Лекция №3 Применение эксперимента для построения математических моделей статики объектов автоматизации
| Вид материала | Лекция |
- Учение студентов основам математического моделирования, необходимых при проектировании,, 28.67kb.
- Рабочая программа разработана в соответствии с государственными требованиями к минимуму, 189.13kb.
- Исследование математических моделей, 9.9kb.
- Лекции по дисциплине «Математическое моделирование» для студентов и магистрантов специальности, 21.92kb.
- Лекция №8 Построение математических моделей технологических объектов и систем аналитическим, 98.99kb.
- Рабочая программа дисциплины методы построения и анализа сложных математических моделей, 104.9kb.
- Лекция 3 курса «Методы автоматизации тестирования», 155.54kb.
- Задачи, объем, степень, очередность автоматизации технологических процессов. 17. Технические, 11.55kb.
- Тематический план учебной дисциплины, 52.63kb.
- Рабочая программа учебной дисциплины непрерывные математические модели Наименование, 113.71kb.
Лекция №3
Применение эксперимента для построения математических моделей статики объектов автоматизации
Математическая модель статики объекта управления – это экспериментально найденная зависимость отклика объекта управления от совокупности входных факторов в виде так называемого уравнения регрессии.
Данная зависимость позволяет получать значения функции отклика при заданном режиме протекания управляемого процесса и может служить основой для его оптимизации.
Процесс определения явного вида уравнения регрессии получил название регрессионного анализа.
Для различных математических планов эксперимента уравнение регрессии содержит различные составляющие:
а) для планов первого порядка уравнение регрессии включает линейные эффекты и парные взаимодействия –
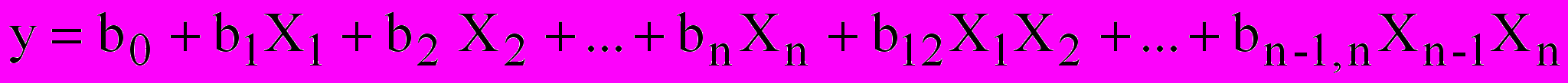 ; (1)
; (1)б) для планов второго порядка уравнение регрессии включает линейные эффекты, парные взаимодействия и квадратичные эффекты –
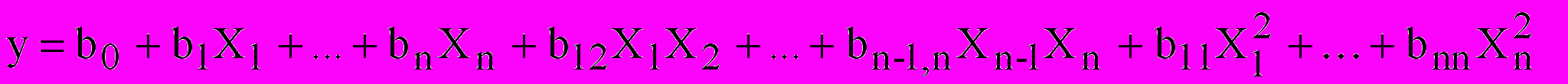 (2)
(2)где b0 – свободный член уравнения регрессии,
bn, b12…bn-1,n, b11…bnn – коэффициенты регрессии,
Xn – условное значения фактора хn. (формулы для его расчета приводились на прошлой лекции)
В практике определения статических характеристик объектов автоматизации нашли применение три метода построения уравнений приближенной регрессии: метод наименьших квадратов, метод средних и метод минимакса.
^ Метод минимакса позволяет построить такое уравнение регрессии, в котором наибольшее из отклонений расчетного значения отклика объекта от измеренного принимает минимально возможную для заданного вида аппроксимации величину.
^ Метод средних позволяет определить аналитическое выражение уравнения регрессии так, что сумма отклонений по всем экспериментально найденным точкам буде равна нулю.
Однако наиболее точным методом, который чаще всего применяют для построения уравнений регрессии, является метод наименьших квадратов. Суть данного метода заключается в выполнении условия: сумма квадратов отклонений S, вычисленных по уравнению регрессии значений
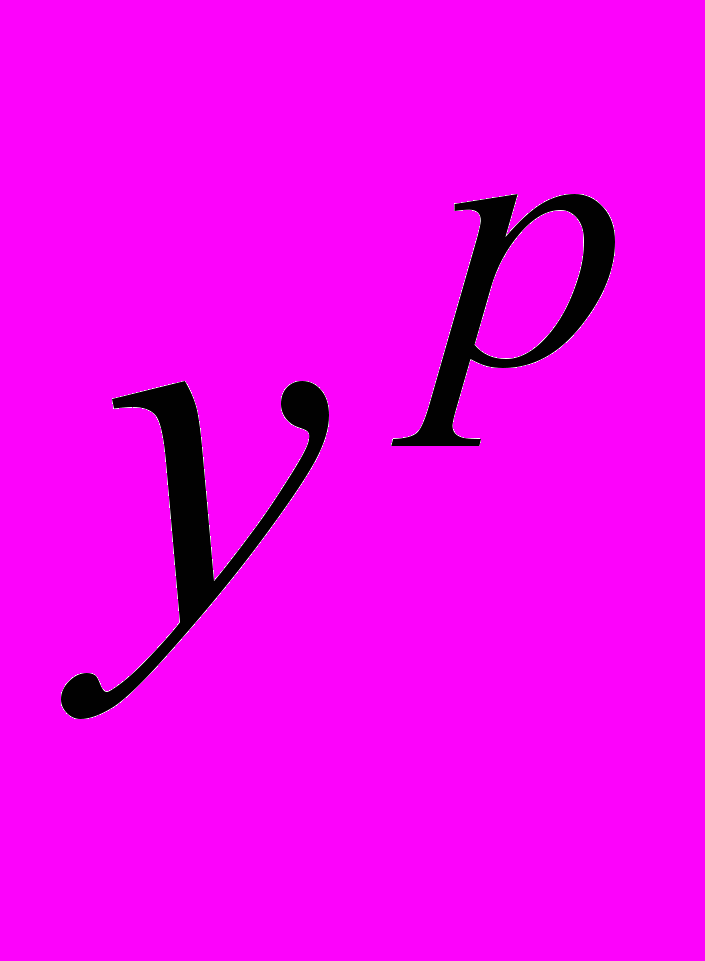 от измеренных y, должна быть минимальной:
от измеренных y, должна быть минимальной: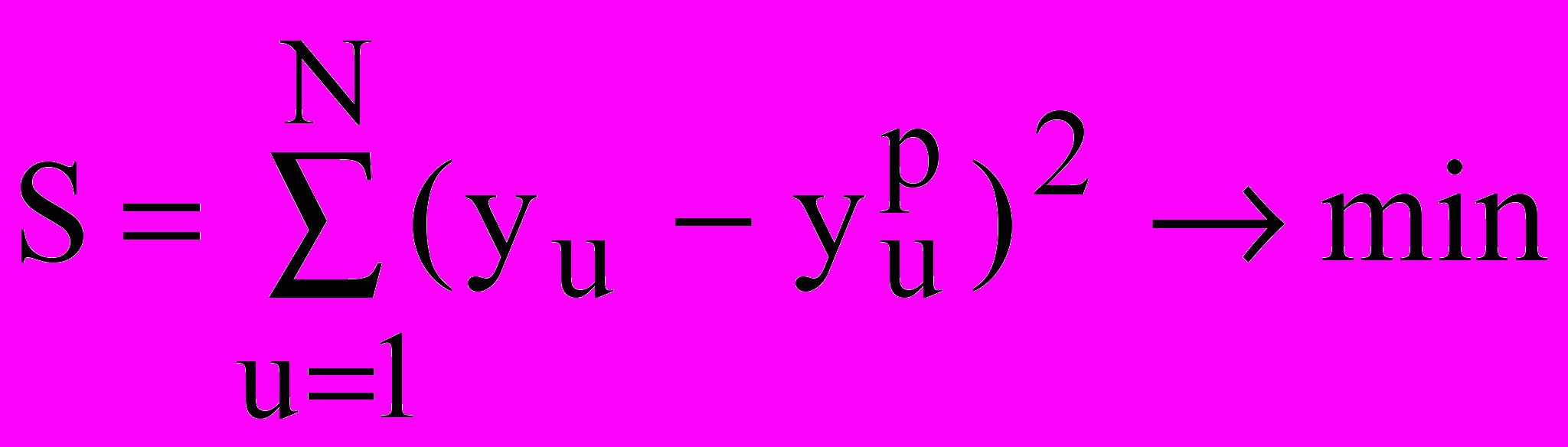 , (3)
, (3)где
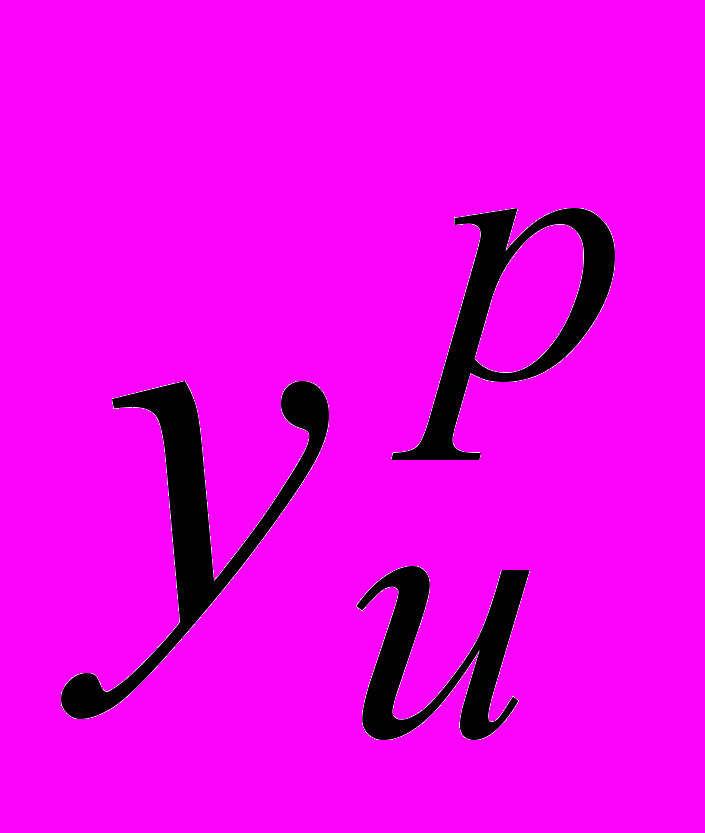 и уu – вычисленное и измеренное значение выходной величины для условий u-го опыта;
и уu – вычисленное и измеренное значение выходной величины для условий u-го опыта;N – общее количество опытов в эксперименте.
Наилучшая точность данного метода вытекает из общего положения математической статистики, согласно которому в качестве меры рассеяния всегда берется дисперсия (среднее из суммы квадратов отклонений. Принцип наименьших квадратов теоретически позволяет сравнивать пригодность любого количества функций для их использования в качестве уравнения приближенной регрессии. Однако на практике обычно сравнивают совокупность функций зафиксированного типа, но с произвольными коэффициентами. В этом случае поиск коэффициентов регрессии может быть осуществлен путем решения системы нормальных уравнений, получаемой в результате частного дифференцирования
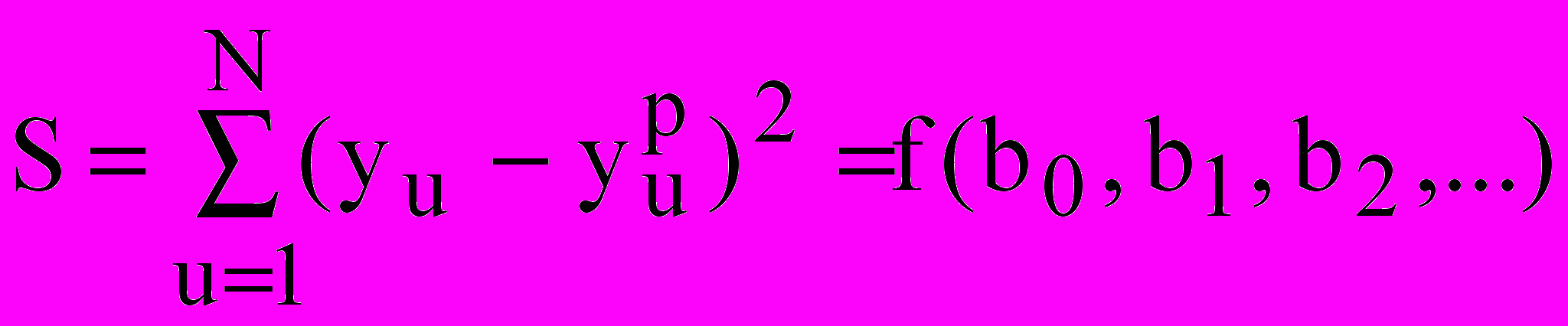 по неизвестным коэффициентам регрессии и их приравнивания к нулю:
по неизвестным коэффициентам регрессии и их приравнивания к нулю: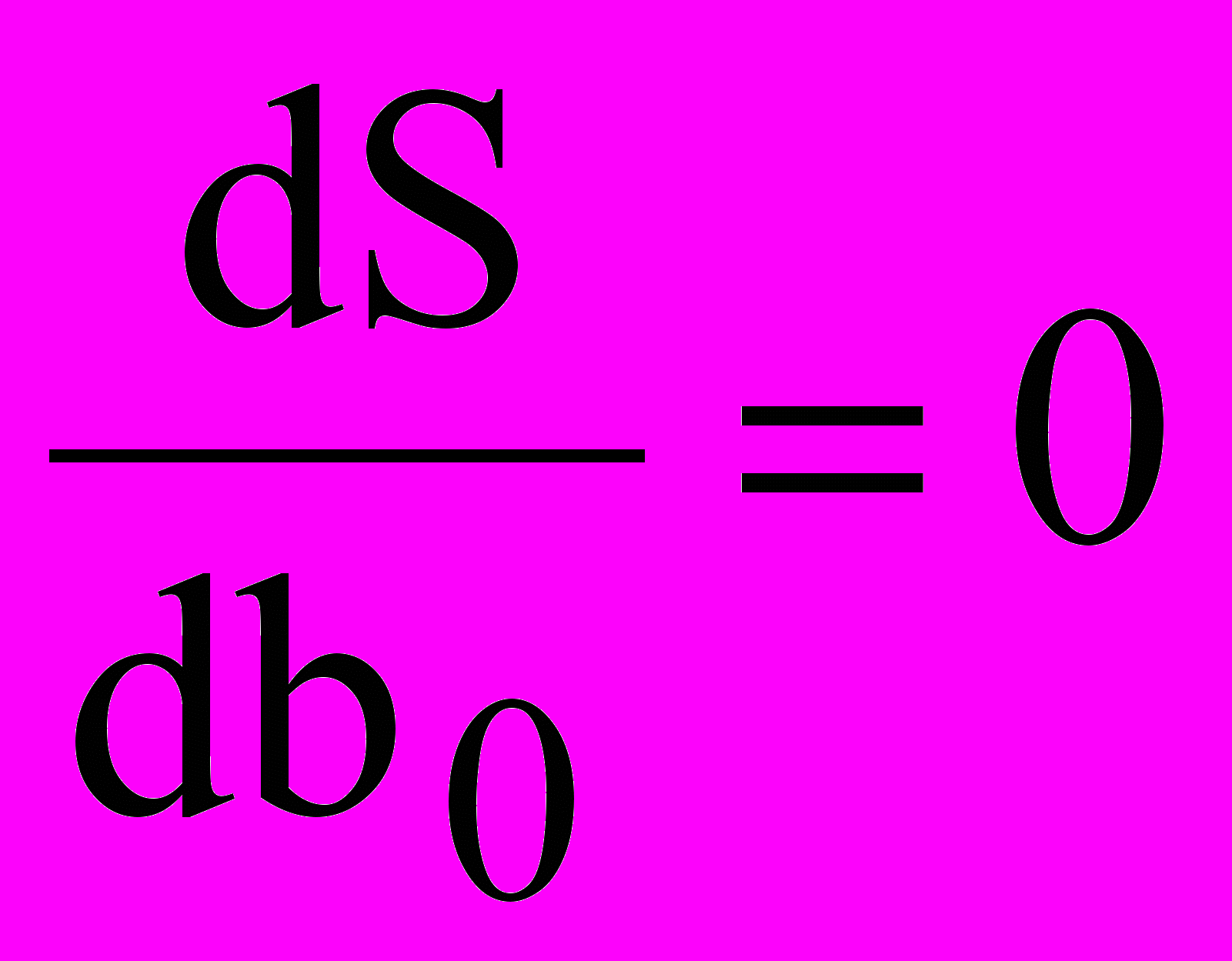 ,
, 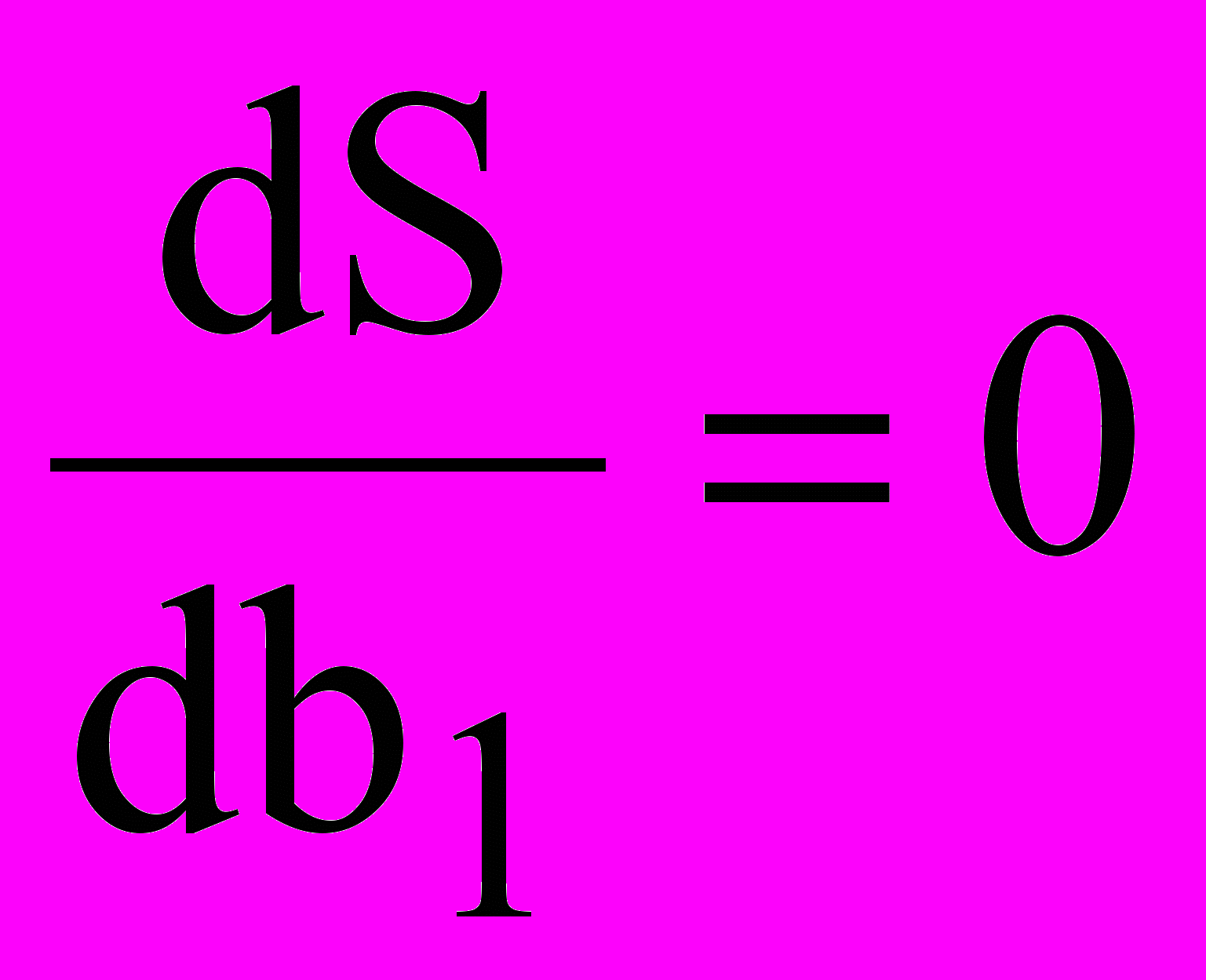 ,
, 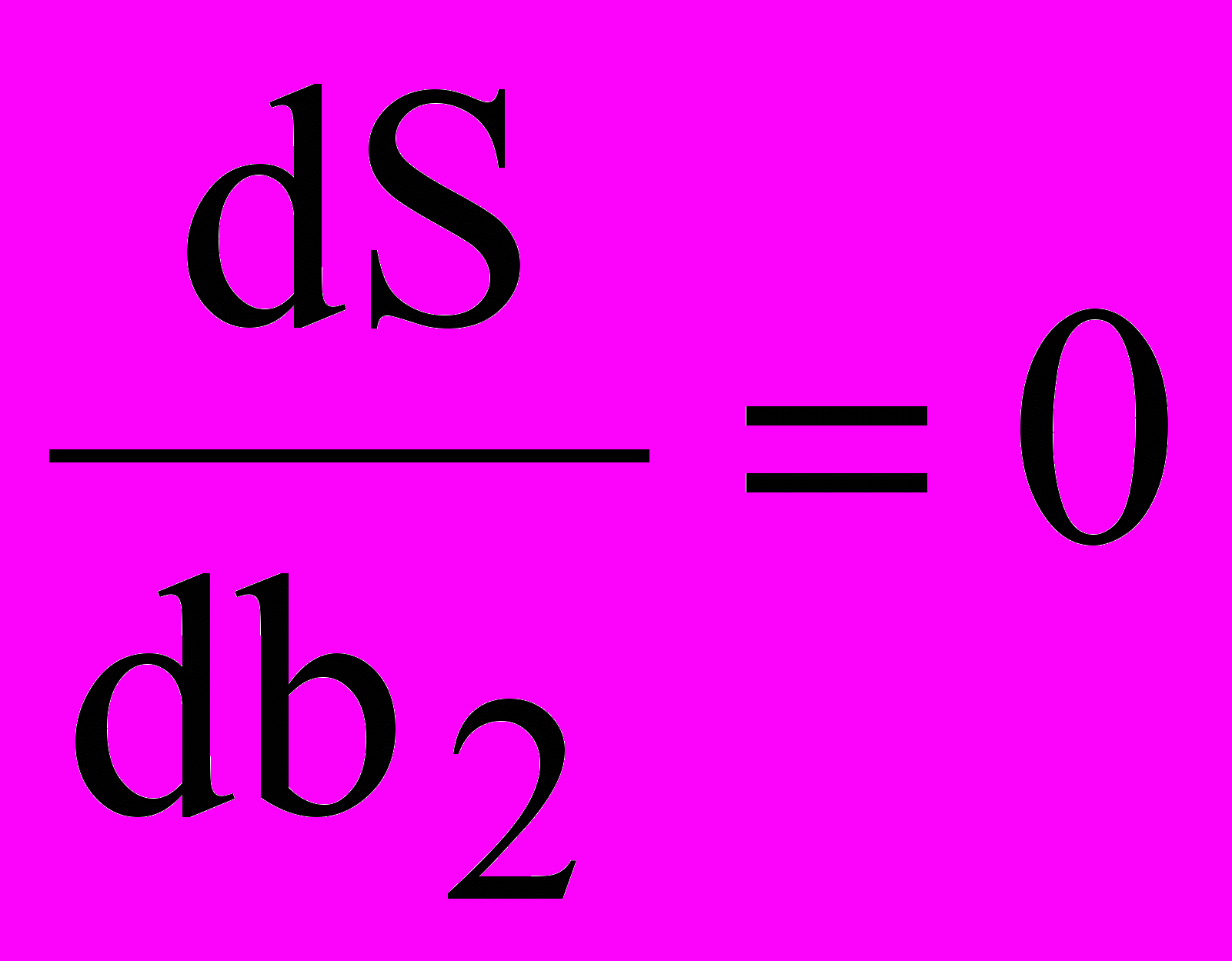 , … (4)
, … (4)Используя правила дифференцирования, системе (4) можно придать следующий вид, который позволяет определить значения искомых коэффициентов регрессии известными методами решения линейных систем уравнений:
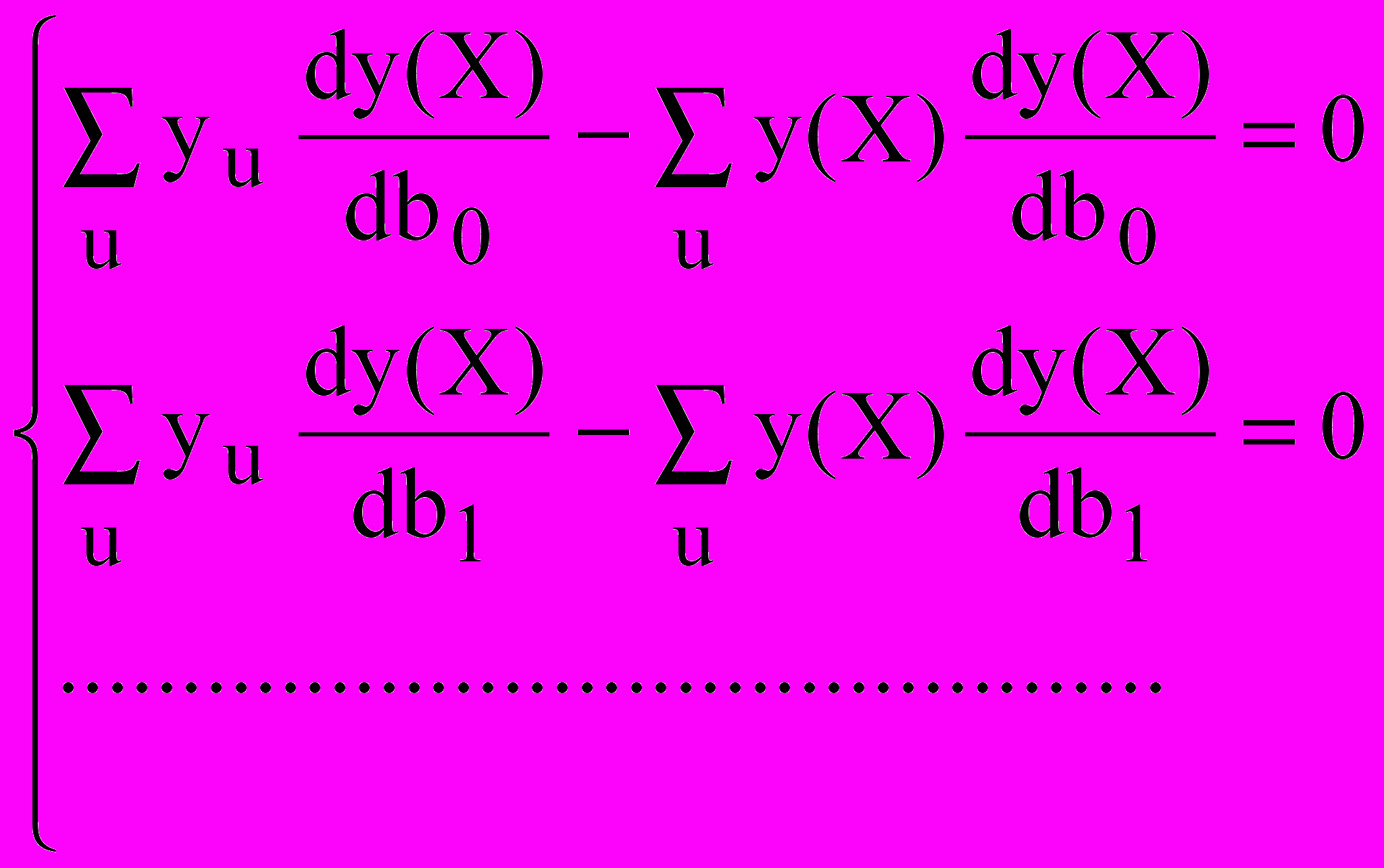 . (5)
. (5)В тех случаях, когда количество эффектов, учитываемых в уравнении велико, для решения системы (5) используют специальные методы расчета на ЭВМ. Для этого полученный в ходе эксперимента статистический материал представляют в матричной форме.
Запишем уравнение регрессии (2) в виде:
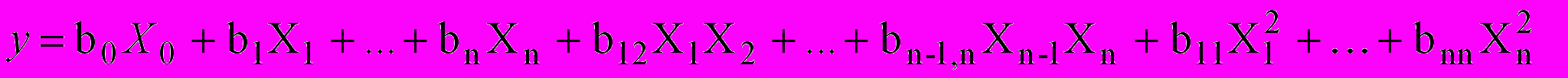 где Х0 – фиктивная переменная, принимающая во всех опытах значение 1.
где Х0 – фиктивная переменная, принимающая во всех опытах значение 1. Выявляемые эффекты и результаты каждого опыта представим в виде табл.1.
Таблица 1
| № опыта | Х0 | Х1 | Х2 | … | Хn-1 | Xn | X1X2 | … | Xn-1Xn | X12 | … | Xn2 | 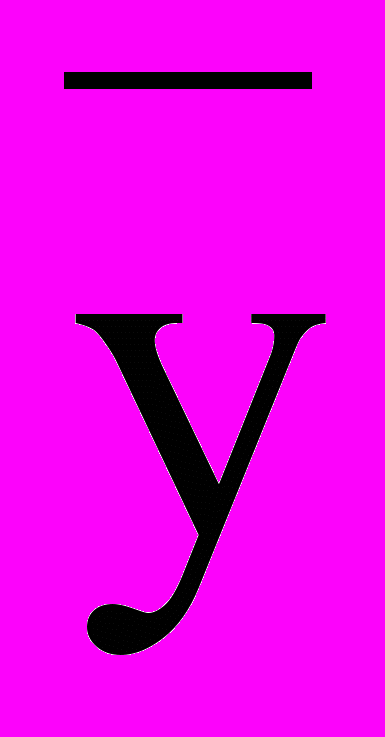 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | +1 | -1 | -1 | | -1 | -1 | +1 | | +1 | +1 | | +1 | 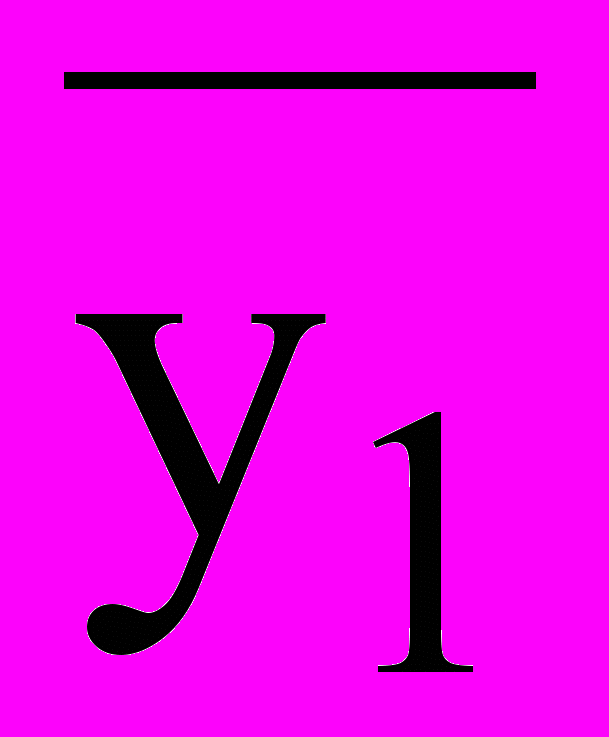 |
| 2 | +1 | +1 | -1 | | -1 | +1 | -1 | | -1 | +1 | | +1 | 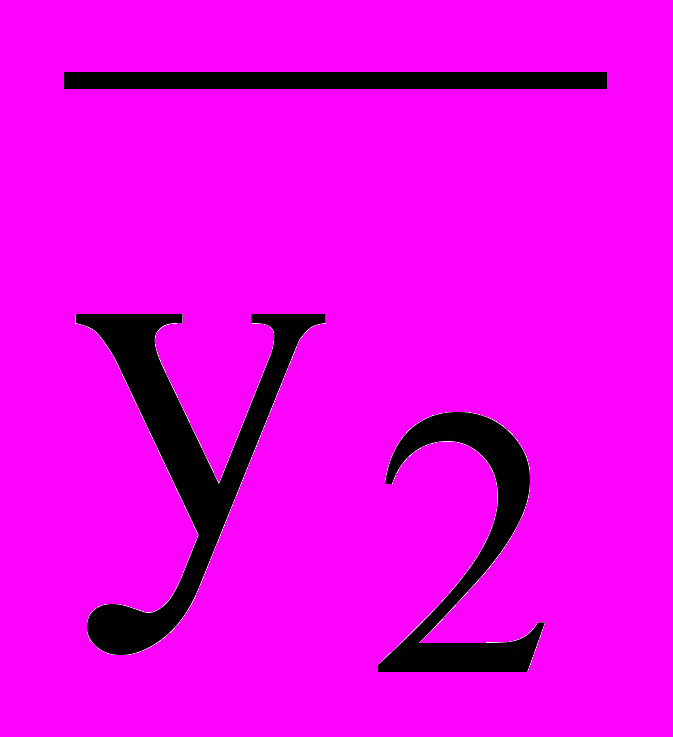 |
| . . . | | | | | | | | | | | | | |
| u | +1 | -1 | +1 | Xiu | +1 | -1 | -1 | XijuXijw | -1 | +1 | Xiiu | +1 | 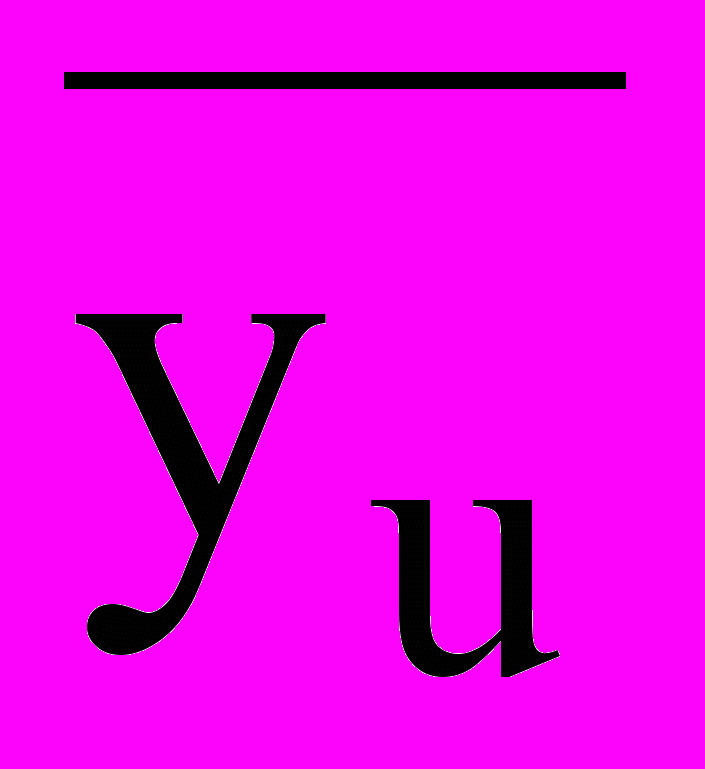 |
| . . . | | | | | | | | | | | | | |
| N-2 | +1 | 0 | 0 | | 0 | α | 0 | | 0 | 0 | | α2 | 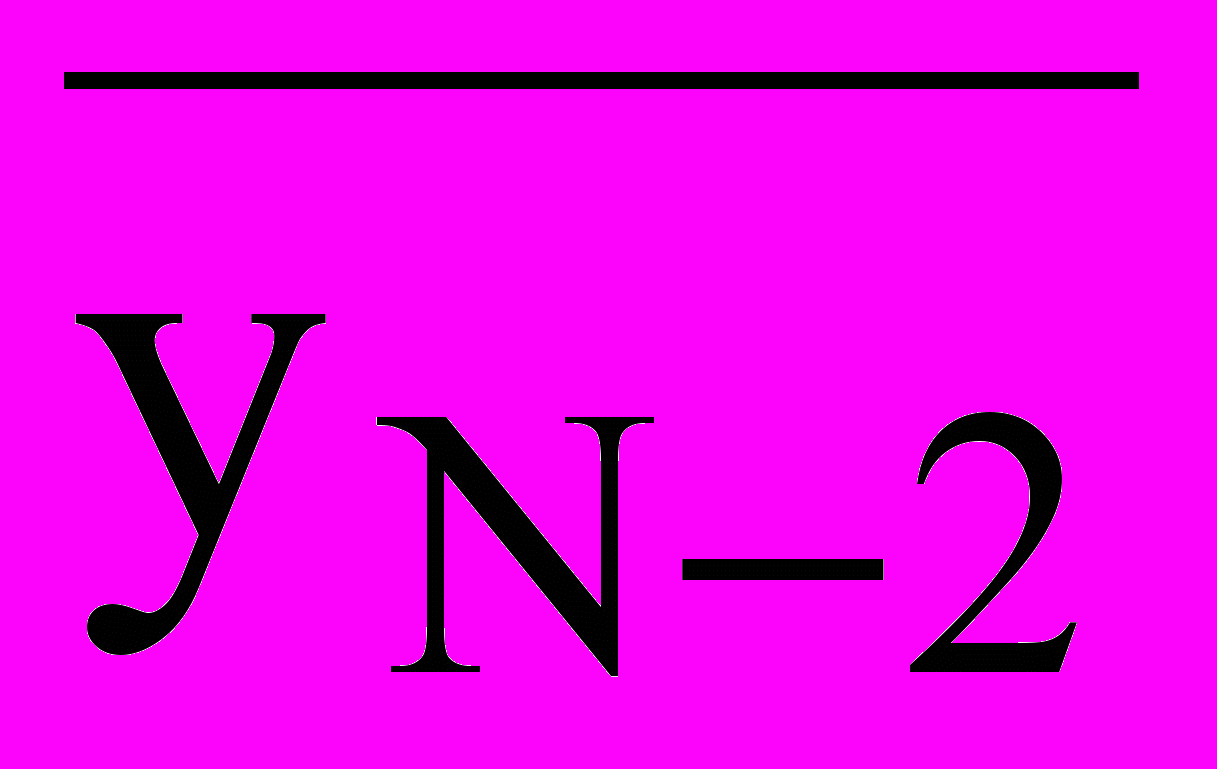 |
| N-1 | +1 | 0 | 0 | | 0 | -α | 0 | | 0 | 0 | | α2 | 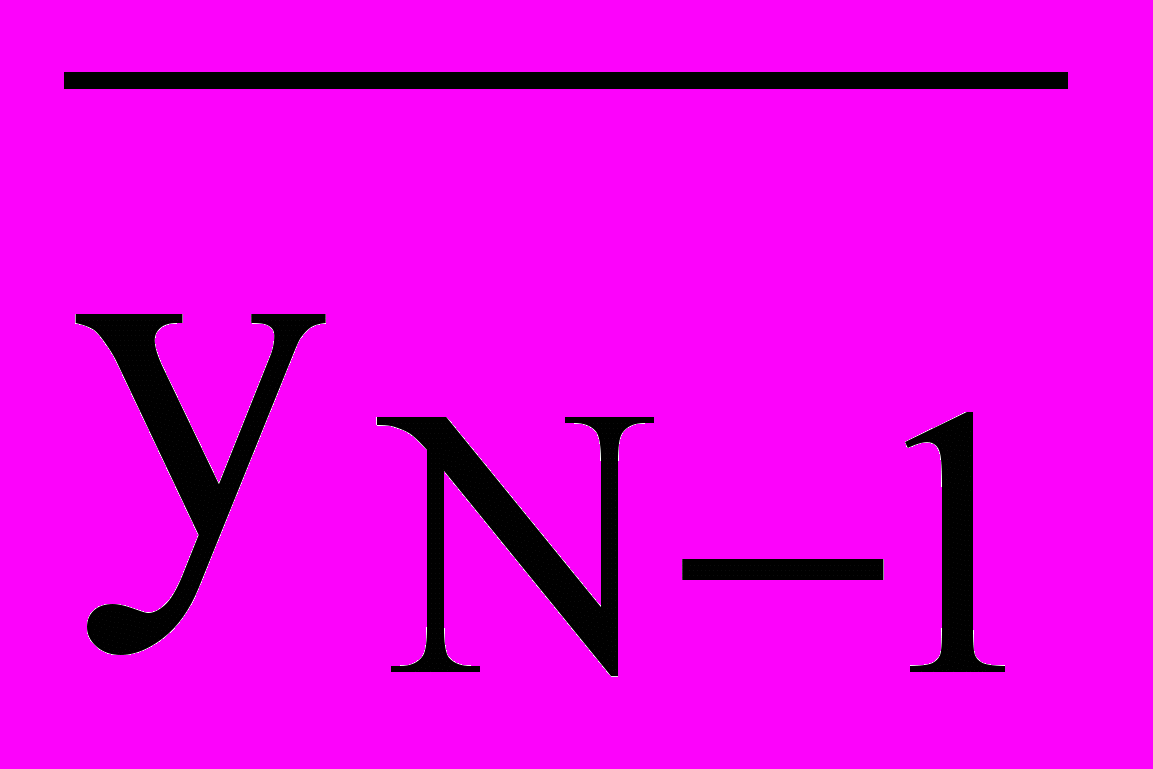 |
| N | +1 | 0 | 0 | | 0 | 0 | 0 | | 0 | 0 | | 0 |  |
Данная таблица по существу является матрицей планирования эксперимента. Графы 2-13 образуют матрицу независимых переменных Х. Графа 14 образует вектор результатов опытов У.
В матричной форме система линейных нормальных уравнений для определения вектора коэффициентов регрессии В будет иметь вид:
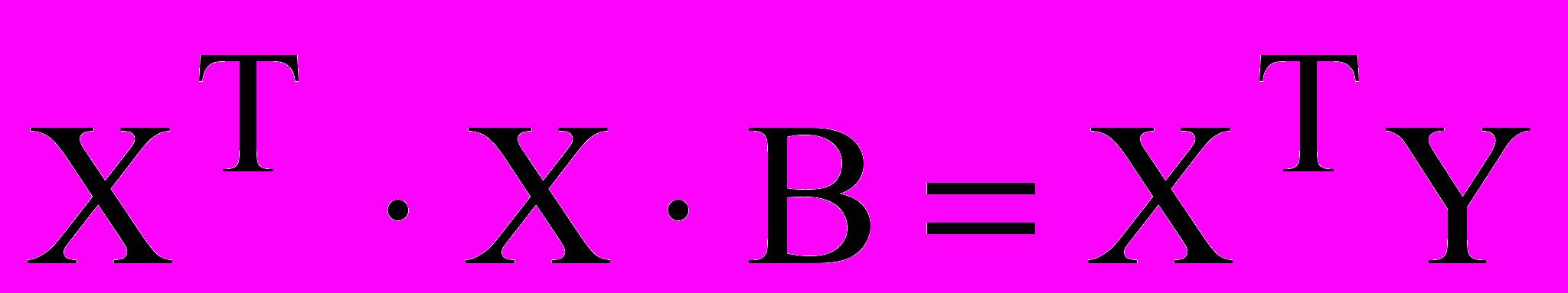 , (6)
, (6)где XT – матрица, транспонированная к Х (поменяны местами столбцы и строки);
В и У – вектор-столбцы вида В=[b0, b1, …, bn, b12, …,bn-1,n, b11,…,bnn],
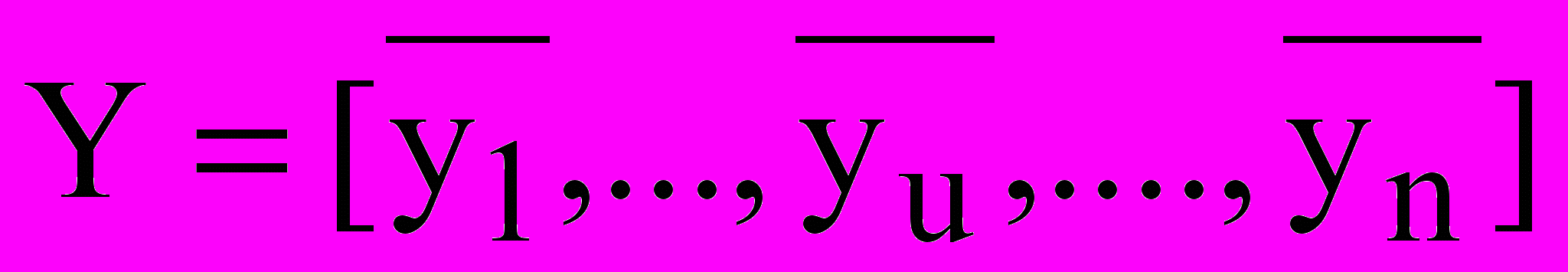 ,
,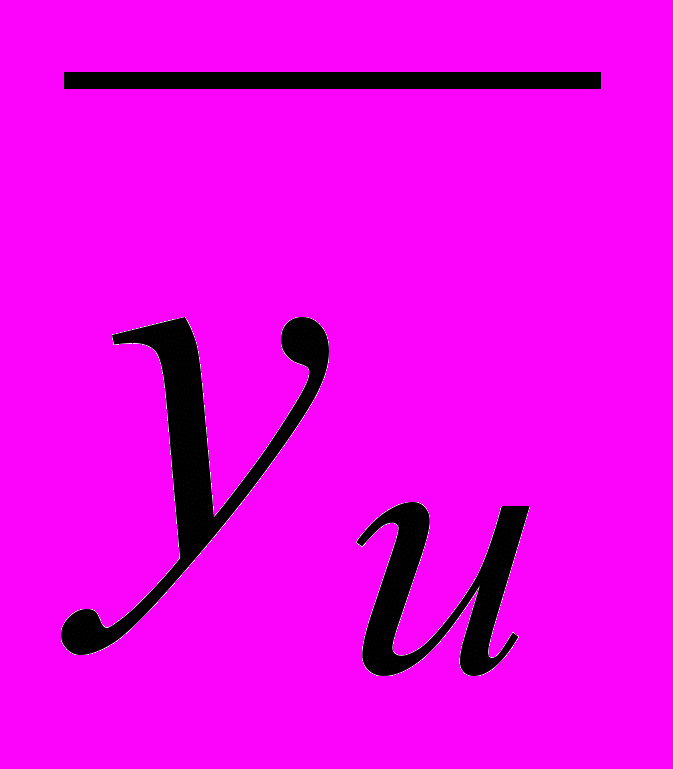 - среднее значение выходной величины в u-м опыте.
- среднее значение выходной величины в u-м опыте.Отсюда вектор-столбец коэффициентов регрессии вычисляется по соотношению:
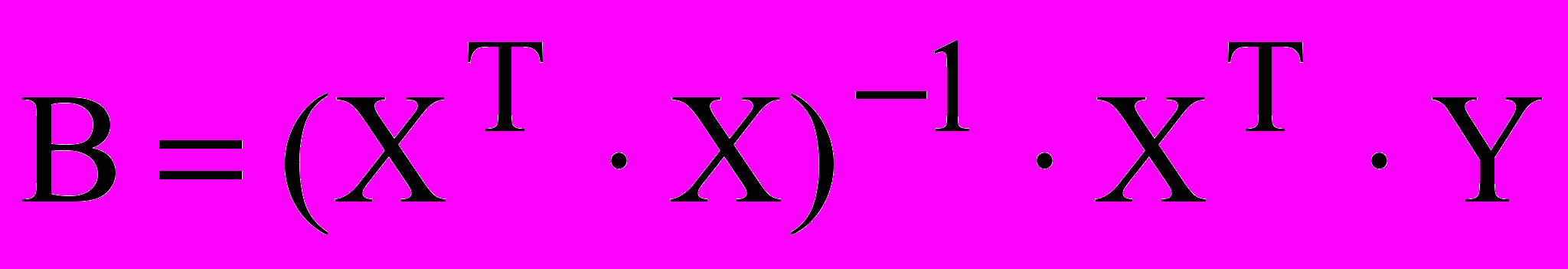 , (7)
, (7)где (XT X)-1 – ковариационная матрица, обратная матрице (XT X).
При использовании ортогональных матриц планирования эксперимента (то есть планов первого порядка, которым соответствуют уравнения регрессии вида (1)) матрица коэффициентов нормальных уравнений (XТ X) содержит лишь диагональные элементы. Тогда коэффициенты регрессии могут быть вычислены по простым формулам. Для ПФЭ и дробных реплик эти формулы имеют вид:
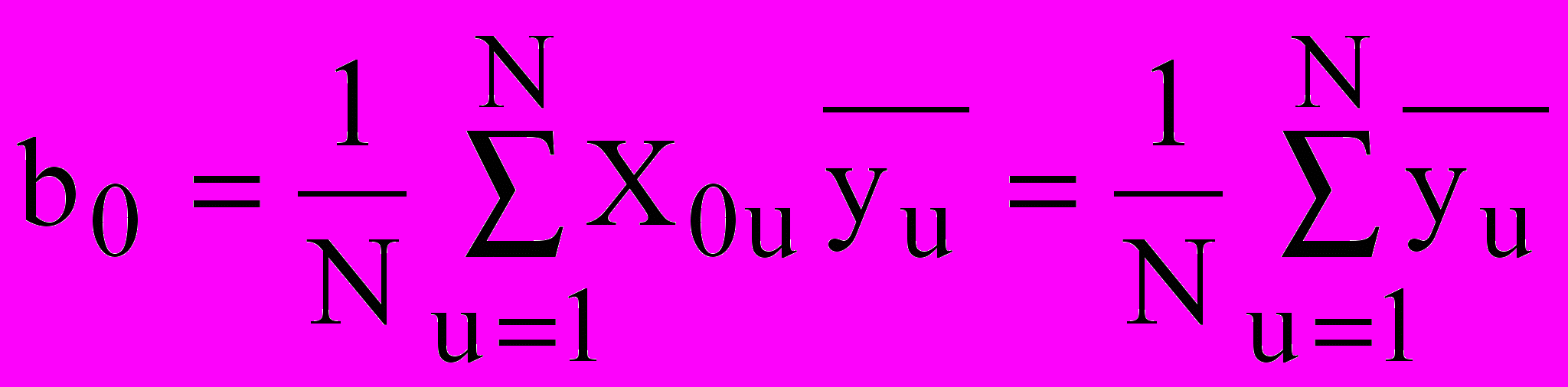 ;
; 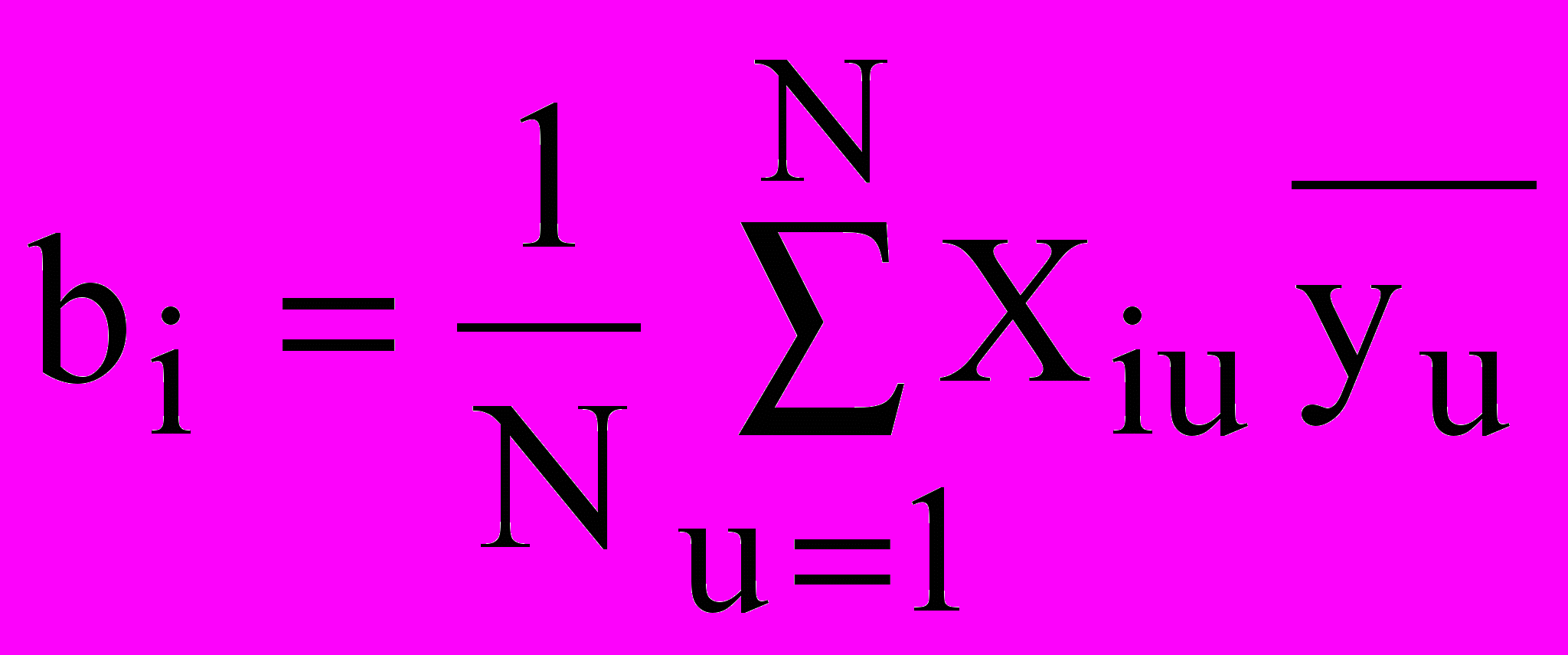 ; (8)
; (8)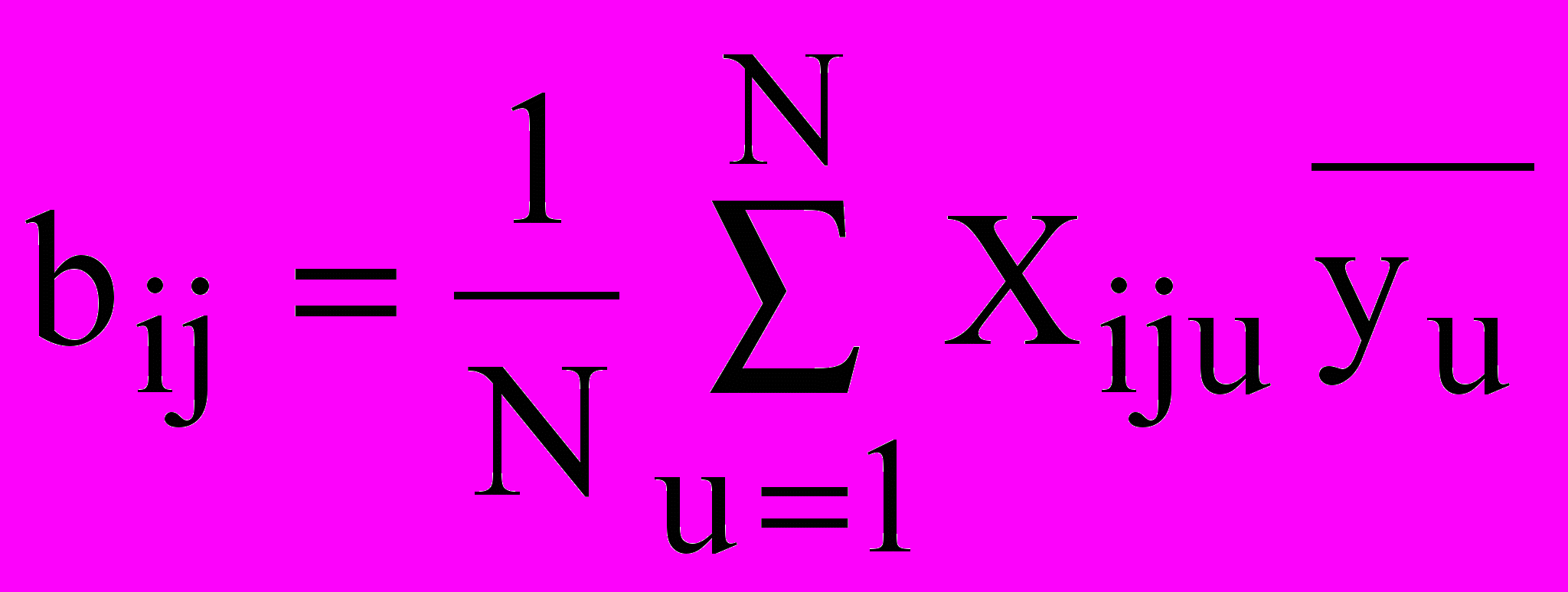 ; (
; ( 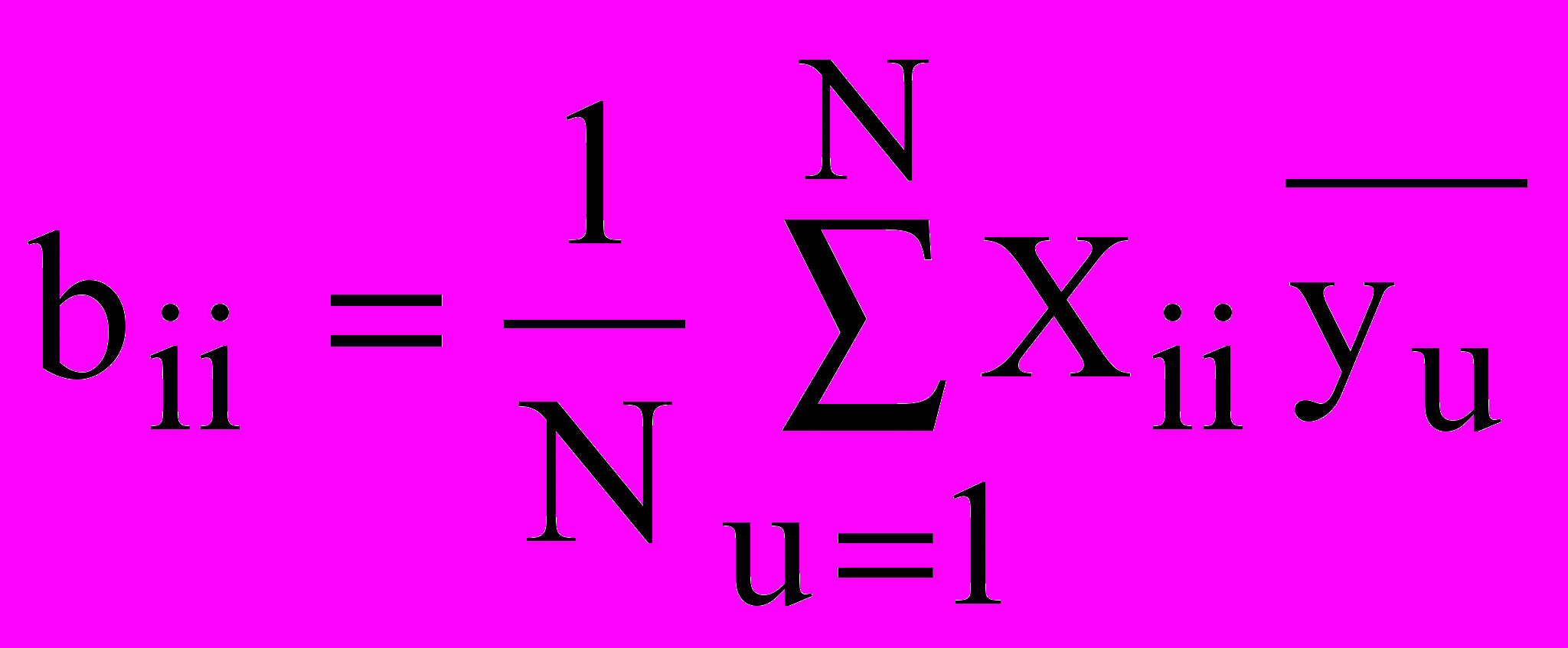 ) .
) . Регрессионный анализ обеспечивает теоретически обоснованные результаты, если выполняются следующие исходные предпосылки:
а) результаты измерений выходной величины в каждом опыте активного эксперимента являются независимыми случайными величинами и распределены по нормальному закону; при пассивном эксперименте совместное распределение выходной величины и входных переменных должно быть нормальным;
б) выборочные дисперсии выходной величины в опытах
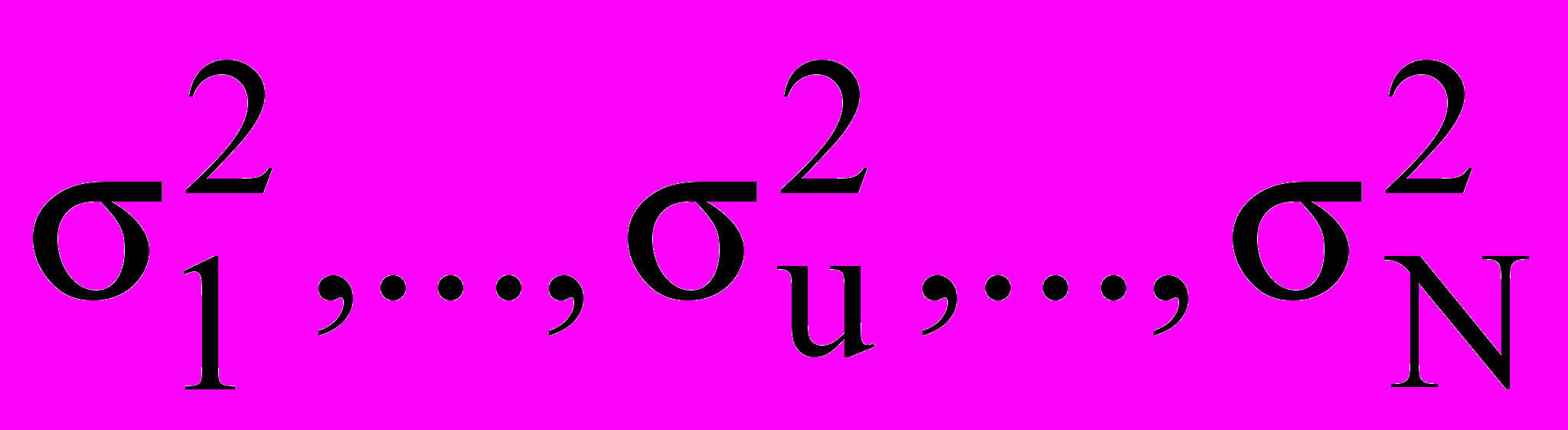 (
(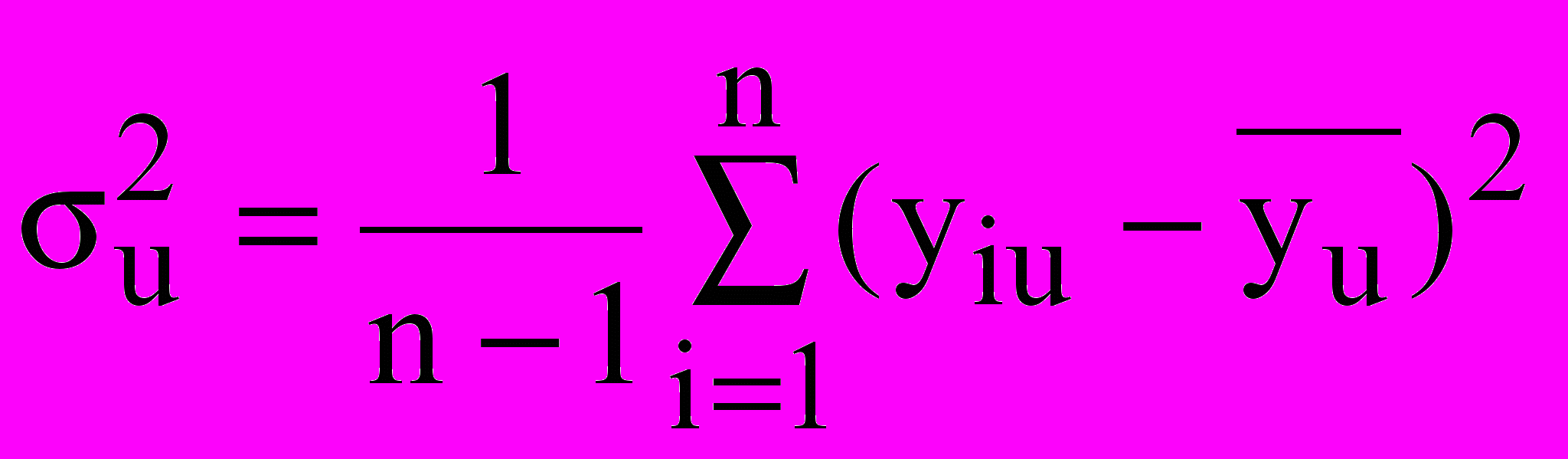 , где n – количество измерений в опыте) - однородны;
, где n – количество измерений в опыте) - однородны;в) основные факторы имеют пренебрежимо малую дисперсию по сравнению с дисперсией выходной величины.
На практике регрессионный анализ иногда возможно формально использовать и при невыполнении его исходных предпосылок. При этом добиваются требуемой для производственных условий точности, хотя применение этого метода в этом случае и лишено теоретического обоснования.
^ После определения коэффициентов регрессии производят статистический анализ результатов, задачами которого являются проверка значимости коэффициентов регрессии и проверка гипотезы об адекватности полученного уравнения.
^ Проверка значимости коэффициентов регрессии производится, как правило, для тех коэффициентов, значения которых близки к нулю. То есть фактически выдвигают нулевую гипотезу (гипотезу о равенстве значения данного коэффициента нулю и его исключении из уравнения регрессии). Для проверки нулевой гипотезы используют критерий Стьюдента, в соответствии с которым коэффициент регрессии b считается значимым при выполнении следующего условия:
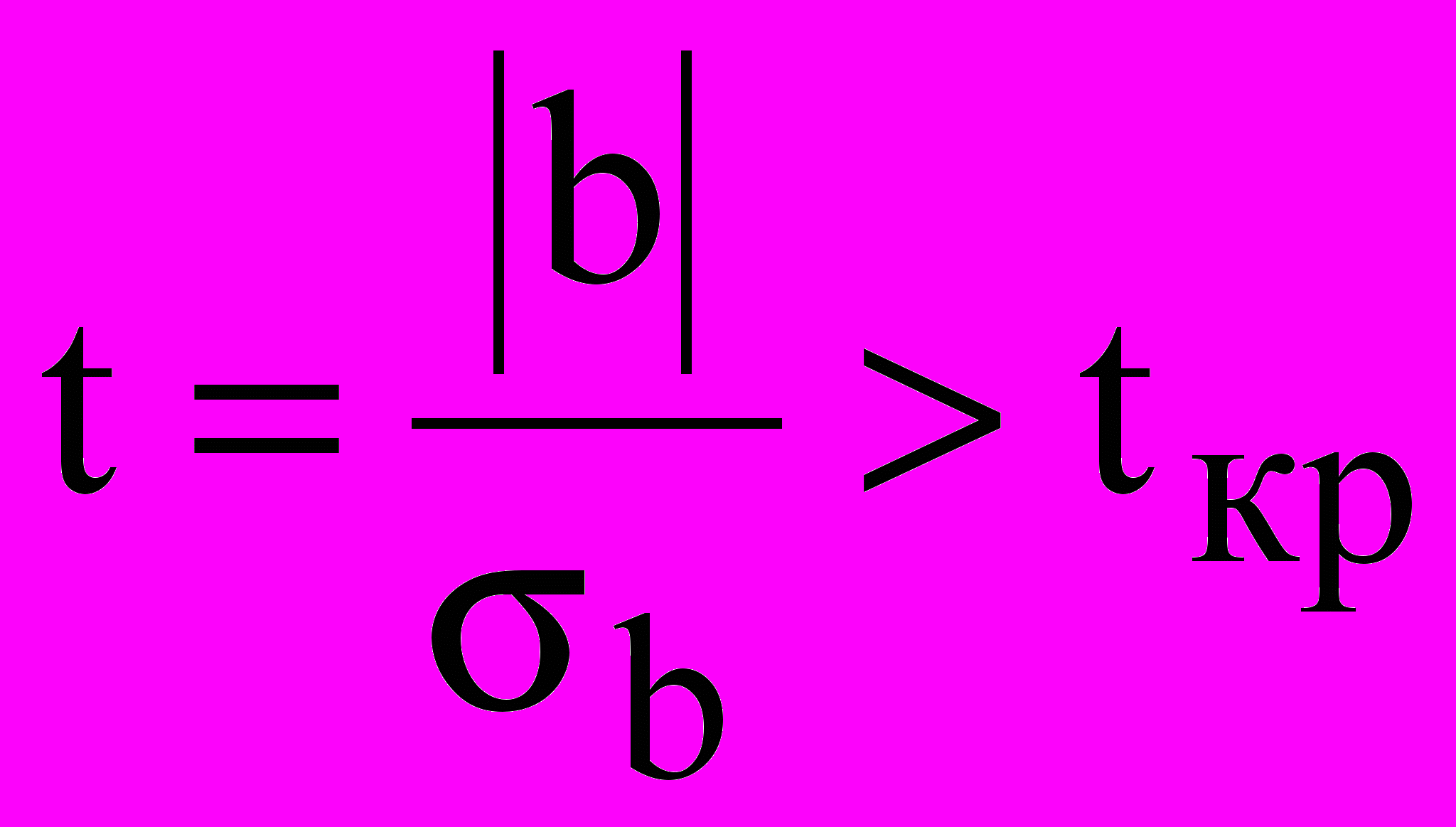 , (9)
, (9)где
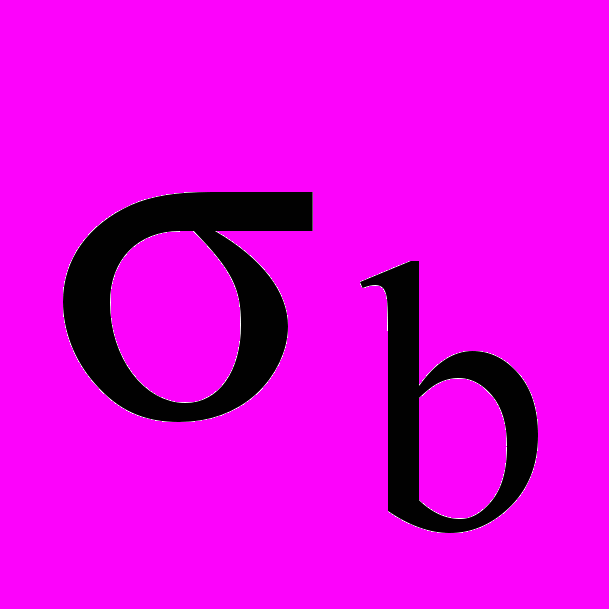 - среднее квадратичное отклонение, рассчитываемое на основе выборочной дисперсии
- среднее квадратичное отклонение, рассчитываемое на основе выборочной дисперсии 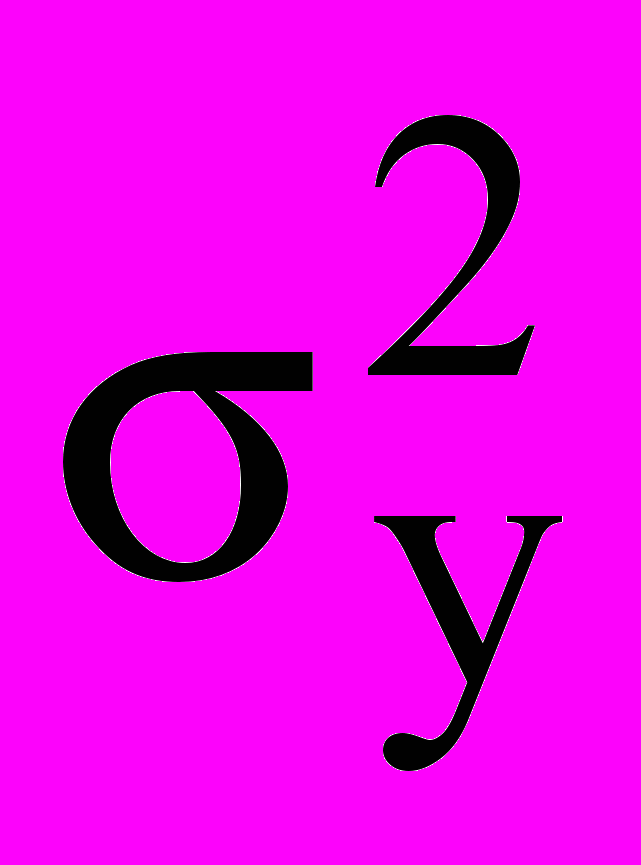 :
: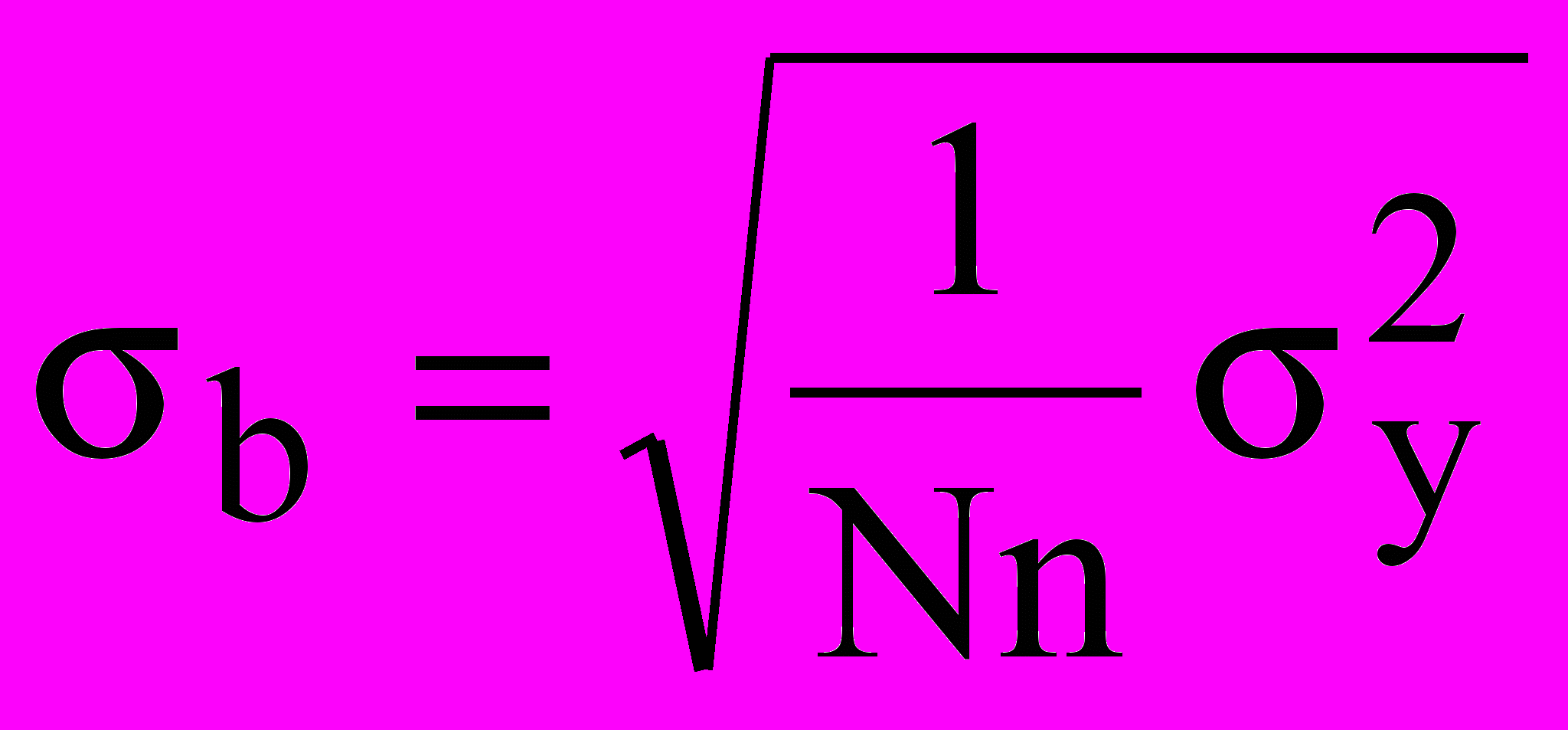 ,
, 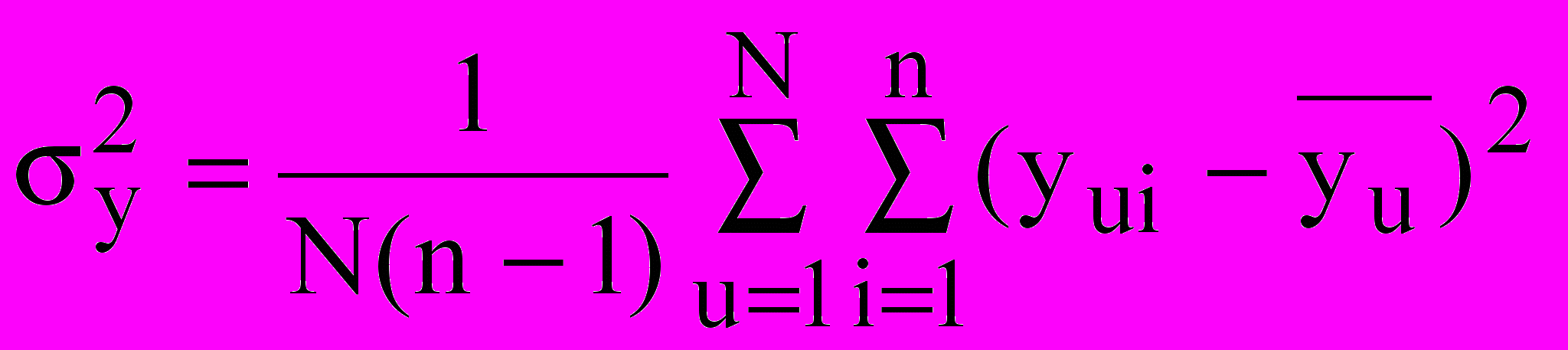 , (10)
, (10)N – количество опытов,
n – количество измерений в каждом опыте;
tкр – табулированное значение квантиля t-распределения Стьюдента для принятого уровня доверительной вероятности и соответствующего числа степеней свободы
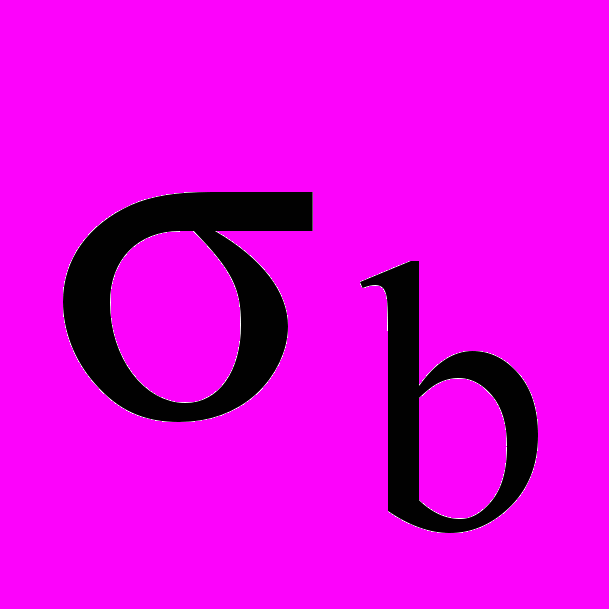 f=N(n-1).
f=N(n-1).Незначимые коэффициенты регрессии вместе с переменными, которые они идентифицируют, исключают из уравнения регрессии.
^ Адекватность уравнения регрессии (то есть способность достоверно и точно описывать функцию отклика) проверяют по критерию Фишера, в соответствии с которым уравнение регрессии считается адекватным при выполнении следующего условия:
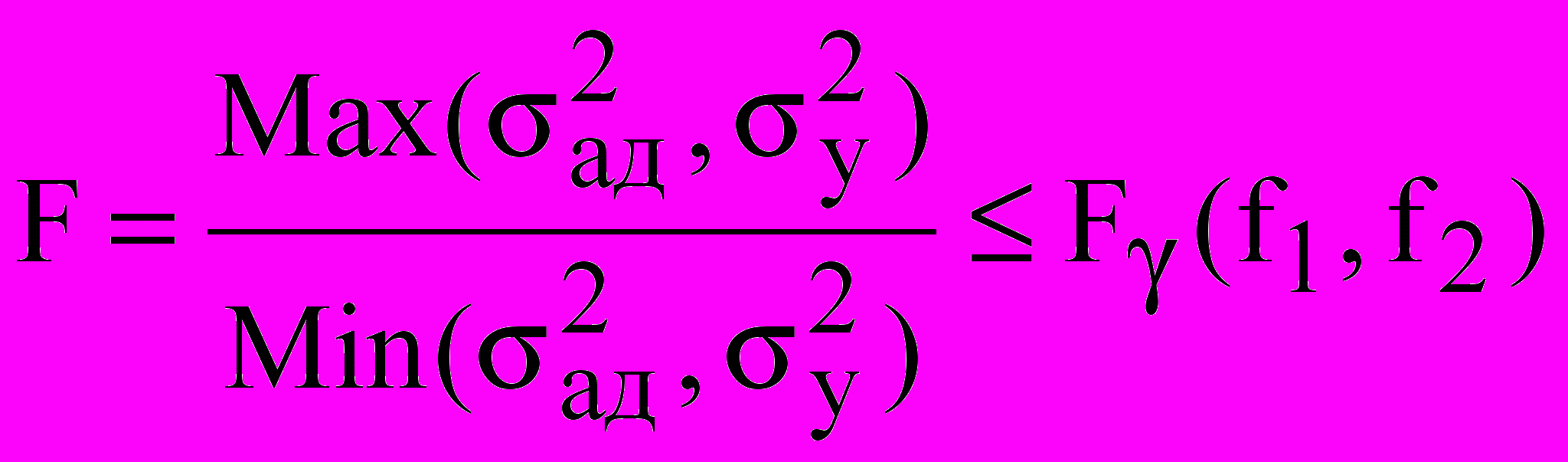 , (11)
, (11)где
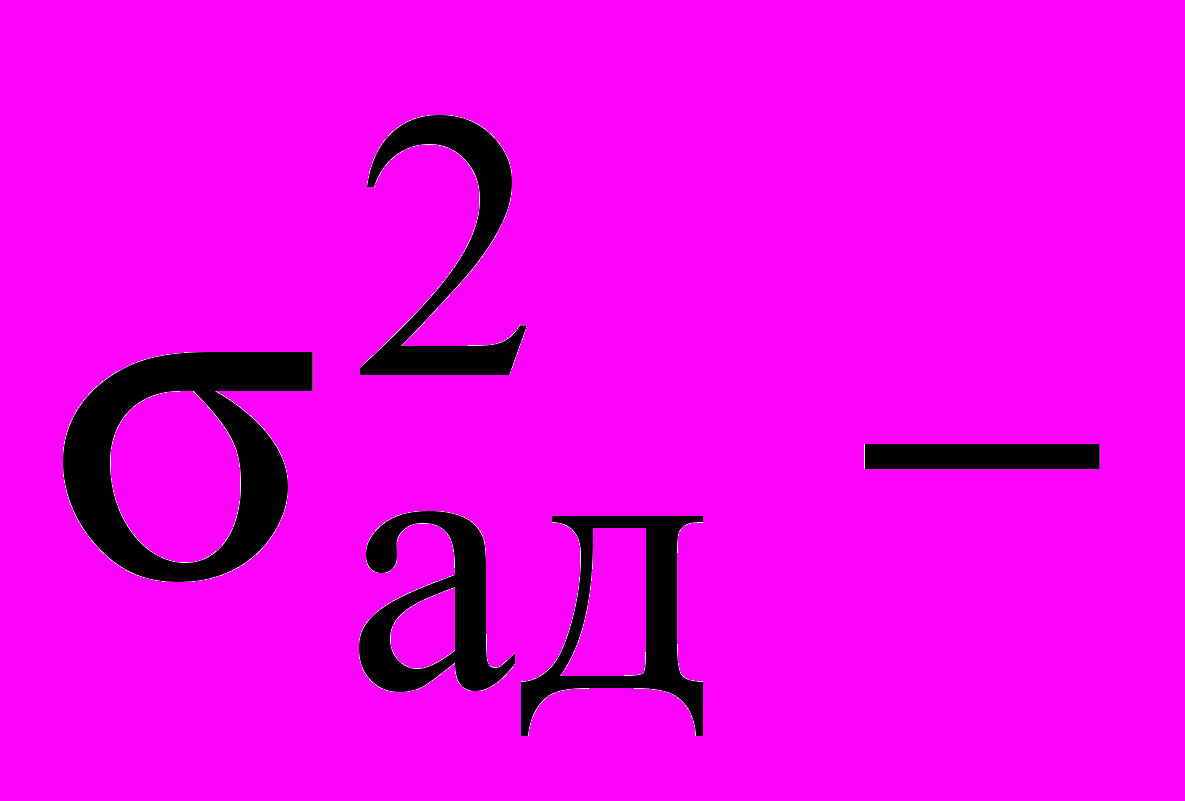 оценка дисперсии адекватности, рассчитываемая по формуле
оценка дисперсии адекватности, рассчитываемая по формуле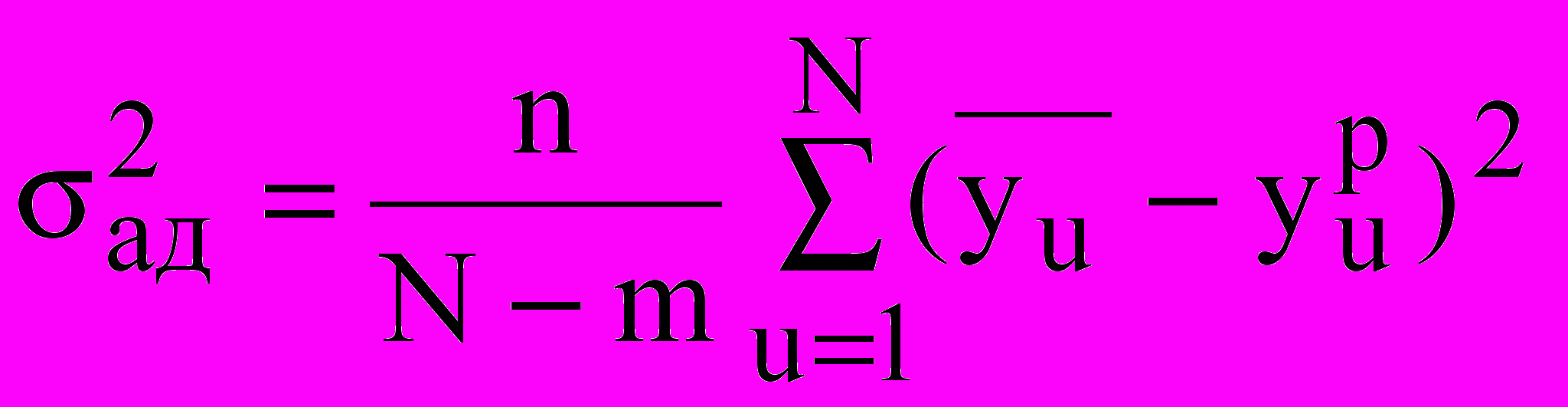 , (12)
, (12)m – число значимых коэффициентов регрессии;
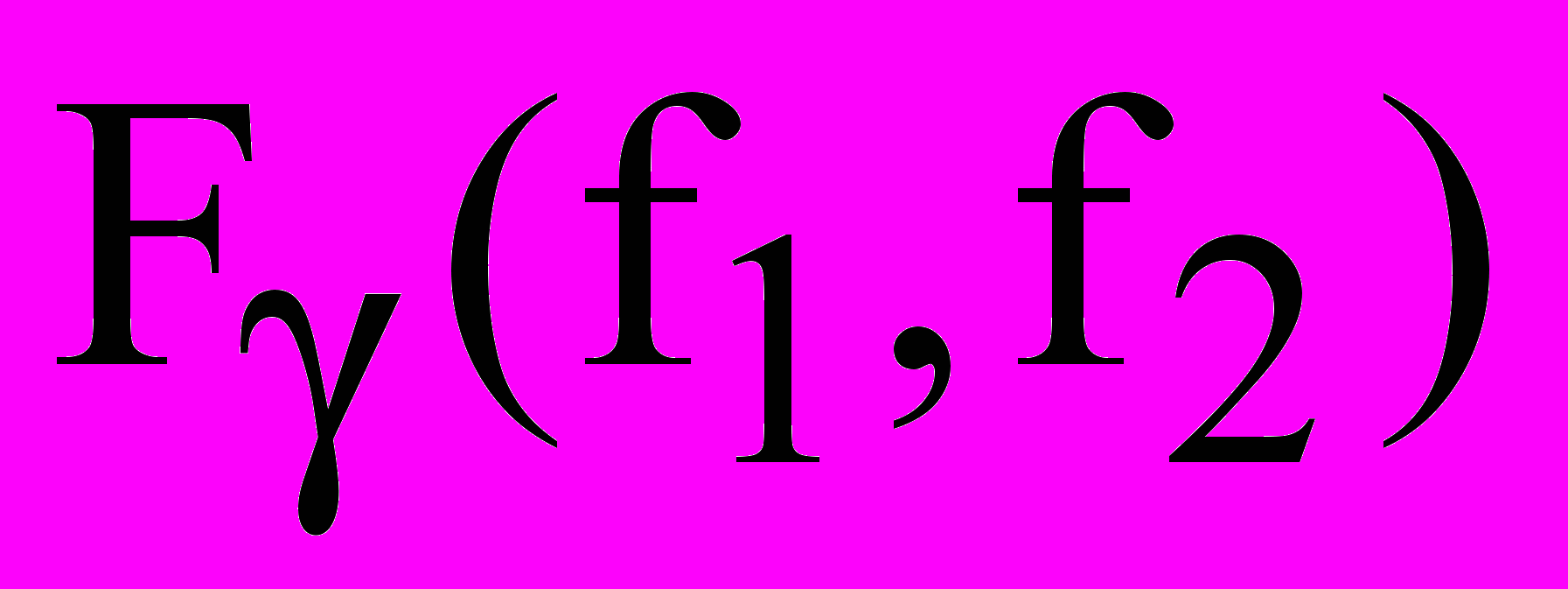 - табличное значение F-распределения для выбранной доверительной вероятности γ и степенях свободы f1 и f2 сравниваемых дисперсий (f1 – дисперсии, стоящей в числителе, f2 –дисперсии, стоящей в знаменателе).
- табличное значение F-распределения для выбранной доверительной вероятности γ и степенях свободы f1 и f2 сравниваемых дисперсий (f1 – дисперсии, стоящей в числителе, f2 –дисперсии, стоящей в знаменателе).То есть f1 и f2 могут принимать следующие значения:
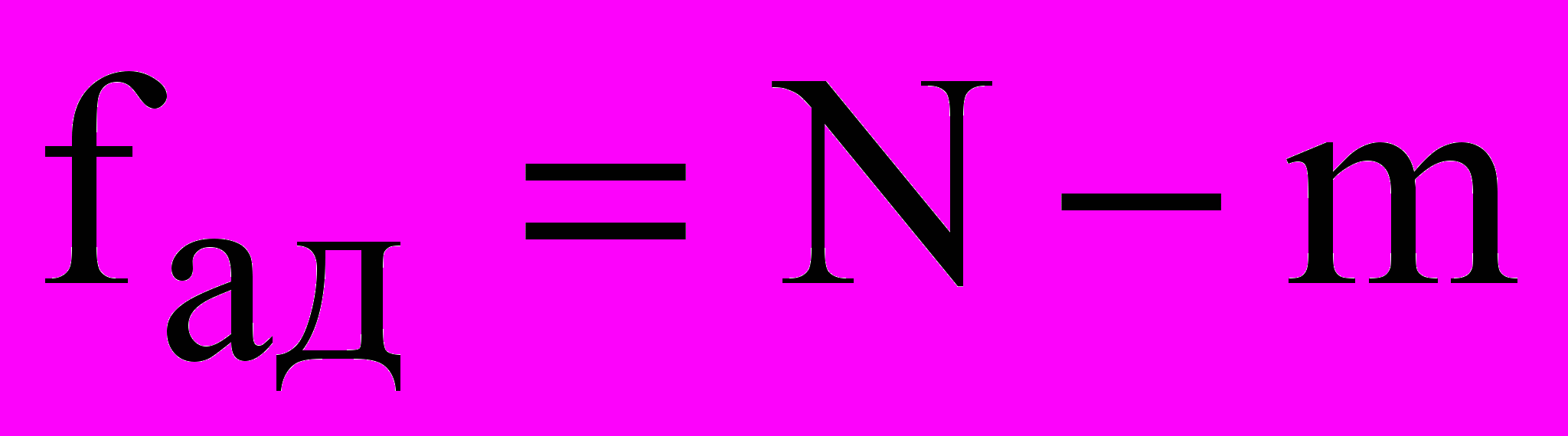 ,
, 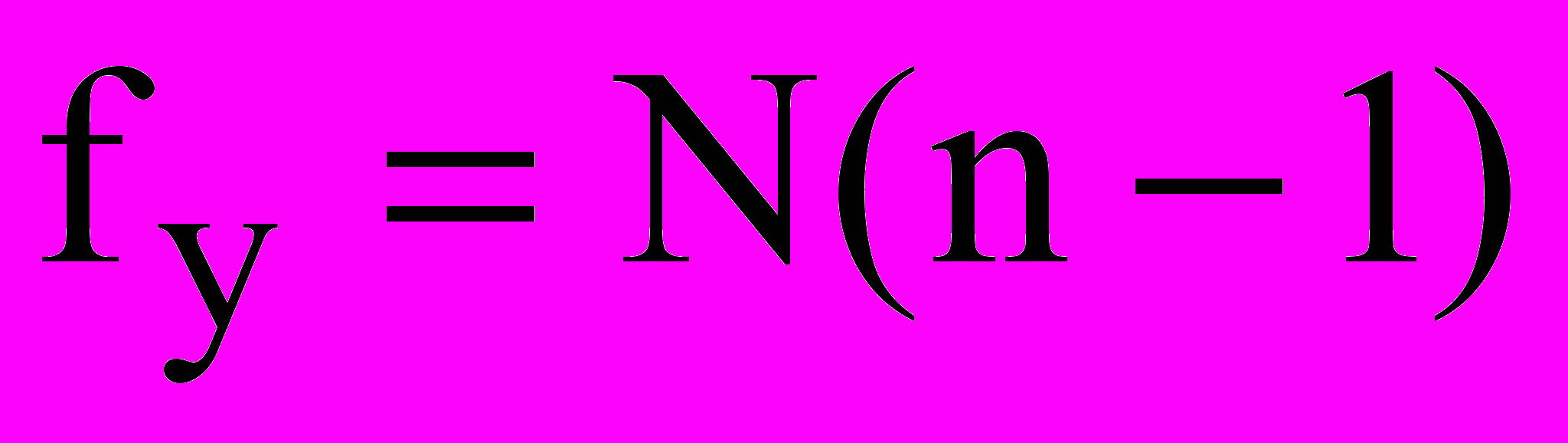 .
.Иногда в результате анализа оказывается, что полученное уравнение регрессии неадекватно. Возможны два пути получения адекватного уравнения:
- уменьшение диапазона изменения входных факторов и повторении эксперимента по тому же плану,
- увеличение числа членов в уравнении регрессии добавлением эффектов более высокого порядка.
Помимо регрессионного анализа экспериментально полученных результатов, который фактически позволяет построить математическую модель статики объекта управления, для получения более узких (в математическом плане) зависимостей между входными переменными и выходными величинами используют методы корреляционного и дисперсионного анализа.
В общем случае зависимость между двумя случайными величинами оказываются сильно завуалированными влиянием «собственных» для каждой из них случайных факторов. Поэтому изменение одной случайной величины, соответствующее изменению другой, разбивается на две компоненты: стохастическую зависимость
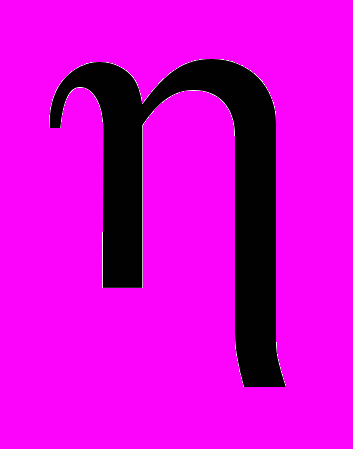 от
от  и случайную составляющую, обусловленную «собственными» случайными факторами величин
и случайную составляющую, обусловленную «собственными» случайными факторами величин 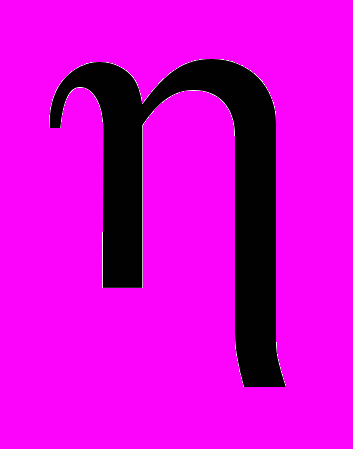 и
и  . Если стохастическая компонента отсутствует, то случайные величины
. Если стохастическая компонента отсутствует, то случайные величины 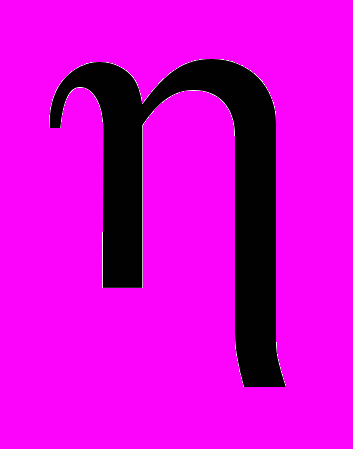 и
и  независимы, в противном случае – между ними существует стохастическая связь. ^ Корреляционный анализ позволяет выявить стохастическую связь между случайными величинами наблюдаемыми и фиксируемыми в процессе эксперимента.
независимы, в противном случае – между ними существует стохастическая связь. ^ Корреляционный анализ позволяет выявить стохастическую связь между случайными величинами наблюдаемыми и фиксируемыми в процессе эксперимента. Как известно, дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин. Следовательно, невыполнение данного условия является верным признаком наличия зависимости между
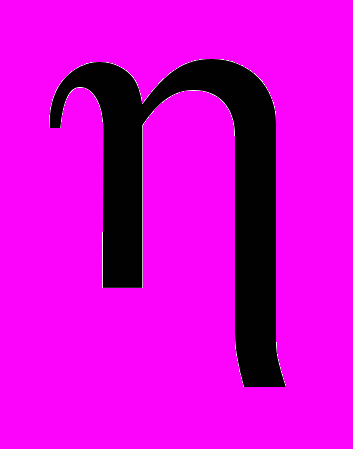 и
и  . Корреляцией называется та часть стохастической связи между
. Корреляцией называется та часть стохастической связи между 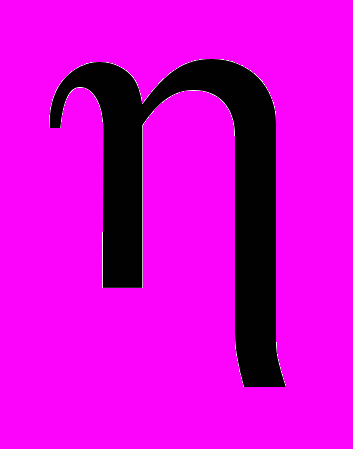 и
и  , которая сказывается на отличии
, которая сказывается на отличии 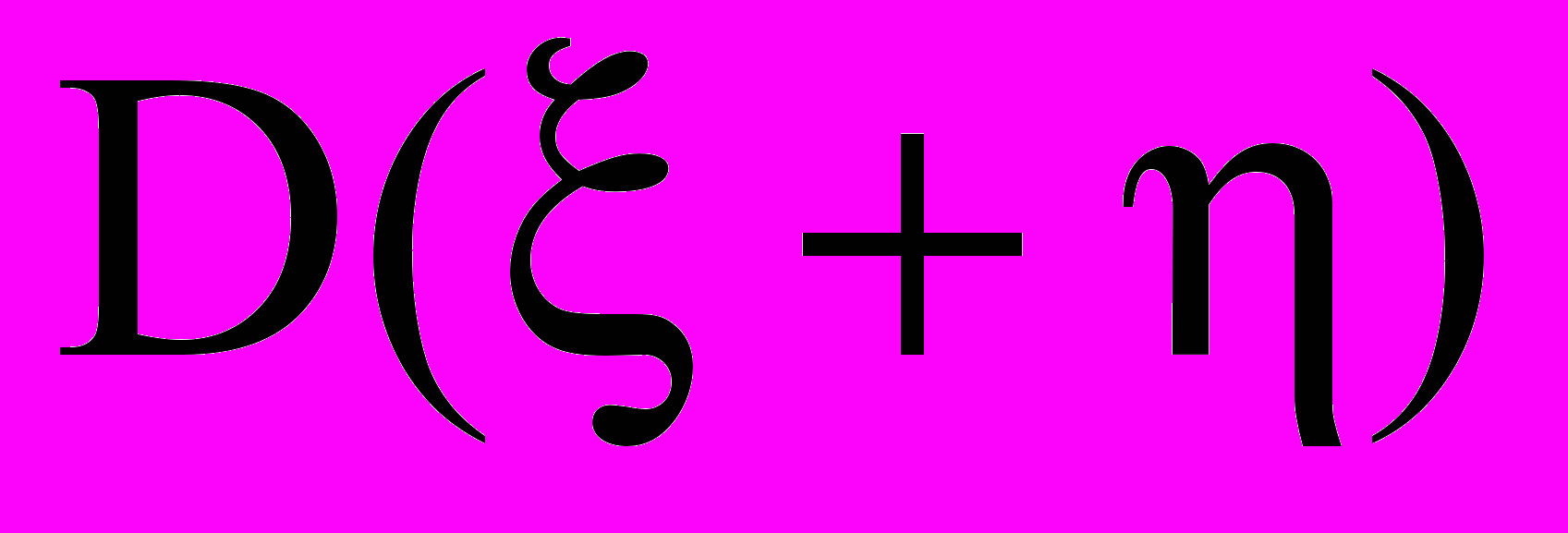 от
от 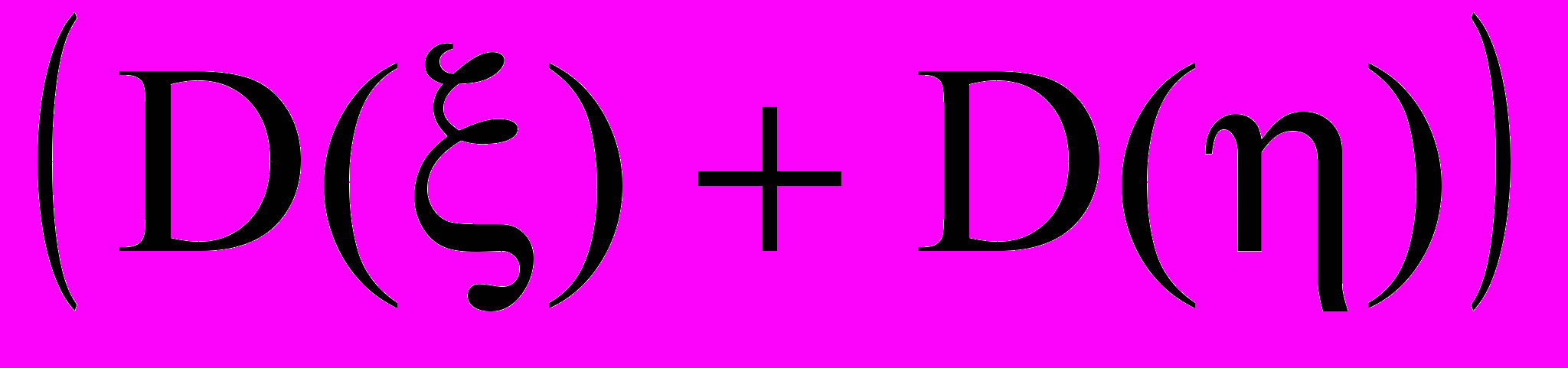 . В качестве показателя данной связи используется так называемый коэффициент корреляции, который для генеральной совокупности измерений двух случайных величин ξ и η имеет вид:
. В качестве показателя данной связи используется так называемый коэффициент корреляции, который для генеральной совокупности измерений двух случайных величин ξ и η имеет вид: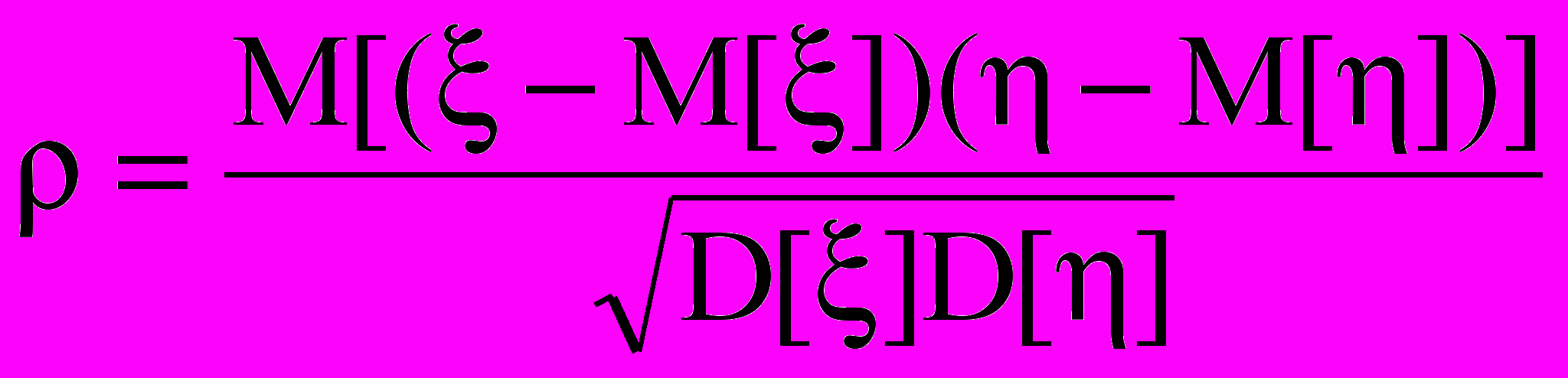 , (15)
, (15)где M и D – соответственно математические ожидания и дисперсии сравниваемых случайных величин.
Отметим некоторые важные свойства коэффициента корреляции:
- коэффициент корреляции независимых случайных величин равен 0,
- коэффициент корреляции не меняется от прибавления к случайным величинам каких-либо постоянных (неслучайных) слагаемых,
- своей величиной коэффициент корреляции характеризует не только наличие, но и силу стохастической связи между
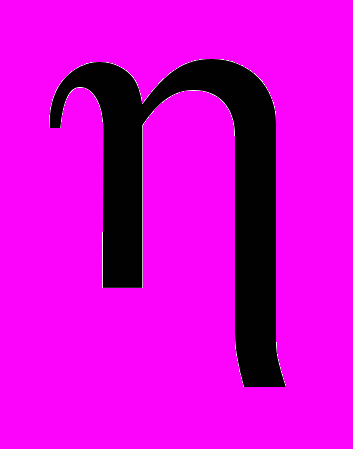 и
и  , чем выше абсолютная величина
, чем выше абсолютная величина  , тем сильнее корреляция между
, тем сильнее корреляция между 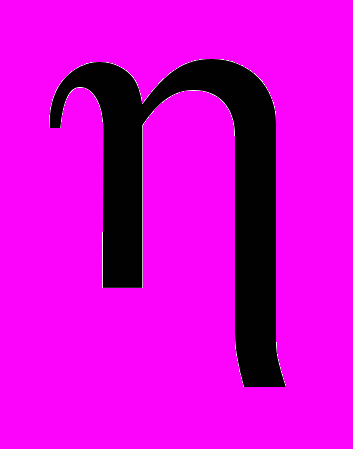 и
и  ,
,
- максимальная корреляция соответствует значению
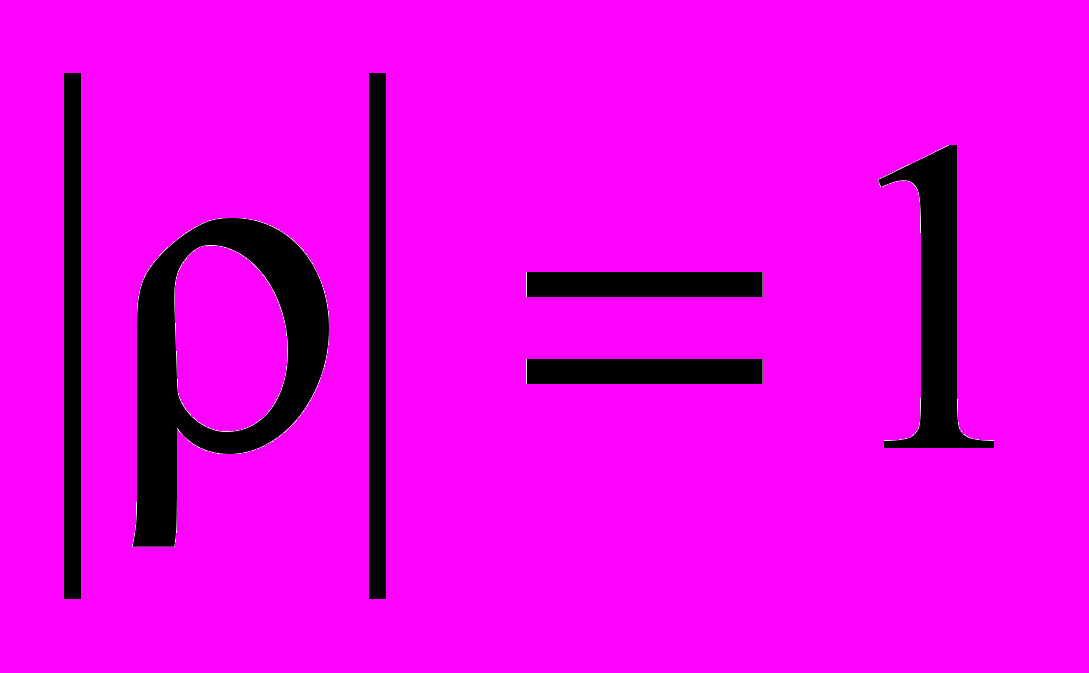 , то есть имеет место функциональная (нестохастическая) зависимость сравниваемых величин,
, то есть имеет место функциональная (нестохастическая) зависимость сравниваемых величин,
- в случае когда
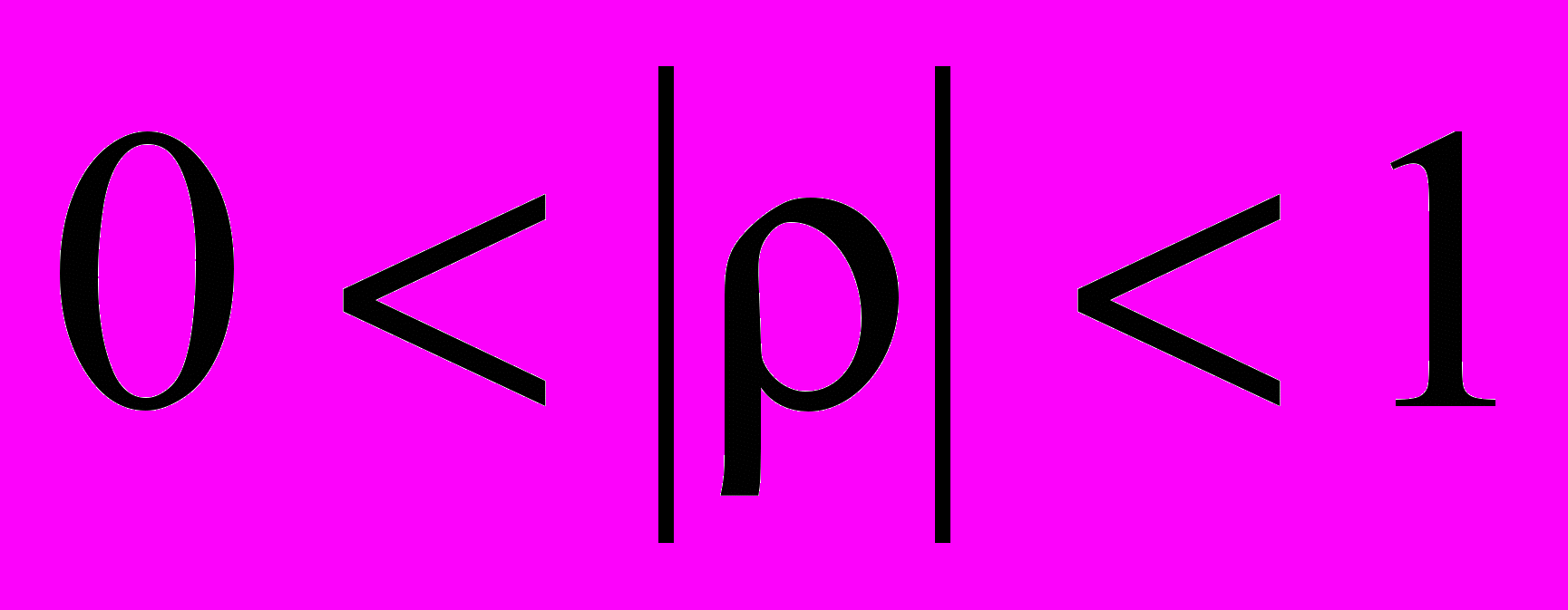 говорят либо о линейной корреляции с рассеянием, либо о наличии нелинейной корреляции.
говорят либо о линейной корреляции с рассеянием, либо о наличии нелинейной корреляции.
При корреляционном анализе результатов эксперимента оценку зависимости случайных величин производят по выборочному коэффициенту корреляции:
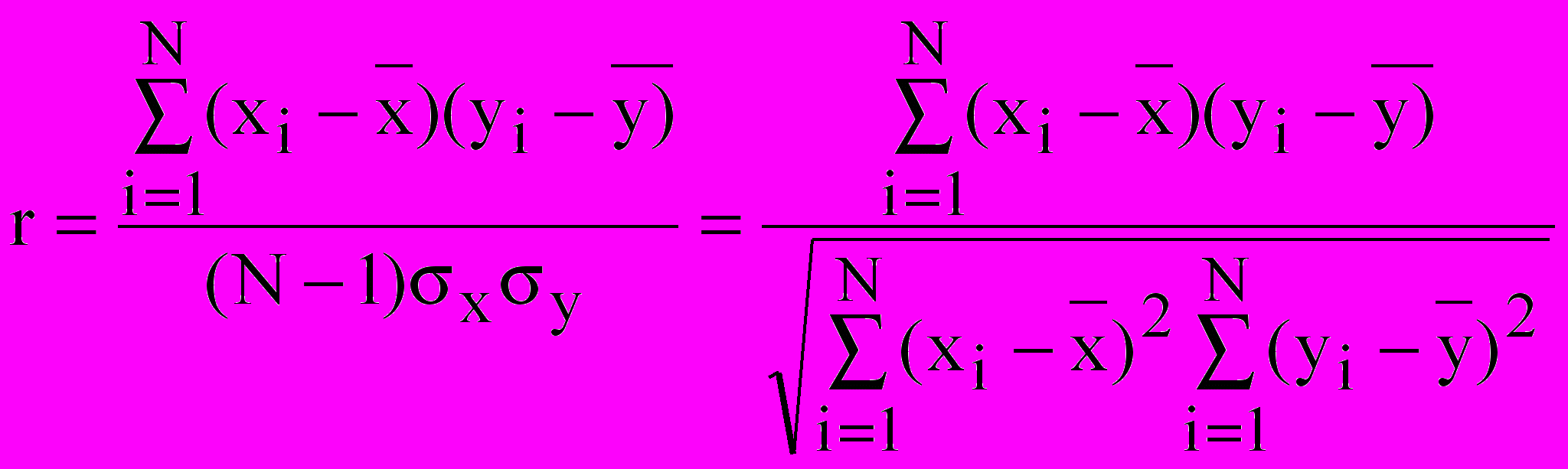 , (16)
, (16)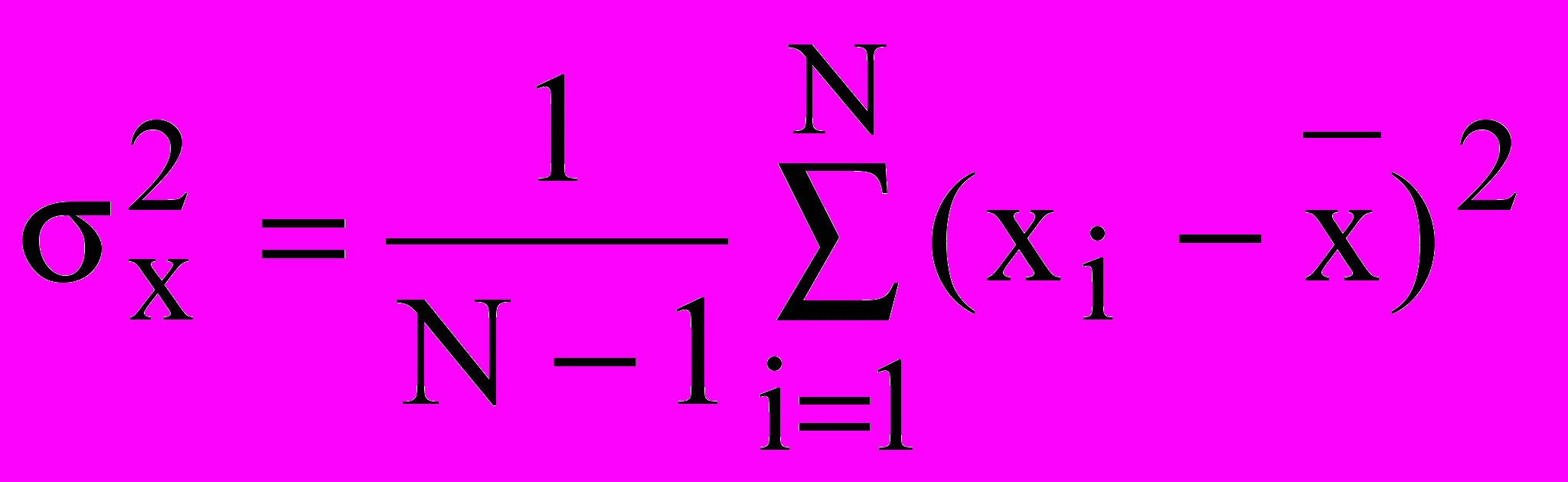 ,
, 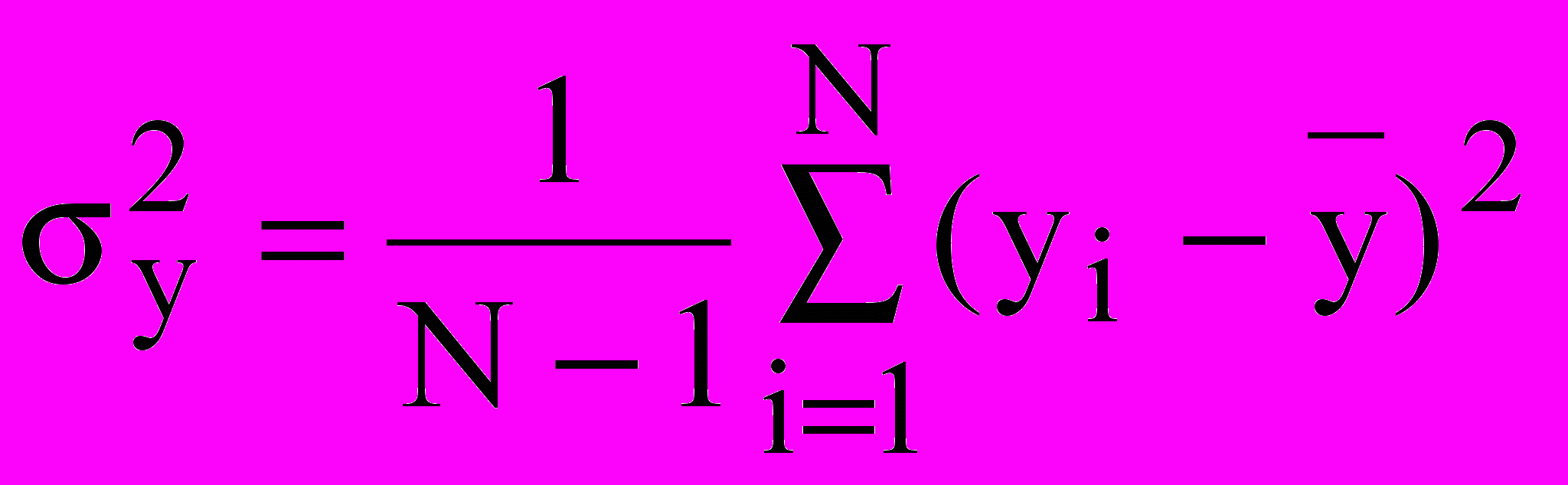 .
.При достаточно большом объеме выборки N выборочный коэффициент корреляции r приближенно равен генеральному коэффициенту
 (хотя и с определенной погрешностью). На практике выборочный коэффициент корреляции используют в основном для проверки общей гипотезы о наличии корреляции между наблюдаемыми величинами.
(хотя и с определенной погрешностью). На практике выборочный коэффициент корреляции используют в основном для проверки общей гипотезы о наличии корреляции между наблюдаемыми величинами. ^ Дисперсионный анализ позволяет оценить влияние переменных факторов на генеральное среднее наблюдаемого распределения путем анализа дисперсий факторов. То есть определить влияние того или иного фактора в целом на отклик (реакцию) исследуемого объекта.
Влияние фактора оценивается так называемой факторной дисперсией:
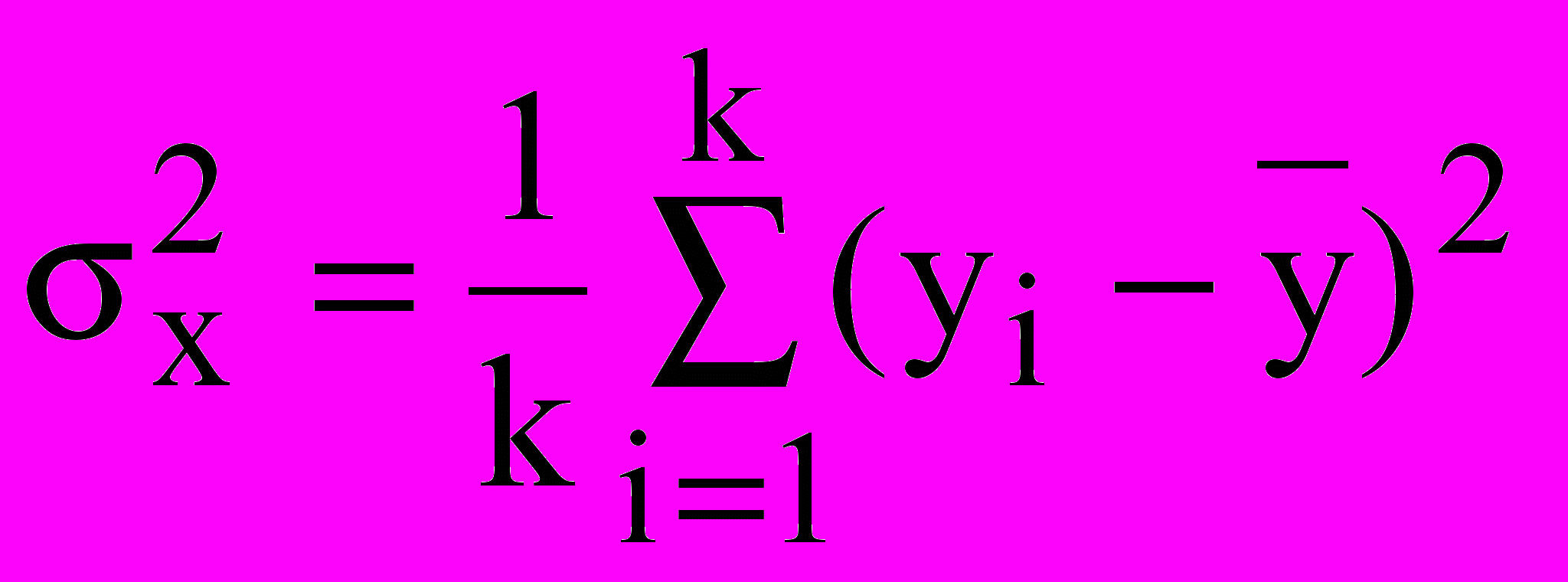 , (18)
, (18)где
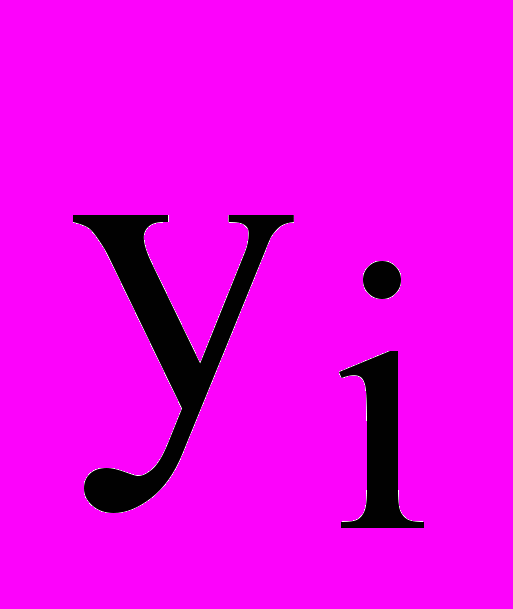 - результаты наблюдения реакции объекта при изменении фактора x,
- результаты наблюдения реакции объекта при изменении фактора x,k – количество уровней факторов и соответственно наблюдений.
В самом простом случае, когда генеральная дисперсия наблюдений D[y] известна и исследуется один фактор х, оценку значимости фактора осуществляют путем сравнения выборочной и генеральной дисперсий по критерию Фишера:
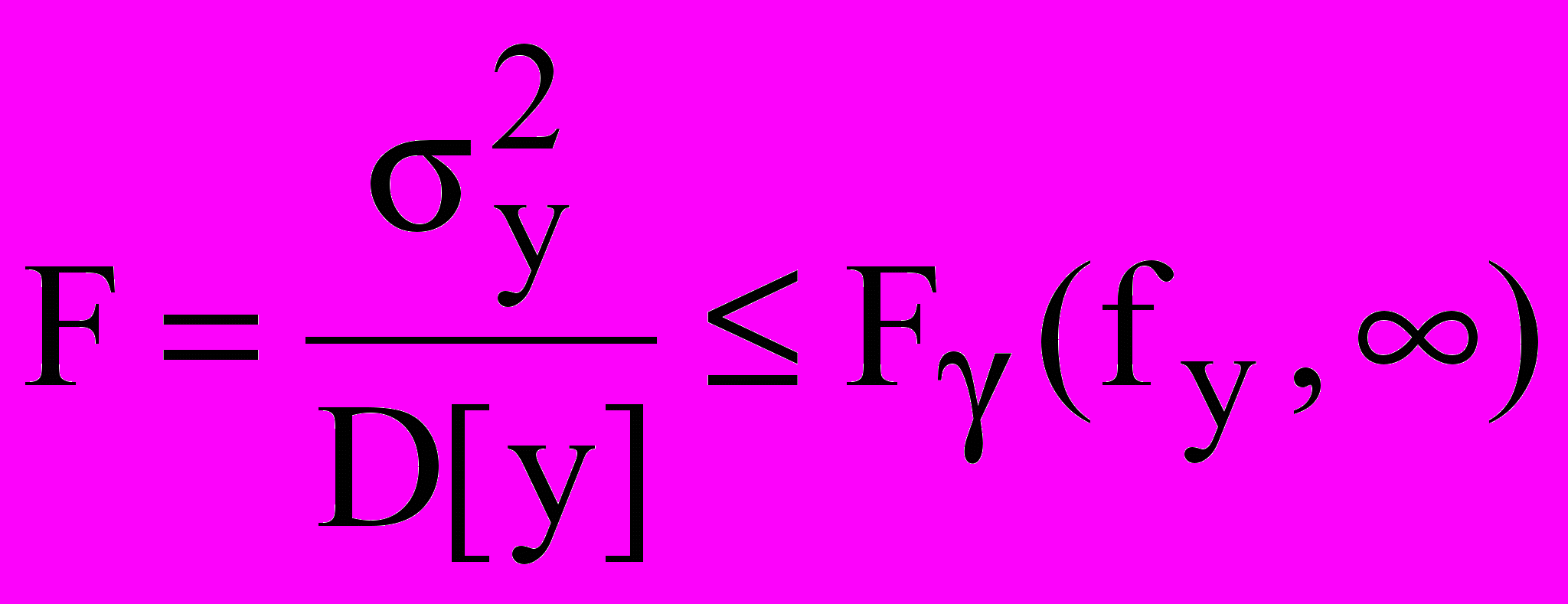 , (19)
, (19)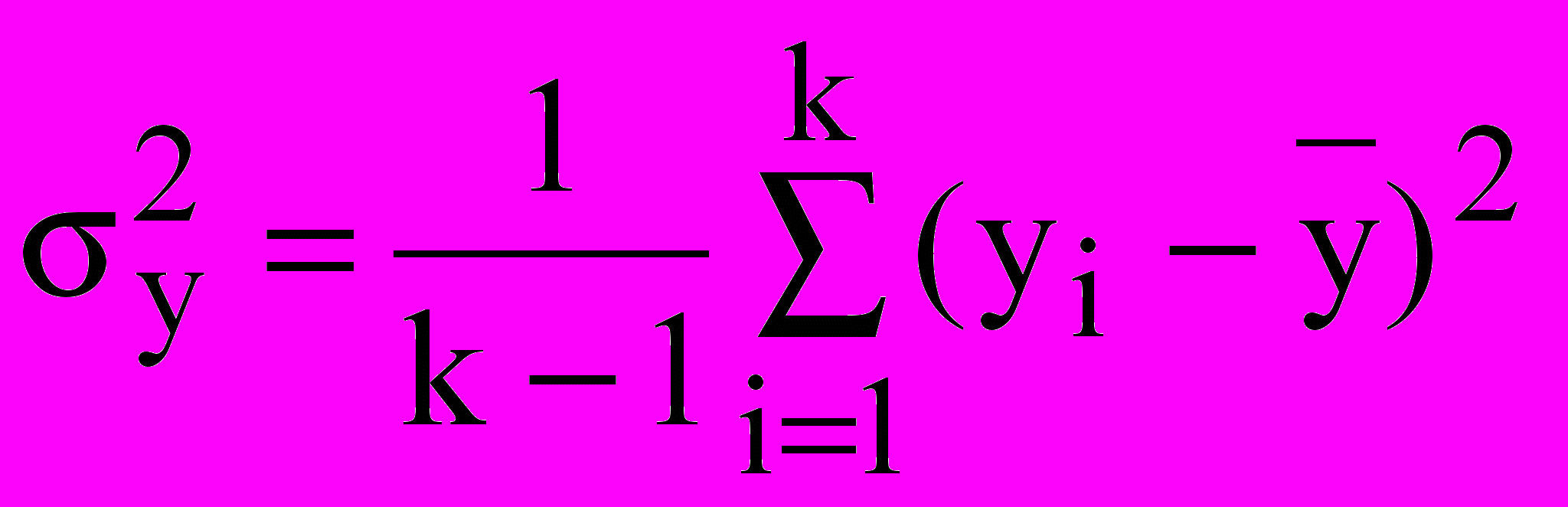 .
. Если условие (19) выполняется, то влияние фактора незначительно, в противном случае влияние фактора значимо.
В случаях, когда значение генеральной дисперсии заранее неизвестно, применяют другие схемы. Рассмотрим решение задачи однофакторного дисперсионного анализа.
Основная задача дисперсионного анализа состоит в том, чтобы разложить общую дисперсию на составляющие, характеризующие влияние фактора x и фактора случайности процесса измерений. Это обусловлено тем, что оценка генеральной дисперсии, связанной со случайностью
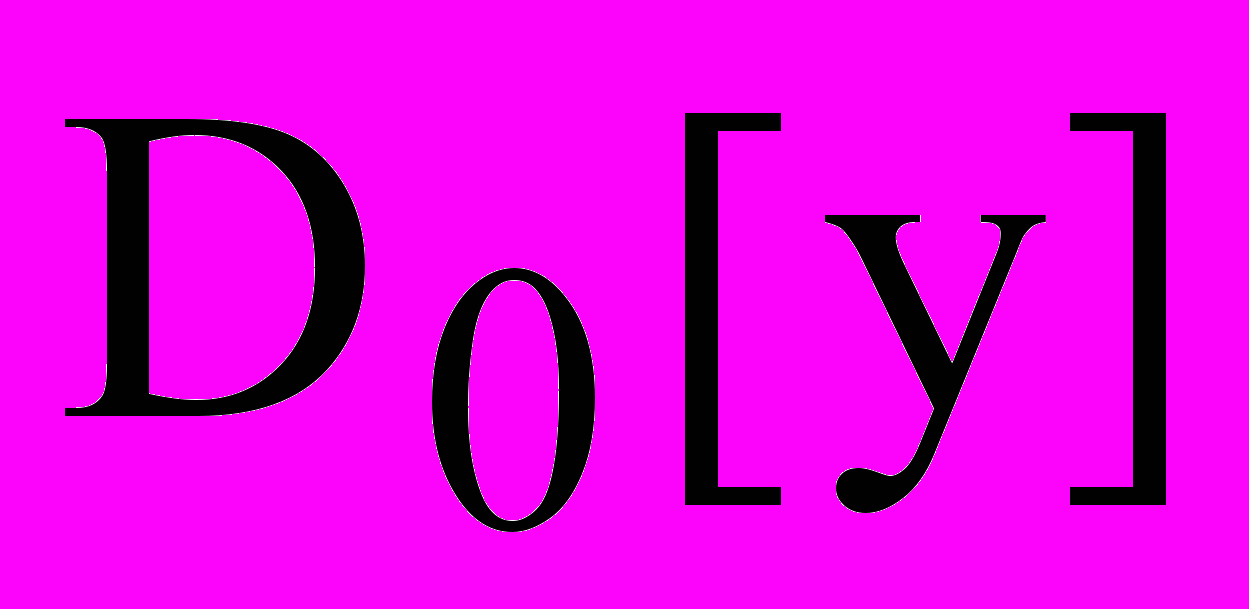 , дает приближенную оценку для дисперсии фактора:
, дает приближенную оценку для дисперсии фактора: 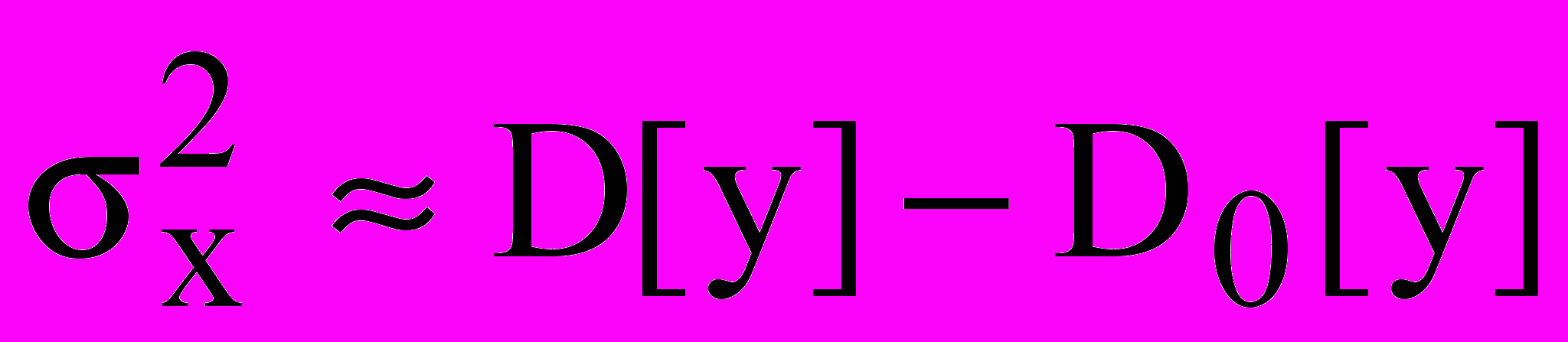 . (20)
. (20)Не вдаваясь в теоретические выкладки, рассмотрим алгоритм оценки значимости фактора x по результатам проведенного эксперимента:
1) На каждом уровне фактора х проделывается n наблюдений и определяется оценка генеральной дисперсии
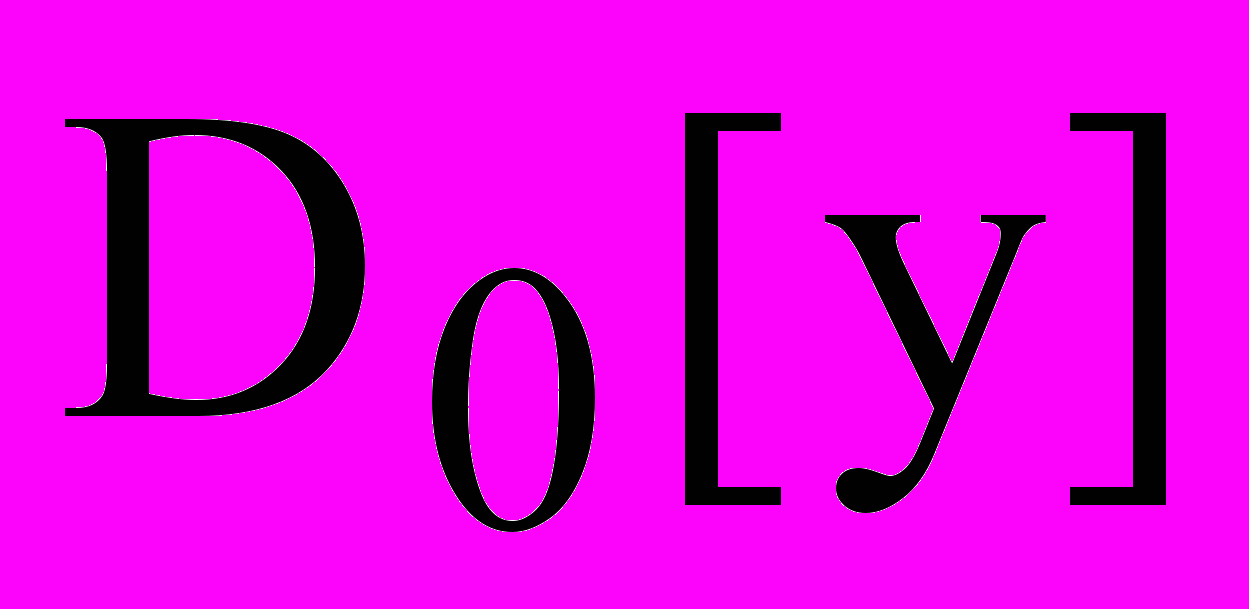
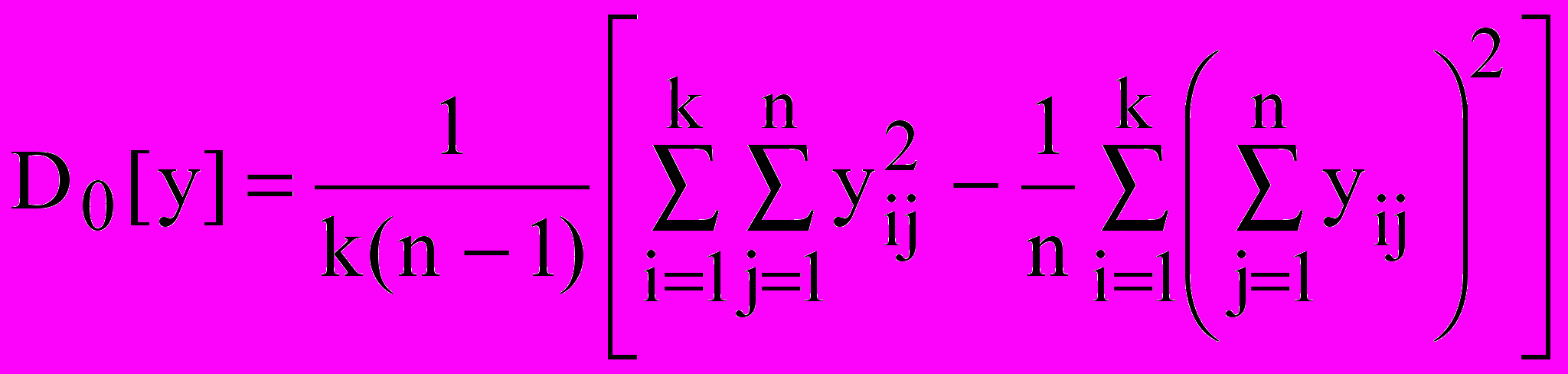 . (21)
. (21)2) Учитывая, что факторная дисперсия наиболее заметна при анализе средних значений на i-м уровне фактора, а дисперсия случайности (остаточная дисперсия) для средних значений в n раз меньше, чем для отдельных измерений, выражение для факторной дисперсии может быть записано в виде:
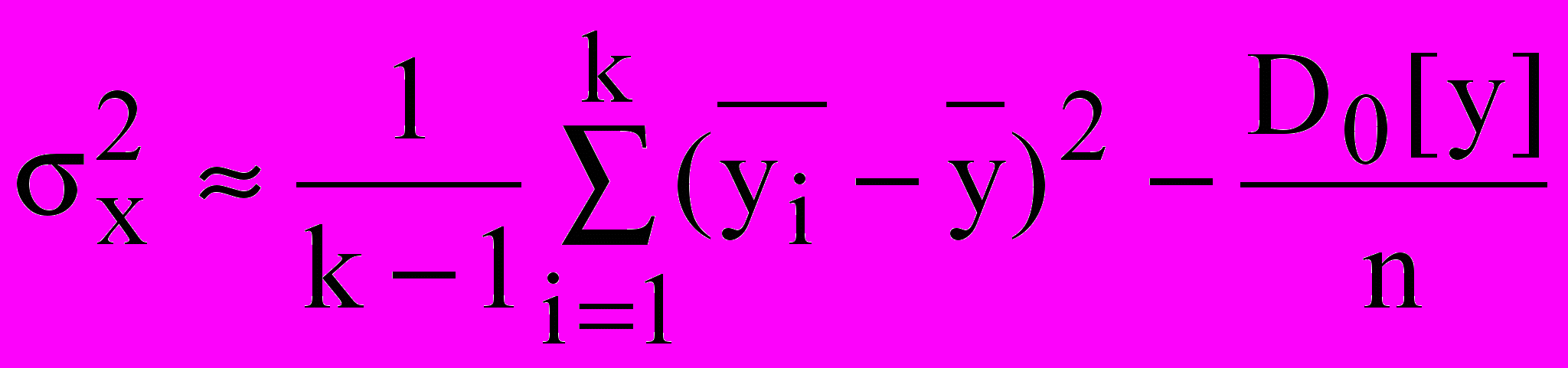 , (22)
, (22)где
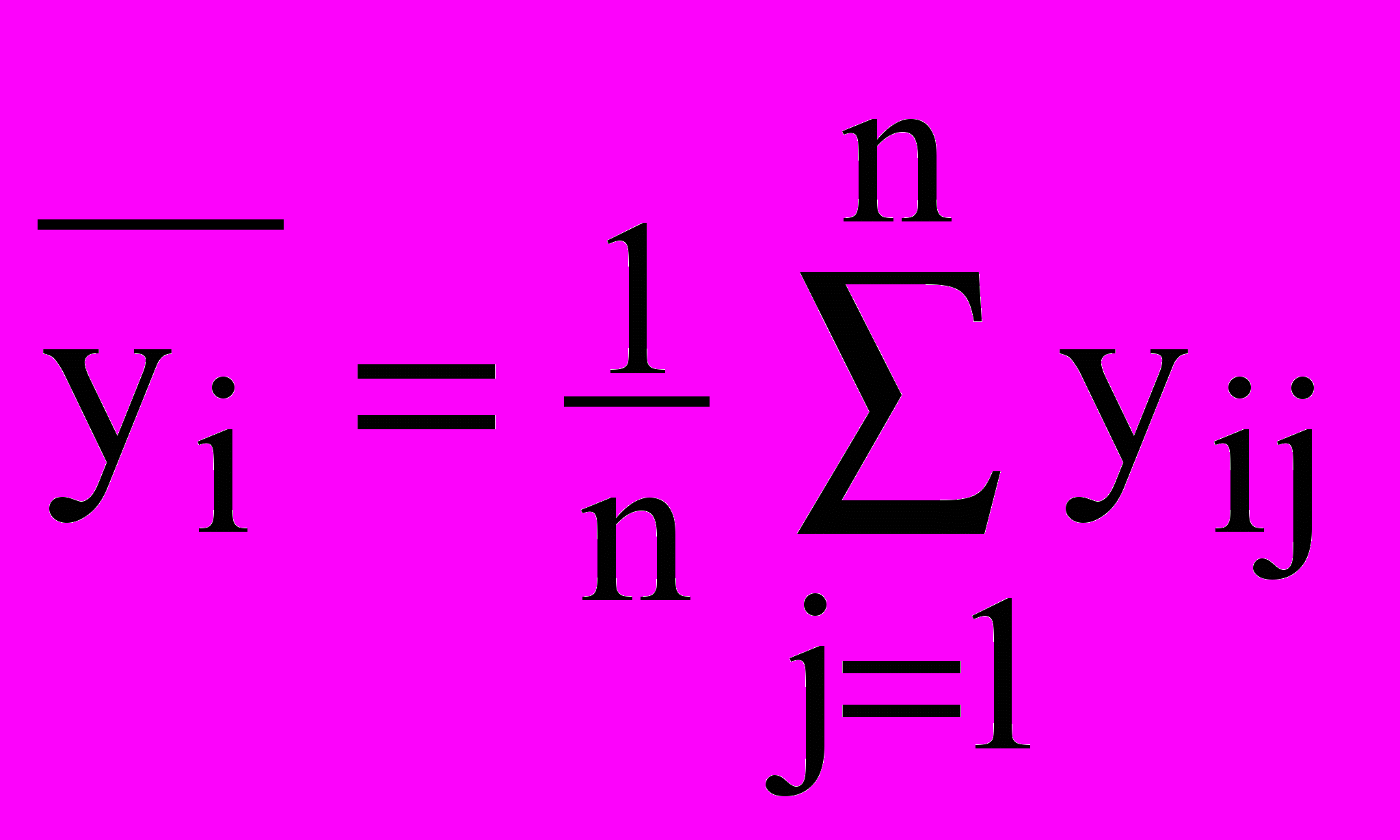 - среднее для i-го уровня фактора,
- среднее для i-го уровня фактора, 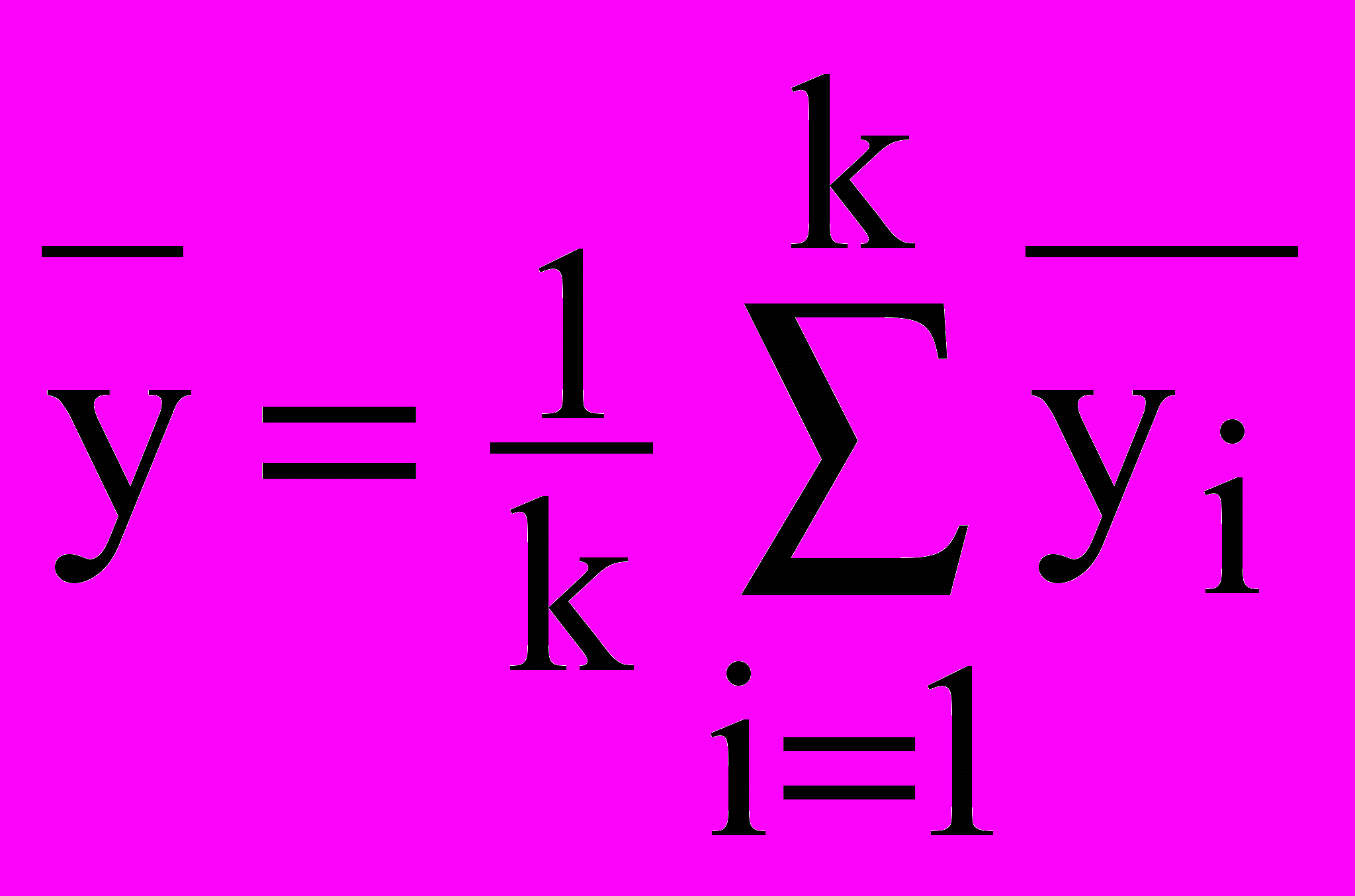 - среднее всех наблюдений.
- среднее всех наблюдений.Выражение (22) преобразуем путем введения дисперсии
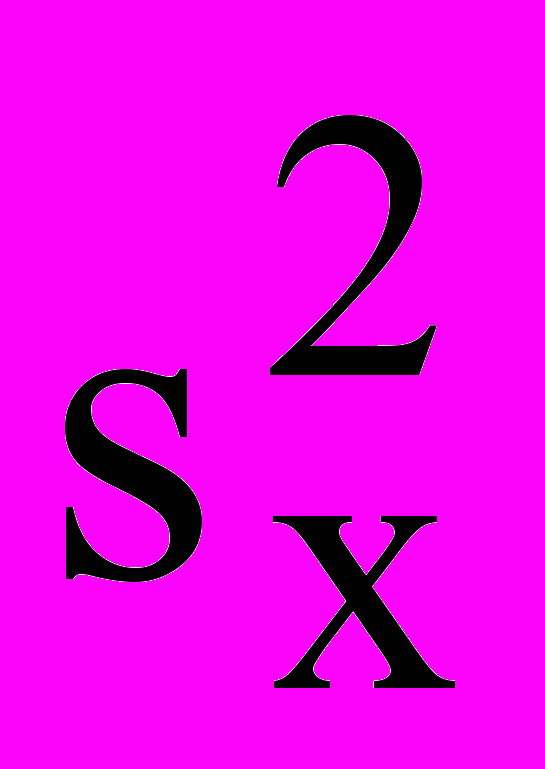 следующим образом:
следующим образом: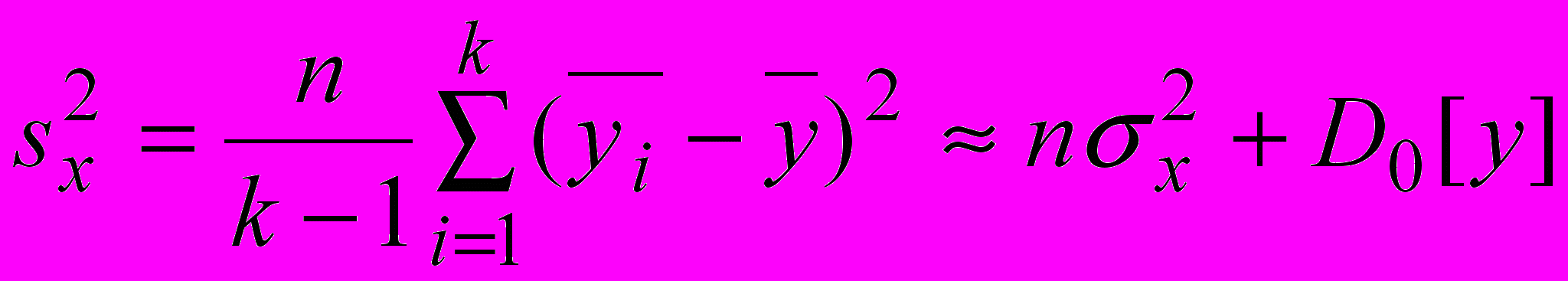 . (23)
. (23)Данная дисперсия имеет (k-1)-ю степень свободы.
3) Определение значимости влияния фактора x осуществляем на основе критерия Фишера:
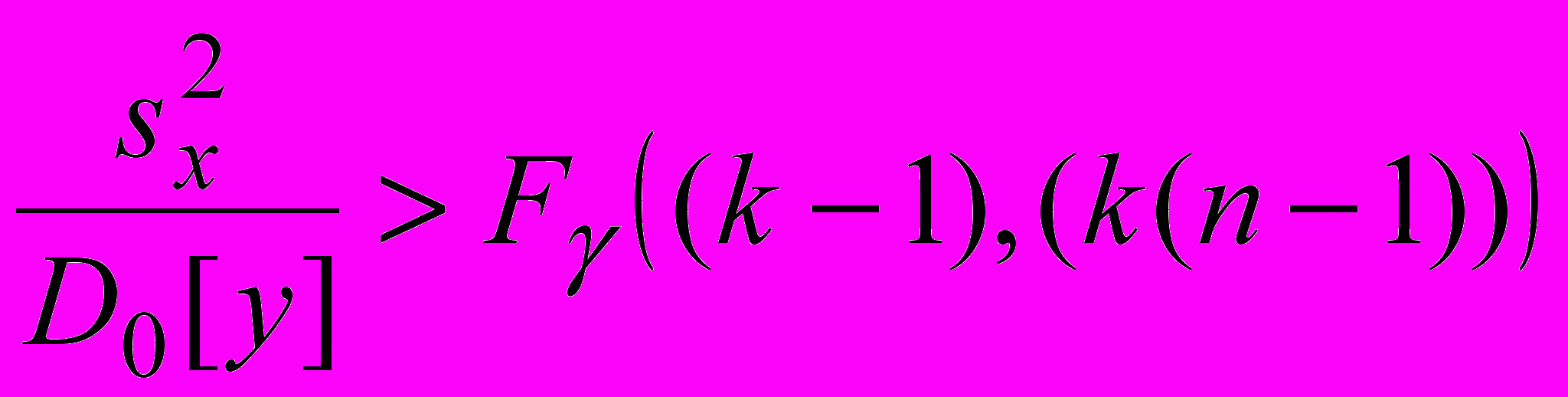 . (24)
. (24)При выполнении данного неравенства влияние фактора считается значимым.
Наилучшие результаты метод дисперсионного анализа дает при обработке результатов ПФЭ и ДФЭ.
