Лекция №8 Построение математических моделей технологических объектов и систем аналитическим методом

Вид материала

Лекция

Содержание Уравнение закона сохранения энергии Уравнение закона сохранения количества движения Уравнение материального баланса Топологические уравнения Физическое описание объекта моделирования. Составление уравнений статики или динамики объекта моделирования. Определение начальных и граничных условий моделирования. Выбор метода решения уравнений математического описания объекта, разработка алгоритма и составление программы. Проверка соответствия (адекватности) модели объекту.

Подобный материал:

• Утверждаю, 89.56kb.
• Программа по курсу " Моделирование систем управления, 30.71kb.
• План изучения дисциплины № п/п, 155.57kb.
• Моделирование и оптимизация систем с распределенными параметрами, 14.61kb.
• Лекция 1 Виды математических моделей сложных систем, 201.52kb.
• Лекции по дисциплине «Математическое моделирование» для студентов и магистрантов специальности, 21.92kb.
• Учение студентов основам математического моделирования, необходимых при проектировании,, 28.67kb.
• Название Лекция-семинар: Построение математических моделей целочисленного линейного, 64.42kb.
• К. А. Тимирязева Экономический факультет Кафедра экономической кибернетики Светлов, 241.83kb.
• 1. Введение Основы анализа данных. Методология построения моделей сложных систем. Модель, 399.94kb.

Лекция № 8

Построение математических моделей технологических объектов и систем аналитическим методом


В основу аналитического метода составления математических моделей положен теоретический анализ конструкции исследуемого объекта (системы) и происходящих в нем физических процессов. Основу данного анализа составляют фундаментальные физические законы, к которым, прежде всего, относятся законы сохранения (массы, энергии, количества движения).

Общая формулировка закона сохранения следующая: изменение во времени некоторой субстанции в элементарном объеме равно сумме притока-стока этой субстанции через его поверхность с учетом скорости генерации или уничтожения субстанции в этом объеме.

Уравнение, соответствующее данной формулировке, имеет вид –

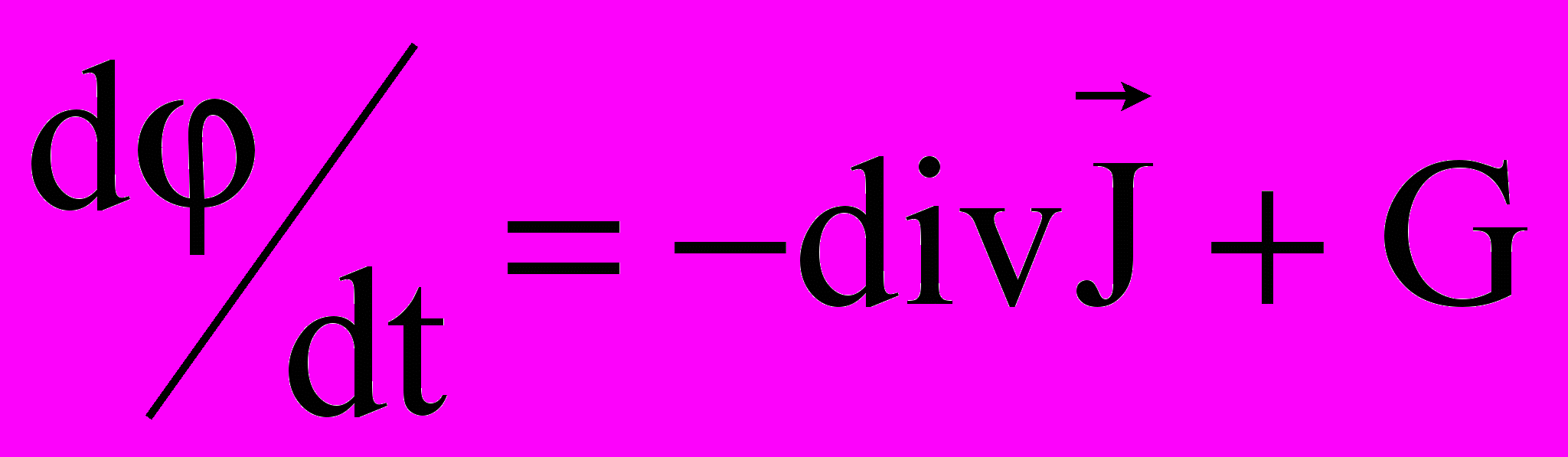, (1)

где - фазовая переменная (координата), выражающая субстанцию;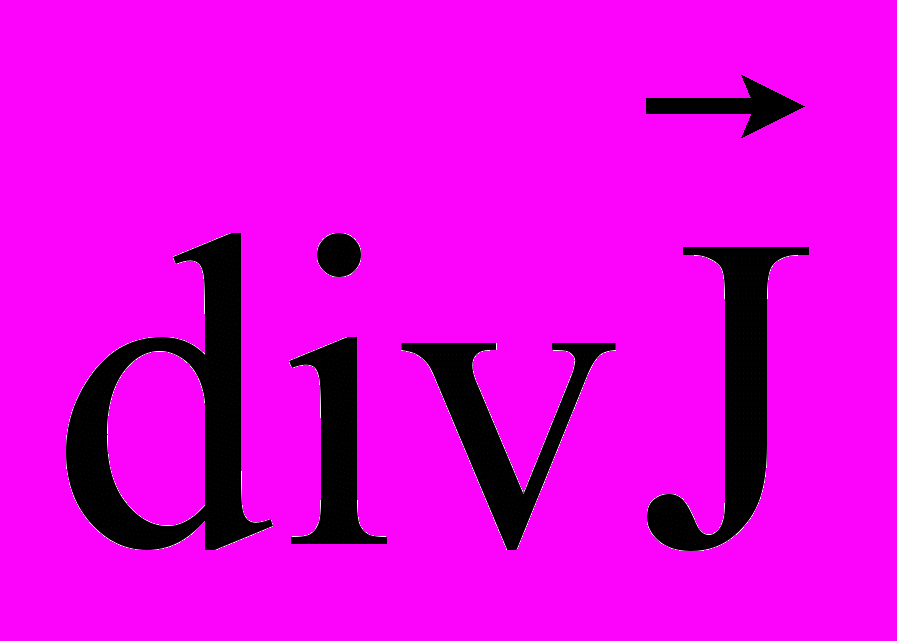

- дивергенция вектора плотности потока фазовой переменной;

G – скорость генерации или уничтожения субстанции.

Дивергенция вектора плотности потока характеризует сумму притока-стока субстанции через поверхность элементарного объема и представляет собой скалярную величину, образуемую суммой частных производных вектора 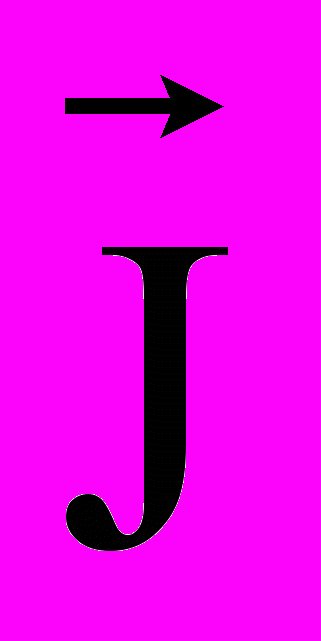в системе координат исследуемого объекта. Например, для трехмерного технического объекта –

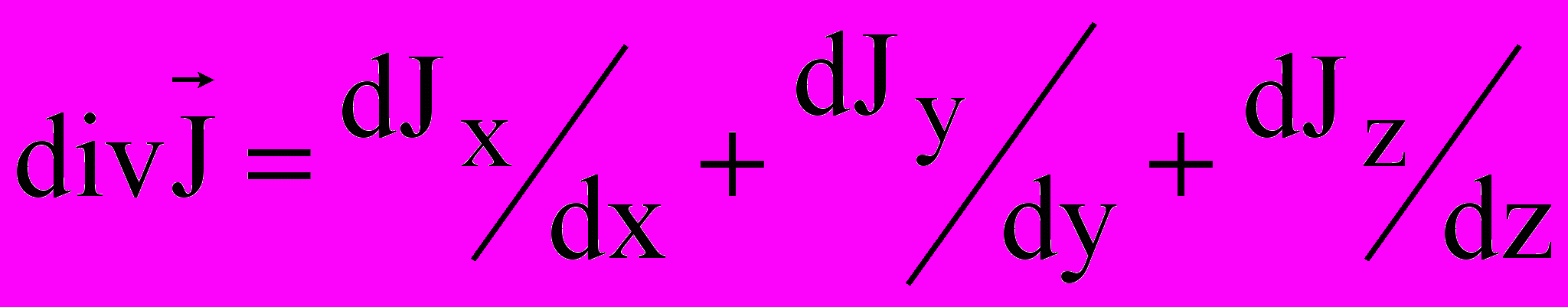. (2)

На основе общей трактовки закона сохранения могут быть получены уравнения для различных субстанций. В частности, уравнение закона сохранения массы имеет вид –

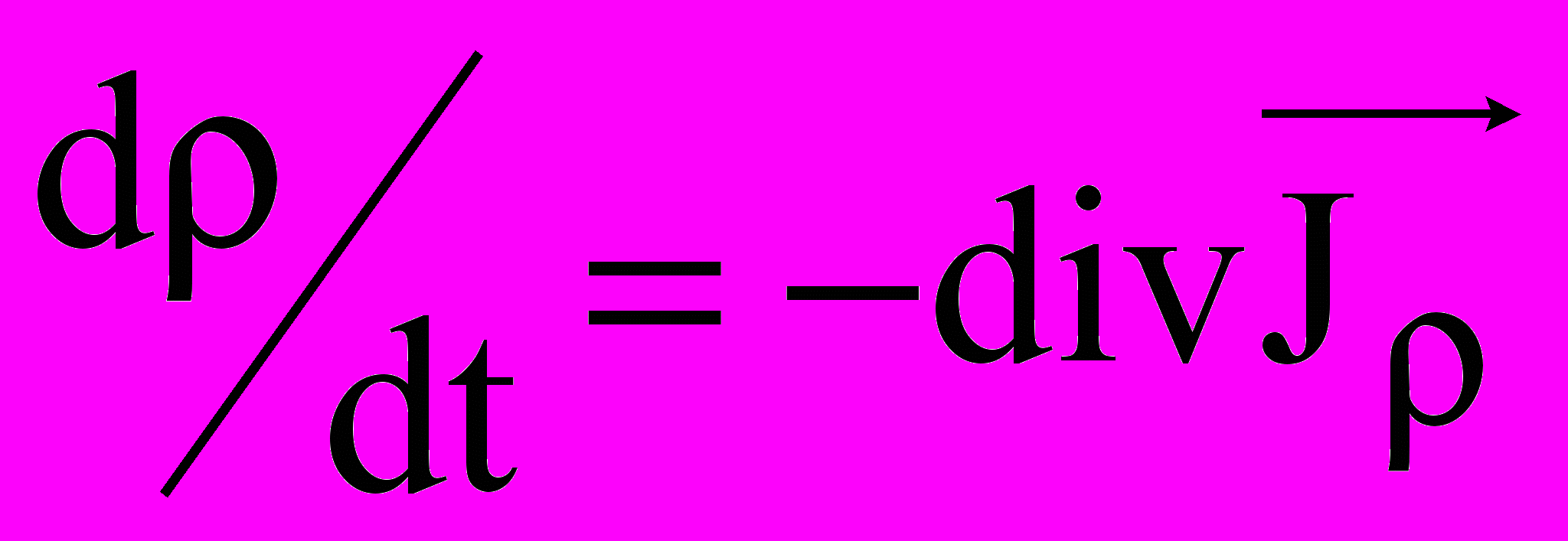, (3)

где - плотность массы, кг/м³,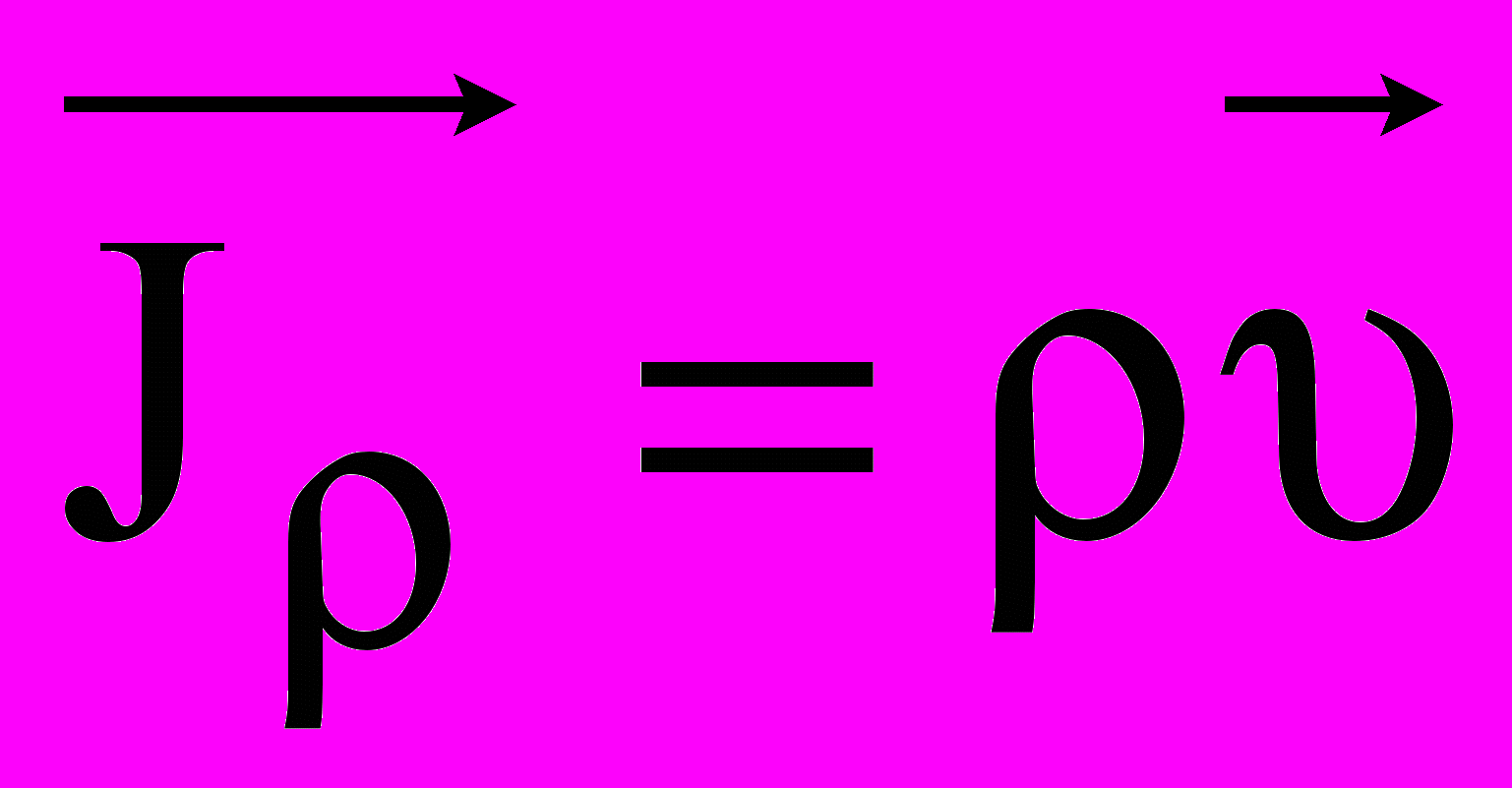

- вектор плотности потока массы, 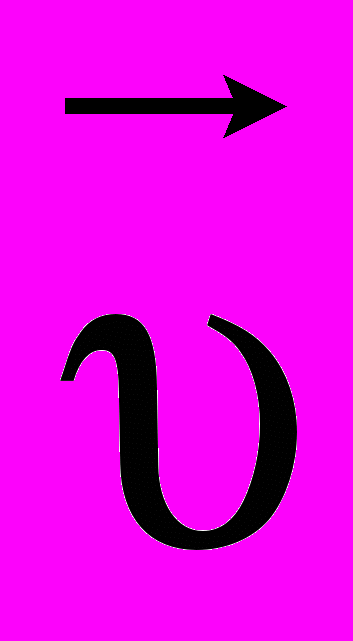- вектор скорости переноса массы.

В одномерном случае, когда скорость направлена вдоль одной оси декартовой системы координат, плотность потока массы измеряется в кг/(м²с). Примером использования данного закона является описание свойства непрерывности потока жидкости в трубопроводе –

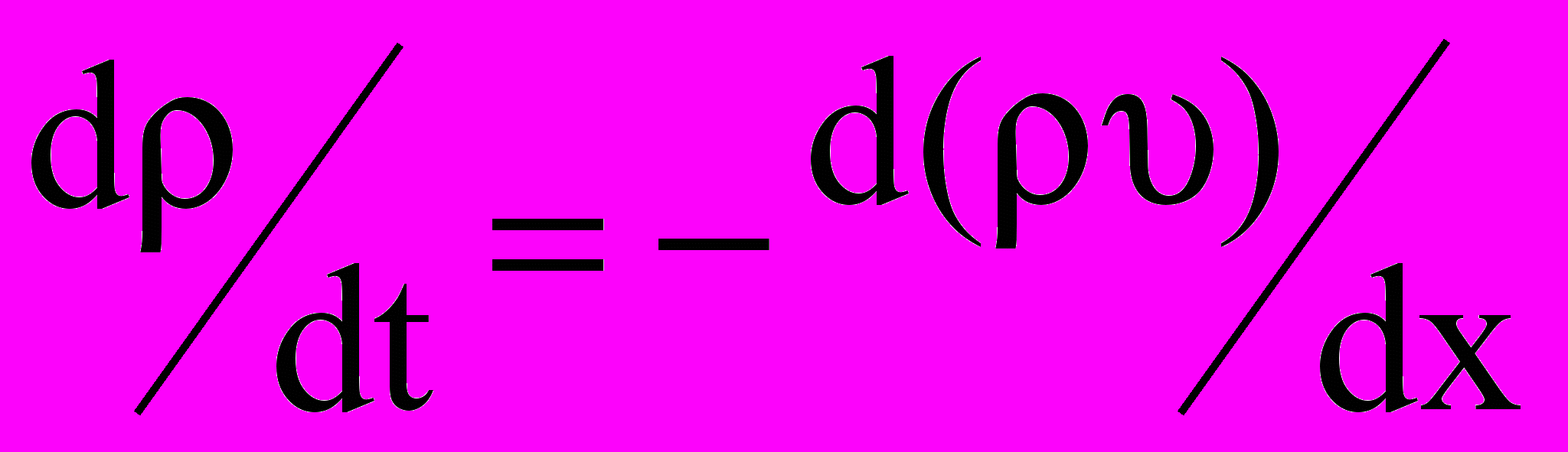. (4)

Уравнение закона сохранения энергии может быть представлено в виде –

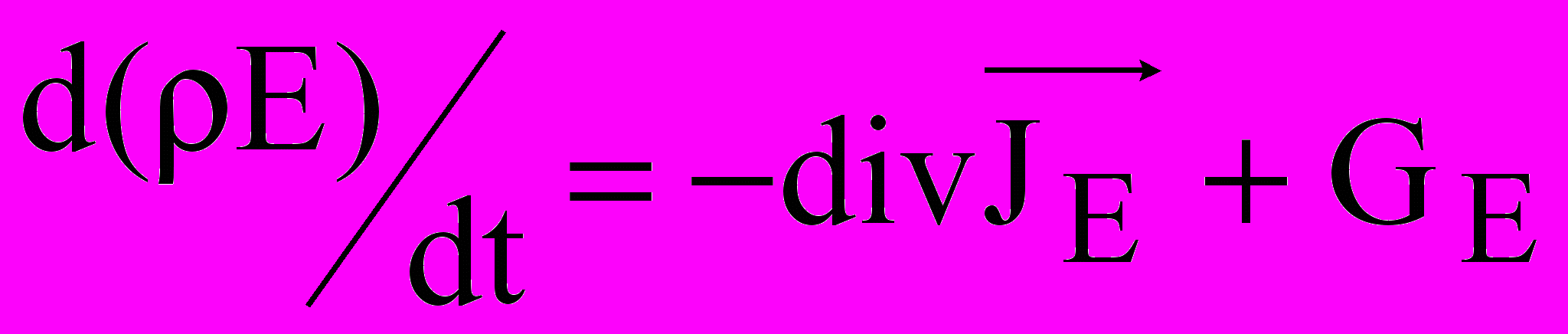, (5)

где 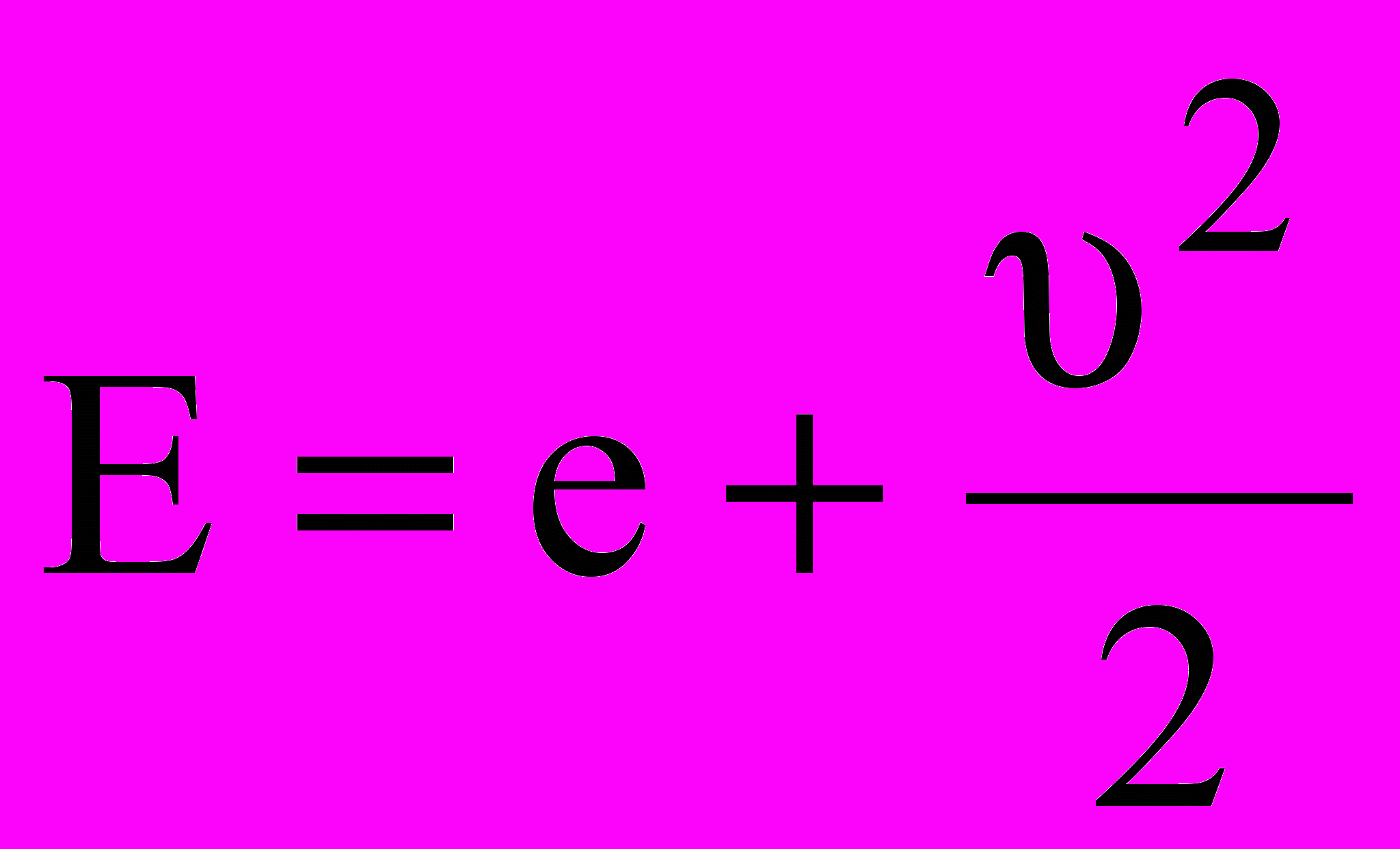- полная энергия единицы массы, е – внутренняя энергия единицы массы,

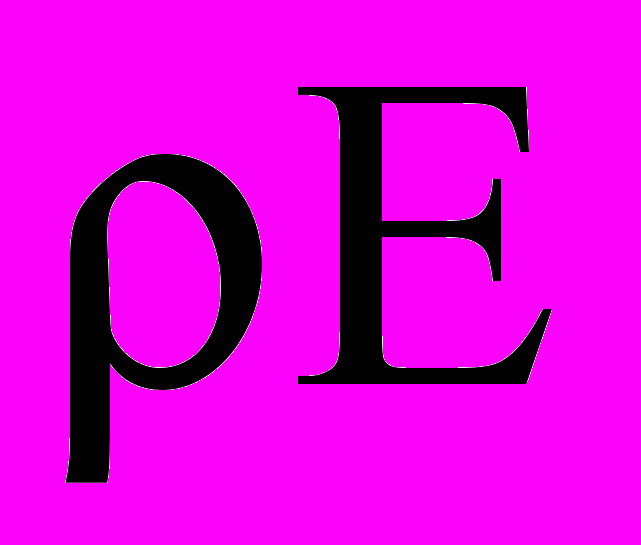- энергия единицы объема, Дж/м³, - вектор плотности потока энергии, 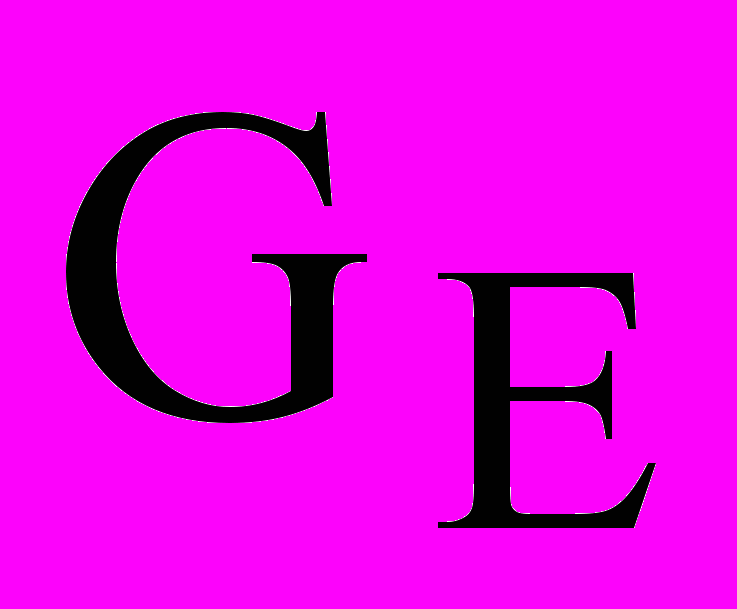- скорость генерации или поглощения энергии в единице объема, Дж/(м³с).

В одномерном случае плотность потока энергии измеряется в Дж/(м²с). Примером использования данного закона является уравнение теплопроводности, связывающее изменение температуры во времени и пространстве со свойствами среды –

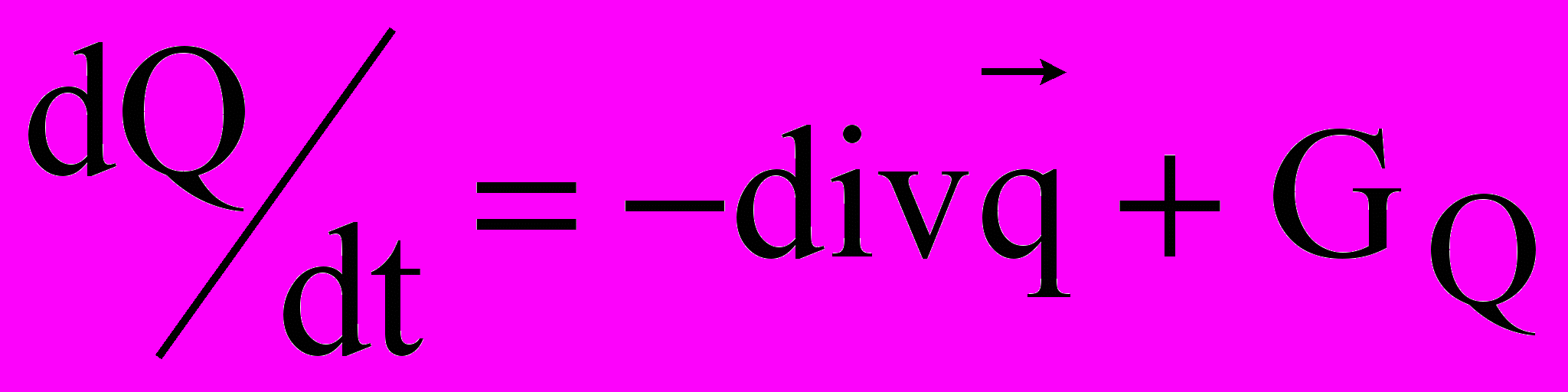, (6)

где Q – количество тепловой энергии в единице объема, Дж/м³, 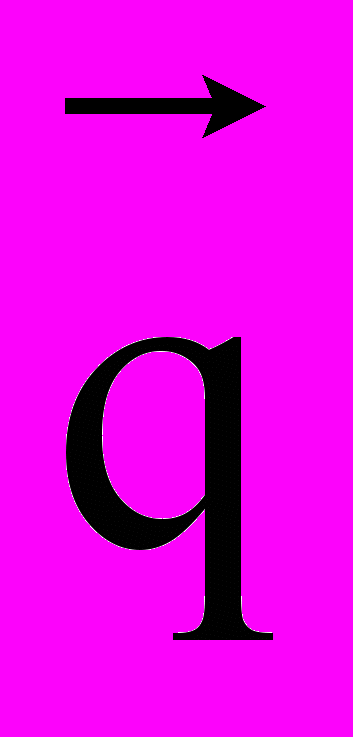- вектор плотности теплового потока, Дж/(м²с), 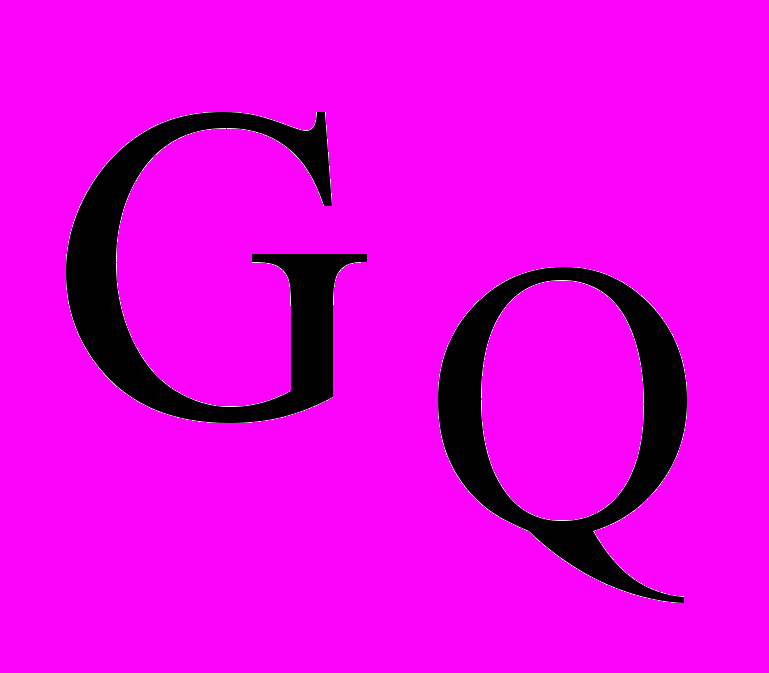- количество тепловой энергии, выделяемое в единицу времени в рассматриваемом элементарном объеме, Дж/(м³с).

Уравнение закона сохранения количества движения для потока идеальной жидкости (без учета сил трения, обусловленных вязкостью) имеет вид –

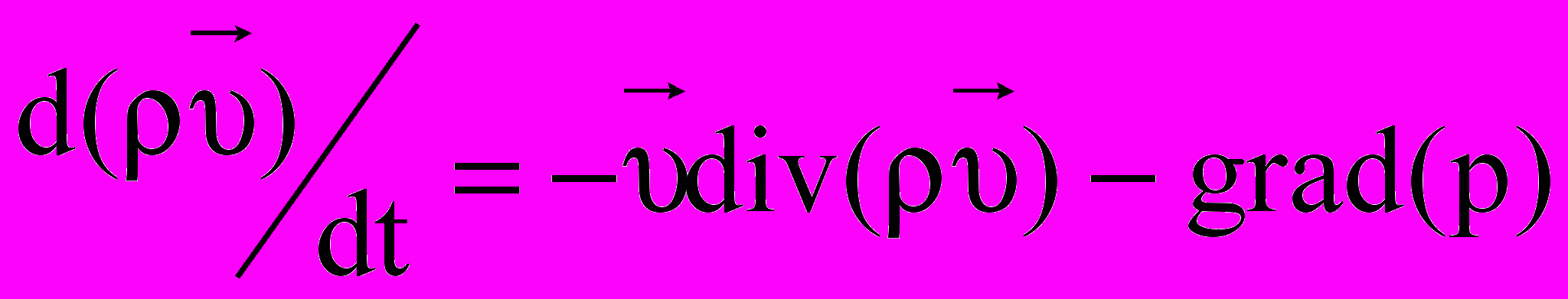, (7)

где 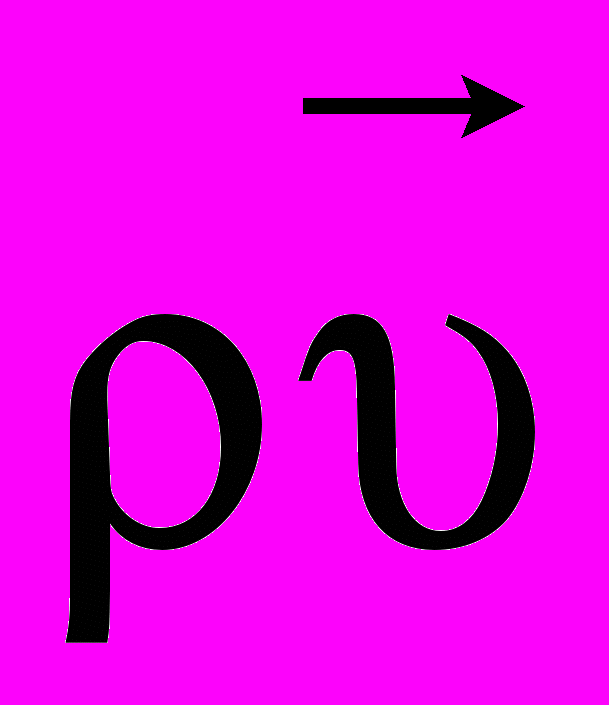- вектор количества движения единицы объема жидкости, p – давление жидкости,

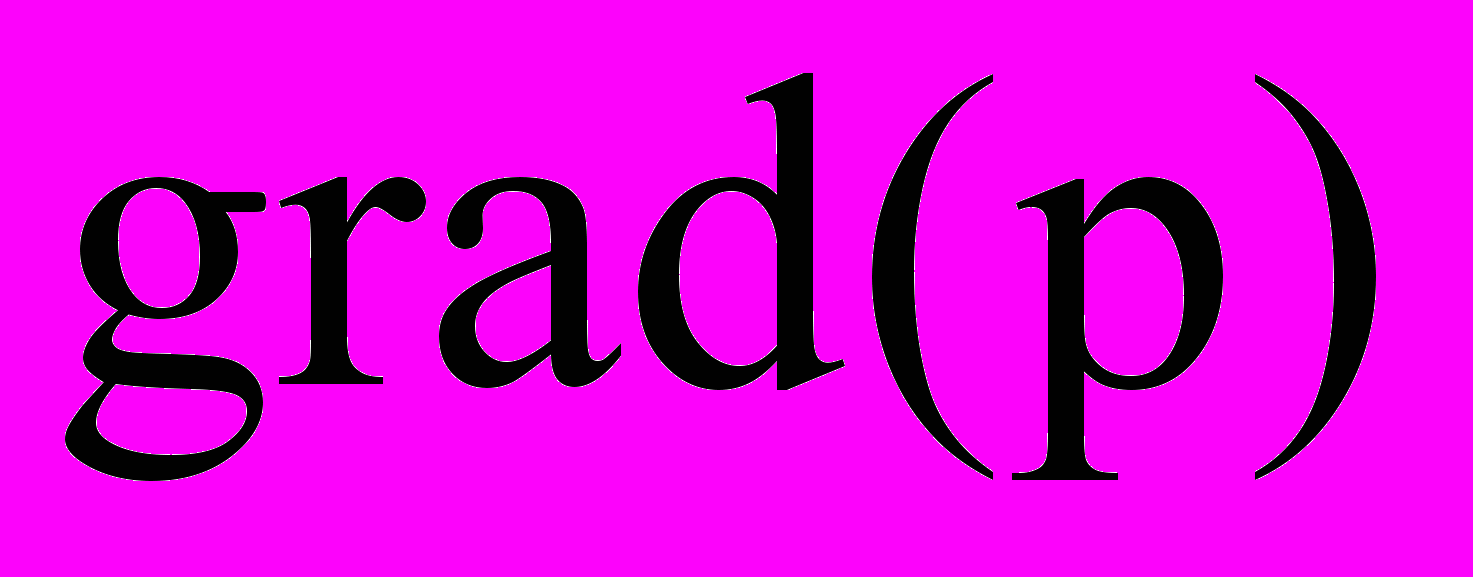- градиент давления, компонентами которого являются частные производные аргумента по пространственным координатам.

Примером использования данного закона является уравнение Навье-Стокса, приближенная форма которого для анализа движения жидкости в трубопроводе имеет вид –

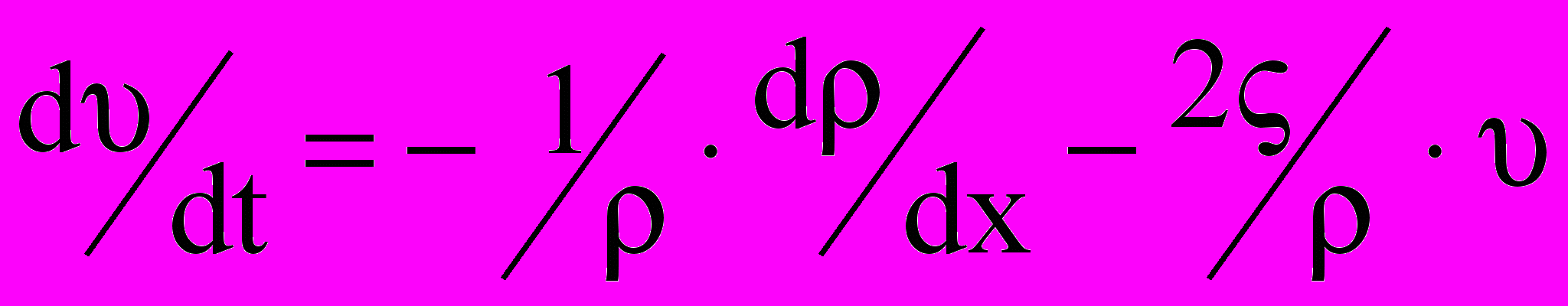, (8)

где 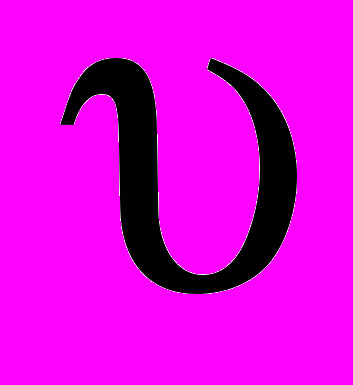- скорость потока жидкости, - плотность потока жидкости, 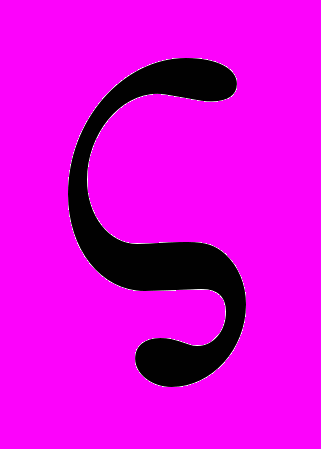- коэффициент линеаризованного вязкого трения в трубопроводе.

Практика показывает, что при разработке математических моделей чаще всего используются закономерности, носящие характер уравнений баланса. К ним относятся уравнения материального и энергетического баланса, уравнения экономического баланса, а также уравнения равновесия сил.

Уравнение материального баланса основано на законе сохранения массы вещества и может быть записано в следующей форме:

Приход вещества – Расход вещества = Накопление вещества

Разность между приходом и расходом вещества равна изменению его количества в рассматриваемом объекте. В стационарном (установившемся) режиме не может происходить ни убыль, ни накопление. В этом случае уравнение материального баланса для n-го количества веществ может быть записано в виде:

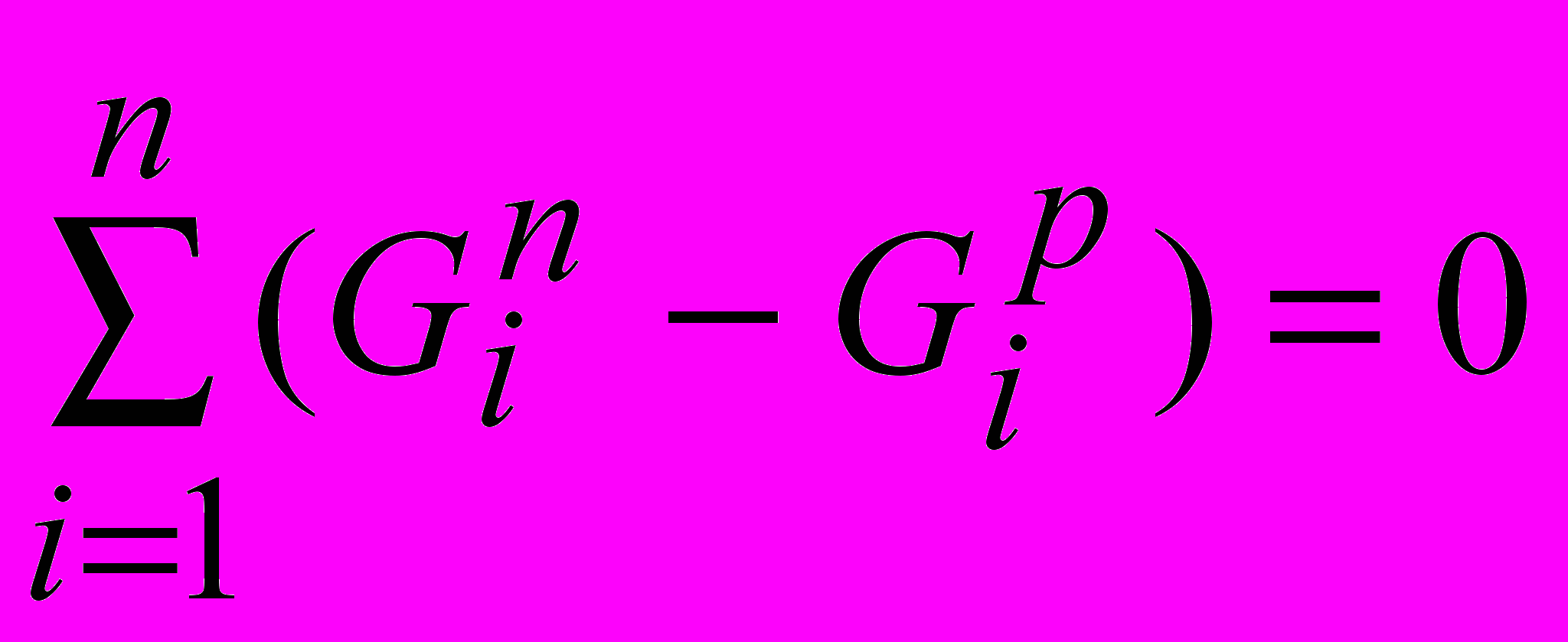, (9)

где 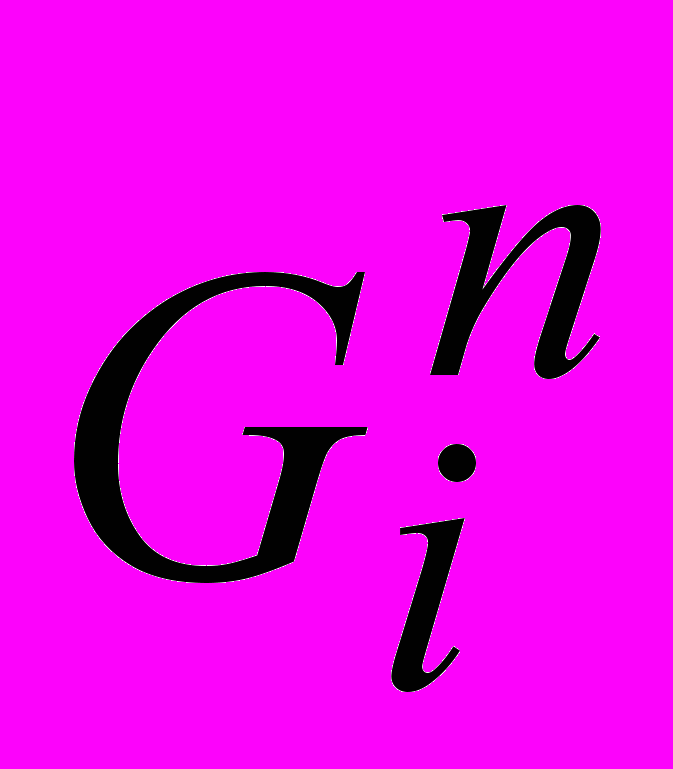- весовой приход i-го вещества;

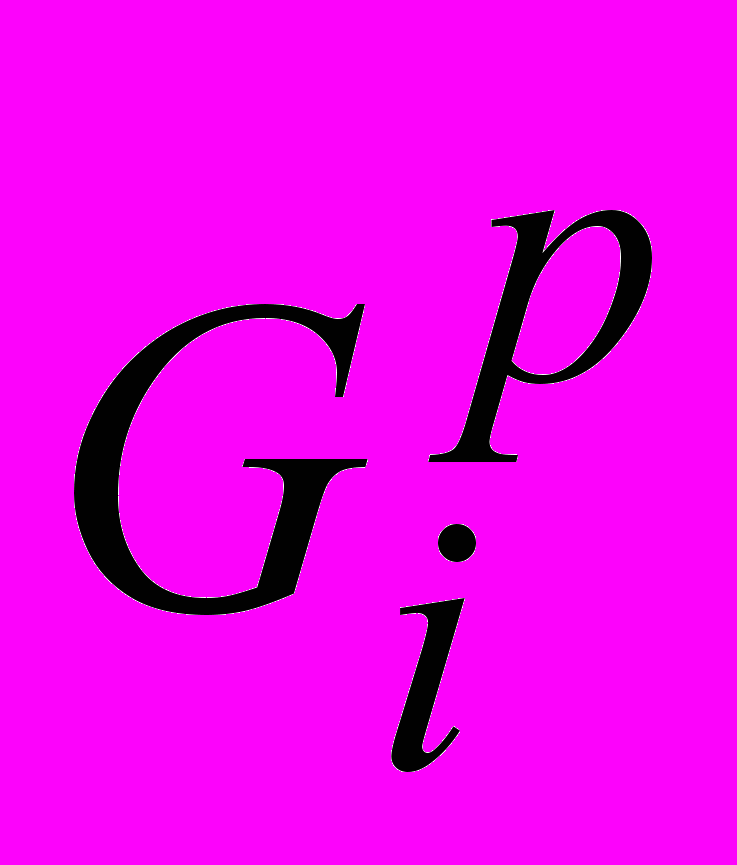- весовой расход i-го вещества.

С учетом изменения количества вещества в объекте уравнение материального баланса может быть записано в виде:

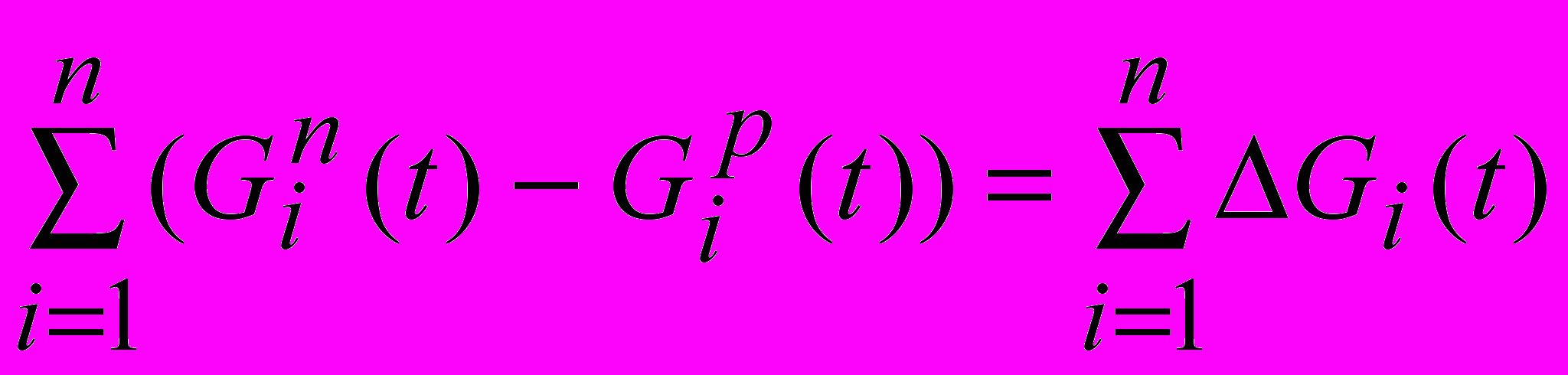, (10)

где 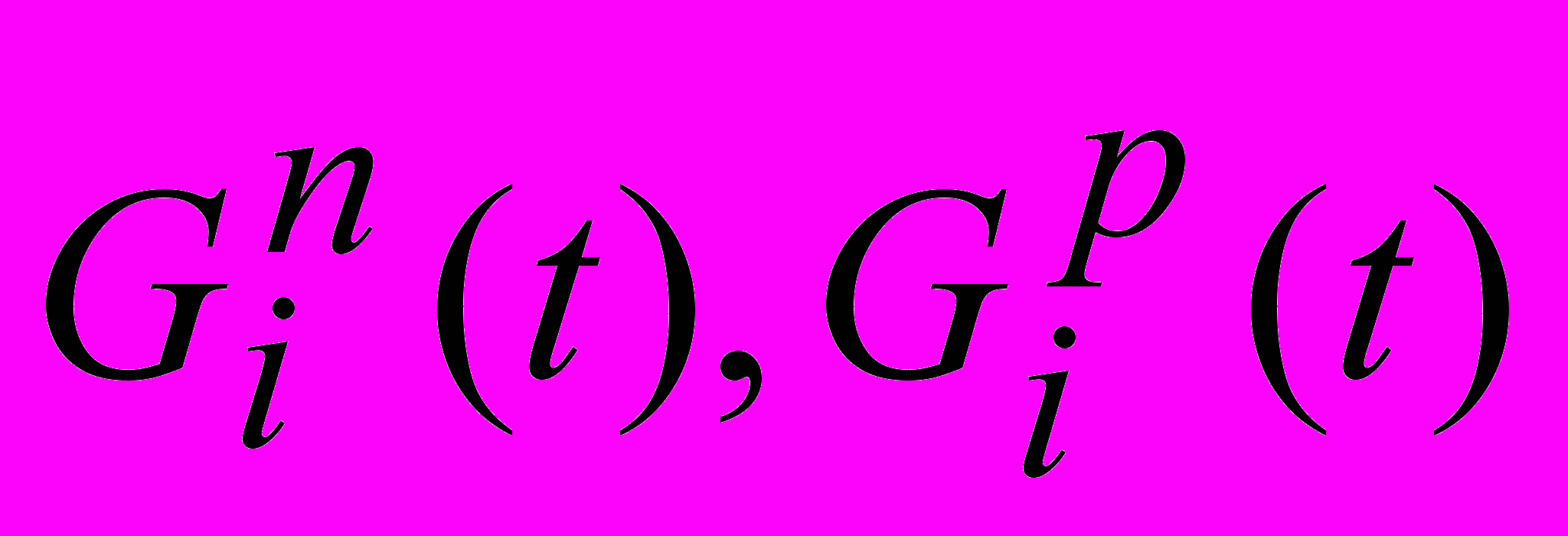- мгновенные значения весового прихода и расхода i-го вещества соответственно;

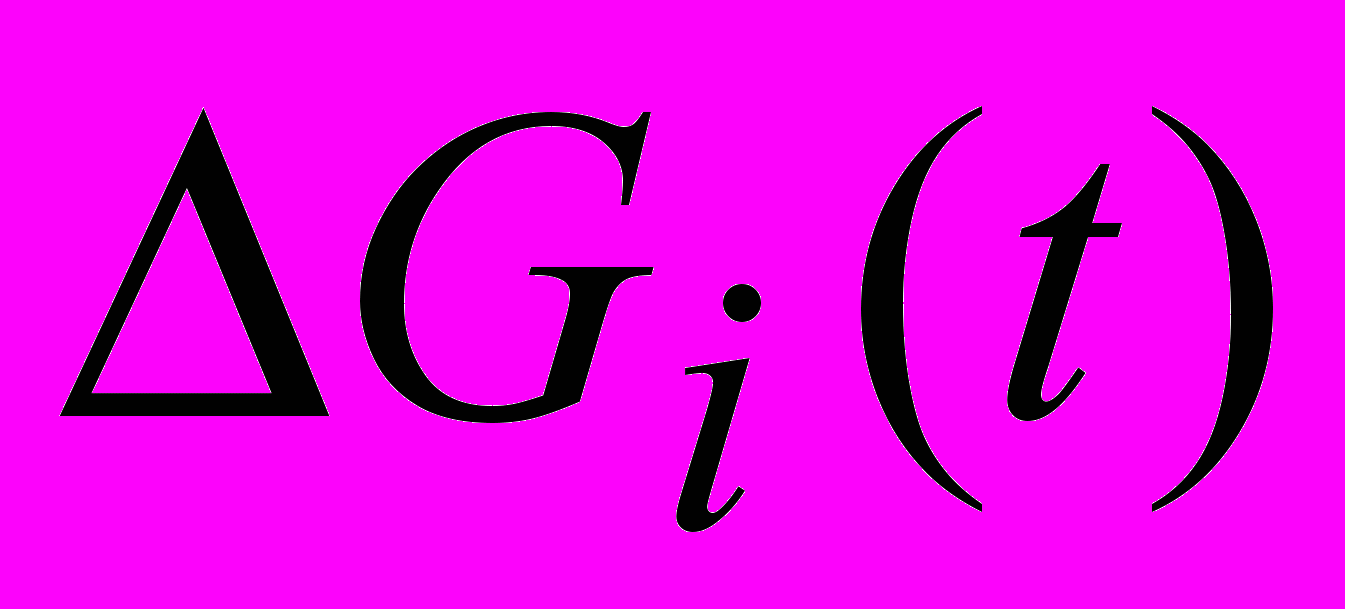- мгновенное значение накопления i-го вещества.

При определении статистических зависимостей можно воспользоваться интегральной записью уравнения материального баланса в следующей форме:

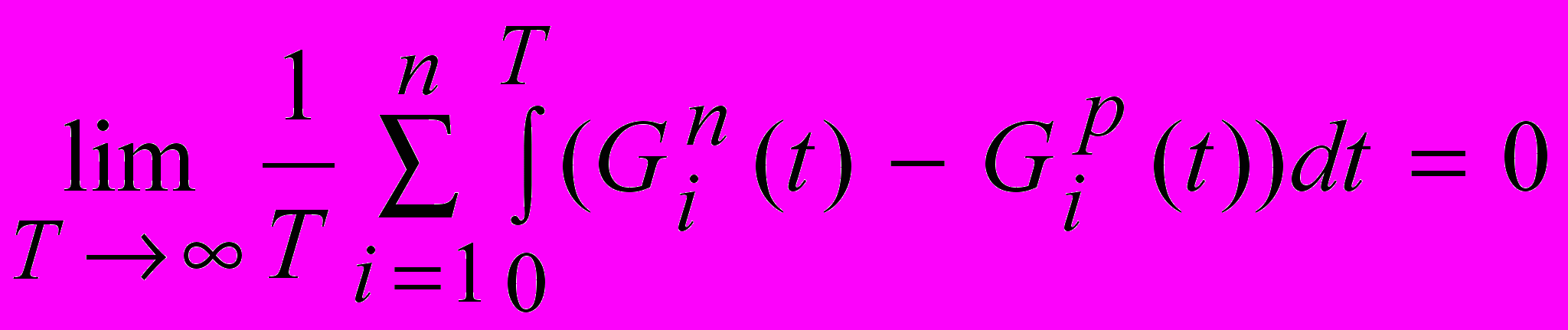(11)

В качестве примера использования уравнения материального баланса рассмотрим получение модели, описывающей смешивающее устройство, в которое поступает два потока веществ, а выходит один смешанный поток.

Материальный баланс в переходном процессе может быть выражен как изменение количества вещества, находящегося в растворе емкости, равное разности между количеством притекающих веществ и количеством вытекающего вещества за одно и то же время:

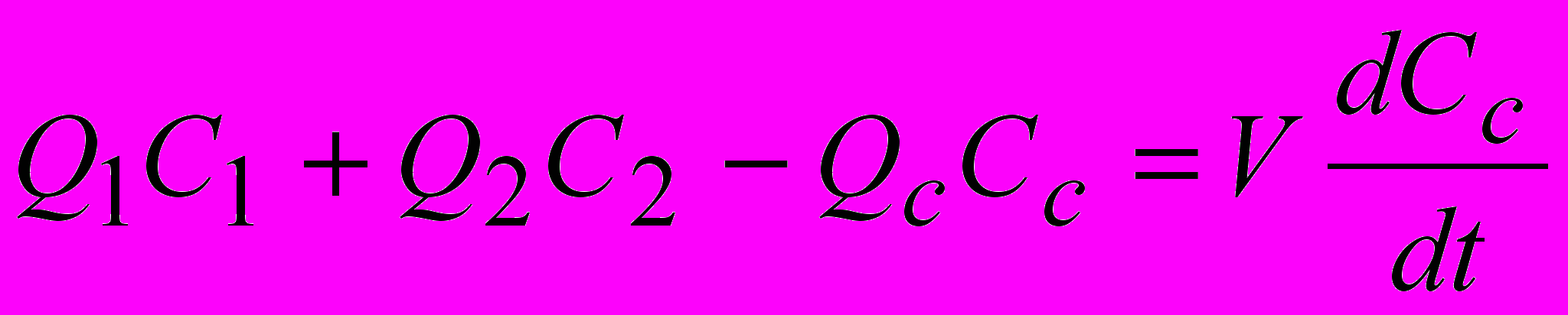, (12)

где Q₁, Q₂ – потоки поступления в смешивающее устройство 1 и 2 вещества соответственно;

C₁, C₂ – концентрация веществ 1 и 2 в приходящих потоках;

Q_c, C_c – расход вещества из емкости и его концентрация;

V – объем смешивающего устройства.

В установившемся режиме количество вносимого вещества должно быть равно количеству выносимого раствора, то есть:

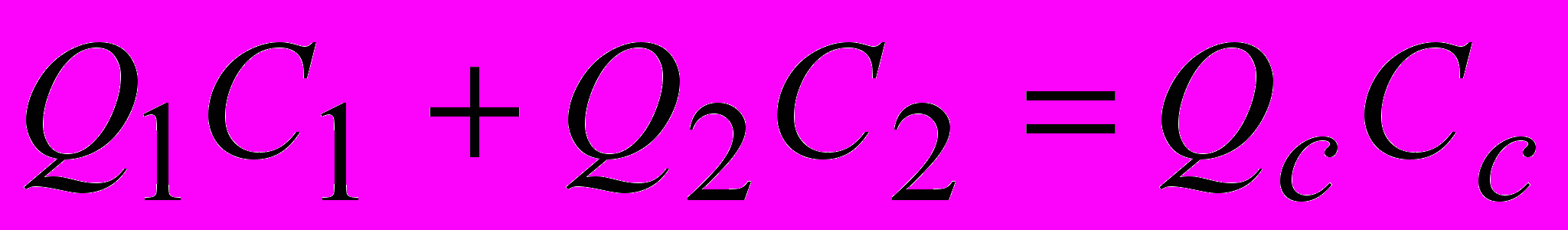(13).

Уравнения (12) и (13) могут быть записаны и в стандартном виде через «вход – выход»:

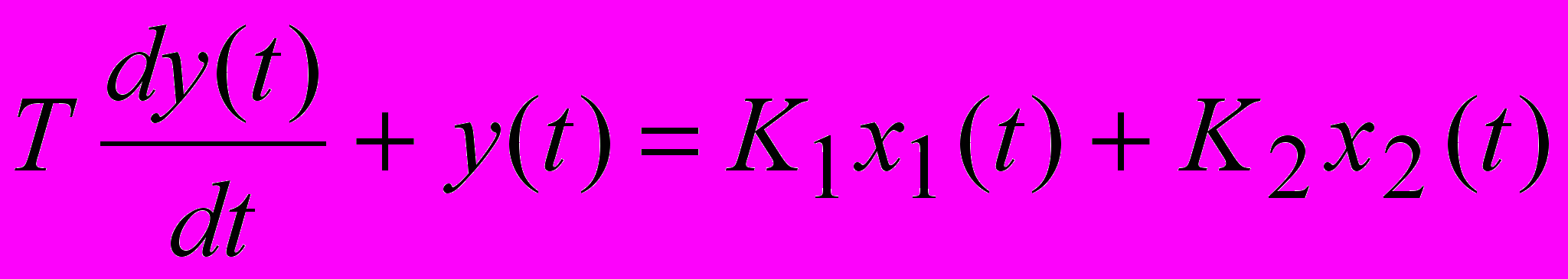, (14)

где ;

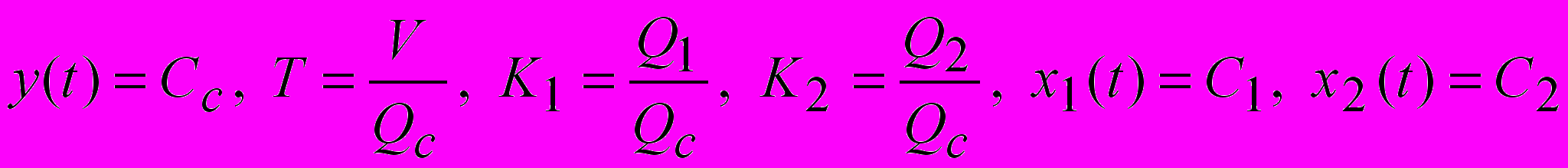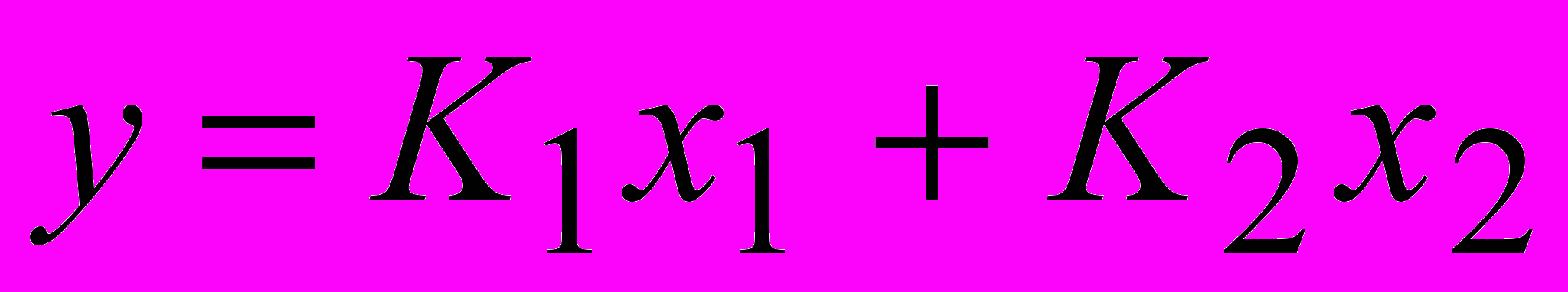(15).

Не менее редко, чем материальный баланс применяется энергетический баланс, основанный на законе сохранения энергии. В установившемся режиме количество энергии, притекающей в объект, равно количеству энергии, уходящей из него. По аналогии с выражением (9) уравнение энергетического баланса может быть записано в виде:

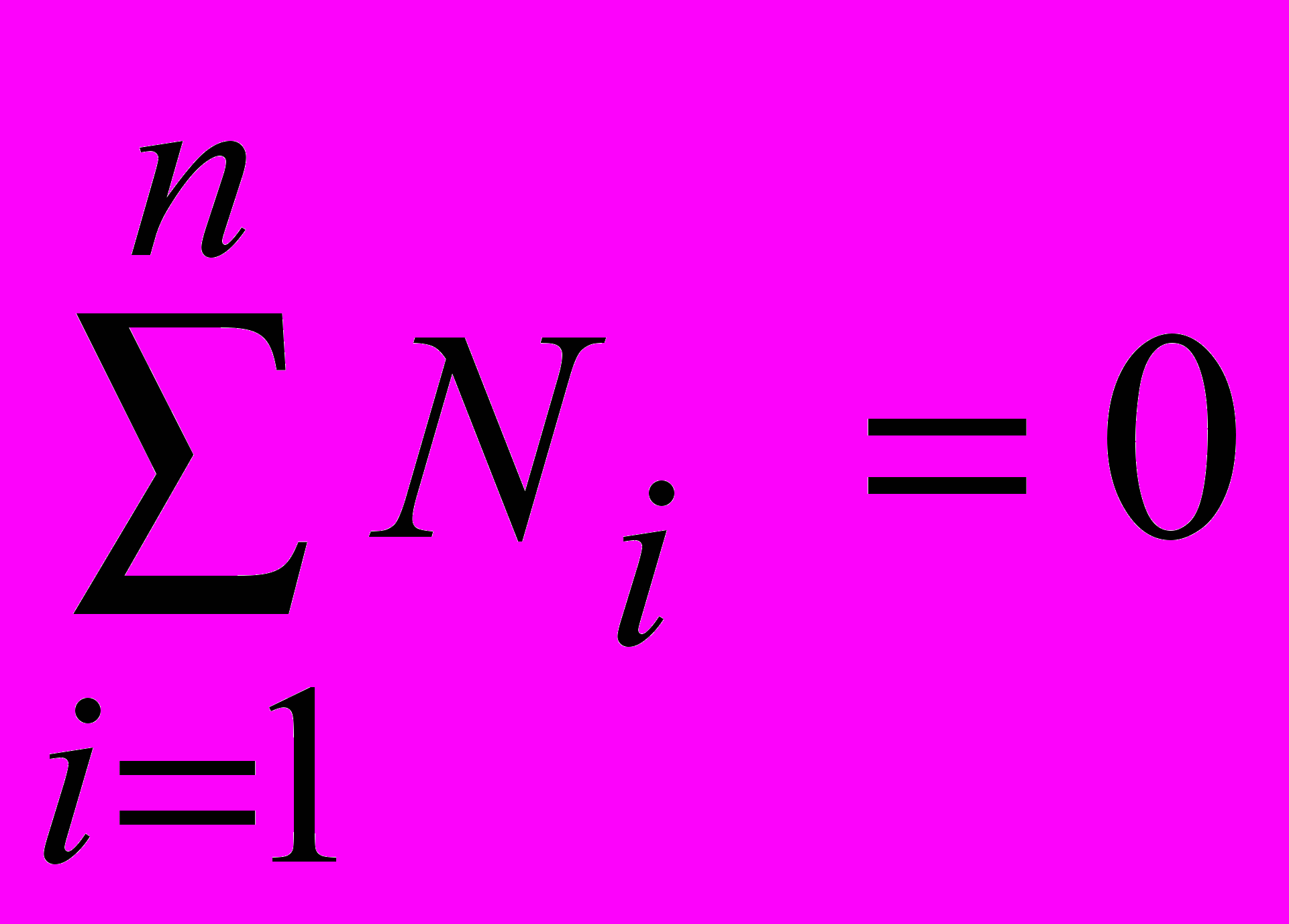, (16)

где 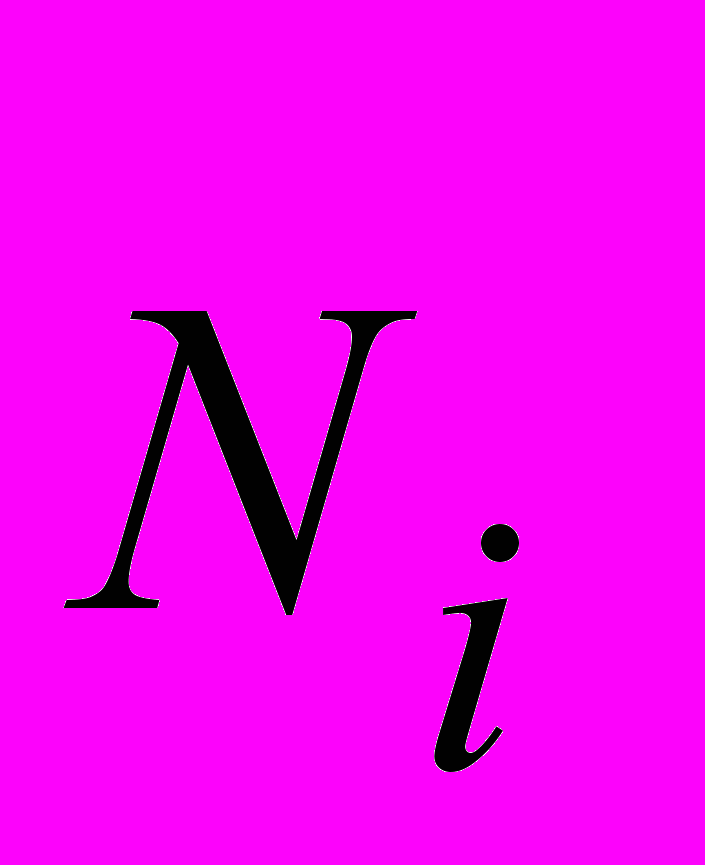- i-й поток энергии (притекающие со знаком +, а уходящие со знаком -).

Примером использования данного типа уравнений является уравнение описания процессов в электрическом колебательном контуре, которое получается на основе 2 закона Кирхгофа (Для любого контура электрической цепи с сосредоточенными параметрами алгебраическая сумма напряжений на ветвях контура равна нулю), отражающего по сути энергетический баланс в электрической цепи:

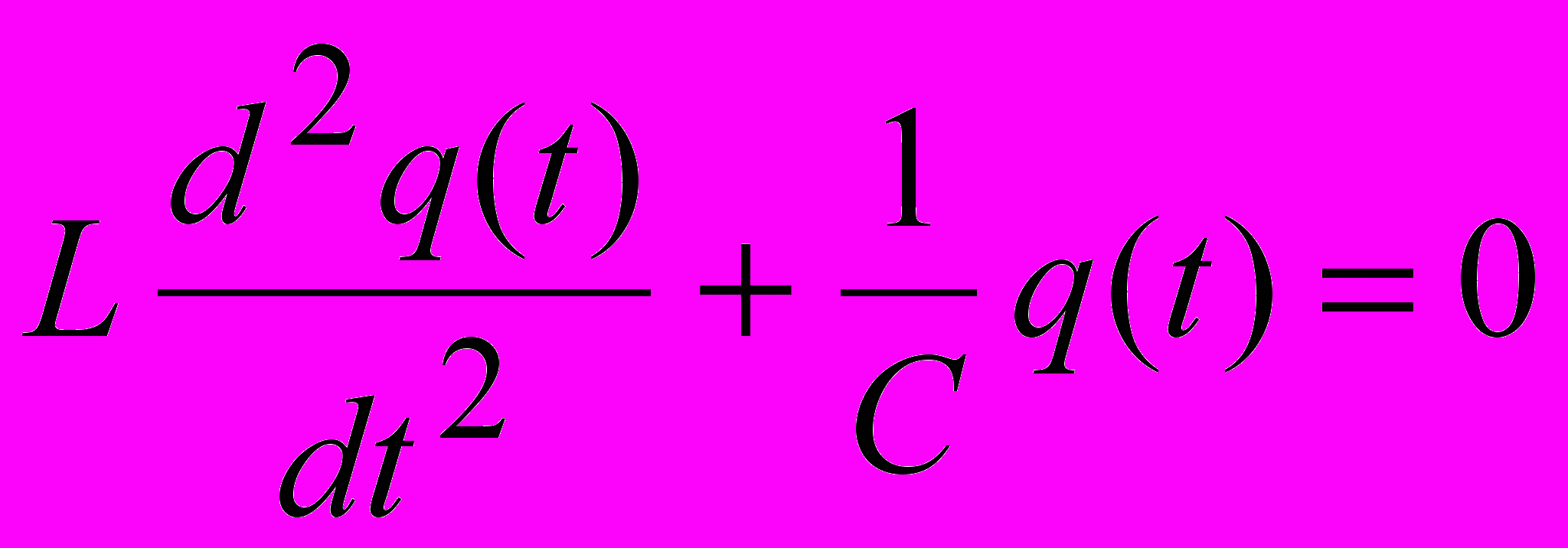, (17)

где q(t) – заряд конденсатора в момент времени t.

Аналитические соотношения, основанные на экономическом балансе, описывают показатели эффективности процессов управления производством. Эти уравнения отражают прибыль, себестоимость продукции, приведенные затраты, производительность и другие экономические характеристики производства.

Кроме указанных уравнений баланса для математического описания объектов также используют:

- уравнения элементарных процессов для локальных элементов объектов (уравнения теплообмена, уравнения химических реакций, уравнения напряжений и токов элементов электрических цепей и т.п.);

- ограничения на параметры процесса (например, при моделировании технологических процессов химического производства на концентрации компонентов в многокомпонентных смесях накладывают ограничения по их значениям от 0 до 1).

Все уравнения, описывающих физические процессы в моделируемой системе можно условно разделить на компонентные и топологические. Компонентные уравнения отражают свойства отдельных элементов моделируемой системы и основываются на физических законах протекания элементарных процессов. Примерами компонентных уравнений для различных систем являются:

- уравнение поступательного движения твердого тела, полученное на основе второго закона Ньютона - 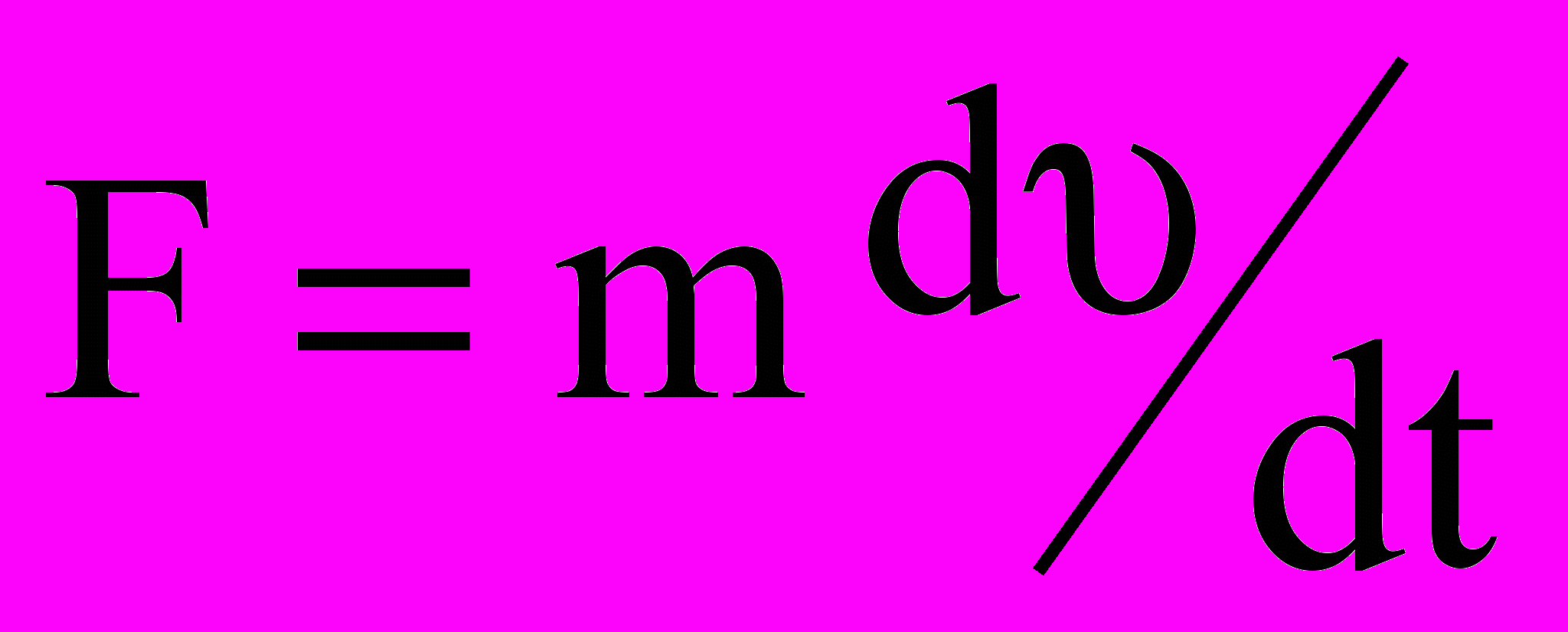, F- сила инерции, m- масса тела, 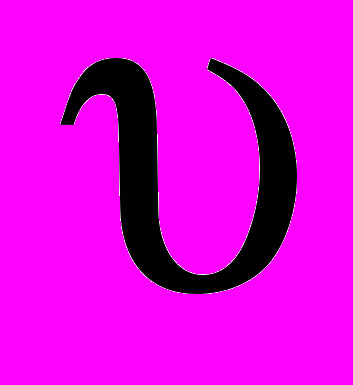- линейная скорость тела;

- уравнение Эйлера для трубопровода постоянного сечения - 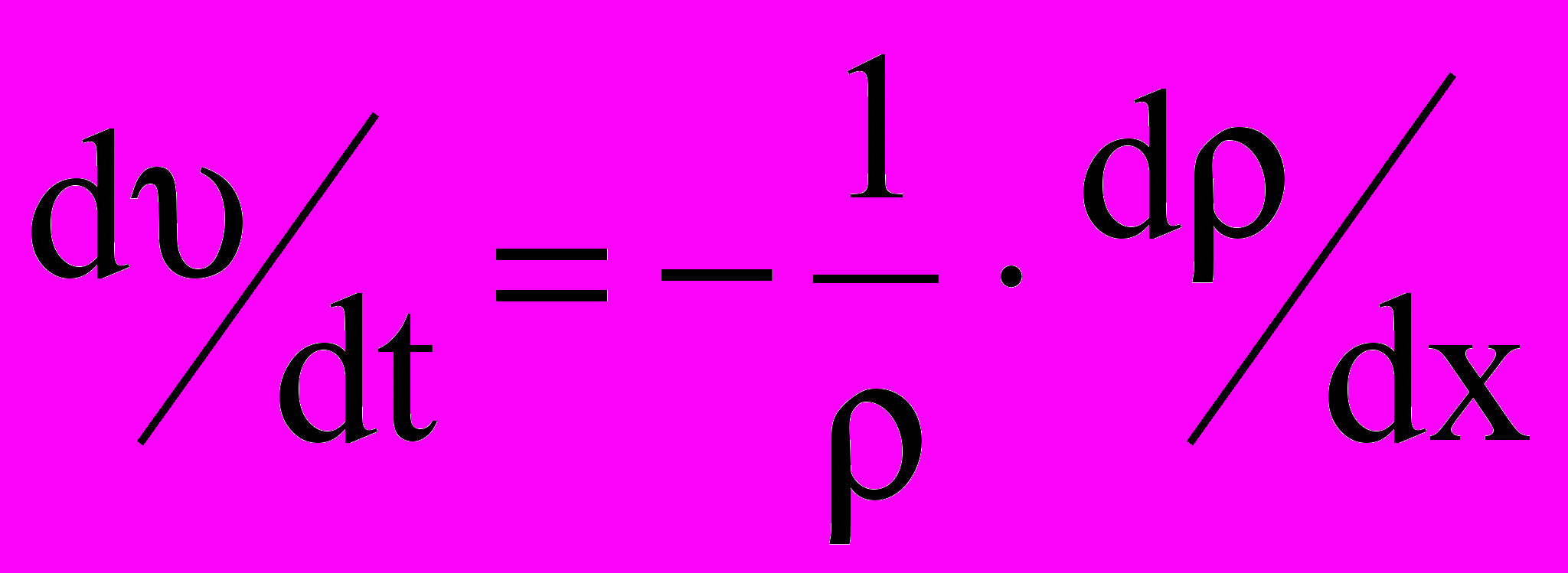, 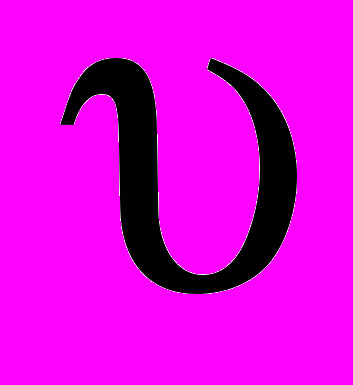- скорость потока жидкости в трубопроводе, - плотность жидкости, х- геометрическая координата;

- уравнение резистора, полученное на основе закона Ома - .

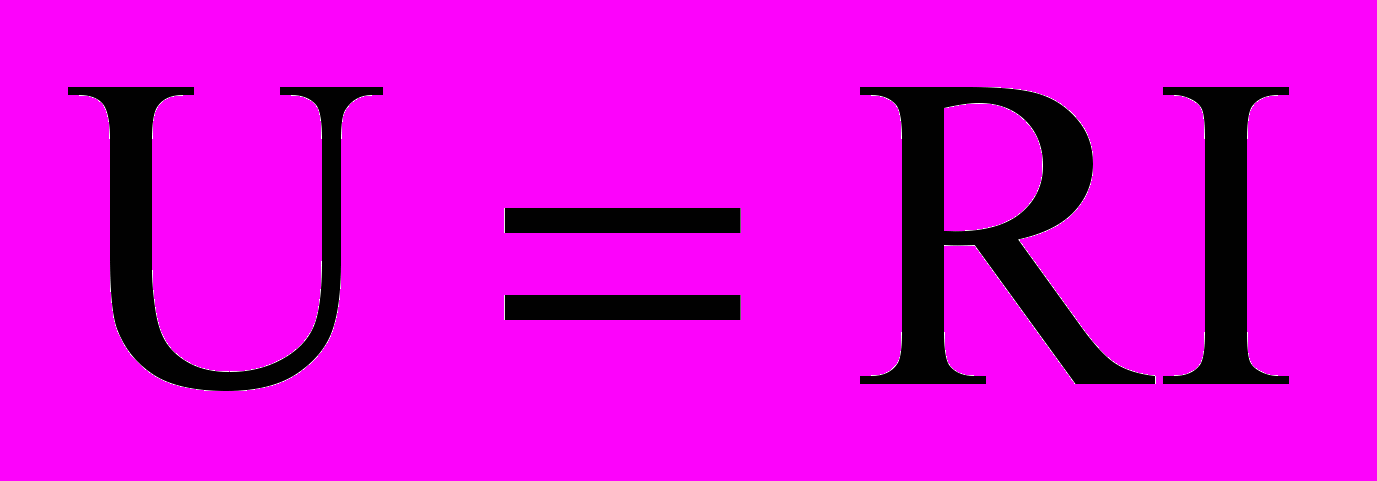Топологические уравнения базируются на физических законах, выражающих условия равновесия и непрерывности фазовых переменных и описывают взаимодействия между элементами моделируемой системы через соотношения между однотипными фазовыми переменными. В частности, к топологическим относятся приведенные выше уравнения баланса. Примерами топологических уравнений для различных систем являются:

- уравнение равновесия сил механической системы, основанное на принципе Даламбера (геометрическая сумма всех сил, приложенных к твердому телу, включая силу инерции, равна нулю) - ;

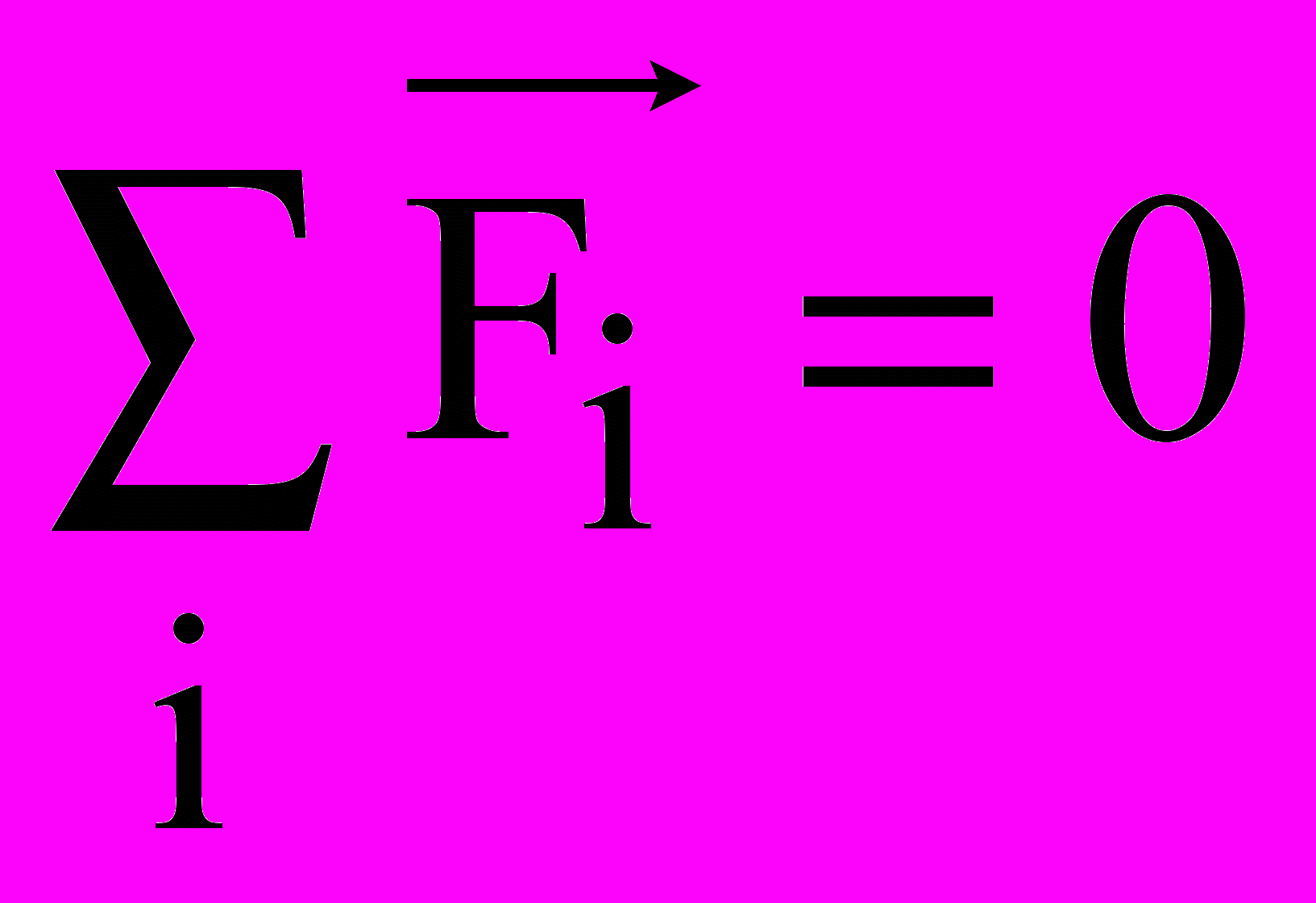- балансное уравнение (13), отражающее условие непрерывности потоков жидкости;

- уравнение (17), базирующееся на втором законе Кирхгофа.

Одним из важнейших свойств аналитического метода построения математических моделей является идентичность структуры уравнений, описывающих совершенно разные процессы. В этом проявляется единство физических законов, несмотря на многообразие форм существования материи. Один и тот же тип элемента в системах различных видов описывается аналогичными по структуре компонентными уравнениями.


Моделирование систем автоматического управления осуществляется, как правило, с использованием алгебраических и дифференциальных уравнений. К алгебраическим уравнениям обычно сводится математическое описание стационарных режимов работы объектов. Для описания динамики исследуемых объектов используют дифференциальные уравнения.

Рассмотрим решение уравнения динамики САУ операционным методом при ненулевых начальных условиях в общем виде. Пусть уравнение имеет вид:

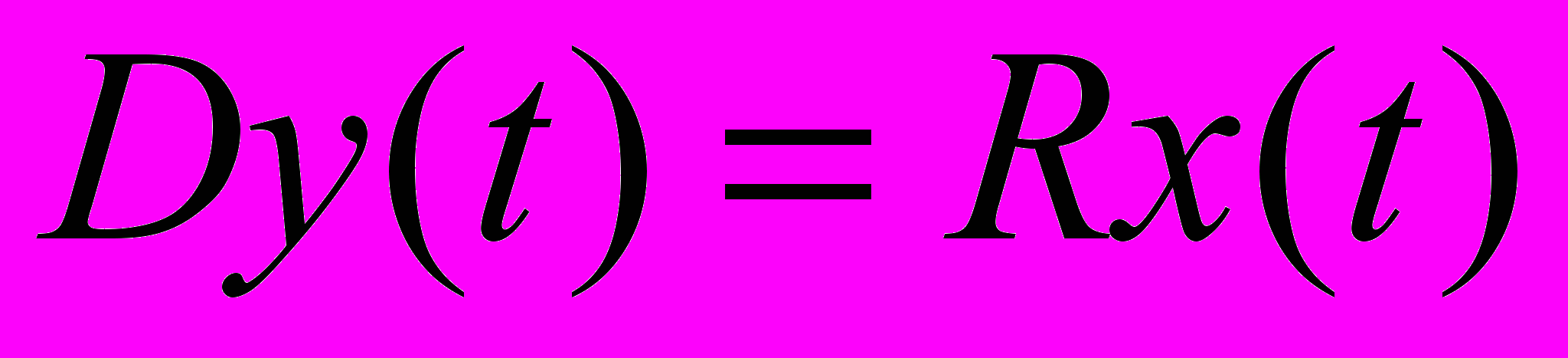, (22)

где ,

, .

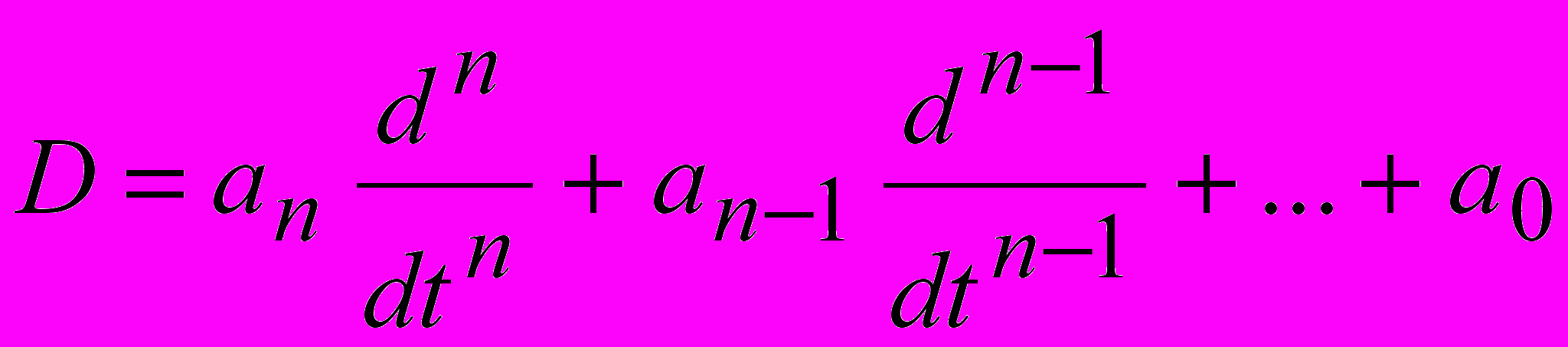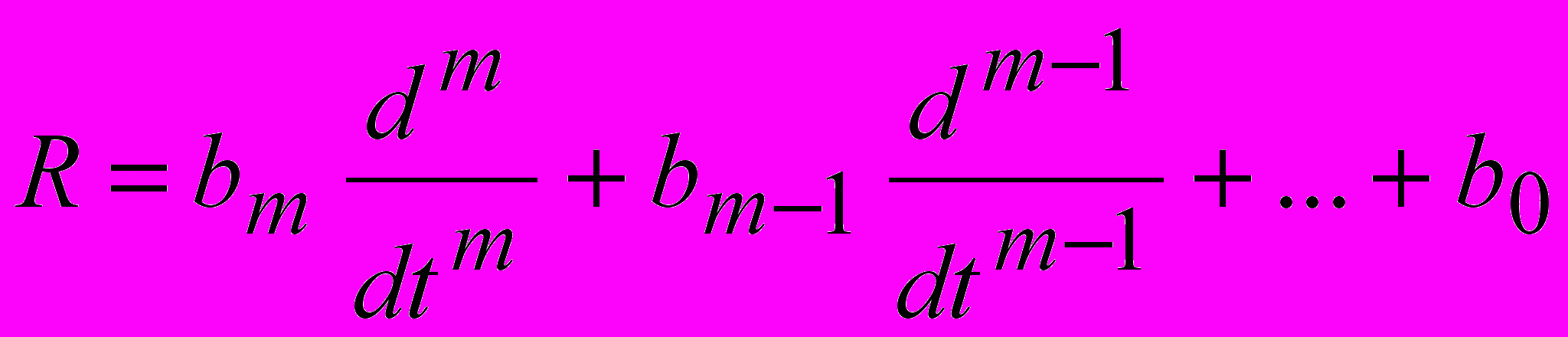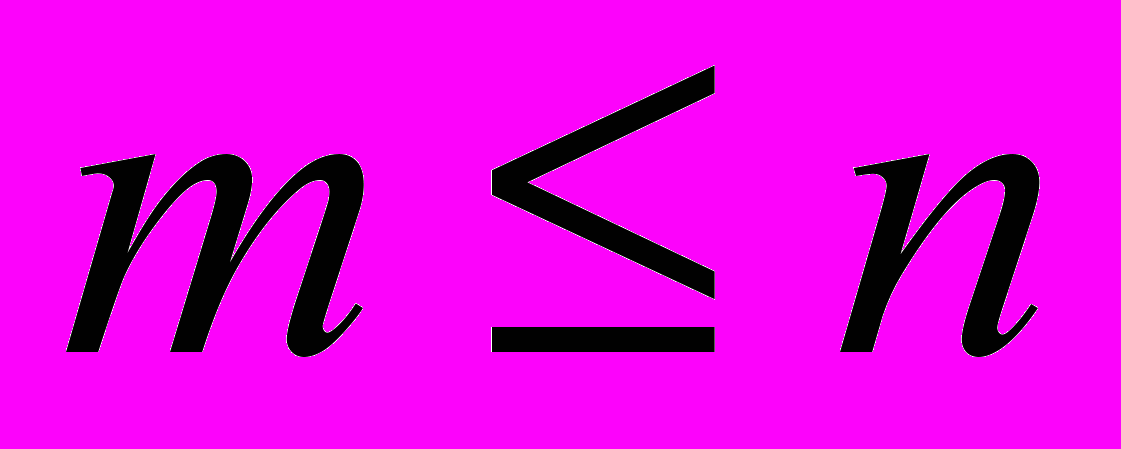Уточним понятие начальных условий для уравнения (22). Под начальными условиями понимают совокупность начальных значений искомой функции y(t) и ее производных до (n-1)-й включительно. Различают левые (y(-0), y’(-0) …) и правые (y(+0), y’(+0) …) начальные условия, различие между которыми заключается в направлении подхода к точке t=0. Левые начальные условия (называемые также предначальными) характеризуют систему до начала динамического процесса, создаваемого воздействием x(t). Если в момент времени t=0 входное воздействие и его производные отличны от нуля и происходит мгновенное изменение выходной величины, то начальные условия будут отличны от предначальных. ( При этом количество начальных условий, отличных от предначальных определяется видом передаточной функции объекта W - чем меньше степень числителя W отличается от степени знаменателя, тем большее число начальных условий отличается от предначальных ).

Если заданы предначальные условия, то преобразование уравнения (22) по Лапласу в соответствии с известной теоремой дифференцирования оригинала (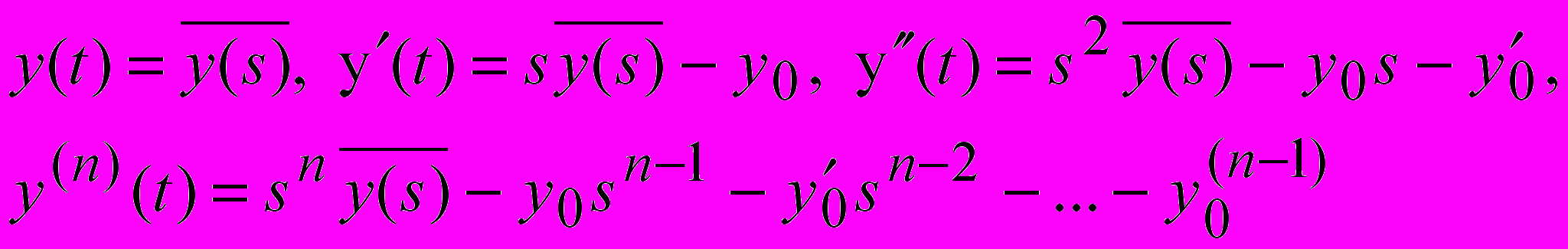) и с учетом того, что при t=-0 внешнее воздействие еще не влияет на систему будет иметь вид:

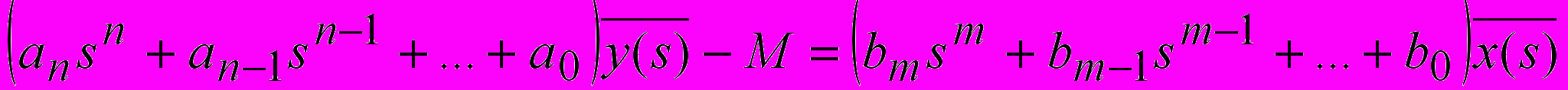, (23)

где 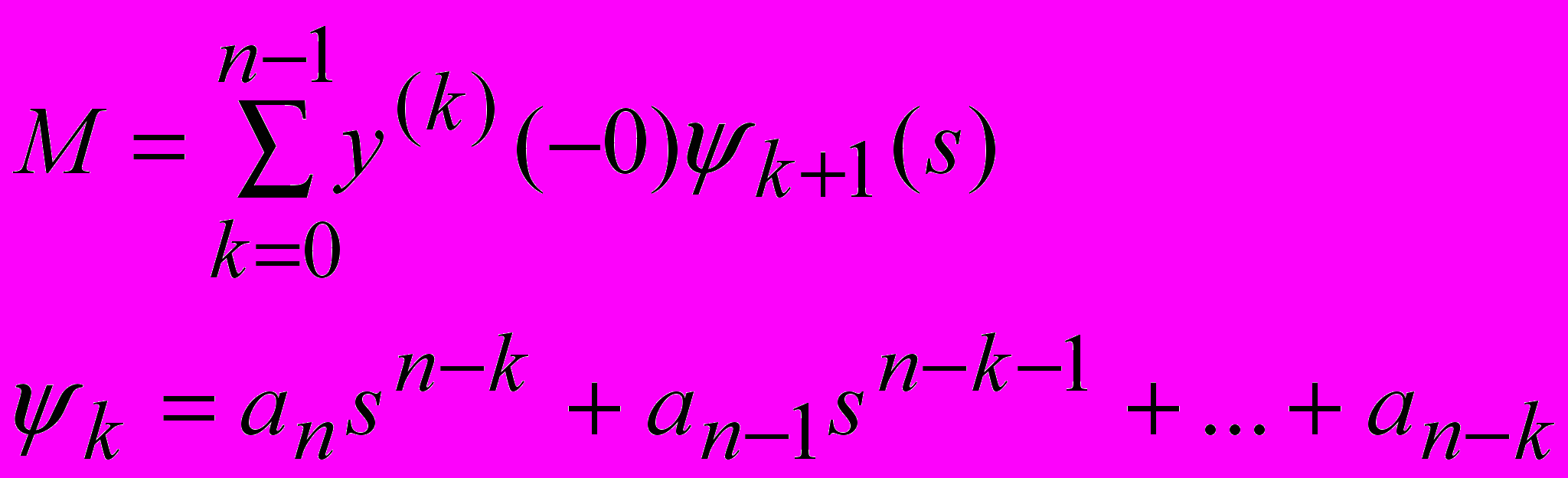(24)

Если выражение (24) разложить на суммы и сгруппировать слагаемые относительно множителей «s в степени», то получим следующее выражение для М:

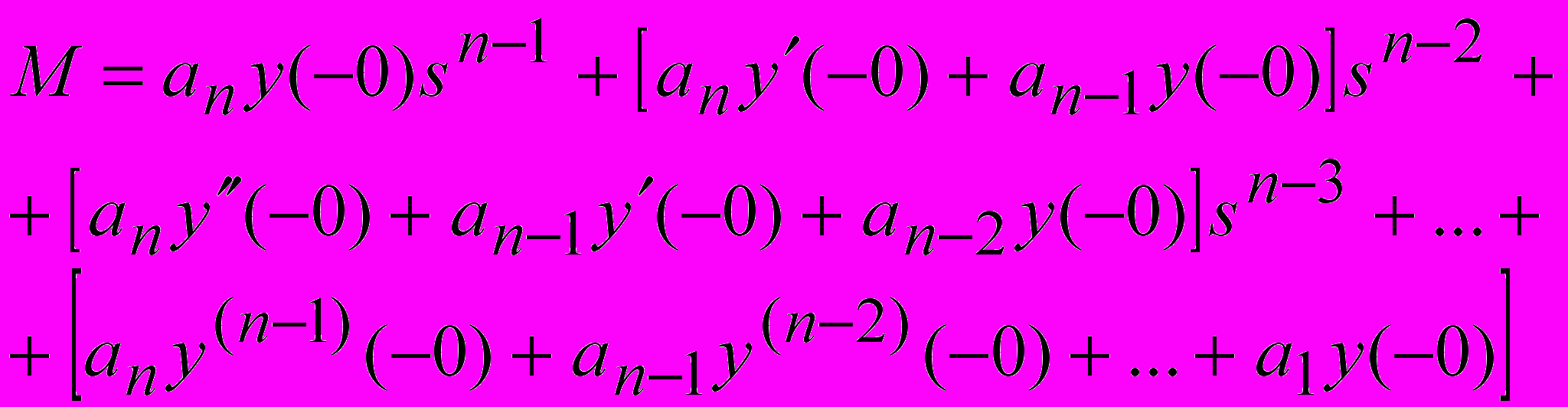(25)

Из уравнения (23) легко найти изображение искомой функции:

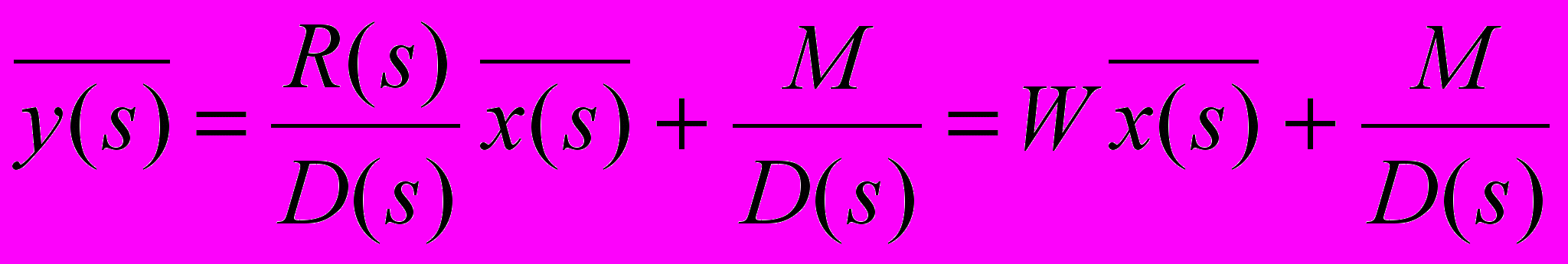(26)

Если передаточная функция W имеет полюсы (корни полинома D(s)) 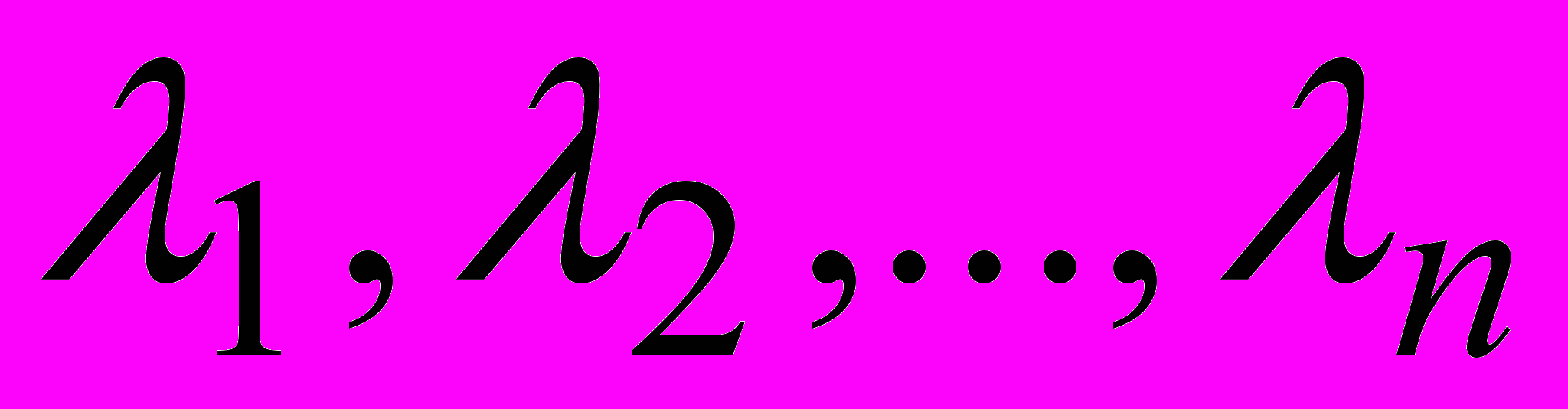и нули (корни полинома R(s)) 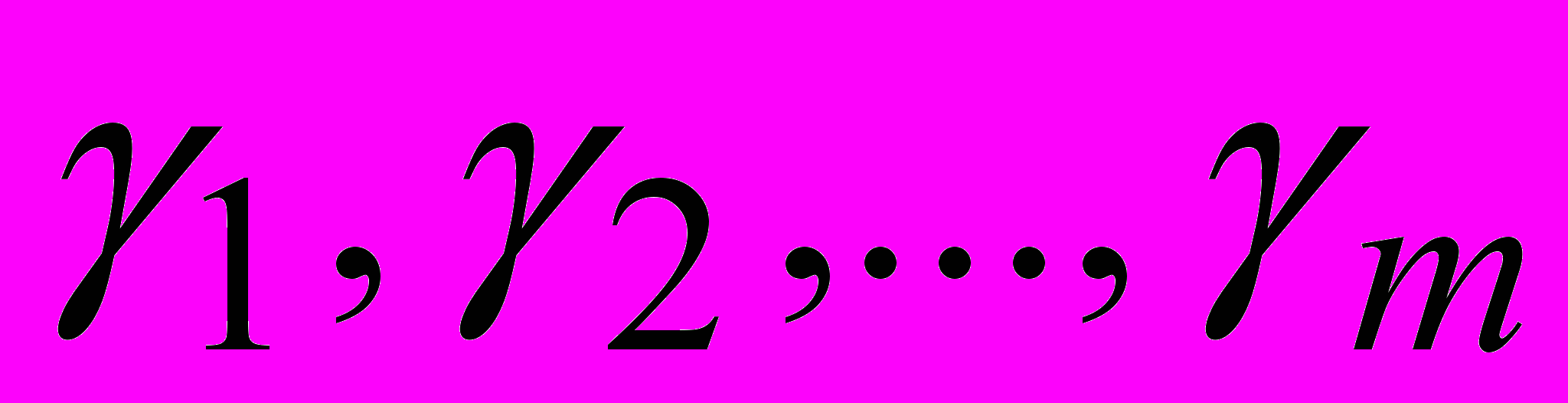, а изображение 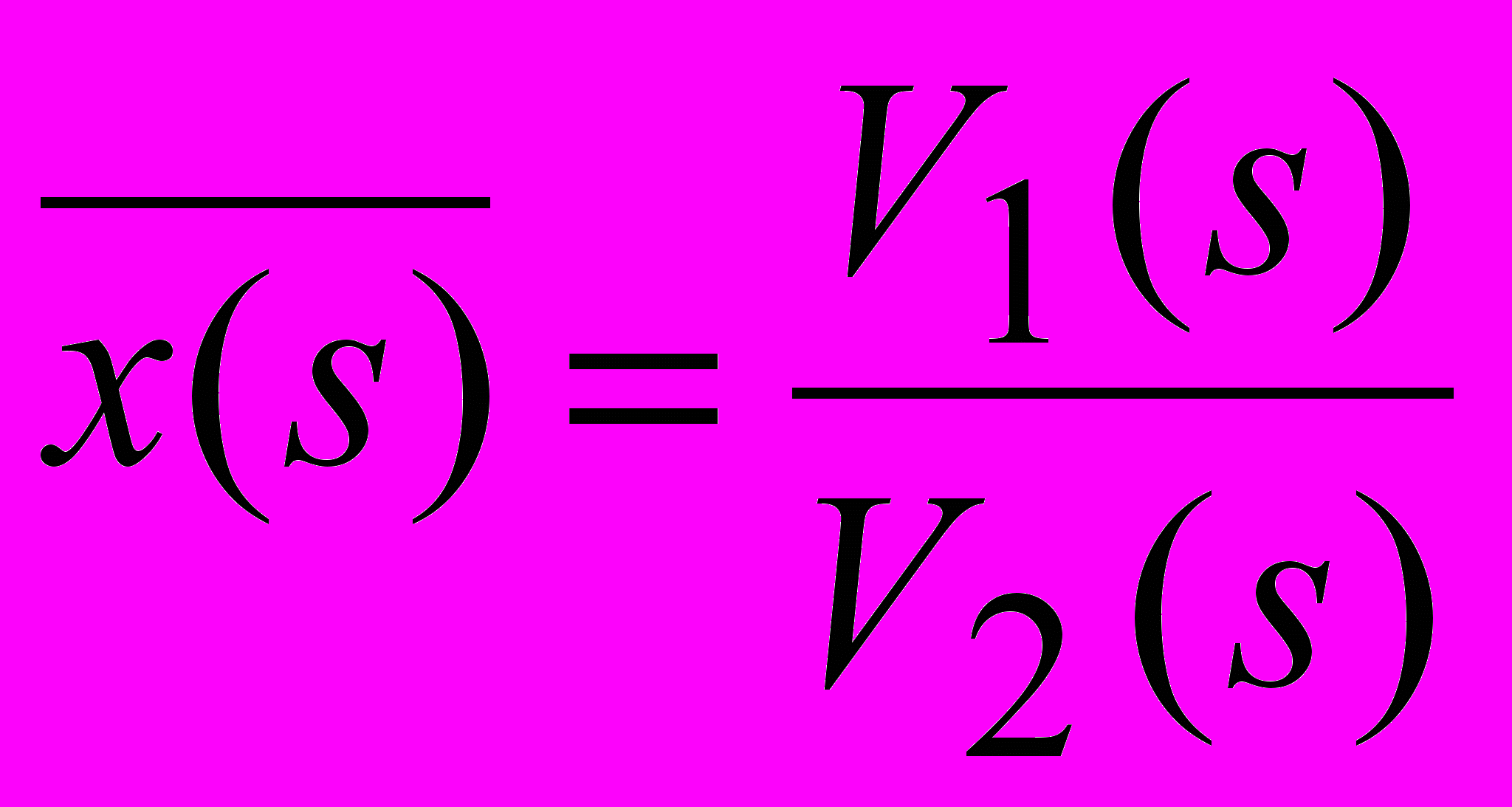имеет полюсы (корни полинома V₂(s)) 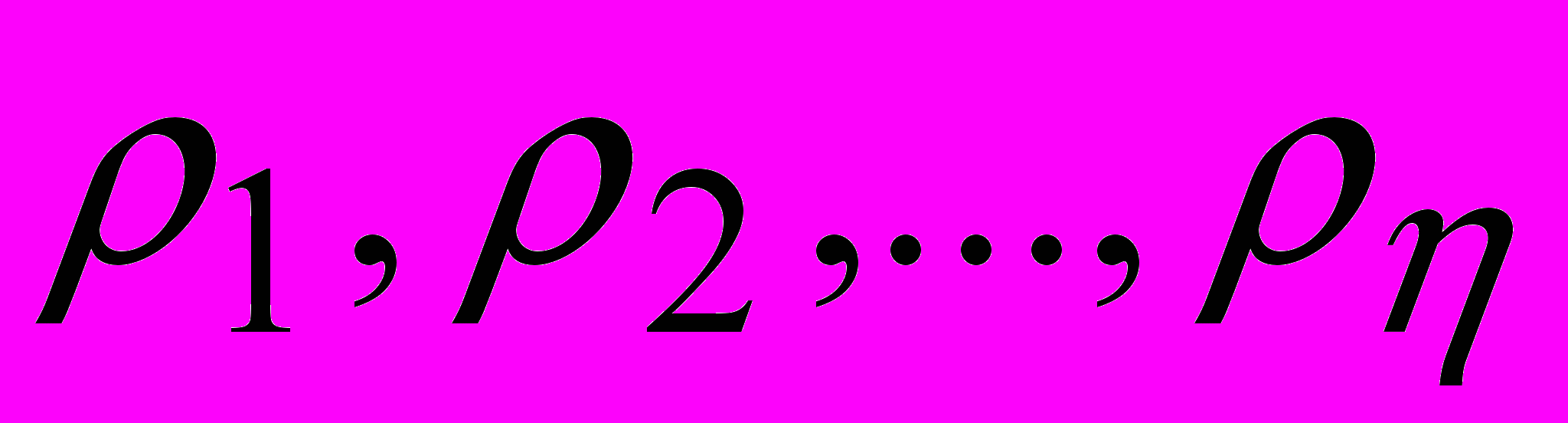и нули (корни полинома V₁(s)) 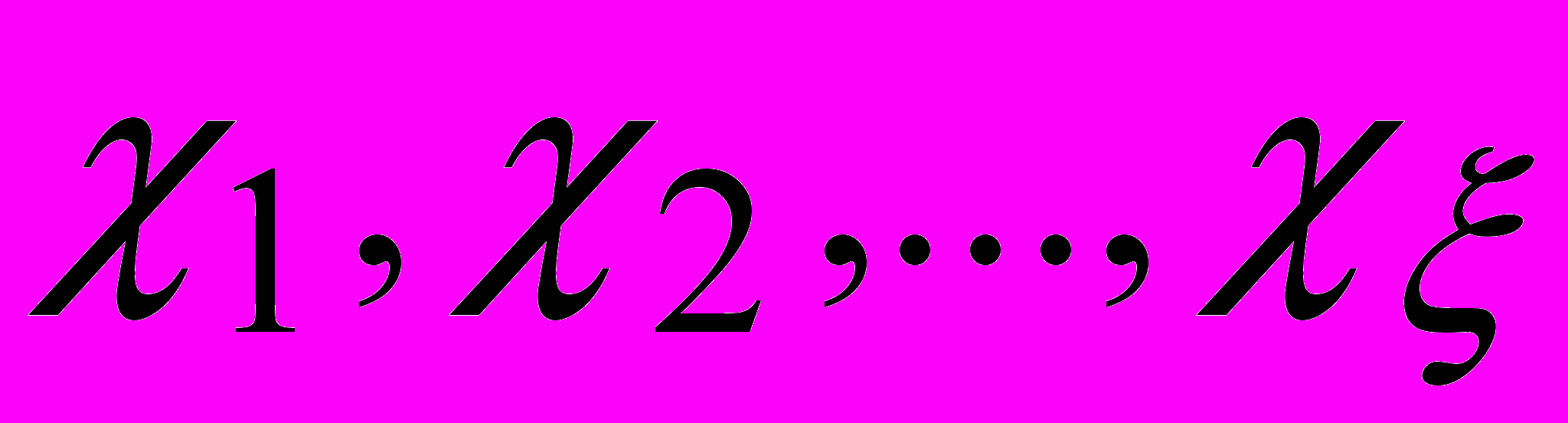, то выражение (26) можно записать в виде:

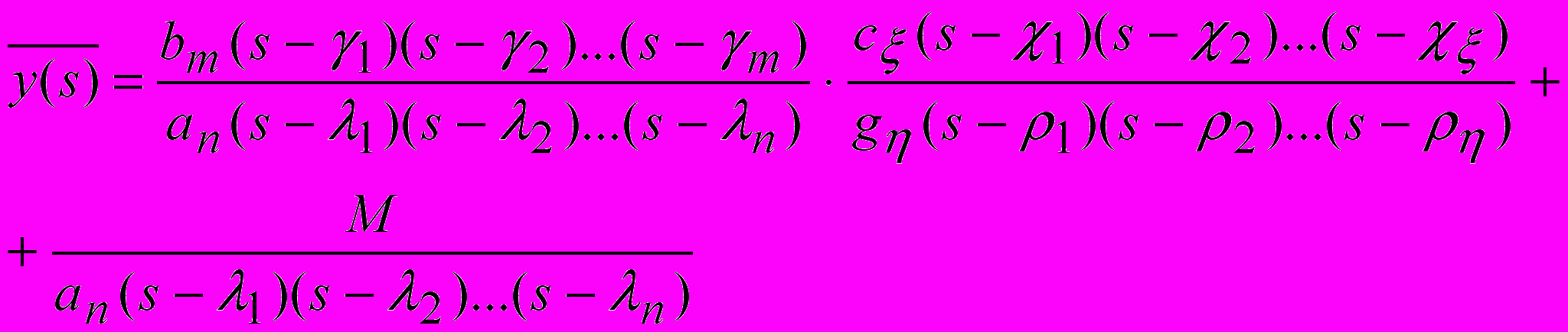(27)

Если заданы начальные условия, то осуществляя преобразование по Лапласу уравнения (22) необходимо учитывать как начальные значения искомой переменной и ее производных, так и начальные значения внешнего воздействия и его производных. Тогда после преобразования по Лапласу уравнение (22) примет вид:

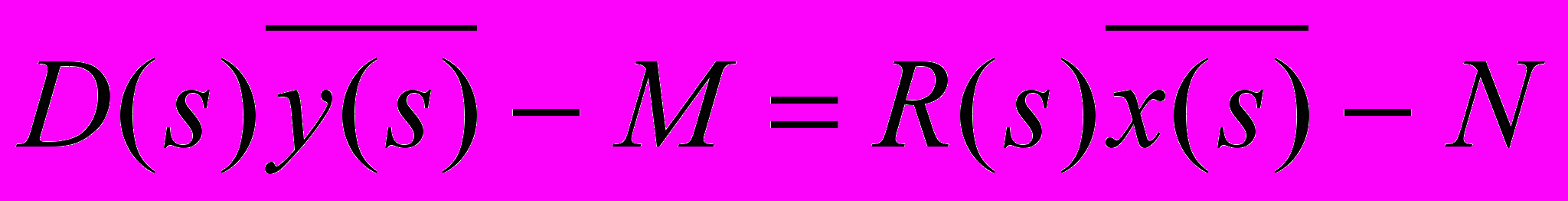, (30)

где ,

.

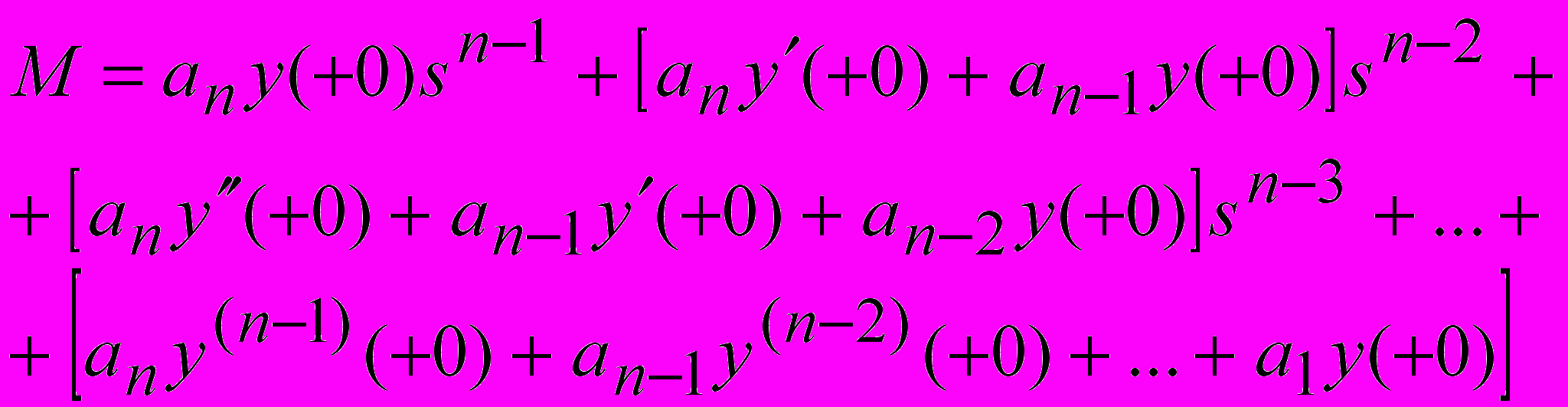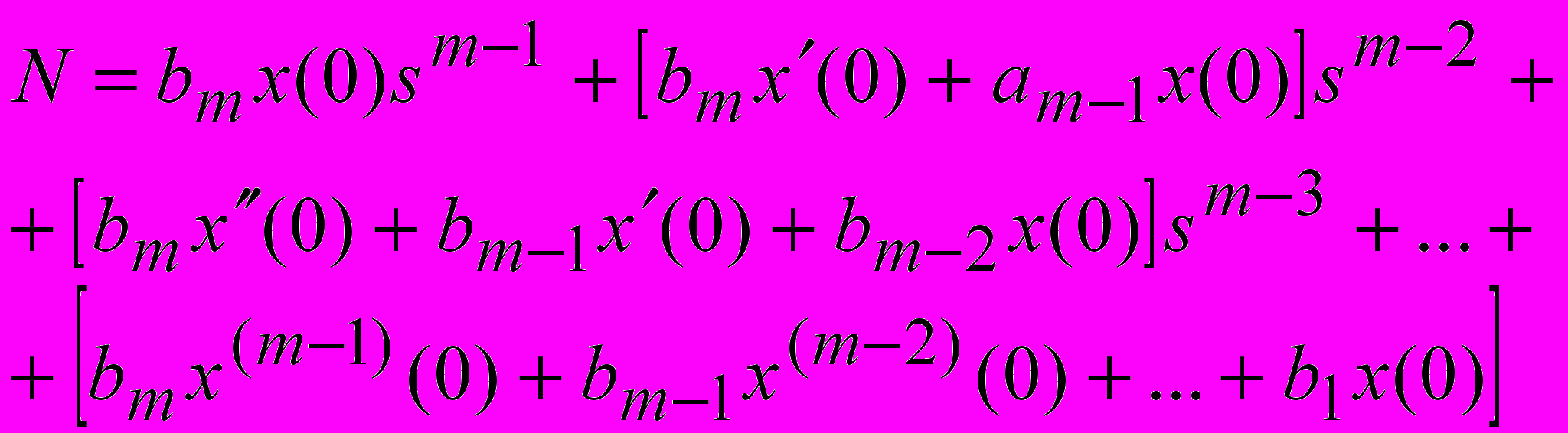Начальные значения 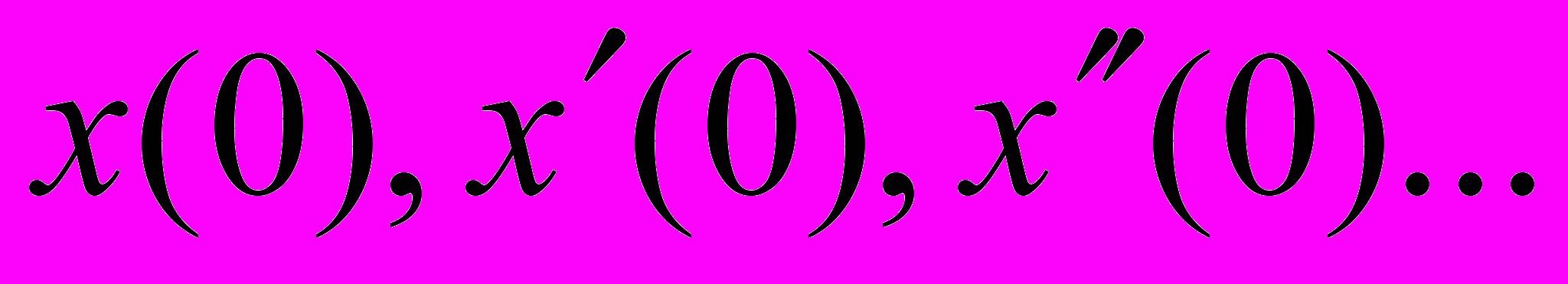определяются в результате подстановки t=0 в функцию x(t) и ее производные.

Заключительным этапом решения дифференциального уравнения операционным методом является отыскание оригинала (искомой функции времени) по изображению. Для отыскания оригинала по известному изображению в операционном исчислении используются так называемые теоремы разложения и теорема свертывания оригиналов, с которыми вы можете познакомиться в специальной литературе по операционному исчислению.

Исходя из вышеизложенного, методика построения математических моделей объектов аналитическим методом сводится к следующей последовательности действий:

1. Физическое описание объекта моделирования. При этом выделяют «элементарные» процессы, протекающие в объекте моделирования, которые подлежат математическому описанию, и формулируют основные допущения, принимаемые при их описании, а также определяются фундаментальные законы, которые должны быть положены в основу составления математических уравнений исследуемого объекта (системы).
   
2. Составление уравнений статики или динамики объекта моделирования. Данный этап включает составление компонентных и топологических уравнений на базе выделенных на первом этапе физических законов в алгебраической или дифференциальной форме.
   
3. Определение начальных и граничных условий моделирования. Данные условия выбираются исходя из особенностей функционирования моделируемого объекта, обусловленных технологическим процессом, в котором он задействован или для которого он разрабатывается.
   
4. Выбор метода решения уравнений математического описания объекта, разработка алгоритма и составление программы. При выборе метода решения системы уравнений обычно руководствуются требованиями обеспечения максимальной быстроты получения решения.
   
5. Проверка соответствия (адекватности) модели объекту. Математическая модель объекта является лишь его определенным в рамках принятых допущений аналогом. Адекватность модели проверяется путем сравнения значений переменных, получаемых на модели и на реальных объектах, и проверки выполнимости критериев адекватности, которые базируются на методах дисперсионного анализа и анализа остатков, существо которых мы с вами рассматривали на прошлых лекциях.
   
6. Изучение свойств объекта моделирования на математической модели. Данное изучение осуществляется в целях определения оптимальных условий протекания процесса, оптимизации управления процессом, а также выработки решений на создание новых объектов.
   

При проектировании принципиально новых процессов и объектов аналитический метод является единственным приемлемым методом математического описания исследуемых объектов.