Лекция 1 Виды математических моделей сложных систем

Вид материала

Лекция

Содержание Переменные, которые претерпевают изменения на каждой ступени, называются переменными состояния. Регрессионный анализ. Корреляционный анализ. Многомерный статистический анализ. Прямой метод вычислений. Классический метод дифференциального исчисления. Метод множителей Лагранжа. Вариационное исчисление. Линейное программирование Квадратичное программирование. Нелинейное программирование. Принцип максимума. (принцип быстродействия)

Подобный материал:

• Лекции по дисциплине «Математическое моделирование» для студентов и магистрантов специальности, 21.92kb.
• Рабочей программы дисциплины Методы управления развитием сложных технических систем, 23.23kb.
• Лекция №8 Построение математических моделей технологических объектов и систем аналитическим, 98.99kb.
• Программа по курсу " Моделирование систем управления, 30.71kb.
• Утверждаю, 89.56kb.
• Магистерская программа: Энергетика теплотехнологии (кафедра эвт); Форма обучения: очная, 55.97kb.
• Исследование математических моделей, 9.9kb.
• План изучения дисциплины № п/п, 155.57kb.
• Самостоятельная работа 2 часа в неделю всего часов, 42.13kb.
• 1. Введение Основы анализа данных. Методология построения моделей сложных систем. Модель, 399.94kb.

ЛЕКЦИЯ 1

Виды математических моделей сложных систем


Одной из проблем современной науки является разработка и внедрение в практику математических методов исследования динамики (во времени)функционирования сложных систем, к которым относится ЛПК.

Под математическим моделированием будем понимать исследование процессов как математических моделей.

Математическая модель должна воспроизводить исследуемый процесс с сохранением его физической природы (физика-наука о природе).

Математическое моделирование обладает широкими возможностями аналитического обобщения различных процессов (механических, тепловых, электрических и др.), описывая их одинаковыми математическими соотношениями.

Примеры: колебания механического (пружинного) маятника и электрических зарядов в колебательном контуре.

Немного терминологии:

Процесс- последовательное состояние системы во времени.

Система- комплекс механизмов, машин, оборудования и т.д..

Состояние системы параметризируется во времени, и они становятся характеристиками процесса.

При математическом моделировании необходима информация не только о параметрах системы, но и о начальных и граничных состояниях, необходимых для решения интегро-дифференциальных уравнений, описывающих процесс.

Математическая модель реального процесса это математический объект, поставленный в соответствие реальному динамическому объекту.

Математическая модель это совокупность формул, уравнений, неравенств, логических условий и т.д..

В силу различных причин характеристики процесса становятся случайными функциями.

Аналитическое исследование процесса предполагает такое исследование, при котором результат достигается аналитическими методами: построение формул, уравнений и т.д; оно является первым необходимым шагом.

Моделирование с учетом случайных процессов: средние, дисперсии, корреляции и т.д.

Математическая модель является результатом формализации процесса. с необходимым приближением к реальному.

Фазовое пространство процесса.

Математическая модель: система соотношений в целом. Разбиение процесса на подпроцессы. Анализ-синтез систем. Подпроцессы подбирают подходящие математические схемы: динамические, массового обслуживания, вероятностных и т.д..

Лесопромышленное производство состоит из последовательных выполняемых технологических операций.

Построение математической модели как сложного процесса в целом, так и для составляющих его элементарных актов в конечном счете сводится к получению соотношений, описывающих зависимость характеристик процесса от соответствующих параметров.

Случайные величины. Законы распределения случайных величин.

Современным производственным процессам свойственна частичная или полная синхронизация последовательно выполняющихся операций. Интервалы времени, характеризующие синхронность, часто являются случайными. Это приводит к нарушению синхронности процесса в целом, когда операции или перегружаются, или недовыполняются.; возникает или очередь или простой. Процесс флуктуируется во времени, создается своеобразный динамический режим занятости производственного оборудования и машин.

Системы массового обслуживания.

Надежность комплексов ( отказы, за критические параметры, износ деталей машин и т.д.).

Содержательное описание сложных систем.

Эргодический процесс: позволяет моделирование большого количества реализаций заменить одной достаточно длинной реализацией, так что результаты моделирования по нескольким реализациям статистически равнозначны результатам моделирования по одной реализации (достатачно длинной). При моделировании эргодических процессов обеспечение заданной точности (при заданной достоверности) достигается достаточно большой длинной реализации (точность зависит от длительности реализаций).

Показатели эффективности сложного процесса, как показатели свойства самого процесса, показатели количественной меры свойства производственных процессов.

Производительность. Мощность оборудования. Средние показатели.

Модернизация процесса сложных систем. Оптимизация.

Синергетический принцип функционирования.

Статистический детерминизм: определяющие факторы

детерминированы, сопутствующие – случайные.

Гармония по представлению древних греков – соединение частей в единое целое.

Этапы математического моделирования:

- формулирование законов, связывающих основные объекты модели,

- исследование математических задач, к которым приводят

математические модели, это прямая задача, т.е. получение исходных

данных результатов для сопоставления с получаемыми результатами,

- адекватность принятой модели, обратная задача,

- развитиемодели.


ЛЕКЦИЯ 2


Многоступенчатые управляемые процессы.


Многоступенчатый управляемый процесс можно рассматривать как абстрактное понятие, с помощью которого можно представлять многие аспекты человеческой деятельности. Процессы могут быть как детерминированными, так и стохастическими. Поскольку многоступенчатый управляемый процесс представляет собой совокупность определенного числа ступеней, его природа определяется типом ступеней, которые его образуют, и способами их соединения.

Каждая ступень может представлять собой реальный или абстрактный объект (технологические операции, периоды времени, экономическая деятельность и т.д.), в котором происходят определенные изменения.

Переменные, которые претерпевают изменения на каждой ступени, называются переменными состояния.

Желаемые изменения с переменными состояния достигаются путем манипуляции с управляющими переменными.

Изменения, происходящие в каждой ступени , полностью определяются системой уравнений преобразования.

Ступень может иметь несколько входов и выходов, по которым в неё поступают или выводятся значения переменных состояния. По числу входов и выходов ступени классифицируются:

- ступень с одним входом и выходом называется связующей,

- ступень с несколькими входами и одним выходом – смесительная;

- ступень с одним входом и несколькими выходами – разделительная,

- ступень с несколькими входами и выходами – сложная.

Процессы разделяются на стационарные (гомогенные) и нестационарные (гетерогенные).

В задачах оптимизации многоступенчатых управляемых процессах целевая функция, подлежащая максимизации или минимизации, представлена как функция переменных состояния на выходе последней ступени, зависящая от условий сопряжения всех ступеней процесса.

Пример. В распоряжении имеется определенное количество ресурса ( сырье, капитал, технологии и т.п.). Он может быть использован различным образом, каждому из которого соответствует определенный результат. Целевая функция - результирующий доход.

Регрессионный анализ. Регрессионные зависимости являются одними из самых распространённых видов моделей, описывающих зависимость одной случайной величины от других случайных или не случайных величин. Регрессионная зависимость, или регрессия, записывается в виде функции, линейной или нелинейной, которая описывает зависимость «в среднем», т.е. приближенно с различной степенью приближения.

Слово «регрессия» введено ученым-естественником Гальтоном.

В инженерной практике приходится решать задачу зависимости наблюдаемой случайной величины У от одной или нескольких случайных (неслучайных) величин Х₁, Х₂, Х₃ ,… . Величина У называется откликом, Х – факторами, влияющими на отклик, а (У,Х) – выборкой. Для определения зависимости отклика от факторов вводится между ними функциональная связь

У = f (Х).

Общая постановка задачи регрессионного анализа: по выборке (У,Х) наблюдаемых (экспериментальных) данных о значениях факторов и отклика

У_к = f (Х_к ) + о_к, к = 1, 2, 3,…,

где о – случайная величина, называемая ошибкой регрессионной модели,

требуется построить оценку функциональной зависимости У = f(Х) , как закономерной зависимости при наличии случайной составляющей.

Гауссовая модель. Метод наименьших квадратов: минимизация суммы квадратов откликов.

Корреляционный анализ. Раздел математической статистики, исследующий зависимость между случайными величинами на основе различных выборочных оценок коэффициентов корреляции.

Применение методов корреляционного анализа позволяет произвести отбор среди факторов с целью выявления наиболее информативных из них, наиболее существенно влияющих на отклик.

Коэффициент корреляции Пирсона

r = [n^-1Σxy – ([xy)_cp ] / [(n^-1Σx² – x²_cp)(n^-1Σy² – y²_cp)]^1/2 .

Выборочный множественный коэффициент корреляции

r_yz = [n^-1Σ(y – y_cp)(z – z_cp)] / [(n^-1(Σ(y – y_cp)² x²_cp)(Σ(z – z_cp)²]^1/2 ,

z = b₀ + b₁x₁ + b₂x₂ +……+ b_kx_k .

Многомерный статистический анализ. Раздел математической статистики, который исследует многомерные наблюдения: наблюдение представляется не одним числом, а целым набором чисел, которые определяют ортогональную систему координат пространства наблюдений.

Дискриминантный анализ Совокупность объектов разбита на группы. Представление группы.

Кластерный анализ. Разбиение «схожих» групп. .


Лекция 3


Математические модели оптимизации


Оптимизация представляет собой математическую задачу максимизации или минимизации некоторой функции нескольких переменных при наличии ограничений.

Процессу оптимизации соответствуют этапы:

1. Определение цели, возможностей системы, независимых переменных,, ограничений и внешних воздействий.
   
2. Анализ и упрощение: исключение второстепенных переменных и несущественных процессов, представление процесса в виде ступеней.
   
3. Моделирование или математическая запись целевой функции и уравнений преобразования. Решение.
   
4. Проверка: соответствие теоретических уравнений реальной системе (адекватность).
   
5. Оптимизация: определение экстремума функций.
   

Прямой метод вычислений. Если известна функциональная связь между целевой функцией и управляющей переменной, то можно непосредственно вычислить значение целевой функции для некоторого фиксированного значения управляющей переменной.

Эффективен при наличии одной управляющей переменной или нескольких в небольшом диапазоне изменения.

Классический метод дифференциального исчисления. Целевая функция f(х₁, х₂,…, х_п) обладает непрерывными частными производными по своим аргументам, тогда положив частные производные от f по х равными нулю и решая совместно n уравнений

(∂f/∂x_i) = 0 , i =1, 2,…, n ,

найдем значения x , дающие стационарное значение целевой функции. Экстремум определяется по исследованию старших производных.

Метод множителей Лагранжа. Найти экстремум целевой функции

f(х₁, х₂,…, х_п) при ограничениях

g_j (x₁, x₂, …, x_n) = 0, j = 1, 2, …, m, m < n .

Вводятся m неопределенных коэффициентов (множителей) λ_j и выстраивается вспомогательная функция

F = f + λ₁g₁ + λ₂g₂ + …

После чего решается система n + m уравнений

∂F/∂x = 0 , g_j = 0 .

Найденная совокупность значений х определяет стационарное значение целевой функции. Экстремум определяется по исследованию старших производных

Вариационное исчисление. Требуется найти функцию у = у(х), доставляющую экстремум интегральному функционалу

Р = ∫ F[x, y(x), dy/dx]dx ,

При граничных условиях y(x₁) = y₁ , y(x₂) = y₂ ; функция y(x) определяется из решения уравнения Эйлера

∂F/∂y – d(∂F/∂y^,)/dx = 0 , y^, = dy/dx.

Пример. Минимальному значению работы

W = ∫ N dt = ∫ Svdt ,

(здесь N - мощность, S - сила, скорость движения v = dx/dt , x – прямолинейная координата) соответствует решение уравнения Эйлера

dS/dt = 0 , S = 0 , const ;

это означает, что движение должно быть равномерным или с постоянным ускорением.

Линейное программирование (ЛП) является одним из востребованных методов решения оптимизационных задач, как в научных исследованиях, так и в практической деятельности: распределение ресурсов между работами машин, оборудования, бригадами, предприятиями, оптимизация технологических операций, экономических задач и др. В задачах, решаемых этим методом, целевая функция и область ограничения задаются линейными функциями.

В стандартной форме задачи ЛП формулируются в виде:

- найти экстремум целевой функции ( min или max)

F = с₁х₁ + с₂х₂ + …+ с_пх_п → min (max) ,

- при заданной системе ограничений

а₁₁х₁ + а₁₂х₂ +…+ а_1п x_n = С₁ ,

а₂₁х₁ + а₂₂х₂ +…+а_2п x_n = С₂ ,

…

а_к1х₁ + а_к2х₂ + …+ а_кпх_п = С_к .

х ≥ 0 , с ≥ 0.

Это задача поиска экстремума линейного функционала на линейных ограничениях.

Геометрическое представление этих задач: область ограничения С представляет собой выпуклый многоугольник, образованный пересечением плоскостей ограничений, построенных в n-мерной прямоугольной системе координат, n-мерной плоскостью так же является целевая функция F.

Здесь целевая функция достигает минимум (максимум) как касание n-плоскостью границы области ограничений, и методы дифференциального исчисления для его определения становятся не пригодными.

Основным методом решения задач линейного программирования является симплекс-метод, основанный на итеративной процедуре.

В том случае, когда область ограничения задается одним линейным уравнением, задача не имеет решения для всех х > 0.

Квадратичное программирование. Представлению задач линейного программирования n-мерными плоскостями и гипервыпуклыми многоугольниками поставим в соответствие n-мерными векторами в n-мерной ортогональной системе координат:

- целевая функция n- мерный вектор

V = e₁с₁х₁ + e₂с₂х₂ + …+ e_nс_пх_п ,

- ограничения n-мерные вектора

е₁а₁₁х₁ + е₂а₁₂х₂ +…+ е_п а_1п x_n = В₁ ,

е₁а₂₁х₁ + е₂а₂₂х₂ +…+ е_п а_2п x_n = В₂ ,

…

е₁а_к1х₁ + е₂а_к2х₂ + …+ е_па_кпх_п = В_к .

здесь е_i – единичные базисные вектора, для которых выполняются условия ортогональности e_i e_j = 0 , e²_i = 1 , i, j = 1, 2, …

Векторным представлениям построим в соответствие квадратичные формы как квадраты длин векторов для целевой функции

V² = (e₁с₁х₁ + e₂с₂х₂ + …+ e_nс_пх_п )² = с²₁х²₁ + с²₂х²₂ +…+ с²_пх²_п ,

и ограничений в виде произведения единичного вектора и векторов ограничений

(е₁ + е₂ +…+ е_п ) (е₁а₁₁х₁ + е₂а₁₂х₂ +…+ е_п а_1п x_n ) =

= а₁₁х ₁ + а₁₂х₂ +…+ а_1п x _n = С₁ ,

(е₁ + е₂ +…+ е_п) (е₁а₂₁х₁ + е₂а₂₂х₂ +…+ е_п а_2п x_n) =

= а₂₁х₁ + а₂₂х₂ +…+ а_2п x_n = С₂ ,

…

(е₁ + е₂ + …+ е_л) (е₁а_к1х₁ + е₂а_к2х₂ + …+ е_па_кпх_п) =

= а_к1х₁ + а_к2х₂ + …+ а_кпх_п = С_к .

Таким образом, линейное программирование на линейных формах отображается на программирование квадратичных форм как квадратов длин векторов целевой функции при ограничениях на линейных формах, и становится возможным сделать переход от методов не дифференциального исчисления линейного программирования к дифференциальным.

На квадратичных формах целевой функции и линейных форм ограничений стандартная задача оптимизации ставится следующим образом:

- найти минимум целевой функции как минимальной длины вектор

(минимальный квадратичный функционал)

Ф =V² = с²₁х²₁ + с²₂х²₂ +…+ с²_пх²_п → min ,

при ограничениях

а₁₁х₁ + а₁₂х ₂ +…+ а_1п x _n = С ₁ ,

а₂₁х₁ + а₂₂х₂ +…+ а_2п x_n = С₂ ,

…

а_к1х₁ + а_к2х₂ + …+ а_кпх_п = С_к .

Здесь целевая функция Ф обладает непрерывными частными производными первого и второго порядка по своим аргументам.

В рассматриваемых условиях задачу оптимизации, как минимизации целевой функции, можно решать известным методом множителей Лагранжа. Метод заключается в введении множителей λ₁ , λ₂ , …, λ_к и построении вспомогательной функции

Т = с²₁х²₁ + с²₂х²₂ +…+ с²_пх²_п +

+ λ₁(а₁₁х ₁ + а₁₂х ₂ +…+ а_1п x_n – С₁) + ,

+ λ₂(а₂₁х₁ + а₂₂х₂ +…+ а_2п x_n – С₂) +

…

+ λ_к(а_к1х₁ + а_к2х₂ + …+ а_кпх_п – С_k).

Минимизация целевой функции обеспечивается условием ∂²Ф/∂х² > 0.

Стационарное значение целевой функции Ф находится путем решения системы ( n + k ) уравнений, получаемых из условий

∂Т / ∂х_i = 0 , i = 1, 2, …, n ,

и ∂Т / ∂λ_j = 0 , j = 1, 2, …, k ,

таких как

2с²₁ х₁ + ∑а_j1 λ_j = 0 ,

2с²₂ x₂ + ∑a_j2 λ_j = 0 ,

…

2с²_п x_n + ∑a_jk λ_k + 0 ,

а₁₁х₁ + а₁₂х₂ +…+ а_1п x_n = С_1,

а₂₁х₁ + а₂₂х₂ +…+ а_2п x_n = С₂

…

а_к1х₁ + а_к2х₂ + …+ а_кпх_п = С_к ..

Размерность пространства решения задачи равна ( n + k ).

Система уравнений является линейной и замкнутой по числу неизвестных x и l, поэтому её решение находится по формуле Крамера

X_i = d_i / d ,

где d – определитель основной матрицы системы уравнений , d_i – определитель матрицы, получающейся из определителя основной матрицы путем замены i-того столбца столбцом из свободных членов.

Таким образом, решением задачи становится пересечение гиперплоскостей, представленных системой уравнений.

Квадратичный функционал связан с линейным условием

V² = F² n .

В качестве иллюстрации представления предлагаемого метода оптимизации запишем решения линейной, плоской и 4-х мерной задач.

Линейная задача:

Найти минимальный квадратичный функционал

с²₁ х²₁ + с²₂ х² ₂ → min ,

при линейном ограничении

х₁ + х₂ = С₁ ,

решение имеет вид

х₁ = с²₂ С₁(с²₁ + с²₂) . х₂ = с²₁ С₁ / (с²₁ + с²₂) .

Плоская задача:

Найти минимальный квадратичный функционал

с²₁ х²₁ + с²₂ х² ₂ + с²₃ х²₃ → min ,

при линейном ограничении

х₁ + х₂ + х₃ = С₁ ,


решение имеет вид

х₁ = с²₂ с²₃ С₁ / ( с²₁ с²₂ + с²₁ с²₃ + с²₂ с²₃) ,

х₂ = с²₁ с²₃ С₁ / ( с²₁ с²₂ + с²₁ с²₃ + с²₂ с²₃) ,

х₃ = с²₁ с²₂ С₁ / ( с²₁ с²₂ + с²₁ с²₃ + с²₂ с²₃) ,

4-х мерная задача:

Найти минимальный квадратичный функционал

с²₁ х²₁ + с²₂ х² ₂ + с²₃ х²₃ + с²₄ х²₄ → min ,

при линейном ограничении

х₁ + х₂ + х₃ + х₄ = С₁ ,

решение имеет вид

х₁ = с²₂ с²₃ с²₄ С₁ / ( с²₁ с²₂ с²₃ + с²₁ с²₃ с²₄ + с²₁ с²₂ с²₄ + с²₂ с²₃ с²₄) ,

х₂ = с²₁ с²₃ с²₄ С₁ / ( с²₁ с²₂ с²₃ + с²₁ с²₃ с²₄ + с²₁ с²₂ с²₄ + с²₂ с²₃ с²₄) ,

х₃ = с²₁ с²₂ с²₄ С₁ / ( с²₁ с²₂ с²₃ + с²₁ с²₃ с²₄ + с²₁ с²₂ с²₄ + с²₂ с²₃ с²₄) ,

х₄ = с²₁ с²₂ с²₃ С₁ / ( с²₁ с²₂ с²₃ + с²₁ с²₃ с²₄ + с²₁ с²₂ с²₄ + с²₂ с²₃ с²₄) ,

Решения позволяют выстраивать оптимальную организацию

общего лесозаготовительного процесса при наличии нескольких технологий, имеющих различную себестоимость единицы лесопродукции. В этом случае с – стоимость 1м³ лесопродукции для отдельной технологии, х – объем лесопродукции, производимой отдельной технологией, а С – общий объем заготовки леса.

В том случае, когда имеется информация о часовой или сменной производительности каждой технологии, можно найти технологическое время для каждой технологии, обеспечивающее минимальные затраты выполнения всего комплекса работ:

t_i = x_i / n_i ,

здесь n_i – производительность огдельной технологии в комплексе.

Задачи на максимум выстраиваются как двойственная минимуму

Н – Ф → mах ,

Где Н – постоянная, и условием – ∂²Ф/∂х² < 0.

Представленное построение показывает, что решение задачи оптимизации данным методом квадратичного программирования возможно при минимальном числе условий ограничения (к = 1), что в принципе не возможно при линейном программировании.

В тоже время множество задач линейного программирования можно решать представленным методом квадратичного программирования.

Нелинейное программирование. Задача представлена нелинейными формами.

Динамическое программирование. Метод основан на принципе оптимальности, сформулированным Беллманом: оптимальная политика обладает тем свойством, что каково бы ни было начальное состояние и управление в начале процесса, последующие управления должны составлять оптимальную стратегию относительно состояния, полученного после начальной стадии процесса.

Пример. Процесс состоит из ступеней: n, n-1, n-2,.., 1. Преобразование и доход определяются функциями T(x,D) и P(x,D) соответственно (x- переменная состояния, D – управляющая переменная)

Целевая функция f_n(x) и управление D_n на n–й ступени удовлетворяют функциональному уравнению

f_n(x) = ext (D_n) {f_n-1[T(x,D_n)] + P_n(x,D_n)},

Принцип максимума. (принцип быстродействия) Состояние процесса задается числами х₁, х₂, …,х_п , называемыми координатами фазового пространства процесса, движение объекта управляется параметрами u₁, u₂,…, u_r; координаты фазового пространства и управляющие переменные зависят от времени, управляемый процесс описывается системой дифференциальных уравнений

dx_i/dt = f_i (x₁,…, x_n , u₁, …, u_r) , i = 1, 2, .., n.

или в векторной форме

dx/dt = f [x(t), u(t)] ,

интегральный функционал

J = ∫f(x₁, x₂,.., x_n, u₁, u₂,…,u_r)dt ,

на отрезке времени принимает определенное значение; переход из одного состояния процесса в другое должен происходить при минимальном значении интегрального функционала.


Лекция 4

Стохастические модели оптимизации


При решении конкретных задач с учетом неопределенностей приходится сталкиваться с тремя типами6

- неопределенность целей,

- неопределенность информации,

- неопределенность действий партнера или противника.

Неопределенность не следует путать со случайностью. Неопределенность подразумевает недостаточность знаний (понимания) проблемы и неясность взаимодействия различных факторов.

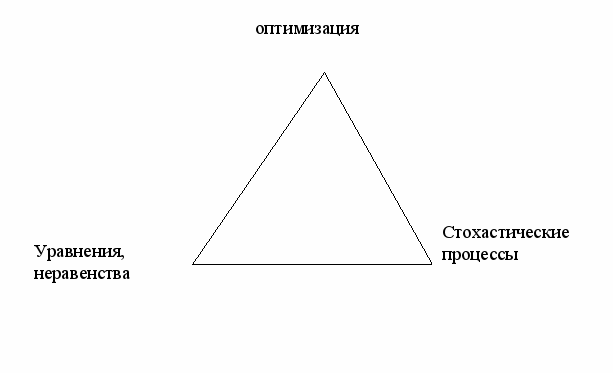
Математические методы можно разделить на три взаимосвязанных класса:

1. детерминированные модели,
   
2. модели оптимизации,
   
3. вероятностные модели.
   

Связь между ними можно представить в виде треугольника.

Проблема может не иметь математического представления по следующим причинам:

1. структура очень сложна,
   
2. структура ясна, но включает неопределенность, вероятности не могут быть определенными,
   

3. орошо понимаемо эмпирически, но теоретическая структура неясна,
   
4. структура понятна, но нерешаеаа даже приближенными методами,
   

Неопределенность надо учитывать по отношению к случайности.:

-стохастическая неопределенность при статистической устойчивости,

- нестохастическая неопределенность, когда не существует никаких предположений.

Возникает риск принятия решений.

Принятие решений в условиях риска основывается на критериях:

- ожидаемого значения,

- комбинация ожидаемого значения и дисперсии,

- известного предельного уровня,

- наиболее вероятного события в будущем.

Если неопределенные факторы заданы законом распределения:

- случайные факторы заменяются математическим ожиданием и

производится оптимизация в среднем.

Стохастическое программирование:

Оптимизация математического ожидания целевой функции

W= М (Σc_ix_i) → ext,


W= М (Σc_ix_i) = Σc_icx_i → ext,

Теоретической основой нахождения решения в условиях неопределенности и конфликтных ситуаций является теория игр.

Теория игр как раздел оптимизации. исследующий методы разрешения конфликтов, в которых сталкиваются интересы нескольких сторон, и непосредственноне затрагивающие максимизацию или минимизацию.

Основу оптимизации с позиции теории игр составляет теория полезности. Оптимизация как предпочтение полезности. Предпочтение альтернатив. Функция полезности на множестве альтернатив. Предпочтение не числовая характеристика, а упорядочение. Поиск лучшей альтернативы.

Теория игр, исследующая интересы не одной стороны, а нескольких сторон, это другой путь оптимизации принятия решений.

Решение, полезность, предпочтение.

Решить – сделать выбор среди альтернатив. Для выбора надо знать порядок предпочтений.

Когда функция полезности определена и известны ограниченияна применение предпочтений, тогда выбирается методика оптимизации в смысле предпочтения среди альтернатив.

Упорядоченная полезность – порядковая полезность. Числовая полезность Эвристические критерии полезности:

1. Сопоставимость: для двух альтернатив либо предпочтение,
   

либо сопоставимость.

2. Транзитивность: если а > в и в> с, то а > с.
   
3. Недополнительность: если а > в, р – вероятность а, (1-р) – вероятность в, то а > ра + (1-р)в,
   

и др..

Метод Парето: сохранение множества возможных вариантов и выделение области , из которой необходимо выбрать наиболее предпочтительные.