Geum.ru

Рабочая программа разработана в соответствии с государственными требованиями к минимуму содержания и уровню подготовки по специальности 210200. Составитель: канд техн наук, доц

Вид материалаРабочая программа

Содержание


1.2. Задачи изучения дисциплины. В результате изучения дисциплины студент должен
Раздел 1. Общие вопросы теории моделирования
Раздел 2. Методы построения математических моделей
Раздел 3. Применение математических моделей
3. Перечень тем лекционных занятий
4. Перечень тем лабораторных занятий
Общие указания
На рис. 1 приняты следующие обозначения
В контрольной работе представить
Исходные данные
Методические указания
W(р) — передаточная функция разомкнутой системы W
Подобный материал:
Рабочая программа разработана в соответствии с государственными требованиями к минимуму содержания и уровню подготовки по специальности 210200.

Составитель: канд. техн. наук, доц. Л.А. Осипов

Рецензент: канд. физ.-мат. наук, доц. Е.А. Носиловский

Всего часов — 68 ч

Лекции — 8 ч

Лабораторные занятия — 4 ч

Самостоятельная работа — 41 ч

Контрольная работа (количество) — 1 ч

1 Экзамен (количество) — 1 ч

РАБОЧАЯ ПРОГРАММА


1. Цель и задачи дисциплины

1.1. Целью изучения дисциплины является обучение студентов общим вопросам теории моделирования, методам построения математических моделей и формального описания процессов и объектов, применению математических моделей для проведения вычислительных экспериментов и решения задач оптимизации.

1.2. Задачи изучения дисциплины. В результате изучения дисциплины студент должен:

— Ознакомиться с основными понятиями моделирования и теорий подобия, теоретическими положениями и методикой экспериментальных исследований, используемых для построения математических моделей;

— получить навыки постановки задачи моделирования, математического описания моделируемого процесса (объекта), численных методов реализации математических моделей на ЭВМ и применения интегрированных пакетов;

— освоить метод подхода к математическому моделированию процессов и объектов, начиная с постановки задачи и кончая составлением программ и реализацией математических моделей на ЭВМ.

Материал дисциплины основывается на знаниях, полученных студентами при изучении курсов «Информатика», «Высшая математика», общенаучных и общеинженерных дисциплин.

2. Содержание дисциплины

2.1. Введение

Раздел 1. Общие вопросы теории моделирования


2.1.1. Понятие объекта и его модели. Роль моделирования в процессах познавательной и практической деятельности человека.

2.1.2. Понятие математической модели (ММ). Формы представления ММ. Соответствие между объектом и его ММ. Основные понятия теории подобия. Коэффициенты и критерии подобия. Подобие ММ.

2.1.3. Классификация моделей, области их применения. Роль математического моделирования в ускорении научно-технического прогресса.

2.1.4. Обзор математических методов качественного и количественного исследования ММ.

[4]

Раздел 2. Методы построения математических моделей


2.2.1. Основные этапы математического моделирования.

2.2.2. Описание объектов моделирования. Упрощение ММ объекта (идеализация, допущения). Исследование условий подобия ММ и моделируемого объекта (процесса).

2.2.3. ММ механических систем. Составление дифференциального уравнения. Определения краевых условий и диапазона изменения параметров. Примеры,

2.2.4. ММ процессов, происходящих в электрических цепях. Составление дифференциального уравнения, моделирующего процесс в электрической цепи. Определение краевых условий и диапазона изменения параметров. Примеры.

2.2.5. ММ системы автоматического управления. Составление дифференциального уравнения, моделирующего систему автоматического управления. Определение краевых условий и диапазона изменения параметров. Примеры.

2.2.6. Сравнение ММ. Выявление аналогии между их параметрами. Определение областей устойчивости ММ. Методы исследования на полноту, непротиворечивость, адекватность (изоморфность) и устойчивость по отношению к возмущениям.

2.2.7. Методы решения систем алгебраических и дифференциальных уравнений (методы итераций, метод Рунге-Кутты и др.). Применение конечно-разностных преобразований для дифференциальных уравнений в частных производных.

2.2.8. Методы реализации ММ (аналитические, численные, аналоговые). Применение пакетов прикладных программ.

2.2.9. Способы оценки адекватности ММ, универсальности и экономичности.

2.2.10. Общие сведения о ММ систем массового обслуживания (СМО) на железнодорожном транспорте. Примеры ММ СМО с потерями и с очередями. Их сравнение. Применение.

[1-4]

Раздел 3. Применение математических моделей


2.3.1. Вычислительный эксперимент (прогноз). Натурный (физический) эксперимент. Сравнение их преимуществ и недостатков на примере ММ.

2.3.2. Использование результатов вычислительного эксперимента (прогноза) для построения ММ.

2.3.3. Понятие об оптимизационных задачах. Критерии оптимальности. Примеры оптимизации ММ. Использование пакетов прикладных программ для решения задач оптимизации. Характеристики и оценка методов оптимизации.

[5-9].

3. Перечень тем лекционных занятий

№ п/п
Наименование темы
Количество часов

1
Моделирование, математические модели и их особенности. Вычислительный эксперимент.
4

2
Интегрированные пакеты для моделирования. Основные сведения о пакете и его использование.
4


4. Перечень тем лабораторных занятий

№ п/п
Название работы
Количество часов

1
Подготовка программы и решение задач, описанных в пп. 2.2.3, 2.2.4, 2.2.5 на одном из языков программирования (по выбору студента)
4

Информационно-методическое обеспечение дисциплины

1. Осипов Л. А. Решение прикладных задач на ЭВМ: Учеб. пос. М.: РГОТУПС, 1995.

2. Осипов Л. А. Математическое моделирование. Моделирование: Рабочая программа и задание на контрольную работу с методическими указаниями. М.: РГОТУПС, 1997.

3. Осипов Л. А. Эффективные алгоритмы и программы цифровой обработки сигналов. Учеб. пос. М.: РГОТУПС, 1999.

4. Советов Б. Я., Яковлев С.А. Моделирование систем: Учебник для вузов. М.: Высшая школа, 1998.

5. Очков В. Ф. Mathcad 6.0 для студентов и инженеров. М.: ТОО фирмы «Компьютер Пресс», 1996.

6. Алейников И. А., Ларченков А.М., Умаров С.А. Использование пакета Mathcad+ при решении задач теоретической механики: Учеб. пос. М.: РГОТУПС, 1998.

7. Дьяконов В. П. Справочник по Mathcad plus 6.0 PRO. М.: СК Пресс, 1997.

8. Осипов Л. А. Использование ЭВМ в инженерных расчетах. Рабочая программа для студентов V курса специальности «Вагоны». М.: РГОТУПС, 1998.

9. Осипов Л. А. Обработка сигналов на цифровых процессорах. Линейно-аппроксимирующий метод: Справ. пос. М,: Горячая линия - Телеком, 2001.


ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ

Общие указания


Задание составлено на основе того, что студенты владеют навыками составления алгоритмов и программ, полученными при изучении дисциплины «Информатика».

Контрольная работа выполняется по варианту, который определяется двумя последними цифрами учебного шифра студента. Если учебный шифр представляет собой однозначное десятичное число, то в предпоследнем разряде его нужно записать ноль. Например, если номер шифра имеет цифру 3, то следует преобразовать его в 03. Контрольная работа, выполненная по варианту, не отвечающему шифру студента, зачету не подлежит.

Задание


Задана структурная схема системы автоматического регулирования - рис. 1, являющаяся одинаковой для всех вариантов контрольной работы.



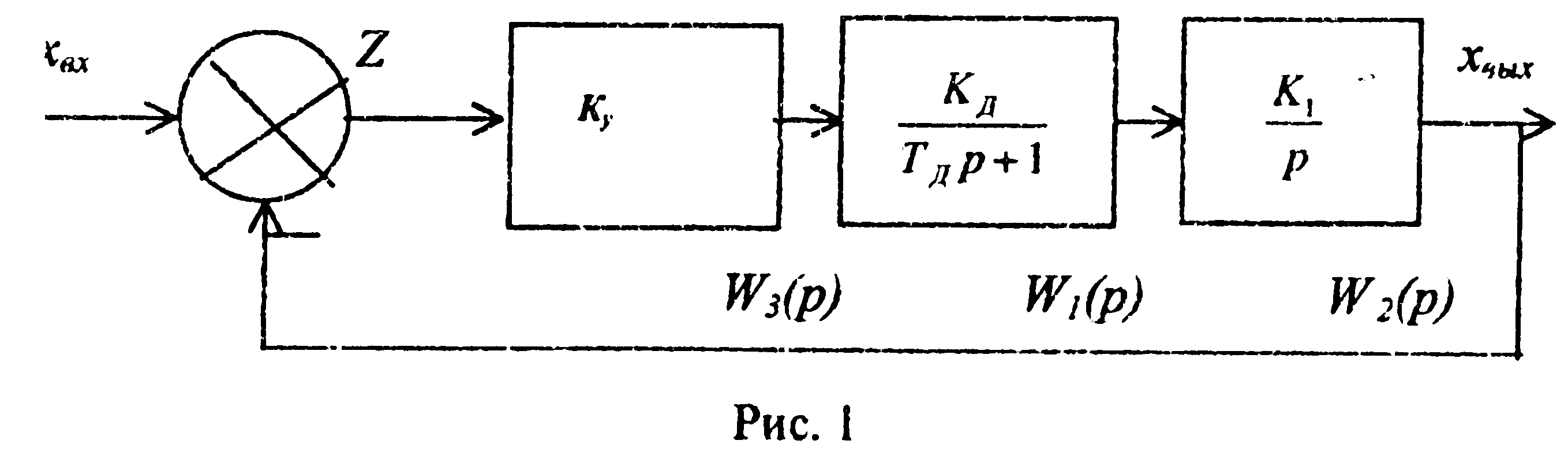
На рис. 1 приняты следующие обозначения:

xвх хвых - входной и выходной сигналы;

Z - рассогласование между входным и выходным сигналами Z = xвх - хвых;

W1(Р), W2(Р), W3(Р) — передаточные функции звеньев системы;

р - оператор дифференцирования ;

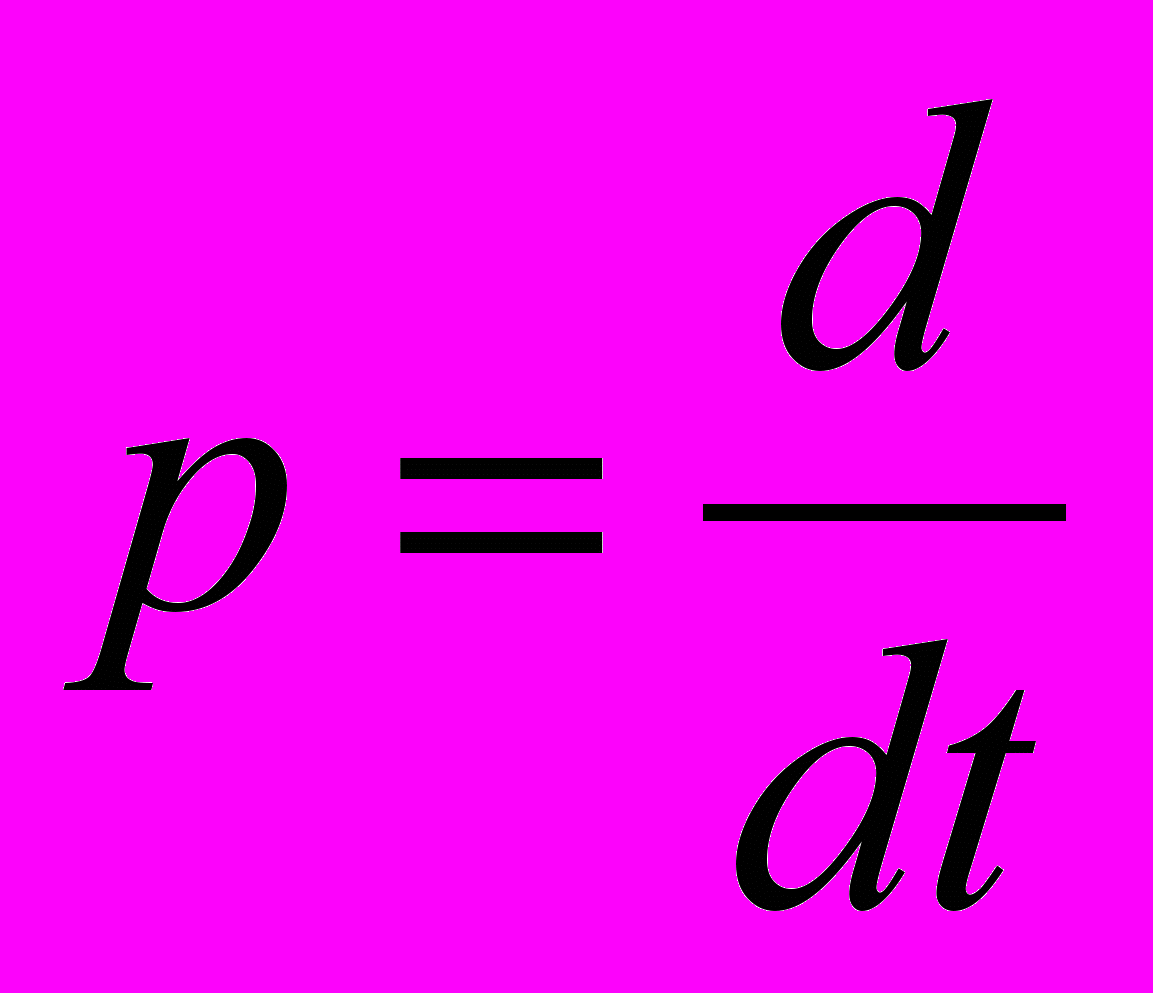Кy, КД, К1 — постоянные коэффициенты;

ТД — постоянная времени передаточной функции апериодического звена W2(Р).

Требуется:

1. Составить дифференциальное уравнение системы регулирования, найти точную формулу для переходного процесса.

2, Составить графическую схему алгоритма решения дифференциального уравнения методом Рунге-Кутты и дать письменное пояснение операторам этой схемы.

3. Составить программу решения дифференциального уравнения на языке программирования или с помощью интегрированного пакета.

4. Полученную программу отладить и решить дифференциальное уравнение на ЭВМ (при выполнении практических работ на лабораторной сессии).

В контрольной работе представить


следующие материалы:

а) исходные данные, соответствующие варианту, включая схему моделируемой системы;

б) вывод дифференциального уравнения моделируемой системы, формулу для переходного процесса;

в) графическую схему алгоритма решения дифференциального уравнения с кратким пояснением;

г) программу решения дифференциального уравнения на языке программирование или для интегрированного пакета;

д) результаты решения дифференциального уравнения на ЭВМ и анализ их (после выполнения практических работ, при подготовке к зачету контрольных работ);

е) график переходного процесса хвых(t) для заданных условий, соответствующего единичному возмущению



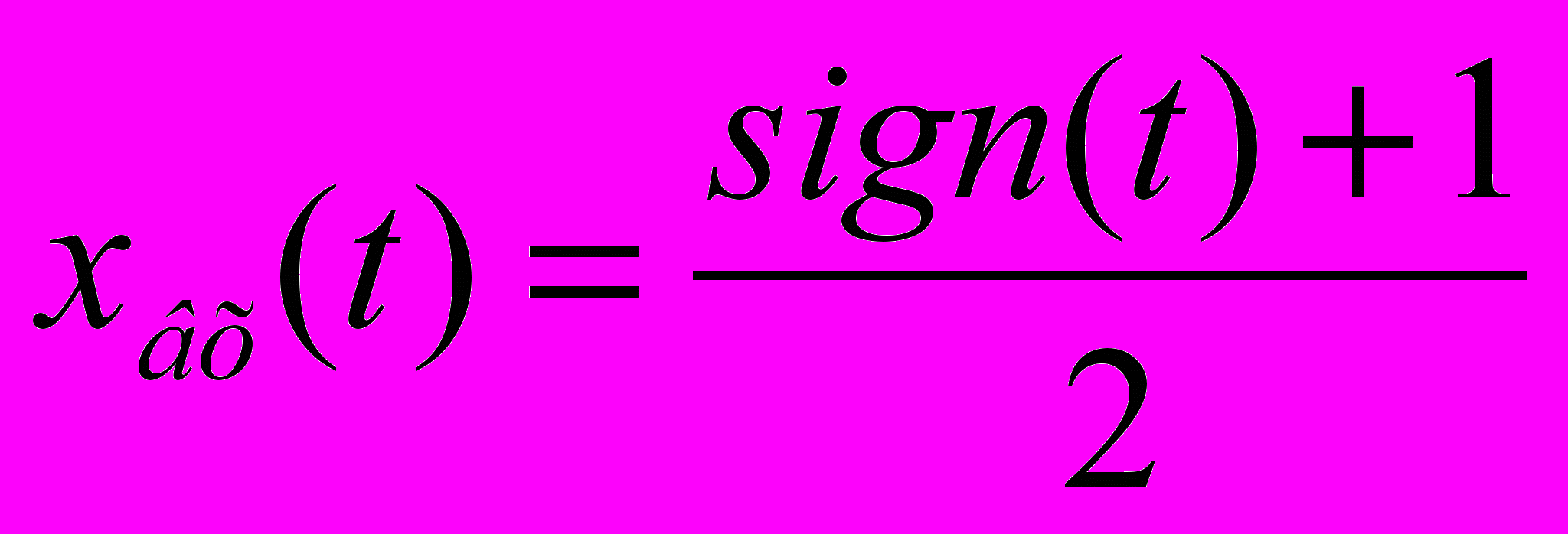
ж) результаты решения на ЭВМ задачи расчета переходного процесса при оптимальных параметрах;

з) график переходного процесса, полученного после оптимизации;

и) выводы по проведенному исследованию.
Исходные данные

Значения параметров передаточных функций заданы в табл. 1 и 2.

Таблица 1.

Последняя цифра шифра
Параметры звеньев системы

ТД, с
КД
Тип метода Рунге-Кутты

(по табл.3)

0
0,50
5
5

1
0,51
10
1

2
0,52
2,5
2

3
0,53
1
3

4
0,54
1,1
4

5
0,55
1,43
5

6
0,56
1,39
1

7
0,57
3,33
2

8
0,58
1,52
3

9
0,59
1,7
4

Таблица 2.

Предпоследняя цифра шифра
Параметры звеньев системы

К1
Ку

0
0,01
10

1
0,015
3,3

2
0,02
10

3
0,025
20

4
0,03
15

5
0,035
10

6
0,045
8

7
0,05
3

8
0,055
6

9
0,06
5




№ вариантов
Расчетные формулы

()

1
xK=(1K+42K+3K)/6

1K=fK(t, x1, x2, ….., xN)H

2K=fK(t+H/2, x1+11/2, x2+12/2, ….., xN+1N/2)H

3K=fK(t+H, x1+21, x2+22, ….., xN+2N)H

2
xK=(1K+33K)/4

1K=fK(t, x1, x2, ….., xN)H

2K=fK(t+H/3, x1+11/3, x2+12/3, ….., xN+1N/3)H

3K=fK(t+2H/3, x1+221/3, x2+222/3, ….., xN+22N/3)H

3
xK=(1K+42K+3K)/6

1K=fK(t, x1, x2, ….., xN)H

2K=fK(t+H/2, x1+11/2, x2+12/2, ….., xN+1N/2)H

3K=fK(t+H, x111+221, x212+222, ….., xN1N+22N)H

4
xK=(1K+32K+33K +4K)/8

1K=fK(t, x1, x2, ….., xN)H

2K=fK(t+H/3, x1+11/3, x2+12/3, ….., xN+1N/3)H

3K=fK(t+2H/3, x111/3+21, x212/3+22, ….., xN1N/3+2N)H

4K=fK(t+H, x1+1121+13, x2+1222+32, ….., xN+1N2N+3N)H

5
xK=[(1K+(2q)2K+(2+q)3K +4K)]/6

1K=fK(t, x1, x2, ….., xN)H

2K=fK(t+H/2, x1+11/2, x2+12/2, ….., xN+1N/2)H

3K=fK(t+H/2, x1+(1/q1/2)11+(11/)21, x2+(1/q1/2)12+(11/q)22, ….., xN+(1/q1/2)1N+(11/q)2N)H

4K=fK(t+H, x121/q+(11/q)13, x222/q+(11/q)32, ….., xN2N/q+(11/q)3N)H

Рис. 4


МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К КОНТРОЛЬНОЙ РАБОТЕ

1. Общие сведения

Из теории подобия известно, что подобны те явления, которые описываются одними и теми же математическими уравнениями (теорема Кирипичева), Большой интерес с точки зрения подобия вызывает аналогия механических, электрических систем и систем автоматического регулирования. В их состав могут входить как активные, так и пассивные элементы.

К активным элементам относятся источники механической или электрической энергии, моментов, скоростей, силы, электрического напряжения и т.п.

К пассивным элементам можно отнести массу, упругость (пружины), фрикционные элементы, электрические сопротивления, индуктивности, электрические емкости и др. Рассмотрим математические модели (дифференциальные уравнения), описывающие системы автоматического регулирования, система автоматического регулирования 2-го порядка описывается уравнением:

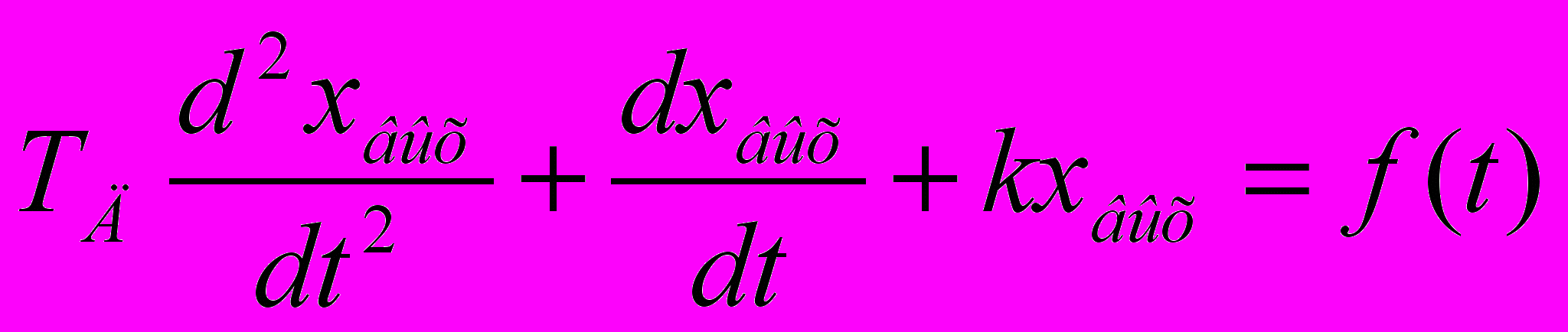(1)

где TД —постоянная времени;

k — постоянный коэффициент;

хвых (t) — выходная величина (зависимая переменная);

f(t) — внешнее возмущение, примем f(t)= kхвх(t);

Подобными математическими уравнениями могут описываться различные по физической природе процессы и системы.

2. Вывод уравнения системы регулирования

Рассмотрим порядок определения передаточной функции К(р) замкнутой системы со структурной схемой, изображенной на рис.1 по известным правилам автоматики запишем:

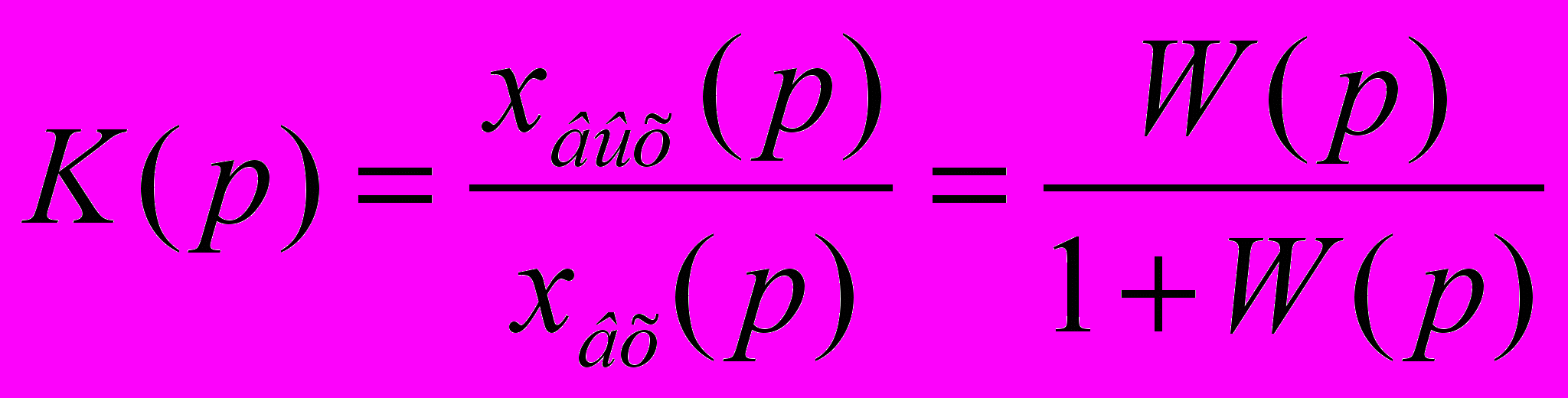(2)

где W(р) — передаточная функция разомкнутой системы

W(p) = W1(p) W2(p) W3(p) (3)

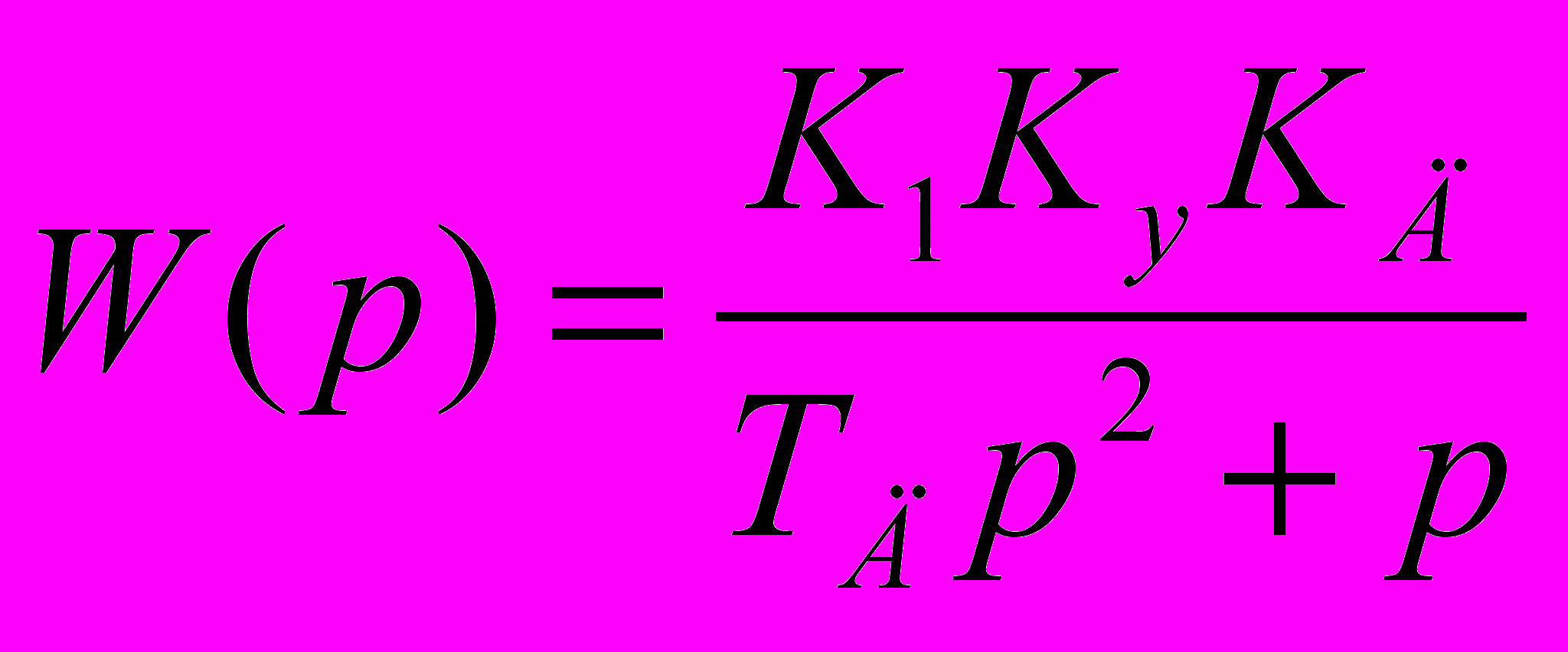(4)

Подставляя в уравнение (3) выражения доя передаточных функций звеньев из схемы рис. 1, получим

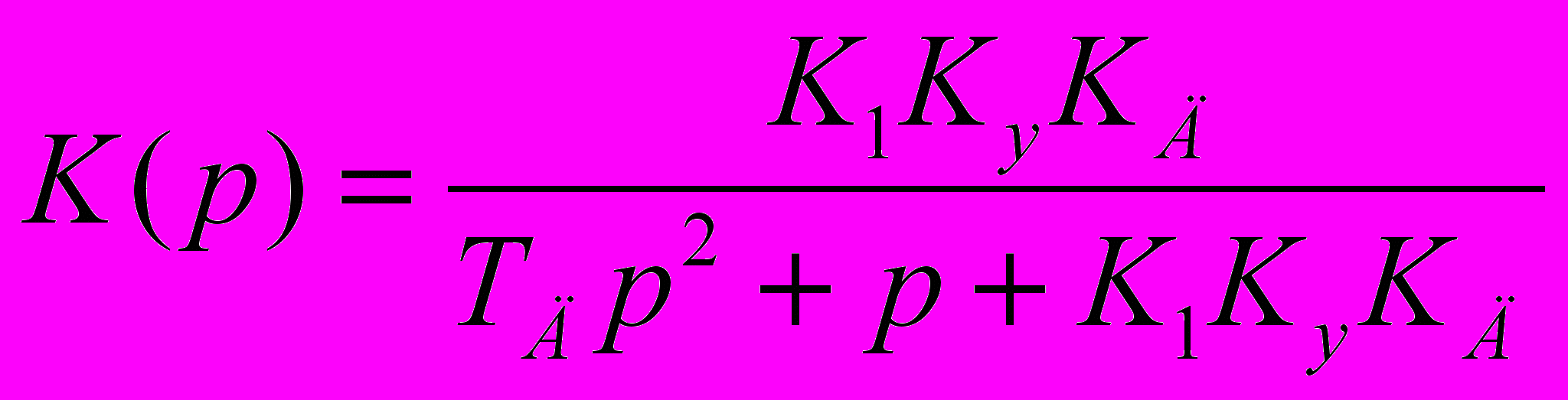(5)

Подставляя выражение (4) в формулу (2), найдем передаточную функцию замкнутой системы

Отсюда найдем уравнение системы

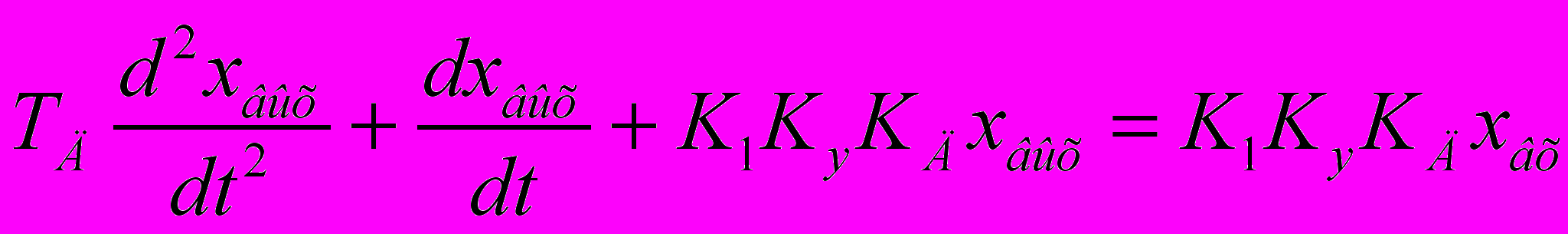(6)

Разделив обе части уравнения на ТД, получим

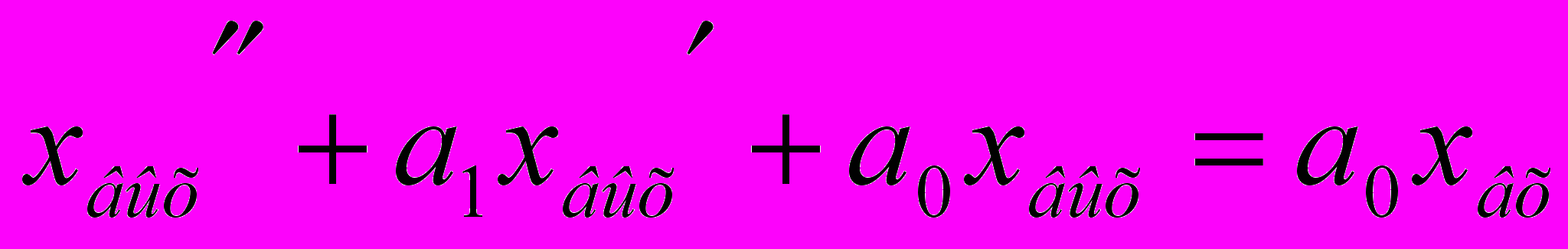, (7)

где 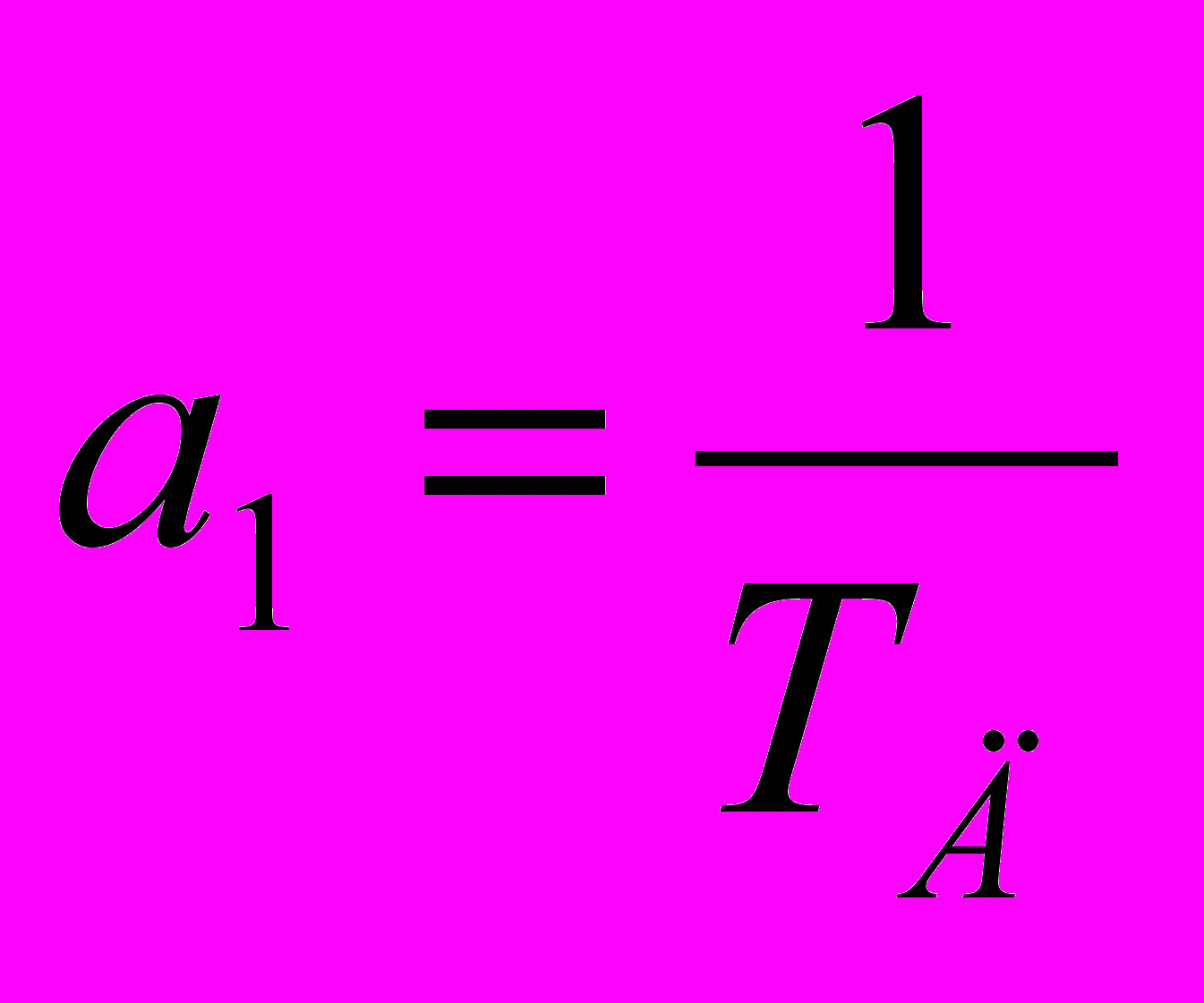; ; 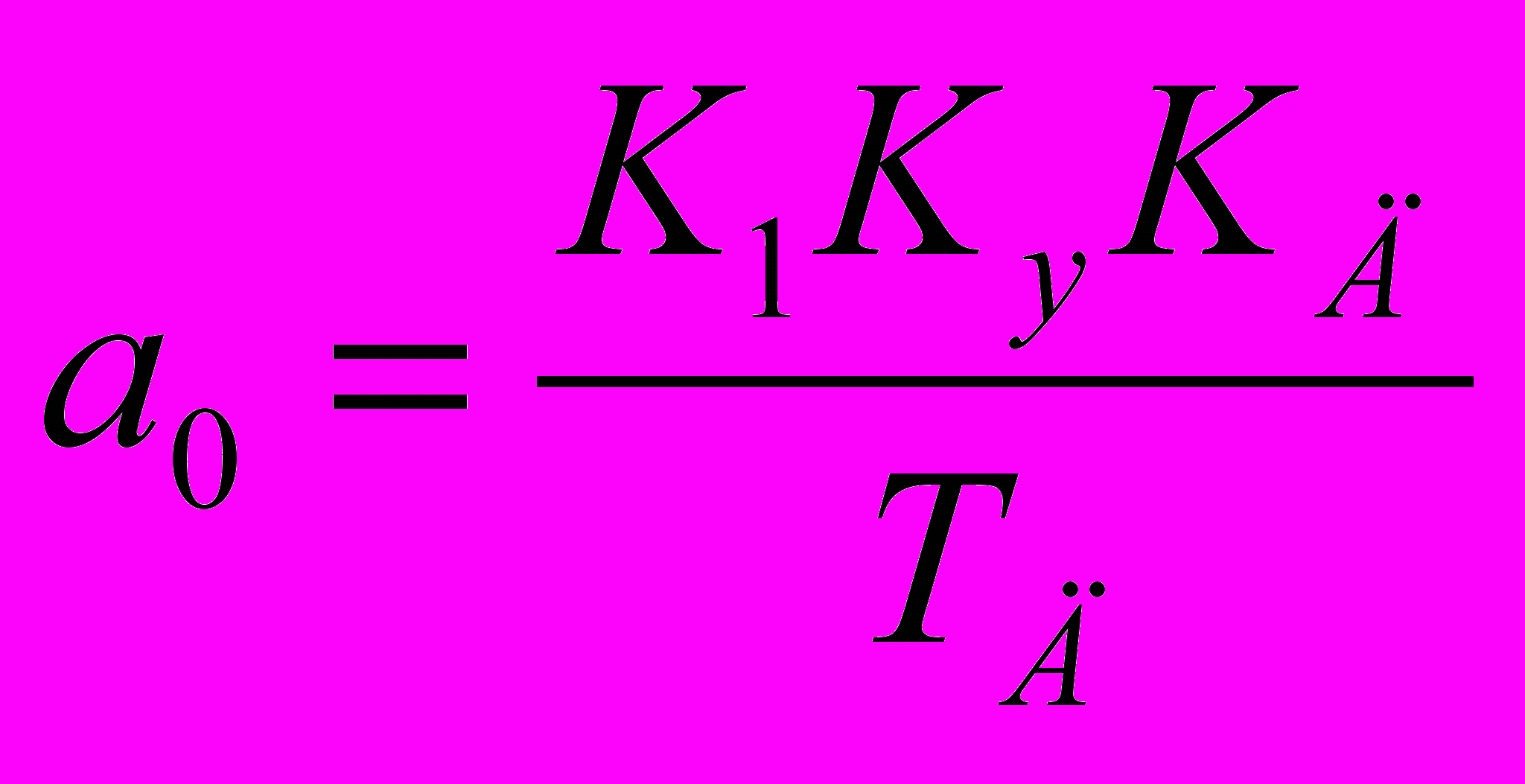xвх = 1;

начальные условия при t=0: хвых(0) = х0; хвых(0) = х0.

3. Методы Рунге-Кутты

интегрирования дифференциальных уравнений

Для решения на ЭВМ обыкновенных дифференциальных уравнений применяют различные методы численного интегрирования. Решение уравнения производится по шагам с вычислением приращений переменных в конце каждого шага. чтобы получить такое решение, уравнение N-го порядка

x(N) = f(t, x, x, x, …, x(N-1)) (8)

приводится к системе N уравнений 1-го порядка (к форме Коши) после замены переменных

x = x2, x = x3, …, x(N-1) = xN

;

;

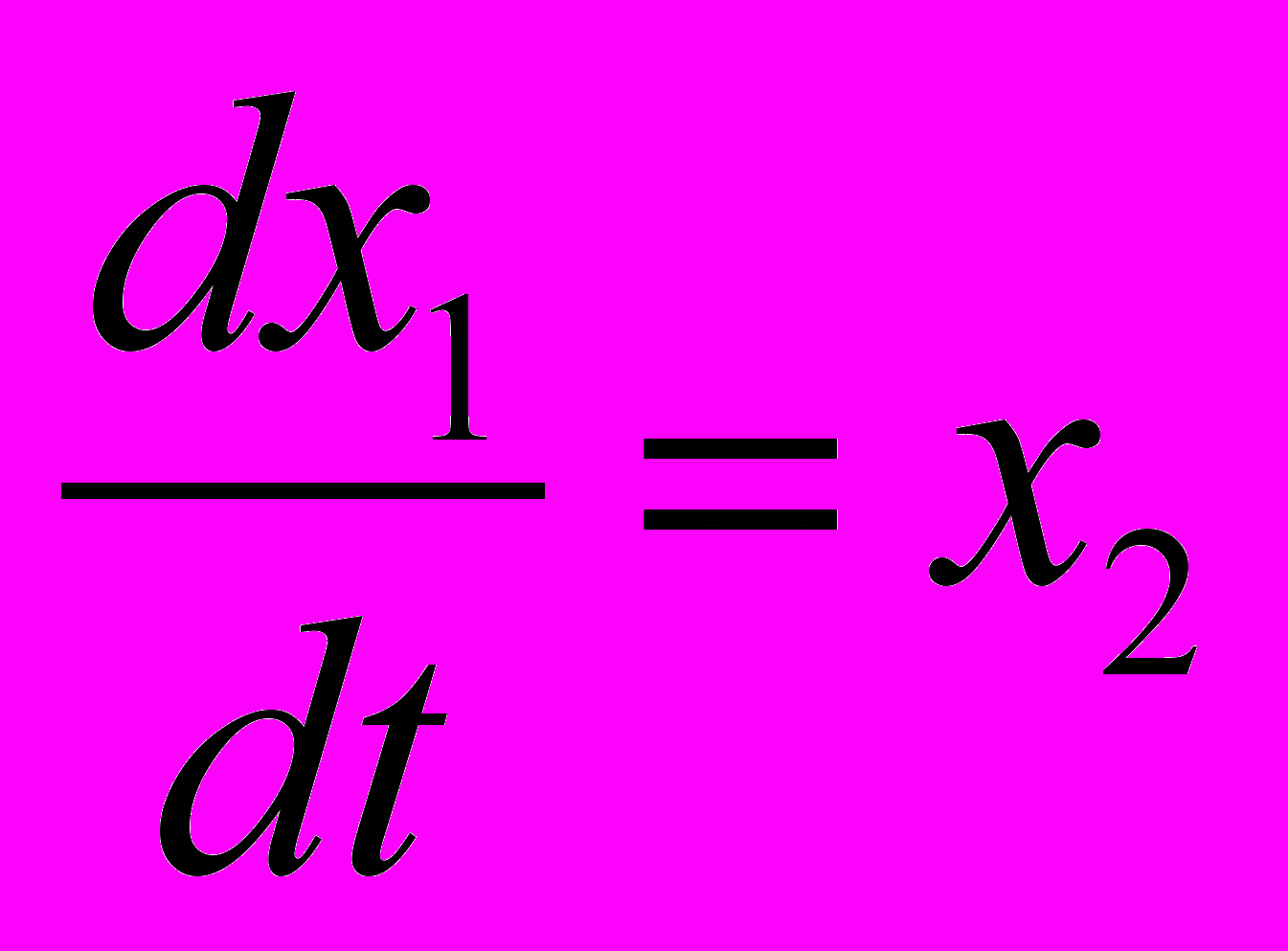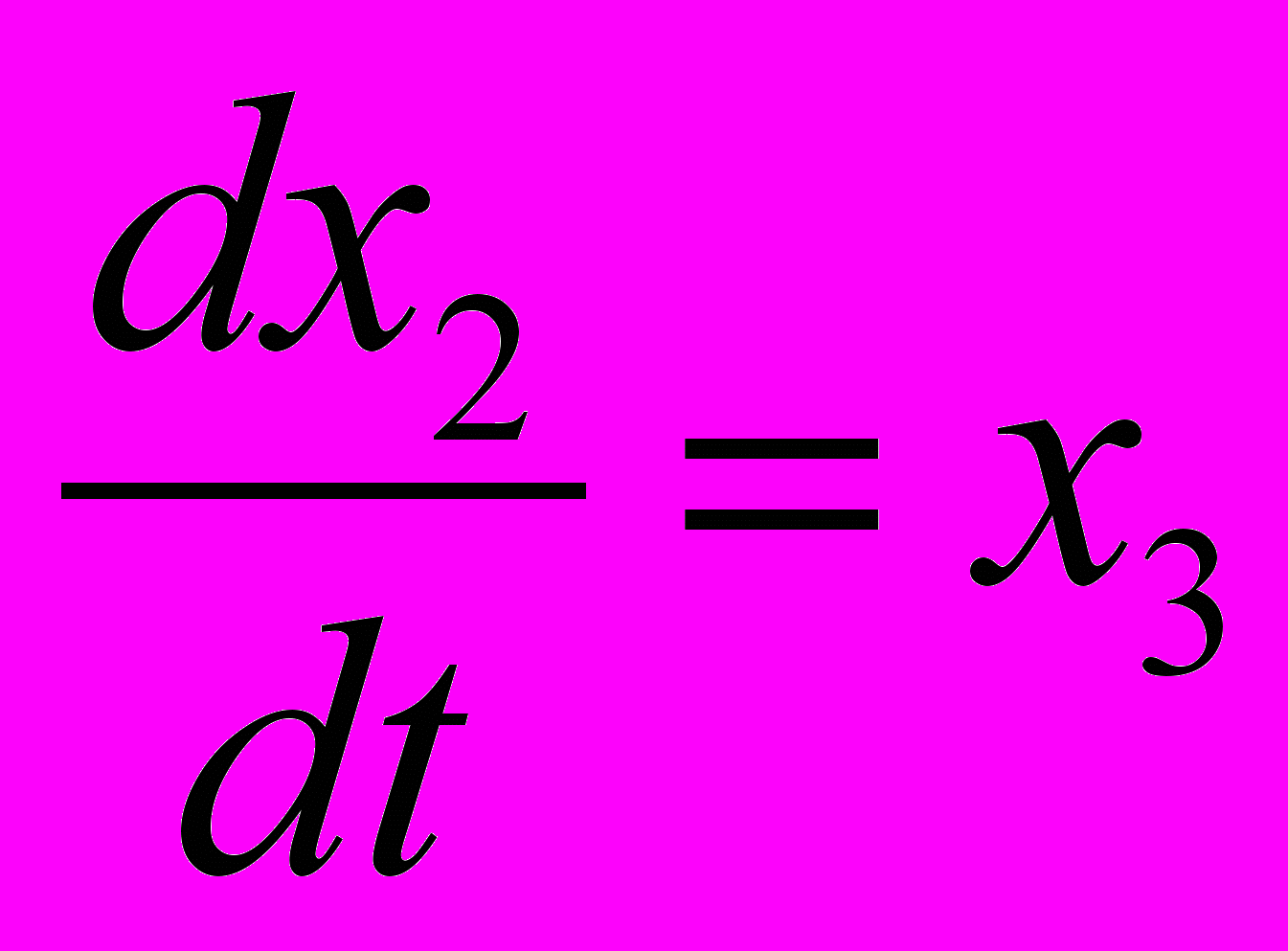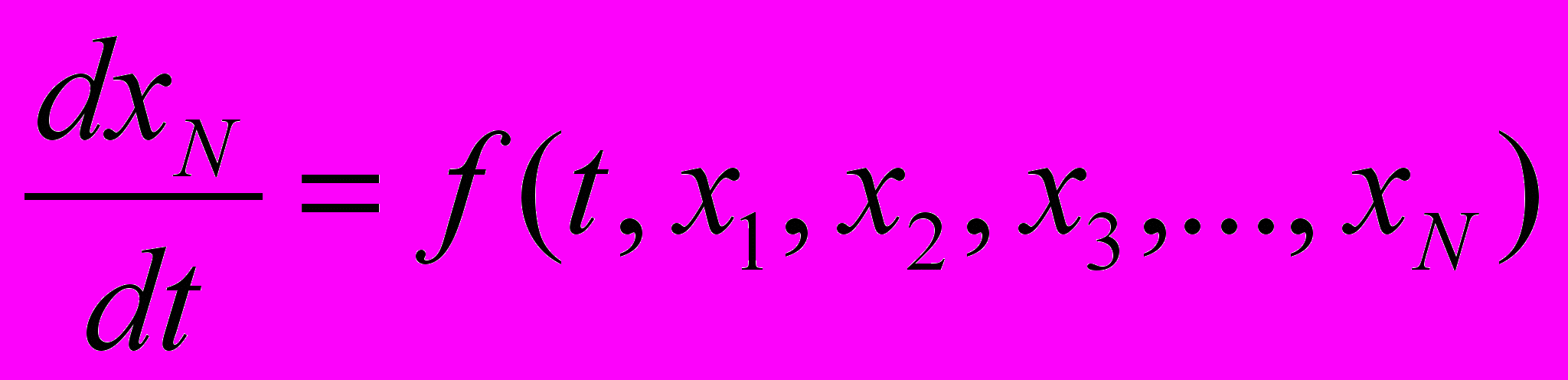. (9)

Для решения уравнения должны быть заданы начальные условия при t = t0.

При выбранном шаге t = Н значения переменных в конце шага могут быть определены из (9) при допущении, что производные на отрезке t не меняют своих значений:

x1(t0+H)=x10+x20H; x2(t0+H)=x20+x30H; ………….

xN(t0+H)=xN0+f(x0, x10, x20, …, xN0)H; t1 = t0+H (10)

Решение на следующем шаге (при t2 = t1+H) определяют по тем же формулам, приняв полученные значения (10) за начальные для очередного шага. Вычисления продолжают до заданного значения аргумента t. Такой алгоритм вычислений называется методом Эйлера.

Пошаговое решение приводит к определенным погрешностям, так как фактически на отрезке t производные не являются постоянными. Значения ошибок можно снизить, уменьшая шаг Н или применив методы с уточнением решения. В качестве последних, чаще всего используют методы Рунге-Кутты [1]. В этих методах находят приращения переменных в конце шага как осредненные значения приращений, полученных в различных точках отрезка t. Основные варианты методов Рунге-Кутты приведены в табл. 3. в ней вычисляются приращения по каждой k-ой переменной, k = 1, N.

Функция fk(t, x1, x2, …, xN) определяет выражение для производной 1с-ой переменной. Применительно к (9) имеем

f1 = x2; f2 = x3;

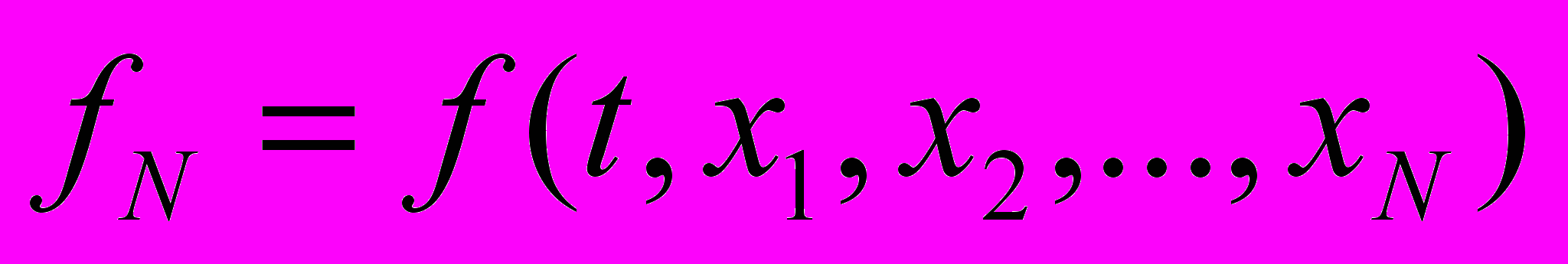
Алгоритм и программа решения задачи

В качестве примера рассмотрим решение уравнения

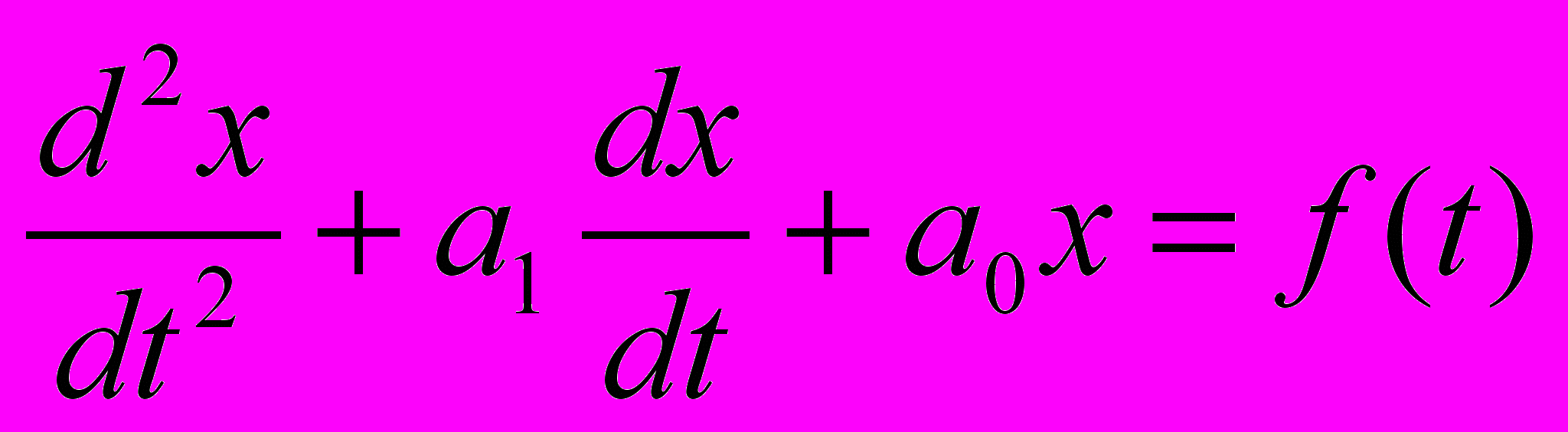на интервале t от 0 до 4 с шагом H = 0,1 при начальных условиях x(t0)=0, x(t0)=0.

Уравнение приводится к системе

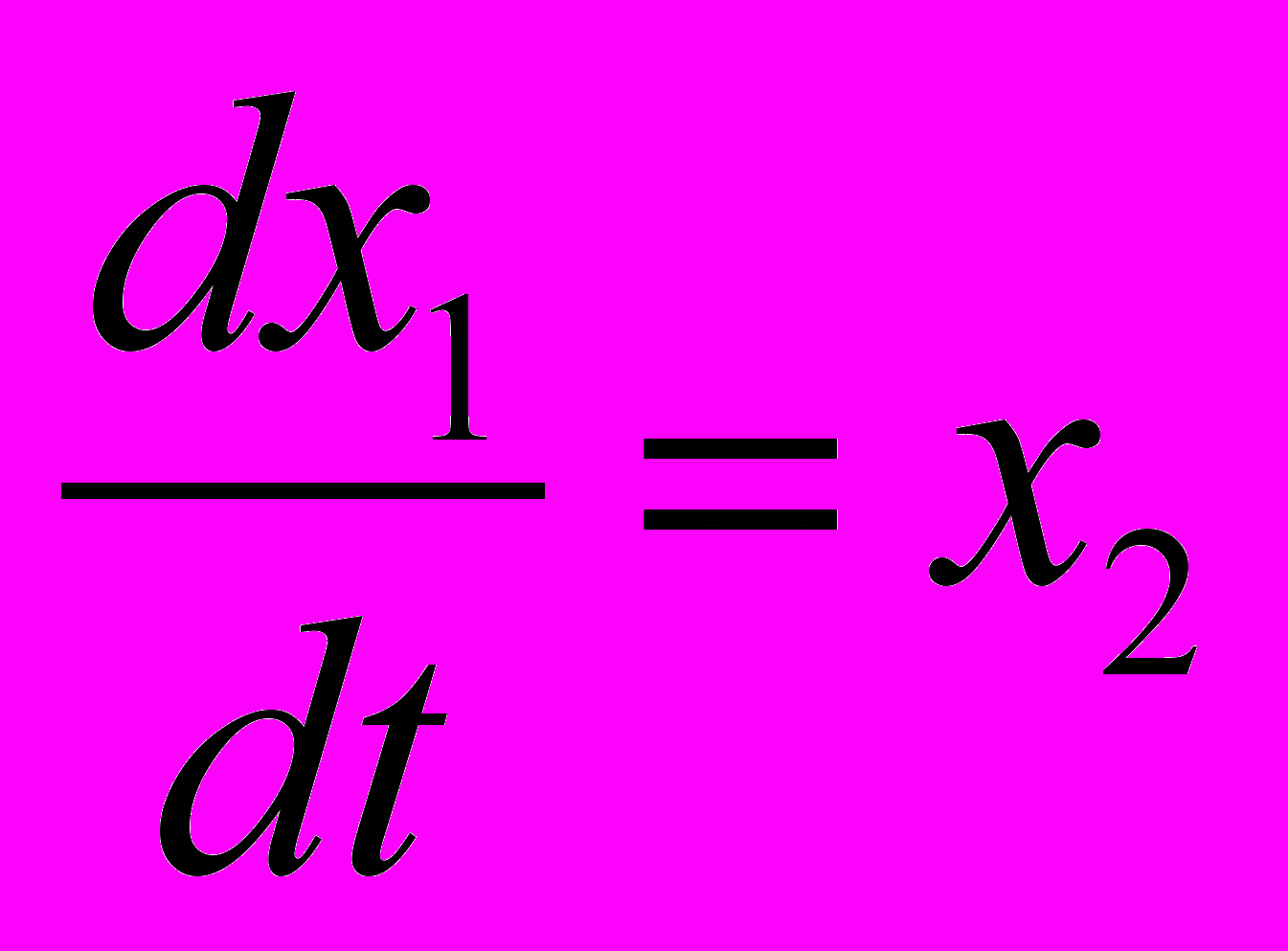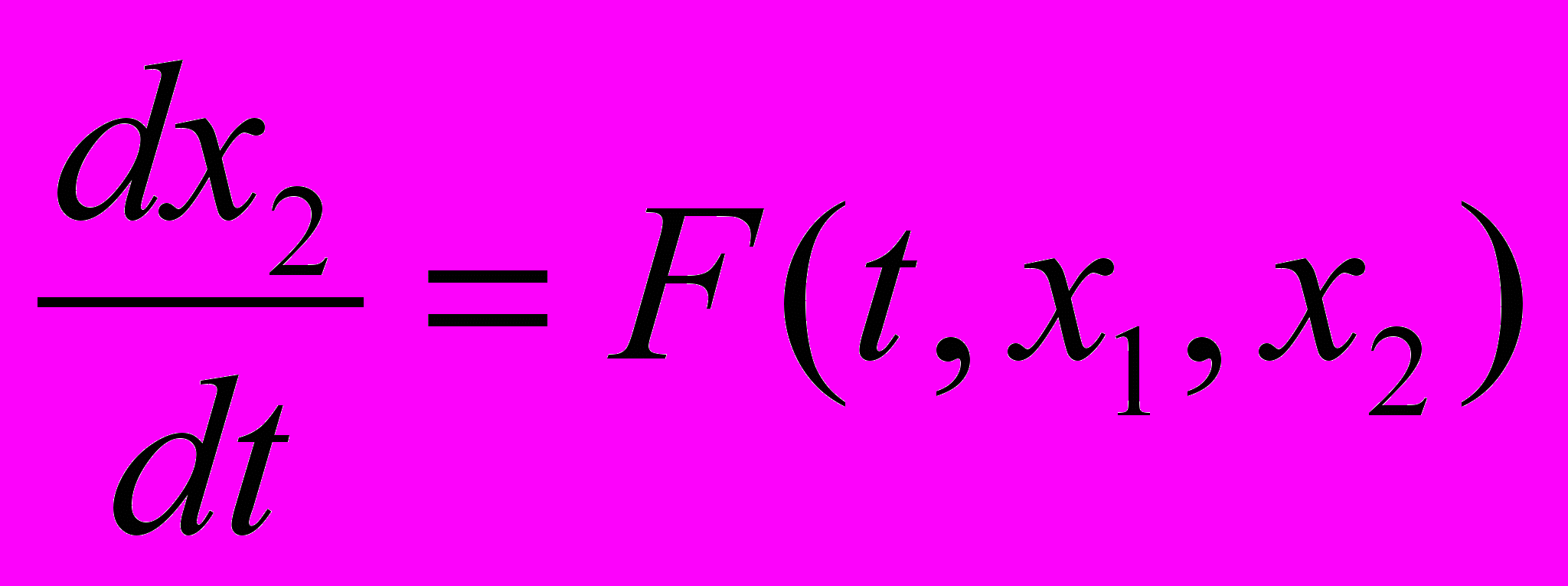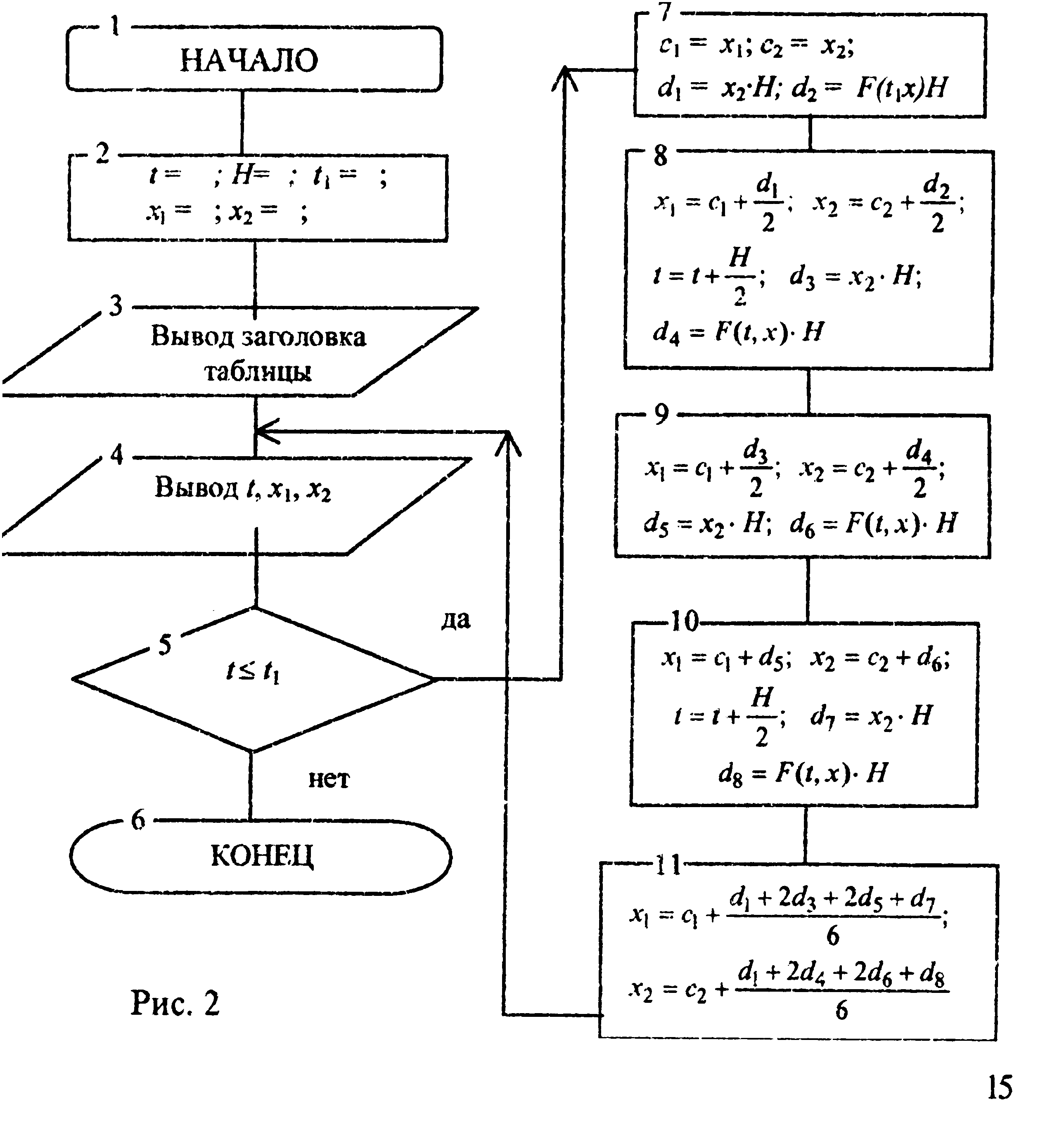
; , где F(t, x1, x2) = f(t) – a0x1 – a1x2.

Для решения применим метод Рунге-Кутты, при котором приращения переменных определяются по формулам:

x1 = (d1 + 2d3 + 2d5 + d7)/6;

x2 = (d2 + 2d4 + 2d6 + d8)/6;

где d1 = x2H; d2 = F(t, x)H; t = t + H/2;

x1 = x1 + d1/2; x2 = x2 + d2/2;

d3 = x2H; d4 = F(t, x)H;

x1 = x1 + d3/2; x2 = x2 + d4/2;

d5 = x2H; d6 = F(t, x)H; t = t + H/2;

x1 = x1 + d5/2; x2 = x2 + d8/2;

d7 = x2H; d8 = F(t, x)H; (11)

В конце шага х1 = х1+ х1, х2 = х2+ х2.

Схема алгоритма численного решения дифференциального уравнения по методу Рунге-Кутты дана на рис. 2.





В верхней части рис. 3 представлена программа на Маткаде (МаthCAD, программы с результатом, в котором называют документом) численного интегрирования уравнения

x + 1,7 x + x 0,9 = 0,9

при нулевых начальных условиях, шаг решения принят Н = 0,8, а время ограничено N = 20 шагами. Сравнение формул (11) с записью на Маткаде легко установить их соответствие.









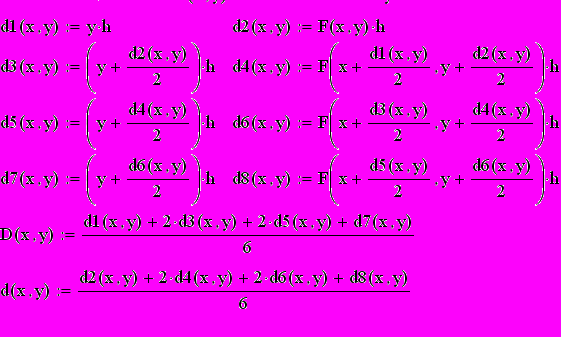
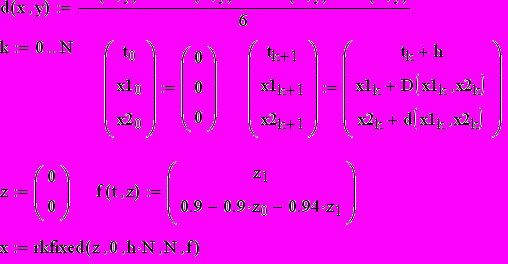
4. Методы оптимизации

В инженерных расчетах ЭВМ используют в основном для выполнения объемных вычислений или для выбора оптимальных параметров проектируемых объектов или процессов. Ряд алгоритмов оптимизации приведен в [1].

При исследовании моделируемых процессов и объектов, кроме устойчивости интересует качество переходных процессов, происходящих в моделируемом объекте. Важнейшими показателями качества переходного процесса являются: время регулирования и колебательность переходного процесса. Характер переходного процесса определяется порядком и коэффициентами дифференциального уравнения, являющегося математической моделью исследуемого процесса или объекта.

Если в переходном процессе отклонение переменной дифференциального уравнения от установившегося значения по абсолютной величине только уменьшается, процесс называют монотонным. Если за время переходного процесса первая производная по времени изменяет знак, то процесс называют колебательным.

Колебательность переходного процесса для уравнения второго порядка может быть оценена по наличию комплексных корней в характеристическом уравнении. Для уравнений более высокого порядка наличие комплексных корней или их отсутствие еще не характеризует колебательности или монотонности переходного процесса.

Для оценки качества переходного процесса используют интегральные оценки:



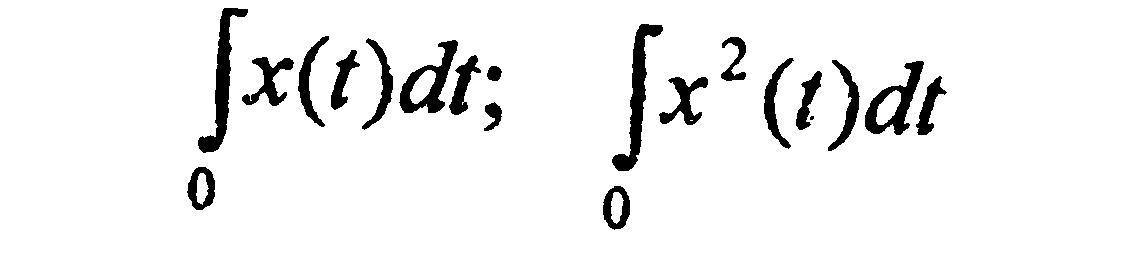
и др. Наибольшее распространение получила квадратичная интегральная оценка вида



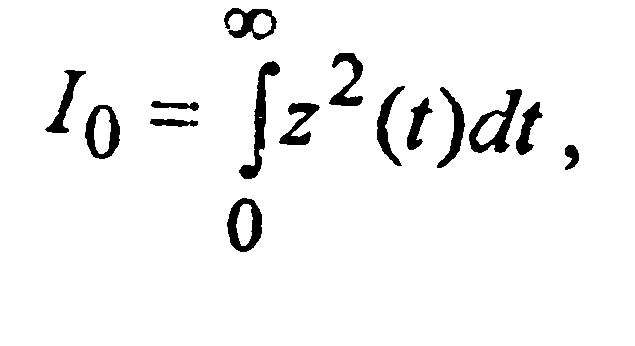
где z — разность между ординатами идеального и данного процессов; в нашем случае

z(t)=хвх—хвых.

Эту оценку можно получить двумя путями:

1) вычислением I0 после решения дифференциального уравнения;

2) вычислением I0, не прибегая к решению дифференциального уравнения.

С точки зрения затрат машинного времени наиболее выгоден второй путь.

Применительно к уравнению 2-го порядка:

(a2p2+a1p+a0)xвых = b0xвх (13)

Интегральная оценка по методу Красовского А.А. имеет вид:



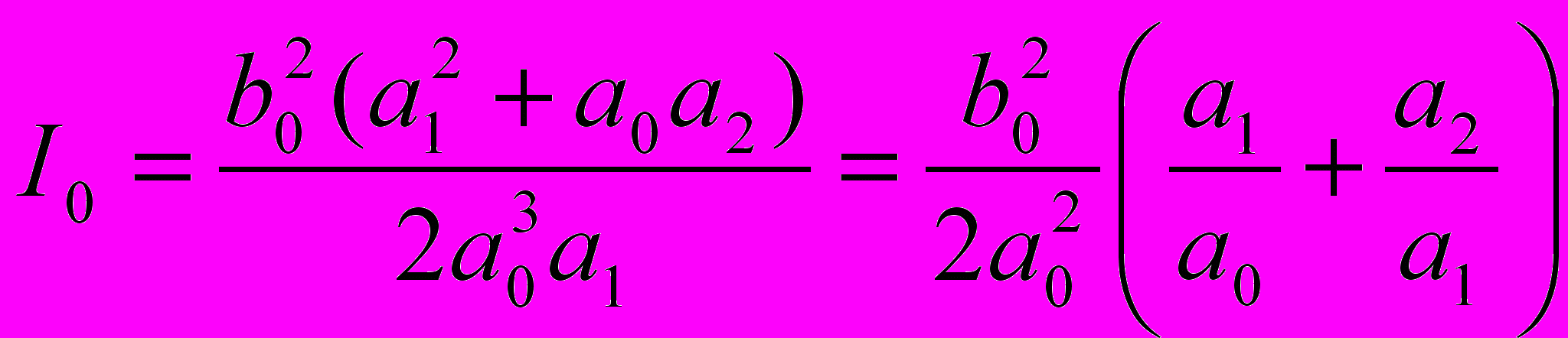
В нашем случае перед скобкой стоит постоянная величина, а коэффициент а2 =1, поэтому достаточно найти минимум:

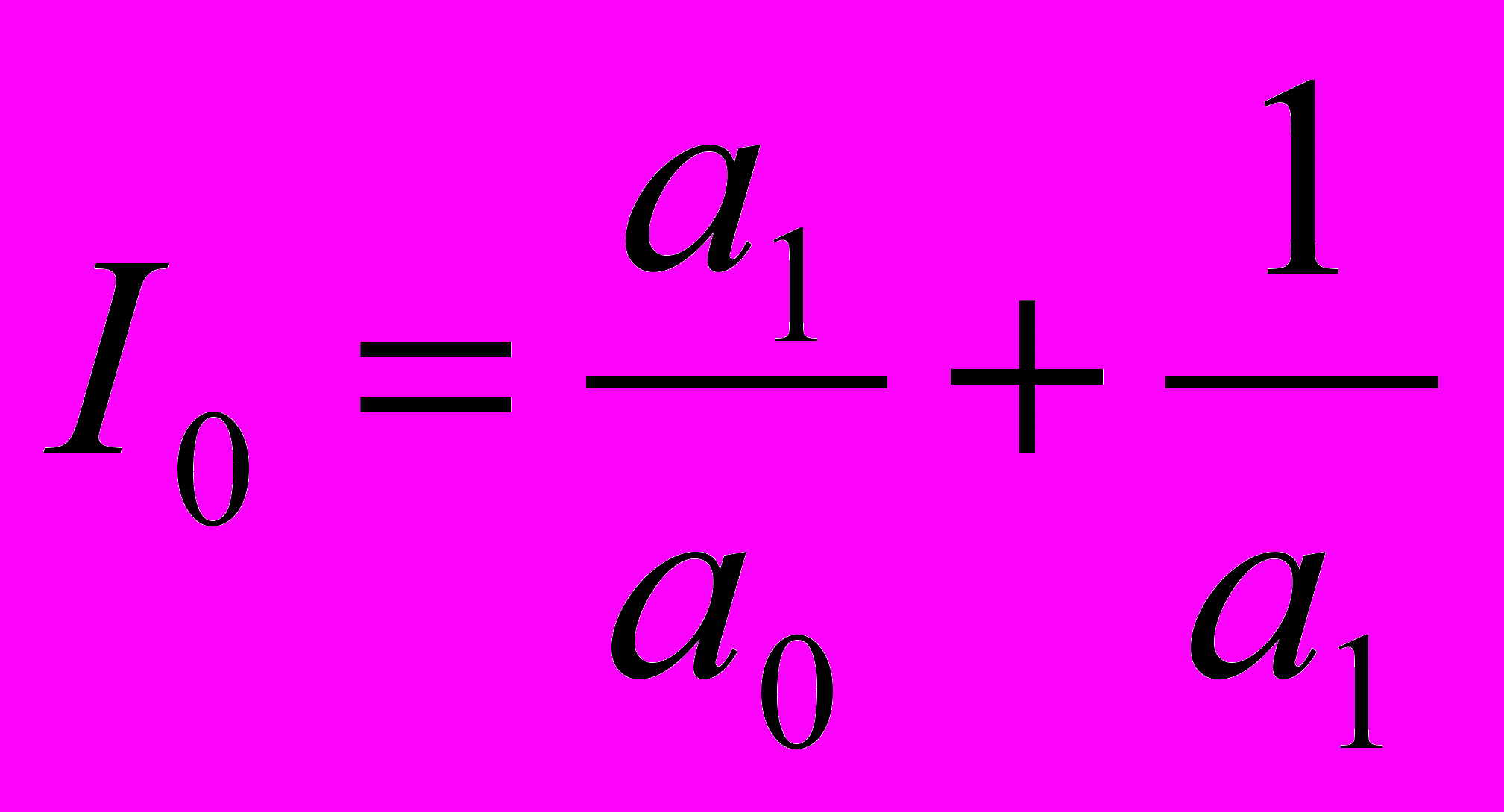(14)

В задании требуется найти оптимальное значение коэффициента демпфирования а1 минимизирующее оценку (14). Это можно сделать, взяв производную 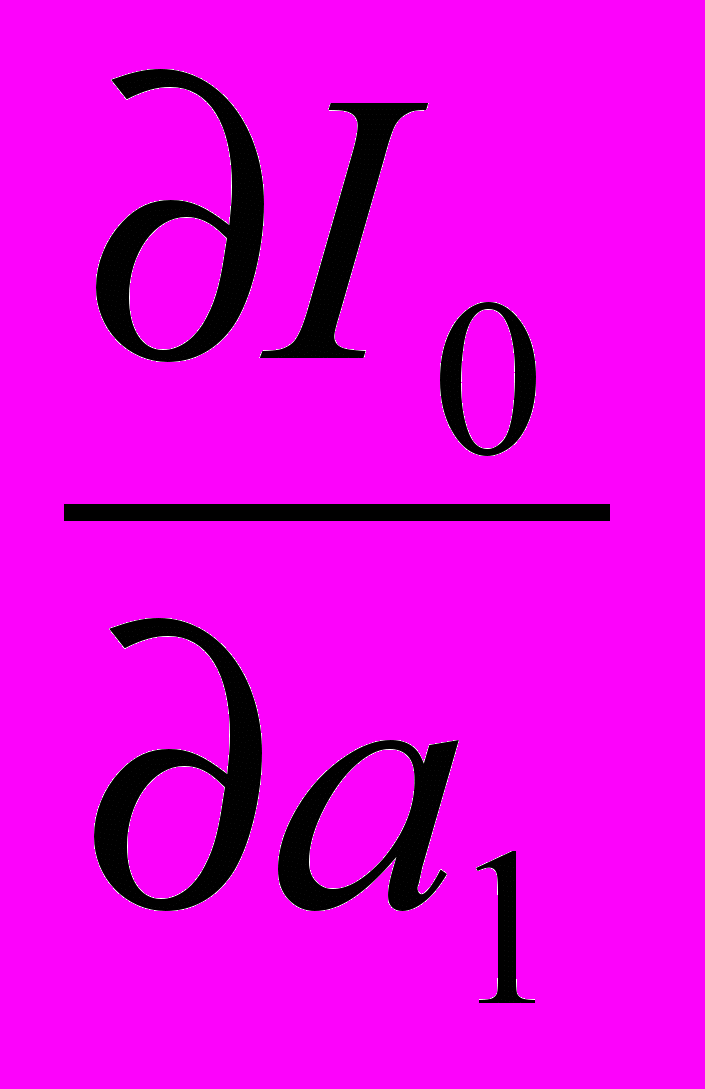— и приравняв ее к нулю.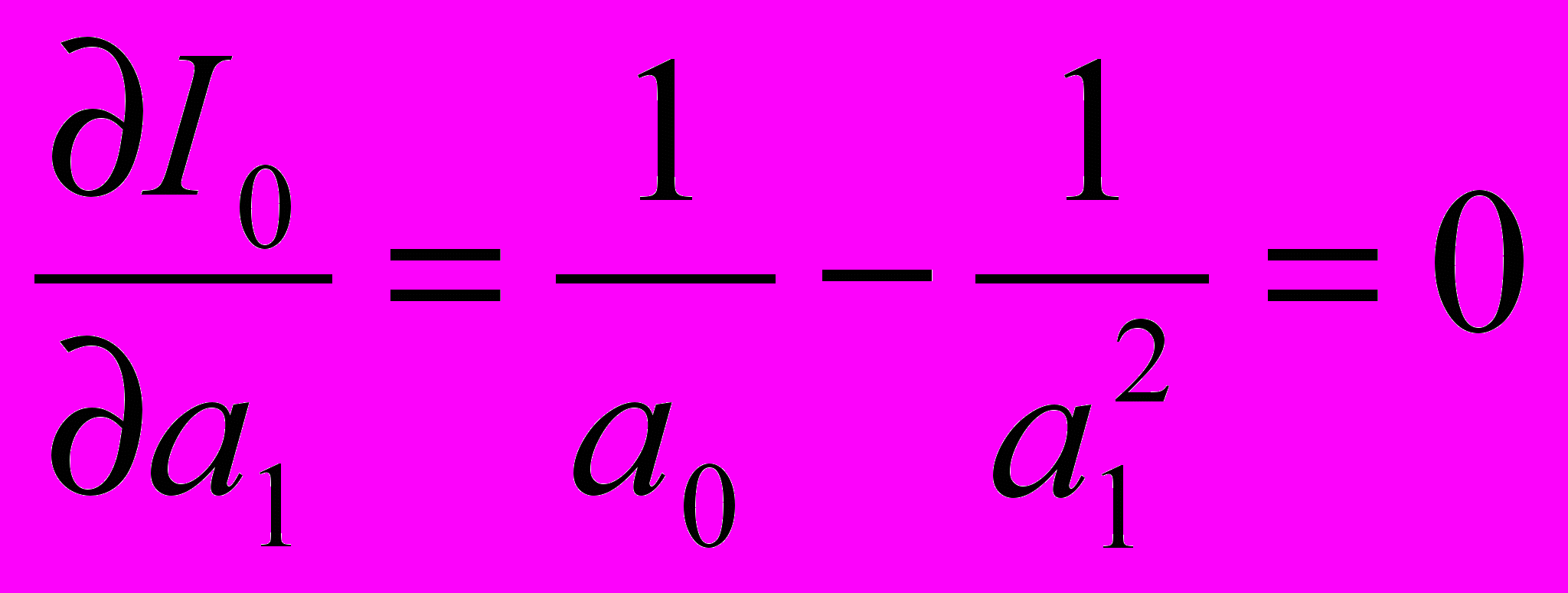



Отсюда .

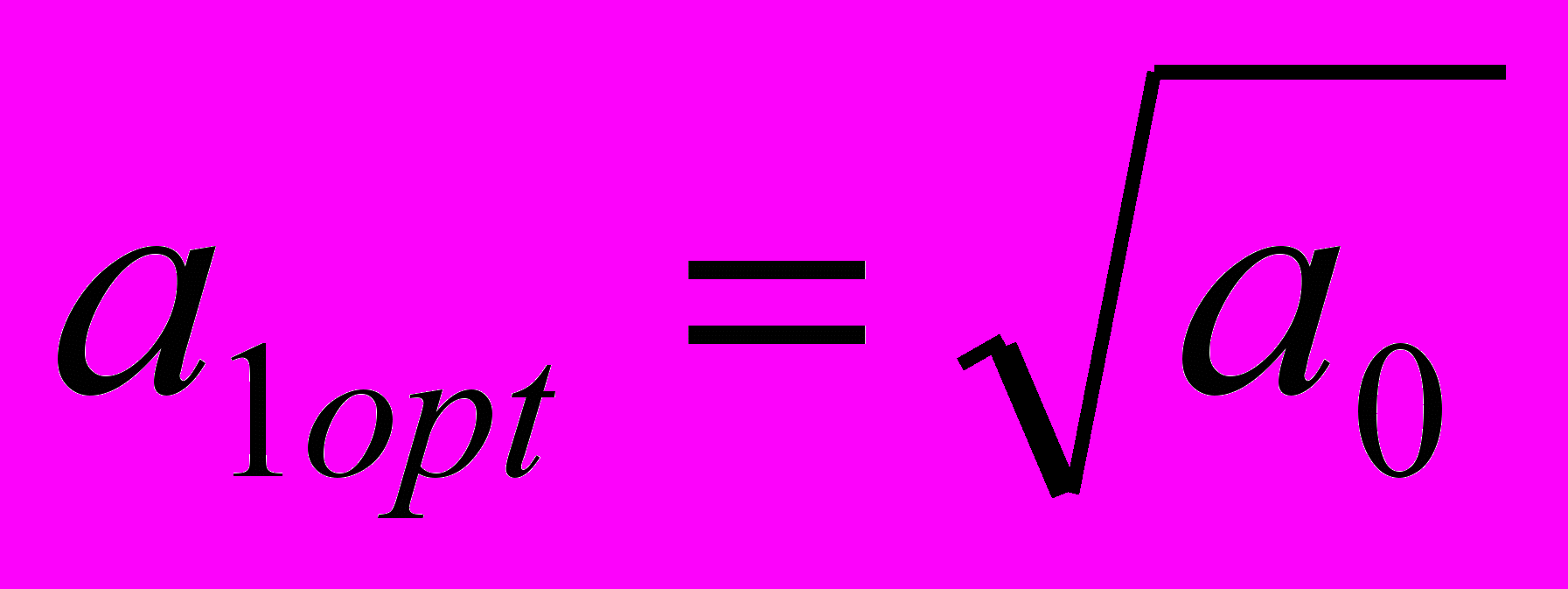Полученное значение а1opt следует подставить в программу Рунге-Кутты и определить новый вид переходного процесса.

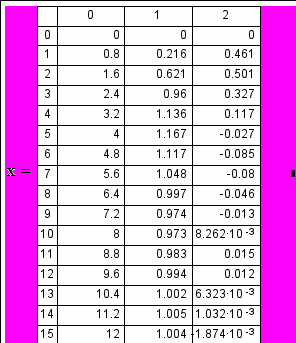
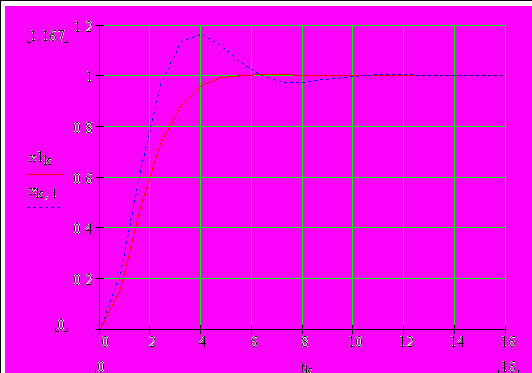
Для этого воспользуемся стандартной процедурой rkfixed, имеющейся в библиотеке Маткада. Эта программа приведена в нижней части рис. 3. Оба графика переходных процессов изображены для наглядности на одном поле. Кроме того, для контроля выведена таблица значений хвых и х'вых в зависимости от текущего времени t.

По полученному результату следует сделать выводы, а также определить оптимальные значения постоянной времени инерционного звена: ТДopt =1/a1opt