Geum.ru

Рабочая программа учебной дисциплины математические методы и комплексы программ решения задач устойчивости наименование магистерской программы

Вид материалаРабочая программа

Содержание


010400.68 Прикладная математика и информатика
Место дисциплины в структуре ООП ВПО
Требования к результатам освоения дисциплины
Структура и содержание дисциплины
Раздел учебной дисциплины
Формы текущегоконтроляуспеваемости(по неделямсеместра)
Образовательные технологии
Подобный материал:

Министерство образования и науки Российской Федерации

ГОУВПО «Мордовский государственный университет им. Н. П. Огарева»

Факультет математический

Кафедра систем автоматизированного проектирования

УТВЕРЖДАЮ

Декан математического факультета

проф. ______________ И. И. Чучаев

«____»_______________2011 г.

РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

МАТЕМАТИЧЕСКИЕ МЕТОДЫ И КОМПЛЕКСЫ ПРОГРАММ
РЕШЕНИЯ ЗАДАЧ УСТОЙЧИВОСТИ

Наименование магистерской программы Математическое и программное обеспечение вычислительных машин

Направление подготовки ^ 010400.68 Прикладная математика и информатика

Квалификация (степень) выпускника Магистр

Форма обучения Очная

г. Саранск – 2011 г.
  1. Цель освоения дисциплины

Целью освоения дисциплины является изучение методов математической теории устойчивости и их применение при моделировании различных объектов и процессов, описываемых системами обыкновенных дифференциальных уравнений большой размерности.

Она достигается решением следующих задач:
  • приобретение знаний о методах решения задач устойчивости решений линейных систем дифференциальных уравнений с постоянными и периодическими матрицами и нелинейных автономных систем дифференциальных уравнений, обладающих положениями равновесия;
  • приобретение навыков в построении математических моделей, описываемых системами обыкновенных дифференциальных уравнений, на примере электрических систем;
  • реализация математических моделей электрических систем и алгоритмов анализа их устойчивости в системе компьютерной математики MATLAB/Simulink.
  1. ^ Место дисциплины в структуре ООП ВПО

Данная дисциплина относится к циклу М.2 Профессиональный цикл и является дисциплиной по выбору студента. Для ее освоения необходимы знания, умения и компетенции, приобретенные в результате изучения следующих дисциплин:
  • Математический анализ – I;
  • Комплексный анализ;
  • Алгебра и геометрия;
  • Физика;
  • Основы информатики;
  • Дифференциальные уравнения;
  • Языки и методы программирования;
  • Численные методы.

Знания и умения, полученные в результате освоения данной дисциплины, могут быть использованы при подготовке студентом магистерской диссертации, а также в научной и практической деятельности после окончания университета.
  1. ^ Требования к результатам освоения дисциплины

Процесс изучения дисциплины направлен на формирование следующих компетенций:
  • способность использовать углубленные теоретические и практические знания в области прикладной математики и информатики (ОК-3);
  • способность проводить научные исследования и получать новые научные и прикладные результаты (ПК-1);
  • способность разрабатывать концептуальные и теоретические модели решаемых научных проблем и задач (ПК-2);
  • способность углубленного анализа проблем, постановки и обоснования задач научной и проектно-технологической деятельности (ПК-3).

В результате изучения дисциплины студент должен:

знать: методы решения задач устойчивости систем дифференциальных уравнений, сводящиеся к вычислению собственных значений матриц;

уметь: проводить доказательства утверждений, составляющих теоретическую основу дисциплины; применять изученные методы для исследования устойчивости решений систем дифференциальных уравнений; проводить программную реализацию изученных методов для решения задач устойчивости на персональном компьютере;

владеть: навыками решения задач устойчивости электрических систем.


  1. ^ Структура и содержание дисциплины

№
п/п
^ Раздел учебной дисциплины
Семестр
Неделя
семестра
Виды учебной
работы и
трудоемкость
(в часах)
^ Формы текущего
контроля
успеваемости
(по неделям
семестра)
Форма
промежуточной
аттестации

лекц.
лабор.
зан.
сам.
раб.

1
2
3
4
5
6
7
8
9

1
Предварительные сведения из теории матриц
1
1, 3
1 – 3
3



6
проверка выполнения лабораторных работ и контрольных заданий (1 – 3 недели)



2
Предварительные сведения из теории линейных систем дифференциальных уравнений
1
3, 5
4 – 6
2



6
проверка выполнения лабораторных работ и контрольных заданий (4 – 6 недели)



3
Общие теоремы об устойчивости линейных систем дифференциальных уравнений
1
5, 7
7, 8
2



4
проверка выполнения лабораторных работ и контрольных заданий (7, 8 недели)



4
Устойчивость линейных систем дифференциальных уравнений с постоянными матрицами
1
7, 9
2, 4, 6, 8, 10, 12
9, 10
2
12
4
проверка выполнения лабораторных работ и контрольных заданий (2, 4, 6, 8 – 10, 12 недели)



5
Устойчивость линейных систем дифференциальных уравнений с непрерывными ограниченными матрицами
1
9, 11
11, 12
3



4
проверка выполнения лабораторных работ и контрольных заданий (11, 12 недели)



6
Устойчивость приводимых систем дифференциальных уравнений
1
13
13, 14
2



4
проверка выполнения лабораторных работ и контрольных заданий (13, 14 недели)





1
2
3
4
5
6
7
8
9

7
Устойчивость линейных систем дифференциальных уравнений с непрерывными периодическими матрицами
1
15
14, 16
15, 16
2
4
4
проверка выполнения лабораторных работ и контрольных заданий (14 – 16 недели)



8
Устойчивость квазилинейных систем дифференциальных уравнений
1
17
18
17, 18
2
2
4
проверка выполнения лабораторных работ и контрольных заданий (17, 18 недели)
зачет
  1. ^ Образовательные технологии

Изучение данной дисциплины предполагает использование коллективных способов обучения, технологий личностно-ориентированного, проблемного, модульного и дифференцированного обучения. Для студентов, проявляющих повышенный интерес к изучению дисциплины, возможно применение технологий проектной деятельности и исследовательского обучения. В рамках изучения дисциплины имеют место также интерактивные формы обучения с применением информационных технологий.
  1. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов

Текущий контроль успеваемости проводится в форме проверки правильности выполнения лабораторных работ и контрольных заданий.

В процессе изучения дисциплины магистрант должен выполнить 10 лабораторных работ и 24 контрольных задания по темам лекционных занятий. Лабораторные работы выполняются на лабораторных занятиях, контрольные работы – в рамках самостоятельной работы.

Темы лабораторных работ:
    1. Моделирование простейшего трехфазного источника напряжения в системе MATLAB.
    2. Моделирование нерегулируемого трехфазного источника напряжения в системе MATLAB.
    3. Моделирование трехфазного источника напряжения с автоматическим регулятором возбуждения в системе MATLAB.
    4. Моделирование трехфазной симметричной статической нагрузки в системе MATLAB.
    5. Моделирование трехфазной электромеханической системы с симметричными статическими нагрузками в системе MATLAB.
    6. Анализ устойчивости трехфазной электромеханической системы с симметричными статическими нагрузками в системе MATLAB.
    7. Моделирование трехфазной несимметричной статической нагрузки в системе MATLAB.
    8. Моделирование и анализ устойчивости трехфазной электромеханической системы с несимметричной статической нагрузкой в системе MATLAB.
    9. Моделирование трехфазного источника напряжения с регулятором частоты в системе MATLAB.
    10. Моделирование и анализ устойчивости нелинейной трехфазной электромеханической системы в MATLAB.

Методические указания для выполнения лабораторных работ имеют вид раздаточных материалов и выдаются магистрантам непосредственно на лабораторных занятиях.

Темы контрольных заданий:
  1. Доказать утверждение, связанное с векторной нормой, например: если 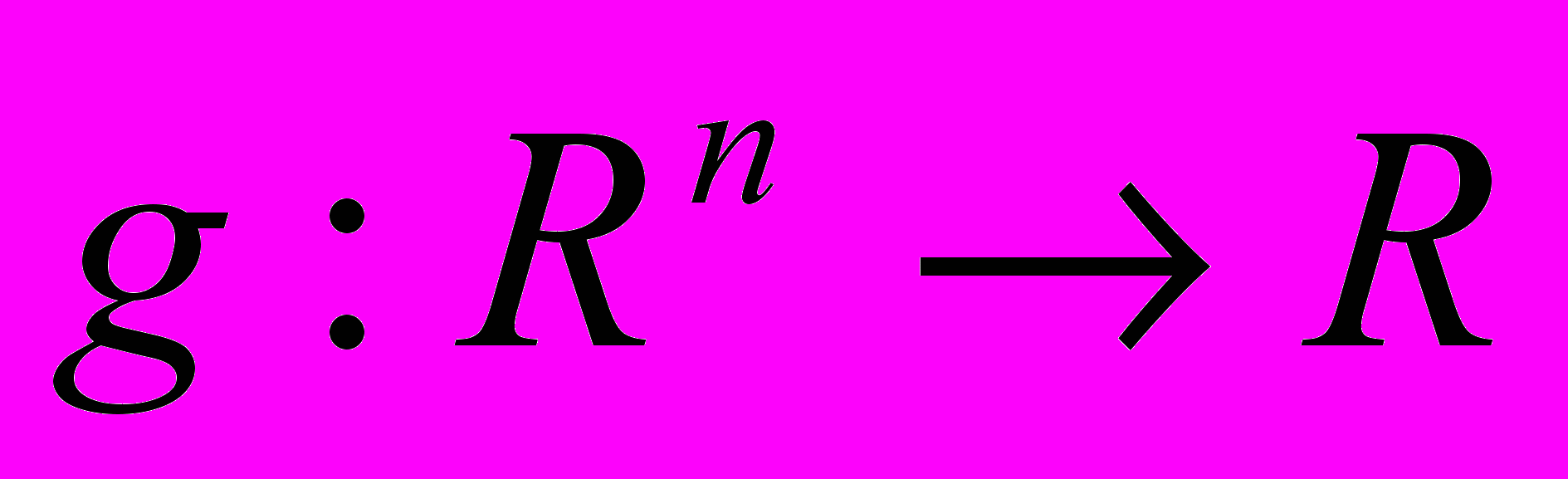– векторная норма и 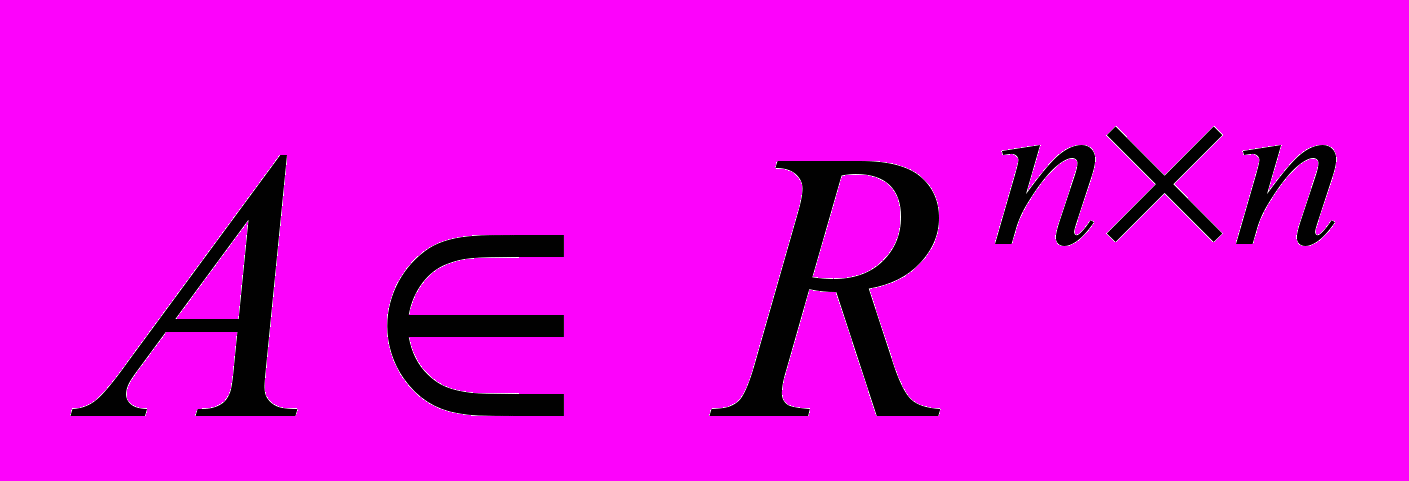– неособенная матрица, то функция 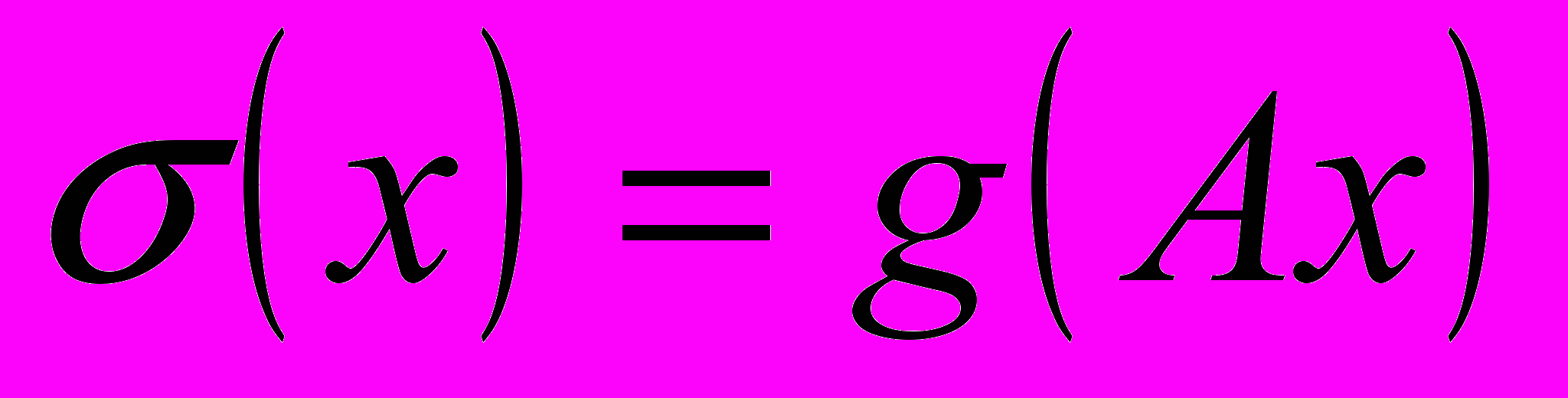также будет являться векторной нормой.
  2. Доказать утверждение, связанное с матричной нормой, например: используя определение матричной нормы, проверить, будет ли являться функция .
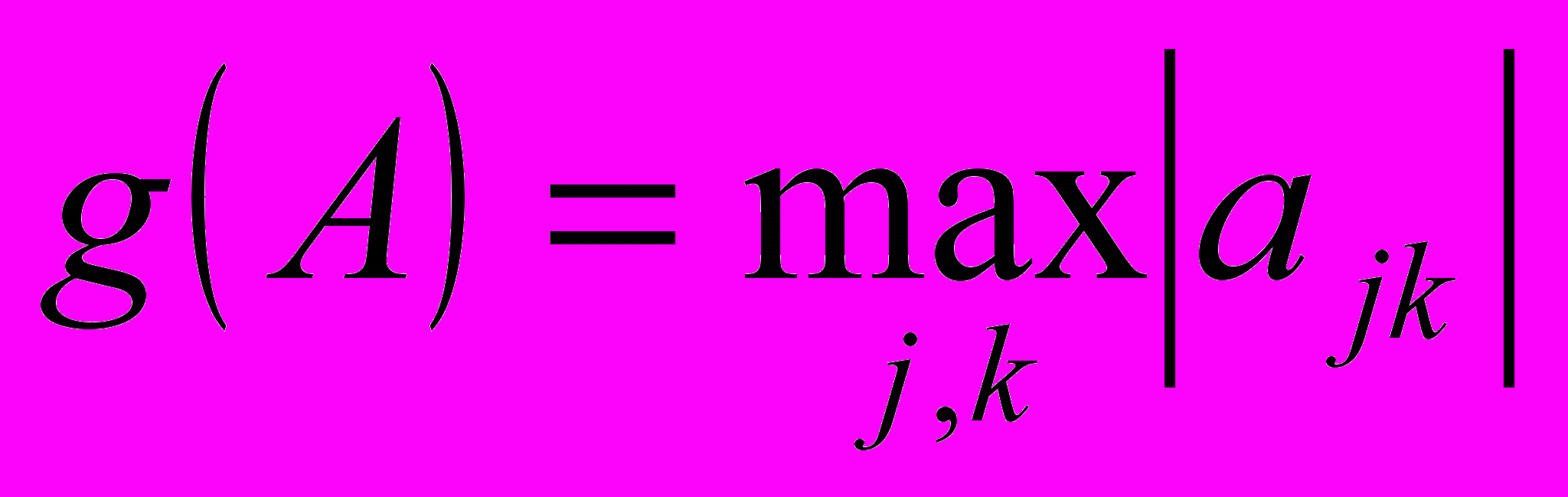  3. Привести к жордановой форме квадратную матрицу и определить матрицу 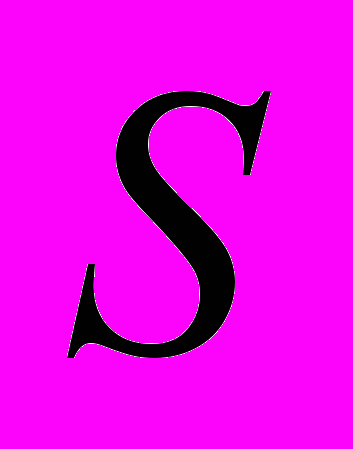, которая преобразует к жордановой форме.
  4. Определить нормальную форму экспоненты квадратной матрицы .
  5. Определить главное значение логарифма квадратной матрицы .
  6. Для линейной однородной системы дифференциальных уравнений 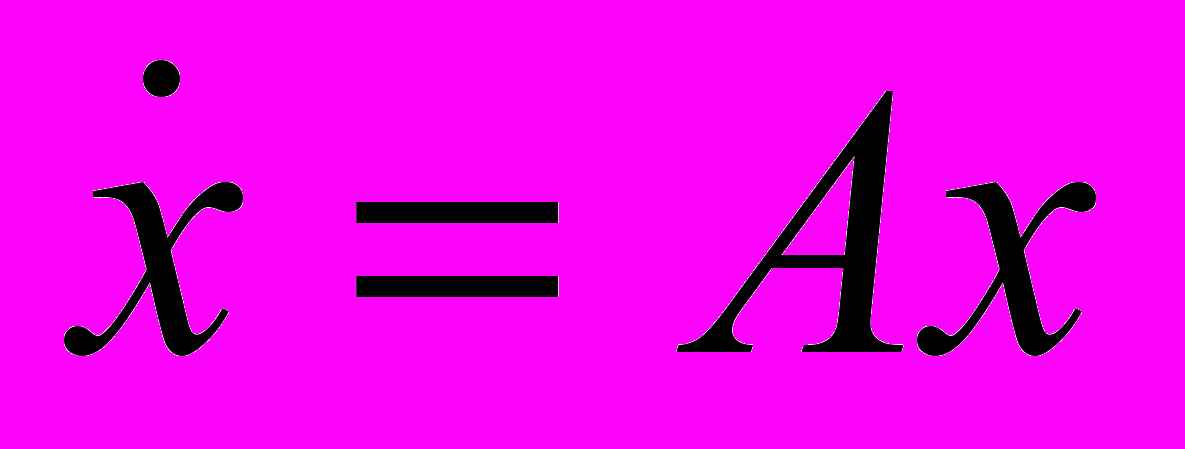с постоянной матрицей найти общее решение и частное решение, удовлетворяющее начальному условию .
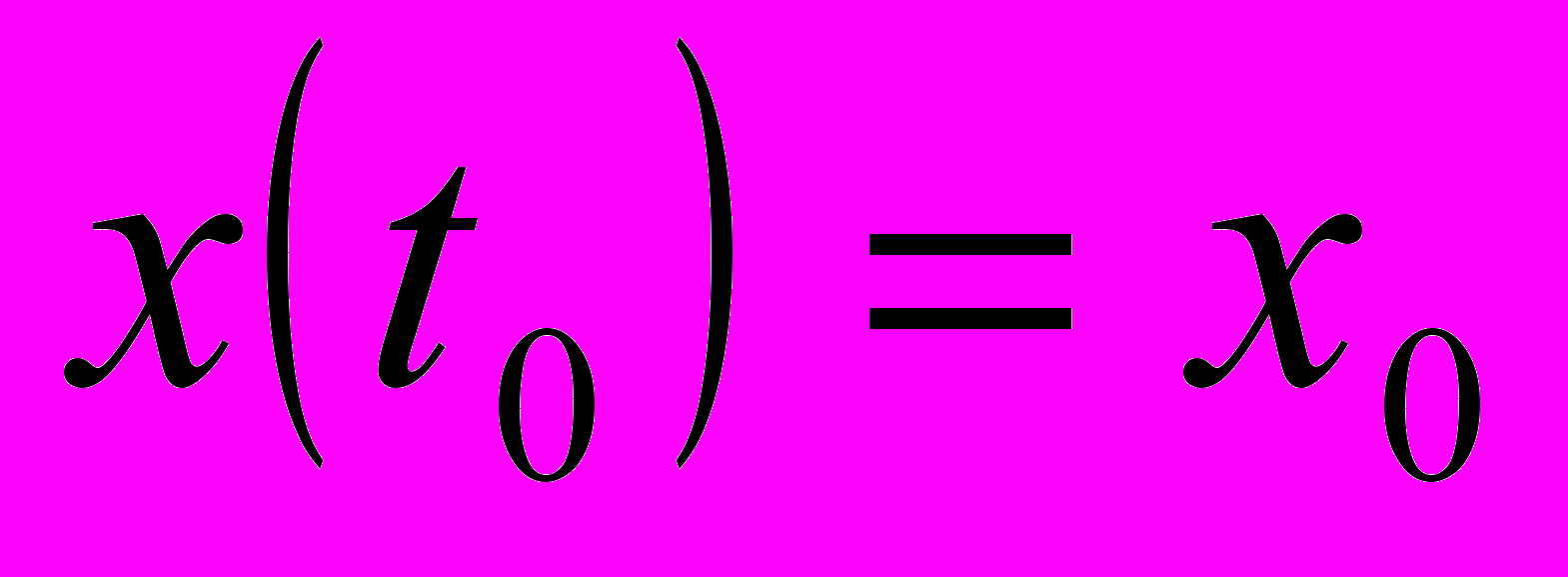  7. Используя определение устойчивости по Ляпунову, доказать, что дифференциальное уравнение 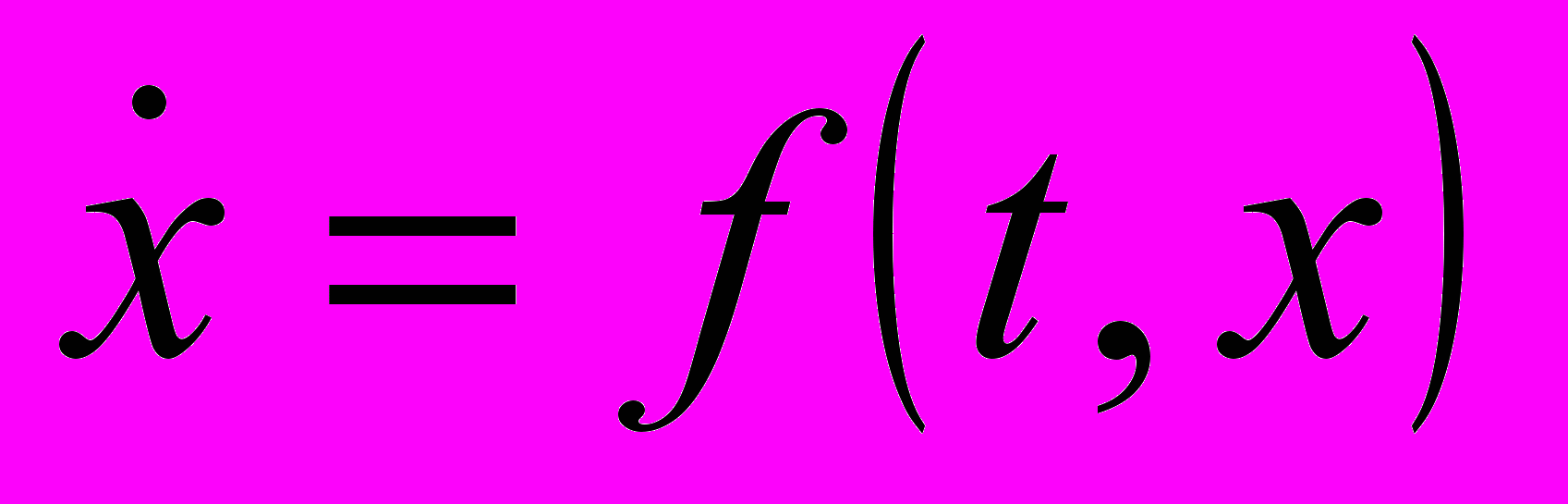, удовлетворяющее начальному условию 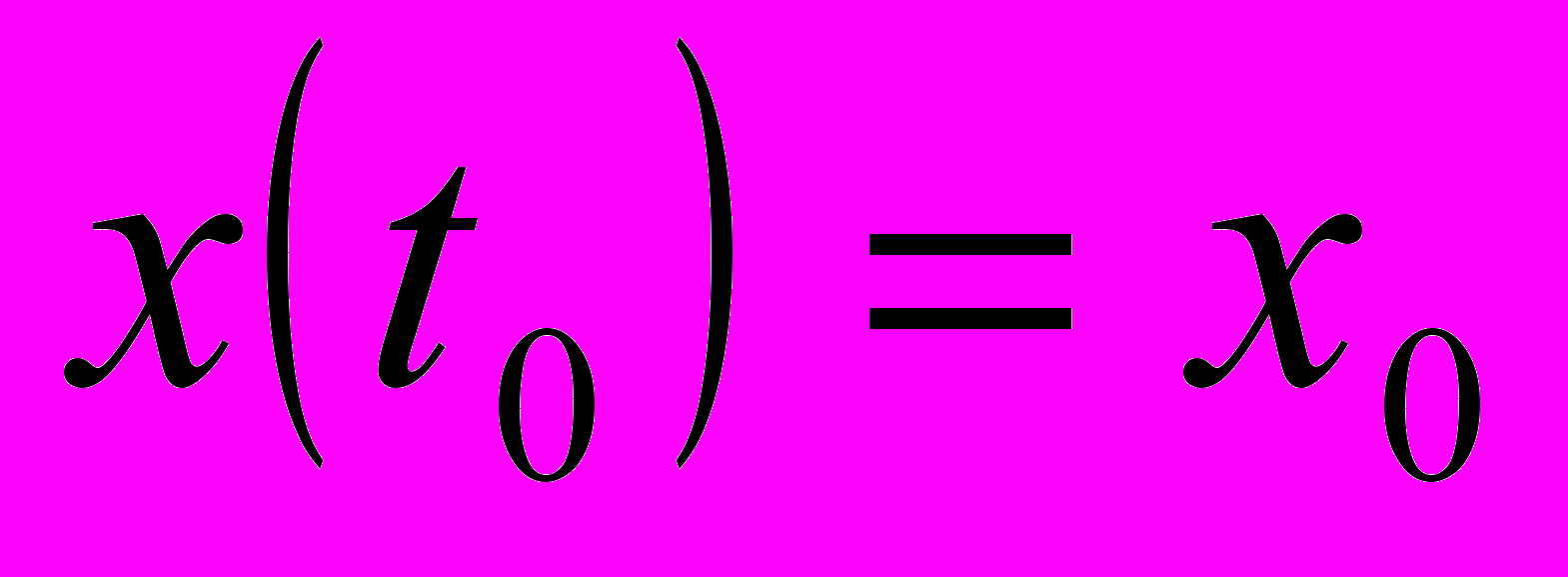, является устойчивым.
  8. Используя определение неустойчивости по Ляпунову, доказать, что дифференциальное уравнение 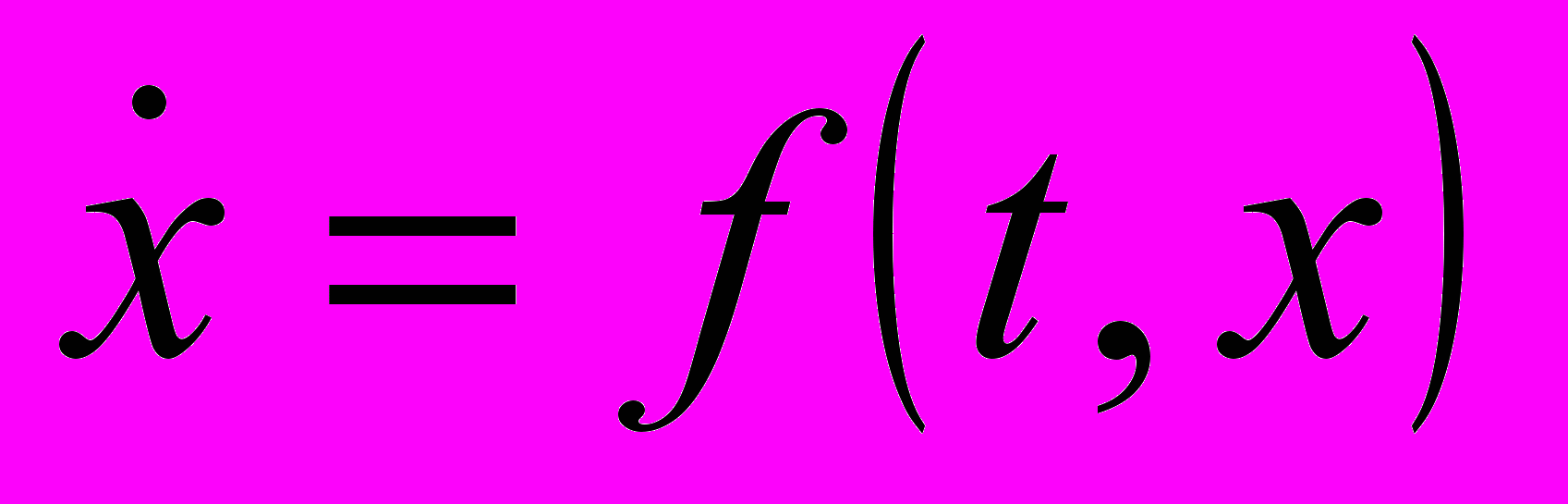, удовлетворяющее начальному условию 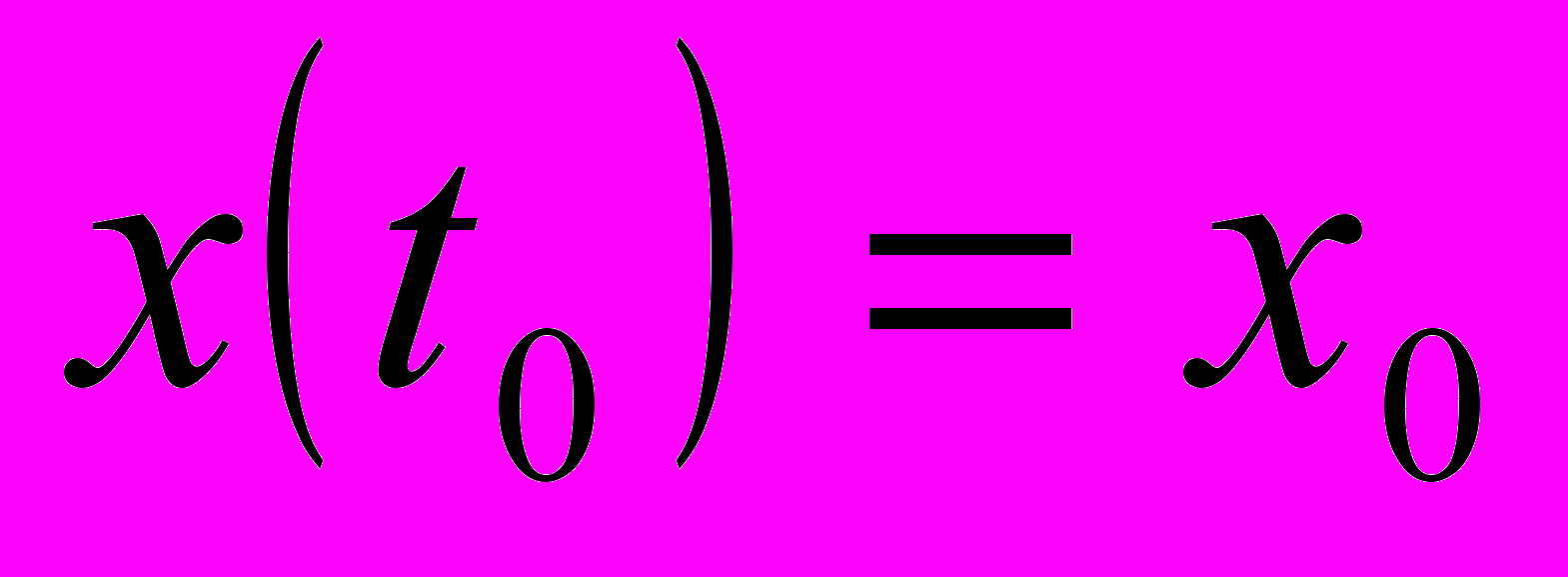, является неустойчивым.
  9. Используя определение асимптотической устойчивости по Ляпунову, доказать, что дифференциальное уравнение 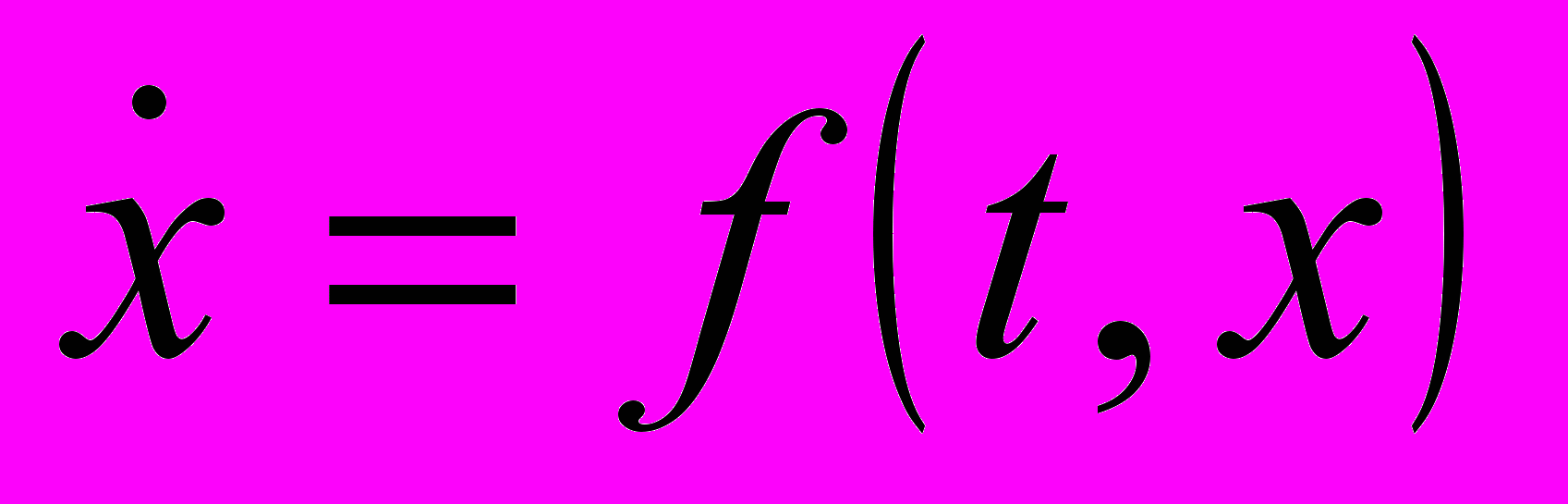, удовлетворяющее начальному условию 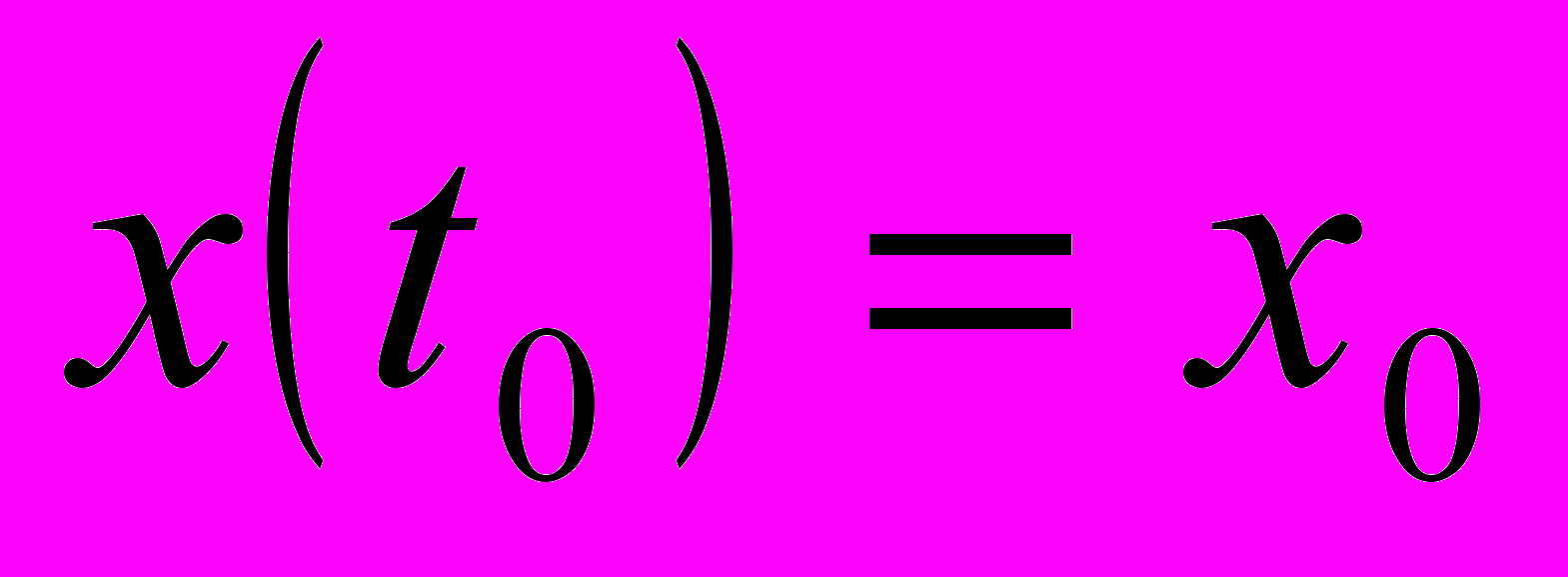, является асимптотически устойчивым.
  10. Используя одно из определений устойчивости, исследовать устойчивость тривиального решения дифференциального уравнения .
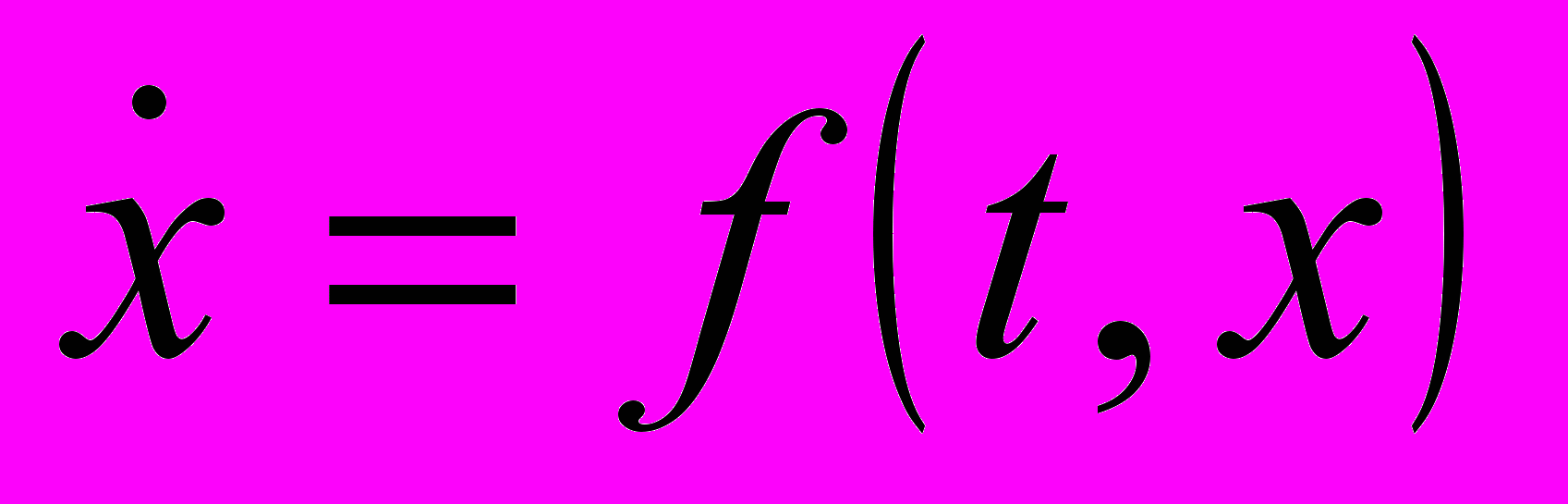  11. Используя теоремы об устойчивости линейной однородной системы дифференциальных уравнений, исследовать устойчивость системы .
  12. Используя теоремы об устойчивости линейной однородной системы дифференциальных уравнений с постоянной матрицей, исследовать устойчивость системы .
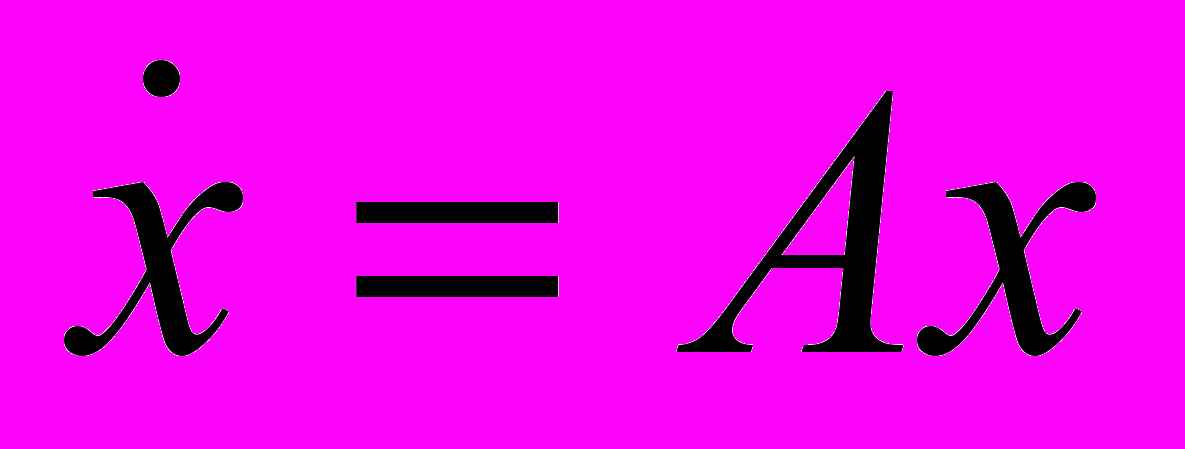  13. Используя теоремы Рауса-Гурвица, исследовать устойчивость линейной однородной системы дифференциальных уравнений 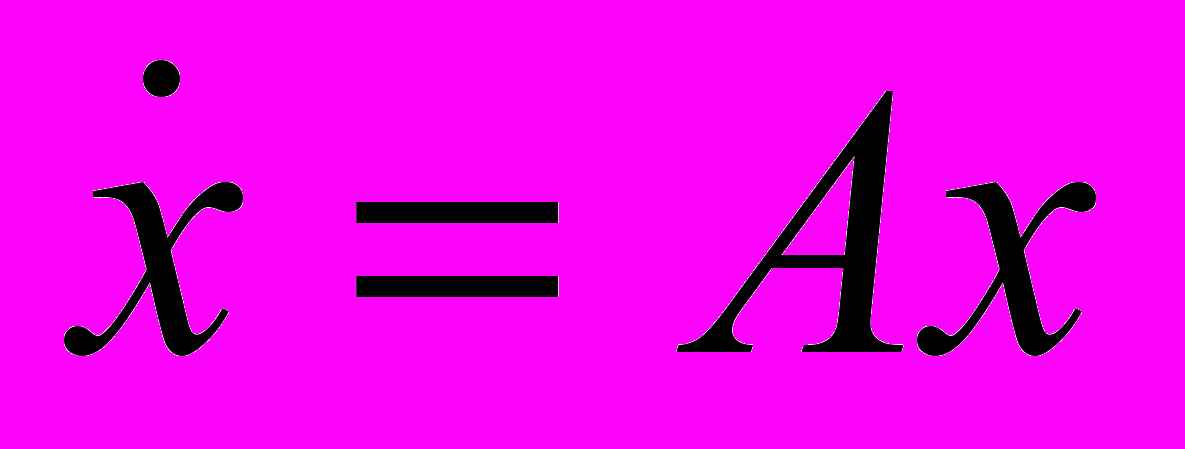с постоянной матрицей .
  14. Используя теоремы Рауса-Гурвица, определить область асимптотической устойчивости линейной однородной системы дифференциальных уравнений с постоянной матрицей относительно параметра .
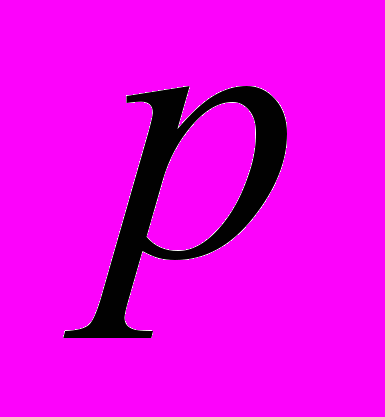  15. Определить спектр линейной однородной системы дифференциальных уравнений .
  16. Определить, является ли матрица 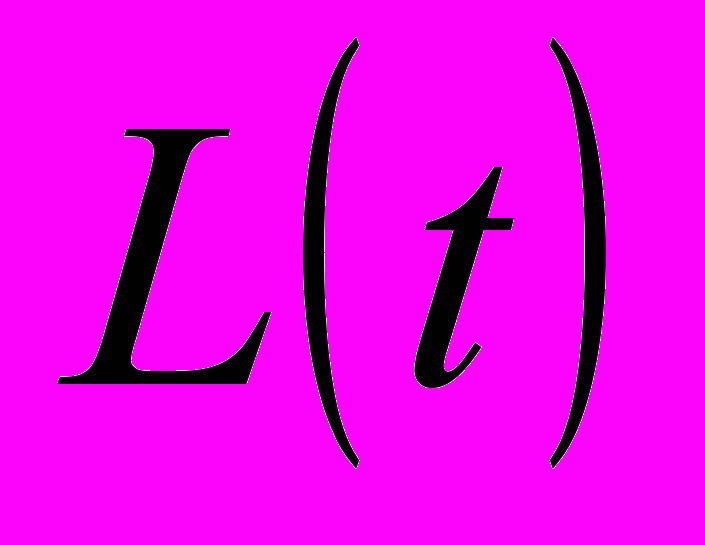матрицей Ляпунова.
  17. Доказать, что линейная однородная система дифференциальных уравнений 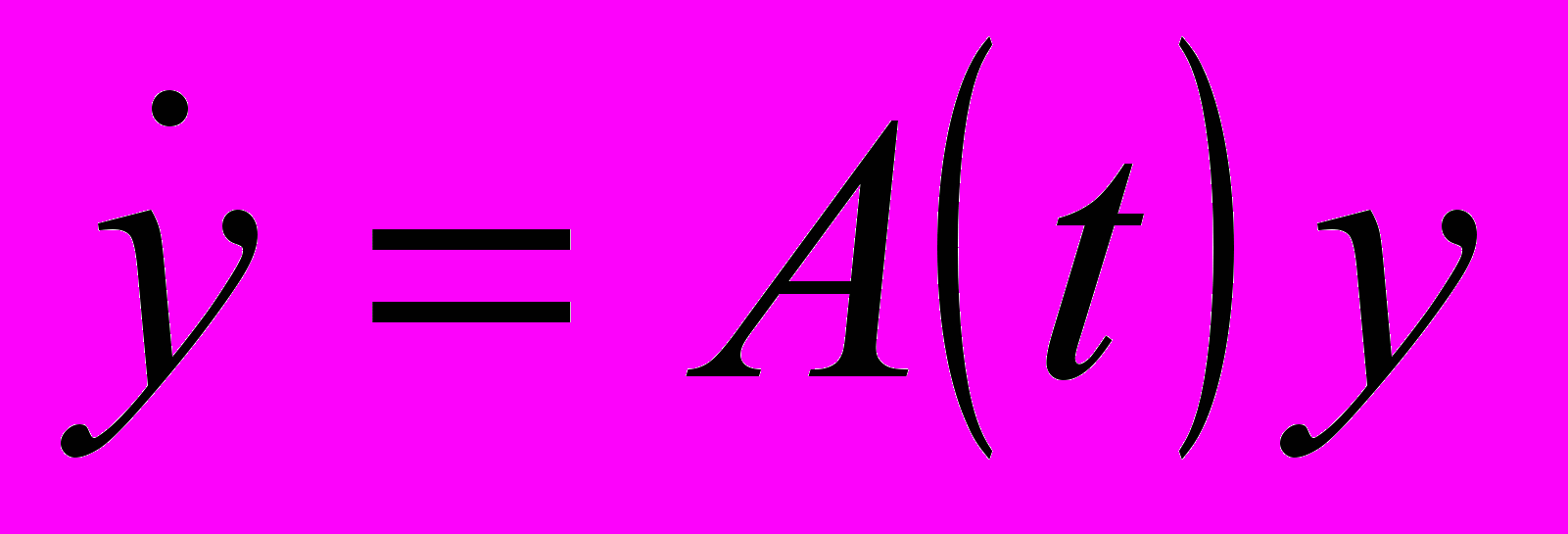с помощью преобразования Ляпунова 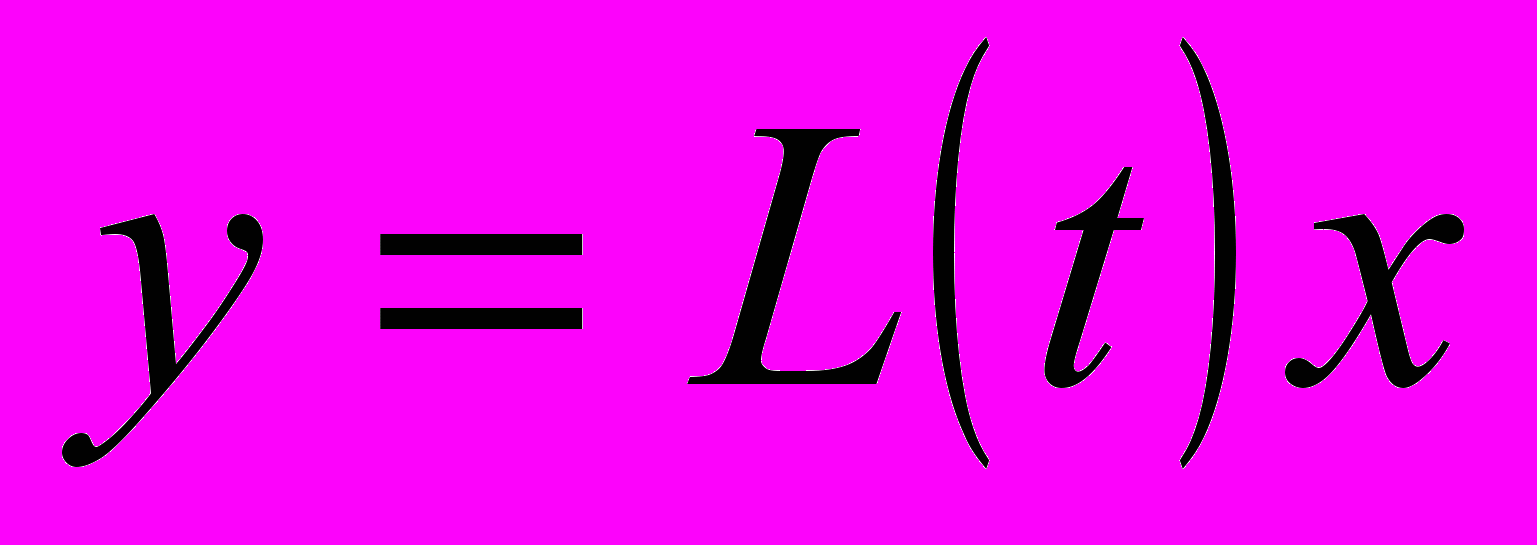приводится к системе с постоянной матрицей.
  18. Определить мультипликаторы и характеристические показатели линейной однородной системы дифференциальных уравнений с непрерывной периодической матрицей .
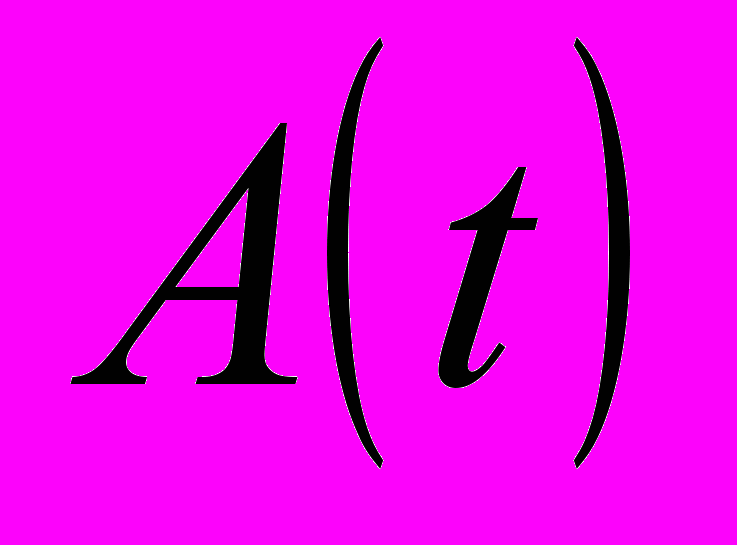  19. Для линейной однородной системы дифференциальных уравнений с непрерывной периодической матрицей 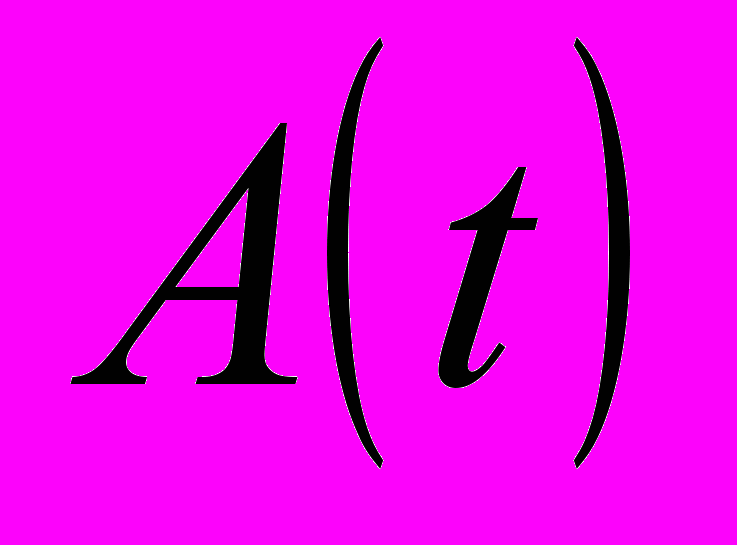определить матрицу Ляпунова 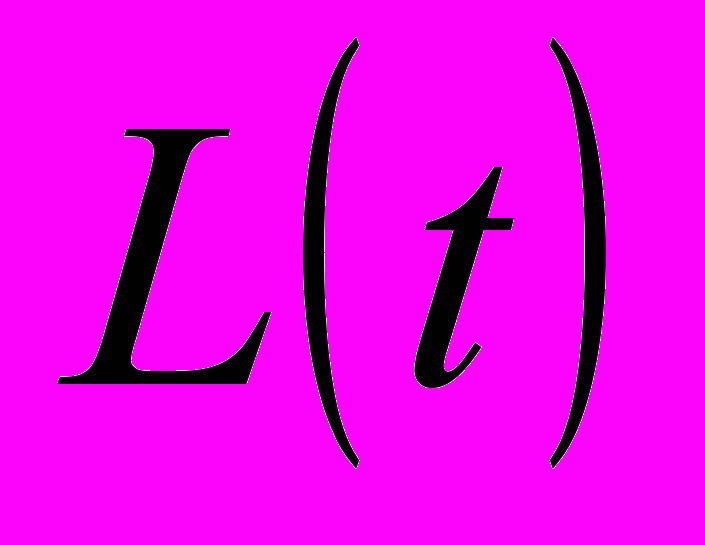, с помощью которой она приводится к системе с постоянной матрицей.
  20. Исследовать устойчивость линейной однородной системы дифференциальных уравнений с непрерывной периодической матрицей .
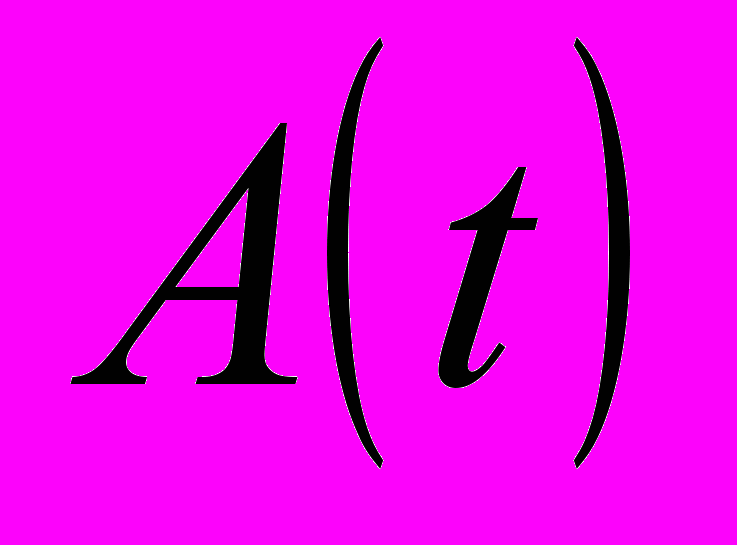  21. Используя алгоритм приближенного построения матрицы монодромии, вычислить мультипликаторы линейной однородной системы дифференциальных уравнений с непрерывной периодической матрицей 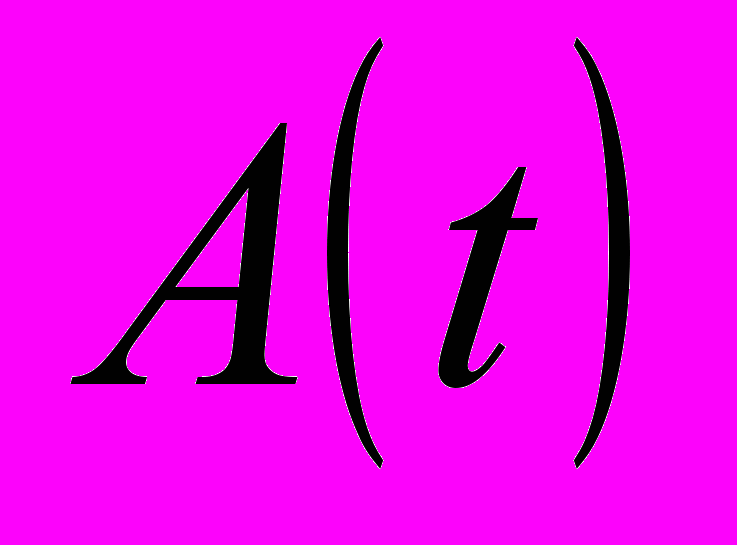и исследовать устойчивость системы.
  22. Исследовать по первому приближению устойчивость тривиального решения нелинейной автономной системы дифференциальных уравнений .
  23. Определить, при каких значениях параметров и тривиальное решение нелинейной автономной системы дифференциальных уравнений 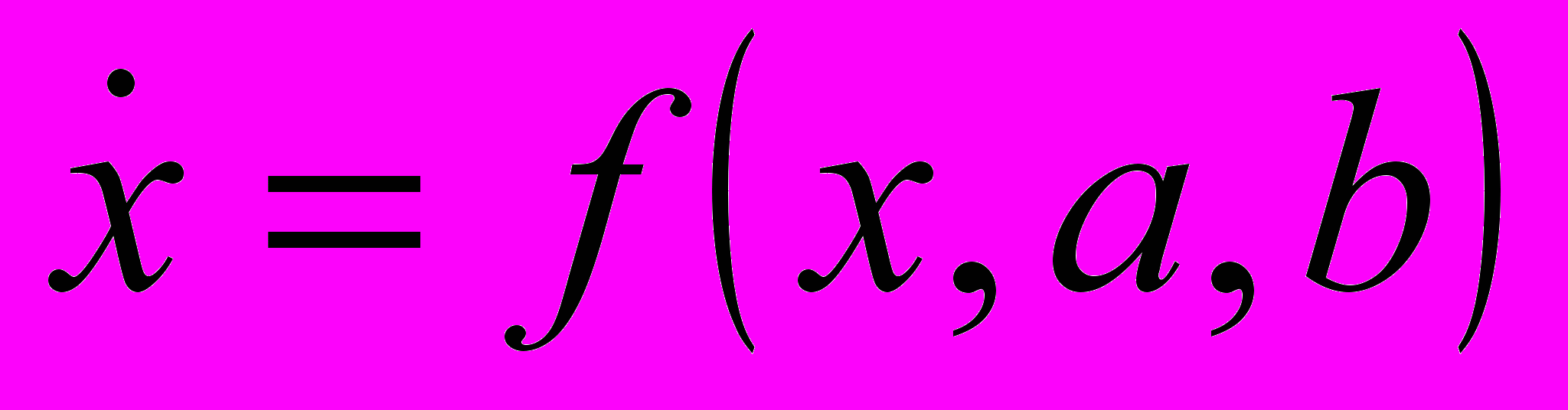является асимптотически устойчивым.
  24. Вычислить все положения равновесия нелинейной автономной системы дифференциальных уравнений и исследовать их устойчивость.

Методические указания для выполнения контрольных заданий предоставляются магистрантам в процессе чтения лекций. Варианты заданий выдаются в электронной форме в формате документа Microsoft Word.

По каждой лабораторной работе и каждому контрольному заданию магистрант готовит отчет. Отчет по лабораторным работам выполняется в форме компьютерной презентации, в процессе которой и проверяется работоспособность моделируемой системы. Отчет по контрольным заданиям выполняется в рукописной форме и оформляется в тетради для контрольных работ. Если лабораторная работа или контрольное задание выполнены верно, то за их выполнение ставится отметка «зачтено», в противном случае работа или задание возвращается магистранту на доработку.

Результаты выполнения лабораторных работ и контрольных заданий и являются допуском магистранта к зачету, который является формой промежуточной аатестации. Для допуска к зачету должны быть выполнены все лабораторные работы и контрольные задания.

На зачете магистранту предлагается ответить на один теоретический вопрос и решить практическое задание по одной из тем дисциплины. Если магистрант дает развернутый ответ на теоретический вопрос, решает практическое задание, не допуская грубых ошибок, и отвечает на дополнительные вопросы в рамках программы дисциплины, то ему выставляется отметка «зачтено». В противном случае выставляется отметка «не зачтено». В этом случае должна быть проведена пересдача магистрантом зачета в соответствии с правилами, установленными в университете.
  1. Учебно-методическое и информационное обеспечение учебной дисциплины
  1. основная литература
    1. Беллман Р. Теория устойчивости решений дифференциальных уравнений: пер. с англ. / Р. Беллман. – 2-е изд., стер. – М.: Едиториал УРСС, 2003. – 216 с.
    2. Демидович Б. П. Лекции по математической теории устойчивости / Б. П. Демидович. – 3-е изд., стер. – М.: Лань, 2008. – 480 с. – (Серия «Учебники для вузов. Специальная литература»).
    3. Дьяконов В. П. MATLAB R2006/2007/2008. Simulink 5/6/7. Основы применения / В. П. Дьяконов. – М.: СОЛОН-Пресс, 2008. – 800 с. – (Серия «<Библиотека профессионала»).
    4. Малкин И. Г. Теория устойчивости движения / И. Г. Малкин. – 3-е изд. – М.: Лань, 2010. – 432 с.
  2. дополнительная литература
    1. Алфутов Н. А. Устойчивость движения и равновесия / Н. А. Алфутов, К. С. Колесников. – 2-е изд., стер. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2003. – 256 с. – (Серия «Механика в техническом университете»).
    2. Белов В. Ф. Функциональное моделирование в системе компьютерной математики MATLAB : учеб. пособие / В. Ф. Белов, Д. В. Логинов, А. Н. Мадонов. – Саранск: Изд-во Мордов. ун-та, 2006. – 168 с.
    3. Гелиг А. Х. Устойчивость и стабилизация нелинейных систем / А. Х. Гелиг, И. Е. Зубер, А. Н. Чурилов. – СПб.: Изд-во Санкт-Петерб. ун-та, 2006. – 270 с.
    4. Краснов М. Л. Операционное исчисление. Теория устойчивости: Задачи и примеры с подробными решениями / М. Л. Краснов, А. И. Киселев, Г. И. Макаренко. – 4-е изд. – М.: Либроком, 2009. – 176 с. – (Серия «Вся высшая математика в задачах»).
    5. Ляпунов А. М. Общая задача об устойчивости движения / А. М. Ляпунов. – М.: Меркурий-Пресс, 2000. – 386 с.
    6. Меркин Д. Р. Введение в теорию устойчивости движения / Д. Р. Меркин. – 4-е изд., стер. – М.: Лань, 2003. – 304 с. – (Серия «Учебники для вузов. Специальная литература»).
    7. Меркин Д. Р. Задачи по теории устойчивости / Д. Р. Меркин, С. М. Бауэр, А. Л. Смирнов. – М.-Ижевск, Институт компьютерных исследований, 2002. – 128 с.
    8. Филатов А. Н. Теория устойчивости / А. Н. Филатов. – М.-Ижевск: Институт компьютерных исследований, 2003. – 220 с.
  1. Материально-техническое обеспечение дисциплины

Для проведения лекционных занятий и практических занятий по учебной дисциплине необходима аудитория на 30 посадочных мест, оборудованная доской. Лекции проводятся в форме компьютерных презентаций, поэтому аудитория должна быть укомплектована следующим оборудованием:
  • портативным персональным компьютером класса «ноутбук» или «нетбук»; на нем должно быть установлено программное обеспечение, включающее операционную систему MS Windows XP (или более поздней версии) и редактор презентаций MS PowerPoint (версии 2002 или более поздней);
  • настенным экраном или интерактивной доской.

Лабораторные занятия требуют использования персональных компьютеров. Поэтому для их проведения необходима лаборатория на 15 рабочих мест. Каждое рабочее место должно быть оборудовано персональным компьютером конфигурации IBM PC или совместимой с ней, двумя электрическими розетками для подключения системного блока и периферийных устройств и компьютерным столом для их размещения. Все компьютеры должны быть объединены в локальную сеть с возможностью доступа к ресурсам сети Internet.

Каждый компьютер должен иметь следующую аппаратную конфигурацию:
  • 4-ядерный процессор семейства Intel Core 2 Quad или более производительный;
  • оперативную память объемом не менее 4 Гб;
  • жесткий диск объемом не менее 500 Гб;
  • дисковод оптических дисков класса DVD-RW;
  • монитор с диагональю не менее 17";
  • стандартную клавиатуру (102 клавиши или более);
  • манипулятор «мышь» оптического типа с тремя кнопками и колесом прокрутки;
  • коврик для манипулятора «мышь» оптического типа.

На каждом компьютере должно быть установлено следующее программное обеспечение:
  • сетевая операционная система семейства Microsoft Windows (Windows XP или более поздняя);
  • система компьютерной математики MATLAB версии R13 или более поздней, включающая оба первичных программных продукта (MATLAB и Simulink) корпорации The MathWorks, Inc.

Желательно, не реже чем один раз в два года, проводить обновление аппаратного и программного обеспечения лаборатории, поскольку развитие информатики и информационных технологий приводит к их быстрому моральному устареванию, что естественным образом отрицательно повлияет на качество подготовки студентов.

Авторы (разработчики):

кафедра САПР доцент А. Н. Мадонов

(место работы) (занимаемая должность) (инициалы, фамилия)

Рецензенты (эксперты):

(место работы) (занимаемая должность) (инициалы, фамилия)

Программа ободрена на заседании _______________________________________________________
от «___» _________________ 2011 г., протокол № ___.