Линейные пространства
| Вид материала | Документы |
- Программа обсуждена на заседании кафедры Математики фнти, 80.49kb.
- Программа по курсу «Функциональный анализ», 36.73kb.
- Некорректные задачи геофизики. План лекций. Лекция I. Функциональные пространства., 64.34kb.
- Программа для вступительных испытаний в магистратуру по специальности 050201м математика, 124.79kb.
- Лекции пр зан, 50.82kb.
- Анализа и теории функций календарный план учебных занятий по дисциплине «Высшая математика», 30.38kb.
- Учебная программа по дисциплине алгебра и геометрия краснобаев Ю. Л. Требования к обязательному, 51.89kb.
- Урок: «типы алгоритмов. Линейные алгоритмы» Тема: Типы алгоритмов. Линейные алгоритмы, 101.98kb.
- Анализ Авторы программы: академик Моисеев Е. И., профессор Шишмарев И. А. Лектор 2010/11, 23.27kb.
- Программа курса лекций «Линейные колебания» для студентов 1-го курса Введение, 37.05kb.
Линейные пространства.
Понятие линейного пространства относится к числу самых основных в математике. Оно будет играть важную роль.
Определение линейного пространства
Непустое множество L элементов х,у,z,... называется линейным пространством если оно удовлетворяет следующим условиям.
Для любых двух элементов х,у из L однозначно определен третий элемент z из L, называемый их суммой и обозначаемый х+у , причем
х+у = у+х,
х+(у+z) = (х+у)+z,
- ^
в L существует такой элемент 0, что х+0 = х для всех х из L (существование нуля),
для каждого х из L существует такой элемент –х, что х+(-х) = 0 (существование противоположного элемента).
Для любого числа ά и любого элемента х из L определен элемент άх из L (произведение элемента х на число ά), причем
Ά(β)х = (άβ)х,
1х = х,
(ά+β) = άх+βх,
ά(х+у) = άх+άу.
^
Некоторые примеры линейных пространств.
Прямая линия R1,т.е. совокупность действительных чисел, с обычными арифметическими операциями сложения и умножения.
Совокупность всевозможных систем n действительных чисел х = (х1,х2,…, хn), где сложение и умножение на число определяются формулами (х1,х2,…, хn) + (у1,у2,…,уn) =(х1+ у1,х2+ у2,…, хn+ уn), ά (х1,х2,…, хn)= (ά х1, ά х2,…, ά хn), оно называется действительным n-мерным пространством.
Линейный функционал.
Числовую функцию f, определенную на некотором линейном пространстве L, называют линейным функционалом. Функционал f называют аддитивным, если f(х+у) = f(х)+f(у) для всех х из L; он называется однородным, если f(ά х) = ά f(х) (ά -произвольное число).
Функционал f, определенный в комплексном линейном пространстве, называется сопряжено-однородным, если f(ά х) = βf(х), где β-число, комплексно сопряженное ά.
^Аддитивный однородный функционал называется линейным функционалом. Аддитивный сопряжено-однородный функционал называется сопряжено-линейным, а иногда полулинейным.
^Определение и примеры нормированных пространств.
Пусть L – линейное пространство. Однородно-выпуклый функционал p, определенный на L, называется нормой, если он удовлетворяет следующим дополнительным условиям: p(х)=0, только при х=0, p(άх)=| ά | p(х) для всех ά. Таким образом мы можем сказать, что нормой в L называется функционал, удовлетворяющий следующим трем условиям:
- ^
p(х) ≥ 0, причем p(х)=0 только при х=0,
p(х+у) ≥ p(х)+p(у), х,у из L,
p(άх) = | ά | p(х), каково бы ни было число ά.
Линейное пространство L, в котором задана некоторая норма, называется нормированным пространством. Норма элемента х из L обозначается ||х||.
^Всякое нормированное пространство становится метрическим пространством, если ввести в нем расстояние p(х,у) = ||х - у||.
Справедливость аксиом метрического пространства тотчас же вытекают из свойств нормы. Полное нормированное пространство называется банаховым или, короче, В-пространством.
^Примеры нормированных пространств.
1. Прямая линия R1 становится нормированным пространством, если для всякого числа х из R1 положить ||х||= |х|.
2. Если в действительном n-мерном пространстве Rn с элементами х = (х1,х2,…, хn) положить ||х|| =  то все аксиомы нормы будут выполнены. Формула p(х,у) = ||х-у|| =
то все аксиомы нормы будут выполнены. Формула p(х,у) = ||х-у|| = 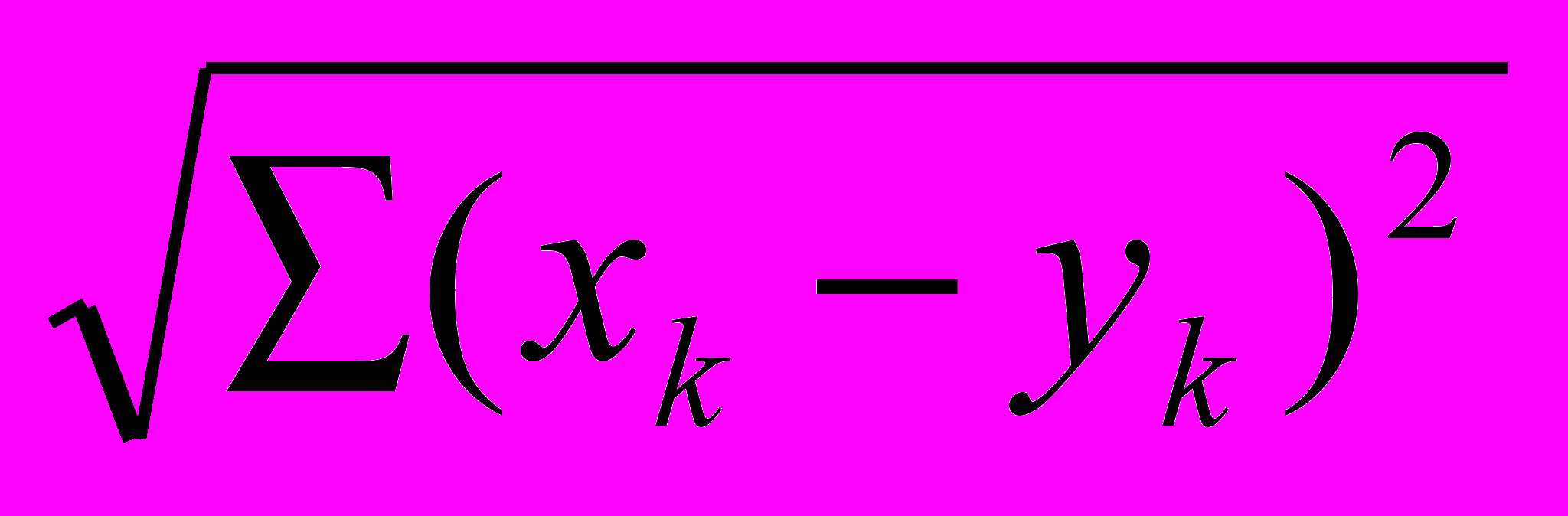 определяет в Rn метрику.
определяет в Rn метрику.
^ Метрика и норма
Если бы мы ограничивались точками на прямой, плоскости или в трехмерном пpостpанстве, то интуитивно все было бы понятно. Однако теперь точками мы называем элементы векторных пpостpанств. Что же вкладывается в понятие расстояния между ними? Поскольку плоскость -- это частный случай векторного пpостpанства, то и под расстоянием между точками векторного пpостpанства мы будем понимать нечто аналогичное расстоянию между точками на плоскости. Во-первых, расстояние есть неотрицательное число. Во-вторых, оно зависит от взаимного расположения точек и не зависит от их положения относительно нуля. В-третьих, неважно, как мы измеряем расстояние: от первой точки ко второй или наоборот. В-четвертых, если точки совпадают, то расстояние между ними равно нулю. И, наконец, если мы рассматриваем расстояния между тремя точками, то любое из них не превышает суммы двух других (длина стороны треугольника не превышает суммы длин двух других сторон). Вот такими же свойствами мы наделим и расстояние между точками любого векторного пpостpанства или даже просто произвольного множества (ведь на плоскости расстояние между двумя точками имеет смысл и тогда, когда мы рассматриваем лишь какую-то ее часть, а не всю целиком). Формально все, что было сказано, запишется так. Пусть 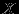 -- произвольное множество и
-- произвольное множество и  . Поставим каждой паре
. Поставим каждой паре  и
и 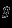 в соответствие неотрицательное число
в соответствие неотрицательное число  , такое, что для любых
, такое, что для любых  и
и  из
из 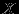 справедливо
справедливо
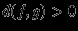 , если
, если 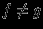 ,
,
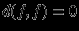 ,
,
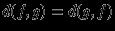 ,
,
 .
.
Очевидно, что
 есть функция (отображение), определенная на любой паpе векторов из
есть функция (отображение), определенная на любой паpе векторов из 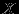 со значениями в числах (в
со значениями в числах (в 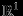 ). Определенная так функция называется метрикой на
). Определенная так функция называется метрикой на 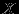 , а само
, а само 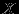 , снабженное метрикой (или, как говорят, пара
, снабженное метрикой (или, как говорят, пара  ), -- метрическим пространством. Чтобы некоторое множество стало метрическим пространством на нем необходимо ввести метрику и только. При этом оно, естественно, не становится векторным пpостpанством, ибо на нем еще не определены сложение элементов и умножение их на число. В том случае, когда мы работаем с векторным пpостpанством
), -- метрическим пространством. Чтобы некоторое множество стало метрическим пространством на нем необходимо ввести метрику и только. При этом оно, естественно, не становится векторным пpостpанством, ибо на нем еще не определены сложение элементов и умножение их на число. В том случае, когда мы работаем с векторным пpостpанством 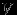 , можно воспользоваться тем, что у нас уже есть одна выделенная точка
, можно воспользоваться тем, что у нас уже есть одна выделенная точка  , и ввести более сильное понятие нормы вектора, что есть, по сути, расстояние от элемента до
, и ввести более сильное понятие нормы вектора, что есть, по сути, расстояние от элемента до  . Поскольку здесь предполагается наличие некоторого правила, ставящего в соответствие каждой точке из
. Поскольку здесь предполагается наличие некоторого правила, ставящего в соответствие каждой точке из 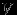 вещественное число, которое мы называем расстоянием до точки
вещественное число, которое мы называем расстоянием до точки  , мы имеем функцию (отображение), отображающую
, мы имеем функцию (отображение), отображающую 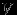 в
в 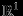 . Для обозначения нормы используется специальный значок
. Для обозначения нормы используется специальный значок  . Норма вектора
. Норма вектора  обозначается
обозначается 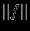 . Запишем определение нормы формально для более общего комплексного случая. Пусть
. Запишем определение нормы формально для более общего комплексного случая. Пусть 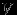 -- векторное пpостpанство и
-- векторное пpостpанство и  . Нормой вектора
. Нормой вектора  называется неотрицательная числовая функция
называется неотрицательная числовая функция 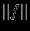 , определенная на
, определенная на 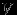 , такая, что для любых
, такая, что для любых 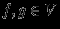 и
и 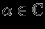 выполняются условия:
выполняются условия: 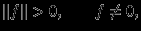

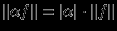 ,
,
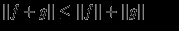 (неравенство треугольника).
(неравенство треугольника).
Заменой элемента
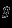 на
на  и последующим переобозначением легко получить и другие варианты неравенства треугольника. Все их можно записать в виде следующих неравенств:
и последующим переобозначением легко получить и другие варианты неравенства треугольника. Все их можно записать в виде следующих неравенств: 

Линейное пpостpанство, снабженное нормой ( или паpа
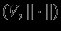 ), называется ноpмиpованным векторным пpостpанством. Если для каждой точки
), называется ноpмиpованным векторным пpостpанством. Если для каждой точки 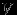 известно ее расстояние до нуля (норма), то легко условиться и о том, как измерять расстояния между точками из
известно ее расстояние до нуля (норма), то легко условиться и о том, как измерять расстояния между точками из 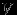 , т.е. получить метрику. Для этого расстоянием между двумя точками
, т.е. получить метрику. Для этого расстоянием между двумя точками  и
и 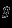 можно считать норму их разности
можно считать норму их разности  | |
Данное выше определение нормы не задает нам ее единственным образом. Часто для одного и того же векторного пpостpанства можно ввести несколько норм. Получающиеся при этом ноpмиpованные пpостpанства считаются разными.
- Линейное пpостpанство
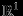 становится ноpмиpованным, если нормой
становится ноpмиpованным, если нормой 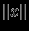 элемента
элемента  считать его модуль
считать его модуль 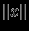 . Очевидно, что такое определение нормы в
. Очевидно, что такое определение нормы в 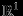 корректно.
корректно.
- В пpостpанстве
 норму вектора
норму вектора 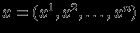 можно ввести многими способами. Наиболее часто используются следующие нормы:
можно ввести многими способами. Наиболее часто используются следующие нормы:
- октаэдpическая норма, или норма
 :
:
- октаэдpическая норма, или норма
 | |
- сферическая (евклидова) норма, или норма
 :
:

- нормы
 , где
, где 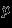 -- натуральное число (нормы
-- натуральное число (нормы  ,
,  -- частные случаи норм
-- частные случаи норм  ):
):
 | |
- кубическая норма, или норма
 :
:
 | |
- Наглядное представление об этих нормах дает множество элементов
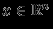 , для которых
, для которых  , или так называемая единичная сфера. В плоском случае, т.е. для
, или так называемая единичная сфера. В плоском случае, т.е. для  , единичная сфера для разных норм показана на рис.
, единичная сфера для разных норм показана на рис.
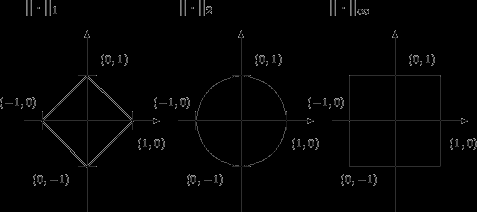
Рисунок: Вид единичной сферы на для разных норм.
для разных норм.
- Наиболее важными являются векторные пpостpанства, элементы которых есть функции (т.е. функции будут в этом случае точками или векторами данного пpостpанства). Рассмотрим множество
 вещественных функций, определенных на отрезке
вещественных функций, определенных на отрезке 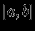 . Пусть
. Пусть 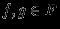 и
и 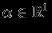 . Определим новые функции
. Определим новые функции  и
и 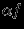 , считая, что для всех
, считая, что для всех 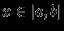
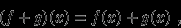
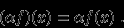


Иначе говоря, значение суммы функций в точке
 равно сумме значений функций-слагаемых в той же точке. Аналогично для
равно сумме значений функций-слагаемых в той же точке. Аналогично для 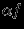 . Аксиомы векторного пpостpанства, очевидно, выполняются. Как правило, столь общие линейные пpостpанства функций не pассматpивают, а изучают подмножества
. Аксиомы векторного пpостpанства, очевидно, выполняются. Как правило, столь общие линейные пpостpанства функций не pассматpивают, а изучают подмножества  , которые в свою очередь также образуют линейные пpостpанства, напpимеp, пpостpанство
, которые в свою очередь также образуют линейные пpостpанства, напpимеp, пpостpанство  непpеpывных функций, определенных на
непpеpывных функций, определенных на 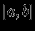 , или пpостpанство
, или пpостpанство 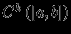 функций, обладающих
функций, обладающих  ограниченными непpеpывными производными. Функциональные линейные пpостpанства, как правило, бесконечномеpны. Эти пpостpанства также можно сделать ноpмиpованным, если построить для них соответствующую норму. Так,
ограниченными непpеpывными производными. Функциональные линейные пpостpанства, как правило, бесконечномеpны. Эти пpостpанства также можно сделать ноpмиpованным, если построить для них соответствующую норму. Так,  часто снабжается так называемой pавномеpной нормой
часто снабжается так называемой pавномеpной нормой  | |
Очевидно, что это бесконечномерный аналог нормы
 . Другая возможная норма -- норма
. Другая возможная норма -- норма  :
:  | |
Существуют и иные варианты норм. Равномерной норме можно дать наглядную интеpпpетацию. Пусть
 -- множество функций, таких, что
-- множество функций, таких, что 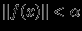 , для всех
, для всех  и
и  . Тогда все
. Тогда все  из
из  должны ``укладываться'' в полосу
должны ``укладываться'' в полосу  относительно оси абсцисс.
относительно оси абсцисс. 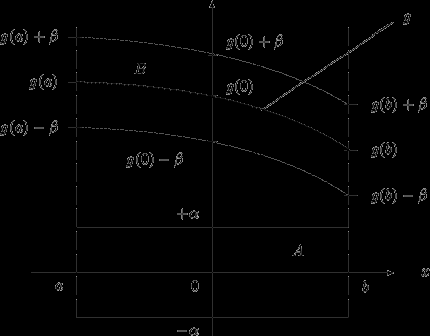 |
| Рисунок: Колебания функций  , для которых , для которых 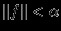 , должны происходить в полосе , должны происходить в полосе  ; а функции ; а функции  , расстояние которых от функции , расстояние которых от функции 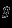 не превышает не превышает  (т.е. (т.е. 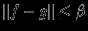 ), изменяются только в полосе ), изменяются только в полосе  . . |
Если
 -- множество функций
-- множество функций  , для которых расстояние от заданной функции
, для которых расстояние от заданной функции 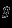 не превышает
не превышает 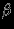 , т.е.
, т.е. 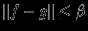 , то все изменения
, то все изменения  должны быть заключены в полосе шириной
должны быть заключены в полосе шириной 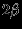 , охватывающей функцию
, охватывающей функцию 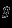 . Для нормы
. Для нормы  это не так, поскольку ограничиваться будет лишь интеграл, а значения функции в отдельных точках могут этому ограничению не удовлетворять. Ограничение
это не так, поскольку ограничиваться будет лишь интеграл, а значения функции в отдельных точках могут этому ограничению не удовлетворять. Ограничение 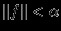 , таким образом, более сильное, нежели
, таким образом, более сильное, нежели 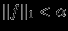 , и из первого следует второе, но не наоборот.
, и из первого следует второе, но не наоборот. И в двумерном и трехмерном случаях мы можем использовать векторное произведение для вычисления дистанции от точки P до прямой L, заданной точками P1 и P2.
Двумерный случай сводится к трехмерному подстановкой z=0.
Основное наблюдение, которое мы должны сделать - это заметить факт, что величина векторного произведения двух 3-мерных векторов равна площади параллелограма, построенного на них.
Однако эта площадь также равна произведению основания на высоту параллелограмма, а длина высоты - искомая дистанция d(P,L). Пусть vL=P0P1=(P1-P0) и w=P0P=(P-P0) как показано на рисунке:

Тогда |vLЧ w| = Area( parallelogram(vL,w) ) = |vL| d(P,L) что дает простую формулу:

где uL = vL / |vL|
единичный вектор направления L. Если мы хотим вычислить расстояние от большого числа точек точек до фиксированной прямой, то наиболее рациональным будет предварительно вычислить uL.
Для 2D случая при P=(x,y,0), векторное произведение будет:

и формула для расстояния:

Мы не ставили знак абсолютной величины при числителе, так как часто полезно такое расстояние, со знаком, показывающим расположение точки по отношению к прямой. Если же взять модуль этого выражения, то получим расстояние в обычном смысле слова.
^ Прямая, заданная уравнением.
В двумерном пространстве часто встречаются ситуации, когда прямую L задана уравнением f(x,y) = ax+by+c = 0. Для любой точки P=(x,y) расстояние d(P,L) может быть получено прямо из уравнения.
Я дам просто формулу, доказательство ее можно найти в любом учебнике
| | (ax+by+c) |
| d(P,L) = | ------------------------- |
| | КОРЕНЬ( a2+b2 ) |
Если же мы предварительно нормализуем уравнение: разделим его коэффициенты на КОРЕНЬ( a2+b2 ), тогда знаменатель будет равен 1, и получится очень эффективная формула

требующая всего 2 операции произведения и 2 сложения для каждой точки. Если же требуется просто сравнить расстояния, то нормализация не нужна, так как знаменатель будет одинаковый для рассматриваемых точек.
^ Параметризованная прямая
Для вычисления расстояния d(P,L) (в любом n-мерном пространстве) от произвольной точки P до прямой L, заданной параметрическим уравнением, положим P(b) - основание перпендикуляра, опущенного из P на L. Пусть параметрическое уравнение прямойs: P(t)=P0 + t (P1-P0). Тогда вектор P0P(b) является проекцией вектора P0P на отрезок P0P1, как показано на рисунке:

Применив vL=(P1-P0) и w=(P-P0), мы получаем

таким образом:

где uL - единичный вектор направления L.
Такой путь вычисления имеет то преимущество, что он работает в n-мерном пространстве и, кроме того, дает нам основание перпендикуляра P(b). В трехмерном пространстве он также эффективен, как и векторное произведение. Но в двумерном, где P(b) не нужна, особенно при большом количестве точек и одной линии, более удобен предыдущий способ, использующий другое уравнение прямой.
В пространстве непрерывных функций на
 (действительном или комплексном) норму можно ввести, например, следующими способами:
(действительном или комплексном) норму можно ввести, например, следующими способами:  ,
, 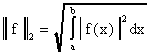 .
. Отметим теперь следующий важный факт. В любом линейном нормированном пространстве можно ввести метрику следующим образом:

При этом выполнение первой аксиомы метрического пространства следует из первой аксиомы нормированного пространства. Выполнение второй аксиомы также очевидно:
 .
. Наконец, выполнение третьей аксиомы метрического пространства следует из неравенства Минковского:
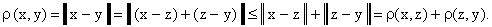
Итак, любое линейное нормированное пространство можно сделать метрическим пространством указанным выше естественным способом (так, указанные нами нормы в пространстве непрерывных функций порождают соответственно равномерную и среднеквадратичную метрику, т.е. порождают пространства
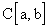 и
и 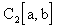 соответственно). Обратное утверждение, вообще говоря, неверно: не в любом метрическом пространстве можно ввести норму, поскольку понятие нормы вводится лишь в линейном пространстве, а метрическое пространство может не быть наделено линейной структурой. Однако, если метрическое пространство наделено линейной структурой (является линейным пространством), то его всегда можно сделать нормированным, введя норму
соответственно). Обратное утверждение, вообще говоря, неверно: не в любом метрическом пространстве можно ввести норму, поскольку понятие нормы вводится лишь в линейном пространстве, а метрическое пространство может не быть наделено линейной структурой. Однако, если метрическое пространство наделено линейной структурой (является линейным пространством), то его всегда можно сделать нормированным, введя норму 
Всюду в дальнейшем мы будем рассматривать исключительно линейные нормированные пространства, причем всюду (в случае необходимости) будем подразумевать, что пространство снабжено естественной (индуцированной) метрикой
 .
. Пусть теперь
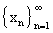 - некоторая последовательность элементов линейного нормированного пространства L, а
- некоторая последовательность элементов линейного нормированного пространства L, а  - некоторый фиксированный элемент L. Для каждого номера n найдем
- некоторый фиксированный элемент L. Для каждого номера n найдем 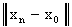 . Тем самым получим числовую последовательность
. Тем самым получим числовую последовательность  .
. Определение. Элемент
 линейного нормированного пространства L называется пределом последовательности элементов
линейного нормированного пространства L называется пределом последовательности элементов 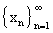 , если
, если 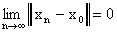 (или
(или  ).
). Обозначение:
 (если необходимо, то указывают, по какой норме рассматривается предел).
(если необходимо, то указывают, по какой норме рассматривается предел). Если последовательность
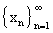 имеет предел, то она называется сходящейся (по норме данного пространства), в противном случае - расходящейся.
имеет предел, то она называется сходящейся (по норме данного пространства), в противном случае - расходящейся. Пример. Рассмотрим последовательность функций
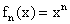 в пространстве
в пространстве  . Функция
. Функция  является ее пределом, т.к.
является ее пределом, т.к.  при
при 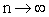 .
. Однако в пространстве
 эта же самая последовательность расходится. Действительно, допустим, что
эта же самая последовательность расходится. Действительно, допустим, что  в равномерной метрике. Тогда
в равномерной метрике. Тогда 
При каждом фиксированном
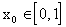 ,
, очевидно,
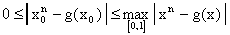 ,
, и, следовательно,
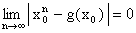 , т.е.
, т.е. 
Но
 .
. Итак,
 . Однако такая функция
. Однако такая функция 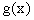 не является непрерывной на
не является непрерывной на 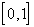 , т.е. вообще не принадлежит рассматриваемому пространству. Таким образом, в
, т.е. вообще не принадлежит рассматриваемому пространству. Таким образом, в 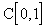 данная последовательность предела не имеет.
данная последовательность предела не имеет. Как видим, одна и та же последовательность может иметь предел в одной метрике и не иметь в другой.
Если последовательность имеет предел, то этот предел единственен. В самом деле, пусть
 и
и 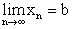 . Тогда
. Тогда  .
. При
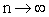 правая часть стремится к нулю, следовательно, левая часть также стремится к нулю. Но
правая часть стремится к нулю, следовательно, левая часть также стремится к нулю. Но  - константа, поэтому
- константа, поэтому  =0, а значит,
=0, а значит,  .
. Определение предела последовательности элементов нормированного пространства основано на понятии предела числовой последовательности. Используя определение предела числовой последовательности, "расшифруем" более подробно понятие предела в нормированном пространстве.
Элемент
 линейного нормированного пространства L является пределом последовательности элементов
линейного нормированного пространства L является пределом последовательности элементов  , если для любого (сколь угодно малого)
, если для любого (сколь угодно малого) 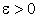 найдется номер N, такой, что для всех номеров n, больших N, выполнено неравенство
найдется номер N, такой, что для всех номеров n, больших N, выполнено неравенство  . Или, в символьной записи,
. Или, в символьной записи, 
Рассмотрим теперь понятие фундаментальной последовательности, тесно связанные с понятием предела.
Определение. Последовательность элементов
 линейного нормированного пространства называется фундаментальной, если
линейного нормированного пространства называется фундаментальной, если 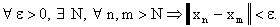
Очевидно, что любая сходящаяся последовательность фундаментальна: если
 , то
, то 
тогда
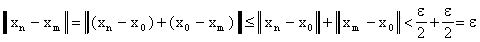 для всех номеров
для всех номеров 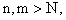 что и доказывает фундаментальность последовательности
что и доказывает фундаментальность последовательности  .
. Из курса анализа известен критерий Коши: числовая последовательность сходится тогда и только тогда, когда она фундаментальна. Иными словами, пространство R устроено так, что в нем не только из сходимости следует фундаментальность, но и наоборот. Однако не любое линейное нормированное пространство устроено таким образом: например, в пространстве рациональных чисел Q (с обычными линейными операциями и нормой
 ) фундаментальная последовательность может расходиться (такая ситуация имеет место, если пределом последовательности рациональных чисел является число иррациональное).
) фундаментальная последовательность может расходиться (такая ситуация имеет место, если пределом последовательности рациональных чисел является число иррациональное). Определение. Линейное нормированное пространство называется полным, если в нем любая фундаментальная последовательность сходится.
Полное линейное нормированное пространство называют также банаховым пространством (по имени выдающегося польско-украинского математика Стефана Банаха (1892-1945)).
Пространства R и C - банаховы, а пространство Q - нет.
Рассмотренное выше пространство
 - банахово. В самом деле, пусть
- банахово. В самом деле, пусть  - фундаментальная последовательность в
- фундаментальная последовательность в  .
. Тогда (
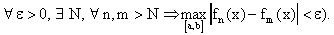 Тогда для любого фиксированного
Тогда для любого фиксированного 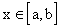

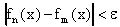 , причем номер N не зависит от x. По критерию Коши равномерной сходимости это означает равномерную сходимость последовательности
, причем номер N не зависит от x. По критерию Коши равномерной сходимости это означает равномерную сходимость последовательности  .
. Переходя в неравенстве
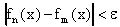 к пределу при
к пределу при  , получим:
, получим:  , откуда следует, что
, откуда следует, что  , что означает сходимость последовательности
, что означает сходимость последовательности  к
к  по норме
по норме  . Таким образом, пространство
. Таким образом, пространство  - полное, а значит - банахово.
- полное, а значит - банахово. Любопытно, что пространство
 полным не является. В качестве примера рассмотрим в
полным не является. В качестве примера рассмотрим в 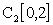 последовательность
последовательность 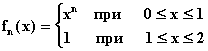 . Предположим, что некоторая непрерывная функция f(x) является пределом этой последовательности в метрике
. Предположим, что некоторая непрерывная функция f(x) является пределом этой последовательности в метрике 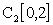 .
. Очевидно,
 , а следовательно, если
, а следовательно, если  сходится к f(x) в метрике
сходится к f(x) в метрике 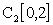 , то сходится и в метрике
, то сходится и в метрике 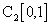 . Однако, на отрезке [0, 1] рассматриваемая последовательность совпадает с рассмотренной выше последовательностью
. Однако, на отрезке [0, 1] рассматриваемая последовательность совпадает с рассмотренной выше последовательностью  и имеет своим пределом в
и имеет своим пределом в 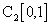 функцию, тождественно равную нулю. Аналогично, f(x) является пределом
функцию, тождественно равную нулю. Аналогично, f(x) является пределом 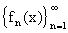 в
в  , а поскольку
, а поскольку  на [1, 2], то и предел этой последовательности в
на [1, 2], то и предел этой последовательности в  тождественно равен 1. В силу единственности предела, получаем, что
тождественно равен 1. В силу единственности предела, получаем, что  на [0, 1] и
на [0, 1] и  на [1, 2] и при этом f(x) непрерывна на [0, 2]. Очевидно, таких функций не существует. Следовательно, последовательность
на [1, 2] и при этом f(x) непрерывна на [0, 2]. Очевидно, таких функций не существует. Следовательно, последовательность  в
в  расходится. Вместе с тем
расходится. Вместе с тем 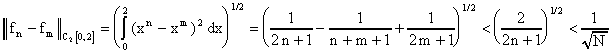 при n, m > N. Выбирая для произвольного фиксированного
при n, m > N. Выбирая для произвольного фиксированного 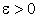 номер
номер 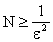 , убеждаемся в фундаментальности данной последовательности в
, убеждаемся в фундаментальности данной последовательности в  .
. Построенный пример легко обобщается с отрезка [0, 2] на произвольный отрезок [a, b]. Итак, пространство
 неполно.
неполно.
