Программа по курсу «Функциональный анализ»

Вид материала

Программа

Содержание Основные принципы теории линейных непрерывных операторов Гильбертовы пространства Вопросы спектральной теории линейных непрерывных операторов. Интегральные уравнения. Производная Фреше

Подобный материал:

• Программа кандидатского экзамена по специальности 01. 01. 01 Вещественный, комплексный, 118.98kb.
• Программа дисциплины Функциональный анализ для направления 010100. 62 «Математика», 242.48kb.
• Список литературы по курсу «Функциональный анализ» 2011-2012, 41.23kb.
• Функциональный анализ направление подготовки, 15.46kb.
• Программа-минимум кандидатского экзамена по специальности, 37.75kb.
• Функциональный подход, 291.02kb.
• Утверждаю, 105.37kb.
• В. М. Земсков Вопросы к зачету по курсу Анализ финансовой отчет, 19.8kb.
• Функциональный анализ. Лекции читает Шаповаленко Василий Всеволодович, 30.76kb.
• I функциональный анализ морфемы, лексемы, фраземы, 91.7kb.

ПРОГРАММА

по курсу «Функциональный анализ»


Факультет математический

Специальность 010101 – Математика

Семестр 5 – 6

Лекции 76 час.

Практические занятия 68 час.

Самостоятельная работа 84 часа

Форма проверки экзамен 5 – 6 семестр

зачет 5 семестр

Составитель: Пуляев В. Ф., профессор, доктор физ.-мат. наук

Содержание лекционного материала

Линейные нормированные пространства ( ЛНП )

Введение. Линейные пространства: определение, примеры. Линейная независимость, базис. Конечномерные пространства. Примеры.

Вспомогательные неравенства (Гельдера, Минковского). Норма в линейном пространстве. Примеры норм.

Шары и топология в ЛНП. Предел в ЛНП и его свойства. Сходимость в конкретных пространствах. Ряды в ЛНП.

Полные (банаховы) ЛНП. Полнота пространств 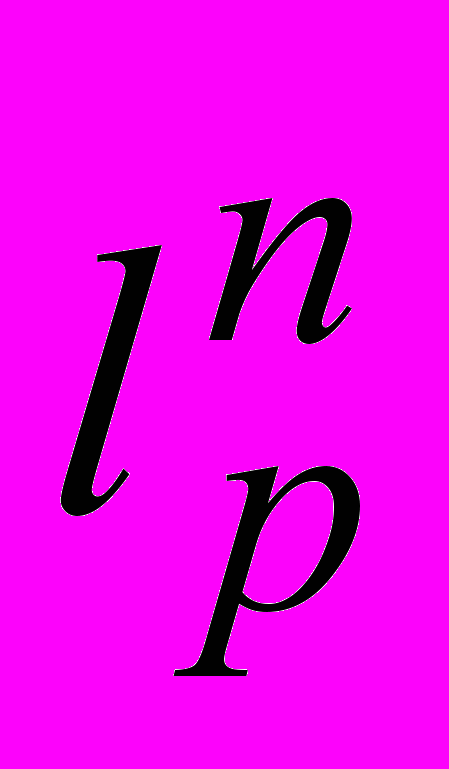, , 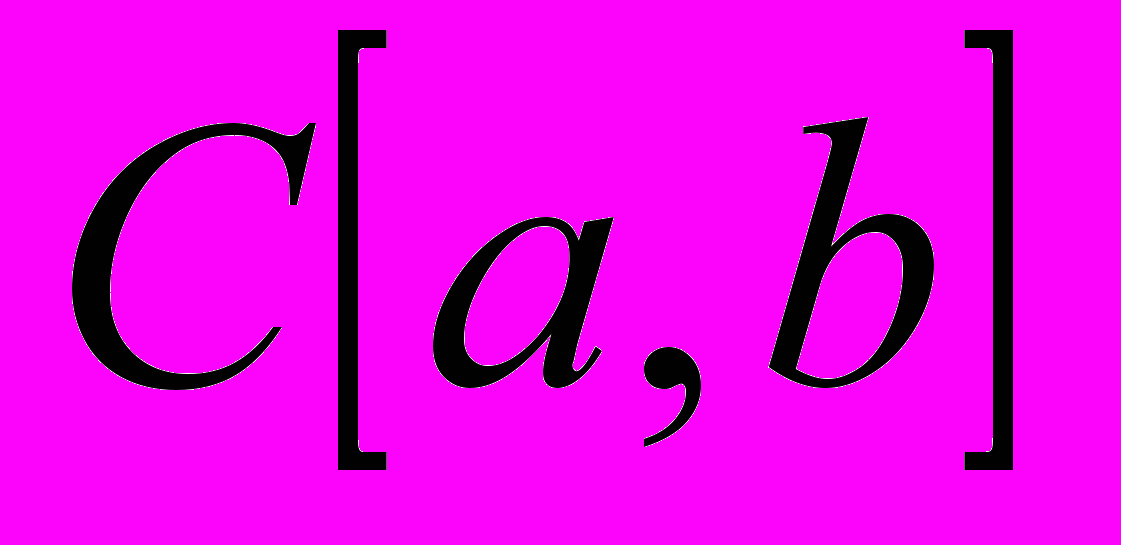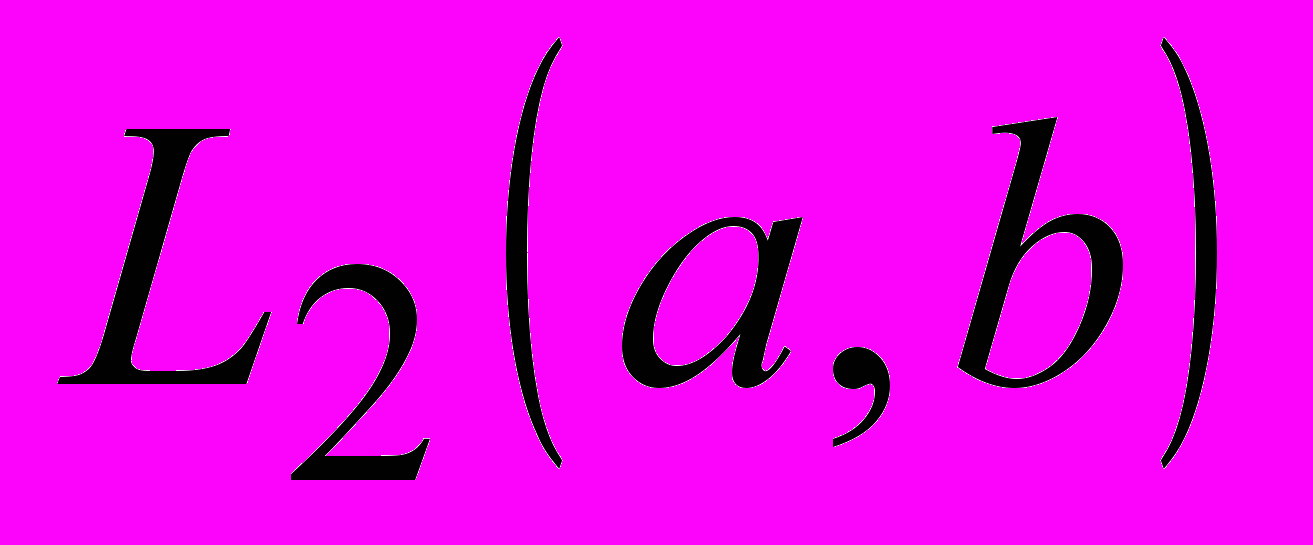. Примеры пространств, не являющихся полными.

Доказательство полноты пространства.

Теорема о вложенных шарах. Замкнутые множества. Теорема Бэра. Пополнение пространства.

Теорема об эквивалентности норм в конечномерном пространстве и следствия из неё.

Принцип сжимающих отображений: непрерывные отображения в ЛНП, сжимающие отображения. Доказательство принципа сжимающих отображений.

Применение принципа сжимающих отображений к скалярным уравнениям, алгебраическим системам, интегральным и дифференциальным уравнениям.

Основные принципы теории линейных непрерывных операторов

Линейные непрерывные операторы и их свойства: определение, примеры. Критерий непрерывности линейных операторов.

Алгебраические операции над операторами. Норма линейного оператора, её свойства. Полнота пространства .

Принцип равномерной ограниченности. Равномерная и поточечная сходимость операторов.

Применение принципа равномерной ограниченности к задачам анализа.

Обратимые операторы и их свойства. Теорема Банаха об обратном операторе: доказательство вспомогательного утверждения.

Доказательство теоремы Банаха. Применение теоремы Банаха для получения оценок решения уравнений.

Линейные непрерывные функционалы. Общий вид функционалов в конкретных пространствах. Теорема Хана – Банаха и следствия из неё.

Доказательство теоремы Хана – Банаха. Применение теоремы Хана – Банаха к задаче об отделимости выпуклых множеств.

Гильбертовы пространства

Пространство со скалярным произведением. Неравенство Коши – Буняковского. Гильбертово пространство. Ортогональность.

Ортогональное дополнение к подпространству. Проекция вектора на подпространство; её вычисление в случае конечномерного подпространства. Теорема о существовании проекции.

Ортонормированные системы. Критерий полноты. Ряды Фурье. Равенство Парсеваля – Стеклова. Общий вид функционалов в .

Вопросы спектральной теории линейных непрерывных операторов.

Теория Фредгольма – Рисса – Шаудера

Обратимые операторы: обратимость 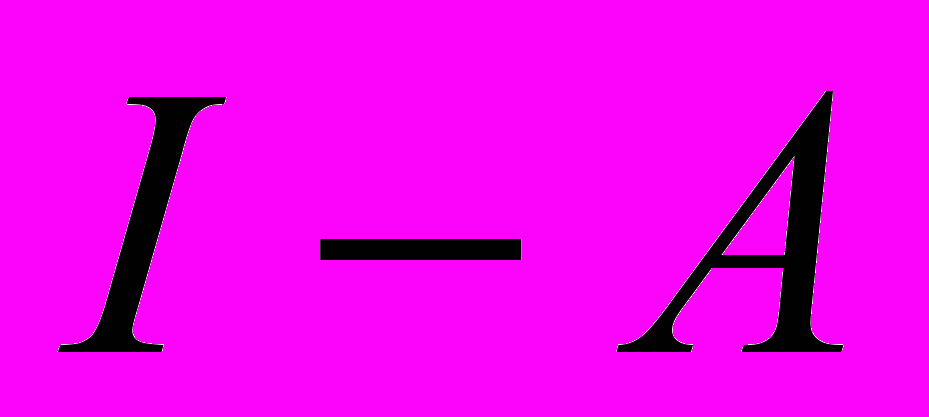. Свойства обратимых операторов.

Спектр линейного непрерывного оператора, его свойства. Непустота спектра. Спектральный радиус.

Формула для вычисления спектрального радиуса.

Компактность множеств в нормированных пространствах. Примеры. Критерий компактности в конкретных пространствах.

Вполне непрерывные операторы и их свойства. Вполне непрерывность оператора Гильберта – Шмидта.

Сопряженные операторы: определение, существование и свойства. Примеры. Вполне непрерывность сопряженного оператора.

Свойства решений линейных уравнений. Замкнутость образа оператора 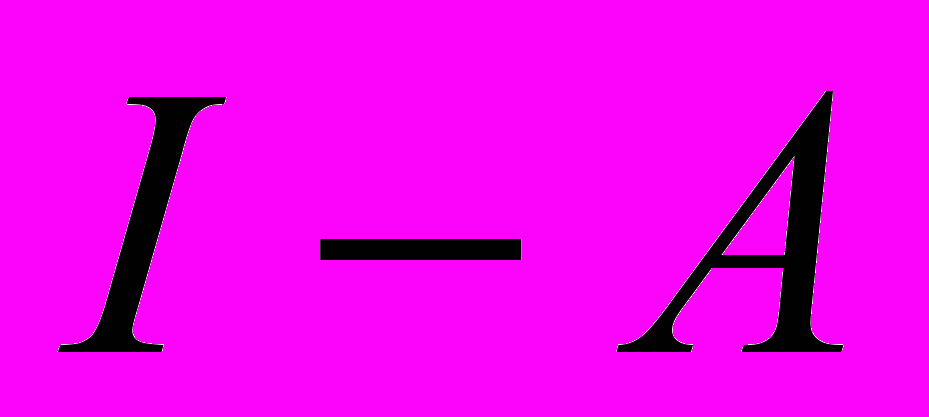, где – вполне непрерывный оператор.

Доказательство теоремы Фредгольма.

Спектр вполне непрерывного оператора.

Вполне непрерывные самосопряженные операторы. Теорема Гильберта – Шмидта.

Интегральные уравнения. Производная Фреше

Линейные интегральные уравнения. Характеристические числа и собственные функции. Теоремы Фредгольма. Уравнения с вырожденными ядрами.

Интегральные уравнения с симметричными ядрами.

Производная отображений, её свойства. Дифференцирование сложной функции.

Применение производной к нахождению экстремумов функционалов.


Литература

Учебники:

1. Основная:
   

1. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа.
   
2. Люстерник Л. А., Соболев В. И. Краткий курс функционального анализа.
   
3. Шилов Г. Е. Математический анализ (спецкурс).
   

2. Дополнительная:
   

1. Канторович Л. В., Акилов Г. П. Функциональный анализ.
   
2. Садовский В. А. Теория операторов.
   

Задачники:

1. Очан Ю. С. Сборник задач и теорем по теории функций действительной переменной.
   
2. Пуляев В. Ф., Цалюк З. Б. Задачи по функциональному анализу.
   
3. Антоневич А. Б., Князев Н. П., Радыно Я. В. Задачи и упражнения по функциональному анализу.