Функциональный анализ направление подготовки

Вид материала

Документы

Подобный материал:

• Программа кандидатского экзамена по специальности 01. 01. 01 Вещественный, комплексный, 118.98kb.
• Программа дисциплины Функциональный анализ для направления 010100. 62 «Математика», 242.48kb.
• Аннотация рабочей программы учебной дисциплины математический анализ Направление подготовки, 95.49kb.
• Аннотация рабочей программы учебной дисциплины бизнес- планирование и экономический, 60.52kb.
• Функциональный подход, 291.02kb.
• Основная образовательная программа высшего профессионального образования Направление, 506.79kb.
• Рабочая программа дисциплины «Компьютерная диагностика» Направление подготовки, 209.63kb.
• Рабочая программа дисциплины технические измерения и приборы Направление подготовки, 496.12kb.
• Рабочая программа дисциплины «Вычислительные машины, системы и сети» Направление подготовки, 231.13kb.
• Рабочая программа дисциплины «Интегрированные системы проектирования и управления», 208.14kb.

ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ


Направление подготовки

010800 механика и математическое моделирование


Профиль подготовки

Теоретическая механика и управление движением


Цель курса:

изложить основные разделы линейного функционального анализа, продемонстрировать их связь с другими разделами математики, показать, как общие методы функционального анализа могут быть использованы для решения задач современной теоретической и прикладной математики; подготовить возможность применения аппарата функционального анализа в следующих курсах, читаемых студентам-механикам: теоретическая механика, теория устойчивости, дифференциально-разностные уравнения, динамические системы, теория управления и др.


Содержание дисциплины:

Возникновение функционального анализа как самостоятельного раздела математики, его современное состояние и связь с приложениями. Метрические пространства: определение и примеры; топология метрических пространств; полнота; компактность; непрерывные отображения, их свойства на компактах; принцип сжимающих отображений. Линейные нормированные пространства; линейные непрерывные операторы; конечномерность и компактность. Евклидовы пространства; гильбертовы пространства; ортогональное разложение гильбертова пространства; ортогональные, полные и замкнутые системы; ряд Фурье. Интеграл и мера; измеримые функции; предельный переход под знаком интеграла Лебега; неравенства Гельдера и Минковского; пространства 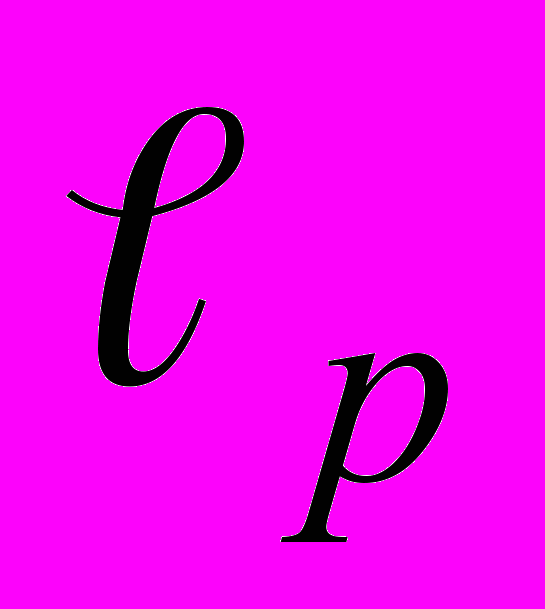, 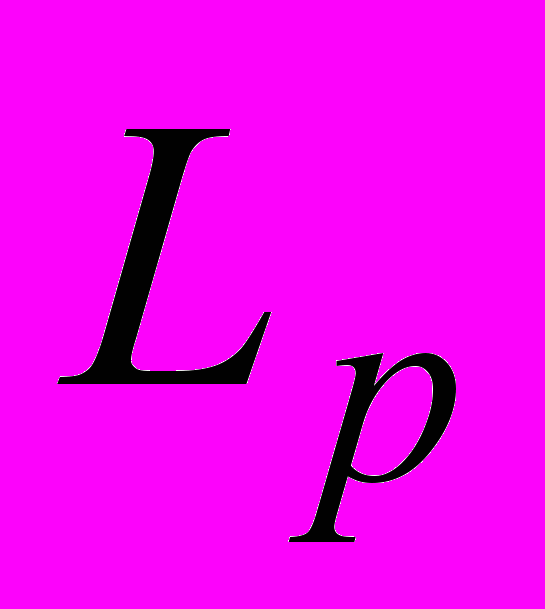. Линейные непрерывные операторы и функционалы; норма оператора; сопряженное пространство; теорема Хана – Банаха и ее следствия; общий вид линейных непрерывных функционалов в классических пространствах. Вполне непрерывные операторы; сопряженные и эрмитово-сопряженные операторы. Обратные операторы. Спектр линейного непрерывного оператора. Операторные уравнения. Теоремы Фредгольма (формулировки). Линейные интегральные уравнения, некоторые задачи, приводящие к интегральным уравнениям. Методы решения интегральных уравнений (метод неопределенных коэффициентов для уравнений с вырожденным ядром, метод малого параметра). Интеграл Фурье в 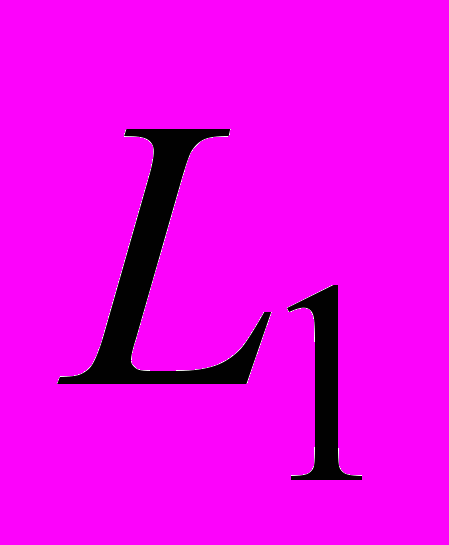, преобразование Фурье в 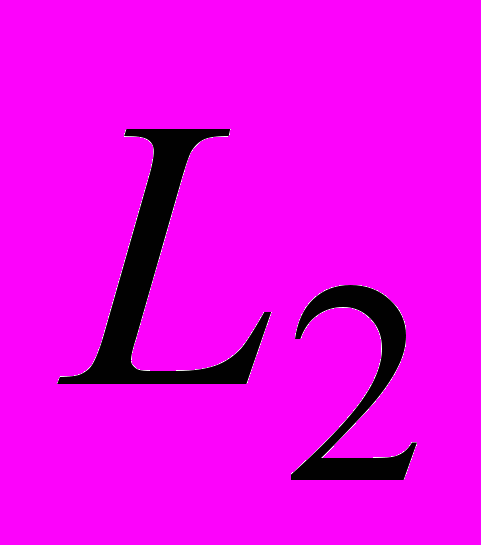. Основные и обобщенные функции, операции над обобщенными функциями.