Утверждаю

Вид материала

Рабочая программа

Содержание 2.Место дисциплины в структуре ООП бакалавриата 3 Компетенции обучающегося, формируемые в результате освоения дисциплины «Функциональный анализ». 4. Структура и содержание дисциплины «Функциональный анализ» Формы текущего контроля успеваемости (по неделям семестра) Форма промежуточной аттестации (по семестрам) 5. Образовательные технологии

Подобный материал:

• Утверждаю утверждаю, 21.26kb.
• «утверждаю» «утверждаю», 262.03kb.
• Утверждаю утверждаю, 393.06kb.
• «Утверждаю» «Утверждаю» Председатель Совета доу заведующий мдоу №25, 113.74kb.
• Кикбоксинг против наркомании и детской преступности «Утверждаю» «Утверждаю», 78.29kb.
• Утверждаю: утверждаю, 156.74kb.
• «утверждаю» «утверждаю» Председатель республиканского Директор маоудод «цдтт №5» совета, 42.86kb.
• Утверждаю» «Утверждаю», 163.81kb.
• «Динамо», 49.89kb.
• Утверждаю: утверждаю: Председатель Глава администрация оо «Гомельский рыболовный клуб», 78.23kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ


Томский государственный университет


Факультет прикладной математики и кибернетики


УТВЕРЖДАЮ


Декан ФПМК А.М. Горцев

"_____"__________________2011__ г.


Рабочая программа дисциплины

Функциональный анализ


Направление подготовки

010400 Прикладная математика и информатика


Квалификация выпускника

Бакалавр


Форма обучения

очная


Томск

2011г.

1. Цели освоения дисциплины

Целями освоения дисциплины «Функциональный анализ» являются:

–изучение основных методов современного анализа, используемого в теоретических и прикладных исследованиях, создание математической основы для изучения дисциплин: теория вероятностей, дифференциальные уравнения, уравнения математической физики;

–обучить студентов методам решения типовых задач анализа, возникающих в приложениях;

–привить навыки исследовательской работы с помощью логически строгого построения доказательств.

В результате освоения данной дисциплины обеспечивается достижение целей основной образовательной программы «Прикладная математика и информатика»; приобретенные знания, умения и навыки позволяют подготовить выпускника к научно-исследовательской деятельности в области прикладной математики, к производственно-технологической деятельности в области создания современных систем для решения прикладных задач и педагогической деятельности.


2.Место дисциплины в структуре ООП бакалавриата_

Дисциплина «Функциональный анализ» находится в цикле Б.2 Математический и естественнонаучный цикл (Базовая часть).

Для изучения курса необходимы знания по предметам: математический анализ, алгебра и геометрия. Знания, полученные при изучении данного курса, используются при изучении «Уравнений математической физики», «Дифференциальных уравнений», «Теории вероятностей», «Теории случайных процессов», в научно-исследовательской работе в области прикладной математики, при создании современных систем управления и в педагогической деятельности.


3 Компетенции обучающегося, формируемые в результате освоения дисциплины «Функциональный анализ».

В результате освоения дисциплины обучающийся должен обладать общекультурными компетенциями:

–способностью осознать социальную значимость своей будущей профессии, обладать высокой мотивацией к выполнению профессиональной деятельности (ОК-9).


В результате освоения дисциплины обучающийся должен обладать профессиональными компетенциями:

–способностью понимать и применять в исследовательской работе и прикладной деятельности современный математический аппарат (ПК-3);

–способностью формировать суждения о значении и последствиях своей профессиональной деятельности с учетом социальных, профессиональных и этических позиций (ПК-8);

– способностью собирать, обрабатывать и интерпретировать данные современных научных исследований, необходимые для формирования выводов по соответствующим научным, профессиональным, социальным и этическим проблемам (ПК-7);

–способностью в составе научно-исследовательского и производственного коллектива решать задачи профессиональной деятельности (ПК-4).


В результате освоения дисциплины обучающийся должен знать:

–основные результаты современного анализа из теории меры и интеграла, функциональных пространств и операторов, используемых в прикладных исследованиях;

–возможности применения общих математических конструкций для решения прикладных задач;

–основные понятия и факты, используемые в физике , кибернетике, экономике.


В результате освоения дисциплины обучающийся должен уметь:

–решать типовые задачи, способствующие углубленному пониманию основных математических объектов;

–применять общие методы к решению конкретных задач, связанных с дифференциальными и интегральными уравнениями;

–логически выстроить обоснование основных фактов.

В результате освоения дисциплины обучающийся должен владеть:

–навыками анализа свойств основных математических объектов, широко применяемых в прикладных задачах;

–общим пониманием аппарата современного анализа, методами и подходами, используемыми в теории меры и интеграла и теории операторов в основных функциональных пространствах.

4. Структура и содержание дисциплины «Функциональный анализ»

Общая трудоемкость дисциплины составляет 7,3 зачетных единиц (264 часов).

Содержание курса

III семестр

4.1. Вводная часть.


Тема 1. Основные задачи функционального анализа и их связь с физикой. Роль функционального анализа в прикладных исследованиях.


4.2. Элементы теории множеств.


Тема 2. Множества, операции над множествами. Классы множеств, замкнутые относительно данного набора теоретико-множественных операций. Кольца, полукольца, алгебры, σ-алгебры. Построения минимальных φ-классов: минимальной алгебры (по разбиению, по конечной системе множеств, по произвольному классу), минимального кольца по полукольцу. Леммы о полукольцах.


4.3. Теория меры.


Тема 3. Мера Лебега на числовой прямой и на плоскости. Продолжение меры с полукольца на минимальное кольцо. Построение меры Лебега плоских множеств. Мера Лебега в .


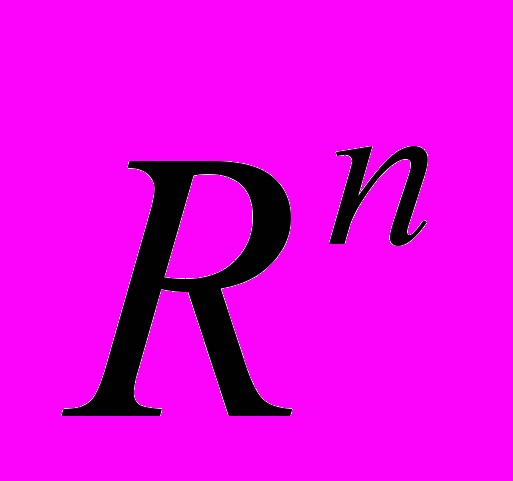Тема 4. Мера абстрактных множеств. Продолжение меры с полукольца на кольцо. Аддитивность и σ-аддитивность. Способы задания мер на измеримых метрических пространствах.

4.4. Измеримые функции.

Тема 5. Функции, образы и прообразы множеств и классов множеств. Свойства обратных отображений. Измеримые функции, дескриптивные и конструктивные определения. Борелевские функции в метрических пространствах.

4.5. Теория интеграла.

Тема 6. Интеграл Лебега на абстрактном множестве на основе конструкции 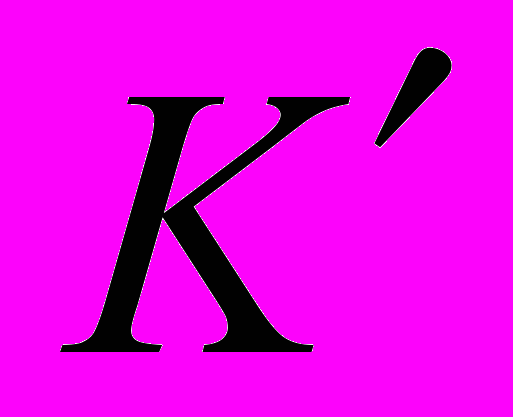-измеримых функций. Определение, корректность определения, свойства. Индуцированные меры. Теорема о замене переменной в интеграле Лебега.

IV семестр.

Тема 7. Продолжение меры с алгебры на σ-алгебру. Внешняя мера. Теорема Каратеодори. Связь интеграла Римана и Лебега. Произведение измеримых пространств. Теорема Фубини о повторных интегралах. Применение в теории вероятностей.

4.6. Метрические пространства


Тема 8. Множества в метрических пространствах. Полные метрические пространства. Теорема Рисса о полноте 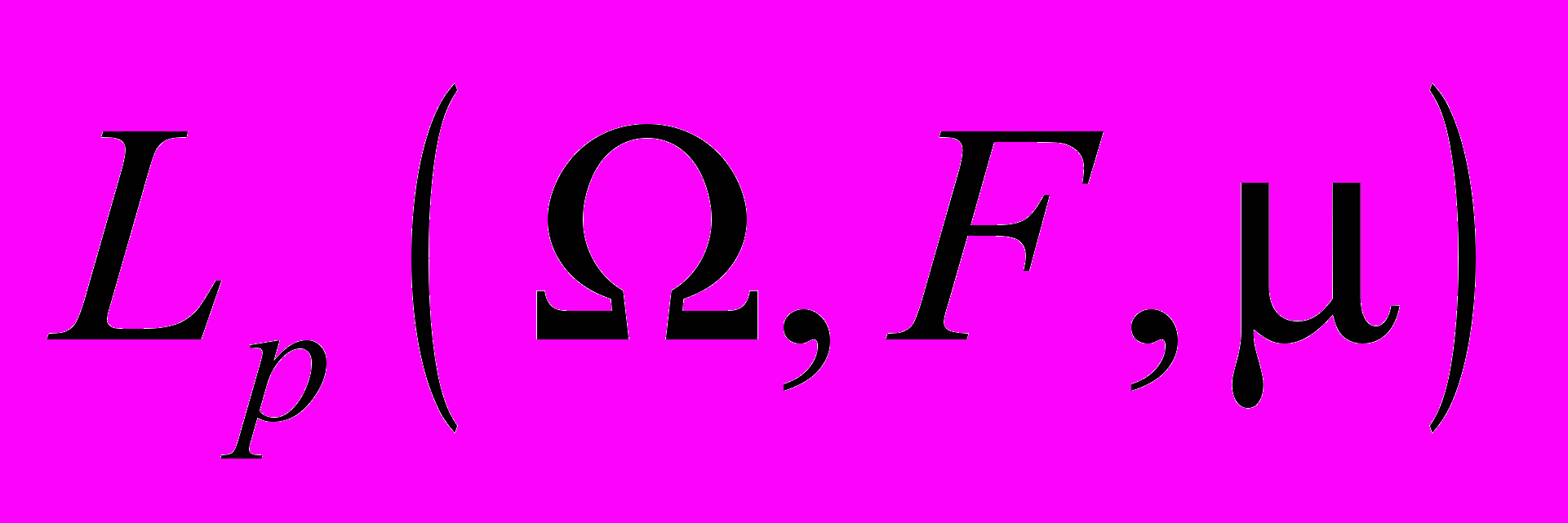. Пополнение метрических пространств. Компактные

множества в метрических пространствах. Теорема Хаусдорфа.


Тема 9. Принцип сжимающих отображений и его применение к задаче Коши для обыкновенных дифференциальных уравнений, интегральным уравнениям Фредгольма и Вольтерра, для доказательства эргодической теоремы.


4.7. Линейные пространства.


Тема 10. Линейные нормированные пространства. Теорема об эквивалентности норм. Банаховы пространства.


Тема 11. Гильбертовы пространства. Геометрия гильбертова пространства. Ортогональные базисы в гильбертовом пространстве. Теорема о базисах. Теорема о полноте тригонометрической системы в 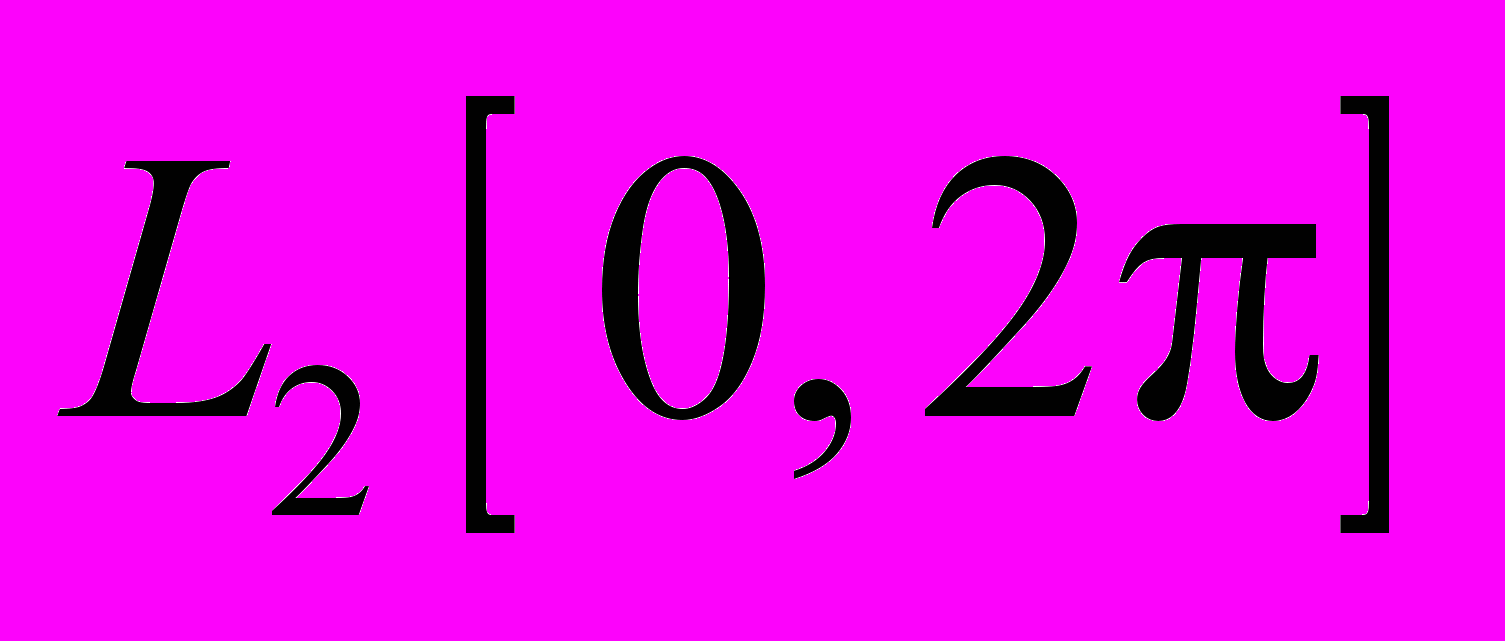. Теорема о проекциях.


4.8. Линейные функционалы и операторы.


Тема 12. Функционалы и операторы. Норма. Теорема Рисса. Абсолютная непрерывность мер, теорема Радона--Никодима. Пространства операторов. Симметричные операторы в гильбертовых пространствах.


Темы практических занятий.


Тема 1. Неравенства Коши--Буняковского, Юнга, Гельдера, Минковского, 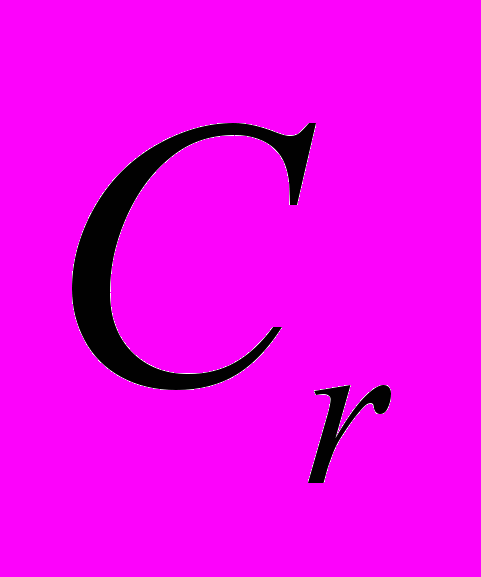-неравенство.


Тема 2. Множества, операции над множествами, системы множеств: алгебры, σ-алгебры, полуалгебры, полукольца, топологии. Построения минимальных алгебр по конечным разбиениям множества.


Тема 3. Метрические пространства, множества в метрических пространствах.


Тема 4. Полнота метрических пространств 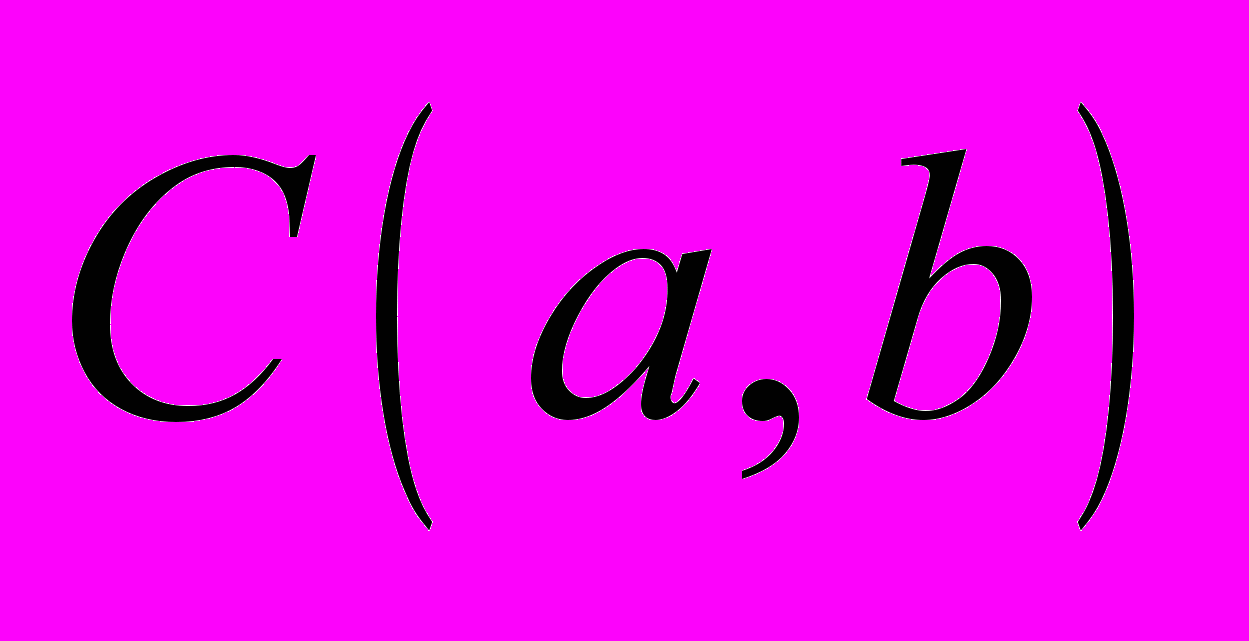, , 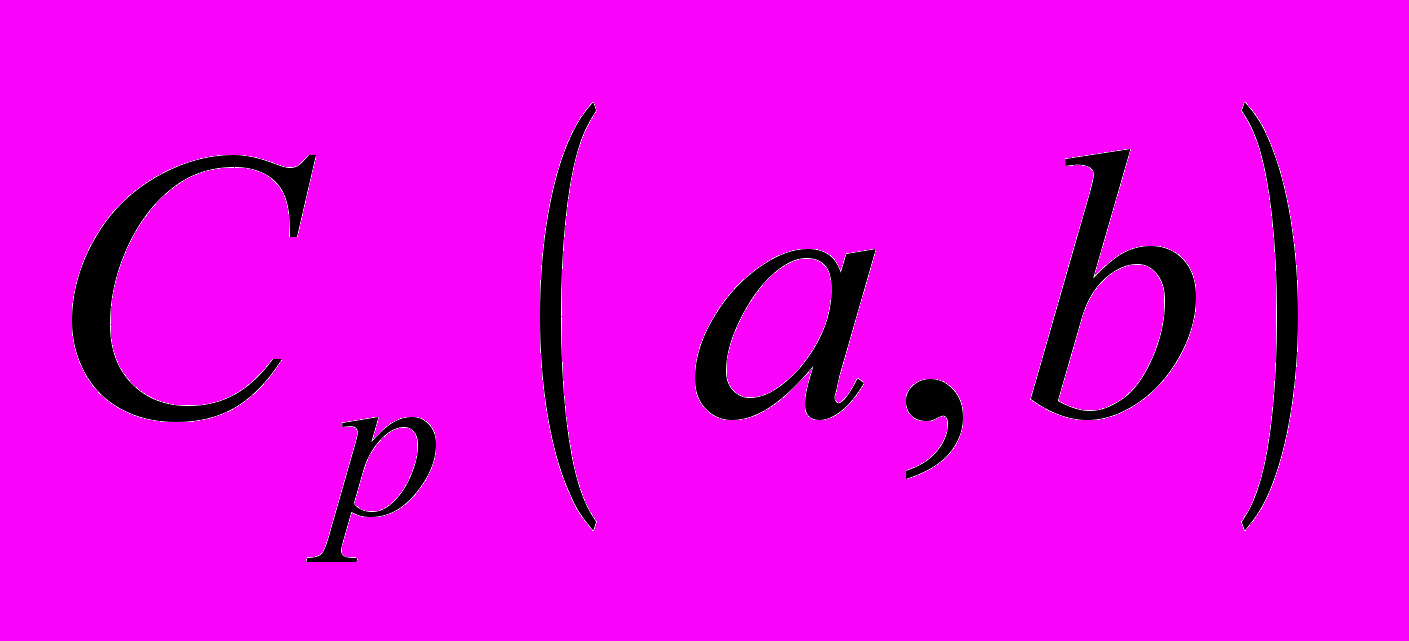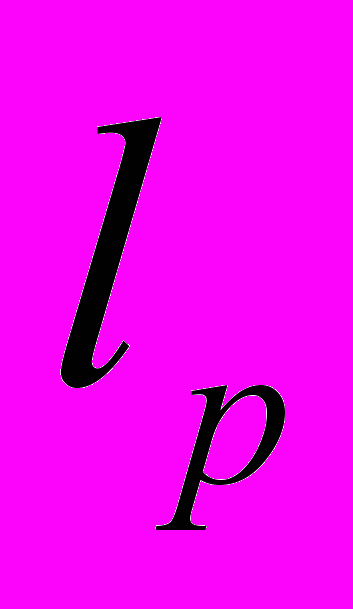. Принцип сжимающих отображений и его применения: задача Коши, интегральные уравнения, эргодическая теорема.


Тема 5. Меры на прямой и на плоскости. Измеримые функции. Сходимость последовательностей измеримых функций по мере и почти всюду.


Тема 6. Компактные множества. Сепарабельность. Плотные множества в .


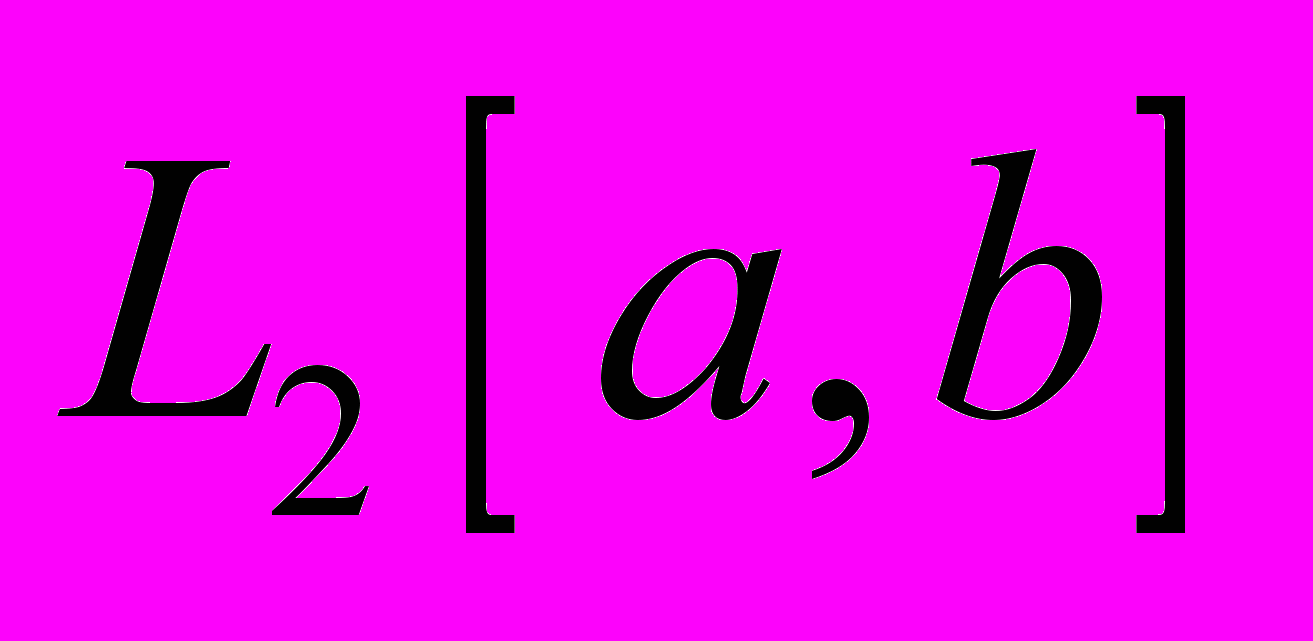Тема 7. Базисы в гильбертовых пространствах. Функции Хаара. Тригонометрические базисы.


Тема 8. Функционалы и операторы. Нахождение норм для линейных функционалов и операторов.

№ п/п	Раздел Дисциплины	Семестр	Неделя семестра	Виды учебной работы, включая самостоятельную работу студентов и трудоемкость (в часах)			Формы текущего контроля успеваемости (по неделям семестра)
				лекции	практические занятия	самостоятельная работа	Форма промежуточной аттестации (по семестрам)
1	Вводная часть.	3	1	1	0	0
2	Элементы теории множеств. Множества в метрических пространствах.	3	1–3	5	12	10	Опрос на занятия, проверка домашних заданий. Контрольная работа.
3	Теория меры.	3	4–7	8	4	10	Опрос на занятия, проверка домашних заданий
4	Измеримые функции.	3	8–11	8	8	10	Опрос на занятия, проверка домашних заданий. Доклады студентов.
5	Теория интеграла.	3 4	12–16 1–2	10 4	8 4	10 4	Опрос на занятия, проверка домашних заданий. Зачет, экзамен.
6	Метрические пространства	4	3–5	6	4	6	Опрос на занятия, проверка домашних заданий. Контрольная работа.
7	Линейные пространства.	4	6–10	10	12	12	Опрос на занятия, проверка домашних заданий. Контрольная работа.
8	Линейные функционалы и операторы.	4	11–15	10	10	18	Опрос на занятия, проверка домашних заданий. Доклады студентов. Контрольная работа. Зачет, экзамен.
	Итого			62	62	80	60

5. Образовательные технологии

В процессе обучения для достижения планируемых результатов освоения дисциплины используются следующие методы образовательных технологий:

– работа в команде;

– опережающая самостоятельная работа;

– междисциплинарное обучение;

– проблемное обучение;

– обучение на основе опыта.

Для изучения дисциплины предусмотрены следующие формы организации учебного процесса: лекции, практические занятия, самостоятельная работа студентов, индивидуальные и групповые консультации.


6. Учебно-методическое обеспечение самостоятельной работы студентов. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины.

Контроль самостоятельной работы студентов и качества освоения дисциплины осуществляется посредством:

– опроса студентов при проведении практических занятий;

– проведения контрольных работ;

– выполнения студентами домашних работ по вариантам;

– проверки выполнения домашних заданий;

– докладов студентов по выбранным темам.

Итоговая аттестация предусматривает предусматривает сдачу зачетов по темам практических занятий и экзаменов по темам лекций. Для итоговой аттестации подготовлены список задач для сдачи зачета (100 задач) и билеты для экзамена (25 билетов по 2 вопроса).


Темы докладов.

1. Обобщенный принцип сжимающих отображений.
   
2. Применение принципа сжимающих отображений к решению систем линейных уравнений.
   
3. Применение принципа сжимающих отображений к решению интегральных уравнений.
   
4. Применение принципа сжимающих отображений к решению задачи Коши для обыкновенных дифференциальных уравнений.
   
5. Вариация функционалов. Задача о брахистохроне.