[по имени амер физика И. А. Раби (I. I. Rabi)], резонансный метод исследования магн моментов ядер, атомов и молекул и внутримол
| Вид материала | Документы |
- 32. Эволюция понятия элементарная частица. Неизменность свойств ядер, атомов, молекул, 827.07kb.
- Молекулярная физика и термодинамика статистический и термодинамический методы Молекулярная, 12.67kb.
- Элементы квантовой механики и физики атомов, молекул, твердых тел, 156.85kb.
- X международная конференция Импульсные лазеры на переходах атомов и молекул ampl, 299.2kb.
- Магнитные свойства молекул, 29.04kb.
- Моделирование структур молекул по Огжевальскому, 61.04kb.
- Десятая новая лекция аксиомы единства канарёв, 209.76kb.
- Программа-минимум кандидатского экзамена по специальности, 79.71kb.
- Молекулярная физика и термодинамика. Лекция №1 Молекулярно-кинетическая теория Основные, 10053.18kb.
- Вегето- резонансный тест Оценка по методу Кузьменко (метод Накатани) Диабат (метод, 12.28kb.
Р
РАБИ МЕТОД [по имени амер. физика И. А. Раби (I. I. Rabi)], резонансный метод исследования магн. моментов ядер, атомов и молекул и внутримол. вз-ствий в молекулярных и атомных пучках. Резонансное высокочастотное магн. поле, через к-рое пролетают ч-цы, вызывает переориентацию магн. моментов, обнаруживаемую по изменению их траекторий в неоднородном магн. поле.
РАБОТА силы, мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения. Если сила F численно и по направлению постоянна, а перемещение М0М1 прямолинейно (рис. 1), то P. A = F•s•cos, где s=M0M1, — угол между направлениями силы и перемещения. Когда <90°, Р. силы положительна, при 180°>90° — отрицательна, а при =90°, т. е. когда сила перпендикулярна перемещению, А=0. Единицы измерения Р.: джоуль (в СИ), 1 эрг=10-7 Дж и килограмм-сила на метр (1 кгс•м=9,81 Дж).
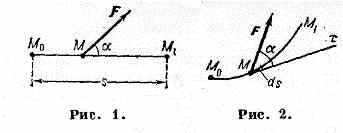
В общем случае для вычисления Р. силы вводится понятие элементарной работы dA=Fdscos, где ds — элем. перемещение, — угол между направлениями силы и касательной к траектории точки её приложения, направленной в сторону перемещения (рис. 2). В декартовых координатах
dA=Fxdx+Fydy+Fzdz, (1) где Fx, Fy, Fz — проекции силы на координатные оси, х, у, z — координаты точки её приложения. В обобщённых координатах
dA=Qiqi. (2)
где qi — обобщённые координаты, Qi — обобщённые силы. Для сил, действующих на тело, имеющее неподвижную ось вращения, dA=Mzd, где Mz — сумма моментов сил относительно оси вращения z, — угол поворота. Для сил давления dA=pdV, где р — давление, V — объём.
Р. силы на конечном перемещении определяется как интегральная сумма элементарных Р. и при перемещении М0М1 выражается криволинейным интегралом:
A=∫M0M1)(Fcos)ds или
A=∫M0M1(Fxdx + Fydy + Fzdz). (3)
Для потенциальных сил dA=-dП и А= П0-П1, где П0 и П1 — значения потенциальной энергии П в нач. и конечном положениях системы; в этом случае Р. не зависит от вида траекторий точек приложения сил. При движении механич. системы сумма работ всех действующих сил на нек-ром перемещении равна изменению её кинетической энергии Т, т. е. Аi=T1-T0. Понятие «Р. силы» широко используется в механике, а также в др. областях физики и в технике.
С. М. Тарг.
Р. в термодинамике — обобщение понятия «Р. в механике» [выраженного в дифф. форме (2)]. Обобщённые координаты в термодинамике -это внеш. параметры термодинамич. системы (объём, напряжённость внеш. магн. или электрич. поля и т. п.), а обобщённые силы (давление и др.) — величины, зависящие не только от координат, но и от внутр. параметров системы (темп-ры или энтропии). Р. термодинамич. системы над внеш. телами заключается в изменении состояния этих тел и определяется кол-вом энергии, передаваемой системой внеш. телам при изменении внеш. параметров системы. В квазистатических (т. е. бесконечно медленных) адиабатических процессах Р. равна изменению внутренней энергии системы, в квазистатич. изотермических процессах — изменению Гельмгольца энергии. В ряде случаев Р. может быть выражена через др. потенциалы термодинамические. В общем случае величина Р. при переходе системы из нач. состояния в конечное зависит от способа (пути), каким осуществляется этот переход. Это означает, что бесконечно малая (элементарная) Р. системы не явл. полным дифференциалом к.-л. функции состояния системы; поэтому элем. Р. обозначают обычно не dA (как полный дифференциал), а А. Зависимость Р. от пути приводит к тому, что для кругового процесса, когда система вновь возвращается в исходное состояние, Р. системы может оказаться не равной нулю, что используется во всех тепловых двигателях. Работа внеш. сил над системой А=-A, если энергия вз-ствия системы с внеш. телами не меняется в процессе совершения Р. Примерами Р. при изменении одного из внеш. параметров системы могут служить: Р. сил давления р при изменении объёма V системы A=pdV, Р. сил поверхностного натяжения при изменении поверхности системы A=-d ( — коэфф. поверхностного натяжения, d — элемент поверхности); Р. намагничивания системы A=-HdJ (H — напряжённость внеш. магн. поля, J — намагниченность в-ва) и т. д. Р. системы в неравновесном (необратимом) процессе всегда меньше, чем в равновесном.
• Леонтович М. А., Введение в термодинамику, 2 изд., М.—Л., 1952; Р е й ф Ф., Статистическая физика, пер. с англ., М., 1972 (Верклеевский курс физики, т. 5).
Г. Я. Мякишев.
^ РАБОТА ВЫХОДА, энергия Ф, к-рую необходимо затратить для удаления эл-на из твёрдого или жидкого в-ва в вакуум (в состояние с равной нулю кинетич, энергией). Р. в. Ф=е, где — потенциал Р. в., е — абс. величина электрич. заряда электрона. Р. в. равна разности между мин. энергией эл-на в вакууме и Ферми энергией эл-нов внутри тела. Если электростатич. потенциалы в вакууме вак, в толще в-ва об, а ξF — энергия Ферми, отсчитываемая от энергии неподвижного эл-на в точке вакуума, где потенциал равен вак, то Р. в. (в случае однородной поверхности)
Ф=e(об-вак)-ξF.
В приповерхностной области любого тела образуется двойной электрич. слой. Он возникает даже на идеально чистой поверхности кристалла в результате того, что «центр тяжести» плотности эл-нов в поверхностной крист. ячейке не совпадает с плоскостью, в к-рой расположены ионы. При этом
вак-об=4PS. где PS — дипольный момент двойного слоя, приходящийся на ед. площади поверхности (РS>0, если дипольный момент направлен наружу). Р. в.— характеристика поверхности тела: грани одного и того же кристалла, образованные разными кристаллографич. плоскостями или покрытые разными в-вами, имеют разные РS и разную Р. в. Вблизи этих поверхностей вак также не совпадают и между поверхностями возникают контактная разность потенциалов и электростатич. поле.
В металлах при низких темп-рах уровень Ферми совпадает с самым высоким заполненным энергетич. уровнем эл-нов и Р. в. имеет смысл наименьшей энергии, требуемой для удаления эл-на в вакуум. В полупроводниках такой смысл Р. в. придавать нельзя. В металлах двойной электрич. слой сосредоточен на самой поверхности и толщина его — порядка межатомного расстояния. В ПП заряд одного знака находится на поверхности (эл-ны или дырки в поверхностных состояниях), а заряд противоположного ' знака распределён в слое, толщина к-рого зависит от концентраций примесей и темп-ры и может достигать многих тыс. межатомных расстояний.
600
РАБОТА ВЫХОДА (в эВ) НЕКОТОРЫХ ПОЛИКРИСТАЛЛИЧЕСКИХ МЕТАЛЛОВ, Q1=0, Q2=0, . . ., Qs=0. (2)
^ ПП И ОТДЕЛЬНЫХ ГРАНЕЙ МОНОКРИСТАЛЛА ВОЛЬФРАМА

Р. в. может быть сильно изменена адсорбцией разл. атомов или молекул на поверхности (адсорбированные ч-цы изменяют РS). Атомы металлов с малой энергией ионизации (напр., Cs) при адсорбции приобретают дипольный момент, направленный в сторону вакуума, и снижают Р. в. Покрытие Cs уменьшает Р. в. для нек-рых металлов и ПП до 1 эВ (4—6 эВ в отсутствие Cs, см. табл.).
В ПП с гомополярными межатомными связями (Ge, Si и т. п.) Р. в. практически не изменяется даже при сильном изменении ξF в объёме кристалла (при изменении темп-ры или введении примеси): изменение ξF вызывает такое изменение заполнения поверхностных состояний эл-нами и, следовательно, такое изменение об — вак, к-рое компенсирует изменение ξF. Плотность состояний на чистых поверхностях ионных ПП в области запрещённой зоны невелика и допускает изменение Р. в. с изменением положения уровня Ферми в объёме ПП (напр., введением примесей).
Абс. величину Р. в. измеряют по кол-ву теплоты, к-рое нужно подводить к телу при отборе из него термоэмиссионного тока (см. ^ Термоэлектронная эмиссия), чтобы темп-ра тела оставалась неизменной; по температурной зависимости и полной величине термоэмиссионного тока, а в металлах и вырожденных ПП — также по красной границе фотоэлектронной эмиссии. Контактная разность потенциалов Uк двух тел равна разности их Р. в.; измеряя Uк между исследуемой поверхностью и эталонной, находят и Р. в. первой.
•Добрецов Л. Н., Гомоюнова М. В., Эмиссионная электроника, М., 1966; Ривьере X., Работа выхода. Измерения и результаты, в сб.: Поверхностные свойства твердых тел, под ред. М. Грина, М., 1972; Фоменко В. С., Эмиссионные свойства материалов, К., 1981.
^ С. Г. Дмитриев, Ш. М. Коган.
РАБОТОСПОСОБНОСТЬ, термин, применяемый в технической термодинамике для обозначения макс. работы, к-рую может совершить система при переходе из данного состояния в равновесие с окружающей средой.
^ РАБОЧИЕ СРЕДСТВА ИЗМЕРЕНИЙ, применяются для практич. измерений при науч. исследованиях, в произ-ве и др. областях. Этим они отличаются от образцовых средств измерений, применяемых только для поверки др. средств измерений.
^ РАВНОВЕСИЕ МЕХАНИЧЕСКОЙ СИСТЕМЫ, состояние механич. системы, находящейся под действием сил, при к-ром все её точки покоятся по отношению к рассматриваемой системе
отсчёта. Если система отсчёта явл. инерциальной (см. ^ Инерциальная система отсчёта), равновесие наз. абсолютным, а если неинерциальной, то относительным. Изучение условий Р. м. с.— одна из осн. задач статики. Условия Р. м. с. имеют вид равенств, связывающих действующие силы и параметры, определяющие положения системы; число этих условий равно числу степеней свободы системы. Условия относит. Р. м. с. составляются так же, как и условия абс. равновесия, но к действующим на точки силам прибавляют соответствующие переносные силы инерции. Условия равновесия свободного тв. тела состоят в равенстве нулю сумм проекций сил на три координатные оси Oxyz и сумм моментов всех приложенных к телу сил относительно этих осей, т. е.
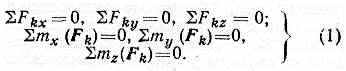
При выполнении условий (1) тело будет по отношению к данной системе отсчёта находиться в покое, если скорости всех его точек относительно этой системы в момент начала действия сил были равны нулю. В противном случае тело при выполнении условий (1) будет совершать т. н. движение по инерции, напр. двигаться поступательно, равномерно и прямолинейно. Если тв. тело не явл. свободным (см. Связи механические), то условия его равновесия дают те из равенств (1) (или их следствий), к-рые не содержат реакций наложенных связей; остальные равенства дают ур-ния для определения неизвестных реакций. Напр., для тела, имеющего неподвижную ось вращения Oz, условием равновесия будет mz(Fk)=0; остальные равенства (1) служат для определения реакций подшипников, закрепляющих ось. Если тело закреплено наложенными связями жёстко, то все равенства (1) дают ур-ния для определения реакций связей.
Согласно отвердевания принципу, равенства (1), не содержащие реакций внеш. связей, дают одновременно необходимые (но недостаточные) условия равновесия любой механич. системы и, в частности, деформируемого тела. Необходимые и достаточные условия равновесия любой механич. системы могут быть найдены с помощью возможных перемещений принципа. Для системы, имеющей s степеней свободы, эти условия состоят в равенстве нулю соответствующих обобщённых сил:
Из состояний равновесия, определяемых условиями (1) или (2), практически реализуются лишь те, к-рые явл. устойчивыми (см. Устойчивость равновесия). Равновесия жидкостей и газов рассматриваются в гидростатике и фэростатике.
С. М. Тарг.
^ РАВНОВЕСИЕ СТАТИСТИЧЕСКОЕ, состояние замкнутой статистич. системы, в к-ром ср. значения всех физ. величин, характеризующих состояние, не зависят от времени. Р. с.— одно из осн. понятий статистической физики, играющее такую же роль, как равновесие термодинамическое в термодинамике. Р. с. не явл. равновесным в механич. смысле, т. к. в системе при этом постоянно возникают малые флуктуации физ. величин около ср. значений. Теория Р. с. даётся в статистич. физике, к-рая описывает его при помощи разл. Гиббса распределений (микроканонич., канонич. или большого канонического) в зависимости от типа контакта системы с окружающей средой, запрещающего или допускающего обмен с ней энергией или ч-цами. В теории неравновесных процессов важную роль играет понятие неполного Р. с., при к-ром параметры, характеризующие состояние системы, очень слабо зависят от времени. Широко применяется понятие локального Р. с., при к-ром темп-ра и химический потенциал в малом элементе объёма зависят от времени и пространств. координат её ч-ц. См. Кинетика физическая.
Д. Н. Зубарев.
^ РАВНОВЕСИЕ ТЕРМОДИНАМИЧЕСКОЕ, состояние термодинамич. системы, в к-рое она самопроизвольно приходит через достаточно большой промежуток времени в условиях изоляции от окружающей среды. При Р. т. в системе прекращаются все необратимые процессы, связанные с диссипацией энергии: теплопроводность, диффузия, хим. реакции и др. В состоянии Р. т. параметры системы не меняются со временем (строго говоря, те из параметров, к-рые не фиксируют заданные условия существования системы, могут испытывать флуктуации — малые колебания около своих ср. значений). Изоляция системы не исключает определённого типа контактов со средой (напр., теплового контакта с термостатом, обмена с ним в-вом). Изоляция осуществляется обычно при помощи неподвижных стенок, непроницаемых для в-ва (возможны также случаи подвижных стенок и полупроницаемых перегородок). Если стенки не проводят теплоты (как, напр., в сосуде Дьюара), то изоляция наз. адиабатической. При теплопроводящих (д и а т е р м и ч е с к и х) стенках между системой и внеш.
601
средой, пока не установилось Р. т., возможен теплообмен. При полупроницаемых для в-ва стенках Р. т. наступает, когда в результате обмена в-вом между системой и внеш. средой выравниваются химические потенциалы, среды и системы. Переход системы в Р. т. наз. релаксацией.
Одно из условий Р. т.— механич. равновесие, при к-ром невозможны никакие макроскопич. движения частей системы, но поступат. движение и вращение системы как целого допустимы. В отсутствие внеш. полей и вращения системы условием её м е х а н и ч е с к о г о р а в н о в е с и я явл. постоянство давления во всём объёме системы. Др. необходимые условия Р. т.— постоянство темп-ры и хим. потенциала в объёме системы, они определяют т е р м и ч е с к о е и х и м и ч е с к о е р а в н о в е с и е системы.
Достаточные условия Р. т. (у с л о в и я у с т о й ч и в о с т и) могут быть получены из второго начала термодинамики; к ним, напр., относятся: возрастание давления при уменьшении объёма (при пост. темп-ре) и положит. значение теплоёмкости при пост. давлении. В общем случае система находится в Р. т. тогда, когда термодинамич. потенциал системы, соответствующий независимым в данных условиях переменным, минимален (см. Потенциалы термодинамические), а энтропия — максимальна.
• Леонтович М. А., Введение в термодинамику, 2 изд., М.—Л., 1952; К у б о Р., Термодинамика, пер. с англ., М., 1970; Мюнстер А., Химическая термодинамика, пер. с нем., М., 1971.
Д. Н. Зубарев.
^ РАВНОВЕСИЯ СОСТОЯНИЕ колебательной системы, состояние динамич. системы, к-рое не изменяется во времени. Р. с. могут быть устойчивыми, неустойчивыми и безразлично-устойчивыми. Движение системы вблизи положения равновесия (при малом от него отклонении) может быть существенно разным в зависимости от характера типа) Р. с.
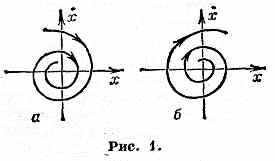
Для систем с одной степенью свободы, если Р. с. устойчиво, при малом возмущении (отклонении) система возвращается к нему, совершая затухающие колебания (на фазовой плоскости — см. Фазовое пространство — такому движению соответствует устойчивый фокус; рис 1, а), или апериодически (устойчивый узел; рис. 2, а). Вблизи неустойчивого Р. с. малые отклонения нарастают, совершая колебания
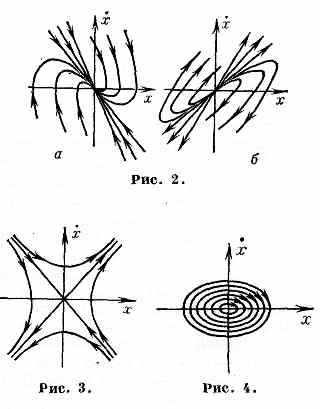
(неустойчивый фокус; рис. 1, б), или апериодически (неустойчивый узел; рис. 2, б); вблизи седлового Р. с. (рис. 3) возможно вначале приближение к Р. с., а затем уход. Наконец, в случае безразлично-устойчивого Р. с. (центр; рис. 4) малые отклонения приводят к незатухающим колебаниям вблизи Р. с. Для систем с неск. степенями свободы движение вблизи Р. с. может быть более сложным и существенно зависеть от характера нач. отклонения. Движение динамич. системы вблизи Р. с. чаще всего описывается линеаризованными ур-ниями, имеющими решение в виде суммы экспонент aeit с комплексными (в общем случае) характеристич. показателями i. Р. с. устойчиво, если действит. части всех характеристич. показателей отрицательны (Rei<0); если же имеется хотя бы один i с положительной действительной частью, то Р. с. неустойчиво. Если же часть характеристич. показателей имеет Rei=0, а для остальных Rei<0, то исследование устойчивости становится более сложным. Для систем с одной степенью свободы (напр., матем. маятник) этих показателей два: 1 и 2. В зависимости от их величины на фазовой плоскости системы возможны четыре типа Р. с.: узел (Im1,2=0, Re1•Re2>0) — рис. 2, фокус (Im1,20, Re1=Re20) — рис. 1, седло (Im1,2=0, Re1•Re2<0) — рис. 3 и центр (Im1,20, Re1=Re2=0) — рис. 4.
• Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, [3 изд.], М., 1981; Меркин Д. Р., Введение в теорию устойчивости движения, 2 изд., М., 1976.
М. И. Рабинович.
^ РАВНОВЕСНОЕ ИЗЛУЧЕНИЕ, тепловое излучение, находящееся в термодинамич. равновесии с в-вом. Р. и.— излучение абсолютно чёрного тела. Спектр Р. и. не зависит от состава в-ва излучающей системы и определяется только темп-рой, одинаковой для всех частей системы (см. Планка закон излучения).
^ РАВНОВЕСНЫЙ ПРОЦЕСС (квазистатический процесс) в термодинамике, процесс перехода термодинамич. системы из одного равновесного состояния в другое, столь медленный, что все промежуточные состояния можно рассматривать как равновесные, т. е. характеризующиеся очень медленным (в пределе — бесконечно медленным) изменением термодинамич. параметров состояния. Р. п.— одно из осн. понятий термодинамики равновесных процессов. Всякий Р. п. явл. обратимым процессом и, наоборот, любой обратимый процесс явл. равновесным.
РАВНОДЕЙСТВУЮЩАЯ системы сил, сила, эквивалентная данной системе сил и равная их геом. сумме: R=Fk. Система сил, приложенных в одной точке, всегда имеет Р., если R0. Любая другая система сил, приложенных к телу, если R0, имеет Р., когда главный момент этой системы или равен нулю, или перпендикулярен R. В этом случае замена системы сил их Р. допустима лишь тогда, когда тело можно рассматривать как абсолютно твёрдое, и недопустима, напр., при определении внутр. усилий или решении др. задач, требующих учёта деформации тела. Примеры систем сил, не имеющих Р.,— пара сил или две силы, не лежащие в одной плоскости.
^ РАВНОМЕРНОЕ ДВИЖЕНИЕ, движение точки, при к-ром численная величина её скорости v постоянна. Путь, пройденный точкой при Р. д. за промежуток времени t, равен s=vt. Тв. тело может совершать п о с т у п а т е л ь н о е Р. д., при к-ром всё сказанное относится к каждой точке тела, равномерное вращение вокруг неподвижной оси, при к-ром угловая скорость тела постоянна, а угол поворота тела =t, и равномерное винтовое движение.
^ РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ, движение точки, при к-ром её касательное ускорение w (в случае прямолинейного Р. д. всё ускорение w) постоянно. Скорость v, к-рую имеет точка через время t после начала движения, и её расстояние s от нач. положения, измеренное вдоль дуги траектории, определяются при Р. д. равенствами: v= v0+wt, s=v0t+wt2/2, где v0 — нач. скорость точки. Когда знаки v и w одинаковы, Р. д. явл. ускоренным, а когда разные - - замедленным.
Тв. тело может совершать поступательное Р. д., при к-ром всё сказанное относится к каждой точке тела, и равнопеременное вращение вокруг неподвижной оси, при к-ром угловое ускорение тела постоянно, а угловая скорость и угол поворота тела равны:=0+t, =0t+et2/2, где 0 — нач. угловая скорость.
^ РАВНОРАСПРЕДЕЛЕНИЯ ЗАКОН, закон классич. статистической физики, утверждающий, что для статистич. системы в состоянии термодина-
602
мич. равновесия на каждую трансляц. и вращат. степень свободы приходится в среднем кинетич. энергия kT/2, а на каждую колебат. степень свободы — в среднем энергия kT (где Т -абс. темп-ра системы, k — Больцмана постоянная). Р. з.— приближённый закон; он нарушается в тех случаях, когда становятся существенными квант. эффекты (а в случае колебат. степеней свободы — также и ангармоничность колебаний). Р. з. позволяет легко оценить предельные значения теплоёмкостей многоатомных газов и тв. тел при высоких темп-рах.
РАД (рад, rad, сокр. от англ. radiation absorbed dose — поглощённая доза излучения), внесистемная ед. поглощённой дозы излучения, соответствует энергии излучения 100 эрг, поглощённой веществом массой 1 г.
1 рад = 100 эрг/г = 0,01 грэй=2,388•10-6 кал/г.
РАДИАН (от лат. radius — луч, радиус) (рад, rad), единица плоского угла; 1 рад равен углу между двумя радиусами окружности, длина дуги между к-рыми равна радиусу. 1 рад=57°17'44,8"3,44•103 угл. минут2,06•105 угл. секунд63,7g (см. Град).
^ РАДИАН В СЕКУНДУ (рад/с, rad/s), единица угл. скорости; 1 рад/с — угл. скорость равномерно вращающегося тела, при к-рой за время 1 с тело совершает поворот относительно оси вращения на угол 1 рад. 1 рад/с=0,159 об/с57,3°/c.
^ РАДИАЦИОННАЯ ТЕМПЕРАТУРА (Тr), физ. параметр, определяющий суммарную (по всему спектру) энергетич. яркость Вэ излучающего тела; Р. т. равна такой темп-ре абсолютно чёрного тела, при к-рой его суммарная энергетич. яркость В0э=Вэ.
Законы теплового излучения (см. Стефана — Больцмана закон излучения и Кирхгофа закон излучения) позволяют выражение В0э=Вэ записать в виде Т4r=TT4, где T — излучательная способность (коэфф. черноты) тела, — Стефана — Больцмана постоянная. Если известна T и измерена Тr (радиац. пирометром), то можно вычислить темп-ру тела Т— = Тr•T-1/4. Для теплового излучения
всех тел, кроме чёрного, T<1, поэтому Тr<Т, но при люминесценции Тr может быть больше Т.
• Г о р д о в А. Н., Основы пирометрии,
2 изд., М.. 1971.
^ РАДИАЦИОННОЕ ДАВЛЕНИЕ в акустике, то же, что давление звукового излучения.
РАДИАЦИОННОЕ МАТЕРИАЛОВЕДЕНИЕ, совокупность методов для:
1) создания материалов (конструкционных, полимерных, ПП и др.), устойчивых к воздействию яд. излучений;
2) придания материалам нужных св-в путём их дозированного облучения. ^ Радиационные дефекты способны изменить объёмные и поверхностные св-ва материалов. В металлах можно изменять уд. электросопротивление и пластичность (у Cu, Аl, Аu, Pt, F, Ni и др. удвоение наблюдается при концентрации вакансий и междоузлий ~1% от концентрации атомов). В результате ядерных реакций (n, ), (р, ) и т. п. образуются пузырьки газа (4Не), что в сочетании с вакансиями определяет изменение пластич. св-в металлов. После длит. облучения (напр., нейтронами) металлы упрочняются, а нек-рые переходные металлы с объёмно-центрир. решёткой приобретают повыш. хрупкость при низких темп-рах.
Облучение полимеров сопровождается разрывом молекул и образованием химически активных радикалов, взаимодействующих между собой и с кислородом воздуха. В результате у мн. полимеров вместо слабо связанных между собой длинных полимерных молекул образуется жёсткий трёхмерный каркас. Напр., полиэтилен, полихлорвинил, мн. резины становятся жёсткими, теряют пластичность (несколько увеличивается их термостойкость), а фторированные полимеры при облучении в присутствии кислорода теряют прочность и пластичность, превращаясь в порошок. Наибольшей устойчивостью к облучению обладают материалы на основе ароматич. углеводородов.
Наибольшую чувствительность к радиации имеют полупроводники. Радиац. дефекты создают в запрещённой зоне разрешённые состояния, что приводит к энергетич. перераспределению носителей заряда и интенсифицирует процессы рекомбинации. В результате время жизни неравновесных носителей изменяется даже при незначит. дозах облучения. В меньшей степени изменяется ПП. Изменяются также оптич. и фотоэлектрич. свойства ПП. Ядерные реакции под действием тепловых нейтронов на нек-рых изотопах Ge и Si приводят к образованию примесных атомов Ga и Р, что открыло возможность р а д и а ц и о н н о г о л е г и р о в а н и я, отличающегося высокой степенью однородности (недостижимой в традиц. способах).
• Конобеевский С. Т., Действие облучения на материалы, М., 1967; Томпсон М., Дефекты и радиационные повреждения в металлах, пер. с англ., М., 1971.
Я. А. Ухин.
^ РАДИАЦИОННОЕ ТРЕНИЕ, то же, что реакция излучения.
РАДИАЦИОННЫЕ ДЕФЕКТЫ, структурные повреждения, образующиеся при облучении тв. тел потоками ч-ц и жёстким электромагн. (гамма- и рентгеновским) излучением. Переданная тв. телу энергия расходуется (частично) на разрыв межатомных связей. Для образования простейшего Р. д.— вакансии и междоузельного атома (п а р а Ф р е н к е л я) необходима энергия, превышающая пороговую п (14—35 эВ). При облучении быстрыми ч-цами (нейтронами, протонами с энергией в десятки МэВ и др.) энергия, сообщаемая смещаемым атомам, может достигать десятков кэВ, т. е. в неск. сотен и в тысячи раз превышать ξп. Ускоренный смещённый атом, двигаясь в плотной среде, ионизует атомы вдоль своей траектории и образует каскад смещений. Р. д. явл. также примеси, образующиеся в результате деления атомных ядер, хим. и ядерных реакций, а также сами бомбардирующие ч-цы (ионное внедрение). В результате в сравнительно небольшой области, размером в сотни А, возникают сотни и тысячи точечных дефектов, образующих скопления (дивакансии, тривакансии, тетравакансии и т. д.).
Нагреванием можно изменить концентрацию Р. д. вплоть до полного их исчезновения (отжиг). Р. д. типа скоплений или разупорядоченных областей можно наблюдать с помощью электронных микроскопов, а точечные Р. д.— с помощью ионных проекторов. Исследования Р. д. позволяют создавать радиационно-стойкие материалы и использовать облучение для целенаправленного изменения их св-в (см. Радиационное материаловедение).
• Емцев В. В., Машовец Т. В., Примеси и точечные дефекты в полупроводниках, М., 1981; Болотов В. В., Васильев А. В., Герасименко Н. Н., Физические процессы в облученных полупроводниках, под ред. Л. С. Смирнова, Новосиб., 1977.
Н. А. Ухин.
^ РАДИАЦИОННЫЕ ПОПРАВКИ, в квантовой электродинамике поправки к значениям нек-рых физ. величин и к сечениям разл. процессов (вычисленным по ф-лам релятивистской квант. механики), обусловленные вз-ствием заряж. ч-цы с собственным эл.-магн. полем. Р. п. рассчитывают по методу теории возмущений, представляя их в виде ряда по степеням постоянной тонкой структуры =e2/ћnc1/137 (где е — заряд эл-на), n-й член к-рого можно рассматривать как результат испускания и поглощения n виртуальных фотонов или электрон-позитронных пар. При вычислении Р. п. используется процедура перенормировки массы и заряда ч-цы.
Наибольший интерес представляют Р. п. к магн. моментам эл-на и мюона, к сверхтонкому расщеплению ат. уровней, радиац. смещение ат. уровней энергии (сдвиг уровней), Р. п. к сечениям рассеяния эл-на эл-ном или ат. ядром. Результаты расчётов Р. п. вплоть до величин 3-го порядка по степеням а блестяще согласуются с эксперим. данными и свидетельствуют о справедливости квант. электродинамики по крайней мере на расстояниях, больших 10-15 см. Р. п. растут с ростом энергии, и эфф. параметром разложения (эффективным зарядом) при высоких энергиях явл. величина •ln(ξ/m), где ξ — энергия ч-цы в системе центра инерции, m — её масса в энергетич. единицах.
603
Р. п. могут быть в ряде случаев подсчитаны не только для электродииамич. процессов, но и для процессов, вызванных др. вз-ствиями. Напр., в квантовой хромодинамике вычисляются Р. п. к сечениям глубоко неупругих процессов или к вероятностям распада мезонов со скрытым «очарованием».
При вычислении Р. п. к электродинамич. величинам с точностью выше 3-го порядка существ. вклад вносят процессы виртуального рождения адронов и эффекты слабого взаимодействия.
• Фейнман Р., Теория фундаментальных процессов, пер. с англ., М., 1978; Бьёркен Дж., Дрелл С. Д., Релятивистская квантовая теория, пер. с англ., т. 1—2, М.,. 1978.
^ Б. Л. Иоффе.
РАДИАЦИОННЫЕ ПОСТОЯННЫЕ (постоянные излучения), физ. константы с1=2hc2 и c2=hc/k, входящие в Планка закон излучения ,T =
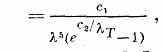
где ,T — объёмная плотность излучения с длиной волны К и абс. темп-рой Т. Первая Р. п. c1=3,741832(20) •10-16 Вт•м2, вторая Р. п. с2=0,01438786(45) м•К.
^ РАДИАЦИОННЫЕ ПОЯСА ЗЕМЛИ, внутренние области земной магнитосферы, в к-рых магн. поле Земли удерживает заряж, ч-цы (протоны, эл-ны, альфа-частицы и ядра более тяжёлых хим. элементов), обладающие кинетич. энергией от десятков кэВ до сотен МэВ. Выходу заряж. ч-ц из Р. п. 3. мешает особая конфигурация силовых линий геомагн. поля, создающего для заряж. ч-ц магн. ловушку. Р. п. 3. были открыты в 1958: внутр. пояс группой амер. учёных под руководством Дж. Ван Аллена, внеш. пояс сов. учёными во главе с С. Н. Верновым и А. Е. Чудаковым. Потоки ч-ц Р. п. 3. были зарегистрированы счётчиками Гейгера, установленными на ИСЗ.
Принципиальная возможность существования магн. ловушки в магн. поле Земли была показана расчётами норв. геофизика К. Стёрмера (1913) и швед. физика X. Альфвена (1950), но лишь эксперименты на спутниках показали, что ловушка реально существует и заполнена ч-цами высоких энергий. Захваченные в магн. ловушку Земли ч-цы под действием Лоренца силы совершают сложное движение, к-рое можно представить как колебат. движение по спиральной траектории вдоль силовой линии магн. поля из Сев. полушария в Южное и обратно с одновременным более медленным перемещением (долготным дрейфом) вокруг Земли (рис. 1). Когда ч-ца движется по спирали в сторону увеличения магн. поля (приближаясь к Земле), радиус спирали и её шаг уменьшаются. Вектор скорости ч-цы, оставаясь неизменным по величине, приближается к плоскости, перпендикулярной направлению поля.
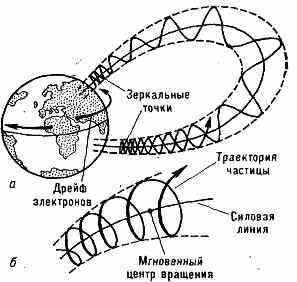
Рис. 1. Движение заряж. ч-ц, захваченных в гоомагн. ловушку (а). Ч-цы движутся по спирали вдоль силовой линии магн. поля Земли (б) и одновременно дрейфуют по долготе.
Наконец, в нек-рой точке (наз. зеркальной) происходит «отражение» ч-цы. Она начинает двигаться в обратном направлении — к сопряжённой зеркальной точке в др. полушарии. Одно колебание вдоль силовой линии из Сев. полушария в Южное протон с энергией ~100 МэВ совершает за время ~0,3 с. Время нахождения («жизни») такого протона в геомагн. ловушке может достигать 100 лет (~3•109 с), за это время он может совершить до 1010 колебаний. Долготный дрейф происходит со значительно меньшей скоростью. В зависимости от энергии ч-цы совершают полный оборот вокруг Земли за время от неск. минут до суток. Положит. ионы дрейфуют в зап. направлении, электроны — в восточном. Движение ч-цы по спирали вокруг силовой линии магн. поля можно представить как состоящее из вращения около т. н. мгновенного центра вращения и поступат. перемещения этого центра вдоль силовой линии.
При движении заряж. ч-цы в магн. поле Земли её мгновенный центр вращения находится на одной и той же поверхности, получившей назв.
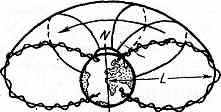
^ Рис. 2. Поверхность, описываемая ч-цей (эл-ном) радиац. пояса; осн. характеристикой поверхности явл. параметр L; N и S — магн. полюсы Земли.
магн. оболочки (рис. 2). Магн. оболочку характеризуют параметром ^ L, его численное значение в случае дипольного поля (см. Диполь) равно расстоянию, выраженному в радиусах Земли, на к-рое отходит магн. оболочка в экваториальной плоскости диполя от центра диполя. Для реального магн. поля Земли параметр L приближённо сохраняет такой же
простой смысл. Энергия ч-ц связана со значением параметра L; на оболочках с меньшими значениями L находятся ч-цы, обладающие большими энергиями. Это объясняется тем, что ч-цы высоких энергий могут быть удержаны лишь сильным магн. полем, т. е. во внутр. областях магнитосферы.
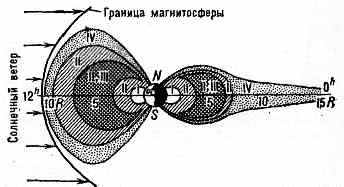
Рис. 3. Структура радиац. поясов Земли (сечение соответствует полуденному меридиану): I —внутр. пояс, II —пояс протонов малых энергий, III — внеш. пояс, IV— зона квазизахвата.
Обычно выделяют внутр. и внеш. Р. п. 3., пояс протонов малых энергий (пояс кольцевого тока) и зону квазизахвата ч-ц (рис. 3) или авроральной радиации (по латинскому названию полярных сияний). Внутр. Р. п. 3. характеризуется наличием протонов высоких энергий (от 20 до 800 МэВ) с максимумом плотности потока протонов с энергией ξр>20 МэВ до 104 протон/(см2•с•ср) на расстоянии L~l,5. Во внутр. поясе присутствуют также эл-ны с энергиями от 20—40 кэВ до 1 МэВ; плотность потока эл-нов с ξр40 кэВ составляет в максимуме ~106—107 эл-н/(см2•с•ср). С внеш. стороны этот пояс ограничен магн. оболочкой с L=2, к-рая пересекается с поверхностью Земли на геомагн. широтах ~45°. На ниж. границе внутр. пояса (на высотах 200—300 км) ч-цы, испытывая частые столкновения с атомами и молекулами атм. газов, теряют свою энергию, рассеиваются и «поглощаются» атмосферой.
Внеш. Р. п. 3. заключён между магн. оболочками с L=3 и L=6 с макс. плотностью потока ч-ц на L~4—4,5. Для внеш. пояса характерны эл-ны с энергиями 40—100 кэВ, поток к-рых в максимуме достигает 106—107 эл-н/(см2•с•ср). Среднее время «жизни» частиц внеш. Р. п. 3. составляет 105—107 с. В периоды повышенной солнечной активности во внеш. поясе присутствуют также эл-ны больших энергий (до 1 МэВ и выше).
Пояс протонов малых энергий (~0,03 —10 МэВ) простирается от L~l,5 до L~7—8. Зона квазизахвата, или авроральной радиации, расположена за внеш. поясом, она имеет сложную пространс7в. структуру, обусловленную деформацией магнитосферы солнечным ветром (потоком заряж. ч-ц от Солнца). Осн. ч-цами в зоне квазизахвата явл. эл-ны и протоны с энергиями ξ<100 кэВ. Внеш. пояс и пояс протонов малых энергий ближе всего (до высоты 200—300 км) под-
604
ходит к Земле на широтах 50—60°. На широты выше 60° проецируется Зона квазизахвата, совпадающая с , областью макс. частоты появления полярных сияний.
Энергетич. спектры для всех ч-ц Р. п. 3. описываются ф-циями вида: N(ξ)~ξ-, где N(ξ)— число ч-ц с данной энергией ξ, или N(ξ)~e-ξ/ξ0 c характерными значениями 1,8 для протонов в интервале энергий ξ от 40 до 800 МэВ, ξ0~200—500 кэВ для эл-нов внеш. и внутр. поясов и ξ0~100 кэВ для протонов малых энергий.
Происхождение захваченных ч-ц с энергией, значительно превышающей среднюю энергию теплового движения атомов и молекул атмосферы, связывают с действием неск. физ. механизмов: распадом нейтронов, созданных космическими лучами в атмосфере Земли (образующиеся при этом протоны пополняют внутр. Р. п. 3.); «накачкой» ч-ц в пояса во время геомагн. возмущений (магн. бурь), к-рая в первую очередь обусловливает существование эл-нов внутр. пояса; ускорением и медленным переносом ч-ц солнечного происхождения из внеш. во внутр. области магнитосферы (так пополняются эл-ны внеш. пояса и пояс протонов малых энергий). Проникновение ч-ц солнечного ветра в Р. п. 3. возможно через особые точки магнитосферы (т. н. дневные полярные каспы; рис. 4), а также через т. н. нейтральный слой в хвосте магнитосферы (с её ночной стороны). В области дневных каспов и в нейтральном слое хвоста геомагн. поле резко ослаблено и не явл. существенным препятствием для заряж. ч-ц межпланетной плазмы. Частично Р. п. 3. появляются также за счёт захвата
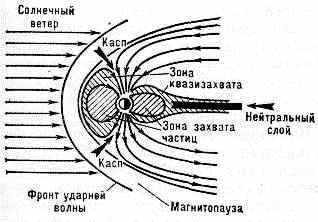
Рис. 4. Строение магнитосферы Земли в плоскости, проходящей через магн. полюсы Земли и линию Земля — Солнце. Стрелками указаны области, через к-рые ч-цы солнечного ветра проникают в магнитосферу.
протонов и эл-нов солнечных косм. лучей, проникающих во внутр. области магнитосферы. Перечисленных источников ч-ц, по-видимому, достаточно для создания Р. п. 3. с характерным распределением потоков ч-ц. В Р. п. 3. существует динамич. равновесие между процессами пополнения поясов и процессами потерь ч-ц. В основном ч-цы покидают Р. п. 3. из-за потери своей энергии на ионизацию (эта причина ограничивает, напр., пребывание протонов внутр. пояса в магн. ловушке временем ~109 с), из-за рассеяния ч-ц при столкновениях с ч-цами окружающей холодной плазмы и рассеяния на магн. неоднородностях и плазменных волнах разл. происхождения (см. Плазма). Рассеяние может сократить время «жизни» эл-нов внеш. пояса до 104—105 с. Эти эффекты приводят к нарушению условий стационарного движения ч-ц в геомагн. поле (т. н. адиабатич. инвариантов) и к «высыпанию» ч-ц из Р. п. 3. в атмосферу вдоль силовых линий магн. поля. Высыпание ч-ц из магн. ловушки, в особенности из зоны квазизахвата (авроральной радиации), приводит к усилению ионизации ионосферы, а интенсивное высыпание — к полярным сияниям.
Р. п. 3. представляют собой серьёзную опасность при длит. полётах в околоземном пр-ве. Потоки протонов малых энергий могут вывести из строя солнечные батареи и вызвать помутнение тонких оптич. покрытий. Длит. пребывание во внутр. поясе может привести к лучевому поражению живых организмов внутри косм. корабля под воздействием протонов высоких энергий. Кроме Земли, радиац. пояса существуют у Меркурия, Юпитера и Сатурна. Радиац. пояса Юпитера и Сатурна имеют значительно большую протяжённость и большие энергии ч-ц и плотности потоков ч-ц, чем Р. п. 3.
• Тверской Б. А., Динамика радиационных поясов Земли, М., 1968; X е с с В., Радиационный пояс и магнитосфера пер. с англ., М., 1972; Шабанский В. П. Явления в околоземном пространстве, М. 1972; Г а л ь п е р и н Ю. И., Г о р н Л. С. Хазанов Б. И., Измерение радиации в космосе, М., 1972; Чемберлен Дж. Теория планетных атмосфер, пер. с англ. М., 1981.
Ю. И. Логачёв
^ РАДИАЦИОННЫЙ ЗАХВАТ, ядерная реакция, в к-рой ядро-мишень захватывает налетающую ч-цу, а энергия возбуждения образующегося ядра излучается в виде -кванта.
^ РАДИОАКТИВАЦИОННЫЙ АНАЛИЗ, то же, что активационный анализ.
РАДИОАКТИВНОЕ ИЗЛУЧЕНИЕ, -частицы, эл-ны, позитроны, антинейтрино, нейтрино, -кванты, испускаемые при радиоактивном распаде (см. Радиоактивность).
РАДИОАКТИВНОСТЬ (от лат. radio -излучаю, radius — луч и activus — действенный), способность нек-рых ат. ядер самопроизвольно (спонтанно) превращаться в др. ядра с испусканием ч-ц. К радиоактивным превращениям относятся: альфа-распад, все виды бета-распада (с испусканием эл-на, позитрона или с захватом орбитального эл-на), спонтанное деление ядер, протонная и двупротонная Р., двунейтронная Р. и др. виды распадов. В случае -распада большое время жизни ядер обусловлено природой слабого взаимодействия, вызывающего -распад. За остальные виды радиоактивных процессов ответственно сильное взаимодействие; замедление таких процессов связано с наличием потенциальных барьеров (кулоновского и центробежного), затрудняющих вылет ч-ц из ядра.
С Р. связаны процессы испускания запаздывающих протонов и нейтронов, а также запаздывающее спонтанное деление ядер. В этих процессах -распад — предварительная стадия, задерживающая испускание яд. ч-ц. Радиоактивный распад часто сопровождается гамма-излучением, испускаемым в результате электромагн. переходов между различными квантовыми состояниями одного и того же ядра.
Открытие Р. датируется 1896, когда франц. физик А. Беккерель обнаружил испускание ураном неизвестного проникающего излучения, названного им радиоактивным. Вскоре была обнаружена Р. тория, а в 1898 франц. физики М. и П. Кюри открыли два новых радиоактивных элемента — полоний и радий. Работами англ. физика Э. Резерфорда и Кюри было установлено наличие трёх видов радиоактивных излучений — -, - и -лучей. Резерфорд и англ. физик Ф. Содди указали, что испускание -лучей сопровождается превращением хим. элементов, напр. превращением радия в радон. В 1913 амер. учёный К. Фаянс и Содди независимо сформулировали т. н. правило смещения, характеризующее перемещение нуклида в периодич. системе элементов при а- и -распадах.
В 1934 франц. физики И. и Ф. Жолио-Кюри открыли искусственную Р., т. е. радиоактивность ядер — продуктов ядерных реакций, к-рая впоследствии приобрела особенно важное значение. Из общего числа (~2000) известных радиоактивных нуклидов лишь ок. 300 — природные, а остальные получены в результате яд. реакций. Между искусств. и естеств. Р. нет принципиального различия. Изучение искусств. Р. привело к открытию новых видов -распада — позитронному + -распаду (И. и Ф. Жолио-Кюри, 1934) и электронному захвату. В 1939 был обнаружен распад с испусканием запаздывающих нейтронов (Дж. Даннинг с сотрудниками, США). В 1940 К. А. Петржак и Г. Н. Флёров открыли спонтанное деление ядер.
Для процессов радиоактивного распада характерен экспоненциальный закон уменьшения во времени ср. числа радиоактивных ядер. Продолжительность жизни радиоактивных ядер характеризуют п е р и о д о м п о л у р а с п а д а T1/2 (промежутком времени, за к-рый число радиоактивных ядер уменьшается в среднем вдвое).
605
Во мн. случаях продукты радиоактивного распада сами оказываются радиоактивными, и тогда образованию стабильных нуклидов предшествует цепочка из неск. актов радиоактивного распада. Характерными примерами систем, в к-рых происходят сложные радиоактивные превращения, явл. радиоактивные ряды изотопов тяжёлых элементов. Мн. радиоактивные ядра могут распадаться по двум или неск. из перечисленных выше осн. типов Р. В результате конкуренции разных путей распада возникают разветвления радиоактивных превращений. Для природных радиоактивных изотопов характерны разветвления, обусловленные возможностью - и -распадов. Для трансурановых элементов наиболее типичны разветвления, связанные с конкуренцией -(реже -)распадов и спонтанного деления. У нейтронодефицитных ядер часто наблюдается конкуренция +-распада и электронного захвата. Для мн. ядер с нечётными Z (число протонов) и чётными А (массовое число) оказываются энергетически возможными два противоположных варианта -распада: -распад и электронный захват или - и +-распады.
Открытие Р. оказало огромное влияние на развитие науки и техники. За работы, связанные с исследованием и применением Р., было присуждено более 10 Нобелевских премий по физике и химии, в т. ч. А. Беккерелю, П. и М. Кюри, Э. Ферми, Э. Резерфорду, Ф. и И. Жолио-Кюри, Д. Хевеши, О. Гану, Э. Макмиллану и Г. Си-боргу, У. Либби.
• Кюри М., Радиоактивность, пер. с франц., 2 изд., М., 1960; Учение о радиоактивности. История и современность, М., 1973.
^ В. И. Гольданский, Е. М. Лейкин.
РАДИОАКТИВНЫЕ РЯДЫ (радиоактивные семейства), ряды генетически связанных радиоактивных нуклидов, в к-рых каждый последующий возникает в результате - или --распадов предыдущего. Каждый Р. р. имеет родоначальника — нуклид с наибольшим периодом полураспада Т1/2 и завершается стабильным нуклидом. В каждом Р. р. массовые числа А нуклидов могут быть либо одинаковыми (--распад), либо различаться на число, кратное 4 (-распад). Если для всех членов ряда А делятся на 4 без остатка, то мы имеем Р. р. 4n (n — целое число). Если же в остатке будет 1,2 или 3, то Р. р. называют (4n+1), (4n+2), (4n+3). Известны четыре Р. р., родоначальниками к-рых являются: 23290Th (ряд 4n), 23793Np (ряд4n+1), 23892U(ряд4n+2), 23592U(ряд 4n+3). Ряд 23892U часто называют рядом урана-радия, а ряд 23592U— рядом актиноурана.
В каждом Р. р. устанавливается т. н. в е к о в о е р а в н о в е с и е, при к-ром скорости образования и
распада промежуточных членов Р. р. равны. Вековое равновесие устанавливается за время ~10•T1/2 наиболее долгоживущего промежуточного члена ряда. Оно объясняет присутствие в земной коре всех членов естеств. Р. р., в т. ч. и быстро распадающихся. Число атомов каждого промежуточного члена ряда N'=N0•T'1/2/T01/2, где N0— число атомов родоначальника ряда, Т01/2 — его период полураспада. Чем меньше Т'1/2 члена Р. р., тем ниже его содержание в земной коре. Напр., на 1 т урана в природе приходится ок. 0,36 г 226Ra и 1,3•10-9 г 218Ро. По мере распада родоначальника общее содержание промежуточных членов естеств. Р. р. в земной коре медленно уменьшается. Для 237Np T1/2=2,14•106 лет, и членов его Р. р. в природе уже нет, все они получены искусственно (см. Трансурановые элементы). Мн. члены естеств. Р. р. обнаружены до открытия изотопов и получили назв. и символы, к-рые частично сохранились.
• См. лит. при ст. Радиоактивность.
^ С. С. Бердоносов.
РАДИОВОЛНОВОДЫ, металлич. трубы и диэлектрич. стержни или каналы, в к-рых распространяются радиоволны. Механизм их распространения в Р. обусловлен многократным отражением эл.-магн. волн от его стенок. Пусть плоская волна падает в вакууме на идеальную отражающую металлич.плоскость х=0 (рис. 1), причём электрич. поле Е волны параллельно этой плоскости. Суперпозиция падающей и отражённой волн образует плоскую неоднородную волну, бегущую вдоль оси oz: exp(it-ikzz), и стоячую волну вдоль оси ох: exp(it)sin(kxx). Здесь kx и kz — проекции волнового вектора k на оси ох и oz, — частота волны. Узлы стоячей волны — плоскости, на к-рых Еу=0, отстоящие друг от друга на расстояниях x=n/kx (n=0, 1, 2, 3, . . .). В них можно помещать идеально проводящие тонкие металлич. листы, не искажая поля. Подобными листами можно ограничить систему с боков,
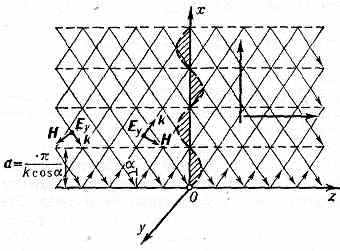
Рис. 1. Падение плоской однородной волны на идеально отражающую поверхность х=0; пунктир — отражённая волна, заштрихованная область — распределение амплитуд поля Еу вдоль оси ох; в узлах этого поля можно помещать идеально проводящий лист, не внося искажений.
перпендикулярно линиям Ey. Т. о., удаётся построить распределение эл.-магн. поля для волны, распространяющейся внутри трубы прямоугольного сечения (прямоугольный Р.). Построение поля путём многократного отражения плоских волн от стенок, поясняющее «механизм» его распространения в Р., наз. к о н ц е п ц и е й Б р и л л ю э н а.
Распространение волн в Р. возможно только при наклонном падении волны на стенки Р. (0). При норм. падении (=0) kz=0, поле перестаёт зависеть от z, и волна оказывается как бы запертой между двумя плоскостями. В результате в Р. образуются нормальные колебания, частоты к-рых n определяются числом полуволн n, укладывающихся между металлич. плоскостями: n=сn/d (d — расстояние между металлич. плоскостями). Эти частоты наз. критич. ч а с т о т а м и Р. Нижняя критич. частота кр=c/d соответствует n=1.
Внутри Р. могут распространяться волны только с частотами >кр,
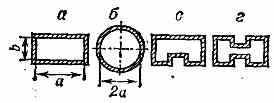
Рис. 2. Формы поперечного сечения некоторых радиоволноводов.
или <кр~2d. Длина волны в Р. (периодичность поля вдоль оси oz):
=(1-(/кр)2): при <кр >,
при кр . Это означает, что при =кр поле в Р. имеет не волновой, а колебат. хар-р. При >кр волна в Р. затухает.
Для длинных волн Р. слишком громоздки. Поэтому они применяются только для 10—20 см. В технике СВЧ используются каналы разл. сечений (рис. 2). Обычно к Р. относят только каналы с односвязными сечениями; каналы с двух- или многосвязными сечениями рассматриваются в теории длинных линий (см. Линии передачи). Но концепция Бриллюэна пригодна в любом из этих случаев.
^ Волновые моды. В Р. могут возбуждаться разл. типы волн, отличающиеся структурой эл.-магн. поля и частотой (моды). Волноводные моды находятся на основании решения Максвелла уравнений при соответствующих граничных условиях (для идеальных проводников равенство нулю тангенциальной составляющей электрич. поля). Поперечная структура полей в Р. определяется скалярной ф-цией (x, у), удовлетворяющей ур-нию мембраны с закреплёнными (=0)
или свободными (д/дn=0, n — нормаль к границе) краями в зависимости от типа поляризации эл.-магн. поля. Задача о собств. колебаниях мембраны имеет бесконечное, но счётное множество решений, соответствующих дискретному набору действительных собств. частот. Каждое из этих собств.
606
колебаний соответствует либо нормальной волне, распространяющейся вдоль Р., либо экспоненциально убывающей или нарастающей колебат. модам. Для прямоугольного Р. спектр собств. частот
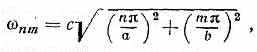
где m и n — числа стоячих полуволн, укладывающихся вдоль а и 6. Чем больше т и n, тем сложнее поле в Р.
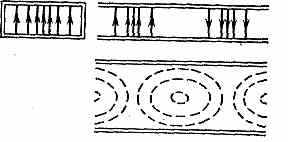
Рис, 3. Структура поля волны ТЕ10 в прямоугольном волноводе; сплошные линии — силовые линии электрич. поля, пунктирные — магн. поля.
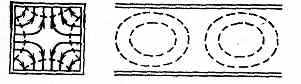
Рис. 4. Структура поля волны ТЕ11 в прямоугольном волноводе.
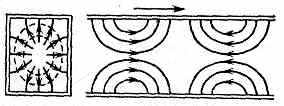
Рис. 5. Структура поля волны TM11 в прямоугольном волноводе.
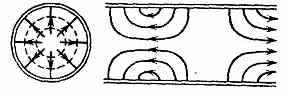
Рис. 6. Структура поля волны TM01 в круглом волноводе.
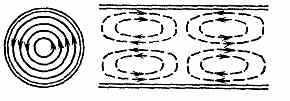
Рис. 7. Структура поля волны ТЕ01 в круглом волноводе.
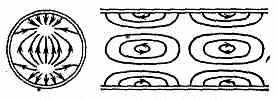
Рис. 8. Структура поля волны TM11 в круглом волноводе.
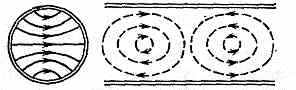
Рис. 9. Структура поля волны ТЕ11 в круг-дом волноводе.
Наименьшее кр соответствует n=1, m=0, если bm=1, если aE поляризовано в плоскости z=const. Эти волны наз. ТE-волнами (от англ. transverse — поперечный) или Н-волнами. Простейшие моды прямоугольного Р.— волны TE10 (рис. 3) и ТЕ11 (рис. 4). Мембранная задача с закреплёнными краями порождает волны типа ТМnm (или Еnm). Здесь n0 и m0, т. к. силовые линии магн. поля не могут упираться в идеально проводящие стенки (они всегда замыкаются сами на себя). Простейшая волна этого типа — ТМ11 (рис. 5). С увеличением размера Р. число мод растёт. При этом поперечное сечение Р. разбивается на ячейки, каждая из к-рых как бы представляет собой элем. Р. с одной из простейших мод — типа ТЕ10, ТЕ11 или ТМ11.
Аналогично можно построить распределение полей в Р. любого поперечного сечения. На рис. 6—9 показаны структуры полей для мод внутри Р. круглого сечения. Простейшей является мода ТЕ11 (рис. 9), к-рая топологически соответствует волне TE10 в прямоугольном волноводе.
Все волноводные моды быстрые, их фазовая скорость v>с (точнее, больше скорости однородной плоской волны в среде, заполняющей Р.) и всегда нелинейно зависит от частоты ,
причём дv/д<0, т. е. Р. подобен среде
с норм. дисперсией (см. ^ Дисперсия волн). Групповая скорость волны любого типа в Р. обратно пропорц. v: vгр=c2/v; она меньше скорости света с в вакууме. Т. к. v и vгр различны для разных мод, то для неискажённой передачи сигналов следует либо работать в диапазоне частот, допускающих распространение только одной, простейшей моды, либо, наоборот, пользоваться «сверхразмерными» многомодовыми Р., когда при vc может быть сформирован почти оторванный от стенок волновой пучок (см. Квазиоптика, Оптический резонатор).
Возбуждение радиоволноводов осуществляется с помощью антенн: металлич. штыря (электрич. диполь), петли (магн. диполь), отверстия или щели (щелевая антенна). Электрич. диполь должен быть ориентирован по силовым линиям поля E нужной моды, петли должны пронизываться линиями Н, а щели прорезываться в стенках поперёк линий тока, т. е. вдоль линий Н. Эффективность возбуждения зависит также от характеристик антенны, оптимальным явл. равенство её внутр. сопротивления сопротивлению излучения в данную моду.
Затухание волн в радиоволноводах обусловлено потерями энергии в металлич. стенках или диэлектрич. среде. Частотная зависимость коэфф.
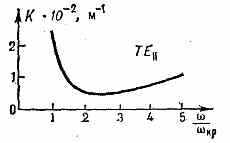
Рис. 10. Частотная зависимость коэфф. затухания К для моды TE11 круглого волновода из-за потерь в проводящих стенках.
затухания K() из-за потерь в стенках показана на рис. 10; при очень больших потери растут с частотой для всех мод, кроме ТЕоп круглого Р.
Диэлектрические радиоволноводы представляют собой стержни из диэлектрика или магнетика (обычно круглые).
В естеств. условиях диэлектрич. Р.— это среды с плавным изменением диэлектрич. проницаемости , обусловливающим формирование волноводного канала. Внутри диэлектрич. Р. плоские волны испытывают на границе раздела с внеш. средой полное внутр. отражение, образуя снаружи экспоненциально убывающие при удалении от Р. поля (поверхностные волны). Это возможно, когда скорость распространения вдоль Р. меньше скорости распространения плоских волн в окружающем пр-ве. Этим диэлектрич. Р. существенно отличаются от металлических. Другая их особенность состоит в том, что из-за неоднородности среды в них могут распространяться т. н. гибридные ЕН- или НЕ-волны. Они возникают и в экранированных системах с неоднородным заполнением. Аналоги таких Р. в оптике — волоконные системы (см. Волоконная оптика). Диэлектрич. Р., образуемые благодаря неоднородному распределению концентрации плазмы в ионосфере, обеспечивают сверхдальнее распространение радиоволн с малым ослаблением сигнала (см. Атмосферный волновод, Распространение радиоволн). При облучении нелинейного диэлектрика, магнетика или плазмы мощными радиоволнами внутри этих сред могут образовываться самоподдерживающиеся Р., но они, как правило, не обладают достаточным запасом устойчивости.
Р. служат фидерными системами в радиолокац. и др. системах для передачи сигнала от передатчика в передающую антенну и от приёмной антенны к приёмнику. Фидерная система на СВЧ имеет вид волнового тракта, состоящего из различных волноводных узлов. Для сочленения Р. с разными поперечными сечениями применяются плавные волноводные переходы с перем. сечением. Осн. преимуществом металлич. Р. по сравнению с линиями передачи (двухпроводной симметричной линией и коаксиальным кабелем) явл. отно-
607
сителъно малые потери энергии. Причина состоит в том, что в экранированных Р. полностью отсутствует излучение энергии в пр-во; кроме того, при одинаковых внеш. размерах Р., и двухпроводной линии (или коаксиального кабеля) поверхность Р., по к-рой протекают электрич. токи (при распространении волны), обычно больше, чем поверхность проводов двухпроводной линии (или жилы коаксиального кабеля). Т. к. глубина проникновения токов во всех случаях определяется скин-эффектом, то плотности токов, а следовательно и джоулевы потери в Р. меньше, чем в линии.
• Каценеленбаум Б. 3., Высокочастотная электродинамика, М., 1966; Лебедев И. В., Техника и приборы СВЧ, 2 изд., т. 1, М., 1970; X а р в ей А. Ф., Техника сверхвысоких частот, пер. с англ., т. 1—2, М., 1965; Фельдштейн А. Л., Явич Л. Р., Смирнов В. П., Справочник по элементам волноводной техники, 2 изд., М., 1967; Фелсен Л., М а р к у в и ц Н., Излучение и рассеяние волн, пер. с англ., т. 1—2, М., 1978; Виноградова М. В., Р у д е н к о О. В., С у х о р у к о в А. П., Теория волн, М., 1979.
^ М. А. Миллер.
РАДИОВОЛНЫ (от лат. radio — излучаю), электромагнитные волны с длиной волны К от 5•10-5 и до 1010 м (частотой (о от 6•1012 Гц до неск. Гц). В опытах Г. Герца (1888) впервые
Таблица 1.

были получены электромагн. волны с в неск. десятков см. В 1895—99 А. С. Попов впервые применил эл.-магн. колебания с ~102—2•104 см для осуществления беспроволочной связи на расстоянии. По мере развития радиотехники расширялся частотный диапазон (табл. 1) радиоволн, к-рые могут генерироваться, излучаться и приниматься радиоаппаратурой. В природе существуют и естеств. источники Р., во всех частотных диапазонах. Источником Р. явл. любое нагретое тело (тепловое излучение). Источниками Р. явл. звёзды, в т. ч. Солнце, галактики и метагалактики. Р. генерируются и при нек-рых процессах, происходящих в земной атмосфере, напр. при разряде молний (а т м о с ф е р и к и), при возбуждении колебаний в ионосферной плазме.
