Geum.ru

Лекция Аксиоматика теории вероятностей

Вид материалаЛекция

Содержание


3.2. Вероятность как нормированная мера
3.3. О борелевской сигма-алгебре и мере Лебега
Борелевская сигма-алгебра на прямой
Мера Лебега
Подобный материал:

Лекция 3. Аксиоматика теории вероятностей

  • Сигма-алгебра событий
  • Вероятность как нормированная мера
  • О борелевской сигма-алгебре и мере Лебега
    • Борелевская сигма-алгебра на прямой
    • Мера Лебега


3.1. Сигма-алгебра событий


   Пусть 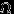 —  пространство элементарных исходов некоторого случайного эксперимента (то есть, вообще говоря, множество произвольной природы). Мы собираемся определить набор подмножеств 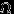, которые будут называться событиями, и затем задать вероятность как функцию, определенную только  на множестве событий.

То есть событиями мы будем называть не любые  подмножества 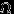, а лишь подмножества из некоторого «множества подмножеств» 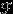. При этом необходимо позаботиться, чтобы это множество 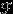подмножеств 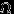было «замкнуто» относительно введенных в параграфе 1.2 операций над событиями, то есть чтобы объединение, пересечение, дополнение событий (то есть элементов 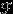) снова давало событие (то есть элемент ).

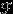Определение 10.

Множество 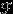, состоящее из подмножеств множества 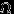(не обязательно всех!) называется -алгеброй событий,  или -алгеброй подмножеств 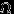, если выполнены следующие условия:

(A1)

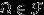          (-алгебра событий содержит достоверное событие);

(A2)

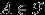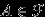     если , то      (вместе с любым событием -алгебра содержит противоположное событие);

(A3)

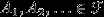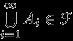    если , то      (вместе с любым конечным или счетным набором событий -алгебра содержит их объединение).

Условия (A1)-(A3) часто называют «аксиомами -алгебры».

Проверим, что этого набора аксиом достаточно для замкнутости множества 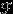относительно других операций над событиями.

Вместо первой аксиомы достаточно предположить, что 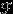не пусто, то есть содержит хотя бы один элемент.  

 

Свойство 1.

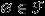        (-алгебра событий содержит невозможное событие).

Доказательство. По (A1), 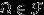, но 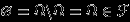в силу (A2).     Q.D.E.

 

Свойство 2.

При выполнении (A1),(A2) свойство (A3) эквивалентно свойству (A4)

(A4)

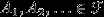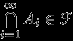    если , то      (вместе с любым конечным или счетным набором событий -алгебра содержит их пересечение).

Доказательство. Докажем, что при выполнении (A1) и (A2) из (A3) следует (A4).

Если , то при всех 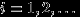по свойству (A2) выполнено 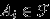. Тогда из (A3) следует, что 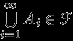, и, по (A2), дополнение к этому множеству также принадлежит 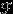, то есть 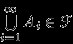. Но, в силу формул двойственности, 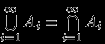, что и требовалось доказать.

Доказательство в обратную сторону выглядит совершенно аналогично.

Q.D.E.

Свойство 3.

Если 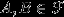, то .

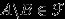Доказательство.

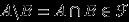 , так как 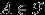, , и по (A4) их пересечение тоже принадлежит .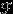

Q.D.E.

  Пример 11.

Пусть 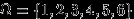 —  пространство элементарных исходов (например, при бросании игрального кубика). Следующие наборы подмножеств 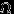являются -алгебрами (доказать! ):

1.

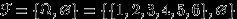   —  тривиальная -алгебра. 

2.

 .

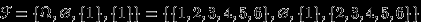3.

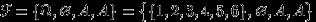 , где 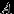 —  произвольное подмножество 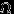(в предыдущем примере ).

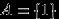4.

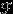   —  множество всех подмножеств .

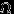Доказать, что если 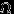 состоит из  элементов, то в множестве всех его подмножеств ровно  элементов.  

Итак, мы определили специальный класс 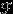подмножеств пространства элементарных исходов 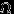, названный -алгеброй событий, причем применение счетного числа любых операций (таких, как объединение, пересечение, дополнение) к множествам из 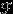снова дает множество из 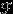(не выводит за рамки этого класса). Множества 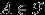мы и назвали «событиями».

Определим теперь понятие «вероятности» как функции, определенной на множестве событий (то есть функции, которая каждому событию  ставит в соответствие число). А чтобы читателю сразу стало понятно, о чем пойдет речь, добавим: вероятность мы определим как неотрицательную нормированную меру,  заданную на -алгебре 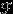подмножеств .


^

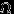3.2. Вероятность как нормированная мера


Определение 11.

Пусть 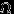 —  некоторое множество и  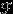—  -алгебра его подмножеств. Функция 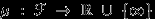называется мерой  на 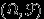, если она удовлетворяет условиям:

(M1)

    Для любого множества 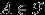его мера неотрицательна: .

(M2)

    Для любого счетного набора попарно непересекающихся множеств 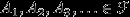(то есть такого, что при всех ) мера их объединения равна сумме их мер:



(«счетная аддитивность» или «-аддитивность»)

Иначе говоря, мера есть неотрицательная, счетно-аддитивная функция множеств.

Определение 12.

Пусть 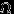 —  некоторое множество и  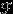—  -алгебра его подмножеств. Мера 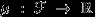называется нормированной,  если 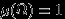. Другое название нормированной меры  —  «вероятность»   или «вероятностная мера».

То же самое еще раз и подробно:

Определение 13.

Пусть 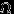 —  пространство элементарных исходов и  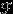—  -алгебра его подмножеств (событий). Вероятностью  или вероятностной мерой  на 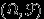называется функция , обладающая свойствами:

(P1)

 Для любого события 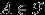выполняется неравенство ;

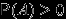(P2)

 Для любого счетного набора попарно несовместных событий 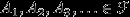имеет место равенство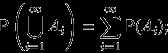



(P3)

 Вероятность достоверного события равна единице: .

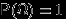Свойства (P1)-(P3) часто называют «аксиомами вероятности».

Определение 14.

Тройка , в которой 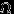 —  пространство элементарных исходов,  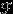—  -алгебра его подмножеств и 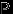 —  вероятностная мера на 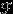, называется вероятностным пространством.

Докажем свойства вероятности, вытекающие из аксиом. Здесь и в дальнейшем под знаком вероятности появляются только события!

 

0.

  .

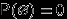Доказательство. События 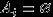, , 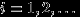попарно несовместны, и их объединение есть также пустое множество. По аксиоме (P2),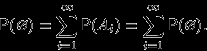



Это возможно только в случае .

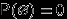1.

  Для любого конечного  набора попарно несовместных событий 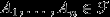имеет место равенство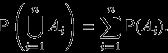



Доказательство. Пусть 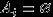при любом 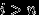. Вероятности этих событий, по предыдущему свойству, равны нулю. События 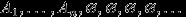попарно несовместны, и, по аксиоме (P2),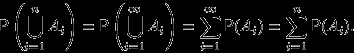



2.

  .

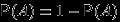Доказательство. 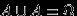, и события 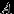, 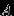несовместны. По аксиоме (P3) и предыдущему свойству,   

3.

  Если 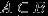, то .

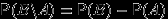Доказательство. 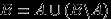, и события 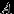, 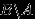несовместны. По аксиоме (P2),    .

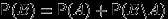4.

  Если 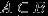, то .

Доказательство. По предыдущему свойству, 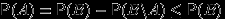. Последнее неравенство следует из (P1), т.к. .

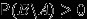5.

   .

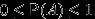Доказательство. 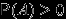по (P1), и т.к. 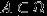, то по предыдущему свойству .

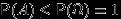6.

   .

Доказательство. , поэтому 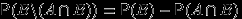. Но события 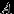и 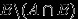несовместны, поэтому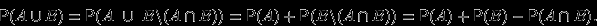



7.

   .

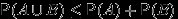Доказательство. Сразу следует из предыдущего свойства и аксиомы (P1).

8.

   .  Доказать методом математической индукции.

9.

  



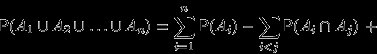
(2)


Доказательство. Воспользуемся методом математической индукции. Базис индукции при 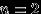 —  свойство 6 выше. Пусть свойство 9 верно при 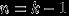. Докажем, что тогда оно верно при .



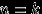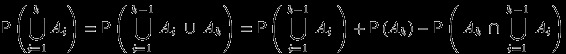
(3)


По предположению индукции, первое слагаемое в правой части (3) равно





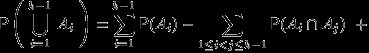
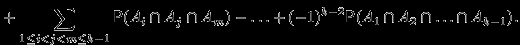
(4)


Вычитаемое в правой части (3) равно





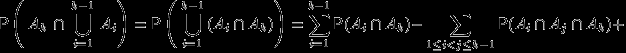
(5)


Подставить (4),(5) в (3) и довести до конца шаг индукции.

Q.D.E.

Приведем пример задачи, в которой использование свойства 9  –  самый простой путь решения.

Пример 12.

Задача.    Есть писем и подписанных конвертов. Письма раскладываются в конверты наудачу. Найти вероятность того, что хотя бы одно письмо попадет в предназначенный ему конверт, и предел этой вероятности при .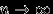

 Решение.   Пусть событие 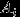, 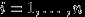означает, что 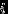-е письмо попало в свой конверт. Тогда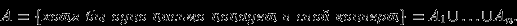



Так как события совместны, придется использовать формулу (2). Нетрудно убедиться, что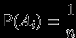

   для всех  ,

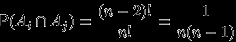    для всех  ,

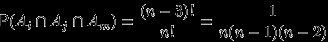   для всех  ,  ,

 

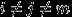Вычислим количество слагаемых в каждой сумме в формуле (2). Например, в сумме ровно слагаемых  —  ровно столько трех-элементных множеств можно образовать из элементов, и каждое такое множество 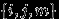встречается в индексах данной суммы единажды.

Подставляя все вероятности в формулу (2), получим:





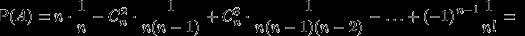
Выписать разложение   в ряд Тейлора и убедиться, что 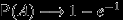  при  .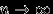


^

3.3. О борелевской сигма-алгебре и мере Лебега


   Следующий параграф предназначен только для тех, кто не испугался всего сказанного выше и хочет познакомиться с понятиями  «-алгебра борелевских множеств» и  «мера Лебега»   (Felix Edouard Justin Emile Borel,  Henri Léon Lebesgue).
^

Борелевская сигма-алгебра на прямой


Пример 13.

Пусть 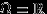 —  вещественная прямая. Рассмотрим некоторые наборы множеств, не являющиеся -алгебрами, и увидим, как их можно дополнить до -алгебр.

 

1.

Множество 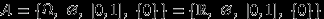не является -алгеброй, так как, например,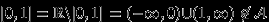

 .

Минимальный набор множеств, содержащий 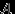и являющийся -алгеброй (минимальная -алгебра), получится, если включить в него всевозможные объединения, пересечения и дополнения множеств из :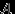

  .

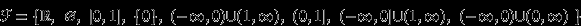Более точно, минимальной -алгеброй, содержащей набор множеств 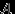, называется пересечение всех -алгебр, содержащих .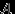

 

2.

Найти минимальную -алгебру, содержащую  .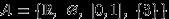

 

3.

Пусть множество 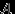подмножеств вещественной прямой 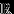состоит из всевозможных открытых интервалов 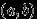, где  :    .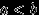

 

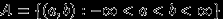(a)

Проверить, что ни в коем случае не является -алгеброй!

Указание: привести примеры двадцати множеств из , дополнения к которым не принадлежат ; привести примеры пяти множеств из , любые объединения которых не принадлежат .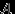
 

(b)

Минимальная -алгебра, содержащая множество 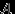всех интервалов на вещественной прямой, называется борелевской -алгеброй в 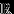и обозначается 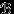или .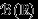


 

(c)

Перечислим некоторые множества на прямой, содержащиеся в 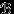. Таковы все привычные нам множества. Чтобы получить множество, не содержащееся в 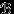, требуются специальные построения.

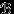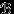Итак, мы знаем, что все интервалы на прямой принадлежат , и  —  -алгебра.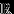

 
  • принадлежит .

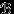Это сразу следует из свойства (A1) -алгебры, но может быть доказано исходя из свойств (A2), (A3).

Действительно, 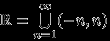. Так как все эти интервалы лежат в 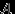, а 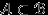, то все эти интервалы принадлежат .
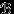Но 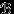 —  -алгебра, поэтому она содержит счетное объединение любых своих элементов. Поэтому .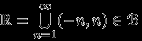

 
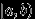  • Любой интервал вида (или , или 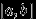), где 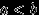, принадлежит .

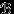Действительно, 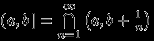, и так как все эти интервалы лежат в 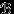, то их счетное пересечение должно по свойству (A4) принадлежать .

 
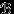  • Любое одноточечное подмножество 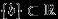принадлежит .

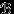Действительно, , а разность двух множеств из -алгебры снова принадлежит -алгебре.

 
  • Докажите, что, например, любые множества вида 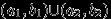  принадлежат  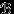, множество натуральных чисел  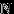 принадлежит  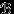, множество рациональных чисел   принадлежит  .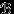

 

4.

Борелевская -алгебра в строится совершенно так же, как в 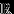. Это должна быть минимальная -алгебра, содержащая все множества вида 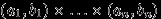(уже не интервалы, как в , а «прямоугольники» в , «параллелепипеды» в и т.д.).

 
^

Мера Лебега


   Когда мы говорили о геометрической вероятности, мы использовали термин «мера области в 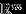», имея ввиду «длину» на прямой, «площадь» на плоскости, «объем» в трехмерном пространстве. Являются ли все эти «длины-площади-объемы» настоящими мерами в смысле определения 11? Мы решим этот вопрос для прямой, оставляя плоскость и пространство большей размерности читателю.

Если вам уже расхотелось читать дальше, сообщаем: мерой Лебега в задачниках и учебниках называют как раз «длину-площадь-объем», так что все в порядке.

Рассмотрим вещественную прямую с -алгеброй борелевских множеств. Эта -алгебра, по определению, есть наименьшая -алгебра, содержащая любые интервалы. Для каждого интервала 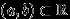число 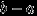назовем «длиной интервала 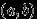». Мы не станем доказывать следующее утверждение:

Лемма 1.

Существует единственная мера   (то есть неотрицательная и -аддитивная функция) на , значение которой на любом интервале равно его длине: . Эта мера называется мерой Лебега.

Это утверждение является следствием теоремы Каратеодори о продолжении меры с алгебры на -алгебру, применительно к .
См.  А.Н.Колмогоров, С.В.Фомин, «Функциональный анализ»   или   А.А.Боровков, «Теория вероятностей» [3].
 

Итак, мы ограничили набор событий только множествами из какой-нибудь -алгебры событий. Мы потребовали, чтобы вероятность была функцией только на множестве событий.

Покажем, что это необходимо: построим пример множества на отрезке, мера Лебега которого («длина») просто не существует (множество Витали).

     То есть: если рассмотреть бросание точки наудачу на отрезок, то вычислить вероятность попадания точки в указанное множество в соответствии с геометрической вероятностью нельзя. Значит, это множество нельзя считать событием  —  мы не умеем вычислить его вероятность!

Пример 14.

Рассмотрим окружность единичного радиуса (реально это тот же отрезок 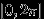). Возьмем любое иррациональное число 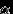. Поскольку оно иррационально, число не является целым ни при каком целом 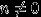(то есть числ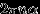о равно 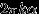лишь при  ).

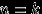Поэтому если взять произвольную точку , то есть точку на окружности, и перечислить все точки, которые получаются поворотом точки 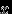на угол 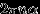, , 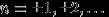то мы ни разу не вернемся в точку 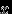. Точек, получившихся из точки 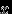такими поворотами, счетное число. Объединим их в один класс. С любой другой точкой окружности можно тоже связать класс точек, получающихся из нее  поворотом на угол 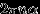при каком-то .

     Таким образом, вся окружность разбивается на классы точек. В каждом классе счетное число точек, и все точки в одном классе получаются друг из друга такими поворотами. Причем эти классы не пересекаются.

Множество 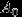определим так: возьмем из каждого такого класса ровно по одной точке. Пусть множество 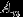получается поворотом всех точек множества 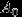на угол , .

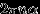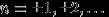     Так как все точки одного класса можно получить, поворачивая любую из них на угол , , 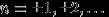а в множестве 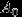собрано по одной точке из каждого класса, то поворачивая это множество, получим все точки окружности.

Очевидно, что 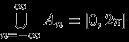. Предположим, что лебегова мера («длина») множества 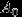существует. Заметим, что тогда все множества 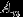имеют ту же лебегову меру, так как получены из 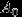поворотом. И так как все эти множества не пересекаются, то мера их объединения равна сумме их мер: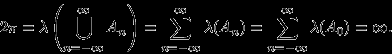



Полученное противоречие означает, что лебегова мера, или длина множества 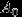не существует.

     Упражнение: какими свойствами «длины» (или меры Лебега) мы воспользовались в этом примере?