Элективный курс «Мир тригонометрии»
| Вид материала | Элективный курс |
- Ф. В. Чижова методическая разработка элективный курс, 490.04kb.
- Элективный курс по истории России в 9 классе Тема: «Быт и традиции русского народа», 53.94kb.
- Элективный курс «глобальные проблемы человечества», 121.74kb.
- Курс «Мой мир мой дом» из цикла «Экология и мир человека. Уроки экологического мышления», 1272.57kb.
- В. А. Ходаков моу воротынская средняя школа Перемышльского района Калужской области, 76.7kb.
- Элективный курс «Мир химии» (9 класс) Курс разработан, 529.48kb.
- Элективный курс по астрономии, 93.86kb.
- Пояснительная записка Элективный курс «Природа тел Солнечной системы» предназначен, 50.52kb.
- Элективный курс «Методы решения задач по физике» 10 11 классы 68 часов, 115.81kb.
- Багровникова Светлана Владимировна, к ф. н., доцент элективный курс, 110.32kb.
Пояснительная записка
Предлагаемый мною элективный курс «Мир тригонометрии» предназначен для изучения в 9 классе в рамках предпрофильной подготовки, так как тригонометрические функции связаны со многими другими классами функций, и рассчитан на 17 часов. Содержание курса расширяет и углубляет знания учащихся по алгебре, так как цель элективного курса – формирование у учащихся представление о единстве алгебры и геометрии; углубление и расширение знаний учащихся по математике, геометрии, физике. Сюда вошел ряд вопросов тригонометрии, которые вообще не рассматриваются и не отрабатываются в рамках базового курса математики или представлены в недостаточном объеме. Данный элективный курс, кроме ориентационной функции, выполняет еще и компенсирующую функцию, так как раздел «Тригонометрические выражения и их преобразование» в 9 классе по новой программе не рассматривается.
Впервые тригонометрические функции появляются в курсе планиметрии тотчас после теоремы Пифагора или непосредственно перед ней. Используются они преимущественно только для решения плоских треугольников. При этом еще отрабатываются начальные навыки работы с таблицами тригонометрических функций и все.
Такой отбор и распределение материала вызывает свои методические трудности. Элементы тригонометрических знаний в ходе преподавания оказываются разъединеными или же слабо связанными. Необходимо найти эффективные методические приемы, позволяющие сохранить единство тригонометрических познаний и возможность широкого их истолкования. Данный элективный курс написан с целью оказания содействия этим поискам. В нем даже освещены основные этапы развития тригонометрии, чего невозможно найти ни в одном учебнике.
Ведущей задачей данного элективного курса “Мир тригонометрии” является создание ориентационной и мотивационной основы для выбора физико-математического профиля обучения. Темы и формы организации занятий элективного курса позволяют учащимся осуществить пробу своих сил в специфических видах деятельности, присущих науке математике, и сделать осознанный выбор дальнейшего профиля обучения. В то же время в содержание курса включены вопросы занимательного характера, что делает данный элективный курс полезным и привлекательным и для тех школьников, которые не планируют изучать математику на профильном уровне.Чтобы заинтерисовать учащихся, запланированы и составлены программы математического вечера, посвященного тригонометрии, игр “Звездный час”, “Поле чудес”, отобраны вопросы для викторины, составлены билеты для проведения зачета как итогового занятия, также выбраны вопросы для “Круглого стола” и т.д.
Курс может изучаться в любое время учебного года.
В процессе изучения представленного элективного курса создаются условия для решения ряда образовательных задач:
- углубление и расширение знаний учащихся по математике, геометрии, физике;
- приобретение предметных умений, связанных с планированием, подготовкой и выполнением проектов и рефератов, самостоятельных и контрольных работ;
Кроме того, учащиеся получают и общеучебные умения:
- информационные - работать со средствами информации (научной, учебной, справочной, научно-популярной литературой, компьютерными программными средствами, средствами дистанционного образования); готовить сообщения, доклады и рефераты, оформлять и представлять их; использовать технические средства обучения и средства новых информационных технологий;
- коммуникативные - работать в группе при выполнении упражнений, заданий, подготовка докладов, сообщений и рефератов, разработка проектов, участвовать в дискуссиях.
Таким образом, цель элективного курса заключается, с одной стороны, в углублении базовых понятий о тригонометрии, что позволяет расширить математический кругозор учащихся, а с другой- в совершенствовании общеучебных коммуникативных умений, навыков, необходимых для общей профессиональной культуры.
Предлагаемая программа носит примерный характер. Она построена по модульному принципу, т.е. каждый тематический блок может быть углублен или расширен, или вынесен как самостоятельный для элективного курса. Учитываются интересы и потребности учащихся и задачи курса в условиях профилизации.
Содержание программы подготавливает девятиклассников к практическому владению первых тем учебника “Алгебра и начала анализа” для 10-11 классов.
Основными принципами организации деятельности учащихся являются: системно-деятельностный, исследовательский, проблемный и творческий.
После изучения курса учащиеся должны:
з н а т ь историю тригонометрии, о тригонометрии как об учебном предмете; как накапливались тригонометрические знания людей; как тригонометрия преобразовалась в самостоятельную часть математики; все тригонометрические функции, основные формулы, тождества;
у м е т ь использовать полученные знания ( формулы, тождества и т.д.) для преобразования тригонометрических выражений и для доказательства тождеств и др.; пользоваться справочной литературой, владеть культурой устного выступления.
Примерный тематический план
(всего 17 часов)
| Наименование разделов и тем курсов | Всего часов | Теоретический материал | Практические заняития | Форма контроля |
| 1.Об истории тригонометрии. | 2 | 2 | | Поисковая работа. Реферат. |
| 2. Тригонометри-ческие функции любого аргумента. | 3 | 2 | 1 | Игра “Поле чудес”. Самостоятельная работа. |
| 3. Основные тригонометричес-кие формулы. | 4 | 3 | 1 | Матем. диктант. Творческая раб. Тест- тренинг. |
| 4. Формулы сложения и их следствия. | 3 | 2 | 1 | Групповая работа. Матем. диктант. |
| 5. Преобразование тригонометричес-ких выражений. | 3 | 1 | 2 | Самост. работа. Круглый стол. |
| 6. Заключительное занятие. Итого | 2 17 | 10 | 2 7 | Матем.вечер. Зачет. Викторина. Игра “Звездный час”. |
Поурочное планирование элективного курса
«Мир тригонометрии»
1. Что такое тригонометрия. Как накапливались тригонометрические знания людей.
Поисковая работа.
2. Знакомство с математиками, внесших свой вклад в развитие тригонометрии.
Реферат.
3. Определение тригонометрических функций. Радианная мера угла.
4. Свойства тригонометрических функций.
5. Свойства тригонометрических функций.
Игра «Поле чудес». Самостоятельная работа.
6. Соотношения между тригонометрическими функциями одного и того же аргумента.
7. Применение основных тригонометрических формул к преобразованию выражений.
8. Формулы приведения.
9. Формулы приведения.
Тест- тренинг. Математические диктанты. Творческая работа.
10. Формулы сложения и двойного угла.
11.Формулы суммы и разности тригонометрических функций.
12. Формулы суммы и разности тригонометрических функций.
Групповая творческая работа. Математический диктант.
13. Преобразование тригонометрических выражений.
14. Преобразование тригонометрических выражений.
15. Преобразование тригонометрических выражений.
Круглый стол. Самостоятельная работа.
16. Заключительный урок-повторение.
17. Математический вечер «История учения о тригонометрических функциях».
Викторина. Зачет. «Звездный час».
Урок №1: Что такое тригонометрия. Как накапливались тригонометрические знания людей.
Тип урока: изучение нового материала.
Форма проведения: лекция.
Цель урока: расскрыть смысл тригонометрии, ознакомить учащихся с ходом накопления тригонометрических знаний.
Оборудование урока: учебник “Геометрия 7-11кл.”,
“История математики в школе” для 7-8 классов,журнал “Математика в школе”,№6, 1984г.
Ход урока
1.Организационный момент.
Приветствие. Ознакомление с целью всего элективного курса. Сообщение цели данного урока.
2. Объяснение новой темы.
а) Что такое тригонометрия? Слово “тригонометрия” означает “измерение треугольников”. Возникновение тригонометрии связано с развитием астрономии - науки о движении небесных тел, о строении и развитии Вселенной - и географии.
Астрономия - одна из древнейших наук, в свою очередь возникшая из потребности знать сроки смены времен года, измерять и считать время, иметь календарь. Она зародилась и развивалась в Вавилоне, Египте, Китае, Индии и других странах древности. В результате произведенных астрономических наблюдений возникла необходимость определения положения светил, вычисления расстояний и углов. Так как некоторые расстояния, например от Земли до планет, нельзя было измерить непосредственно, то ученые стали разрабатывать приемы нахождения взаимосвязей между сторонами и углами треугольника, у которого две вершины расположены на Земле, а третью представляет планета или звезда. Такие соотношения можно вывести, изучая различные треугольники и их свойства. Вот почему астрономические вычисления привели к решению тре-угольника. Этим и занимается тригонометрия.
В современной нам структуре математических наук тригономет-рия определяется как та их часть, где исследуют один из классов аналитических функций, называемых тригонометрическими, а также их приложение. Эти функции чаще всего вводятся с по-мощью специальной конструкции- порождающей окружности. В качестве своих аргументов они могут иметь как действительные, так и комплексные величины, что придает им высокую степень общности. Их специфические свойства: периодичность, четность или нечетность и др. позволяют с помощью формул приведения и иных формул существенно упрощать и облегчать операции с ними.
Для решения многих важных задач, как теоретических, так и в особенности прикладных, тригонометрия является важным инстру-ментом. Значительную роль они играют, например, при изучении явлений, обладающих свойством периодичности.
В геометрической своей части тригонометрия является той математической дисциплиной, где изучают соотношения между сторонами и углами геометрических фигур. В зависимости от того, где расположены фигуры, на плоскости или на сфере, тригонометрия делится на плоскую и сферическую.Формулы сферической тригонометрии находят широкое применение в астрономии.
Таким образом, первоначальный смысл термина тригонометрия буквально означает измерение треугольников.
б) Как же накапливались тригонометрические знания людей? Задачи, в которых требуется измерять углы, появились так же дав-но и столь же настойчиво требовали своего решения, как и задачи, сводящиеся к измерению расстояний.Более того, эти две измери-тельные операции всегда существовали неразделимо. Роль изме-рения углов оказывается особенно значительной в тех случаях, когда непосредственное измерение расстояний оказывается затруд-нительным или невозможным вследствие удаленности или недос-тупности предметов.В свою очередь, измерение углов может быть охарактеризовано измерением специальных отрезков прямых- три-гонометрических линий. Тригонометрия вместе с геометрией начи-нали свой путь с решения практических задач.
Все древние цивилизации вносили свой вклад в дело накопления тригонометрических знаний. История математической науки дает тому немало убедительных примеров. Об этом мы продолжим разговор на следующем уроке.
3. Актуализация знаний: групповая поисковая работа.
( Класс делится на 2 группы и все работают с учебником по геомет-рии для 7-11 классов).
Вопрос всему классу: Что мы знаем об элементах тригонометрии до сегодняшнего урока?
7класс: - п.35, определение прямоугольного треугольника; 8 класс: - п.62, определение косинуса угла и Т.7.1;
- п.67, определение синуса и тангенса;
- п.68, основные тригонометрические тождества;
- п.69, значения синусов, косинусов и тангенсов некоторых углов, Т.7.4;
- п.70, изменения значений синуса, косинуса и тангенса угла при возрастании угла, Т.7.5;
- п.78, угловой коэффициент в уравнении прямой;
- п.81, определение синуса, косинуса и тангенса углов от 0° до 180°;
- п.98, скалярное произведение векторов;
9 класс:- п.109, теорема косинусов;
- п. 110, теорема синусов;
- п.112, решение треугольников.
4. Итог урока:
1) Что такое тригонометрия?
2) Для чего ее изучаем?
3) Как накапливались тригонометрические знания людей?
4) Что мы уже знали об элементах тригонометрии?
Урок №2: Знакомство с математиками, внесших свой вклад в развитие тригонометрии.
Тип урока: изучение нового материала.
Форма проведения: лекция.
Цель урока: продолжить знакомство с историей возникновения и развития тригонометрии.
Оборудование урока: “История математики в школе” для 7-8 классов, журнал “Математика в школе”, №6, 1984г., портреты Архимеда, Фалеса, Виета, Л.Эйлера, Т.Браге.
Ход урока
1. Организационный момент.
Приветствие.Сообщение цели данного урока.
2. Объяснение новой темы.
Все древние цивилизации вносили свой вклад в дело накопления тригонометрических знаний. История математической науки дает тому немало убедительных примеров.
На одной из глиняных табличек из Древнего Вавилона, возраст которой определяют тысячелетием до нашей эры, решается задача:
вычислить длину хорды круга, исходя из величины диаметра и вы-соты сегмента, отсекаемого этой хордой. Описание задачи и прави-ла ее решения таковы, что в них можно заметить использование подобия треугольников и теоремы Пифагора.
Руководитель одной из самых ранних научных школ Древней Греции Фалес из Милета упоминал в числе научных достижений древних египтян метод определения высоты предметов по длине отбрасываемой им тени. Этот метод послужил основой гномоники - учения о солнечных часах. Как широко известно, гномон - это прямой шест, вертикально укрепленный на горизонтальной площадке. Его тень в течение солнечного дня перемещается, “ заметая” некоторую площадь. Середина линии, окаймляющей эту площадь, будучи соединена с основанием гномона, образует полуденную линию: север - юг. Отношение длины тени к длине шеста определяет высоту расстояния Солнца над горизонтом. Деление линии дает части дня. Регулярные замеры позволяют отыскать пункт солнцестояния, определить длину солнечного года и решить много других задач.
Многие сочинения древнегреческих математиков содержали элементы тригонометрии. Например, в трактате Архимеда “Измерение круга” приведена лемма: “Если вписанный в дугу окружности сломанный на две неравные части отрезок прямой принимает опущенный на него из середины дуги перпендикуляр, то этот перпендикуляр разделит всю сломанную линию пополам”. Это, почти очевидно, дает возможность вычислить хорды суммы и разности двух заданных дуг. В сочинениях типа евклидовых “Начал”, где авторы избегают рассуждений метрического, измерительного характера, содержится, разумеется, меньше элементов тригонометрии, хотя и здесь их не столь уж трудно обнаружить и интерпретировать. Например, во второй книге “Начал” теоремы 12 и 13 по существу эквивалентны теореме косинусов.
Одна из самых первых крупных достижений в составлении тригонометрических таблиц относится ко 2 в. нашей эры. Мы имеем в виду знаменитое сочинение К.Птолемея “Математическое собрание в 13 книгах”. При вычислениях Птолемей пользовался 60-ричной системой счисления.Для регулярности в вычислениях и для удобства он делил окружность на 360 частей, диаметр - на 120 частей и т.д.
Таким образом, уже в самые первые века нашей эры, т.е. более двух тысячалетий тому назад, элементы плоской тригонометрии сложились и заняли определенное место в совокупности матема-тических знаний, имевших своей главной целью решение задач практического землемерия практической астрономии и географии. По своему значению они, вероятно, не были столь высоко оцениваемы, как основы сферической тригонометрии, так как теоремы последней непосредственно примыкали к астрономическим суждениям.
Столь же рано и естественно определялись направления развития плоской тригонометрии. Они состояли: во введении других тригонометрических характеристик, помимо птолемеевских хорд; в отыскании формул, выражающих связи между этими характеристиками; в разработке вычислительных приемов, имеющих целью облегчить составление таблиц тригонометрических функций.
Именно по этим направлениям и происходило накопление тригонометрических знаний в последующие века. Подъемы и ускорения происходили в эти времена главным образом в Индии и в государствах Ближнего и Среднего Востока. В науке этих стран накопление и усовершенствование тригонометрических знаний происходило значительно энергичнее.
Математики и астрономы, работавшие на территории Индостанского полуострова, восприняли греческую тригонометрию хорд и широко ее применяли.
Общеизвестно, что становление науки, в том числе математики, в указанных государствах сопровождалось систематическим изучением математических сочинений, написанных в Древней Греции и в других странах.
На этом пути рано стали появляться арабские зиджи. Это было сборники астрономических и тригонометрических таблиц, сопро-вождаемых пояснениями и доказательствами соотношений между тригонометрическими линиями. Из содержания этих зиджей видно, что не позднее 9 в. н.э. были выведены и табулированы вслед за синусом, косинусом новые тригонометрические функции: тангенс, котангенс, секанс и косеканс.
В Европе первое сочинение, в котором тригонометрия была рассмотрена как самостоятельная математическая дисциплина, было написано в 1462-1464 гг. Его автором был Иоганн Мюллер. Вслед за Мюллером тригонометрией много занимался Н.Коперник, посвятивший ей две главы своего знаменитого капитального труда “Об обращениях небесных тел”. Знаменитый астроном Тихо Браге разработал много вычислительных приемов, облегщающих задачу решения треугольников как плоских, так и сферических.Таблицы тригонометрических функций, по форме и по составу близкие к ныне употребляемым, составил и издал в 1551г. ученик Коперника Ретик.
Принципиально новый этап в развитии тригонометрии состоял в установлении связей этой науки с алгеброй. Начало этому этапу было положено в самом конце 16 в. Ф.Виетом. Он вывел, среди многих других тригонометрических формул, выражения для сину-сов и косинусов кратных дуг. С тех пор установление связей между тригонометрией и алгеброй посредством взаимных интерпретаций прочно вошло в практику математических исследований.
Содержание тригонометрии, равно как и средства ее аналитического выражения, достигли состояния, близкого к современному, около 200 лет тому назад, во второй половине 18 в. Решающая роль в этом принадлежит Л.Эйлеру. Свою теорию тригонометрических функций он изложил в 8-ой главе первого тома своей книги “Введение в анализ бесконечных”, завершив тем самым более или менее успешные попытки своих ближайших предшественников. Он ввел в тригонометрию практически совпадающую с привычной нам символику, полностью разъяснил вопрос о знаках всех тригонометрических функций любого аргумента. Тем самым в развитие тригонометрии был сделан очень важный шаг.
В то же примерно время, в 1770г., появился и удержался до нашего времени термин: тригонометрические функции. Его ввел Г.С.Клюгель в работе “Аналитическая тригонометрия”.
3. Итоги урока.
Как видно из рассказанного, тригонометрия прошла следующие этапы своего развития:
1) Она была вызвана к жизни практической необходимостью производить измерения углов. Влияние этих побудительных мотивов прослеживается с давних времен в интеллектуальной деятельности людей.
2) Первыми шагами формирующейся тригонометрии было установление связей между величиной угла и отношением специально при нем построенных отрезков прямых.
3) Аналогичные результаты были получены для сферических поверхностей.
4) Измерительный характер задач тригонометрии приводил к настоятельной необходимости табулировать значения тригонометрических функций. Составление таблиц в течение длительного времени явилось центральной задачей тригонометрии.
5) Примерно в 18в. начался процесс выделения тригонометрии в самостоятельную часть математики, имеющую цель исследовать тригонометрические функции углов, их свойства и взаимоотноше-ния.
6) В конце 16в. были установлены первые связи тригонометрии с алгеброй посредством взаимных интерпретаций между задачами о делении углов и решениями неприводимых алгебраических уравнений.
7) В течение 18в. тригонометрические функции были введены в математический анализ в качестве одного из классов аналитических функций. Они сразу же получили широкую область применения и сделались важной частью аппарата математического анализа, актуальной и для современной математики.
Почти одновременно тригонометрия приобрела более широкие применения в традиционной области ее существования - в геомет-рии.
4. Творческая домашняя работа:
написать реферат об одном из выше перечисленных основателей тригонометрии.
Урок № 3: Определение тригонометрических функций. Радианная мера угла.
Тип урока: комбинированный.
Форма урока: игра “Поле чудес”.
Цель урока: дать понятие радиана; научить пользоваться этой единицей для выражения угловых величин: углов, дуг и поворотов; переводить градусную меру в радианную и наоборот и пользовать-ся соответствующими таблицами; ознакомить учащихся с понятиями синуса, косинуса, тангенса и котангенса числового аргумента,области определения и множества значений этих функций .
Обрудование урока: таблицы “Значения тангенса и котангенса угла α”, “Значения синуса и косинуса угла α”, портреты Л.Эйлера, Евклида, Лейбница, Бернулли, магнитная доска.
Ход урока
1. Организационный момент.
Приветствие. Сообщение цели данного урока, ознакомление с порядком работы.
2. Актуализация знаний.
1) прослушивание реферата об Эйлере;
2) повторение результатов поисковой работы.
3. Объяснение новой темы
Отметим на оси х справа от точки О точку А и проведем через нее окружность с центром в начале координат. Радиус ОА будем называть начальным радиусом.
Повернем начальный радиус около точки О на 70° против часовой стрелки. При этом он перейдет в радиус ОВ. Говорят, что угол поворота равен 70°. Если повернуть начальный радиус около точки О на 70° по часовой стрелки, то он перейдет в радиус ОС. В этом случаи говорят, что угол поворота равен -70°. Углы поворота в 70° и -70° показаны на рис.1.
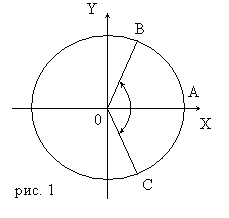
Вообще, при повороте против часовой стрелки угол поворота считают положительным, а при повороте по часовой стрелки - отрицательным.
Угол поворота может быть измерен в градусах, минутах и секундах. Наряду с этими единицами используется еще одна единица, называемая радианом. Один радиан приближенно равен 57°. Точное значение радиана в градусах выражается дробью 180/π: 1рад=(180/π)°= 180°/π = 57°.
Повернем начальный радиус ОА, равный R, на 180° (рис. 2).
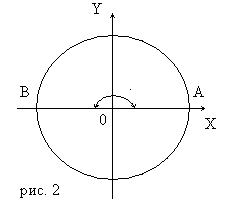
При этом точка А опишет полуокружность, ее длина равна πR. Углу поворота в 1° соответствует дуга, длина которой πR/180. Углу поворота в 1 рад соответствует дуга, длина которой равна R.Действительно, 1рад=180°/π , а 1° соответствует дуга длиной πR/180. Поэтому
πR/180 ·180/π =R.
Таким образом, угол в один радиан - это угол поворота, при котором конец начального радиуса описывает дугу, длина которой равна радиусу.
Рассмотрим примеры перехода от радианной меры к градусной и от градусной меры к радианной.
Пример 1. Выразим в градусах 4,5 рад.
Так как 1рад= 180°/ π , то 4,5 рад= 4,5 · 180°/π = 810°/π =258°.
