Geum.ru

Элективный курс «Мир тригонометрии»

Вид материалаЭлективный курс

Содержание


Синусом угла α называется отношение ординаты точки В к радиусу.
Тип урока
Ход урока
Форма урока
Ход урока
Тип урока
Ход урока
Тип урока
Ход урока
Подобный материал:
1   2   3   4   5

Пример 2. Найдем радианную меру угла в 72°.

Так как 1°= π /180рад, то 72°= 72·π /180рад = 2 π /5рад = 1,3рад.

Выразим в радианной мере углы 30°, 45°, 60°, 90°, 180°, 270° и 360°. Получим:

30°= π /180 · 30= π /6; 90º= π/180 ∙ 90= π /2;

45°= π /180 ∙ 45= π /4; 180º= π /180 ∙ 180= π ;

60°= π /180 ∙ 60 = π /3; 270º= π/180 ∙ 270= 3 π /2;

360°= π /180 ∙ 360= 2 π .

Радианная мера угла часто используется в тригонометрических выражениях.

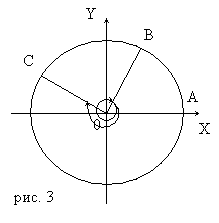
Из курса геометрии знаем, что мера угла в градусах выражается от 0 до 180. Что касается угла поворота, то он может выражаться в градусах каким угодно числом от - ∞ до + ∞. Так, если начальный радиус повернуть против часовой стрелки на 180º, а потом еще на 30º, то угол поворота будет равен 210º. Если начальный радиус сделает полный оборот против часовой стрелки, то угол поворота будет равен 360º; если он сделает полтора оборота в том же направлении, то угол поворота будет равен 540º и т.д. На рис.3 стрелками показаны углы поворота в 405º и -200º.



Рассмотрим радиусы ОА и ОВ (рис.4).



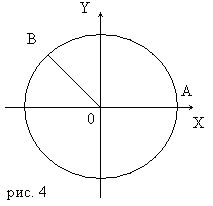
Существует сколько угодно углов поворота, при которых начальный радиус ОА переходит в радиус ОВ. Так, если угол <АОВ=130º, то соответствующие углы поворота будут равны 130º+360ºn, где n - любое целое число.

Например, при n = 0, 1, -1, 2, -2 получаем: 130º, 490º, -230º, 850º, -590º.

Пусть при повороте на угол α начальный радиус ОА переходит в радиус ОВ. В зависимости от того, в какой координатной четверти окажется радиус ОВ, угол α называют углом этой четверти. Так, если 0º < α < 90º, то угол α - угол 1 четверти; если 90º < α < 180º, то α - угол 2 четверти; если 180º < α < 270º, то α - угол 3 четверти; если 270º < α < 360º, то α - угол 4 четверти.

В курсе геометрии были определены синус, косинус, тангенс и котангенс угла α при 0º < α < 180º. Теперь мы рассмотрим эти определения на случай произвольного угла.

Пусть при повороте около точки О на угол α начальный радиус ОА переходит в радиус ОВ (рис.5).



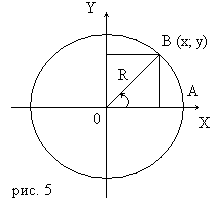
Синусом угла α называется отношение ординаты точки В к радиусу.

Косинусом угла α называется отношение абсциссы точки В к радиусу.

Тангенсом угла α называется отношение ординаты точки В к ее абсциссе.

Котангенсом угла α называется отношение абсциссы точки В к ее ординате.

Синус и косинус являются функциями с областью определения (- ∞ , + ∞ ); тангенс является функцией, область определения которой состоит из всех чисел, кроме ± π /2, ± 3π /2, ±5 π /2, ± 7 π /2,….. ; котангенс – кроме 0, ±π , ±2 π , ± 3 π ,…..

Синус, косинус, тангенс и котангенс называют тригонометрическими функциями.


4. Закрепление.

№1. Окружность разделена на три, четыре и шесть конгруэнтных частей. Чему равна градусная и радианная меры каждой части?

№2. Найдите градусную меру угла, радианная мера которого равна:

0,5; 10; π/5; π/9; 3π/4; - 5π/6; - 9π/2; 12π

№3. Найдите радианную меру угла, равного:

135º; 210º; 36º; 150º; 240º; 300º; - 120º; - 225º

№4. Заполните таблицу углов в градусной или радианной мере:


Градусы


45º
105º



135º





70º






Радианы
π /3






2 π /3



π/5
4 π /5



7 π /9
3π



№5. Начертите окружность с центром в начале координат и изобразите угол поворота, равный: 45º, -30º, 225º, -315º, 210º, 590º, -50º, -410º.

№6. Углом какой четверти является угол α, если:

α = 283º, 190º, 100º, -20º, -110º, 4200º ?

№7. Заполните таблицу:
0º
90º
180º
270º
360º

sin α















cos α















tg α















ctg α
















5. Итог урока.

« Поле чудес» к 300-летию со дня рождения Л. Эйлера.


Первая тройка игроков.

Задание: Уроженцом какого города в Швейцарии был Л.Эйлер?

( Базель)


Вторая тройка игроков.

Задание: Л.Эйлер был очень умным учеником, а может, ему просто повезло с учителем? Его занятиями по математике руководил ближайший последователь Г.В.Лейбница, ученый, оставивший после себя большие математические труды, особенно по решению уравнений и неравенств. Его имя- Иоганн. Назовите его фамилию.

(Бернулли)


Третья тройка игроков.

Задание: Математик Кокстер Г. сказал: “Эйлер внес значительный вклад буквально во все области математики. Некоторые из его простейших открытий таковы, что можно представить себе дух, вопрошающий: “Почему при жизни на земле я не додумался до этого?”

О духе какого ученого шла речь, если известно, что жил он около 300 лет до нашей эры в Александрии и что он является одним из родоначальников изучаемой нами геометрии?

( Евклид)


Игра со зрителями.

Задание: Л.Эйлер усовершенствовал как символику, так и содержание одного из важнейших разделов алгебры, изущающих функции. Что это за раздел?

(Тригонометрия)


Финал.

Задание: Назовите одну из тригонометрических функций, символ которой дал Л.Эйлер. Этим символом мы пользуемся и сейчас.

( Косинус - cos.)


Урок №4: Свойства тригонометрических функций.

Тип урока: комбинированный.

Цель урока:научить учащихся определять знаки значений тригонометрических функций от чисел, находящихся в той или иной четверти; дать определения четной и нечетной функции, периодической функции и соответствующие теоремы; научить применять свойство периодичности тригонометрических функций при решении различных упражнений.

Оборудование: таблица “Значения тангенса и котанегнса угла α”, “Значения синуса и косинуса угла α”, четырехзначная математи-ческая таблица Брадиса.


Ход урока


1.Организационный момент.

Приветствие. Сообщение темы и цели урока.


2. Актуализация знаний.

1) Что понимается под углом поворота?

2) В каком случаи угол поворота считают положительным, в каком- отрицательным?

3) Какие значения может принимать угол поворота?

4) В каком случаи угол поворота называют углом той или иной координатной четверти?

5) Что называется радианом?

6) Чему равна длина дуги в π /2 радиан?

7) Углом какой четверти является угол -35°, 179º, 750º, -280º и им противоположные углы?

8) Дайте определение синуса угла α , косинуса угла α , тангенса угла α и котангенса угла α .Для каких углов α существует синус α, косинус α ?

9) Для каких углов α не существует тангенса α , котангенса α ?

10) Какие значения могут принимать синус, косинус, тангенс и котангенс угла α ?


3. Объяснение новой темы.

Сегодня мы рассмотрим некоторые свойства тригонометрических функций.

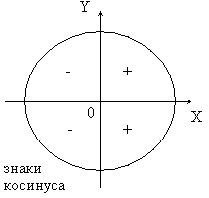
а) Знак синуса α такой же, как у ординаты у; знак косинуса α совпадает со знаком абсциссы х радиус - вектора, образующего угол с ОХ.




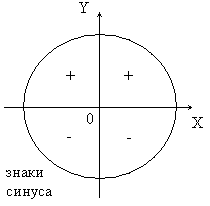
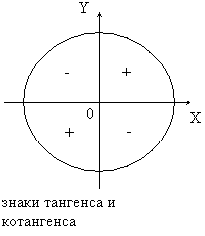Тангенс α и котангенс α положительны там, где sin α и cos α имеют одинаковые знаки. Из определения также следует, что знак sec α совпадает со знаком cos α , а знак cosec α - со знаком sin α.

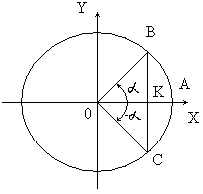б) Пусть при повороте на угол α перемещается к ОВ, а при повороте на угол α – к ОС.

Координаты точки В(х,у), а точки С(х,-y). пользовавшись этим, находим:

sin (-α) = -y/R = - sin α;

cos (-α) = x/R = cos α;

tg(-α) = -y/x = -tg α;

ctg (-α) = x/(-y) = - ctg α;

Например, cos(-40º)=cos40º; tg(-60º)= -tg60º= √3.

Вычислить: sin(-60º)+cos(-30º)+tg45º=-sin60º+cos30º-tg45º=-√3/2+ √3/2 -1= -1.

Если при изменении знака аргумента значение функции не меняется - функция четная; если наоборот, то функция - нечетная.

Таким образом, функции синус, тангенс и котангенс - нечетные, а косинус - четная.


в) Число 2π называют наименьшим периодом для функций синус и косинус, а число π - наименьшим периодом для тангенса и котангенса. Таким образом, тригонометрические функции - периодические, и каждая из них имеет бесконечное множество периодов, получающихся от умножения наименьшего периода на любое число n. Свойство периодичности выражается следующими тождествами:

sin (α + 2πn) = sin α; tg (α + πn) = tg α;

cos (α + 2πn) = cos α; ctg (α + πn) = ctg α;

Запишем область изменения:

- 1 ≤ sin α ≤ 1; - 1 ≤ cos α ≤ 1; -∞ < tg α < +∞; -∞< ctg α < +∞


Например, sin30º = sin (30º + 360º) = sin (30º- 360º) = sin (30º +2· 360º) = sin (30º- 2 ·360º) = …..= 1/2.

sin 765º = sin (2· 360º + 45º) = sin 45º = √2/2;

cos (-1170º) = cos 1170º = cos (3· 360º + 90º) = cos 90º =0.


4. Закрепление.

№1. Какой знак имеет:

sin α , если α = 36º, 117º, 197º, 311º;

cos α , если α = 16º, 108º, 288º, 304º;

tg α , если α =5º, 91º, 183º, 303º;

ctg α , если α = 77º, 97º, 209º, 281º?


№2. Какой знак имеет:

sin 185º , tg116º, cos210º, ctg310º;

sin 510º, cos388º, tg456º, ctg373º;

sin (-16º), cos (-88º), tg (-110º), ctg (-93º) ?


№3. Укажите в таблице соответствующий знак синуса, косинуса, тангенса и котангенса:
135º
216º
400º
460º
-16º
-127º

sin α


















cos α


















tg α


















ctg α



















№4. Определите знак выражения:

sin 92º ·cos 200º sin 143º· cos 311º

sin 116º· cos 116º· tg197º cos 255º· sin 83º· tg 100º


№5. Углом какой четверти является угол α, если известно, что:

sin α < 0 и tg α > 0 cos α > 0 и tg α > 0


№6. Найдите значения выражения:

sin(-60º) cos(-90º) ctg(-30º)

sin(-30º) + tg 45º sin (-90º) –cos0º cos(-180º) sin(-30º)


№7. Вычислите:

sin 390º , tg420º, sin780º, cos405º, ctg750º, cos390º.


5. Итоги урока:

1) Какие знаки имеют синус, косинус, тангенс и котангенс по четвертям?

2) В какой четверти знаки синуса, косинуса, тангенса и котангенса одинаковы?

3) Объясните, почему значения синуса, косинуса, тангенса и котангенса не изменяются при прибавлении к углу целого числа оборотов?

4) Какова зависимость между синусами (косинусами, тангенсами и котангенсами) противоположных углов?

5) Если α = 48º, 137º, 200º, 306º, то какие знаки имеют синус, косинус, тангенс и котангенс угла α?


Урок №5: Свойства тригонометрических функций.

Тип урока: совершенствование знаний· умений и навыков.

Форма урока: семинар.

Цель урока: закрепить умений применять формул, обобщить и систематизировать знания и умения учащихся, контроль знаний по теме для дальнейшей их коррекции.

Оборудование: четырехзначная математическая таблица Брадиса, таблицы «Значения синуса и косинуса угла α », «Значения тангенса и котангенса угла α ».

Ход урока


1. Организационный момент.

Приветствие. Сообщение цели и задач данного урока.


2. Актуализация знаний и умений.

а) Устный опрос.

1) Какой четверти принадлежит: sin α > 0; cos α < 0; tg α > 0?

2) Какие знаки имеют тригонометрические функции от чисел, находящихся в 1 четверти; во 2 четверти; в 3 четверти; в 4 четверти?

3) Почему для чисел, находящихся в 1 или 2 четвертях, значение синуса положительно?

4) Почему для чисел, находящихся во 2 или 4 четвертях, значения тангенса и котангенса отрицательны?

5) Если точка единичной окружности принадлежит оси абсцисс, то что можно сказать о значениях тригонометрических функций от чисел, изображаемых этой точкой?

6) Каким свойством обладает четная функция? Приведите примеры.

7) Что можно сказать об областях определения четных и нечетных функций?

8) Какие из основных тригонометрических функций являются четными, а какие - нечетными?

9) Какая функция называется периодической? Чему равен наименьший положительный период синуса и косинуса, тангенса и котангенса?

б) Письменное выполнение заданий.


№1. Найдите значение выражения:

2 cos 60º + 3 cos 30º 5 sin 30º - ctg 45º

2 sin 60º + 6 cos 60º- 4 tg 45º 3 tg 45º· tg 60º

4 tg 60º· sin 60º 12 sin 60º· cos 60º


№2. Вычислите:

sin 0º + 2cos 60º tg 45º· sin 60º· ctg 30º

4 sin 90º - 3 cos 180º 3 ctg 90º- 3 sin 270º


№3. Углом какой четверти является угол α, если:

sin α > 0 и cos α > 0 sin α > 0 и tg α > 0

sin α < 0 и cos α > 0 tg α < 0 и cos α > 0;

sin α < 0 и cos α < 0 ctg α > 0 и sin α < 0


№4. Найдите значение выражения:

sin (-60º) sin (-90º)

сos (-180º) tg (-900º)

cos (-35º) ctg 190º·tg (-15º)

ctg 178º sin 50º· cos 130º


3. Самостоятельная работа.

№1. Начертите окружность с центром в начале координат и изобразите угол поворота, равный: 45º, -30º, 225º, -315º, 210º, 590º, -50º, -410º.


№2. Укажите в таблице соответствующий знак синуса, косинуса, тангенса и котангенса:
135º
216º
400º
460º
-16º
-127º

sin α


















cos α


















tg α


















ctg α




















№3. Вычислите:

2 sin 30º + 6 cos 60º- 3ctg 30º + 9 tg 30º

sin (-45º) + cos (-45º) + 2 sin (-30º) - 4cos (-60º)

4 sin (-30º) + tg (-45º) ctg (-45°) – 3 cos 90º

3 sin π/2 - 2cos π/3 - tg π/4 + 4ctg π/4

sin (- π/2 ) -3cos (- π/4 ) +3sin (- π/4 ) - 4sin π

2 tg (- π/4 ) · ctg (- π/4 ) + 3 sin (- π/2 ) + 5 cos (- π/6 )


4. Итог урока: смена тетрадей.


Урок № 6: Соотношения между тригонометрическими функциями одного и того же аргумента.

Тип урока: комбинированный.

Цель урока: познакомить учащихся с соотношениями между тригонометрическими функциями одного и того же аргумента, выработать умения применять полученные соотношения к преобразованию выражений.

Оборудование: таблицы «Формулы тригонометрии», «Основные тригонометрические формулы».


Ход урока


1. Организационный момент.

Приветствие. Результаты самостоятельной работы. Выявление недочетов и ошибок. Составление плана по устранению этих ошибок и недочетов.


2. Объяснение новой темы.



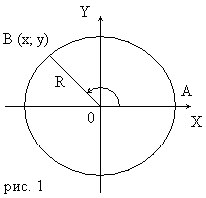
Пусть при повороте радиуса ОА, равного R, на угол α получен радиус ОВ (рис.1). Тогда по определению

sin α = y/R ; cos α = x/R,

где х - абсцисса точки В, у - ее ордината.

Отсюда следует, что х= Rcos α , y= R sin α .

Точка В принадлежит окружности. Поэтому ее координаты удовлетворяют уравнению

x 2+ y2 = R2.

Воспользовавшись тем, что x= R cos α , y= R sin α , получим:

sin2 α + cos2 α = 1.(1)

По определению tg α = y/x= sin α / cos α .Таким образом,

tg α = sin α /cos α . (2)

Аналогично ctg α =x/y= cos α /sin α , т.е.: ctg α= cos α / sin α . (3)

Равенство (1) верно при любых значениях. Равенство (2) верно при всех значениях α, при которых cos α =0, а равенство (3) верно при всех значениях α , при которых sin α =0.

С помощью формул (1)- (3) можно получить другие формулы, выражающие соотношения между тригонометрическими функциями одного и того же аргумента.

Из равенства (2) и (3) получаем:

tg α ctg α = (sin α / cos α) · (cos α / sin α ) =1, т.е.

tg α ·ctg α =1. (4)

Она верна при всех значениях, при которых tg α и ctg α имеют смысл. Заметим, что формулу (4) можно получить и непосредственно из определения тангенса и котангенса.

Выведем теперь формулы, выражающие соотношения между тангенсом и косинусом, а также котангенсом и синусом одного и того же аргумента.

Разделив обе части равенства (1) на cos α , получим:

sin2 α /cos2 +1= 1/ cos2 α , т.е. 1 + tg 2 α = 1/ cos2 α . (5)

Если обе части равенства (1) разделить на sin α , то будем иметь:

1 + cos2 α /sin2 α = 1/ sin 2α , т.е. 1 + ctg2 α = 1/ sin2 α . (6)

Равенство (5) верно, когда cos α =0, а равенство (6)- когда sin α =0.

Равенства (1)- (6) являются тождествами. Их называют тригонометрическими тождествами.

Рассмотрим примеры использования этих тождеств для нахождения значений тригонометрических функций по известному значению одной из них.

Пример 1. Найдем cos α , tg α и ctg α , если известно, что sin α =5/13 , π/2 < α < π .

Найдем сначала cos α . Из формулы sin2 α + cos2 α =1 получаем, что cos2 α = 1- sin2 α .

Так как α является углом 2 четверти, то его косинус отрицателен. Значит, cos α =- √ 1- sin2 α = - √1- 25/169 = -12/13.

Зная синус и косинус угла α, можно найти его тангенс:

tg α = sin α / cos α = 5/13: (-12/13)= - 5/12.

Для отыскания котангенса угла α удобно воспользоваться формулой tg α ·ctg α =1. Имеем: ctg α =1/tg α =-12/5= -2,4 .

Итак, cos α = -12/13; tg α = -5/12; ctg α =-2,4

.

Пример 2. Известно, что tg α =2 и 0 < α < π/2 .

Воспользовавшись формулой 1+ tg2 α = 1/ cos2 α , найдем cos α. Имеем: 1+4 = 1/ cos2 α , cos2 α =1/5.

По условию угол α является углом 1 четверти, поэтому его косинус положителен. Значит, cos α = √ 1/5= √ 5/5.

Зная cos α и tg α , можно найти sin α . Из формулы tg α = sin α /cos α получим: sin α = tg α· cos α =2·√ 5/5= 2 √ 5/5.

По известному tg α легко найти ctg α: ctg α = 1/ tg α =1/2.

Итак, sin α =2 √ 5/5 , cos α = √5/5 , ctg α =1/2.


3. Закрепление.

№1. Известно, что π/2 < α < π. Найдите:

sin α, если cos α =-0,6 cos α , если sin α =1/3

tg α ,если cos α =-15/17 sin α, если ctg α = -2


№2. а) Найдите tg α , если sin α =9/41 и π/2 < α <π;

б) найдите cos α , если ctg α =1/3 и π < α < 3π/2 .


№3. Найдите значения тригонометрических функций угла α, если известно, что: sin α =3/5 и 0 < α <π/2;

cos α = 8/17 и α - угол 1 четверти;

tg α = -√ 3 /3 и π/2 < α <0;

ctg α = -2,5 и α - угол 4 четверти.


№4. Найдите значения тригонометрических функций угла α, если известно, что: sin α = 8/17;

cos α = - 3/2.


№5. Выразите тригонометрические функции угла α:

через sin α; через cos α .


№6. Найдите tg α , если ctg α равен: -3;1/8; 0,6; а/в, где ав≠0; а+в, где а≠в.


№7. Упростить: а) 2- sin2 α - cos2 α ; б) sin(- α ) cos (- α ) tg (- α ) ctg (- α )


4. Итоги урока.

1) Назовите независимые формулы из основных тригонометрических тождеств.

2) Как получить следствия из независимых формул?

3) Какое из основных тригонометрических тождеств верно для любого угла?

4) В каком случае теряют смысл формулы (1)- (6)?

5) Почему по заданному значению синуса угла можно найти только модуль значения косинуса?

Урок №7: Применение основных тригонометрических формул к преобразованию выражений.

Тип урока: комбинированный.

Цель урока: выработать умения применять основных тригонометрических формул для преобразования тригонометрических выражений, развивать разговорную речь и логическое мышление учащихся, воспитывать чувства аккуратности и ответственности.

Оборудование: листы с тестами, портрет Л.Эйлера, таблицы «Формулы тригонометрии», «Основные тригонометрические формулы», « Значения тангенса и котангенса угла α», « Значения синуса и косинуса угла α».

Ход урока


1. Организационный момент.

Приветствие. Сообщение цели урока и плана работы на уроке.


2. Актуализация знаний и умений учащихся.

а) Ответы на вопросы с помощью опорных конспектов:

1) назовите все основные формулы;

2) как они называются?

3) какое из этих основных формул верно для любого угла?

4) в каком случае эти основные формулы теряют смысла?

5) (устно) cos α = 8/17; α - угол 1 четверти. Найти sin α , tg α , ctg α.


б) Выполнение теста.

1· Если α =+98°· то угол α лежит…·.

А. в 1 четверти; Б. во 2 четверти; В. в 3 четверти.


2. cos 0° + 3 sin 90°

А. 1; Б. 2; В. 4.


3. tg 30° + ctg 30°

А. 1 ⅓ √ 3; Б. ⅓ √3; В. ¾ √ 3.


4. Если угол α = 197°, то …·.

А. sin α >0; Б. sin α <0; В. sin α может быть и положительным, и отрицательным.


5. Если α = π /2, то значение 3 sin α - 2 cos α будет…·

А. 5; Б. 3; В.0.

( Проверяем с помощью таблицы).


в) Работа на доске.

Упростить: sin α ·ctg α (1- cos2 α) / 1- sin2 α

tg α / ctg α +1


3. Объяснение новой темы.

Установленные соотношения между тригонометрическими функциями одного и того же аргумента позволяют упрощать тригонометрические выражения и доказывать тригонометрические тождества.

Пример 1. Упростим выражение ctg2 α (cos2 α -1).

Воспользовавшись формулами ctg α = cos α sin α и sin2 α + +cos2 = 1, получим: ctg2 α (cos2 α - 1)= cos2 α / sin2 α (-sin2 α) = = - cos 2 α