Элективный курс «Мир тригонометрии»

Вид материала

Элективный курс

Содержание Ход урока таблица «Формулы тригонометрии». Ход урока 1. Организационный момент. Тип урока Ход урока Тип урока Ход урока Тип урока

Подобный материал:

• Ф. В. Чижова методическая разработка элективный курс, 490.04kb.
• Элективный курс по истории России в 9 классе Тема: «Быт и традиции русского народа», 53.94kb.
• Элективный курс «глобальные проблемы человечества», 121.74kb.
• Курс «Мой мир мой дом» из цикла «Экология и мир человека. Уроки экологического мышления», 1272.57kb.
• В. А. Ходаков моу воротынская средняя школа Перемышльского района Калужской области, 76.7kb.
• Элективный курс «Мир химии» (9 класс) Курс разработан, 529.48kb.
• Элективный курс по астрономии, 93.86kb.
• Пояснительная записка Элективный курс «Природа тел Солнечной системы» предназначен, 50.52kb.
• Элективный курс «Методы решения задач по физике» 10 11 классы 68 часов, 115.81kb.
• Багровникова Светлана Владимировна, к ф. н., доцент элективный курс, 110.32kb.

Пример 2. Упростим выражение sin α / 1+ cos α + 1+ cos α / sin α

Имеем: sin α / 1+ cos α + 1 + cos α / sin α = ( sin ² α + ( 1 + +cos α )² )/ (sin α (1+ cos α )) = ( 2 (1+ cos α)) / (sin α ( 1+ cos α)) = =2/ sin α


Пример 3. Докажем тождество tg² α - sin² α = tg² α · sin² α .

Преобразуем левую часть данного равенства: tg ² α - sin² α = sin² α / cos² α - sin² α = sin² α (1/ cos² α - 1) = sin² α (1+ tg² α - 1)= tg² α · sin² α .

Мы получили выражение, стоящее в правой части равенства. Таким образом, тождество доказано.

Можно воспользоваться несколькими способами доказательства тождеств. Например, 1/ sin² α · cos² α = ( tg α + ctg α) ²·


1- ый способ: ( tg α + ctg α ) ²= ( sin² α / cos² α + cos α / sin α ) ² = ( sin² α + cos² α / sin α cos α ) = ( 1/ sin α cos α )= 1/ sin α cos α


2- ой способ: ( tg α + ctg α ) ² = tg² α + 2 tg α · ctg α + ctg² α = =tg² α + 2+ ctg² α = ( 1+ tg² α ) ( 1+ ctg² α )= 1/ cos² α + 1/ sin² α = sin² α + cos² α / sin² α · cos² α = 1/ sin² α · cos ² α .


3- ий способ: 1/sin² α cos² α = sin² α + cos² α / sin² α · cos² α = sin² α / sin² α cos² α + cos² α / sin² α cos ² α = 1/ cos² α + 1/ sin² α = 1+ tg² α + 1+ ctg² α= tg ² α + 2+ ctg² α = ( tg α + ctg α ) ²·


4- ый способ: (1/ sin² α) · (1/ cos² α) = ( 1+ ctg² α ) ( 1+ tg² α )= =1+ tg² α + ctg² α + tg α · ctg α = 2+ tg² α + ctg² α = ( tg α + ctg α ) ².


Таким образом, надо выбрать тот способ, который вам кажется короче и проще. Для нашего примера, например, подходит 1-ый способ, но решение другими способами тоже ошибкой не будет.


4.Закрепление.

1. Упростить выражение:

sin² α + cos² α + tg² α 1- 1/ cos² α

tg² α · ctg² α - cos² α 2 - sin² α - cos² α

sin α · ctg α ( 1- sin α )· ( 1+ sin α )


2. Преобразуйте выражение:

1- sin² α cos² α - 1

cos α · tg α sin² α - tg α · ctg α

sin² α + cos ² α+ ctg² α


3. Докажите, что при всех допустимых значениях значение выражения не зависит от α:

1/ (1+ tg ² α ) + 1/ (1+ ctg² α )

( 1+ sin α ) / cos α · (1- sin α ) / cos α

4. Преобразуйте выражение:

ctg α sin(- α) – cos (- α)

tg (- α) ctg α + sin² α

cos α tg (- α ) - 1


5. Докажите тождество:

(sin β + sin α)· (sin α - sin β)- (cos α + cos β) · (cos β - cos α)= 0;

(tg α + tg β) / ctg α + ctg β = tg α tg β


5. Итоги урока.

1) Чему мы научились на сегодняшнем уроке?

2) Какие основные тригонометрические тождества чаще используются?

3) Стоит ли все тригонометрические выражения упрощать только одним единственным способом?

Урок №8: Формулы приведения.

Тип урока: комбинированный.

Цель урока: ознакомить учащихся с формулами приведения, выработать умения применять полученные соотношения к преобразованию выражений.

Оборудование: таблица «Формулы тригонометрии».

Ход урока


1. Организационный момент.

Приветствие. Результаты тестов. Выявление и анализ ошибок и недочетов.


2. Актуализация знаний.

Математический д и к т а н т.

1) Чему равна сумма квадратов синуса 73º и косинуса 73º?

( Напишите выражение, тождественно равное единице, деленной на синус квадрат α).

2) Напишите выражение, тождественно равное единице, деленной на косинус квадрат α. (Чему равна сумма квадратов косинуса 37º и синуса 37º?).

3) Вычислите синус острого угла, если его косинус равен 5/13.

( Вычислите косинус острого угла, если его синус равен 12/13).

4) α - угол 3(1) четверти, sin α = - 0,3; (cos α =0,2). Чему равен cos α; (sin α)?

5) sin α =0,6; cos α = -0,4 ( cos α =0,4; sin α =-0,6). Найдите tg α (ctg α).

6) α - угол 2(4) четверти, cos α =-1/3 (cos α =2/7). Найдите tg α .

7) α - угол 1(3) четверти; sin α =1/9 (sin α = 2/3). Чему равен ctg α?

8) tg α =7 (ctg α =-3). Найдите ctg α (tg α).


3. Объяснение новой темы.

Тригонометрические функции углов вида π/2 к ± α, где к - произвольное целое число, могут быть выражены через функции угла α с помощью формул, которые называются формулами приведения.

Выведем сначала формулы приведения для синуса и косинуса. Докажем, что для любого α

sin ( π /2+ α )= cos α и cos( π /2+ α )= - sin α . (1)

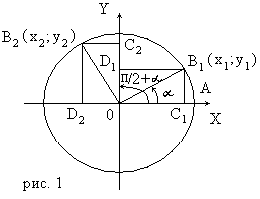Повернем радиус ОА=R на угол α и на угол π /2+ α , при этом радиус ОА перейдет соответственно в радиусы ОВ₁ и ОВ₂ (рис.1). Опустим из точки В перпендикуляры В₁С₁ и В₁Д₁ на оси координат. Получим прямоугольник О Д₁ В₁ С₁.

При повороте около точки О на угол π /2 точка В₁ переходит в точку В₂ , так как угол < В₁ОВ₂ = π/2. Поэтому прямоугольник О Д₁ В₁ С₁ перейдет в равный ему прямоугольник О Д₂ В₂ С ₂, причем точка С₁ оси х перейдет в точку С₂ оси у, а точка Д₁ оси у - в точку Д₂ оси х.

Отсюда следует, что ординатой точки В₂ станет абсцисса точки В₁, а абсциссой точки В₂ – число, противоположное ординате точки В₁. Обозначим координаты точки В₁ через х₁ и у₁, а координаты точки В₂ – через х₂ и у₂. Тогда у₂=х₁ и х₂ = - у₁.

Поэтому y₂/R= x₁ / R x₂ /R= - y₁ /R/

Значит, sin ( π /2+ α)= cos α и cos ( π /2+ α) = - sin α .

Из формулы (1) следует, что

sin ( π/2- α ) = cos α и cos( π /2- α ) = sin α .

Таким образом можно доказать все формулы приведения.

Все формулы приведения сведем в две таблицы, поместив в первой из них формулы для углов π ± α и 2 π ± α , а во второе - для углов π /2± α и 3π /2 ± α .

x	π + α	π - α	2 π + α	2 π - α
sin x	-sin α	sin α	sin α	-sin α
cos x	-cos α	- cos α	cos α	cos α
tg x	tg α	-tg α	tg α	-tg α
ctg x	ctg α	-ctg α	ctg α	-ctg α

x	π /2+ α	π /2- α	3 π /2+ α	3 π /2- α
sin x	cos α	cos α	- cos α	-cos α
cos x	-sin α	sin α	sin α	-sin α
tg x	-ctg α	ctg α	-ctg α	ctg α
ctg x	-tg α	tg α	-tg α	tg α

Из таблиц видны закономерности, которые имеют место для формул приведения.

Функция в первой части равенства берется с тем же знаком, какой имеет исходная функция, если считать, что угол α является углом 1-ой четверти.

Указанные закономерности позволяют записать любую формулу приведения, не прибегая к таблицам.

С помощью формул приведения нахождение значения тригонометрической функции любого угла можно свести к нахождению значения тригонометрической функции угла от 0 до π/2. Приведем примеры.

Пример 1. Найдем значение выражения cos 8 π /3.

cos 8 π /3 = cos ( 2 π + 2 π /3) = cos 2 π /3= cos (π - π/3) = - cos π /3= = -1/2.

Пример 2. Найдем значение выражения sin (-560º).

sin (-560º)= -sin 560º= - sin ( 360º+ 200º)= - sin200º= - sin (180º+ 20º)= = - (- sin 20º)= sin 20º

По таблице синусов находим, что sin 20º= 0,342. Значит,

sin (-560º)= 0, 342.


4. Закрепление.

№1 Замените тригонометрической функцией угла α:

sin (π/2- π) sin ( 2π + α) ctg (π + α)

cos (3π/2 + α) ctg (360º- α) sin(180º+ α)

tg ( 3π/2 – α) cos (90º - α) tg (270º- α)

cos (2π- α) sin (270º- α) tg ( 3π/2 – α)


№2. Выразите sin α , cos α , tg α ,ctg α через тригонометрическую функцию угла из промежутка (0º; 90º), если:

α =130º; α = -320º;

α = 190º; α = -590º.


№3. Приведите к тригонометрической функции угла из промежутка (0º; 90º):

tg 137º sin 680º

sin (-178º) cos (-1000º)


№4. Найдите значение выражения:

sin 240º tg 300º

ctg (- 225º) cos ( - 210º)


№5. Найдите:

cos 120º cos 7π/6 cos 4π/3

tg (– 225º) sin ( -150º)


5. Итоги урока.

1) С какими формулами мы сегодня познакомились? Как они называются?

2) Расскажите, как можно вычислить:

sin 945º; tg 225º; sin 15 π /4; cos (-2π /3);

cos135º; ctg210º; sin (-960º); tg 5 π /3;

ctg2 π /3; tg (-7 π /3);

Урок № 9: Формулы приведения.

Тип урока: совершенствование знаний, умений и навыков.

Форма проведения: семинар·

Цель урока: совершенствовать навыки использования формул приведения для упрощения выражений.

Оборудование: таблица «Формулы тригонометрии».

Ход урока

1. Организационный момент.

Приветствие. Сообщение цели урока.


2. Актуализация и систематизация знаний, умений и навыков.

а) Ответы на вопросы.

• Углом какой четверти является угол – 35º, 179º, им противоположные углы?
  
• Может ли cos принимать значение, равное: - √3; - 1/√ 3; √ 5- 2; √5-1?
  
• Углом какой четверти является угол 750º, -280º?
  
• Существует ли такой угол α, для которого верно равенство: sin α = √1,5; cos α = 2- √ 3; ctg α = (- 2) ¹¹
  
• Какой знак имеет выражение: sin 156º , cos (-35º), tg 365º , ctg 178º , sin 50º cos 130º , ctg 190º tg(- 15º).
  
• Вычислите: cos 0º + sin 360º; tg 45º - ctg 45º; sin 90º - tg 0º ; ctg 90º - cos 60º.
  
• Найдите tg α , если ctg α =3; cos α , если sin α = 1/3 и π /2 < α < π .
  
• Выразите в градусной мере углы π/3, 5 π /6, 3π радиан.
  
• Выразите в радианной мере углы в 45º, 150º, 720º.
  

б) Математический диктант.

1 вариант 2 вариант

sin( 3 π /2 + α ) sin( π - α )

cos( π /2+ α ) cos ( 2 π + α )

tg ( π + α ) tg( 3 π /2- α )

ctg ( π - α ) ctg ( π /2 - α )

cos ( 2 π + α ) cos( 3 π /2+ α )

sin ( 2 π - α ) sin( π /2 + α )

tg (π/2- α) tg (π + α)

ctg(3 π /2- α) ctg (2π - α)


в) Выполнение упражнений.

№1.Найдите числовое значение выражения:

sin (-570º) + 3 cos 150º + tg 315º;

sin 210º + cos (-480º) - √ 3 ctg 480º;

tg 7 π /4 + sin (- 7π /6) – 2 cos (-11 π /6) .


№2. Упростите выражения:

1- cos ( π /2 - α ) sin ( π - α );

cos ( π - α ) cos (2 π - α ) + cos² α ;

cos ( α - π /2) ;

cos( 2 π - α ) cos ( 2 π + α ) – sin² α ;

cos (π - α ) + sin (2 π - α) cos ( π /2 - α ).

sin ( π - α ) ;

tg ( α - π /2);

№3. Определите, чему равен косинус угла, смежного с углом α, если cos α =- 0,6.


№4. Упростите выражение:

sin (α - π/2) cos (α - π) ctg (α-180º)

tg(- α +270º) sin(α -3 π /2); cos (α- 3 π /2).


№5. Упростите выражение:

sin (90º- α) + cos (180º+ α) + tg (270º+ α) + ctg (360º+ α);

sin (π/2 + α ) –cos (α - π) + tg ( π - α ) + ctg (5 π /2- α );

sin (180º- α) + sin (270º- α);

sin (π - α) ·cos (α- π /2) –sin (α + π /2) cos (π - α);

cos (π + α) + cos (π/2 + α);

sin (π + α) cos ( π /2 + α) – cos (2 π + α) sin (3 π /2-α).

№6. Докажите, что:

sin ( 3 π /2+ α ) ctg ( π /2- α ) + sin ( π - α ) +ctg ( 3 π /2 - α ) = tg α .

ctg ²( 2π - α ) - sin ( α - π /2) ·1/sin ( α + π /2) = 1/ sin² α .

( sin β + sin α )( sin α - sin β )- (cos α + cos β )( cos β -cos α ) = 0.

ctg² α - cos² α = ctg² α · cos ² α.


№7. Упростите выражение и найдите его значение:

1- sin α · cos α · tg α , если sin α =0,7.

cos⁴ α + sin² α cos² α , если tg α =2.


3. Итоги урока:

Домашняя творческая работа.


1 вариант. 1. Вычислите:

5 sin 0º + 3 cos 60º 2 sin π /2 – 3 tg π/4

cos 180º + 4 tg 45º 3 cos π /2 – 2 sin π /6

6 sin 30º- 2 tg 45º 4 sin π + 2 cos π /3


2. Упростите выражение:

1- sin α cos α tg α 1- ctg α cos α sin α

(1- sin α)(1+ sin α) (1- cos α)(1+ cos α)

cos (π/2+ α) + sin (π - α) sin(2 π + α)- cos (π/2+ α)

cos (π + α) + sin (π/2- α) tg(π/2- α) + ctg (π - α)


2 вариант. 1. Вычислите:

2cos 60º - 4/5 tg0º + 2 sin 45º

7 ctg π/4 – 6 sin π/2 – 2 sin (- π /3)

6 sin 30º - 2 ctg 45º - cos 0º

2 sin π /4 – ¾ tg π - 2 cos ( - π /6)

3 sin 180º - 2 cos 60º

6 sin π /2 – 5 tg π /4


2. Упростите выражение:

(1 + tg² α) cos² α - sin ² α

( ctg² α +1)sin² α - cos ² α

sin ² ( π + α) + cos² ( α + π)+ ctg² ( π /2 - α )

sin² ( α - π ) + cos² (π + α) + ctg² ( 3 π /2 + α )

( 1- cos α ) ( 1 + cos α )

cos ( π - α) – cos α cos π

sin ( 2 π + α ) – cos ( π /2 + α )

cos (π/2 + α) + sin (π - α)


Урок № 10: Формулы сложения и двойного угла.

Тип урока: комбинированный.

Цель урока: ознакомить учащихся с формулами сложения и формулами двойного угла для синуса и косинуса, выработать умение применять эти формулы при выполнении преобразований несложных тригонометрических выражений.

Оборудование: таблицы «Формулы тригонометрии», «Формулы сложения», «Формулы двойного угла».

Ход урока


1. Организационный момент.

Приветствие. Сообщение цели урока и плана работы. Вопросы и предложения по домашней работе.


2. Объяснение новой темы.

Выразим тригонометрические функции суммы и разности двух углов через тригонометрические функции этих углов:

cos ( α - β ) = cos α cos β+ sin α sin β . (1)

Косинус разности двух углов равен произведению косинусов этих углов плюс произведение синусов этих углов.

Формулу (1) называют формулой косинуса разности.

С помощью формулы (1) легко получить формулу косинуса суммы:

cos ( α + β ) = cos α cos β - sin α sin β . (2)

Косинус суммы двух углов равен произведению косинусов этих углов минус произведение синусов этих углов.

Выведем теперь формулы синуса суммы и синуса разности.

Используя формулу (1) и формулы приведения, получим:

sin ( α + β ) = sin α cos β + cos α sin β . ( 3)

Синус суммы двух углов равен произведению синуса первого угла на косинус второго угла плюс произведение косинуса первого угла на синус второго.

Для синуса разности имеем:

sin ( α - β ) = sin α cos β - cos α sin β . (4)

Синус разности двух углов равен произведению синуса первого угла на косинус второго угла минус произведение косинуса первого угла на синус второго.

Формулы (1) – ( 4) называют формулами сложения.

Приведем несколько примеров использования формул сложения.


Пример 1. Вычислим cos15º и sin 15º.

Представим 15º в виде разности 45º-30º. Тогда

cos 15º = cos( 45º- 30º)= cos45º cos30º + sin45º sin30º= √2/2 ·√ 3/2+ √2/2 · 1/2= √2/4·( √3+ 1).

sin 15º= sin(45º-30º)= sin45º cos30º - cos45º sin30º= √2/2 · √3/2 – √2/2 · 1/2 = √2/4( √3- 1).


Пример 2. Упростим выражение cos (α + β) + cos ( α - β).

Воспользовавшись формулами косинуса суммы и косинуса разности, получим:

cos ( α + β ) + cos ( α - β ) = cos α cos β - sin α sin β + cos α cos β + sin α sin β = 2 cos α cos β .


Формулы сложения позволяют выразить sin2 α , cos2 α и tg2α через тригонометрические функции угла α.

Положим в формулах

sin ( α + β ) = sin α cos β + cos α sin β ,

cos ( α + β ) = cos α cos β - sin α sin β ,

tg ( α + β ) = (tg α + tg β )/ 1 – tg α tg β

β равным α. Получим тождества:

sin2 α = 2 sin α cos α , (1)

cos 2 α = cos² α - sin² α , (2)

tg 2 α = 2tg α / 1- tg² α . (3)

Эти тождества называют формулами двойного угла.

Приведем примеры применения формул двойного угла для нахождения значений тригонометрических функций и преобразования тригонометрических выражений.


Пример 1. Найдем значение sin 2 α , зная, что cos α = - 0,8 и α - угол 2 четверти.

Сначала вычислим sin α . Так как α - угол 2 четверти, то sin α > 0. Поэтому sin α = √1- cos² α = √1- 0,64= √ 0,36 = 0,6.

По формуле (1) находим: sin 2 α = 2 sin α cos α = 2 ·0,6· (- 0,8) = = - 0,96.


Пример 2. Упростим выражение sin α cos³ α – sin³ α cos α .

Вынесем за скобки sin α · cos α и воспользуемся формулами двойного угла: sin α · cos³ α - sin³ α cos α = sin α cos α (cos² α - - sin² α)= ½ (2 sin α cos α)· cos 2α = ½ sin2 α cos 2 α = ¼ sin4α

Из формулы (2) следует, что 1- cos2 α = 2 sin² α . (4)

Действительно, выразив cos 2 α через sin α , получим:

cos 2 α = (1- sin² α )- sin² α = 1 – 2 sin² α .

Отсюда 1 – cos 2 α = 2 sin² α .

Аналогично, выразив cos 2 α через cos α , получим:

1+ сos2 α = 2 cos² α . (5)

Формулы (4) и (5) часто используются в вычислениях и преобразованиях.


3. Закрепление.

№1(устно). а) Используя формулу cos2 α = cos² α - sin² α , замените данное выражение равным ему:

cos 40º cos 80º cos 4 π cos 6 π


б) Используя формулу cos2 α = cos² α - sin² α «справа налево», замените данное выражение равным ему:

cos35º - sin35º cos π/4 - sin π /4 cos5 α - cos5 β


№2. Сократите дробь:

sin40º/ sin20º sin100º/ cos 50º

cos80º/ cos40º+ sin40º cos36º + sin 18º/ cos18º


№3. Упростите выражение:

2 sin 20º cos 20º 1+ cos 4 α

1- cos4 α tg α (1+ cos 2 α )

ctg α (1- cos2 α )


№4. Найдите значение выражения:

cos107º cos17º + sin107º sin17º

cos36º cos24º - sin 36º sin24º


4. Итоги урока.

1. Как записывается формула косинуса разности двух углов?

2. Как получаются формулы cos ( α ± β) , sin (α ± β)?

3. Как получаются формулы двойного угла? Сформулируйте их для синуса и косинуса.


Урок № 11: Формулы суммы и разности тригонометрических функций.

Тип урока: комбинированный.

Цель урока: познакомить учащихся с формулами суммы и разности тригонометрических функций.

Оборудование: таблица «Формулы суммы и разности синусов и косинусов».

Ход урока

1. Организационный момент.

Приветствие. Сообщение цели урока и ознакомление с планом работы.


2. Актуализация знаний.

а) Чему равняются косинус разности и суммы двух углов?

б) Синус суммы и разности двух углов?


в) Упростите:

4sin α cos α

cos( π /3+ α ) cos α + sin( π /3+ α) sin α

sin α cos ( π + α )- cos α sin( π + α )


г) Дано: sin α = ½ ; sin β =1/3 ; α и β - углы 1 четверти. Найти:

sin ( α + β ) , cos( α - β ).

3. Объяснение новой темы.

Сумму и разность синусов и косинусов можно представить в виде произведения.

Чтобы представить в виде произведения сумму sin α + sin β , положим α = х + у и β = х - у и воспользуемся формулами сложения и получим:

sin α + sin β = 2 sin (α + β ) /2 ·cos ( α - β ) /2.

Мы получили формулу суммы синусов двух углов.

Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.

Аналогично можно вывести формулы разности синусов, суммы и разности косинусов.

sin α - sin β = 2 sin (α + β ) /2 · cos ( α - β ) /2.

Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.

cos α + cos β = 2 cos (α + β) /2 · cos (α - β) /2.

Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы этих углов на косинус их полуразности.

cos α - cos β = -2 sin ( α + β) /2 · sin (α - β) /2.

Разность косинусов двух углов равна взятому со знаком «минус» удвоенному произведению синуса полусуммы этих углов на синус их полуразности.

Приведем примеры применения рассмотренных формул.

Пример 1.

Упростим сумму sin10º + sin50º

Воспользовавшись формулой суммы синусов, получим:

sin10º + sin50º= 2 sin (10º+50º)/2 cos (10º-50º)/2 = 2sin 30º cos(-20º)= =2 · ½ cos20º = cos20º.

Пример 2.

Представим в виде произведения разность cos 0,3 π - sin 0,6 π .

Воспользовавшись формулой приведения, представим данное выражение в виде разности косинусов. Тогда

cos 0,3 π - sin 0,6 π = cos 0,3 π - sin (0,5 π +0,1 π )= cos 0,3 π – cos 0,1 π = -2 sin ( 0,3 π + 0,1 π )/2 ·sin (0,3 π - 0,1π) /2= -2 sin 0,2 π sin 0,1 π .


4. Закрепление.

№1. Упростить:

cos20º- cos40º/cos10º.

Воспользуемся формулой cos α -cos β = -2 sin (α + β) /2 ·sin (α - β) /2, т.е.

cos20º- cos40º = -2 sin (20º+40º)/2· sin (20º-40º)/2= -2 sin30º sin(-10º)= =2 · ½ sin10º =sin10º.

sin10º/cos10º=tg10º.

sin20º cos40º+ cos20º sin40º sin α cos 2 α + cos α sin 2 α

cos20º cos40º+ sin20º sin40º cos α cos 2 α + sin α sin 2 α

sin80º cos20º - cos80ºsin20º cos80º cos20º- sin80º sin20º


№2. С помошью формул преобразования суммы тригонометри-ческих функций в произведение разложите на множители выра-жение:

sin 3 α +sin α cos 2x + cos 3x

cos y – cos 3y sin α - sin 5 β


№3. Представьте в виде произведения:

sin40º+ sin16º sin20º- sin40º cos46º- cos74º

cos15º+ cos45º sin12º+ sin20º sin52º- sin32º

cos40º+ cos50º sin15º+ cos65º cos50º+ sin80º

cos40º- sin16º sin40º- cos40º cos18º- sin22º


5. Итоги урока.

1. Запишите формулы сложения для синуса и косинуса суммы (разности) двух углов и сформулируйте соответствующее правило. Используя формулы сложения, вычислите:

sin75º cos15º

sin105º cos105º


2. Запишите формулы двойного угла для синуса и косинуса. Упростите выражение:

sin2 α /2cos α cos α -sin α cos165º- sin165º

sin2 α -( sin α + cos α ) 2 sin75º cos75º


Урок № 12: Формулы суммы и разности тригонометрических функций.

Тип урока: совершенствование знаний, умений и навыков.

Форма урока: семинар.

Цель урока: совершенствовать навыки использования формул суммы и разности тригонометрических функций.

Оборудование: таблица «Формулы суммы и разности тригонометрических функций».