Geum.ru

Колпаков Юрий Алексеевич, кандидат технических наук, доцент кафедры информационных технологий учебно-методический комплекс

Вид материалаУчебно-методический комплекс

Содержание


Тема 1. «Решение уравнений»
Поиск решения
Минимальному значению
Задача 4. Нахождение экстремума без ограничений
Поиска решения
Тема 4. «Задачи на прогнозирование»
Тема 5. «Задачи частотного анализа»
ЧАСТОТА(данные; интервалы
Тема 6. «Аппроксимация»
Подобный материал:
1   2   3   4   5   6   7   8



    1. Темы контрольных работ и методические указания по их выполнению

7.1 Для студентов очной формы обучения


Тема 1. «Решение уравнений»

Решение уравнения в Excel как поиск значения параметра формулы, удовлетворяющего ее конкретному значению.

Эту процедуру используют для поиска такого значения ячейки, при котором значение другой ячейки, вычисляемое по формуле, заранее задано. В формуле должна быть ссылка на ячейку, значения которой ищут. Ограничения на искомое значение ячейки не налагают.


Задача 1

Познакомимся с этой процедурой на примере составления штатного расписания.

Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующая хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 10 000 руб. Необходимо определить, какими должны быть оклады сотрудников больницы.

Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальные оклады будем вычислять, исходя из него: во столько-то раз или на столько-то больше. Говоря математическим языком, каждый оклад Аорется линейной функцией от оклада санитарки: Ai*С+Вi, где С – оклад санитарки; Аi и Вi – коэффициенты, которые для каждой должности определяют следующим образом:
  • медсестра получает в 1,5 раза больше санитарки (А2=1,5; В2=0);
  • врач – в 3 раза больше санитарки (В3=0; А3=3);
  • заведующий отделением – на 30 руб. больше, чем врач (А4=3; B4=30);
  • заведующий аптекой – в 2 раза больше санитарки (А5=2; В5=0);
  • заведующий хозяйством – на 40 руб. больше медсестры (А6=1,5; В6=40);
  • главный врач – в 4 раза больше санитарки (А7=4; В7=0);
  • заведующий больницей – на 20 руб. больше главного врача (А8=4; В8=20);

Зная количество человек на каждой должности, нашу модель можно записать как уравнение

N1*A1*C+N2*(A2*C+B2)+…+N8*(A8*C+B8) = 10000,

где N1 – число санитарок, N2 – число медсестер и т.д.

В этом уравнении нам известны A1…A8, B1…B8 и N1… N8, а С неизвестно.

Анализ уравнения показывает, что задача составления расписания свелась к решению линейного уравнения относительно С. Решим его.

Введите исходные данные в рабочий лист электронной таблицы, как показано ниже.



В столбце D вычислите заработную плату для каждой должности. Например, для ячейки D4 формула расчета имеет вид =B4*$H$8+C4.

В столбце F вычислите заработную плату всех рабочих данной должности. Например, для ячейки F4 формула расчета имеет вид =D4*E4.

В ячейке F12 вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже.



Определите оклад санитарки так, чтобы расчетный фонд был равен заданному:
    • активизируйте команду Подбор параметра из меню Сервис;
    • в поле «Установить в ячейке» появившегося окна введите ссылку на ячейку F12, содержащую формулу;
    • в поле «Значение» наберите искомый результат 10000;
    • в поле «изменяя значение ячейки» введите ссылку на изменяемую ячейку H8 и щелкните на кнопке ОК.

Сохраните таблицу в личном каталоге под именем hospital.xls.

Анализ задачи показывает, что с помощью Excel можно решать линейные уравнения. Конечно, такое уравнение может решить любой школьник. Однако, благодаря этому простому примеру стало, очевидным, что поиск значения параметра формулы, удовлетворяющего ее конкретному значению, - это не что иное, как численное решение уравнений. Другими словами, используя Excel, можно решать любые уравнения с одной переменной.

Контрольное задание

Найти корень уравнения x2-sinx=0.

Указание
В качестве начального приближения возьмите х=0,5.
Обратите внимание, что уравнение имеет два корня: 0 и 0,87, однако Excel может находить только один.

Тема 2. «Задачи оптимизации»

Задачи линейного программирования

Если математическая модель исследуемого процесса и ограничения на значения ее параметров линейны, то задача достижения цели является задачей линейного программирования.


Задача 2. Составление штатного расписания

Усложним рассмотренную в предыдущей главе задачу. Пусть известно, что для нормальной работы больницы необходимо 5-7 санитарок, 8-10 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующая хозяйством и заведующий больницей. Общий месячный фонд зарплаты должен быть минимален. Необходимо определить, какими должны быть оклады сотрудников больницы, при условии, что оклад санитарки не должен быть меньше прожиточного минимума 80 руб.

В качестве модели решения этой задачи возьмем, как и в первой задаче, линейную. Запишем ее так:

N1*A1*C+N2*(A2*C+B2)+…+N8*(A8*C+B8) = Минимум.

В этом уравнении нам не известно число санитарок (N1), медсестер (N2), врачей (N3) и оклад санитарки (С).

Используя Поиск решения, найдем их.

Откройте созданный в предыдущей главе файл hospital.xls.

В меню Сервис активизируйте команду Поиск решения.

В окне Установить целевую ячейку укажите ячейку F12, содержащую модель.

Поскольку необходимо минимизировать общий месячный фонд зарплаты, то активизируйте радиокнопку Минимальному значению.

Используя кнопку Добавить, опишите ограничения задачи.

Окончательно окно Поиска решения будет выглядеть так:



Опишите Параметры поиска, как показано на рис. 7.1.

Щелкните на кнопке ОК, а затем – Выполнить.

Решение приведено на рис. 7.2. Оно тривиально: чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд заработной платы.


Задача 3. План выгодного производства

Предположим, что мы решили производить несколько видов конфет. Назовем их условно «A», «B» и «C». Известно, что реализация 10-и килограмм конфет «А» дает прибыль 9 руб., «В» – 10 руб. и «С» – 16 руб.



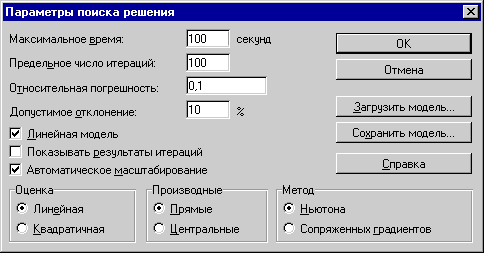
Рис. 7. 1 – Описание параметров поиска решения



Рис. 7. 2 – Решение задачи линейного программирования

Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограмм необходимо произвести, чтобы общая прибыль от реализации была максимальной.

Нормы расхода сырья на производство 10 кг конфет каждого вида приведены ниже.

Сырье
Нормы расхода сырья
Запас сырья

 
А
В
С
 

Какао
18
15
12
360

Сахар
6
4
8
192

Наполнитель
5
3
3
180

Прибыль
9
10
16
 

Введите исходные данные и формулы в электронную таблицу, как указано ниже.



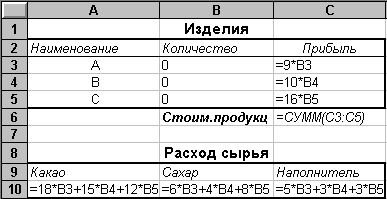
В меню Сервис активизируйте команду Поиск решения и опишите его параметры, как указано на рис 7.3.

Не забудьте указать в Параметрах на Линейность модели.

Запустите Поиск решения. Если Вы сделали все верно, то решение будет таким, как на рис 7.4.

Из решения видно, что оптимальный план выпуска предусматривает изготовление 80 кг конфет «В» и 20 кг конфет «С». Конфеты «А» производить не стоит. Полученная Вами прибыль составит 400 руб.


Задачи книги Solvsamp.xls

Книга Solvsamp.xls, входящая в состав Excel, в папке Examples\Solver содержит более сложные примеры использования средств процедуры Поиска решения.



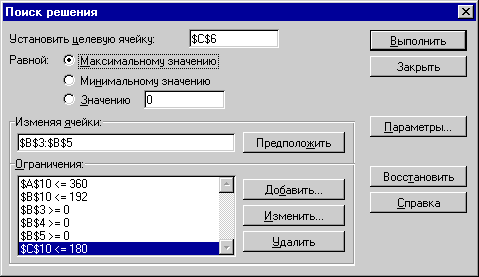
Рис. 7. 3 – Описание параметров поиска решения



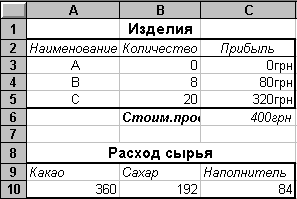
Рис. 7. 4 – План выгодного производства

Листы с примерами расчетов из этой книги можно использовать как образцы решения Ваших задач оптимизации. Чтобы изучить листы с задачами линейного программирования «Перевозка грузов»1), «График работы» и «Оборотный капитал», откройте книгу, перейдите на нужный лист, затем выполните команду Поиск решения из меню Сервис. Целевые ячейки, влияющие ячейки и ограничения на листах уже заданы.


Задача 4. Нахождение экстремума без ограничений

Книга Solverex.xls, входящая в состав Excel, содержит пример решения типичной задачи маркетинга: определения затрат на рекламу, при которых прибыль от реализации товара будет максимальной. Решение этой задачи Аормацет определить: «Стоит ли вкладывать дополнительные средства в рекламу, чтобы увеличить прибыль?».

Задачи, подобные приведенной, демонстрируют использование процедуры Поиска решения для подбора таких значений параметров, которые максимизируют значение нелинейной функции.

Прежде чем знакомиться с примером этого листа, рассмотрим упрощенный вариант этой задачи: поиск максимума функции при изменении одного параметра.

Исходные данные задачи состоят из 2-х блоков: «Планируемые показатели» и «Данные о продукции». Так, в 1-м квартале запланированы следующие показатели реализации:
  • сезонный фактор (ячейка В2) – равным 0.92);
  • затраты на заработную плату персонала (ячейка В9) – 8 тыс. грн;
  • затраты на рекламу (ячейка В10) – 10 тыс. руб.

Данные о продукции:
  • цена реализации (ячейка В17) – 40 грн;
  • себестоимость (ячейка В18) – 25 руб.

Расчет планируемых показателей производят так:
  • объем сбыта продукции3) (ячейка В4) нелинейно зависит от сезонного фактора и затрат на рекламу

=35*B2*(B10+3000)0,5
  • доход с оборота определяется как ожидаемое количество проданных единиц продукции (ячейка В4), умноженное на себестоимость продукции, поэтому в ячейку В5 введем формулу

=B4*B17
  • фраза «себестоимость реализованной продукции» на языке математики выглядит как

B6=B4*B18
  • очевидно, что валовая прибыль, имеющая в электронной таблице адрес В7, определяется как

=B5-B6
  • накладные расходы фирмы будем исчислять в объеме 15% дохода с оборота, то есть в ячейку B11 введем формулу

=0,15*B5
  • валовые издержки рассчитаем как сумму затрат на заработную плату персонала, рекламу и накладные расходы, то есть

B12=СУММ(B9:B11)
  • прибыль от продукции определим как валовую прибыль минус валовые издержки, то есть

B14=B7-B12
  • рентабельность

B15=B14/B5

Если вышеперечисленные данные и формулы ввести в таблицу, то результаты вычислений будут такими, как показано на рис. 7.5.

Активизируем Сервис=>Поиск решения и опишем условия решения задачи:
  • задайте ячейку B14, как содержащую целевую функцию4);
  • определите цель оптимизации – Максимальное значение;
  • укажите ячейку, значение которой будет изменяться при поиске наилучшего решения5) – B10;
  • при назначении параметров укажите на нелинейность модели. Для остальных параметров используйте установки по умолчанию, которые подходят для решения большинства задач.

Щелкнув на кнопке Выполнить, Вы увидите следующий результат оптимизации (рис. 7.6).

Как видно из полученного решения при, затратах на рекламу 17 093 руб. прибыль от реализации товара будет максимальной. Однако следует отметить, что максимизация прибыли не обязательно соответствует наивысшему значению рентабельности. Ее значение уменьшилось до 8%.



Рис. 7. 5 – Данные для поиска экстремума в задаче маркетинга


Контрольное задание

Покажите, что функция

f = (x-1)2 + y2 – 0,5cos(2z)

имеет минимальное значение -0,5 при x=1; y=-7,9E-07 и z=3,14159.

Указание

В качестве исходных данных для поиска минимума примите x=1, y=2 и z=3.



Рис. 7. 6 – Результат оптимизации


Тема 3. Задачи нелинейного программирования

Если математическая модель исследуемого процесса или ограничения на значения ее параметров нелинейны, то задача достижения цели является задачей нелинейного программирования.

Решите предыдущую задачу при условии, что затраты на рекламу не могут превышать 12 000 руб.

Решение задачи – 14 722 руб.

Отметим, что в этом случае с каждой вложенной гривны Вы получите 10 коп. дохода.

Контрольное задание

Покажите, что при ограничениях x + 2y <= 8, 2x – y <= 12, x >= 0, y >= 0 функция

f = x(2 – x) + 2y(2 – y)

имеет максимальное значение 3 при x=1 и y=1.

Указание

В качестве исходных данных для поиска минимума примите x=0 и y=0.



1) Эту задачу иногда называют «Транспортная».

2) Сезонный фактор отражает колебания спроса на товар в зависимости от времени года. Например, зимой чаще покупают теплые вещи.

3) Объем сбыта определяется количеством (штуками) проданной продукции.

4) Помните, что в адресе должна указываться ячейка, в которой содержится формула, а не числовое значение, дата, или текст.

5) Помните, что переменные – это числовые значения, а не даты, формулы или текст.


Тема 4. «Задачи на прогнозирование»

Иногда нам хочется знать, «что будет» заранее. Это облегчает принятие предстоящих решений в свою пользу. Как принято говорить, «подстелить соломку».

В науке предвидение называют прогнозированием. Основой прогнозирования являются наблюдения. Точнее, не сами наблюдения, а числовые значения неких состояний наблюдаемого явления. Например, курс ценных бумаг. Фиксируя значения курса во времени, мы получим табличное описание процесса изменения курса. Понятно, что если описать аналитически этот процесс, то есть поставить ему в соответствие некую функциональную зависимость

ПРОГНОЗ = f(x),

где х – некий момент времени, то ПРОГНОЗ будет не что иное, как значение f(x) в некоторый наперед заданный момент времени х.


Тема 5. «Задачи частотного анализа»

При обработке статистических данных в демографии, маркетинге, при анализе экономических показателей иногда возникает вопрос: «Как часто среди наблюдаемых результатов встречаются значения, входящие в некоторый диапазон?».

Этот вопрос не является праздным. Ответив на него. Можно выработать правильную линию поведения в будущем. Например, спланировать объем выпуска продукции фабрики верхней одежды на основе анализа распределения населения некоторого региона по росту.

Заполните данными рабочий лист электронной таблицы, как показано ниже.



Используя функцию ЧАСТОТА(данные; интервалы), где данные – это множество значений блока A3:D10, а интервалы – блока E3:E9, определим число людей в группах.

Поскольку этих групп на одну больше числа интервалов, то:
  • выделите блок F3:F10;
  • наберите формулу

=ЧАСТОТА(A3:D10;E3:E9);
  • введите ее, нажав комбинацию клавиш Ctrl+Shift+Enter.

Результат анализа будет следующим:



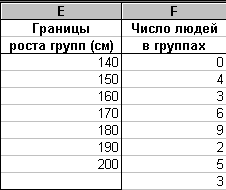
Он показывает, например, что в данном регионе все люди выше 140 см. Людей ростом от 140 см до 150 см – четверо и т.д.

Выполнив подобный анализ, фабрика для обеспечения региона может определить рациональный план выпуска одежды разных размеров. Например, из анализа ясно, что не следует выпускать одежду для людей, чей рост не превосходит 140 см.

Контрольное задание 7.4

Определите, используя результаты предыдущей задачи, сколько необходимо производить верхней одежды для разных групп людей, если для тех, чей рост больше 180 см, но не превышает 190 см пошить 100 единиц.


Тема 6. «Аппроксимация»

Позволяет описать наблюдаемые результаты аналитической функцией.

Продемонстрируем возможность прогнозирования на примере определения зависимости высоты от времени свободного падения тела.

Заполните данными рабочий лист электронной таблицы, как показано ниже.



Постройте диаграмму зависимости высоты времени свободного падения.

Аппроксимируйте полученную кривую с помощью степенной зависимости. Для этого:
  • установите курсор мыши в пределах диаграммы и щелкните два раза ее левой кнопкой;
  • выделите данные диаграммы, установив курсор на графике и щелкнув кнопкой мыши;
  • выберите из меню Вставка команду Линия тренда. На экране появится окно выбора линии тренда.

Сделайте настройку линии тренда:
  • выберите на вкладке «Тип» степенную аппроксимацию;
  • выберите на вкладке «Параметры» «Показывать уравнение на диаграмме»;
  • щелкните на кнопке OK.

Результат аппроксимации показан на рис. 7.7.

Как видно, получена следующая аппроксимирующая функция:

y=5,0118x1,9995.

Если бы мы не знали из школьного курса физики, что точная зависимость

y=gx2/2,

то по полученной с помощью Excel зависимости можно было бы предсказать, например, что за время х=20 сек тело пролетит 1962 м.

Таким образом, как показывает рассмотренный пример, Excel позволяет не только определять аналитическое выражение зависимости таблично представляемых данных, но и предсказывать тенденцию их изменения.



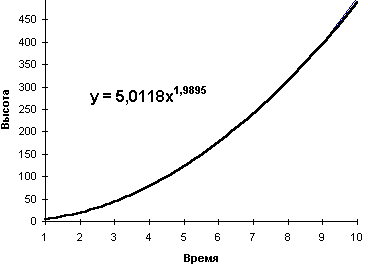
Рис. 7. 7 – Аппроксимирующая кривая


Контрольное задание 7.5

Определите, сколько Вы заработаете, приобретя 10 акций предприятия, если колебания их курса следующие:

Декада
Курс
Декада
Курс

1
6,5
13
14,3

2
6,1
14
16

3
5,6
15
17,3

4
4,9
16
18,2

5
4,2
17
18,8

6
4
18
17,6

7
4
19
16

8
4,8
20
14,1

9
6,1
21
12

10
8,3
22
10

11
10
23
9

12
12,1
24
7,9