Методические указания и задачи для самостоятельной работы студентов по дисциплине «Математическая статистика» для студентов специальностей 060800 («Экономика и управления на предприятии апк») и 060500 («Бухгалтерский учет, анализ и аудит»)

Вид материала

Методические указания

Содержание Задачи для самостоятельного решения Интервалы Частота Статистические гипотезы Дисперсионный анализ Корреляция и регрессия

Подобный материал:

• Методические рекомендации по выполнению практических и лабораторных работ для студентов,, 824.47kb.
• Рабочая программа, методические указания, конспект лекций для студентов заочной формы, 375.73kb.
• Методические указания для выполнения курсовой работы по статистико экономическому анализу, 85.77kb.
• Методические указания по подготовке и защите дипломных работ по специальности 060500, 459.74kb.
• Методические указания по выполнению контрольной работы для студентов заочной формы, 281.98kb.
• Экономика Республики Татарстан Для студентов по специальностям 080101 Экономика и управление, 176.7kb.
• Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
• Методические указания для написания курсовой работы по дисциплине «Деньги, кредит,, 162.15kb.
• Методические указания к изучению дисциплины и к выполнению курсовой работы для студентов, 1275.89kb.
• Методические указания для выполнения курсовой работы по дисциплине «Экономика организаций, 379.4kb.

Министерство сельского хозяйства РФ

Федеральное Государственное образовательное учреждение

высшего профессионального образования

«Пермская государственная сельскохозяйственная академия

им. академика Д.Н. Прянишникова»


Кафедра статистики,

анализа и финансов

Методические указания и задачи

для самостоятельной работы студентов


по дисциплине «Математическая статистика»

для студентов специальностей

060800 («Экономика и управления на предприятии АПК»)

и 060500 («Бухгалтерский учет, анализ и аудит»)

очной и заочной формы обучения


Пермь, 2004

Методические указания подготовлены ст. преподавателем кафедры статистики, анализа и финансов Бодряковой З.П.

Методические указания соответствуют требованиям образовательного стандарта Министерства образования РФ. Предназначены студентам экономического факультета очного и заочного обучения.

Рекомендовано к изданию методической комиссией экономического факультета. Протокол № 12 от 10 февраля 2004 г.

Отпечатано множительным центром академии тиражом 75 экз.


Общие положения


Математическая статистика взаимосвязана с теорией вероятностей и общей теорией статистики.

Математическая статистика изучает закономерности развития массовых социально-экономических явлений с помощью методов теории вероятностей.

Современная математическая статистика разрабатывает методы сбора и обработки статистических данных для получения научных и практических выводов, необходимых для принятия управленческих решений.

Основная цель учебного пособия – выработать у студентов творческий подход к применению методов математической статистики.

Методические указания могут быть использованы студентами для самостоятельной работы по изучению соответствующих разделов курса «Математическая статистика» и преподавателями для контроля знаний студентов.


Тема 1. Ряды распределения. Нормальное распределение.


Ряд распределения – это упорядоченное распределение единиц совокупности на группы по варьирующему признаку. Следовательно, ряд распределения – результат группировки. Различают атрибутивные (по качественному признаку) и вариационные ряды распределения (по количественному признаку).

Вариационный ряд состоит из элементов: вариантов и частот. Варианта - конкретное значение варьирующего признака.

Частота – показатель повторяемости отдельных вариантов (группы). Сумма всех частот равна объему совокупности. Частостями называются частоты выраженные в процентах. Различают локальные и накопленные частоты и частости.

По характеру вариации признака различают дискретные и интервальные вариационные ряды. Вариация количественных признаков может быть дискретной (прерывной) или непрерывной.

В случае дискретной вариации количественный признак принимает только целые значения. При непрерывной вариации величина признака может принимать любые дробные значения в определенных пределах. В этом случае целесообразно построение интервального ряда. Интервальный ряд – ряд с непрерывной вариацией распределения признака, в котором значения признака представлены в виде интервалов.

Для анализа вариационных рядов, изучения формы распределения, применяется графический метод.

Ранжированный ряд изображается графически в виде огивы Гальтона. По оси абсцисс откладываются ранги, по оси ординат – значения варьирующего признака в масштабе.

Наглядное представление о характере изменения частот ряда распределения дают полигон и гистограмма.

Гистограмма применяется для изображения интервального вариационного ряда. На оси абсцисс откладываются интервальные значения признака, а частоты по оси ординат.

Полигон используется при изображении дискретных вариационных рядов. По оси абсцисс откладываются в масштабе ранжированные значения признака, а по оси ординат – частоты.

Кумулятивный ряд представляет собой ряд накопленных частот. При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты, а по оси ординат – накопленные частоты или частости.

Статистические совокупности могут быть расчленены по одному признаку (одномерные ряды распределения) или одновременно по двум и более признакам (двумерные и многомерные распределения).

Ряды распределения анализируют с помощью системы статистических характеристик:

• характеристики центральной тенденции;
  
• показатели вариации;
  
• характеристики формы распределения.
  

Показатели центральной тенденции включают степенные и структурные средние. Из степенных средних наиболее часто применяется средняя арифметическая:

1) простая 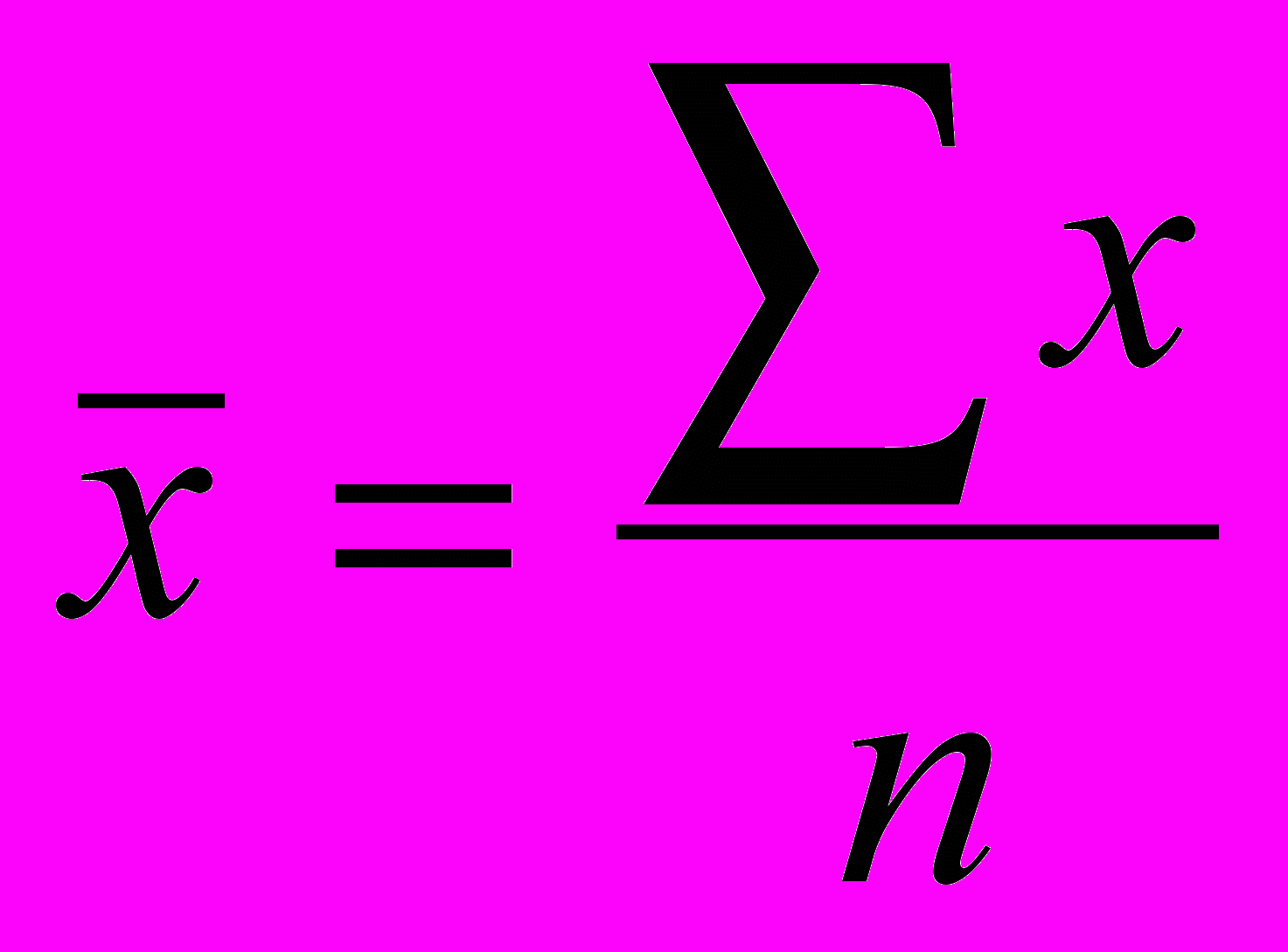; 2) взвешенная 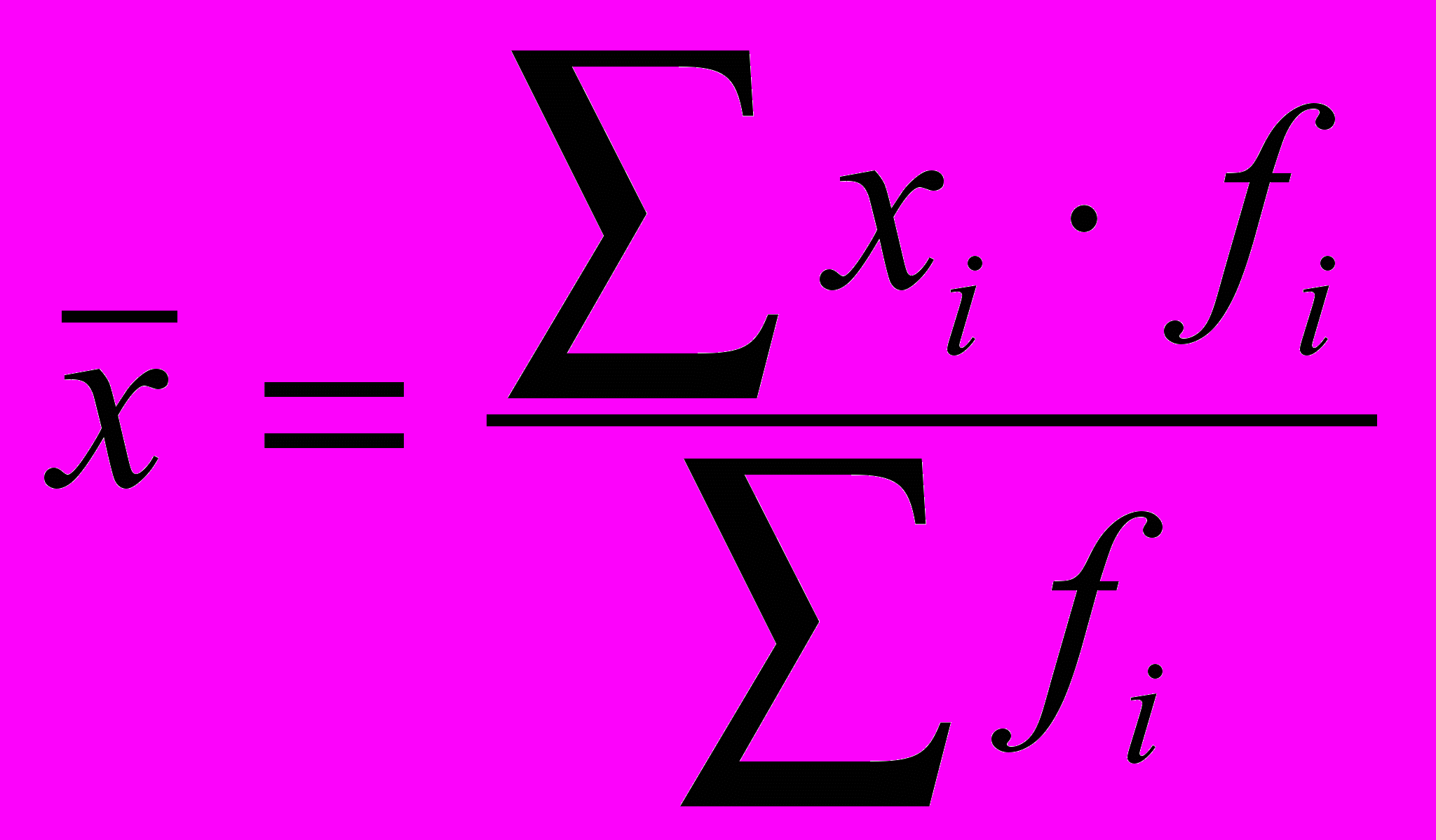, где х_i - отдельные значения признака – варианты, f _i – веса (повторяемость) значений признака.

Для интервальных рядов находят центры (середины) интервалов, которые умножают на веса (взвешенное произведение). Произведения суммируют и делят на сумму весов.

Средняя арифметическая обладает аналитическими свойствами, что позволяет значительно упростить ее расчеты. Из структурных средних широко применяются мода и медиана.

Мода – наиболее часто встречающееся значение признака. Мода в вариационном ряду – это варианта с наибольшей частотой или частостью. В интервальном ряду с неравными интервалами – интервал с наибольшей плотностью.

Для интервального ряда с равными интервалами мода исчисляется по формул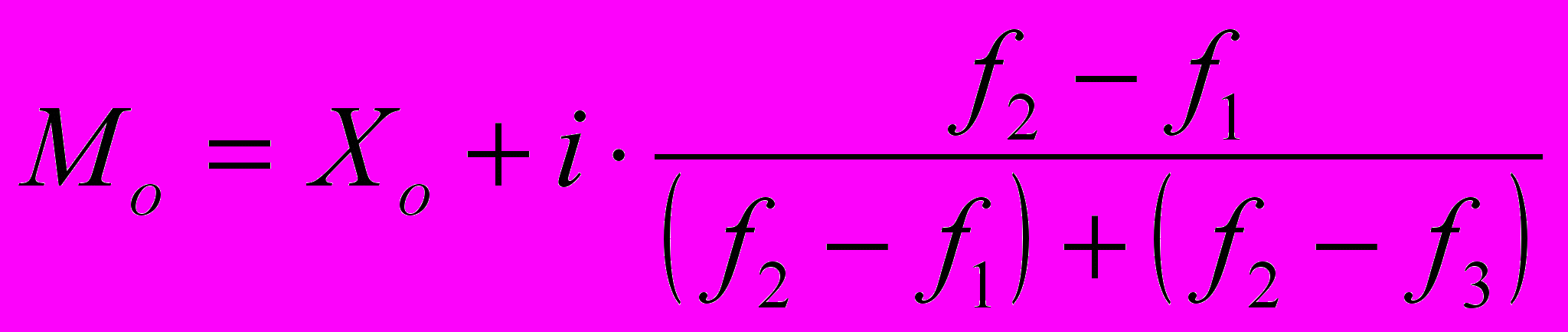е: , где

Хо – начальная (нижняя) граница модального интервала;

i – величина интервала;

f₁ – частота интервала, предшествующего модальному;

f₂ – частота модального интервала;

f₃ – частота постмодального интервала.

Медиана – значение признака, приходящееся на середину ранжированного ряда. В медианном интервале накопленная частота превышает половину объема совокупности.

Медиана определяется способом интерполяции по формуле:

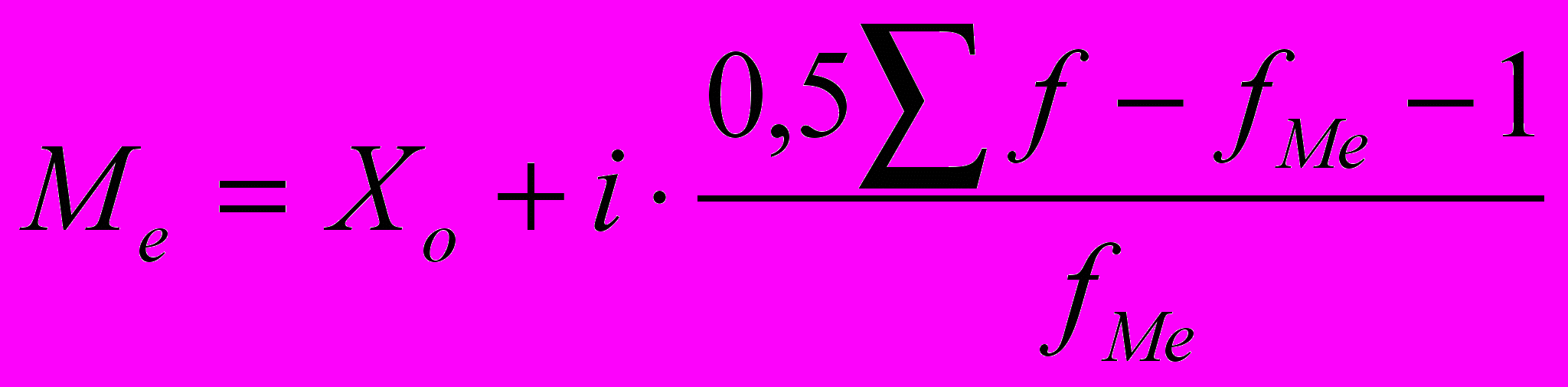, где 0,5 ∑ƒ – порядковый номер медианы;

ƒ_{Μе -1} - накопленная частота интервала, предшествующего медианному.

Структурные средние, следовательно, можно определить двояко:

1. расчетным путем (по формуле);
   
2. на графике мода определяется на полигоне и гистограмме, меридиана – на огиве Гальтона, - кумулятивной кривой.
   

Практическое значение моды: продукция (товар), пользующийся наибольшим спросом, например, модальные размеры одежды и обуви; модальные цены на рынке – наиболее типичные цены.

Свойство медианы практически используется, например, при размещении таких объектов, как телефонов-автоматов, бензоколонок, школ, станций ТО и др.

Структурными характеристиками вариационных рядов выступают квартили, делящие ряд на 4 равные части, децили на 10 частей и перцентили – на 100 равных частей.

Показатели вариации, характеризующие меру колеблем ости признака в совокупности, отражают:

• максимальную вариацию признака (показатель размаха вариации);
  
• среднюю вариацию признака относительно средней арифметической величины в абсолютных единицах (показатели: среднее линейное отклонение
  

и среднее квадратичное отклонение ;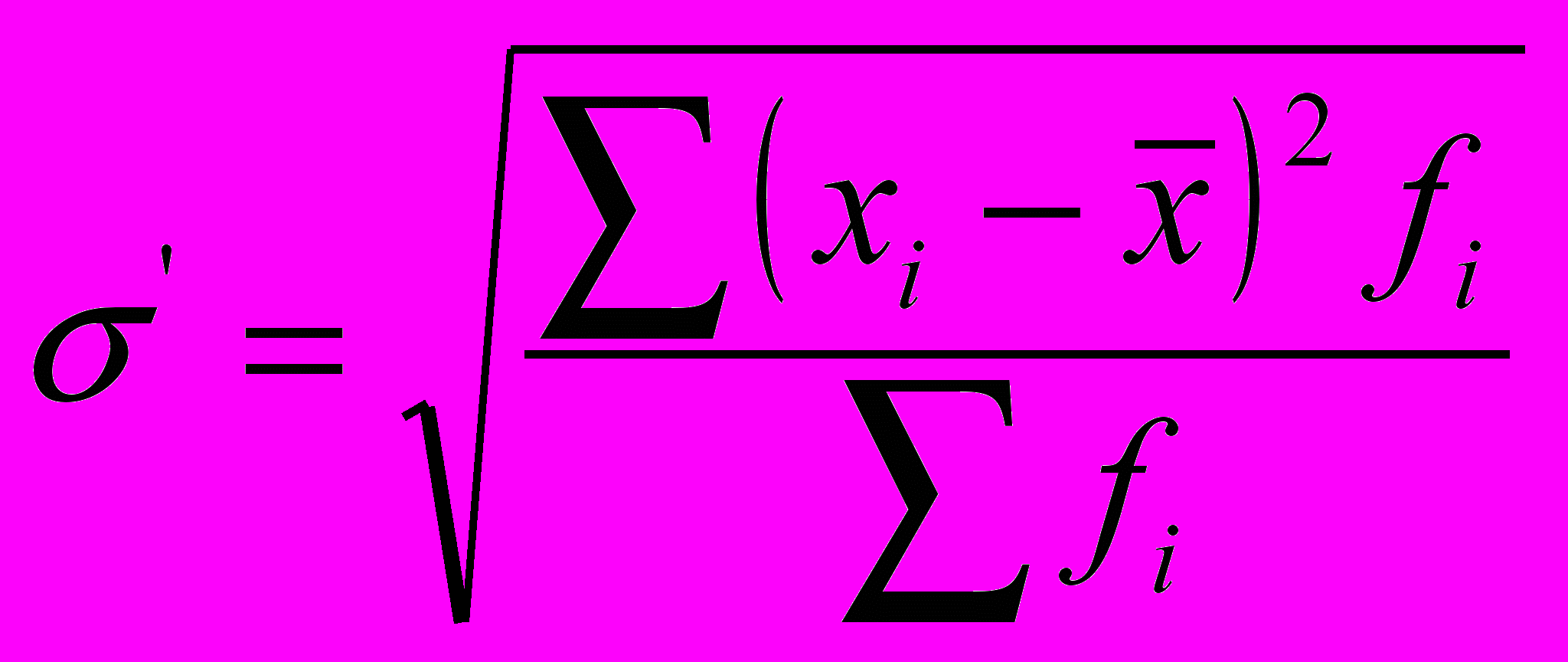

• среднюю меру колеблемости признака относительно средней в относительных единицах (процентах)- (через показатель – коэффициент вариации
  

);

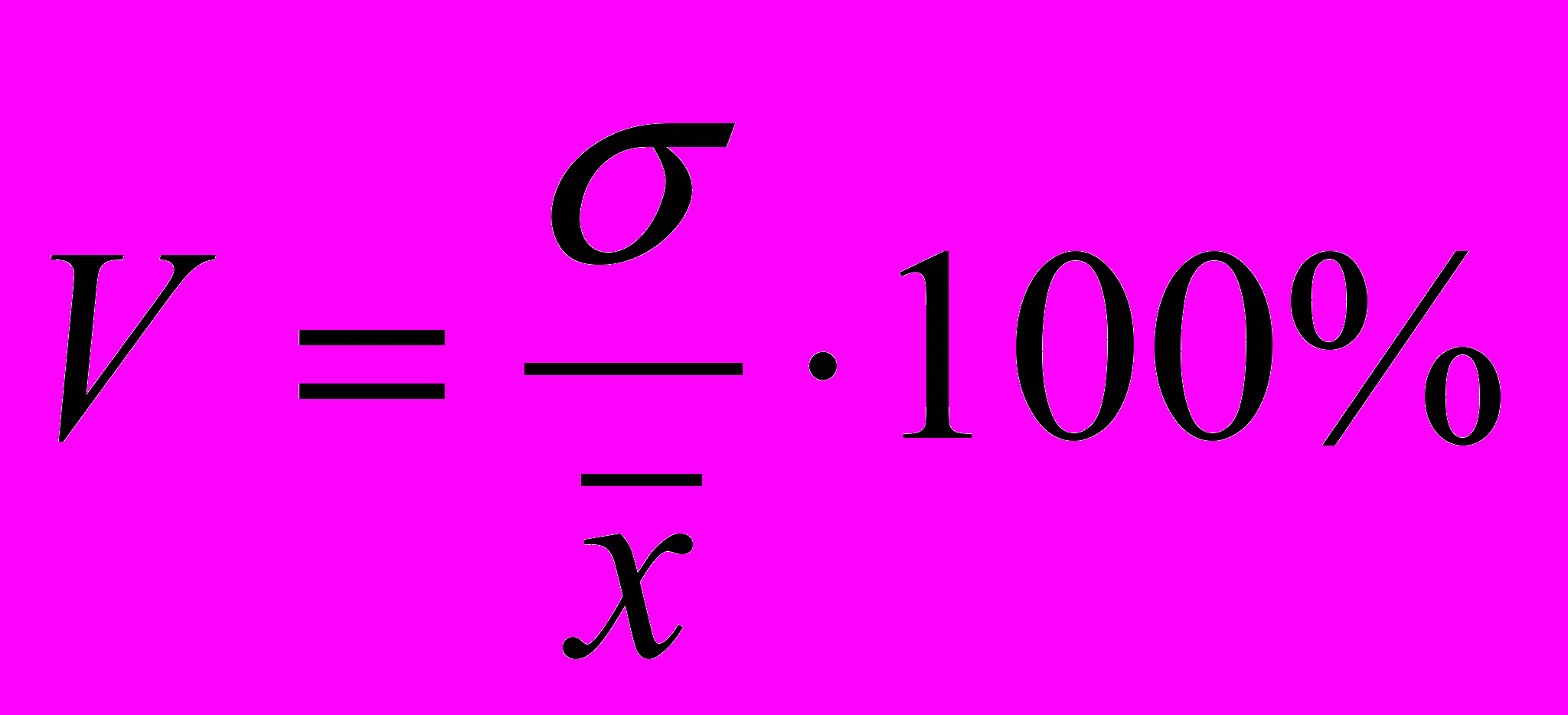• квадрат среднего отклонения индивидуальных значений признака от средней в абсолютном выражении (показатель – дисперсия признака ) .
  

Дисперсия обладает аналитическими свойствами. Применение свойств позволяет упростить расчеты дисперсии.

Для подробного описания особенностей распределения используют дополнительные характеристики – моменты распределения.

Моментом «К» – го порядка называют среднюю из «К» – х степеней отклонений вариантов «Х» от некоторой постоянной величины «А»:

∑(х_i – А)^к f_i

М _к = ———————

∑f _i

где А – величина, от которой определяются отклонения;

К – степень отклонения (порядок момента).

В зависимости от того, что принимается за величину «А», различают 3 вида моментов: начальные моменты получают при А = 0 :

∑х_i^к f_i

М _к = ——————

∑f_i

центральные моменты получают при А = :

∑ (х_i - )^кf_i

М '_к = ——————

∑f _i

условные моменты получают при А = х и отличной от нуля:

∑ (х_i – А)^к

м * = ——————

∑f _i

В статистической практике пользуются моментами первого, второго, третьего и четвертого порядков.

Начальный момент первого порядка М₁ представляет собой среднюю арифметическую и используется как показатель центра распределения.

Центральный момент первого порядка (нулевое свойство средней арифметической) всегда равен нулю: М '₁ = 0.

Центральный момент второго порядка представляет собой дисперсию и служит основной мерой колеблемости признака: М '₂ = σ² .

Центральный момент третьего порядка равен нулю в симметричном распределении и используется для определения показателя асимметрии. Центральный момент четвертого порядка М'₄ применяется при вычислении показателя эксцесса.

Все перечисленные характеристики играют важную роль в анализе вариационных рядов и определении типа кривой распределения и при выравнивании вариационных рядов.

Число наблюдений, по которому строится эмпирическое распределение, обычно невелико и представляет собой выборку из изучаемой генеральной совокупности. С увеличением числа наблюдений и одновременным уменьшением величины интервалов зигзаги полигона сглаживаются и ломаная линия в пределе превращается в плавную кривую, которая называется кривой распределения.

Кривая распределения характеризует теоретическое распределение, закономерность распределения частот внутри однокачественной совокупности явлений. Изучение закономерности (или формы) распределения включает решение задач:

1. выяснение общего характера распределения;
   
2. выравнивание эмпирического распределения, которое состоит в том, что на основании эмпирического распределения строится кривая у = f (х) с заданной формой;
   
3. проверка соответствия найденного теоретического распределения эмпирическому.
   

Кривые распределения могут быть различных типов. В практике социально-экономических исследований широко используется, прежде всего, кривая нормального распределения.

Нормальным называют распределение вероятностей случайной непрерывной величины Х, плотность которого имеет вид:

1

Ф (х) = ——— ℓ^{- (х – а)2 /2σ2}



где а – математическое ожидание;

σ – среднее квадратичное отклонение Х.

Отсюда видно, что нормальное распределение определяется двумя параметрами: а и σ. Достаточно знать эти параметры, чтобы задать нормальное распределение.

Кривая нормального распределения представляет собой симметричную куполообразную фигуру, где вправо и влево симметрично убывают, приближаясь к оси абсцисс.

Симметричным является такое распределение, в котором частоты двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений характерно равенство средней арифметической, моды и медианы.

Асимметрия, эксцесс, мода и медиана соответственно равны: