Стабилизатор магнитного поля для измерителя япр конструктивная схема и модель объекта управленя
| Вид материала | Документы |
- Задание 1 Цель: оценить значение сердечника для получения магнитного поля катушки, 33.68kb.
- Дефицит магнитного поля, 27.98kb.
- Домашнее задание по физике на 4 сессию Учебник, 55.57kb.
- Задачи урока: -обучения: продолжить формирование представлений о магнитном поле; рассмотреть, 35.34kb.
- Урок на тему «Магнитное поле Земли», 31.68kb.
- Лабораторная работа № Исследование магнитного поля модели сверхпроводникового индуктора, 75.13kb.
- А. С. Галюжин Осушка сжатого воздуха с помощью магнитного поля, 167.73kb.
- Источник меняющегося магнитного поля и. С. Кравченко1, А. Ю. Митягин2, М. В. Фесенко1,, 52.78kb.
- Разработка урока в 8-м классе "Магнитное поле. Линии магнитного поля", 33.77kb.
- Магнитное поле. Сила Ампера. Сила Лоренца. Явление электромагнитной индукции, 98.2kb.
Стабилизатор магнитного поля для измерителя ЯПР
Конструктивная схема и модель объекта управленя
М
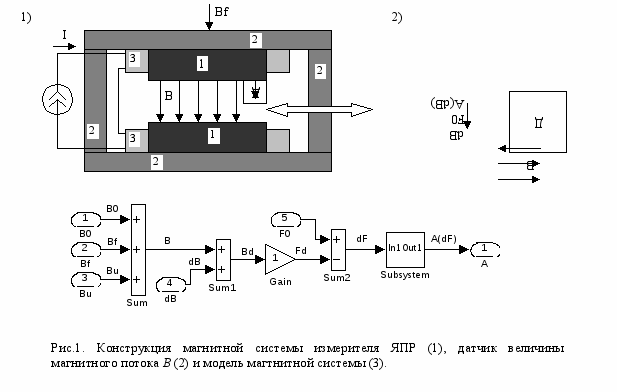агнитная система (рис.1,1) создает в зазоре между полюсами постоянных магнитов 1 с магнитопроводом 2 поток B. От величины B0, требуемой дли измерения сигналов ЯПР, его отклоняют (возмущают) изменения температуры и внешние воздействия Bf. Датчик Д (рис.1,2). измеряет точную величину поля В, что позволяет компенсировать возмущения поля Bf потоком управления Bu, создаваемым током I в обмотках 3. Датчик представляет собой узкополосный резонатор, собственная частота которого пропорциональна величине магнитного поля
Fd = Kd*Bd, (1) где Kd – физическая константа, определяющая зависимость частоты резонанса от величины поля, и Bd - величина потока, действующего непосредственно на датчик.
.Амплитуда сигнала датчика A максимальна при равенстве его собственной частоты Fd частоте внешнего генератора F0 и быстро убывает при отклонении (расстройке)
dF = F0 – Fd (2) частоты резонанса датчика Fd от частоты генератора F0.
Настройка генератора на резонанс позволяет измерять величину магнитного поля по частоте F0 с высокой точностью, определяемой точностью задания физической константы Kd и погрешностями измерениями частоты генератора F0.
Преобразование датчиком отклонений величины магнитного поля Bf от значения
B0 = (1/Kd)* F0, (3) заданного частотой генератора F0, в изменения амплитуды выходного сигнала A(dF) позволяет сформировать сигнал для автоматической компенсации возмущений поля Bf управлением Bu посредством тока I в обмотках 3.
Экстремальная САУ
С точки зрения ТАУ [1], магнитная система вместе с датчиком представляет собой объект управления с нелинейной экстремальной регулировочной характеристикой
y = N(x) = A(dF). (4)
Цель управления состоит в отыскании экстремума (максимума) и далее - в удержании настройки на экстремум как при противодействии возмущениям Bf, так и при программировании величины поля B0 регулировкой частоты генератора F0.
Средством для ее достижения является измерение крутизны наклона S=dN/dx регулировочной характеристики объекта и организация регулятора, обеспечивающего движение системы к желаемому значению крутизны S=0, соответствующему экстремуму регулировочной характеристики Экстремальная система автоматического управления ЭСАУ способна настраиваться как на максимум, так и на минимум регулировочной характеристики. Выбор того или иного экстремума зависит от знака ОС в контуре регулятора.
Методика и техника построения ЭСАУ магнитной системы для ЯПР
Для анализа и моделирования расстройку (и настройку) удобно измерять в относительных единицах – отношением расстройки dF к рабочей полосе частот датчика D,
x = dF/D. (5) Выход датчика удобно измерять как отношение текущего значения амплитуды A к ее максимальному значению Ar при резонансе
y = A/Ar. (6) Возмущения поля Bf также имеет смысл измерять как расстройку Xf. В ее состав можно включить две составляющих – случайные внешние возмущения Xfs и изменения уставки Xg, определяемые детерминированным управлением частотой генератора F0 при программировании величины поля B0 при помощи ЭСАУ.
Для измерения крутизны S к «медленной» (постоянной) составляющей входа X добавляют «быстрые» вариации dX(t), при этом x(t) = X + dX(t). В реальной системе (рис.1.1) датчик Д (рис.1,2) снабжен собственной обмоткой, позволяющей варьировать поле Bd в точке расположения самого датчика. (cумматор Sum1 на рис.1,3). Результатом быстрых вариаций входа являются «быстрые» вариации выхода dY(t) относительно «рабочей точки» - медленной составляющей выхода Y =Y(X), и поэтому y(t) = Y + dY(t)
С
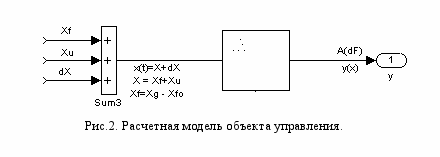
учетом всех описанных выше соображений, модель объекта управления рис.1,3 можно упростить и представить в виде, показанном на рис.2.
Аппроксимация регулировочной характеристики объекта управления.
На рис.3 показаны модели двух вариантов аппроксимации резонансной характеристики объекта безынерционной нелинейностью y = N(x). Аппроксимация Obj1
y = (½)(cos2x +1) при – pi/2
y = 0 при mod(x)>pi/2. (7) похожа на резонансную характеристику, а параболическая аппроксимация Obj2
y = 1 – x*2 при - 1
у = 0 при mod(x)>1 (8) удобна для аналитических исследований. Для модели Obj1 зависимость крутизны от расстройки описывает участок синусоиды
S(X) = - sin2X, -pi/>x>pi/2, (9) для модели Obj2 – прямолинейный отрезок
S(X) = - 2X, -1>x>1. (10) В модели для сравнения характеристик источник сигнала Ramp смещает рабочую точку X по характеристике y=N(x) с постоянной скоростью X(t)=t*1[t] и поэтому блоки дифференцирования правильно рассчитывают величину производной S(X)=dy/dt для каждого из объектов. Мультиплексор группирует сигналы y1, S1, y2, S2, а осциллограф S
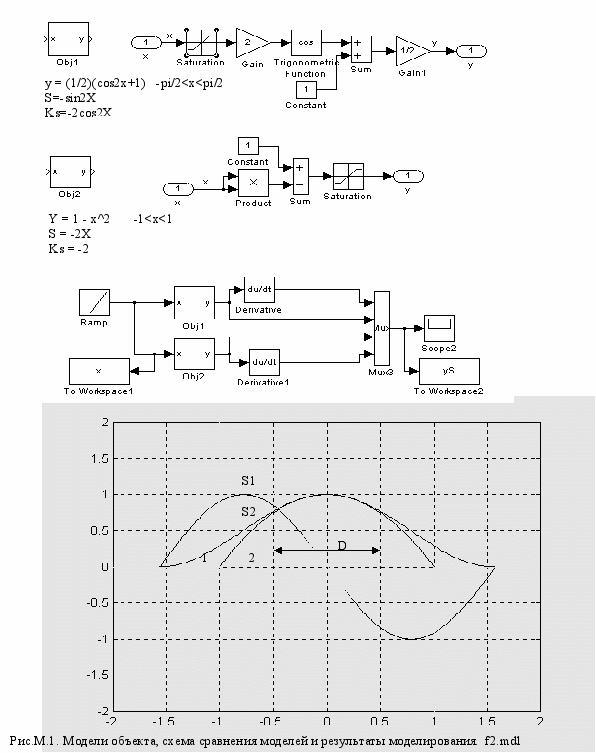
cope позволяет наблюдать результаты моделирования в виде временных графиков – осциллограмм. Блоки To Workspace адресуют переменные в рабочей области Matlab, и поэтому команда plot(x,yS) в командном окне Matlab дает графики регулировочных характеристик y=N(x) и их крутизны S(X) в зависимости от расстройки X, показанные в нижнем окне рис.3. Начало диапазона Х задает начальное значение в источнике сигнала, а конец – время интегрирования в позиции Simulation.
Регулировочные характеристики моделей 1 и 2 и графики зависимости крутизны от расстройки S1 и S2 хорошо совпадают вблизи экстремума (максимума) и заметно расходятся с увеличением расстройки Х.
Измерение крутизны нелинейности при помощи пробного сигнала.
Р
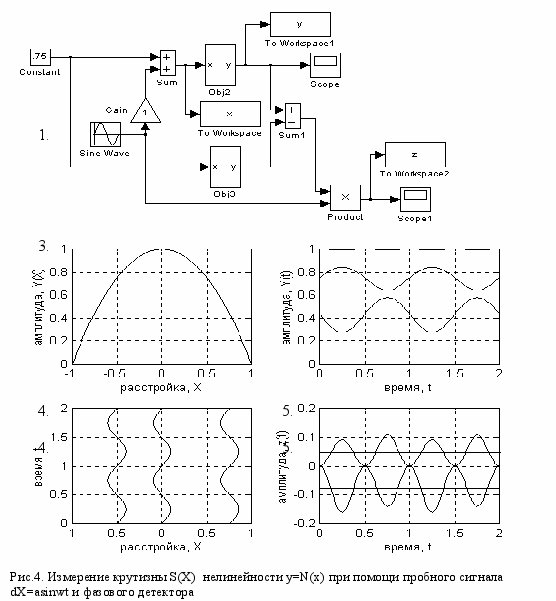
ис.4 иллюстрирует принцип и технику измерения крутизны характеристики S(X) = dN/dx нелинейности y=N(x) при помощи пробного сигнала dX(t) = asinwt и фазового детектора ФД на блoке перемножения Product. В модели рис.4,1 к постоянной составляющей расстройки X = Const добавлены вариации dX = asinwt (генератор Sine Wave, делитель Gain и сумматор Sum ). Сигнал x(t) = X + dX(t) для Х=-0,5, 0 и 0,75 (поз.4) поступает на вход нелинейности Obj2 с характеристикой y=N(x) (поз.2), сигналы на выходе которой y(t) = N[x(t)], представленны осциллограммами поз.3. Эти осциллограммы наглядно демонстрируют зависимость формы, амплитуды и фазы приращений выходного сигнала нелинейности dY(t) от расстройки X. Амплитуду и фазу линейной составляющей приращений выхода с частотой пробного сигнала определяет соотношение
dY(t) = S(X)*a*sinwt (11) Эта составляющая сигнала с выхода нелинейности несет информацию о крутизне в виде амплитуды A1= [S(X)*a], причем знак крутизны S(X) определяет фазу сигнала (11).
Для расчета приращений выхода (11) в модели рис.4.1 использованы второй нелинейный блок Obj3 и сумматор Sum1.
Фазовый детектор
Фазовый детектор ФД должен выделить полезную информацию о крутизне нелинейности, представляемую сигналом (11). Это можно осуществить путем умножения выходного сигнала нелинейности на опорный сигнал Хоп = sinwt, синфазный с пробным сигналом dX = asinwt.
Осциллограммы рис.4,5 представляют сигналы на выходе фазового детектора ФД на блоке перемножения Product - результат умножения приращений выхода dY(t) на опорный сигнал sinwt
z(t) = dY*sinwt~Sa*(sinwt)2=(Sa/2)*(1-cos2wt)=
=Sa/2 – (Sa/2)cos2wt. (12) Постоянная составляющая в его составе
Z = Sa/2 (13) непосредственно представляет крутизну характеристики S(X) с коэффициентом пропорциональности a/2. Величина этой постоянной составляющей показана сплошными линиями для расстроек Х=-0,5 и 0,75.
Р
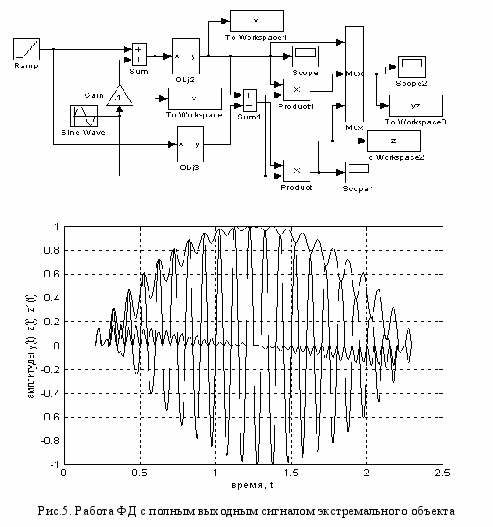
ис.5 представляет работу ФД с полным выходным сигналом объекта y(t)=Y+dY(t). Источник линейного сигнала медленно смещает рабочую точку вдоль оси , начиная с расстройки Х0 = - 1,25 за нижним пределом рабочего диапазона до Хв = 2,5 за его верхним пределом. Блок Product1 умножает выход y(t)=Y+dY(t) на опорный сигнал sinwt. Мультиплексор Mux группирует сигналы выхода объекта y(t) и выходные сигналы двух фазовых детекторов на блоках перемножения Product и Product1.
Умножение постоянной составляющей выходного сигнала Y на опорную синусоиду дает синусоидальныйсигнал
Z1(t)=Ysinwt (14) c частотой, равной частоте опорного сигнала и большой амплитудой Y, намного превышающей постоянную составляющую (13), представляющую крутизну S(X). Сигнал (14) является помехой и должен быть достаточно хорошо подавлен при измерении крутизны и формировании управления на основе полезной постоянной составляющей (13).
Фильтрация сигнала перед входом фазового детектора
Выделить из выходного сигнала объекта y(t) = Y + dY(t) информативные вариации dY(t) и подавить постоянную составляющую Y на входе ФД позволяет фильтр типа дифференцирующей RC–цепочки с передаточной функцией вида
Wф(s) = Ts/(Ts + 1) (15) Уменьшение влияния возникающего при этом фазового опережения основной гармоники вариаций выхода dY(t) на снижение коэффициента передачи ФД можно обеспечить таким же опережением по фазе опорного сигнала.
С той же целью можно использовать режекторный фильтр, подавляющий только сигнал основной частоты помехи. В работе [2] для этого был успешно использован двойной Т-образный RC-фильтр, подавлявший одновременно помеху (14) и наводку с частотой сети 50 Гц, использованную в качестве пробного и опорного сигналов.
Фильтрация сигнала перед входом ФД помогает улучшить его работу и упрощает задачу фильтрации его выходного сигнала.
Фильтрация выхода фазового детектора
Д
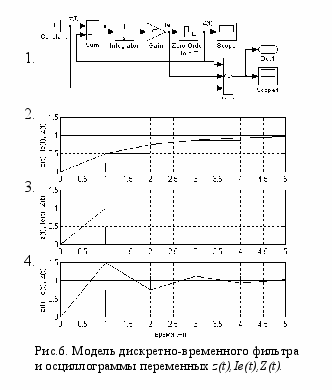ля выделения информативной медленной (постоянной) составляющей (13) и подавления помехи (14) на выходе ФД можно использовать любой низкочастотный фильтр, например интегрирующую RC-цепочку с передаточной функцией апериодического звена. Однако аналоговые фильтры не обеспечивают полного подавления помехи и вносят фазовое запаздывание, ухудшающее устойчивость и качество системы регулирования с ОС [3].На рис.6,1 показана модель дискретно-временного фильтра DTF, работающего по принципу импульсной САУ интегратором с конечной длительностью переходного процесса, равной одному периоду квантования сигналов по времени.
Сумматор Sum вычисляет отклонение текущего непрерывного сигнала z(t) на интервале (n-1)T
e(t) = z(t) – Z[n-1)T] (16) Результат интегрирования отклонения в течение очередного такта с коэффициентом усиления k = 1/T (сигнал Ie(t) ) поступает на вход УВХ. По окончании такта при t = nT УВХ. запоминает конечный результат интегрирования отклонения e(t) на очередном временном интервале Ie(nT) для следующего такта.
Принцип действия фильтра иллюстрируют осциллограммы переменных Ie(t) и Z(t) (поз. 2-4) при отработке единичной ступеньки z(t) для некоторых значений коэффициента усиления интегратора Ки .При Ки < 1/T (Ки=0,5/T для графиков поз.2) реакция фильтра похожа на переходную характеристику апериодического звена. При Kи>1/T (Ки = 1,5(1/T) для поз.4) становится колебательной, при Ки = 2/T колебания становятся незатухающими, при дальнейшем увеличении Kи – расходятся, система становится неустойчивой.
П
ри Kи = 1/T (поз.3) переходной процесс заканчивается за один такт Т.
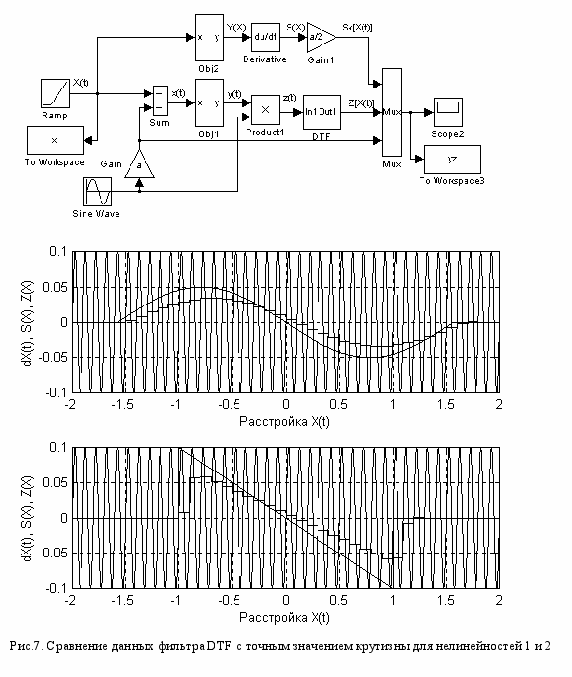
В модели на рис.7 фильтр DTF фильтрует полный сигнал фазового детектора z(t) Преобразователи Obj2 и Derivative верхней цепочки рассчитывают крутизну S(X) ,а блок Gain1 умножает ее на коэффициент a/2 , соответствующий коэффициенту передачи постоянной составляющей (13) фазового детектора.
Осциллограммы обнаруживают:
- DTF вычисляет только величину постоянной составляющей входного сигнала и подавляет все остальные компоненты с нулевым средним значением в течение такта.
- Вычисление очередного значения крутизны Z(X) запаздывает на один такт, равный периоду пробного сигнала, что обусловлено принципом работы DTF.
- Рассчитываемое фильтром значение Z(X) меньше величины крутизны Sk(X)=(a/2)*S(X) из-за высокой скорости сканирования характеристики y=N(X) сигналом X(t) по сравнению с частотой w пробного сигнала dX=asinwt. С увеличением частоты w и амплитуды a эта погрешность уменьшается.
Блок МДМ
С
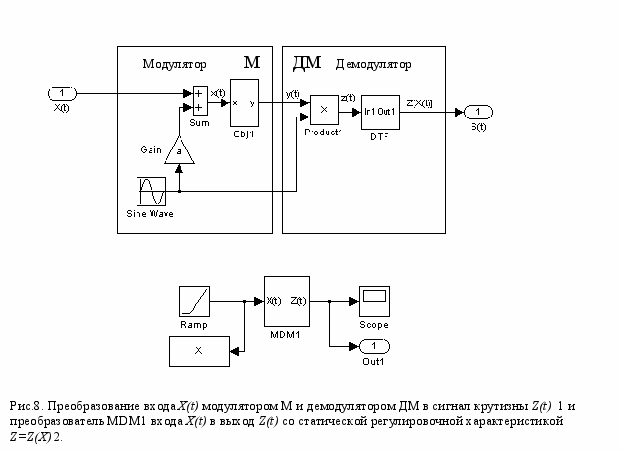
учетом подавления постоянной составляющей Y весь блок, включающий источник пробного сигнала, его суммирование с входным сигналом X(t) и нелинейность y = N(x) (рис.8,1), можно рассматривать как модулятор М несущей sinwt входным сигналом X(t). В соединении с ФД и фильтром – демодулятором ДМ они образуют канал «модулятор-демодулятор» МДМ, преобразующий входной сигнал X(t) в сигнал Z(t) , представляющий крутизну нелинейности S[X(t)]. Блок МДМ на рис.8.2 представляет это преобразование.
Зависимость выхода Z от входа X преобразователя МДМ в статике описывает обычная статическая, в общем случае - нелинейная регулировочная характеристика
Z=Nz(X) = (a/2)*S(X), (17) где
S(X) = dN/dX (18) – крутизна нелинейности) y = N(x).
Н
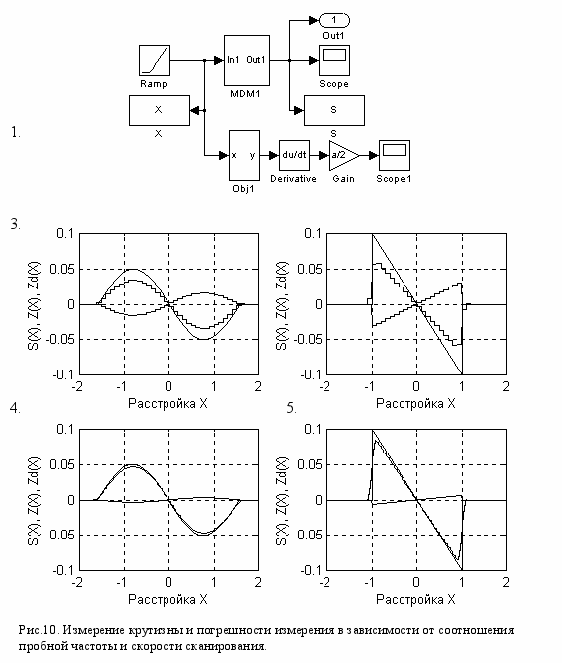
а рис.9.1 показана схема для изучения преобразования блоком МДМ «медленного» входного сигнала X(t) в сигнал крутизныZ(t) и динамических погрешностей этого преобразования в зависимости от соотношения между скоростью сканирования нелинейности сигналом X(t) и частотой w пробного сигнала. Нижняя цепочки рассчитывает точную величину производной и сигнала (17). Графики 2 и 4 представляют результаты моделирования для аппроксимации объекта моделью Obj1, графики 3 и 5 – моделью Obj2..Скорость сканирования для всех графиков одинакова и составляет 1 у.е. в сек. Для графиков 2 и 3 частота пробного сигнала равна 10 Гц, для графиков 4 и 5 – 50 Гц. Графики погрешности получены при амплитуде пробного сигнала а=0. Они обнаруживают, что с увеличением относительной скорости сканирования ФД воспринимает «медленный» сигнал сканирования как «быстры» пробный и рассчитывает соответствующую ему компоненту производной со знаком «минус».
Сравнение графиков показывает, как с увеличением частоты пробного сигнала уменьшается погрешность измерения крутизны.
Блок МДМ как объект регулирования
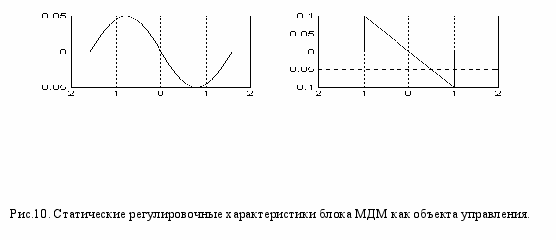
Блок МДМ представляет преобразование «медленного» входа X(t) в сигнал крутизны Z[X(t)]. С точки зрения организации регулятора, блок МДМ можно представить как объект регулирования, преобразование «медленного» входа которого X(t) в «медленный» выход Z(t) описывает безынерционная регулировочная характеристика Z = Nz(X) (17). Ее форму для двух вариантов аппроксимации нелинейности y = N(x) представляют графики на рис.10.
С
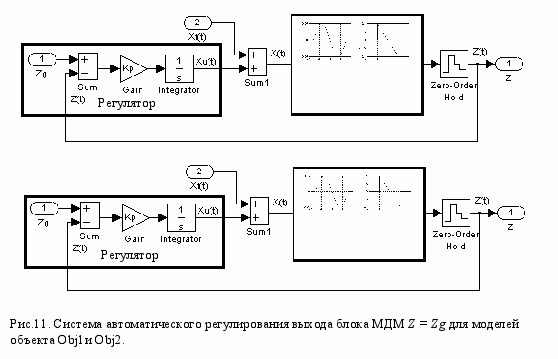
хемы регуляторов для обоих вариантов аппроксимации тождественны и представлены на рис.11.
Следуя общему принципу построения регуляторов с ОС, выходной сигнал объекта Z(t) следует сравнивать с уставкой Zg и использовать сигнал ошибки e(t)=Zg–Z(t) как входной для устройства управления УУ (блоки Gain и Integrator) в составе регулятора. В принципе система может отрабатывать любую уставку крутизны в рабочей области.
Настройке на экстремум соответствует уставка Zg=0. На какой из экстремумов – min или max будет настраиваться ЭСАУ, определяет знак коэффициента Kp усилителя Gain в УУ. Для настройки на max он должен быть отрицательным.
Регулятор настройки ЭСАУ
Интегральный закон регулирования
Wp(s) = Kp/s (19) обеспечивает нулевую установившуюся ошибку.
Einf = 0. (20) Коэффициент усиления регулятора Kр определяет скорость движения к экстремуму как
Vx = dX(t)/dt = Kp*S(X), (21) и поэтому интегральный регулятор технически реализует известный градиентный метод наискорейшего спуска (подъема).
Выход регулятора Xu(t) компенсирует любые возмущения поля Xf(t), вызываемые как неконтролируемыми внешними воздействями на магнитную систему, так и программированием величины поля посредством подстройки частоты задающего генератора.
Линеаризация и анализ ЭСАУ
Для параболической аппроксимацией нелинейности Obj2 в пределах рабочей области зависимость выхода от входа – линейная
S(X) = - 2X. (22) Нелинейный блок САР S(X) можно заменить усилителем с коэффициентом усиления
Kn = (a/2)*(-2) = a, (23) равным амплитуде пробного сигнала. САР оказывается линейной, и для ее анализа можно использовать хорошо известные методы и результаты теории линейных систем.
При небольших расстройках регулировочная характеристика блока МДМ для Obj1 близка к характеристике блока с Obj2 (22). Ее можно линеаризовать, заменив коэффициентом (23), и использовать линейную ТАУ для оценки динамики нелинейной САР.
В общем случае эквивалентный коэффициент усиления при линеаризации экстремальной характеристики равен ее второй производной по входной переменной.
Устойчивость и качество ЭСАУ
При небольших значениях коэффициента усиления регулятора контур ОС ЭСАУ представляет собой просто интегратор, охваченный отрицательной обратной связью с общим коэффициентом усиления K = (Kn*Kp). Такая линейная система устойчива, а реакцию ее выхода X(t) на вход Xf(t) описывает передаточная функция
W(s) = X(s)/Xf(s) = Ts/(Ts + 1), (24) где T = 1/K – постоянная времени. САР обладает астатизмом 1 порядка, и поэтому при отработке ступенчатых воздействий установившаяся ошибка равна нулю (20), а при отработке сигналов, изменяющихся с постоянной скоростью Vf = const, равна
EVinf = Vf/K. (25). Поэтому для повышения быстродействия и динамической точности регулирования общий коэффициент усиления петли ОС следует увеличивать.
Предел увеличения К определяют условия обеспечения устойчивости системы как импульсной САР. Блок МДМ измеряет крутизну в течение одного периода пробного сигнала и выдает это значение в течение следующего периода, что представляет УВХ в схемах САР на рис.11. Вместе с интегратором в УУ и УВХ контур ОС регулятора оказывается похож на контур ОС дискретно-временного фильтра DTF Таким образом, динамические свойства всего регулятора определяют те же обстоятельства, которые описаны ранее – при рассмотрении DTF.
В отличие от DTF, фаза импульсов которого жестко связана с фазой пробного и опорного сигналов, возмущения могут прикладываться к магнитной системе в произвольные моменты времени. Быстрые возмущения «медленной» переменной X(t) блок МДМ воспринимает как компонент «быстрого» пробного сигнала и добавляет к сигналу крутизны Z[X(t)] дополнительный сигнал, чего не учитывает описание блока МДМ только его статической характеристикой. Кроме этого, при больших возмущениях проявляется нелинейность системы, что сказывается на ее движении к экстремуму.
Испытания и характеристики ЭСАУ
На магнитную систему могут воздействовать возмущения, скорость которых определяется тепловыми процессами, флуктуации магнитного поля Земли, перемещения магнитных материалов, наводки от силовой сети и трансформаторов, импульсные поля при включении и выключении различной аппаратуры. Рабочий диапазон датчика потока достаточно мал, и поэтому требуется определить пределы возмущений, не нарушающих нормальной работы ЭСАУ. Определенные вопросы возникают и в отношении з
апуска системы в рабочее состояние.
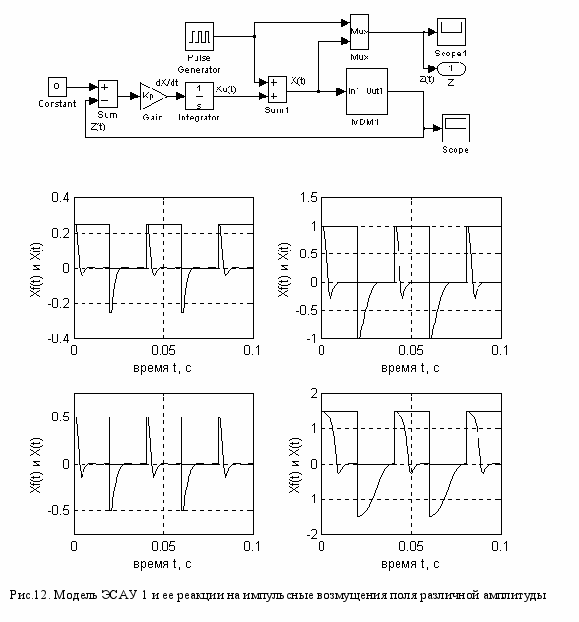
На рис.12 показана модель ЭСАУ для объекта Obj1и приведены результаты ее испытаний при возмущениях поля в виде прямоугольных импульсов различной амплитуды. Частота пробного сигнала принята равной 1кГц, амплитуда а = 0,1 у.е., коэффициент усиления регулятора Кр =.5000, общий коэффициент усиления в петле ОС К=500.
На графиках показаны возмущение Xf(t) в виде однополярных прямоугольных импульсов частотой 25 Гц с амплитудой 0,25, 0,5. 1,0 и 1,5 у.е. и реакция поля в зазоре магнитной системы X(t) в результате компенсации возмущения управлением Xu(t).
Для небольших возмущений переходной процесс заканчивается в течение 4-6 тактов пробного сигнала, что составляет около 5-10 мс. При амплитуде помехи 1,0 у.е. длительность переходного процесса несколько увеличивается. Импульс амплитудой 1,5 у.е. отбрасывает рабочую точку почти на границу рабочего диапазона. Однако и при таком сильном возмущении ЭСАУ возвращается к экстремуму, хотя и затрачивает на это больше времени.
На рис.13 показаны схема испытания ЭСАУ линейным сигналом 1 и его результат 2, а также отработка системой синусоидального возмущения 3.
В
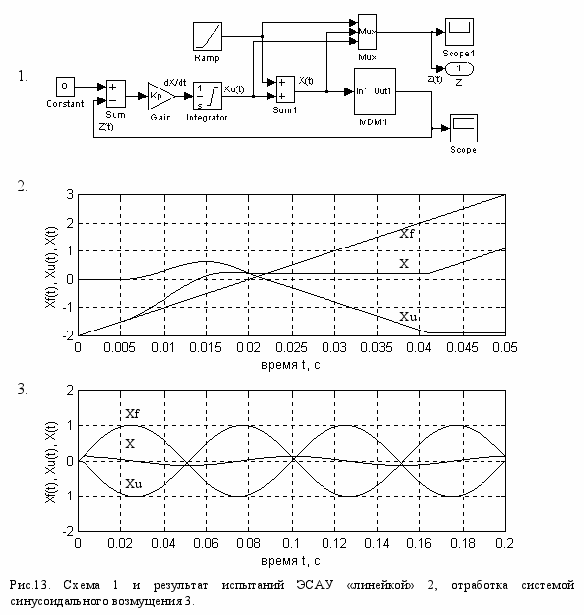
ыходной сигнал генератора (поз.2) изменяется от начального значения Xf0 = -2 у.е. со скоростью 100у.е./с. При t~0,005 с он достигает нижней границы рабочего диапазона ЭСАУ. Начинается процесс входа системы в рабочий режим. К моменту времени t~0,017 с переходной процесс заканчивается, возмущение компенсируется управлением с обратным знаком, и устанавливается скоростная ошибка, равная 0,2 у.е. При t~0,04 c интегратор управляющего устройства достигает насыщения, работа ЭСАУ прекращается и поток магнитной системы начинает расти вслед за возмущением.
На рис.13,3 приведены осциллограммы отработки синусоидального возмущения с частотой w = 10 Гц и амплитудой a = 1 у.е. Управление Xu(t) примерно в 10 раз уменьшает амплитуду пульсаций поля X(t) по сравнению с амплитудой возмущения Xf(t).
Заключение
- Анализ и моделирование ЭСАУ стабилизатора магнитного поля для измерителя ЯПР показывают, что создание системы с требуемыми весьма высокими характеристиками является задачей, решаемой предлагаемыми современными средствами.
- Результаты анализа и моделирования дают методическую основу для теоретических расчетов, проектирования, конструирования, настройки и испытаний практических ЭСАУ для любых экстремальных объектов управления, в частности – стабилизаторов магнитного поля различного назначения и применения.
- Для более полного изучения возможностей ЭСАУ требуется анализ и моделирование ее работы с большой амплитудой вариаций поля, заметно превышающей рабочий диапазон датчика потока, а также работы ФД с опорным сигналом в виде прямоугольных импульсов. Такие решения давно известны и описаны [2], однако для отработки алгоритмов и технических решений на современном уровне целесообразно их дополнительное изучение.
- Реализация ЭСАУ на основе микропроцессорного контроллера в соединении с ПК позволит создать удобный и надежный современный прибор, отвечающий всем методическим, техническим и эргономическим требованиям
Литература:
- Г.Н.Алексаков, В.В.Гаврилин, В.А.Федоров. Персональный аналоговый компьютер/ - М.; Энергоатомиздат, 1992, с.с.181-191.
- Г.Н.Алексаков, Б.М.Жиряков,Е.Д.Проценко, В.Ф.Семенов. Стабилизатор магнитного поля/ Труды МИФИ, М.,1959.