Магнитное поле. Сила Ампера. Сила Лоренца. Явление электромагнитной индукции
| Вид материала | Документы |
- Требования по теме «Магнитное поле» Перечень элементов содержания, проверяемых на едином, 12.18kb.
- B. Как изменится сила Ампера, действующая на проводник, если силу тока уменьшить, 34.54kb.
- Самостоятельная работа Кредитная стоимость Лекции 36 Число недель, 154.88kb.
- Задачи, 847.5kb.
- Магнитные явления, 181.73kb.
- А. С. Галюжин Осушка сжатого воздуха с помощью магнитного поля, 167.73kb.
- Штейн Б. М. Взаимосвязь изучения электромагнитной индукции и электромагнитного поля, 136.4kb.
- 4. Сила тяжести. Сила, возникающая при деформации. Вес. Сложение сил. Сила трения, 99.78kb.
- Магнитное поле. Электромагнитная индукция. Самоиндукция. Часть, 84.18kb.
- Магнитное поле. Электромагнитная индукция. Самоиндукция. Часть, 53.53kb.
Магнитное поле. Сила Ампера. Сила Лоренца. Явление электромагнитной индукции.
1. Взаимодействие между электрическими токами, называемое магнитным, осуществляется посредством магнитного поля. Основной характеристикой магнитного поля является вектор магнитной индукции В.
За направление вектора магнитной индукции принимают направление нормали к рамке с током, имеющей возможность свободно ориентироваться в магнитном поле. Это направление совпадает с направлением магнитной стрелки в поле, т. е. с направлением линии, проведенной от южного полюса стрелки к северному.Модуль вектора магнитной индукции определяется отношением максимального момента сил, действующих на рамку (контур) со стороны магнитного поля, к произведению силы тока в нем на его площадь:
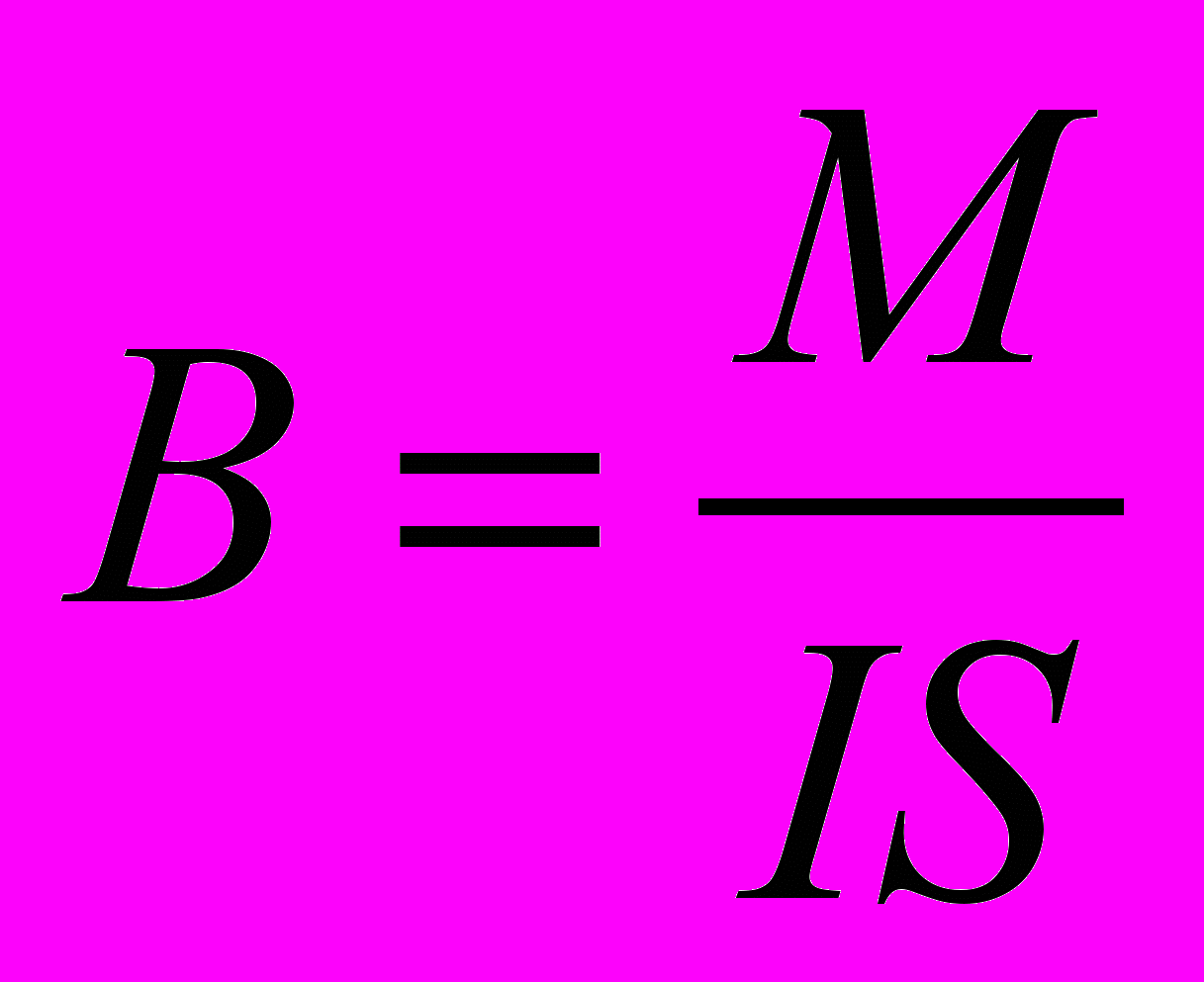
2. По закону Ампера на отрезок проводника с током длиной ℓ со стороны магнитного поля действует сила, модуль которой равен
FA =BΔℓsin α,
где α— угол между направлением тока в проводнике и вектором магнитной индукции В. Направление силы FA определяется по правилу левой руки.
3. На движущуюся заряженную частицу действует сила Лоренца, модуль которой равен
FA =B q0 υ sin α,
где а — угол между скоростью частицы υ и вектором магнитной индукции В. Сила Лоренца перпендикулярна скорости частицы, поэтому не совершает работы. Эта сила изменяет направление скорости частицы, но не меняет ее кинетической энергии.
4. Все тела в магнитном поле намагничиваются, т.е. сами создают магнитное поле. Отношение вектора магнитной индукции в однородной среде В к магнитной индукции в вакууме Во называют магнитной проницаемостью, она характеризует магнитные свойства вещества: μ=В/В0
У большинства веществ магнитные свойства выражены слабо.Лишь у ферромагнитных тел, к которым относится железе, магнитная проницаемость очень велика (μ>1) и зависит от магнитной индукции. Хотя ферромагнетиков сравнительно немного, они имеют очень большое практическое значение, так как позволяют в сотни раз увеличивать магнитную индукцию поля без затрат энергии.Ферромагнитные материалы применяют для изготовления сердечников трансформаторов, генераторов, электродвигателей и т. д., а также для изготовления постоянных магнитов. Ферромагнитные сердечники используют в качестве ячеек памяти в ЭВМ.
5
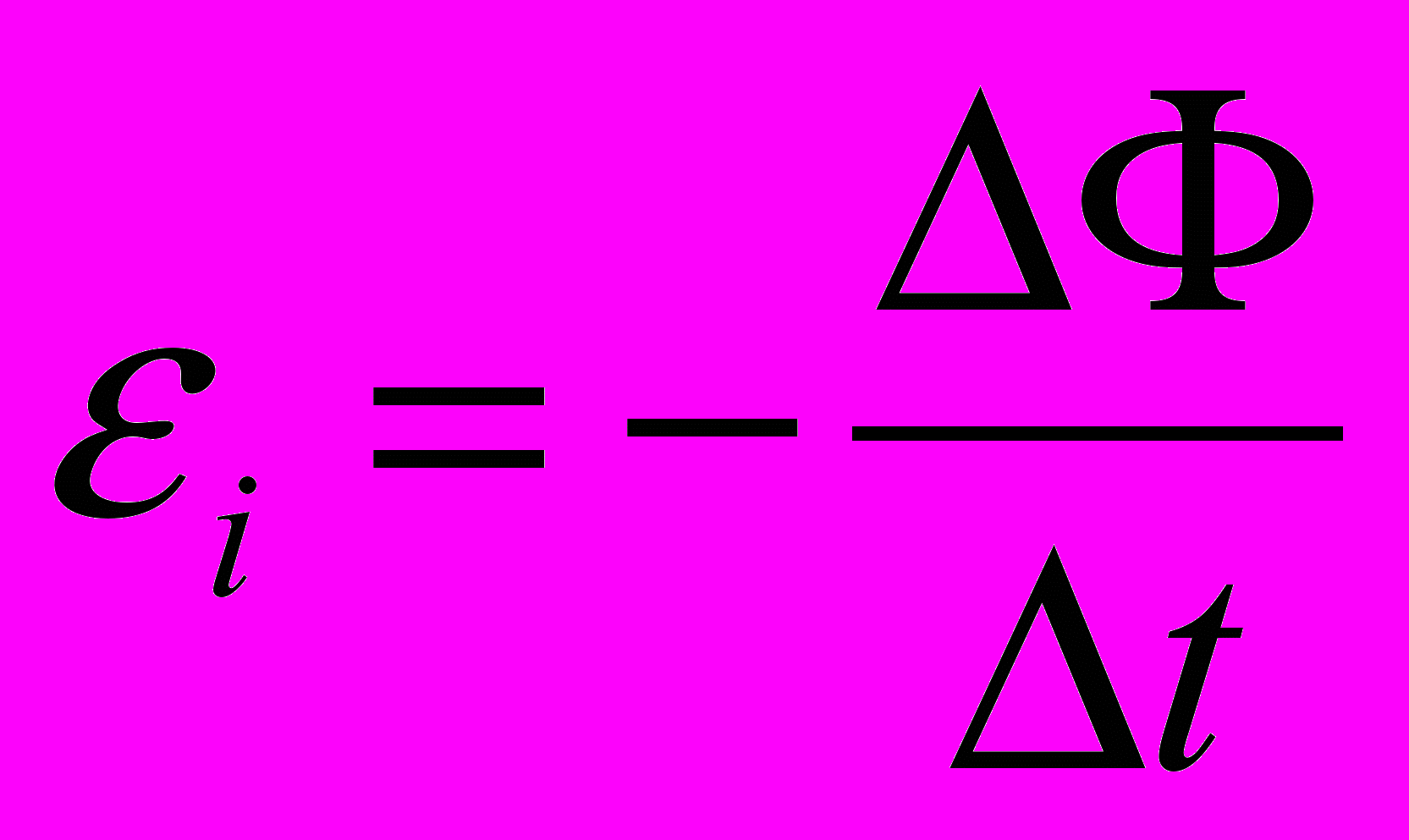 .Явление электромагнитной индукции, открытое М. Фарадеем, состоит в возникновении ЭДС индукции в замкнутом контуре при изменении магнитного потока через площадь, ограниченную этим контуром. Согласно закону электромагнитной индукции ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока, взятой со знаком «минус»:
.Явление электромагнитной индукции, открытое М. Фарадеем, состоит в возникновении ЭДС индукции в замкнутом контуре при изменении магнитного потока через площадь, ограниченную этим контуром. Согласно закону электромагнитной индукции ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока, взятой со знаком «минус»:Здесь Ф = ВnS — поток магнитной индукции через площадь контура S, Вп — проекция вектора магнитной индукции на нормаль к контуру. Знак «минус» объясняется правилом Ленца, определяющим направление индукционного тока: индукционный ток в замкнутом контуре имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать то изменение магнитного потока, которое порождает данный ток.
6.В неподвижном проводнике сторонней силой, создающей ЭДС индукции, является вихревое (индукционное) электрическое поле, порождаемое переменным магнитным полем. В движущемся проводнике источником ЭДС индукции является магнитная сила Лоренца, действующая на движущиеся вместе с проводником заряженные частицы. При движении проводника длиной со скоростью υ в однородном магнитном поле с индукций В возникает ЭДС индукции:
.
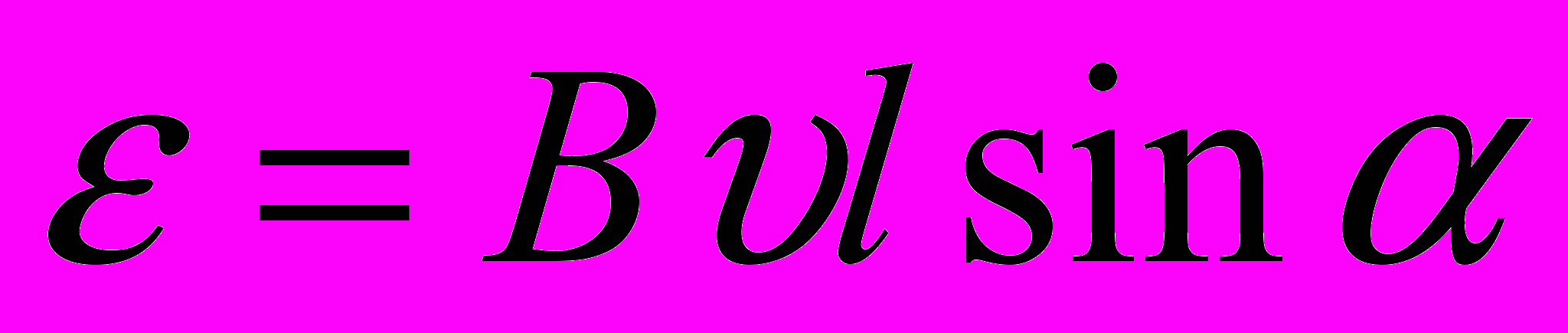
7.Важный частный случай электромагнитной индукции — самоиндукция. При самоиндукции изменяющееся магнитное поле индуцирует ЭДС в том проводнике, по которому течет ток, создающий это поле.
ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока в проводнике:

Коэффициент пропорциональности L называют индуктивностью. Индуктивность зависит от свойств проводника, а также от свойств среды, в которой находится проводник. Измеряют ее в Генри: 1Гн= 1Вс/А
8. Энергия магнитного поля тока равна той работе, которую должен совершить источник, чтобы создать данный ток.
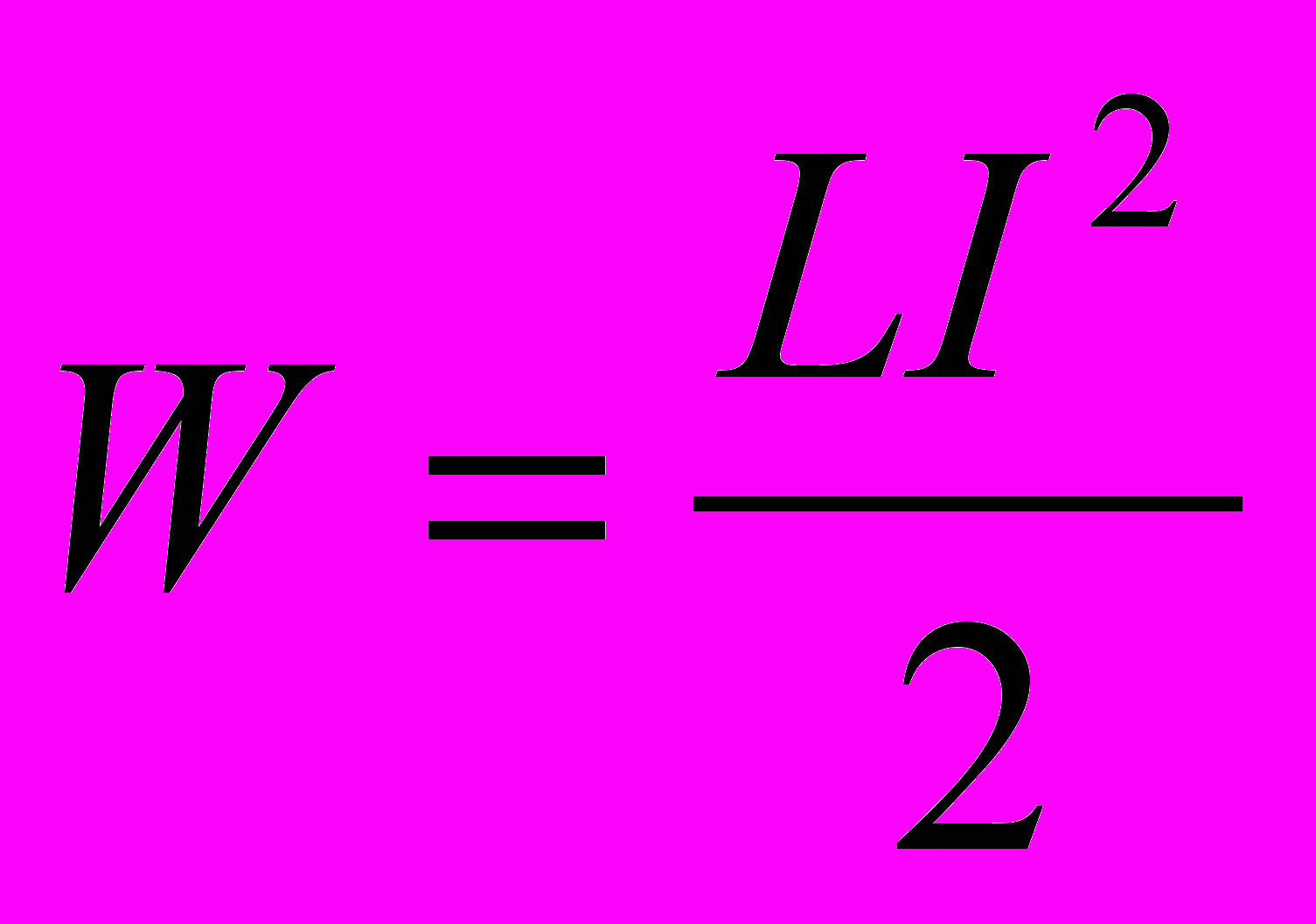
8. Магнитное поле без электрического, так же как электрическое без магнитного, могут существовать только в определенной системе отсчета. Они являются проявлением единого целого — электромагнитного поля, особой формой существования материи. Фундаментальное свойство электромагнитного поля: изменяясь во времени, магнитное поле порождает переменное электрическое поле и наоборот.
Примеры решения задач « Магнитное поле. Электромагнитная индукция».
1. Какова индукция магнитного поля, в котором на прямой провод длиной 10 см, расположенный под углом 30° к линиям индукции, действует сила 0,2 Н, когда по нему проходит ток 8 А? 1)0,2Тл; 2) 0.5 Тл: 3) 5 Тл; 4) 0,8 Тл; 5)1,2Тл.
Решение. Индукцию определим из закона Ампера: F = ІBℓsin α.
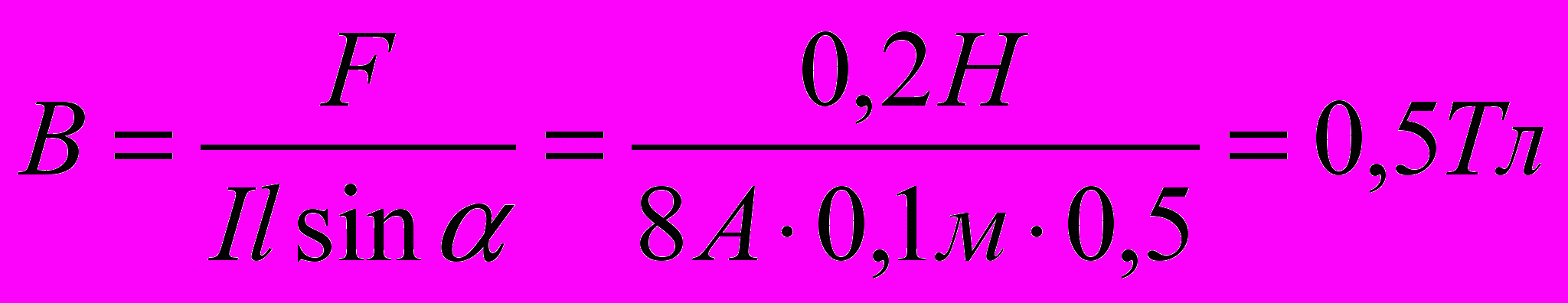
2. Если угол 60° между вектором магнитной индукции однородного магнитного поля и прямолинейным проводником с током, помещенным в это поле, уменьшить в 2 раза, то сила Ампера, действующая на проводник,
- увеличится в 2 раза; 2) уменьшится в 2 раза; 3)увеличится в
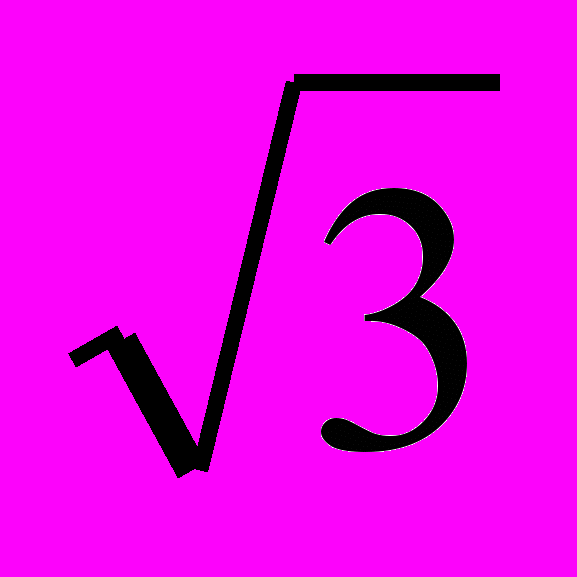 раз; 4)уменьшится в
раз; 4)уменьшится в 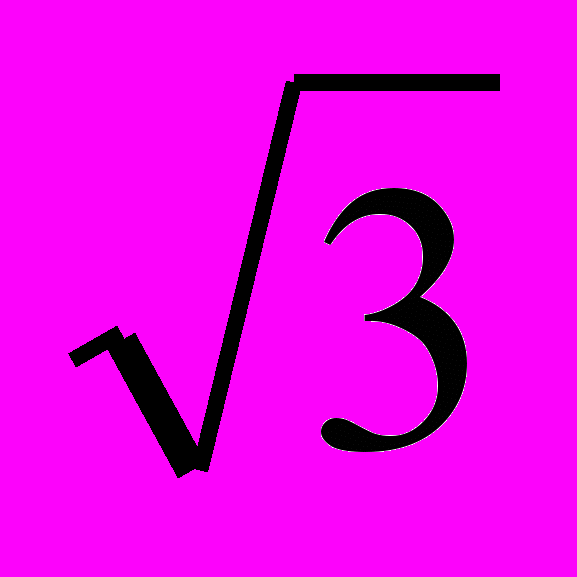 раз;
раз;
Решение.Сила Ампера подсчитывается по формуле F = ІBℓsin α. Для α 1 = 60° сила равна
F1 =
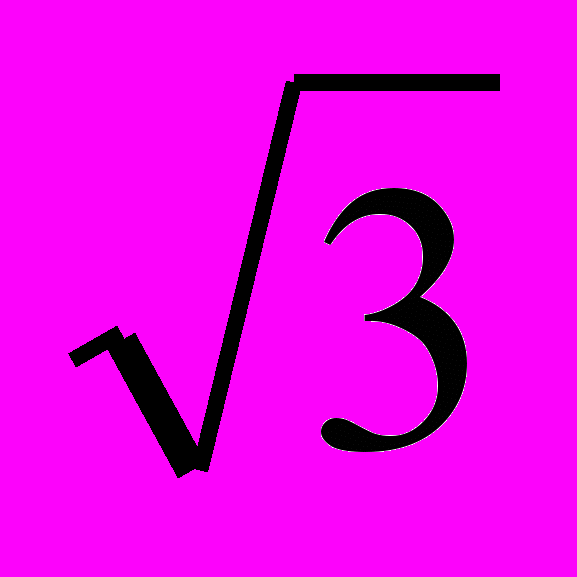 /2 IBℓ, а для α 2 = 30°: F2 = 1/2 IBℓ . Таким образом, при уменьшении угла сила уменьшается в
/2 IBℓ, а для α 2 = 30°: F2 = 1/2 IBℓ . Таким образом, при уменьшении угла сила уменьшается в 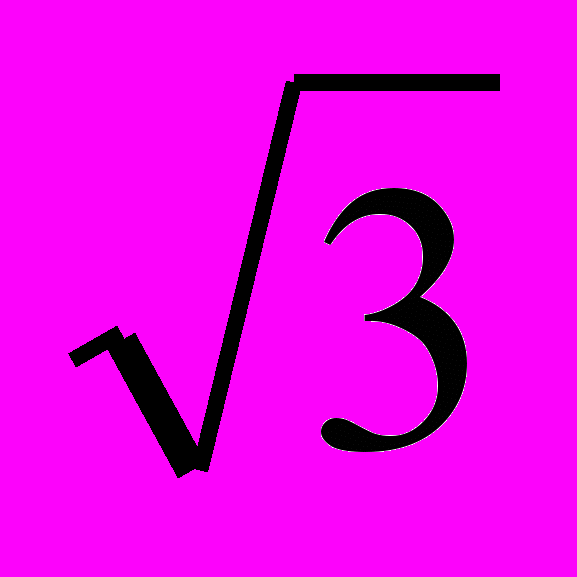 раз.
раз. 3. Для того чтобы сила, действующая со стороны однородного магнитного поля с индукцией 0,1 Тл на прямолинейный проводник длиной 4 м, причем проводник расположен под углом 30° к полю, была равна 1 Н, по проводнику следует пропустить ток 1)_5А; 2) 4 А; 3) 0,2 А; 4) 0,4 А; 5) 2 А.
F 1H
Решение. Из закона Ампера I = = = 5 А.
Blsina О,1Тл·4м·О,5
4. Линейный проводник длиной 60 см при силе тока в нем 3 А находится в однородном магнитном поле с индукцией 0,1 Тл. Если проводник расположен по направлению линий индукции магнитного поля, то на него действует сила, модуль которой равен: 1)0,18Н; 2) 18,00 Н; 3) 2,00 Н; 4) 0,30 Н; 5) 0.00 Н.
Решение. На проводник, в котором ток течет вдоль магнитного поля сила Ампера не действует.
5. Линии индукции однородного магнитного поля с индукцией 4 Тл пронизывают рамку под углом 30° к ее плоскости, создавая магнитный поток, равный 1 Вб. Чему равна площадь рамки?
1) 0.5 м2: 2) 1,0 м2; 3) 1,5 м2; 4) 2,0 м2; 5) 4,0 м2.
Решение. Поток магнитной индукции через площадку находится по формуле Ф = BS cos α, здесь α — угол между перпендикуляром к площадке и вектором В. Это угол, дополняющий заданный до 90°.
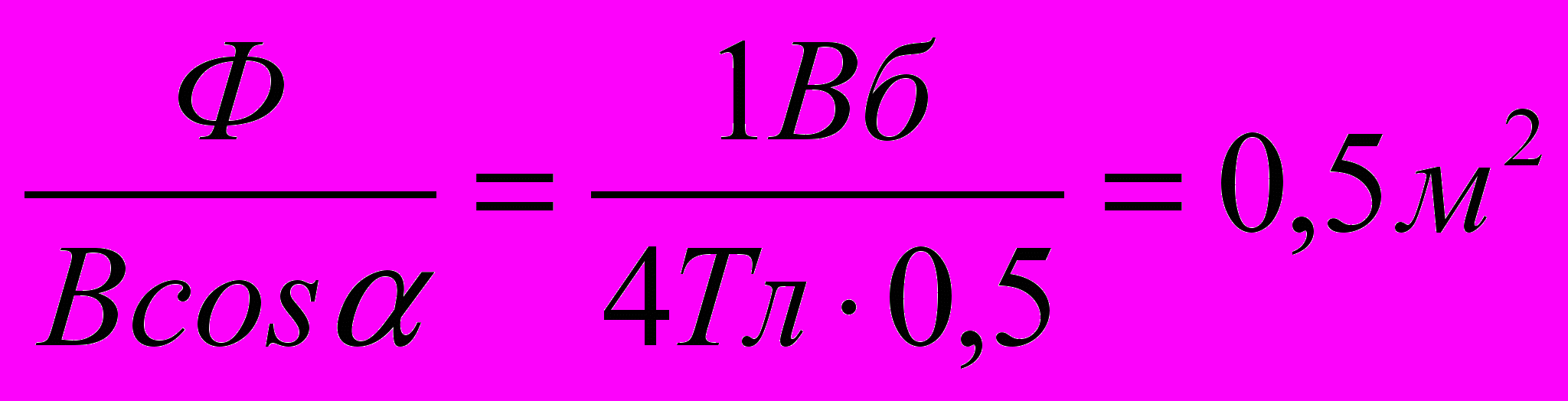
Поэтому S =
6. Магнитный поток через соленоид, содержащий 500 витков провода, равномерно убывает со скоростью 60 мВб/с. Определить ЭДС индукции в соленоиде:
1)12 В; 2) 15 В; 3)150 В? 4) 120 В; 5)3QB.
Решение. ЭДС в каждом витке численно равна скорости убыли тока. ЭДС в соленоиде в N раз больше ЭДС в одном витке
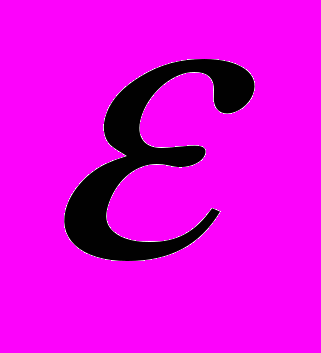 = 60 • 10 -3 Вб/с· 500 = 30 В.
= 60 • 10 -3 Вб/с· 500 = 30 В.7. ЭДС индукции, возникающая в замкнутом контуре, если магнитный поток, пронизывающий контур, равномерно уменьшился с 10 Вб до 2 Вб за 2 с, численно равна:
1
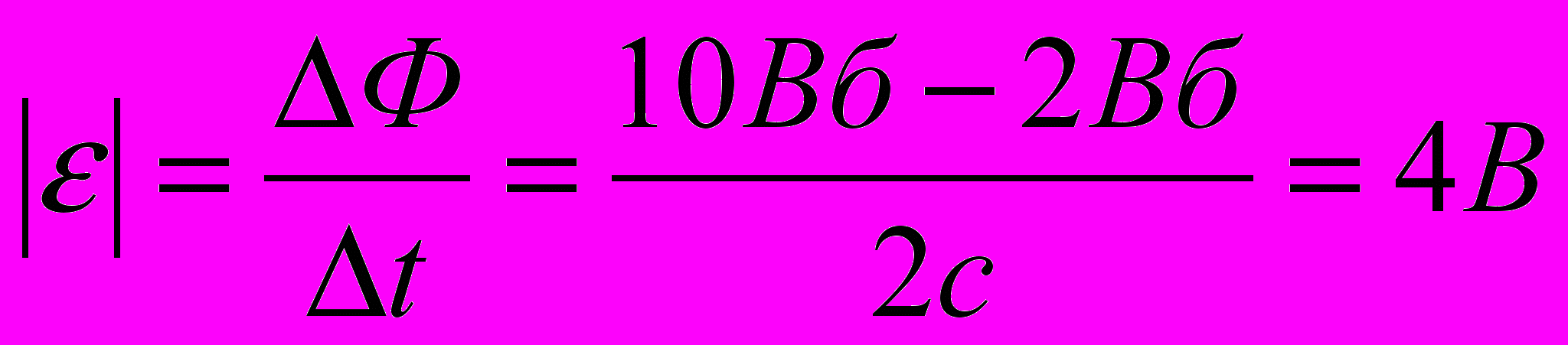 ) 4В; 2) 2 В; 3)8 В; 4) 0,4 В; 5) 6 В.
) 4В; 2) 2 В; 3)8 В; 4) 0,4 В; 5) 6 В.Решение. По основному закону электромагнитной индукции:
8. Чему равна индуктивность катушки, если за 0,5 с ток в цепи изменился от 20 до 5 А? При этом ЭДС самоиндукции на концах катушки равна 24 В.
1)0,4Гн; 2)1,2Гн; 3) 0,6 Гн; 4) 0,2 Гн; 5)0,8Гн.
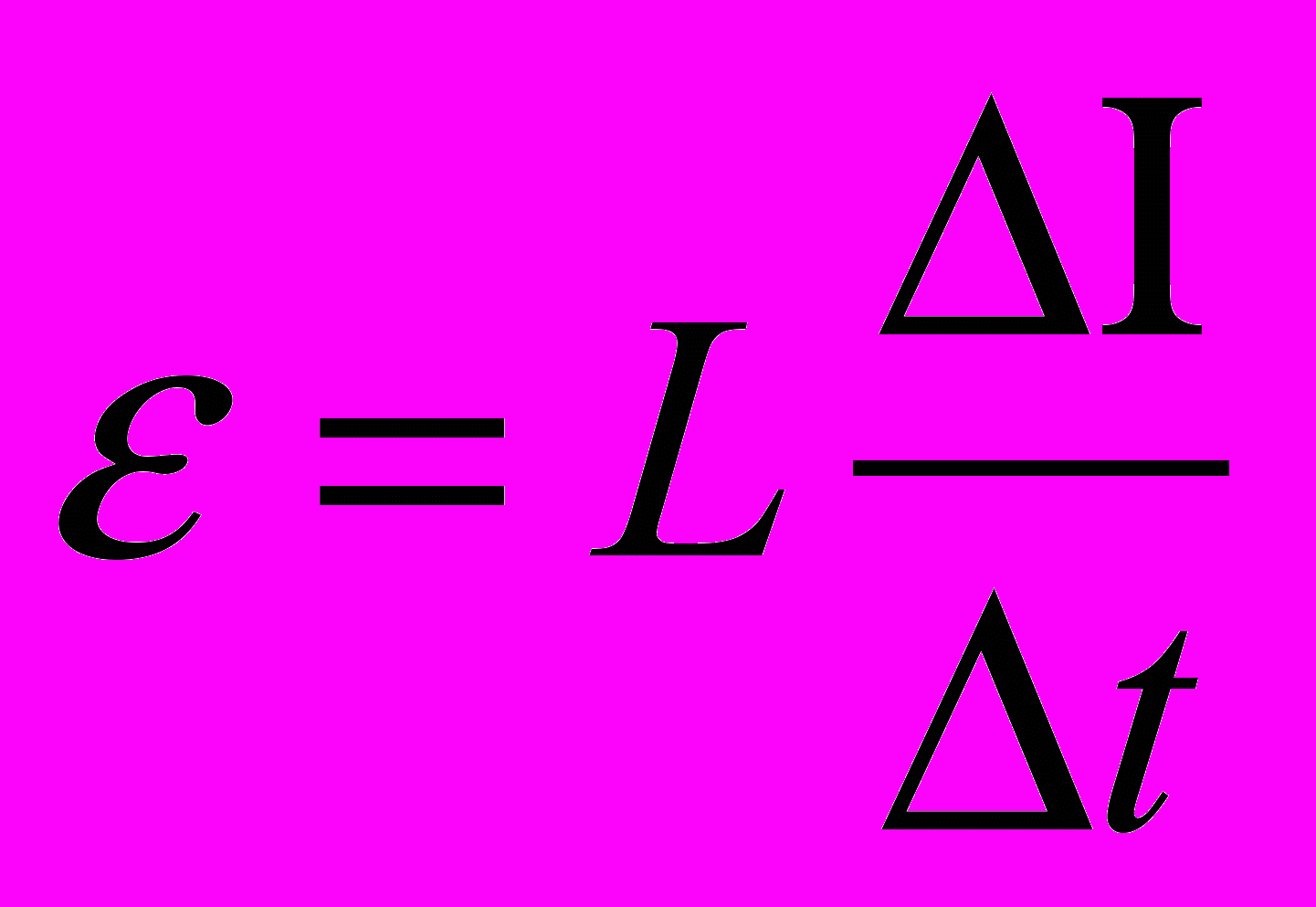
Решение.ЭДС самоиндукции по модулю
О
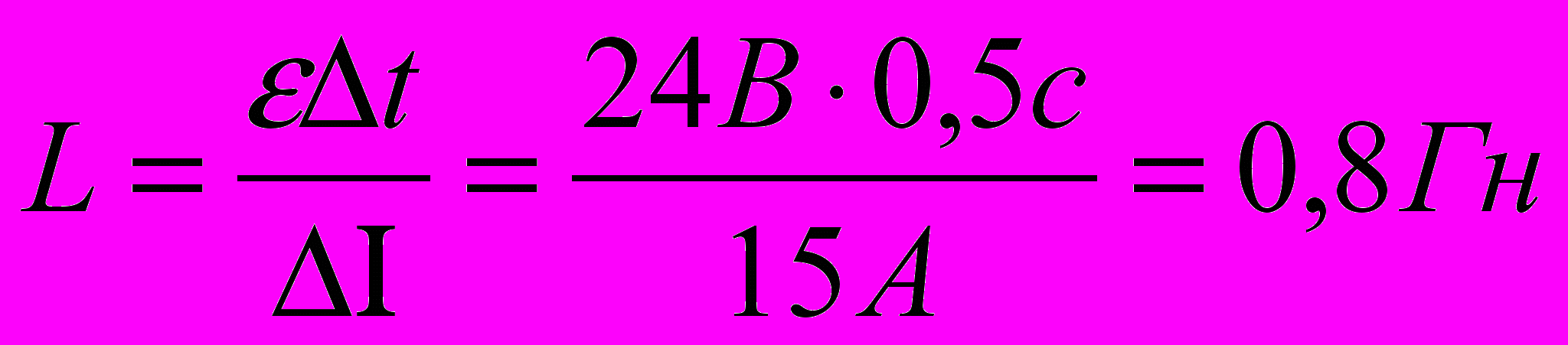 тсюда
тсюда Задачи для самоконтроля.
1. Какое явление наблюдалось в опыте Ампера?
А. Взаимодействие двух проводников с током. Б. Взаимодействие двух магнитных стрелок. В. Поворот магнитной стрелки вблизи проводника с током. Г. Возникновение электрического тока в катушке при вдвигании в нее постоянного магнита.
2. На рисунке 1 изображен проводник, по которому течет электрический ток І. Какое направление имеет вектор В индукции магнитного поля в точке М?
А. 1. Б. 2. В. 3. Г. 4. Д. 5. Е. 6 рис 1
3. Контур площадью 20 см 2 находится в однородном магнитном поле с индукцией 2 Тл. Чему равен магнитный поток, пронизывающий этот контур, если плоскость его перпендикулярна вектору индукции?
А. 40 Вб. Б. 0,1 Вб. В. 10 Вб. Г. 0,4 Вб. Д. 4.10 -3 Вб.
4
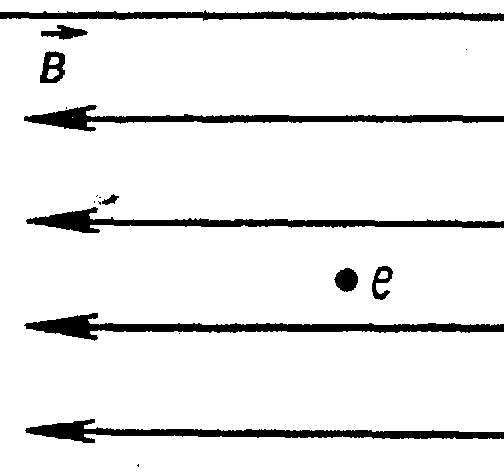 . В какую сторону и как будет двигаться первоначально неподвижный электрон, помещенный в постоянное по времени магнитное поле ?
. В какую сторону и как будет двигаться первоначально неподвижный электрон, помещенный в постоянное по времени магнитное поле ?А. Равноускоренно, вправо. Б. Равноускоренно, влево. В. По окружности, по часовой стрелке. Г. По окружности, против часовой стрелки. Д. Останется неподвижным.
5. В магнитном поле с индукцией 2 Тл движется электрический заряд 10 -10 Кл со скоростью 4 м/с. Чему равна сила, действующая на заряд со стороны магнитного поля, если вектор скорости υ движения заряда перпендикулярен вектору В индукции магнитного поля?
А. 0. Б. 0,5·10 -10 Н. В. 2·10 -10 Н Г. 8·10 -10 Н Д. 4·10 -10 Н
6. Как называют единицу магнитной индукции?
А. Тесла (Тл). Б. Вебер (Вб). В. Вольт (В). Г. Генри (Гн). Д. Ампер (А).
7. Электрический ток 2 А создает в контуре магнитный поток 4 Вб. Какова индуктивность контура?
А. 8 Гн. Б. 0,5 Гн. В. 2 Гн. Г. 1 Гн. Д. 16 Гн.
8. За 2 с магнитный поток, пронизывающий контур, равномерно увеличился с 2 до 8 Вб. Чему при этом было равно значение ЭДС индукции в контуре?
А. 5 В. Б. 20 В. В. 3 В. Г. 12 В. Д. 0.
9. Чему равна энергия магнитного поля катушки индуктивностью 3 Гн при силе тока в ней 2 А?
А. 6 Дж. Б. 3 Дж. В. 18 Дж. Г. 9 Дж. Д. 12 Дж.
10. Контур площадью 40 см 2 находится в однородном магнитном поле с индукцией 5 Тл. Чему равен магнитный поток, пронизывающий контур, если угол между вектором В и нормалью к поверхности контура составляет 60°? А. 10 -2 Вб. Б. 2·10 -2 Тл. В. 100 Вб. Г. 200 Вб.
11.Чему равна ЭДС самоиндукции в катушке с индуктивностью 2Гн, если сила тока в ней за 0,1 с равномерно уменьшалось от 5 до 3 А?
А. 10 В. Б. 0,4 В. В. 40 В. Г. 20 В. Д. 0,8 В
12. Изменения электрического заряда конденсатора в колебательном контуре происходят по закону
q = 10 -2 cos 20t. Определите циклическую частоту колебаний заряда.
А. 10 -2 с -1. Б. cos20t с -1. В. 20t с -1. Г. 20 с -1.
13. Какое из выражений, приведенных ниже, определяет частоту свободных электрических колебаний в контуре, состоящем из конденсатора емкостью С и катушки индуктивностью L?
А.
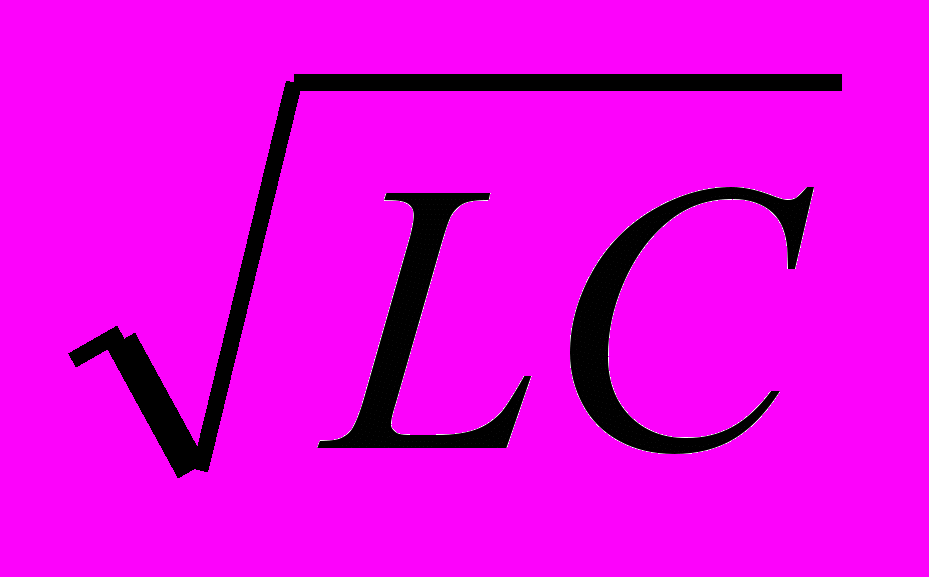 Б.
Б.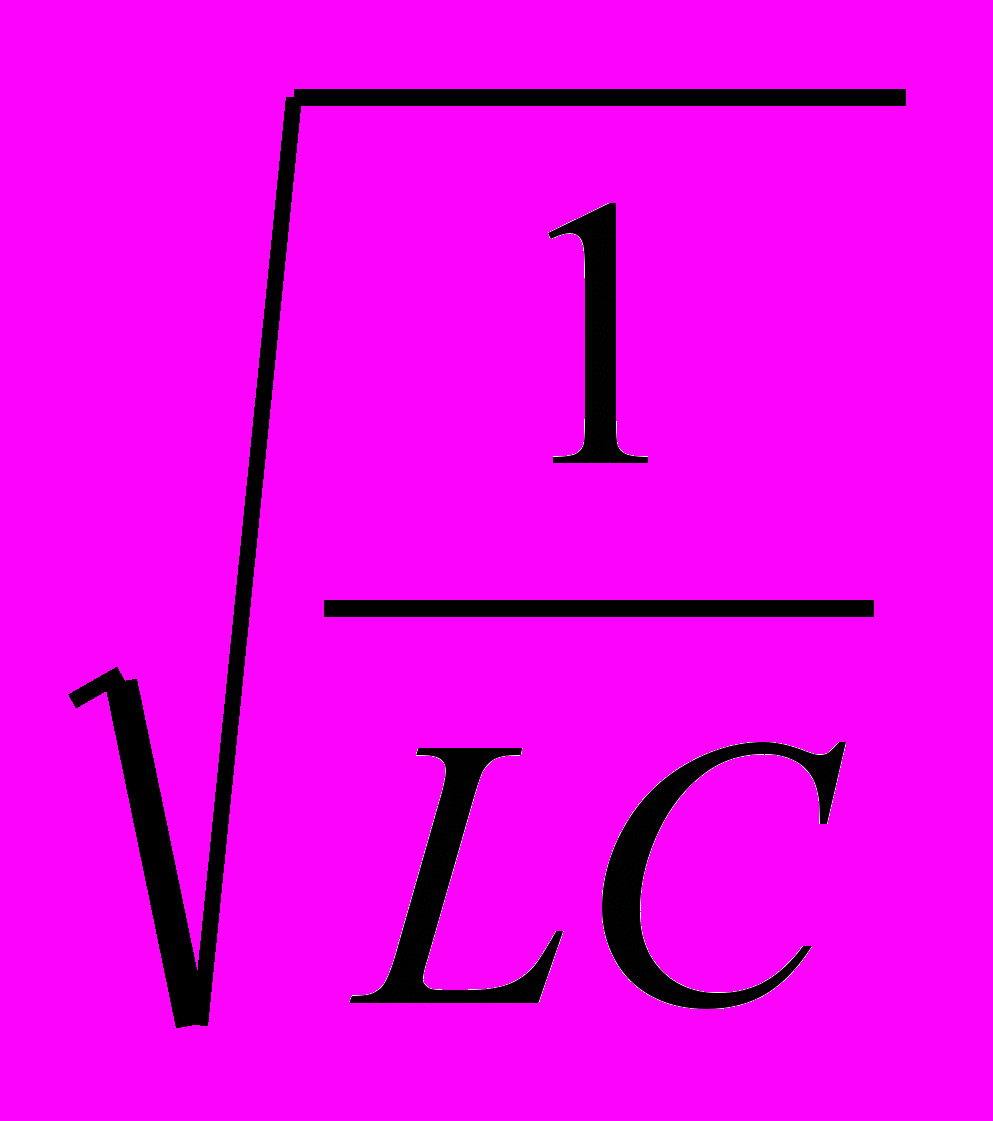 В.
В.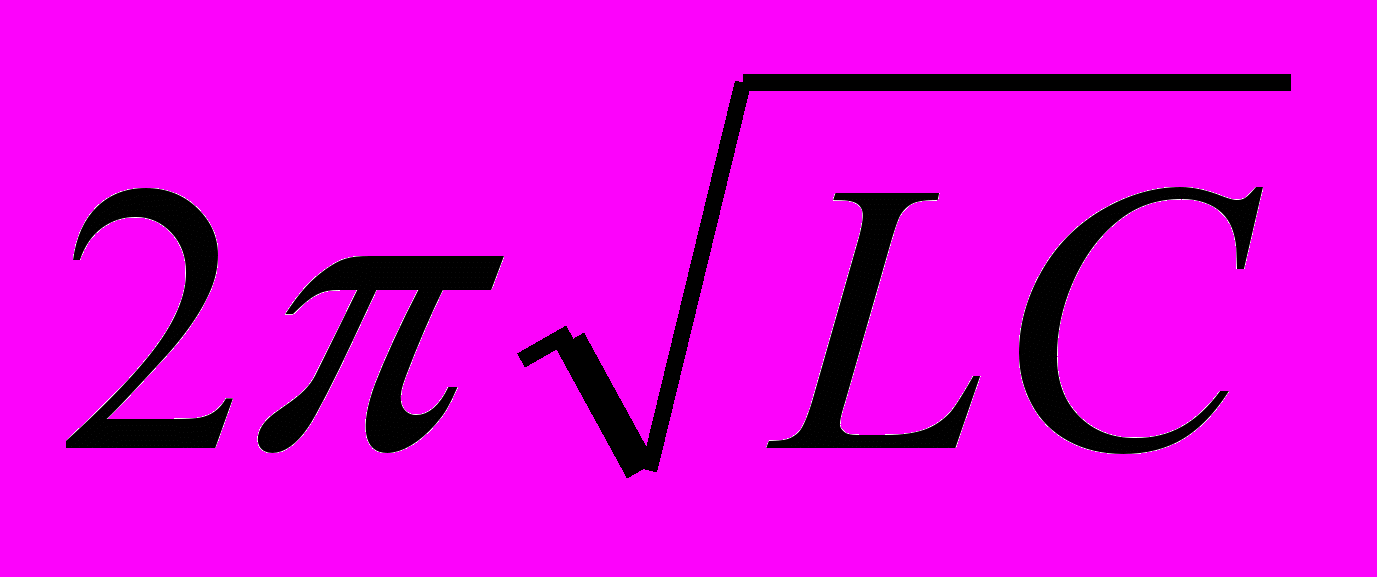 Г.
Г.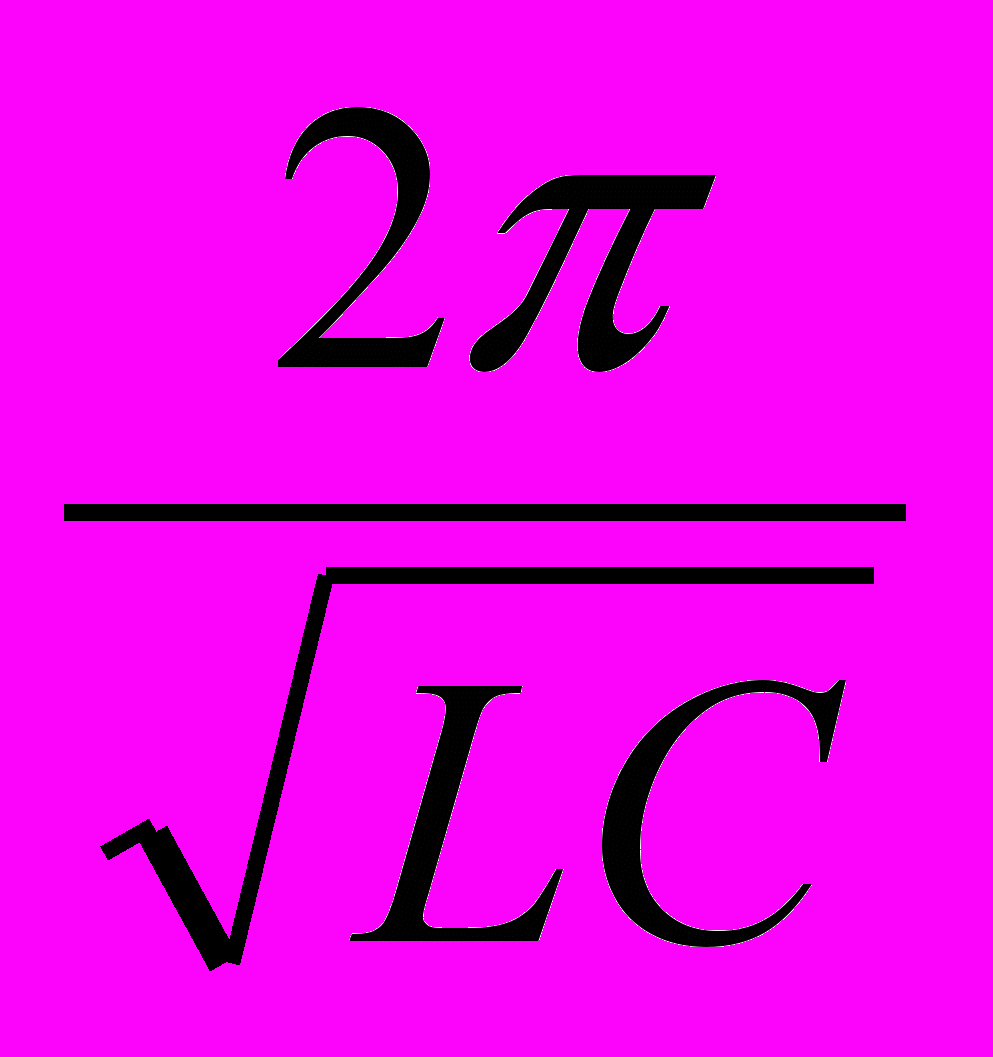 Д.
Д. 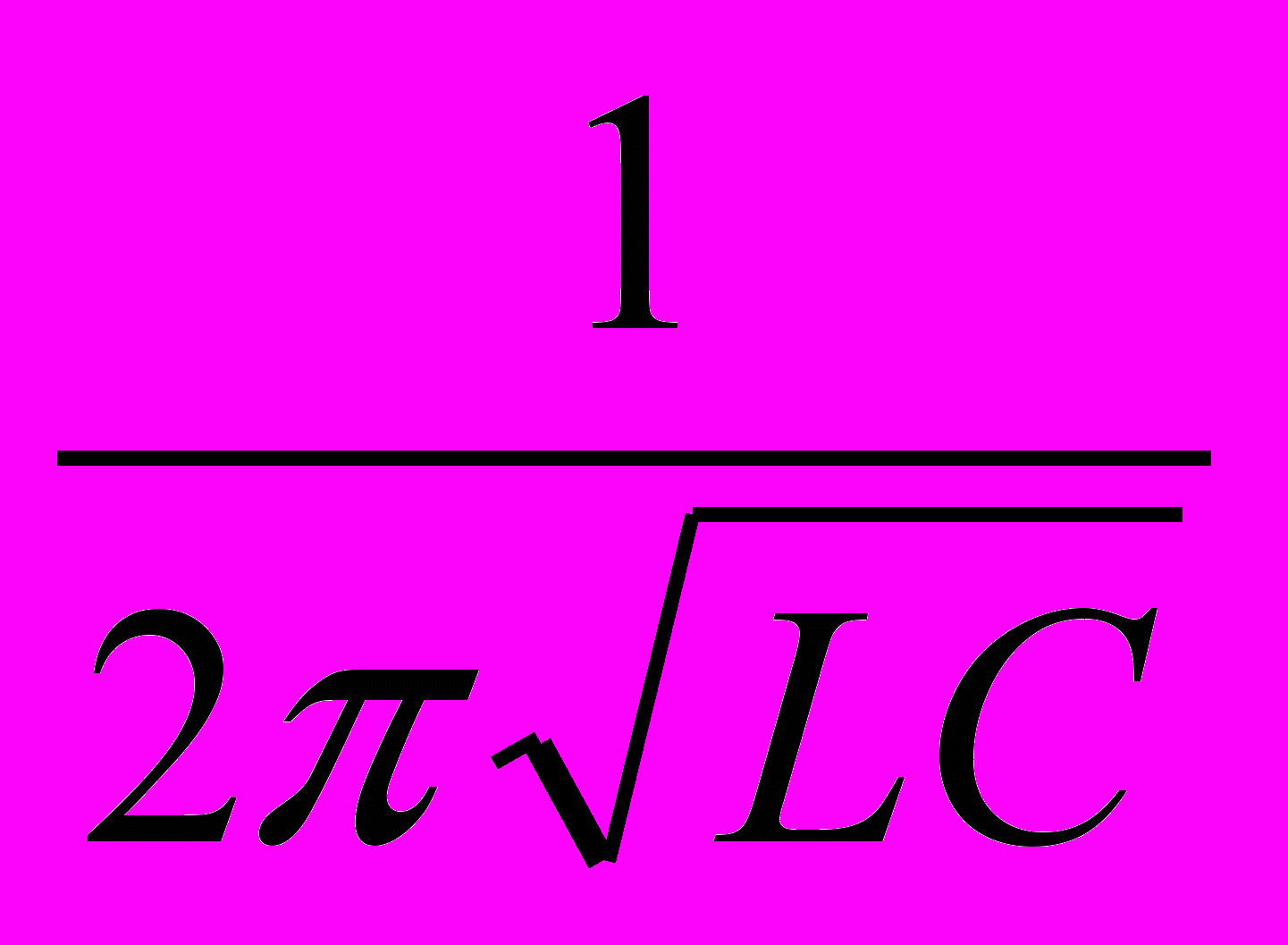
14. Как изменится период свободных электрических колебаний в колебательном контуре, если емкость конденсатора увеличить в 4 раза?
А. Уменьшится в 4 раза. Б. Уменьшится в 2 раза. В. Увеличится в 4 раза. Г. Увеличится в 2 раза. Д. Не изменится.
