Решение неравенств и систем неравенств с одним неизвестным
| Вид материала | Решение |
СодержаниеПродолжи высказывание: (по 1 баллу за правильный ответ) Сравни числа. ( 1 балл) Решите неравенство. Решите системы неравенств. Поставьте знак. (по 1 баллу) |
- Решение неравенств. Равносильные неравенства, 46.71kb.
- Элективный курс по математике, 37.2kb.
- Элективный курс «Решение уравнений и неравенств» Класс: 11 Профиль класса: общеобразовательный, 47.74kb.
- Общий метод решения сюжетных задач состоит в моделировании их в виде уравнений или, 467.25kb.
- Задачи урока: отработать навык решения линейных неравенств с одной переменной, систем, 130.04kb.
- Методические рекомендации к проведению урока: «Методы решения уравнений и неравенств., 15.21kb.
- Защита изображений на основе решения систем диофантовых уравнений и неравенств, 31.25kb.
- Николаев Юрий Викторович г рассказ, 204.59kb.
- «Решение квадратных неравенств», 20.58kb.
- Неравенств и, если «да», то найдите общее решение и частное решение двумя способами:, 11.47kb.
МОУ Ладожская ООШ, Сандовского района, Тверской области
учитель математики: Севастьянова О.В.
Урок алгебры в 8 классе
Тема: Решение неравенств и систем неравенств с одним неизвестным.
Цель:
1. Проверить в игровой форме теоретические знания и умения по теме «Решение неравенств и систем неравенств с одним неизвестным».
2. Активизировать мыслительную деятельность учащихся посредством участия каждого из них в игре.
3. Пробудить интерес к изучению математики.
Предварительная подготовка к уроку:
- Капитаны команд до уроков проверяют домашнее задание своих соперников.
- Учитель консультирует своих 3 помощников из параллельного класса или из числа старшеклассников, задача которых – проверять и подсчитывать баллы в каждой команде.
- Подготовить задания для команд.
Ход урока.
- Оргмомент.
Считайте, ребята, скорее считайте.
Хорошее дело смелей умножайте,
Плохие дела поскорей вычитайте.
Скорее работу свою начинайте!
- Сообщение темы и правил игры.
- Ребята, сегодняшний наш урок пройдет в форме игры. Каждая игра имеет свои правила. Давайте познакомимся с ними.
1. Игра состоит из 2 туров.
I тур - отборочный
II тур – финальный
2. В игре участвуют 3 команды. В каждой команде выбран капитан.
3. В I туре команды отвечают поочередно, но о своей готовности ответить можно, оповестив звуковым сигналом. За правильное выполнение заданий команда получает баллы.
4. Во II туре команда-победительница занимает красный стол и отвечает на вопросы после 1 минуты размышления. Если ответ неверен или не найден, то отвечает команда, подавшая сигнал.
5. Команда, набравшая больше всего очков, побеждает. Ее капитан выставляет отметки игрокам своей команды. Капитаны остальных команд могут выставить отметки 2 игрокам своей команды.
- I тур игры.
- Продолжи высказывание: (по 1 баллу за правильный ответ)
а) Любой член неравенства можно переносить…
б) Обе части неравенства можно умножить или разделить на одно и то же число, отличное от нуля, при этом…
в) Решением неравенства с одним неизвестным называется…
г) Решением системы неравенств с одним неизвестным называется…
д) Неравенством с одним неизвестным называется…
е) Системой неравенств с одним неизвестным называется…
- Сравни числа. ( 1 балл)
- Вам даны числа. Вы должны расставить числа в порядке возрастания. Капитаны команд будут наблюдателями у команды соперника. Закончившие первыми приносят своей команде 3 балла, вторыми – 2 балла, третьими – 1 балл.
-0,36; 0,16; 1,06; -0,63; -0,06; 1,16
-0,24; -0,14; -0,41; 1,02; 1,21; 0,12
-1,25; 2,15; -1,52; 2,51; -1,21; 1,15
3. Решите неравенство.
- Каждая команда получает индивидуальные задания для каждого ученика трех уровней сложности за 3, 2, 1 балл. Задание рассчитано на 5 минут. Каждое верно выполненное задание принесет команде баллы.
| 1 балл. а) - 3x > 0 б) - 6x < - 42 в) - 5x > 2 2 балла. а) 2,5 x – 1 ≤ x + 2 б) 3 x – 2 ≤ 1,5x + 4 в) 1,4 х + 2 ≥ х + 6.4 3 балла. а) 3 + 4(х – 1) < 3х + 8 б) 8 х + 11 ≥ 1 + 2 (х – 7) в) 11 + 5х < 1 – 4 (2 + х) | 1 балл. а) - 2x ≤ - 8 б) - 4x ≥ 10 в) - 7x ≤ - 63 2 балла. а) 0,5 x – 1 > 0 б) x – 2 ≥ 3x - 5 в) 1,7 х - 3 < х + 2,6 3 балла. а) 7 - 3(1 – х) < х + 1,8 б) 4 х - 7 ≥ 1 - 2 (х + 1) в) 7 + 5х < 4 + 2 (х + 3) |
- Решите системы неравенств.
- Каждая команда получает индивидуальные задания для каждого ученика трех уровней сложности за 3, 2, 1 балл. Задание рассчитано на 10 минут.
| 1 балл. а) 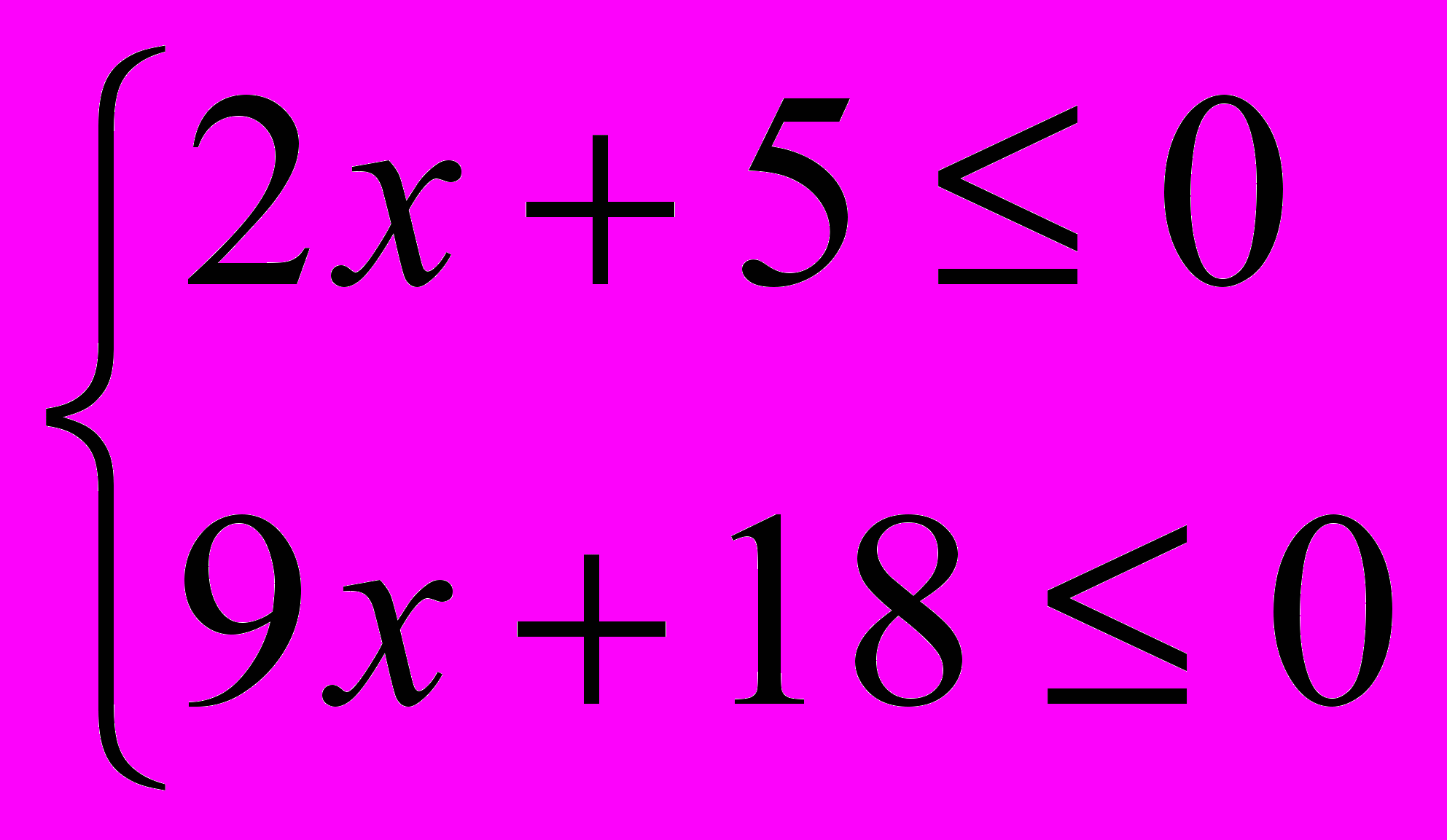 б) 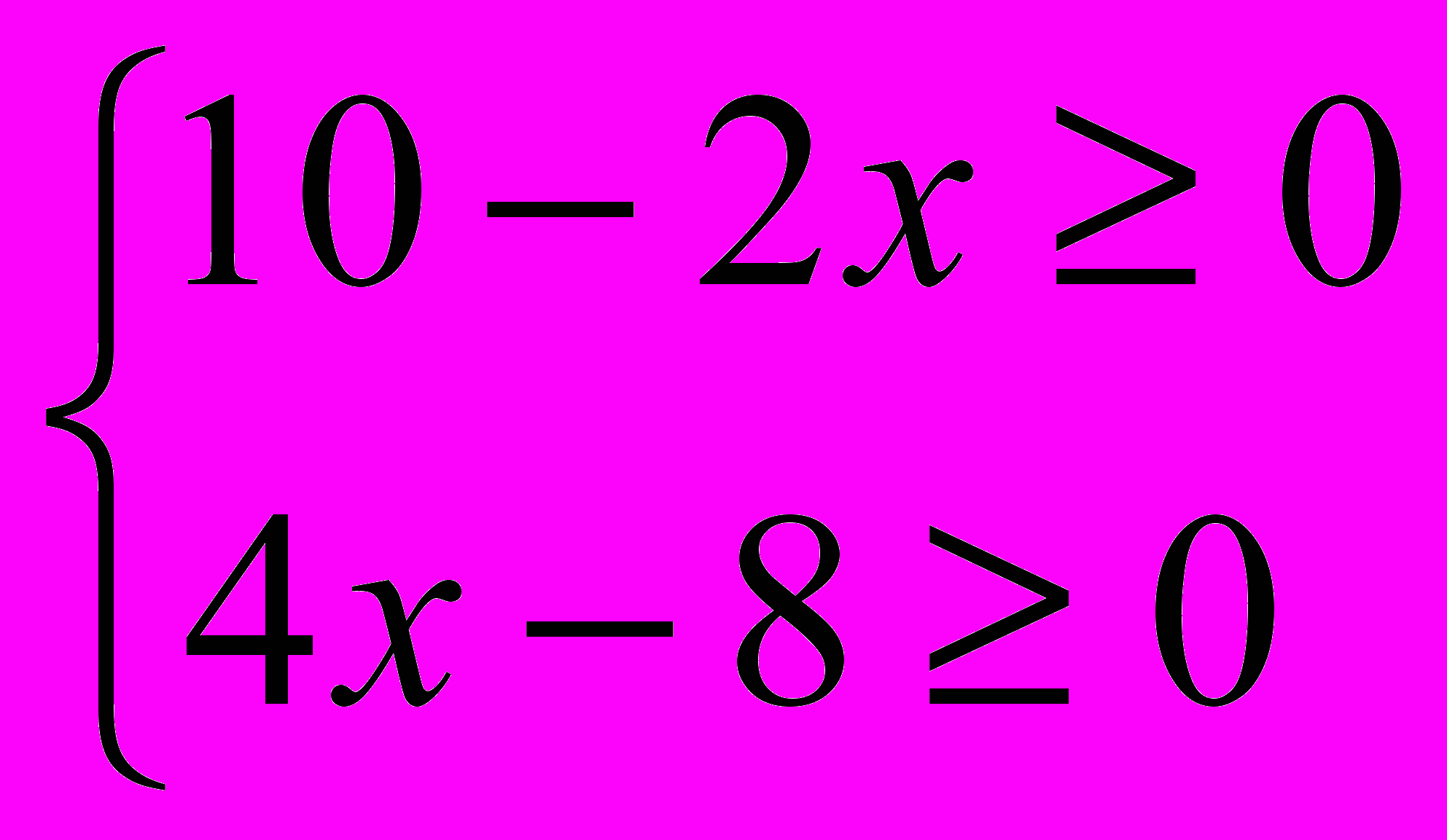 в) 3х – 18 > 0 4х – 12 < 0  2 балла. а) 4х + 2 ≥ 5х +3  2 – 3х < 7 – 2х 2 – 3х < 7 – 2х б) 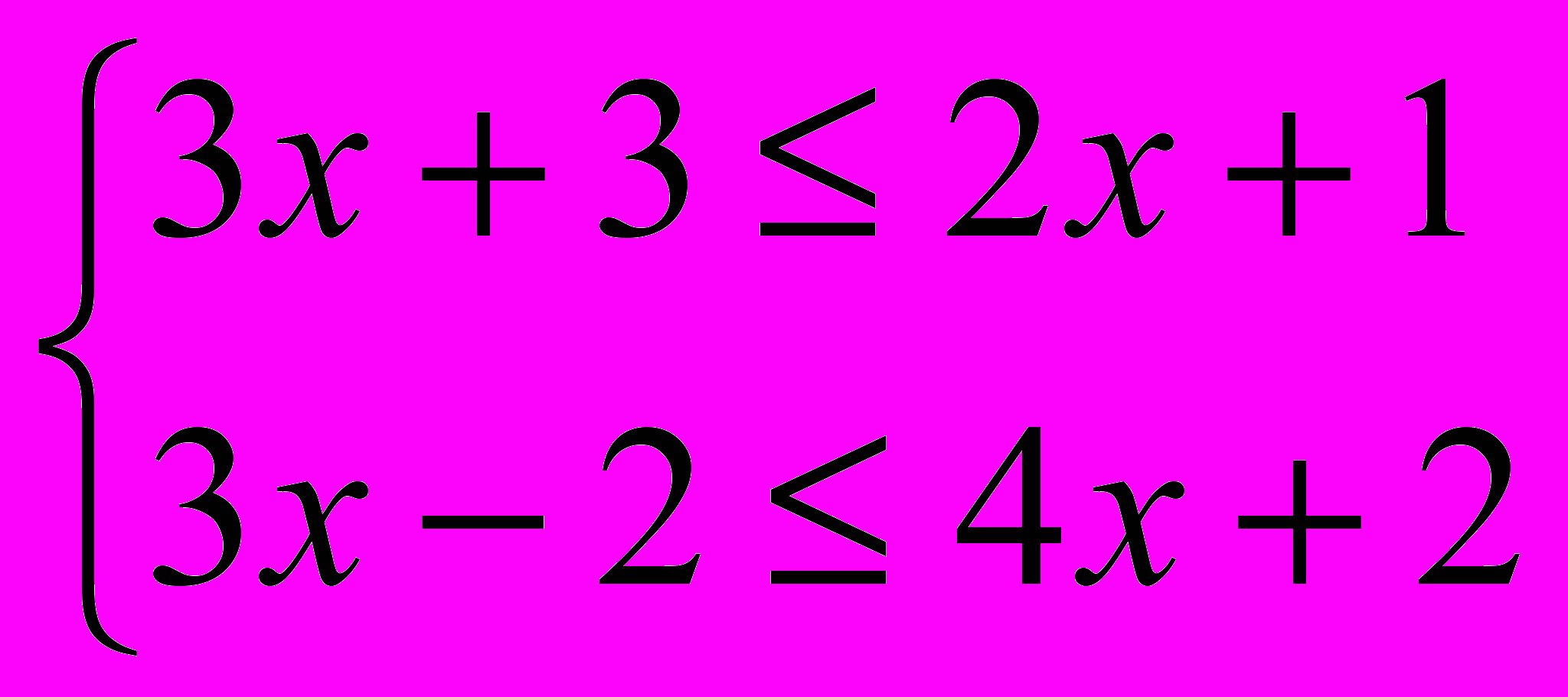  3 балла. 5 (х +1) – х > 2х + 2 4 (х + 1) – 2 ≤ 2 (2х + 1) - х | 1 балл. а) 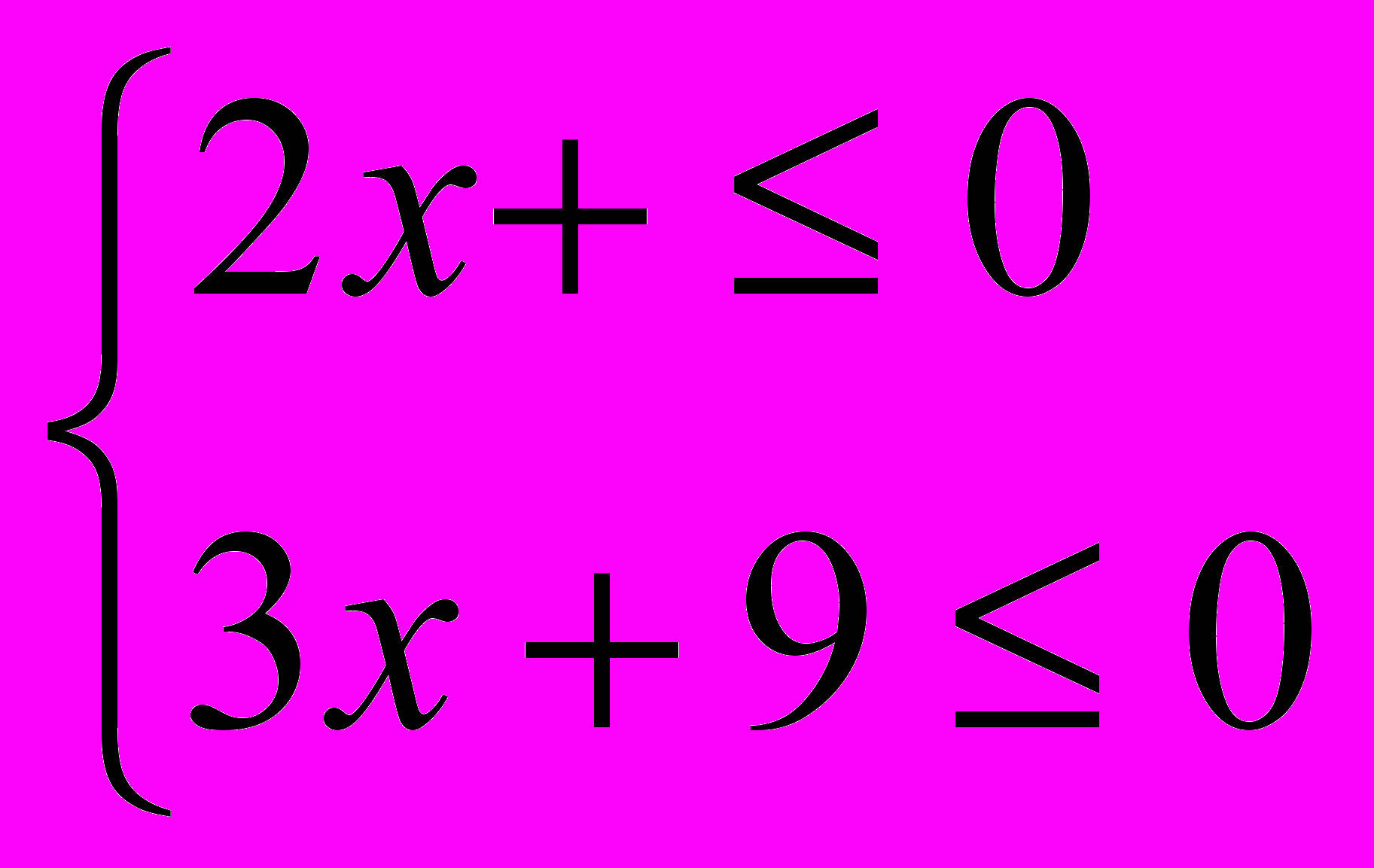  б) б) 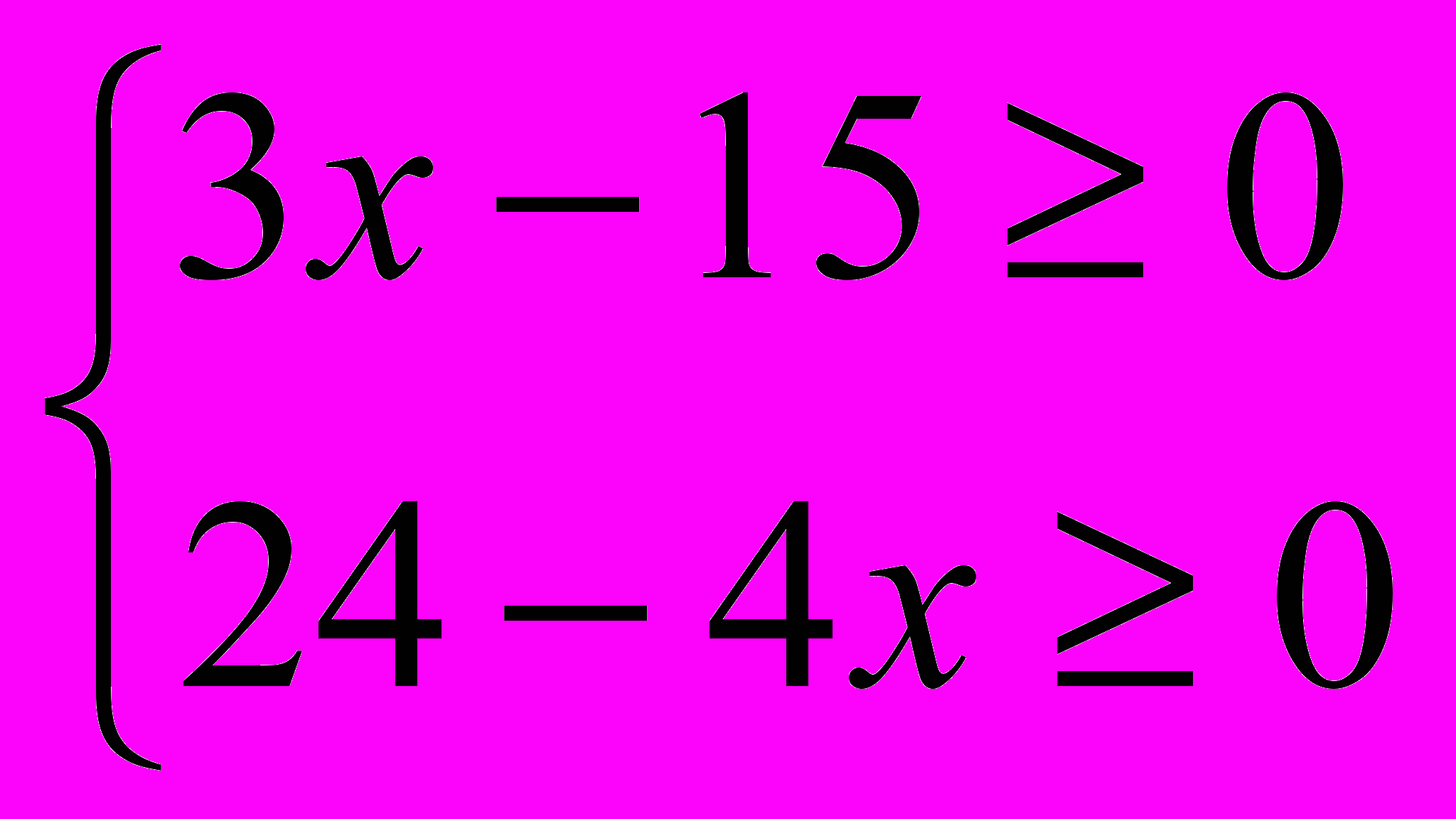 в) 2х + 15 < 0 12 – 2х > 0 2  балла. а) 5х + 3 < 3х – 7 балла. а) 5х + 3 < 3х – 71 – 2х >х + 4 б) 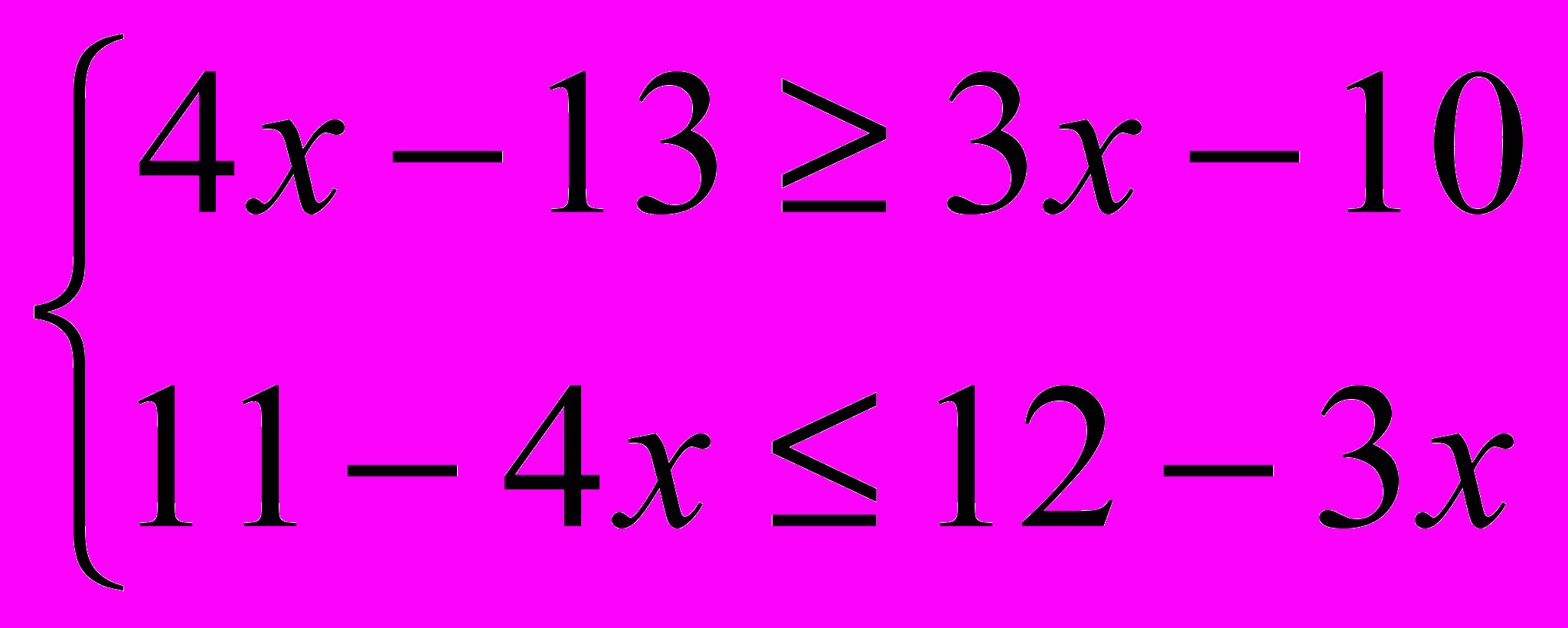 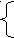 3 балла. 2 (х – 1) – 3 < 5 (2х – 1) – 7х 3 (х+1) – 2 ≤ 6 (1 – х) + 7х |
5. Назовите числа. ( 1 балл)
- Назовите целые числа, принадлежащие промежутку:
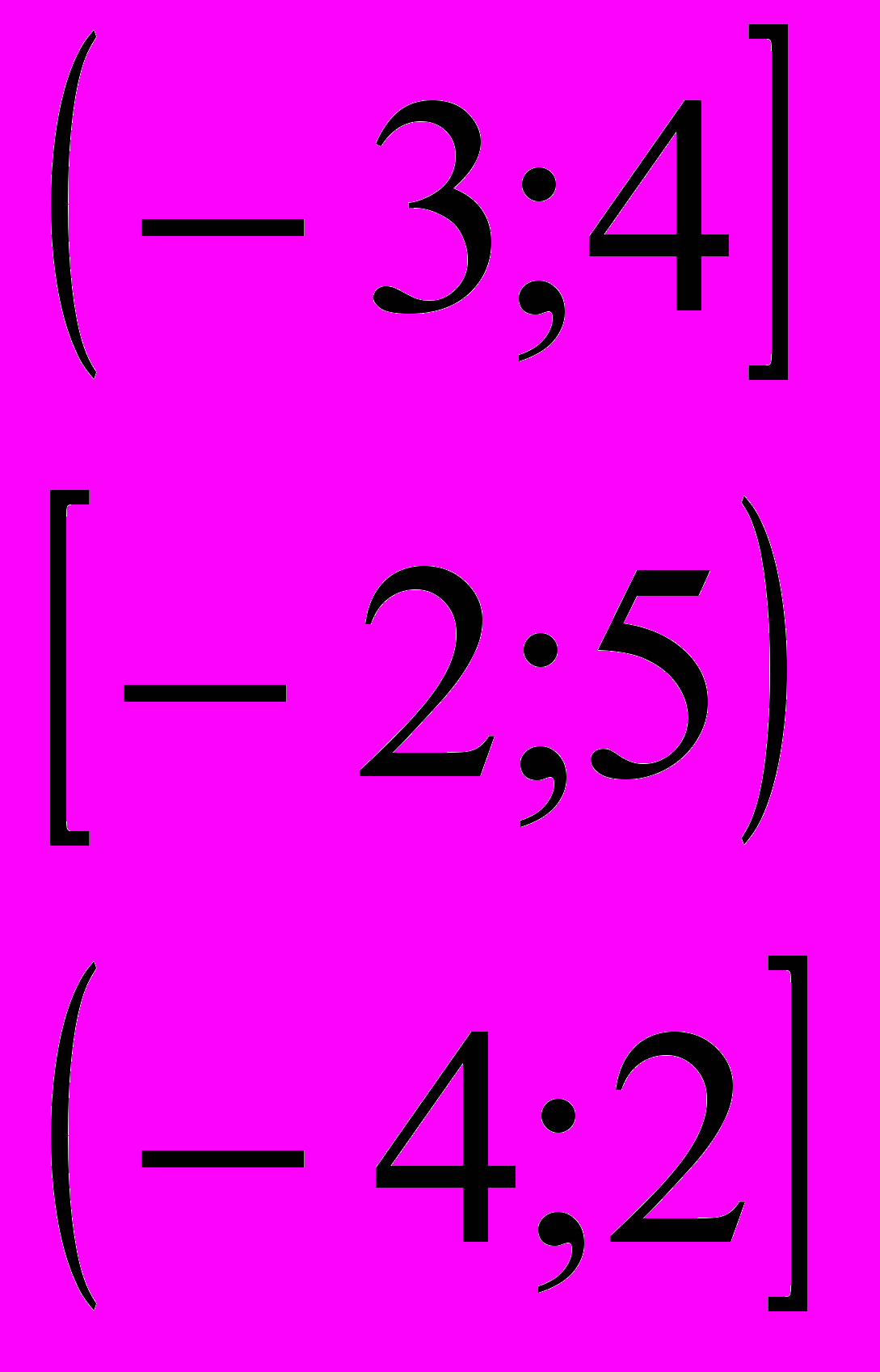
6. Домашнее задание.
- Послушаем капитанов команд о том, как команды справились с домашним заданием. Каждая правильно выполненная работа приносит команде 1 балл.
7. Подведение итогов I тура.
IV. II тур игры.
1. Найдите ошибку. Дайте комментарий. ( по 1 баллу)
| а) 7 – 3х ≤ 2х +2 -5х ≤ - 5 х ≥1  Ответ: 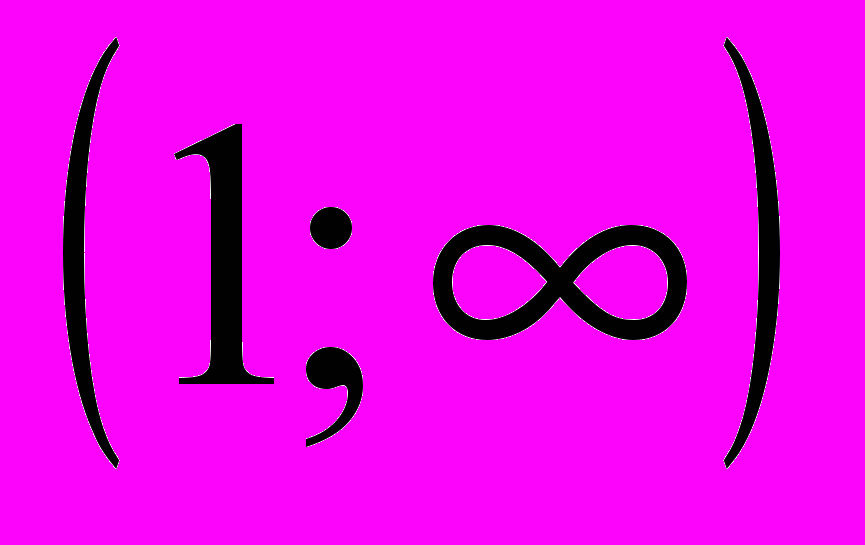 | б  ) 4х – 2 > 2х + 4 ) 4х – 2 > 2х + 47 – 3х < х + 11 4х – 2 > 2х + 4 7 – 3х < х + 11 2х > 6 - 4х < 4 х > 3 х > 1  Ответ: 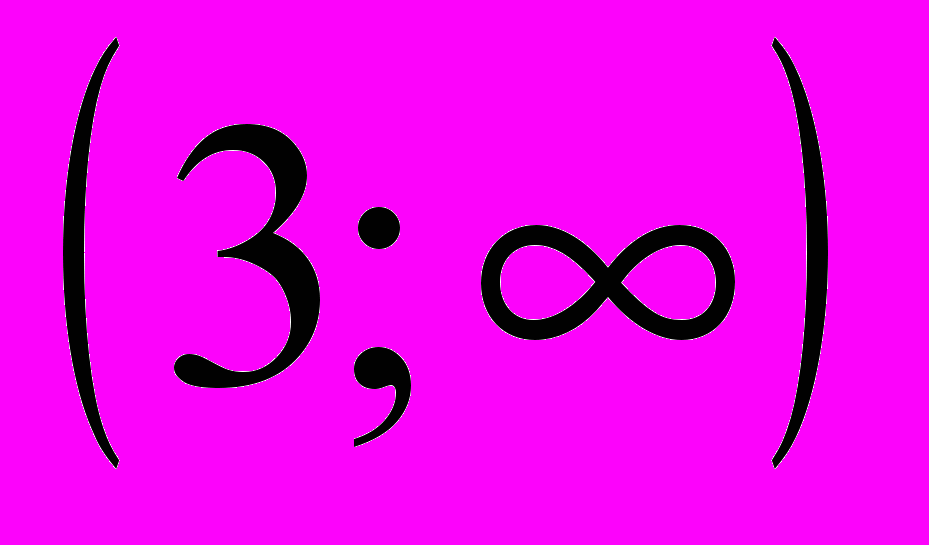 |
2. Поставьте знак. (по 1 баллу)
а) Какой знак надо поставить между числами 0,3, 7,7, 0,125, чтобы в результате выполнения указанных действий получилось 1?
б) Какой знак надо поставить между числами 7 и 8, чтобы получилось число, меньше 8, и не меньше 7?
- Решите неравенство. (3 балла)
Решите неравенство
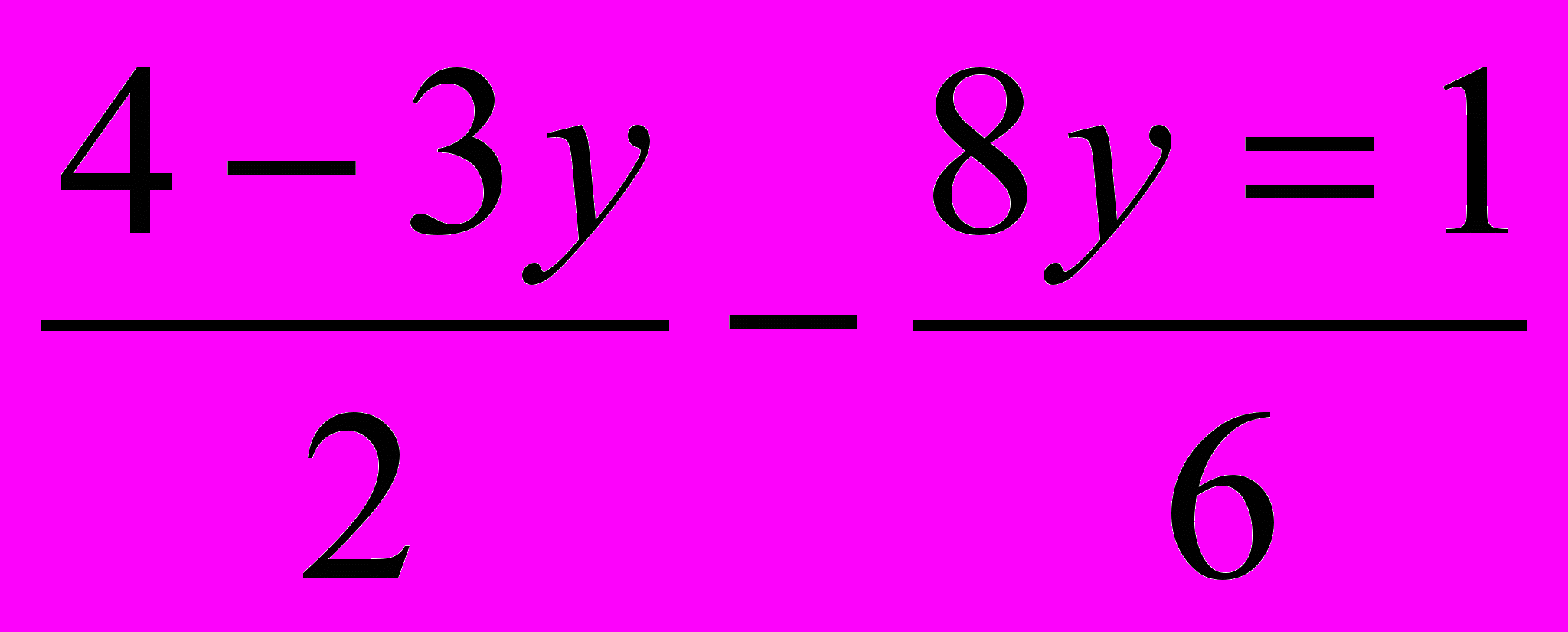 <
<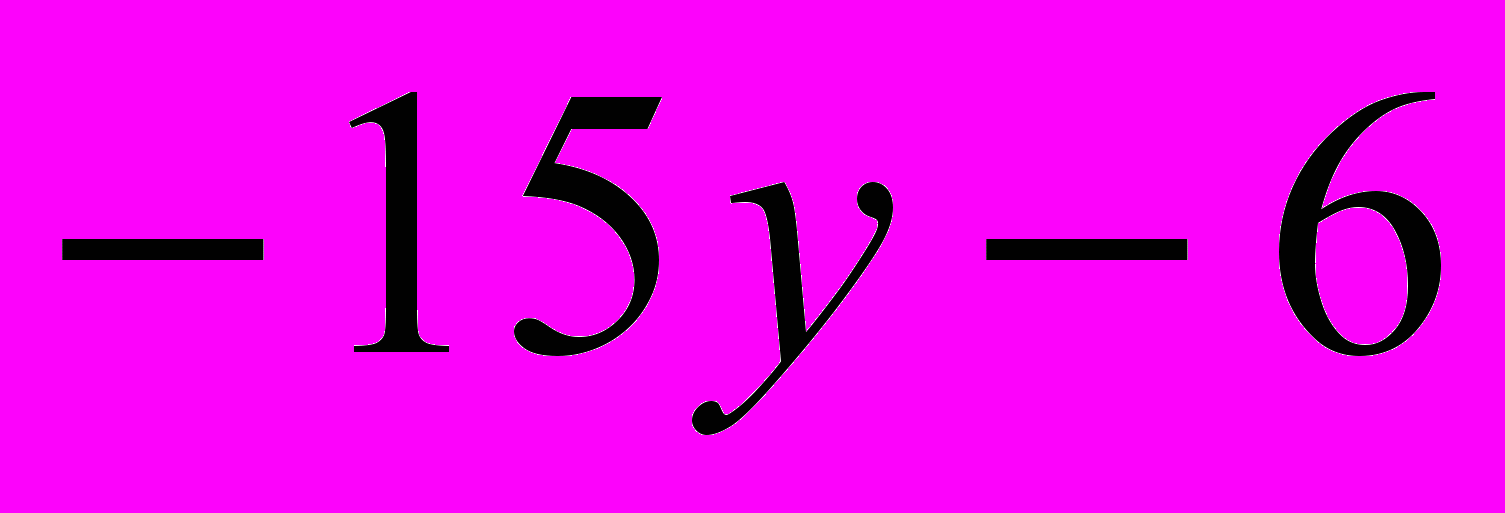 и назовите наибольшее целое число из множества решений.
и назовите наибольшее целое число из множества решений.- Укажите общие точки. (2 балла)
Укажите общие точки промежутков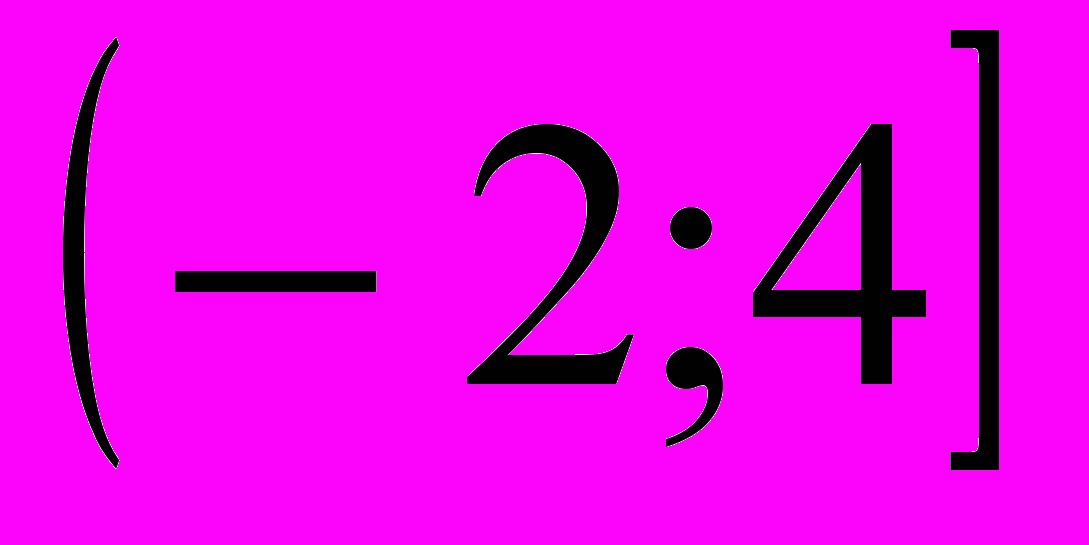 и
и 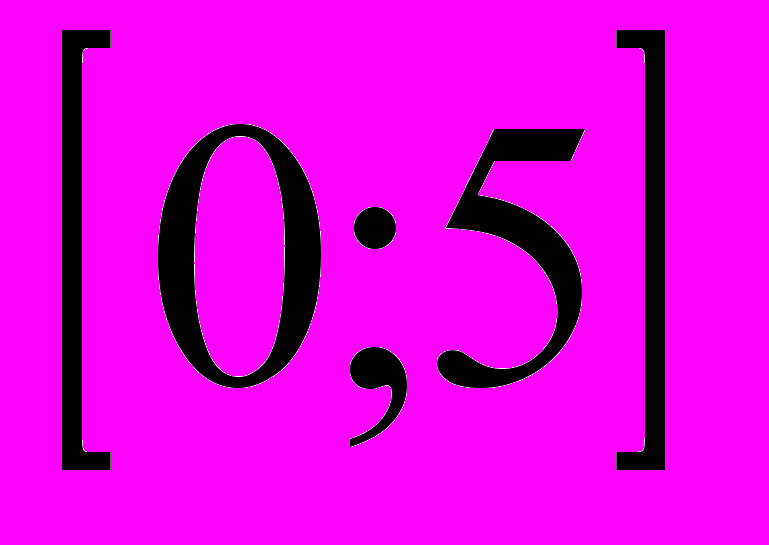 .
.
- Аукцион.
- Вспомните все, что вы знаете о неравенствах и системах неравенств. Ответ формулируйте в виде утверждения. Команда, давшая последнее утверждение, получает 2 балла.
V. Подведение итогов игры. Выставление оценок.
VI. Домашнее задание.
- Домашнее задание у вас будет творческое. Каждый из вас должен составить карточку для устного счета по изученной теме и решить ее.
- Спасибо за урок.
