Задачи урока: отработать навык решения линейных неравенств с одной переменной, систем неравенств

Вид материала

Урок

Содержание Ход урока.

Подобный материал:

• Урок по теме «линейные неравенства с одной переменной», 62.28kb.
• Методические рекомендации к проведению урока: «Методы решения уравнений и неравенств., 15.21kb.
• Общий метод решения сюжетных задач состоит в моделировании их в виде уравнений или, 467.25kb.
• Задачи урока : Проконтролировать знания учащихся по методам решения сложных логарифмических, 83.18kb.
• Васюта Аленой Георгиевной. 2009 г. Набережные Челны решение, 41.28kb.
• Защита изображений на основе решения систем диофантовых уравнений и неравенств, 31.25kb.
• Лаврентьева Светлана Дмитриевна № п/п Раздел, название урок, 308.1kb.
• Решение неравенств. Равносильные неравенства, 46.71kb.
• Решение неравенств и систем неравенств с одним неизвестным, 42.8kb.
• Задачи курса : расширить представления обучающихся о приемах и методах решения уравнений, 223.2kb.

ТЕМА УРОКА: “ Решение неравенств с одной переменной и их систем”

ЦЕЛИ УРОКА: - обобщить и систематизировать знания учащихся по данной

теме,

- поддерживать у учащихся интерес к предмету.

ЗАДАЧИ УРОКА: - отработать навык решения линейных неравенств с одной

переменной, систем неравенств,

- формирование вычислительных навыков,

- выявить степень усвоения учащимися изученного

материала.

ОБОРУДОВАНИЕ:

• Медиа-проектор
  
• Экран
  
• Авторская презентация к уроку
  
• Раздаточный материал
  
• Учебник Алгебра 8 класс Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова
  

ПЛАН УРОКА.(40 мин.)

1. Организационный момент.
   
2. Дифференцированные задания.
   
3. Устный опрос.
   
4. Решение числовых неравенств первой степени с одной переменной.
   
5. Физкультминутка.
   
6. Устный опрос.
   
7. Решение систем числовых неравенств первой степени с одной переменной.
   
8. Историческая справка.
   
9. Зарядка для глаз.
   
10. Выполнение упражнений. Работа с учебником.
    
11. Тестирование.
    
12. “Найди ошибку!”
    
13. Дополнительное задание.
    
14. Домашнее задание.
    
15. Итог урока.
    

ХОД УРОКА.

1. Организационный момент.
   

(Проверка готовности учащихся к уроку. Сообщение темы и целей урока.)

Наш урок я хочу начать со слов персидско-таджикского поэта Рудаки:

«С тех пор как существует мирозданье,
Такого нет, кто б не нуждался в знанье.
Какой мы ни возьмем язык и век,
Всегда стремится к знанью человек »

II. Дифференцированные задания. Учащиеся объединяются в пары (одно и то же задание выполняют два ученика: один у доски, другой на месте). 3 пары. Задания на карточках (1, 2, 3).

Карточка №1

Изобразите числовой промежуток на координатной прямой и запишите соответствующее неравенство:

а) (-1;4]; б) ( -∞;6); в) [8;+∞).

Карточка №2

Запишите промежуток, изображенный на координатной прямой, и составьте соответствующее неравенство:



Карточка №3

Изобразите на координатной прямой множество чисел, удовлетворяющих неравенству:

а) 0<х<3; б) х>12,5; в) -5<х<-3.

III. Устный опрос.

- Является ли решением неравенства 3х - 11>1 число 5?

- Дайте определение решения неравенства с одной переменной.

- Что значит решить неравенство?

- Сформулируйте свойства равносильности, которые используются при решении неравенств.

IV. - Используя свойства, решите следующие неравенства (работа в тетрадях и у доски):

1. 4 + 12х > 7 + 13х;
   
2. – (2 - 3х) + 4(6 + х)> 1; х/2 –( х – 3)/4 – (х + 1)/8≤ 1/2.
   
3. 
   

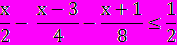
V. – Физкультминутка. «Прививка хорошего настроения».

• Повернитесь лицом друг другу:
  
• Пятачок (показывают на нос)
  
• Улыбочка (разводят руки в стороны)
  
• Колпачок (соединяют руки над головой)
  
• Прививочка (щекочут друг друга).
  

VI. Отдохнули, работаем дальше, ответьте на вопрос:

- Является ли решением системы неравенств 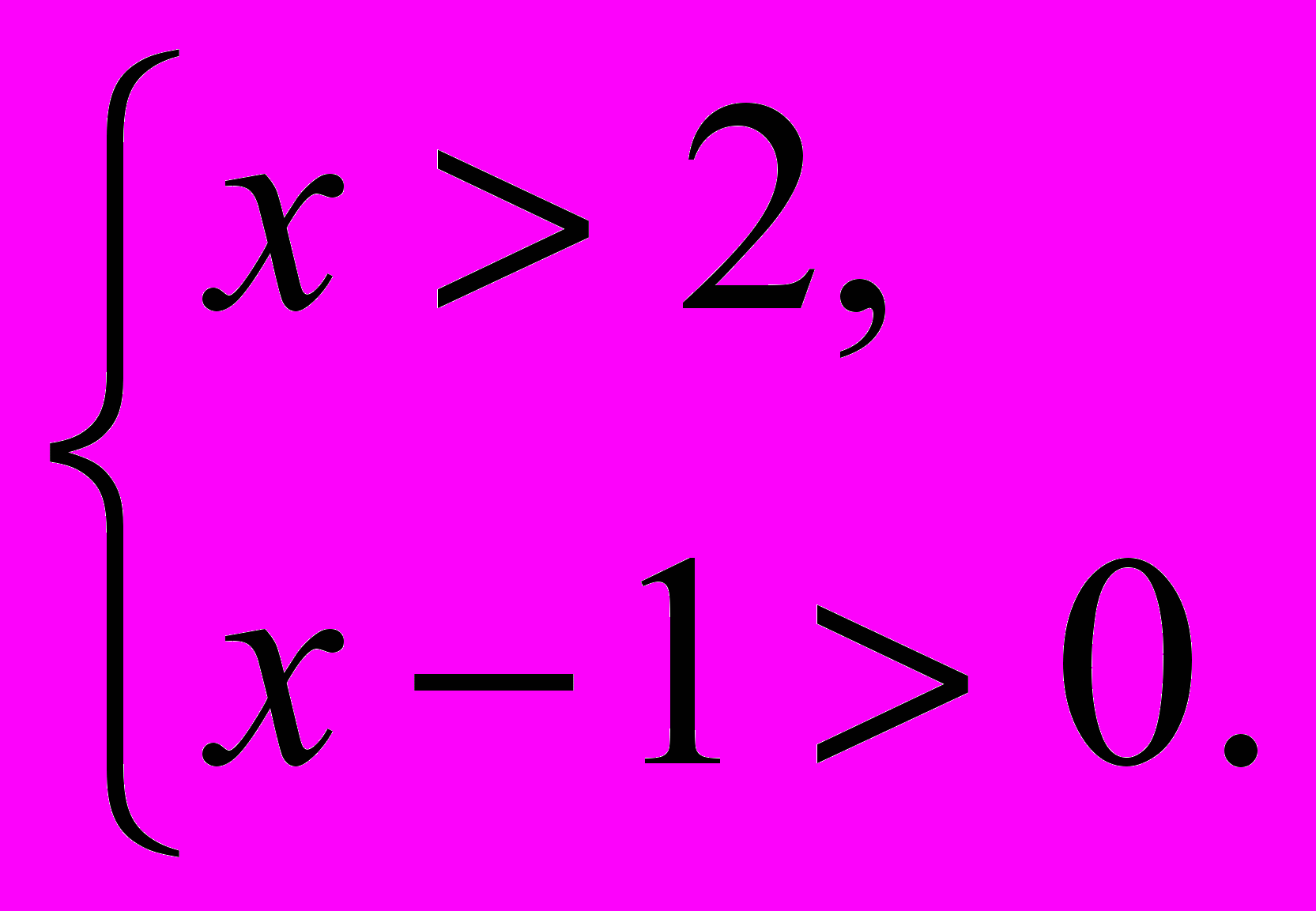число 3?

- Что называется решением системы неравенств?

- Что значит решить систему неравенств?

VII. - Решите системы неравенств:

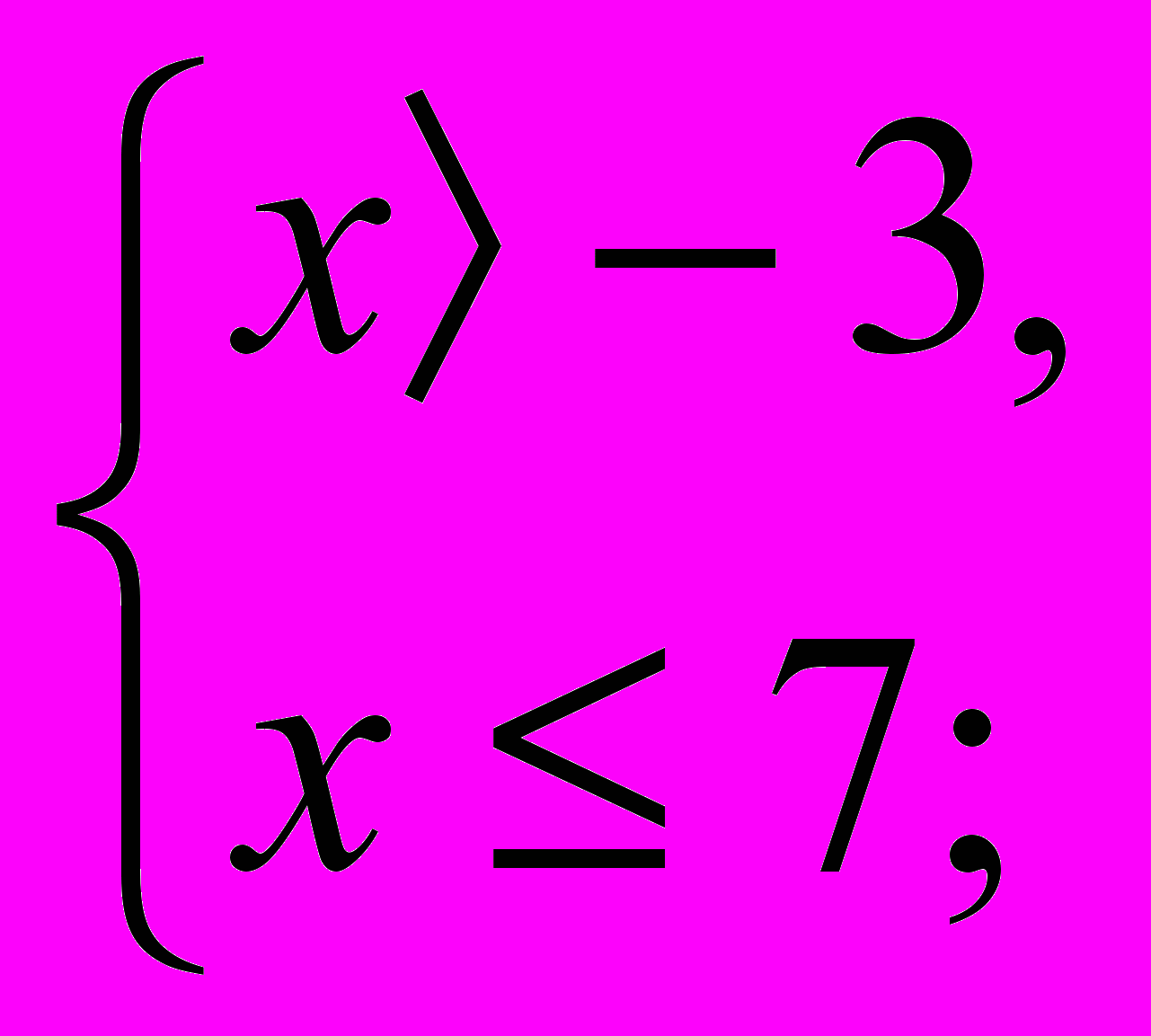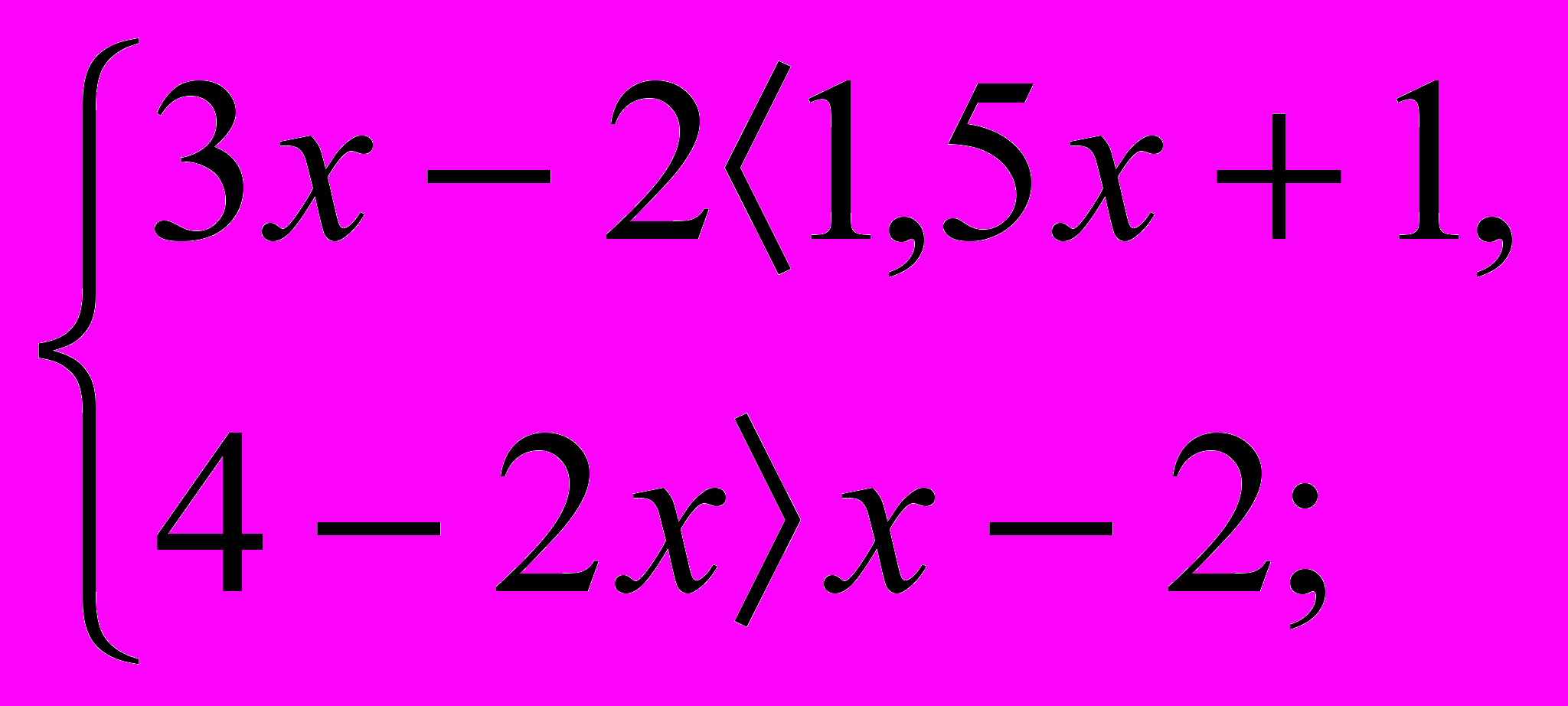а) б) в) г)

VIII. Историческая справка «Происхождение знака неравенства».

Понятия «больше» и «меньше» наряду с понятием равенства возникли в связи со счетом предметов и необходимостью сравнивать различные величины. Понятиями неравенства пользовались уже древние греки. Например Архимед (III в. до н. э.), занимаясь вычислением длины окружности, указал границы числа π.

Ряд неравенств приводит в своем знаменитом трактате «Начала» Евклид. Он, например, доказывает, что среднее геометрическое двух положительных чисел не больше их среднего арифметического и не меньше их среднего гармонического.

Однако все эти рассуждения проводили словесно, опираясь в большинстве случаев на геометрическую терминологию. Современные знаки неравенств появились лишь в XVII— XVIII вв. Знаки < и > ввел английский математик Томас Гарриот (1560—1621) года жизни. Он был первым алгебраистом XVII века, являлся воспитанником Оксфордовского университета составитель ценного описания и карты исследованной им части Северной Америки, карты Луны, которую он наблюдал через зрительную трубу в одно время с Галилеем.

Новыми полезными знаками Гарриота явились знаки > и < для отношений «больше» и «меньше», он их употребил при рассмотрении вопроса о наличии у кубического уравнения положительных корней. Вывод соответствующих условий, предложенный Гарриотом, заслужил впоследствии высокую оценку Жоржа Лагранжа, но по существу эти условия имелись еще у Виета.

Знаки ≤ и ≥ ввел математик Пьер Бугер (1698—1758)года жизни.

Это французский ученый, один из основателей фотометрии, “Трактат о корабле, о его конструкции и о его движении.

Самое интересное, что Бугер сознавал в целом недостаточную теоретическую подготовленность судостроителей того времени, поэтому его книга написана простым языком и не загромождена сложными математическими выкладками, что сделало ее на долгие годы учебником для кораблестроителей.

IX. Физкультминутка для глаз.

• Рисуй глазами треугольник.
  
• Теперь его переверни
  
• Вершиной вниз.
  
• И вновь глазами
  
• Ты по периметру веди.
  
• Рисуй восьмерку вертикально.
  
• Ты головою не крути,
  
• А лишь глазами осторожно
  
• Ты вдоль по линиям води.
  
• И на бочок ее клади.
  
• Теперь следи горизонтально,
  
• И в центре ты остановись.
  
• Зажмурься крепко, не ленись.
  
• Глаза открываем мы, наконец.
  
• Зарядка окончилась.
  
• Ты молодей!
  

X. Выполнение упражнений.

1. № 879(а, в), №881(а, в). Учащиеся объединяются в группы по 4 человека (соседние две парты). Каждый решает по одной системе (сами распределяют в группе).

XI. Тестирование. Каждое задание предполагает ответ «да» или «нет».

1. Является ли число –7 решением неравенства 3 х >12?
   
2. Является ли число 10 решением неравенства 3 х >12?
   
3. Является ли неравенство 2 х – 15 > 3 х + 6 строгим?
   
4. Верно ли что, при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется...
   
5. Можно ли почленно складывать верные неравенства одного знака?
   
6. Является ли число 3 решением системы неравенств
   

7. Верно ли при любом а неравенство: а² + 1 > 0?
   
8. Существует ли целое число, принадлежащее промежутку [-1,8; - 1,6]?
   
9. Верно ли, что: (-5; 5)∩ (-3; 2) = (-3; 2)?
   
10. Верно ли при любом значении а неравенство: – а² – 2 < 0?
    

XII. “Найди ошибку!”



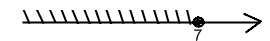
х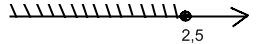≥7


У<2,5



хє(-∞;7]

Ответ: (-∞;7]


Yє(-∞;2,5]

Ответ: (-∞;2,5]


m≥12




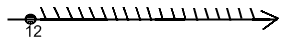
mє(-∞;12)

Ответ: (-∞;12)


-3k≤3,9, k≤-1,3


Kє(-∞;-1,3]

Ответ: (-∞;-1,3]