1. Алфавит, слова, операции над словами

Вид материала

Документы

Содержание 8. Структура цепочек. СУ-схемы Tmt, (mt) Tmt, mt

Подобный материал:

• Исполнительный кодекс Республики Молдова, 2184.07kb.
• Статьи 4 изложить в следующей редакции: "Статья Ответственность физических, юридических,, 41.3kb.
• Республика Молдова, 777.62kb.
• Федеральный закон, 404.04kb.
• Подготовка к операции по прорыву блокады проводилась в глубокой тайне, 18.04kb.
• Игра «Алфавит» Чтобы узнать тему нашего занятия вы должны расшифровать слова. (зашифрованные, 50.79kb.
• «День культуры и славянской письменности», 78.75kb.
• Выполнили: Фурманова Диана 3класс, 121.65kb.
• Работа со словами с непроверяемыми написаниями, 134.51kb.
• Календарно-тематический план учебная дисциплина: «Математика», 34.71kb.

8. Структура цепочек. СУ-схемы

Цепочка – последовательность лексем(терминалов). Структура цепочки – способ задания семантики (смысла) правильной последовательности лексем (т.е. принадлежащей формальному языку).

Структура может выражать непосредственно семантические связи слов (для естественного языка), или, например, порядок вычислений (для арифметических выражений), вложенность конструкций (для языков программирования).

Например, для цепочки ad2+c структура будет выражать порядок действий.



+

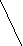
a





c

d

2

Рис.24


Структура этой же цепочки может быть представлена в виде скобочной записи: (( (a)  ( (d)(2)) )+ (c) ).

Нас обычно интересует структура цепочки, построенной в некоторой конкретной грамматике G₁₄.

Пусть дана грамматика G с множеством правил:

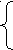S T + ST

T M  T  M

M (S)  i


Пусть анализируемая цепочка Х = i + i  i. Для неё можно построить несколько выводов, различающихся порядком замены нетерминалов, например: S T +S  T + T T+ M  TT + M  M M + M  M i + M  Mi + M  ii + i  i , или S T +S  M + S  i + Ti + M  T i + i  T i + i  Ti + i  Mi + i  i.

Легко заметить, что по существу эти выводы различаются незначительно. Для придания единообразия процессу построения вывода определим:

Вывод, в котором на каждом шаге правило применяется к самому правому (левому) нетерминалу, назувается правым (левым) выводом. Второй из приведенных выводов для цепочки i + i  i является левым выводом, т.к. на каждом шаге правило применяется к самому левому нетерминалу.

Одна из форм представления вывода – синтаксические дерево.

Правила построения синтаксического дерева.

1. Каждому правилу вывода A₁₂…_nR, где _i - некоторые лексемы, сопоставляется куст.

	A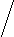
1	2	…	n

2. Строим дерево с корнем, растущее вниз. Корню дерева приписываем начальный символ.

3. Для каждого применяемого правила в выводе приклеиваем соответствующий куст к вершине построенного дерева.

4. Повторяем шаг 3 де тех пор, пока всем висячим вершинам будут сопоставлены терминалы.

Для грамматики G₁₄ синтаксическое дерево для цепочки i + i  i представлено на рис. 25




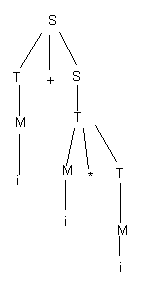
Рис.25

Теорема. Каждому выводу некоторой терминальной цепочки соответствует единственное синтаксическое дерево. Каждому синтаксическому дереву соответствует единственный правый (левый) вывод.

Доказательство:

1. Для построенного вывода дерево единственно по построению.
   
2. Пусть для данной цепочки имеется некоторое синтаксическое дерево. Построим левый вывод, соответствующий этому дереву. Для этого в дереве на каждом шаге применяем соответствующее правило к самому левому нетерминалу. Предположим, что одному дереву соответствует более одного правого (левого) вывода. Если существует 2 вывода, соответствующих этому дереву, то существует нетерминал, к которому применяются разные правила  соответствующие деревья будут различными. Поэтому каждому дереву соответствует единственный правый (левый) вывод.
   

Соответствие дерево – вывод не является взаимно-однозначным, т.к. порядок применения правил не задан и одному дереву может соответствовать более одного вывода, например, правый и левый.

Цепочка xL(G) называется неоднозначной в G, если для неё существует более одного синтаксического дерева в G. Грамматика G называется неоднозначной, если L(G) содержит неоднозначные в G цепочки.

Язык L называется неоднозначным, если для него не существует однозначной грамматики.

Например, L={aⁿbⁿc^m, aⁿb^mc^m , n,m 1} – неоднозначный язык.

Регулярные выражения всегда задают однозначный язык (т.к. можно построить детерминированный автомат, и каждой цепочке – однозначному проходу по диаграмме – соответствует единственное синтаксическое дерево, т.к. это однозначный порядок применения правил).

Неоднозначные грамматики часто проще однозначных, но они пригодны только для построения цепочек, а не для их анализа, т.е. задания семантики.

Для задания структуры цепочек часто используются СУ-схемы, т.е. схемы синтаксически управляемого перевода. СУ- схема T=< V_вх,V_вых, V_N, I, R>, где V_вх – входной алфавит , V_вых – выходной алфавит , V_N – множество нетерминалов, I – начальный нетерминал, R={ A₁,₂}, гдеA V_N, ₁(V_вх V_N)*, ₂(V_вых V_N)*, а «,» - метасимвол, разделяющий ₁ и ₂. При этом количество и состав нетерминалов в₁ и ₂ совпадают. Если в ₁ более одного вхождения некоторого нетерминала А, то устанавливается соответствие между всеми вхождениями А в ₁ и ₂: А⁽¹⁾, А⁽²⁾…А⁽ⁿ⁾.

СУ-схема называется простой, если порядок вхождений нетерминалов в ₁ и ₂ совпадают.

Вывод в СУ-схеме строится из пары начальных символов . Определение выводимости в СУ-схеме подобно определению выводимости (выводимость за один шаг обозначаем )для обычных грамматик:

₁₁ ₂₂ (из ₁₁ непосредственно выводима ₂₂) ₁₁ А ₂, ₂₁ ₁ ₂, ₁=₁ А ₂, ₂ =₁ ₂ ₂, и А₁,₂ R, при этом вхождения А в ₁ и ₁ –соответствующие.

Выводимость является рефлексивным и транзитивным замыканием непосредственной выводимости.

СУ-схема применяется к цепочке следующим образом: правила применяются одновременно к двум входным символам таким образом, чтобы до запятой получилась исходная цепочка, в этом случае после запятой получается перевод этой цепочки.

Перевод, порождаемый СУ-схемой Т:

(T) = (/ ⁺ & xV_вх*, yV_вых*}.

Из СУ—схемы T можно извлечь две грамматики G_вх=вх, V_N, I, R_вх> R_вх={A ₁/ A₁,₂ R} и

G_вых=вых, V_N, I, R_вых> R_вых={A ₂/ A₁,₂ R}.

СУ-схемы позволяют задавать структуры на уровне описания языка, где

(T) = {/ x – входная цепочка, y – выходная цепочка}.

Например, СУ-схема Т, описывающая перевод арифметического выражения, составленного с использованием символов сложения, умножения и скобок, в скобочную запись, отражающую порядок построения формулы (а следовательно, и порядок проведения вычислений), выглядит следующим образом.

S T+S, (T+S)

S T,T

TMT, (MT)

TM,M

M(S),(S)

Mi,(i)

Применение данной СУ- схемы к цепочке i+ii проиллюстрируем выводом(приводится левый вывод):

       

В результате получается перевод цепочки, отражающий порядок её построения.

Можно построить СУ-схему для других преобразований цепочки, например, для построения по цепочке её обратной польской записи, например, соответствующая СУ-схема для построения обратной польской записи для цепочек, использующих только знаки умножения и сложения, выглядит следующим образом:

S T+S, +TS

S T,T

TMT, MT

TM,M

M(S),S

Mi,i

Применение этой схемы к той же цепочке выглядит следующим образом:

<Т+S,+TS>.

Следует обратить внимание, что в обоих случаях применяемые СУ-схемы были простыми.