1. Алфавит, слова, операции над словами

Вид материала

Документы

Содержание 12.Элементы теории конечных автоматов Конечный автомат Мура

Подобный материал:

• Исполнительный кодекс Республики Молдова, 2184.07kb.
• Статьи 4 изложить в следующей редакции: "Статья Ответственность физических, юридических,, 41.3kb.
• Республика Молдова, 777.62kb.
• Федеральный закон, 404.04kb.
• Подготовка к операции по прорыву блокады проводилась в глубокой тайне, 18.04kb.
• Игра «Алфавит» Чтобы узнать тему нашего занятия вы должны расшифровать слова. (зашифрованные, 50.79kb.
• «День культуры и славянской письменности», 78.75kb.
• Выполнили: Фурманова Диана 3класс, 121.65kb.
• Работа со словами с непроверяемыми написаниями, 134.51kb.
• Календарно-тематический план учебная дисциплина: «Математика», 34.71kb.

12.Элементы теории конечных автоматов

Конечный автомат (автомат Мили) S=< V_a, Q, V_b, q₀, F, G>, где

V_a={a₁,a₂,…a_m}, m1 – входной алфавит автомата,

V_b= {b₁, b₂, …, b_n}, n1 – выходной алфавит автомата,

Q= {q₀,q₁,…q_k}, k0 – внутренний алфавит (алфавит состояний),

q₀Q – начальное состояние автомата,

F - функция переходов; F: Q V_a Q,

G - функция выходов, G: Q V_a  V_b .

Автомат однозначно задает отображение V_a*  V_b* (входной цепочки в выходную).

Модель автомата – абстрактное устройство с входной и выходной лентами и управляющей головкой.

В каждый момент времени автомат находится в одном из состояний множества Q, воспринимает один из символов входного алфавита (содержащийся в ячейке, с которой происходит считывание), и печатает один символ выходного алфавита на выходной ленте. Время у нас считается дискретным.

Существуют две традиции в задании автоматов. Первая из них - явное задание дискретного времени, т.е. номера такта tN(= {0,1,2,…}, a(t)V_a, b(t) V_b, q(t) Q.

Тогда работа автомата описывается с помощью рекуррентных соотношений:

q(t+1)=f (q(t),a(t))

b(t)=g(q(t),a(t))

Иногда рассматривается b(t+1)=g(q(t),a(t)) – автомат с задержкой; мы такие автоматы не рассматриваем, т.к. это для некоторых задач неудобно.

Граф переходов автомата определяется следующим образом:

Множество вершин графа – каждая вершина соответствует элементу множества Q, множество ребер определяется отображениями F и G, причём F определяет связи (переходы состояний), а G – выходы. Отображения в общем случае частичные, но если определено f(q_i,a_j), то определено и g(q_i,a_j).

Пример. Пусть граф переходов автомата представлен на рис.26.



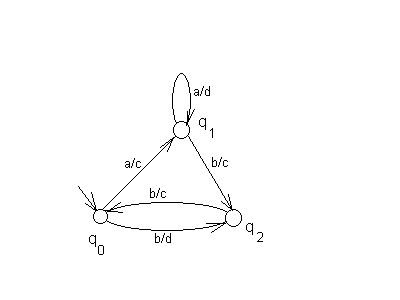
Рис. 26. Пример автомата Мили.

При входной цепочке aabb получается выходная цепочка cdcc.


Функции переходов и выходов определяют автоматное отображение V_a*V_b* . При этом для любой входной цепочки =a₁a₂….a_k f(q₀, a₁a₂….a_k )= f(f(…f(q₀, a₁)a₂)…. a_k )

Или, эквивалентное индуктивное определение:

1. f(q_i, a_j) определяется по таблице перехода автомата,

2. f(q_i,  a_j)= f (f(q_i, ), a_j).

Соответствующая функция выхода:

1. g(q_i, a_j) определяется по таблице перехода автомата,

2. g(q_i,  a_j)= g (f(q_i, ), a_j).

Тогда входному слову =a₁a₂….a_k ставится в соответствие выходное слово ()=g(q₀,a₁)g(q₀,a₁ a₂), …g (q₀, a₁a₂….a_k).

Это отображение, ставящее в соответствие входным словам выходные слова, называется автоматным отображение, или автоматным оператором, реализуемым автоматом S. Будем говорить, что S()=.

Автоматное отображение можно определить индуктивно, как и функцию переходов.

1. S(q₀, a_j)= g(q₀, a_j)

2. S(q_i,  a_j)= S(q0, )g (q₀, a), a_j).

Как и ранее, длина цепочки  обозначается.

Свойства автоматного отображения:

1.  и  = S() имеют одинаковую длину  S(a).

2. Если =₁₂, и S(₁₂)=₁₂, где a₁=₁, то S(a₁)= w₁.

Т.е. автоматный оператор является оператором без «предвосхищения», без заглядывания вперед, например, мы не можем построить инверсию слова.

Говорят, что состояние q_j достижимо из состояния q_i, если  V_a*, такая, что f(q_i, )=q_j.

Автомат S называется сильно связным, если любое состояние достижимо из любого другого.

Два автомата S и T изоморфны, если входы, выходы и состояния автомата S можно переименовать таким образом, чтобы таблица переходов автомата S превратилась в таблицу переходов автомата Т.

Например, автомат на рис. 26 изоморфен автомату на рис. 27. Если же заменить f на c на стрелке из q_C в q_A , то автоматы становятся неэквивалентны.

Соответствия:

a – b, b – a

c – c, d – f

q₀ – q_A

q₁ – q_B

q₂ - q_C




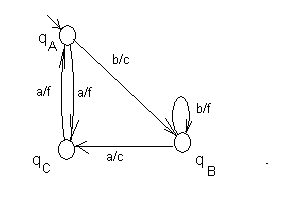
Рис.27. Автомат Мили, изоморфный автомату на рис. 26.

Пусть T и S автоматы с одинаковыми входными и выходными алфавитами. Состояние q автомата S и состояние r автомата T называются неразличимыми, если для любой входной цепочки Va* S(q,)=T(r,). При T=S говорим о неразличимых состояниях одного автомата.

Если неразличимы входные состояния двух автоматов, то они реализуют одно и то же автоматное отображение. В этом случае автоматы эквивалентны.

Переход от автомата к эквивалентному – эквивалентное преобразование автомата.

Автоматы Мура.

Отличаются от автоматов Мили тем, что здесь одному состоянию ( а не переходу) соответствует один выход.

Конечный автомат Мура: S=< V_a, Q, V_b, q₀, F, G>, где

V_a={a₁,a₂,…a_m}, m1 – входной алфавит автомата,

V_b= {b₁, b₂, …, b_n}, n1 – выходной алфавит автомата,

Q= {q₀,q₁,…q_k}, k0 – внутренний алфавит (алфавит состояний),

q₀Q – начальное состояние автомата,

F - функция переходов; F: Q V_a Q,

G - функция выходов, G: Q  V_b .

Приняты две схемы задания автоматов Мура:

Первая схема	Вторая схема
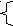q (t+1) =f (q(t), a(t)) b(t)= g(q(t))	q (t+1) =f (q(t), a(t)) b(t)= g(q(t+1))

При работе по первой схеме выход автомата однозначно соответствует состоянию, из которого совершается переход, по второй – состоянию, в которое автомат переходит. Хотя при записи уравнений первая схема выглядит более естественно, условие второй схемы реализовать проще: в соответствующих автоматах Мили для первой схемы должны быть одинаковые выходы на всех дугах, выходящих из состояния, для второй – одинаковые выходы должны быть на дугах, ведущих в состояние.

Рассмотрим автомат Мура, представленный на рис. 28



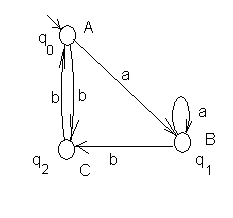
Рис.28 Автомат Мура

Здесь выходы, соответствующие состояниям, изображены справа от состояния. Если рассматривать работу автомата по первой схеме, то входу aabb будет соответствовать выход ABBC, если же по строй схеме, то этому же входу соответствует выход BBCA.

По автомату Мура всегда можно построить автомат Мили.

Автомат Мили, эквивалентный автомату Мура, представленному на рис. 28, при работе по первой схеме, дан на рис. 29, а при работе по второй схеме – на рис.30.



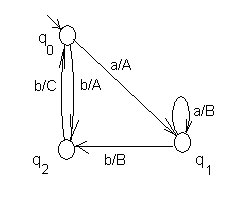
Рис. 29. Автомат Мили, эквивалентный автомату Мура на рис. 28, при работе по 1-ой схеме, здесь все дуги, ведущие из состояния, имеют одинаковые выходы.



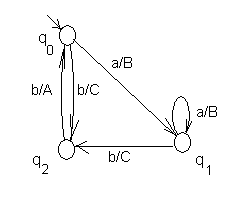
Рис.30. Автомат Мили, эквивалентный автомату Мура на рис. 28, при работе по 2-ой схеме, здесь все дуги, ведущие в состояние, имеют одинаковые выходы.

По выразительной мощности эти модели (автоматы Мили и Мура) эквивалентны, если используется вторая версия для представления автоматов Мура. (Очевидно, что по автомату Мура всегда можно построить автомат Мили.)

Построение автомата Мура (вторая схема) по автомату Мили:

а) Если все дуги, ведущие в некоторое состояние q_k, имеют одинаковые выходные пометки b_s, то эта пометка просто переносится на это состояние (рис.31).



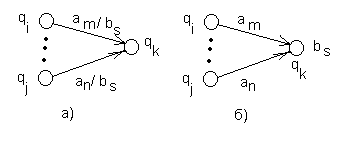
Рис. 31

Формально это условие для состояния q_k и выхода b_s можно записать так:

q_i,q_j,an,a_m (f(q_i,a_n)= f(q_j,a_m)= q_k  g(q_i,a_n)= g(q_j,a_m)= b_s)

б) Общий случай: в некоторые вершины ведут дуги, помеченные разными символами. В этом случае все q_k такие вершины расщепляются на множество вершин (расщепление состояния), помечаемых символами k,b_j> (рис.32).

q_k{k, b_s>/ f(q_i, a)=q_k, g(q_i, a)=b_s}




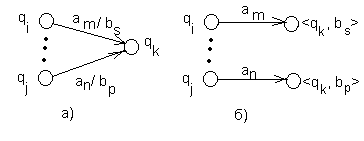
Рис. 32. Расщепление вершины.

В общем случае число состояний увеличивается. Затем для каждого состояния q_i исходного автомата Мили и для каждой дуги из состояния q_i в состояние q_k с пометкой a_p/b_s(a_p - вход, b_s - выход) строятся дуги из всех i,b_j> в k, b_s> и помечаются a_p.

Кроме того, если начальное состояние q0 расщепилось, вводится новое начальное состояние, в которое не ведет ни одна дуга.

Затем приписываем состояниям соответствующие выходы и переобозначаем состояния.

Например, рассмотрим автомат Мили (Рис. 33, а), приведенный так же на рис. 26. У этого автомата состояния q₁ и q₂ расщепляются, а q₀ нет, поэтому нет необходимости вводить новое входное состояние. Полученный эквивалентный автомат Мура приведён на рис. 33.б.





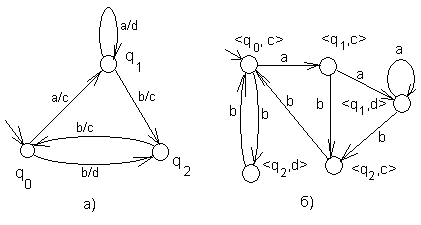
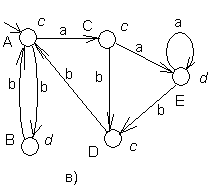
Рис. 33. Автомат Мили(а) и эквивалентный ему автомат Мура(б) до и после (в) переобозначения состояний.

Таким образом, полный алгоритм построения эквивалентного автомата Мура по автомату Мили выглядит следующим образом:

1. Расщепляем состояния.
   
2. Вводим дополнительное входное состояние (если входное состояние расщепилось).
   
3. Строим дуги, соответствующие дугам исходного автомата.
   
4. Переносим выходные символы на соответствующие состояния.
   
5. Переобозначаем состояния.
   

Таким образом, установлено соответствие между разными типами автоматов.

Частичные автоматы

Автомат S называется частичным автоматом, если хотя бы одна из двух функций (F или G) не полностью определена, т.е. для некоторых пар (состояние,вход) значение F или G не определено (обозначается прочерками в таблице).

Состояния A и B называются псевдоэквивалентными (обозначается AB), если они одновременно не определены или определены и равны функции F и G. Эти функции для частичных автоматов определяются следующим образом:

f(q_i,)

1. f(q_i, a_j) – по таблице переходов автомата
   
2. если f(q_i,) определена, то f(q_i, a_j)f(f(q_i,),a_j)
   
3. если f(q_i,) не определена, то не определена и f(q_i, a_j) для всех a_j.
   

g(q_i, a_j)

1. g(q_i, a_j) – по таблице переходов автомата
   
2. g(q_i, a_j)g (f(q_i,), a_j).
   

Автоматное отображение:

1. S(q_i, a_j)= g(q_i, a_j) (если g(q_i, a_j) не определено, то S(q_i, a_j) считаем равным прочерку)
   
2. если f(q_i,) определена, то S(q_i, a_j)=S(q_i,) g(f(q_i,) a_j). Если g(f(q_i,), a_j) не определена, то считаем её равной прочерку)
   
3. если f(q_i,) не определена, то не определена и S(q_i, a_j) для всех a_j.
   

Входное слово , для которого S(q_i,) определено, называется допустимым для S.

Отметим неравноправность функций f и g – неопределенность g не препятствует допустимости слова, а неопределенность функции f для некоторого слова говорит о недопустимости любого его продолжения.

Состояния q_i  S и r_jT псевдонеотличимы (псевдоэквивалентны), если для любой цепочки  S(q_i,)T(rj,) (Т.е. области определённости и неопределённости для q_i и r_j совпадают, и в области определённости отображения совпадают).

Автоматы S и T псевдонеотличимы, если для любого состояния автомата S найдётся псевдонеотличимое от него состояние автомата T, а наоборот, для любого состояния автомата T найдётся псевдонеотличимое от него состояние автомата S.

Для полностью определённых автоматов псевдонеотличимость совпадает с обычной неотличимостью.

Отношение псевдонеотличимости является отношением эквивалентности.

Пример псевдоэквивалентных автоматов приведён на рис.34.



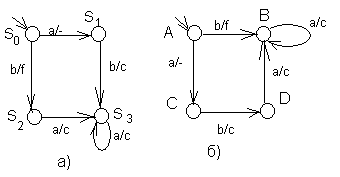
Рис.34. Пример псевдоэквивалентных автоматов. Здесь соответствия состояний

S0 – A S2 – B, D S3 – B, D S4 - C

A – S0 B – S3,S2 C – S1 D – S2,S3

Недостаток введённого определения псевдоэквивалентности – необходимость совпадения областей определения. Можно дать эквивалентное определение, не требующее анализа совпадения областей: вводим новое, дополнительное состояние, переход в которое осуществляется при отсутствии перехода по данному входу, для которого переход по любому входу осуществляется в само себя, а в функции выхода прочерк будем рассматривать как дополнительную букву, таким образом автомат становится полностью определённым.

Минимизация не полностью определённых автоматов возможна двух типов: «строгая», с сохранением областей определения (что производится просто, как для доопределённого автомата), и через покрытия состояний, когда требуется совпадение переходов только в области определённости.

Если проводить строгую минимизацию, то автомат на рис. 34 а минимизируется до автомата, граф переходов которого приведен на рис. 35.



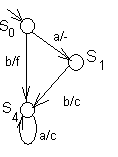
Рис. 35. Минимизированный автомат.

Два основных аспекта работы автомата:

1. Автоматы распознают входные слова, т.е. отвечают на вопрос М? (распознаватели)
   
2. Преобразуют входные слова в выходные( автоматные отображения):
   

с одной стороны, последовательность ответов распознавателя на входные слова а₁, а₁а₂, … образуют выходное слово, которое является автоматным отображением;

с другой стороны, выходные буквы можно разбить на два класса С₁ и С₂, и считаем, что слово распознаётся, если g(q_i,) С₁. Таким образом, эти два представления автоматов являются эквивалентными.

Интерпретация автоматов: Дискретное устройство, входная буква – входной сигнал, выходное слово – последовательность сигналов.

Свойство автоматов:

Теорема:

Существуют события, не представимые в конечных автоматах: никакая непериодическая последовательность не распознаваема в конечных автоматах( например, 010110111011110111110…)

Док-во:

Пусть непериодическая последовательность a₁a₂…a_j… распознаётся автоматом S с n состояниями. Тогда для любого начального отрезка a₁a₂…a_j f(a₁a₂…a_j)= q_k C₁. но тогда проходится последовательность состояний из C₁, а оно конечно, значит, некоторое состояние встретится дважды: q_s=q_s+p. Значит, f(q_s, a_s+1…a_s+p)=q_s, поэтому периодическая последовательность так же будет распознаваться автоматом, и, следовательно, непериодическая последовательность не может распознаваться конечным автоматом вопреки предположению.