1. Алфавит, слова, операции над словами

Вид материала

Документы

Содержание 11. Синтаксический анализ для КС-языков S  abcca S  abcca

Подобный материал:

• Исполнительный кодекс Республики Молдова, 2184.07kb.
• Статьи 4 изложить в следующей редакции: "Статья Ответственность физических, юридических,, 41.3kb.
• Республика Молдова, 777.62kb.
• Федеральный закон, 404.04kb.
• Подготовка к операции по прорыву блокады проводилась в глубокой тайне, 18.04kb.
• Игра «Алфавит» Чтобы узнать тему нашего занятия вы должны расшифровать слова. (зашифрованные, 50.79kb.
• «День культуры и славянской письменности», 78.75kb.
• Выполнили: Фурманова Диана 3класс, 121.65kb.
• Работа со словами с непроверяемыми написаниями, 134.51kb.
• Календарно-тематический план учебная дисциплина: «Математика», 34.71kb.

11. Синтаксический анализ для КС-языков

Может рассматриваться синтаксический анализ в широком или же узком смысле. Синтаксический анализ в узком смысле – по цепочке определить её структуру (или же построить синтаксическое дерево). Т.Е. задача сводится к построению вывода данной цепочки в данной грамматике.

Синтаксический анализ в широком смысле – определение, может ли данная цепочка быть построена с использованием данной грамматики. Это в общем случае гораздо более сложная задача.

Существующие алгоритмы синтаксического анализа классифицируются по:

1. Cпособу построения вывода : нисходящие, восходящие, смешанные
   
2. Способу выбора альтернативы: детерминированные и недетерминированные. В первом случае на каждом шаге выбирается правильная альтернатива, во втором – альтернатива выбирается наугад.
   
3. Способу возврата (для недетерминированного выбора альтернативы): разбор с быстрым или медленным возвратом.
   
4. По степени доступности цепочки: или цепочка доступна вся сразу, или же читается слева направо посимвольно (при этом доступно для анализа определенное число символов).
   

Обычно рассматривается нисходящий или восходящий разбор при чтении цепочки слева направо.

Типовая задача синтаксического анализа:

Имеется активный нетерминал S и множество альтернатив:

S___k и текущее состояние анализируемой цепочки Y. Пусть выбрана альтернатива SX₁X₂…X_n, X_iV_NV_T, при i[1,n]. Если X₁ V_T, то он должен совпадать с первым символом цепочки Y. Если совпадает, то укорачиваем цепочку на этот символ и переходим к X₂. Если не совпадает, то переходим к другой альтернативе.

Если же X_iV_N, тогда из X_i необходимо вывести какое-нибудь начало цепочки Y. Если из X_i нельзя вывести никакое начало цепочки Y, то возможны 2 варианта:

1). Сразу перейти к X_i-1 и попытаться вывести из X_i-1 другое начало и т.д. ( получаем полный перебор вариантов вывода) – разбор с медленным возвратом.

2). Сразу отказаться от альтернативы SX₁X₂…X_n (разбор с быстрым возвратом).

Очевидно, что наиболее удобными при анализе цепочек являются грамматики, допускающие детерминированный разбор, когда на каждом шаге мы можем однозначно выбрать альтернативу, и в случае невозможности подобрать нужную альтернативу цепочка не принадлежит языку (никакой вывод не может быть построен). Одним из таких типов грамматик являются LL(k)-грамматики.

11.1 LL(k)-грамматики

LL(k)-грамматиками называются грамматики, допускающие детерминированное построение левого разбора (left) при чтении анализируемой цепочки слева (left) направо, подсмат­ривая вперед не более чем на k символов.

Например, рассмотрим грамматику с множеством правил:


S 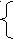a SbB

B  b B


Эта грамматика является LL(1)-грамматик, т.к. для выбора правильной альтернативы на каждом шаге нам достаточно анализировать один (текущий) символ цепочки.

Грамматика называется разделённой, если все правила грамматики имеют вид

Aa₁₁a₂ ₂…a_k_k, причём a_ia_j при ij, a_iV_T, _i(V_TV_N)* при i[1,k]. Очевидно, что в случае разделённой грамматики строится детерминированный нисходящий разбор.

Очевидно, что разделённые грамматики принадлежат к классу LL(1) грамматик. Грамматики могут оказаться LL(k) грамматиками для различных k, например, грамматика может быть LL(3) грамматикой, но не LL(2) грамматикой. Бывают и грамматики, которые не являются LL(k) грамматикой ни для какого k.

Например, рассмотрим грамматику с множеством правил:

S 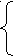0 S0B

A  0 A ac L(G)= {0ⁿ⁺¹ c aⁿ, 0ⁿ⁺¹ d bⁿ, n 0}

B  0 B bd

S_l A ⁿ⁺¹0ⁿ⁺¹ с aⁿ

S_l B ⁿ⁺¹ 0ⁿ⁺¹ d bⁿ ( n  0 ).

Чтобы определить по заданной терминальной цепочке, ка­кое правило ( S  A или S  B ) было применено на первом шаге вывода, нужно прочитать n+1 символ, следовательно данная грамматика не является LL(k) ни при ка­ком k

Дадим формальное определение LL(k) грамматики. Для этого введем определение

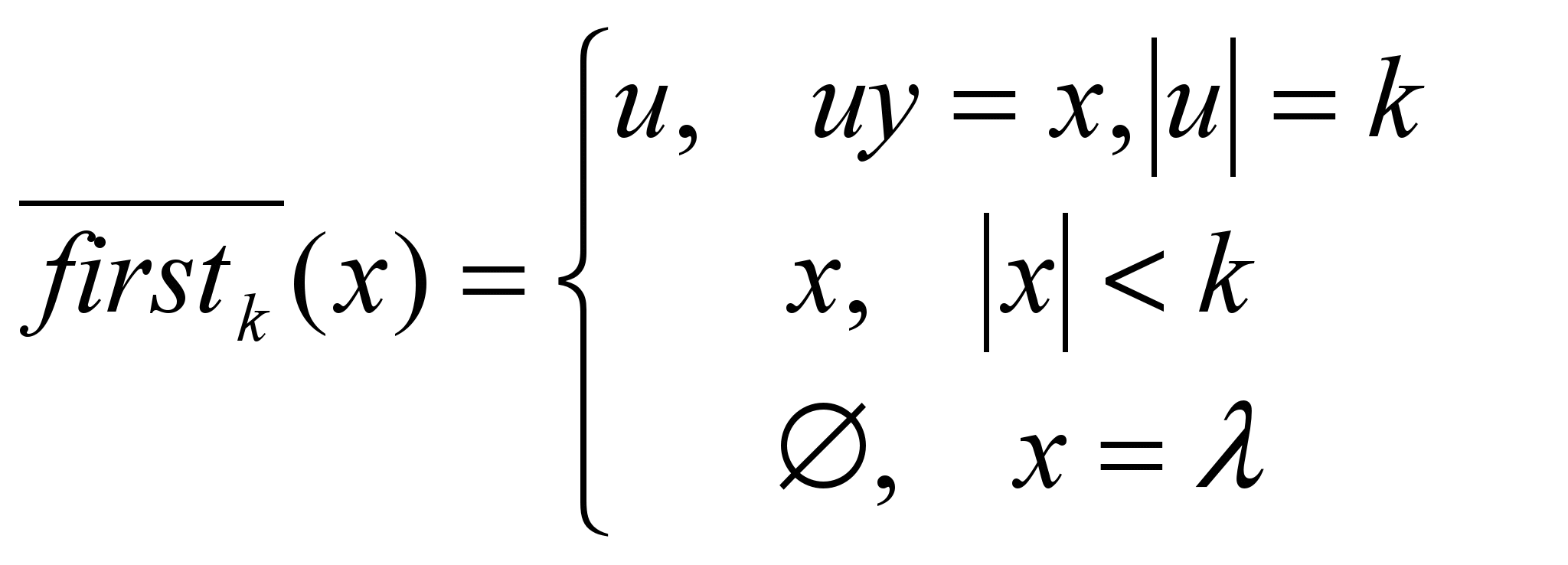
• определяются первые k символов терминальной цепочки. Т.к. для пустой цепочки это пустое множество, то определим для данной грамматики пополненную грамматику, к которой не будут встречаться пустые цепочки:
  

Для грамматики G=< V_T,V_N, S, R> соответствующая пополненная грамматика G’=< V_T{$},V_N{S’}, S’, R’>, где множество правил R’=R{S’ S $ }, где каждая цепочка имеет справа граничный маркер($).

Расширим определение множества first так, чтобы охватить произвольные цепочки (V_TV_N)*:

Для (V_TV_N)* First_k()= { x/ * Z, ZV_T*, x=}.

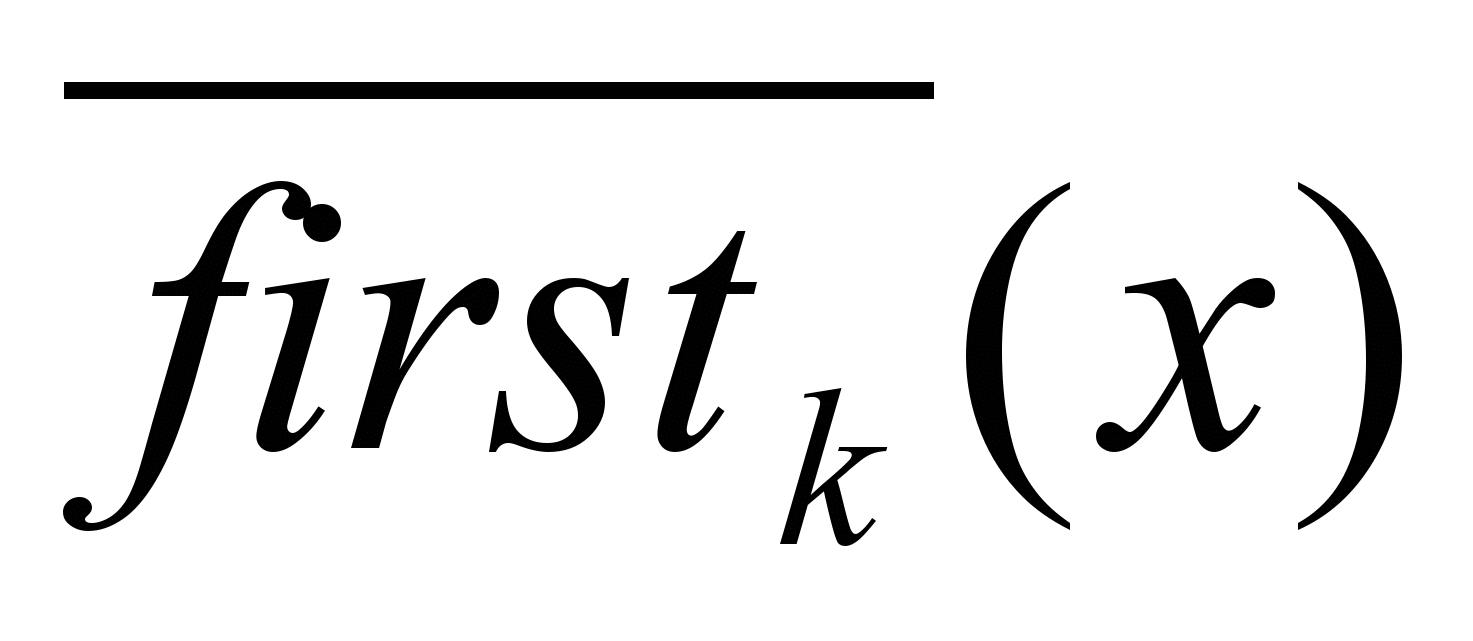Например, рассмотрим грамматику с множеством правил

S 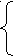 abAabB

A  ab A c L(G)= {(ab)ⁿc, (abc)ⁿ, n 1}

B  cab Bc

Правила соответствующей пополненной грамматики:

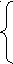S’ S $

S ® abA½abB

A ® ab A ½c

B ® cab B½c


Для данной грамматики

First₁(S)={a}, First₁(A)={a, c}, First₁(B)={c}; First₂(S)={ab}, First₂(A)={ab, c$}, First₂(B)={c$, ca}, First₃(S)={abc}, First₃(A)={abc, c$}, First₃(B)={c$, cab}.

Тогда мы можем формально определить LL(k) грамматику как грамматику, для которой для любых двух левых выводов

S* A      * x

S* A      * y

AV_N, , x, y  V_T*,     (V_N  V_T)*, из условияFirst_k(x)=First_k(y) следует .

Несложно показать, что наше формальное определение соответствует не формальному.

Теорема: LL(k) грамматика является однозначной.

Неоднозначность грамматики противоречит LL(k) свойству. Неоднозначна – значит, существуют два вывода для некоторой цепочки, значит, не сможем определить по k символам, каое из правил следует применить.

Теорема: КС-грамматика G=< V_T,V_N, S, R> является LL(k) грамматикой  для любых двух правил А₁ и А₂ First_k(₁ ) First_k(₂ )= для любой цепочки , такой что S*A.

Использование LL(k) свойства при построении анализатора.

Пусть текущее состояние левого вывода цепочки z=y имеет вид А, где  выведенное терминальное начало цепочки, А – текущий нетерминал( самый левый нетерминал), y не просмотренная часть цепочки.

Рассмотрим First_k(y). Пусть для нетерминала А существуют альтернативы:

А₁₂_n R. Надо найти _i для применения на данном шаге. Для этого надо вычислить 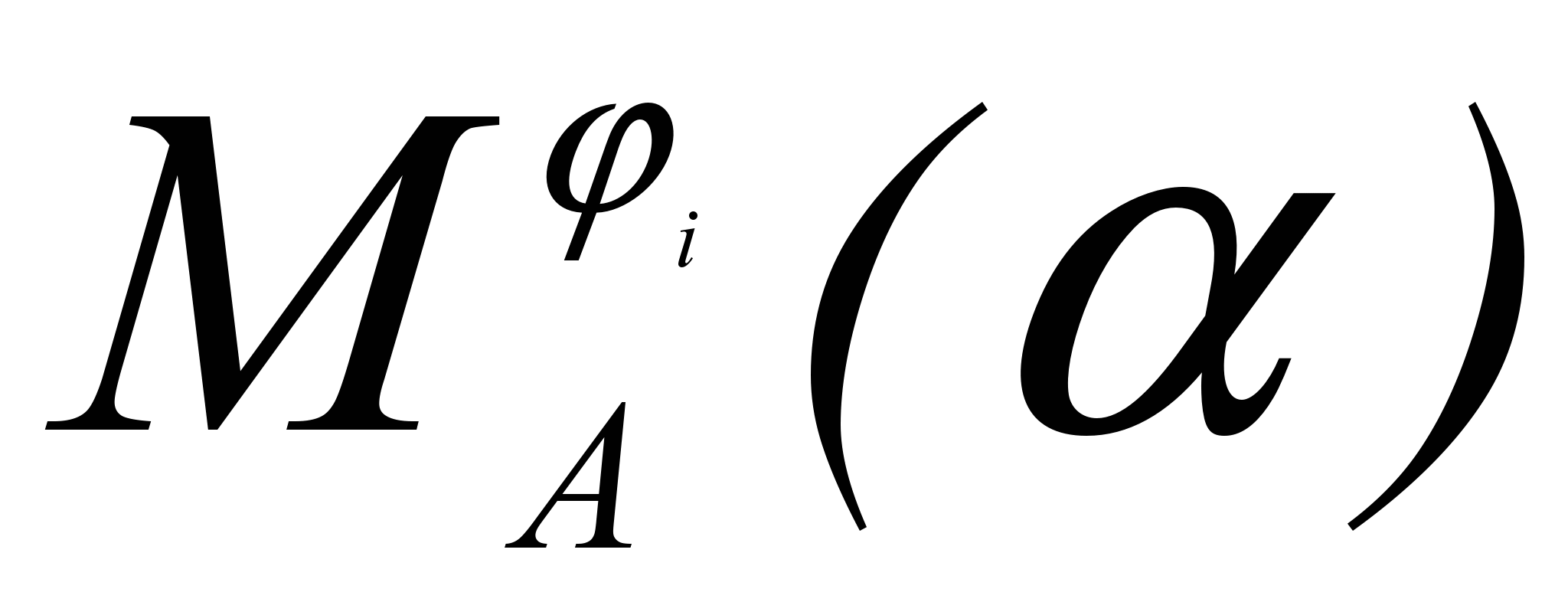=First_k(_i). Это множество может быть заранее вычислено для всех А, , _i. При этом из LL(k) свойства следует, что 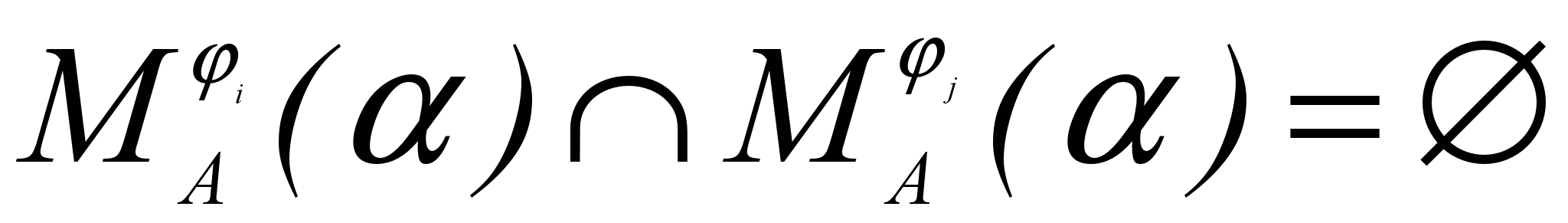при ij.

Выбираем _i, такое, что First_k(y)= First_k(_i). Если такого _i нет, то zL(G).

Затем переходим к анализу полученной цепочки xy’y’, где ’ – терминальное начало цепочки ₁.

Шаги повторяются, пока не разберём всю цепочку, или не установим, что zL(G).

Пример:

Рассмотрим анализ цепочки acbbd в грамматике

S 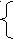ac SbB

B  b Bd


Эта грамматика является LL(1) На первом шаге определяем, какое правило применялось вначале: First₁(acS)={a}, First₁(bB)={b}, поэтому на первом шаге применяется правило S ac S, анализируемая цепочка принимает вид:bbd, First₁(bbd)={b}, поэтому применяется правило S  bB, и анализируемая цепочка принимает вид bd. Определяем First₁(bB)={b}, First₁(d)={d}, поэтому применяемое правило B  b B, анализируемая цепочка принимает вид d, применяем правило B  d, остается пустая цепочка как в выводе, так и анализируемая цепочка, поэтому анализируемая цепочка принадлежит языку, порождаемому грамматикой.

Проблемы, возникающие при построении анализатора для LL(k) грамматик:

1. При k1 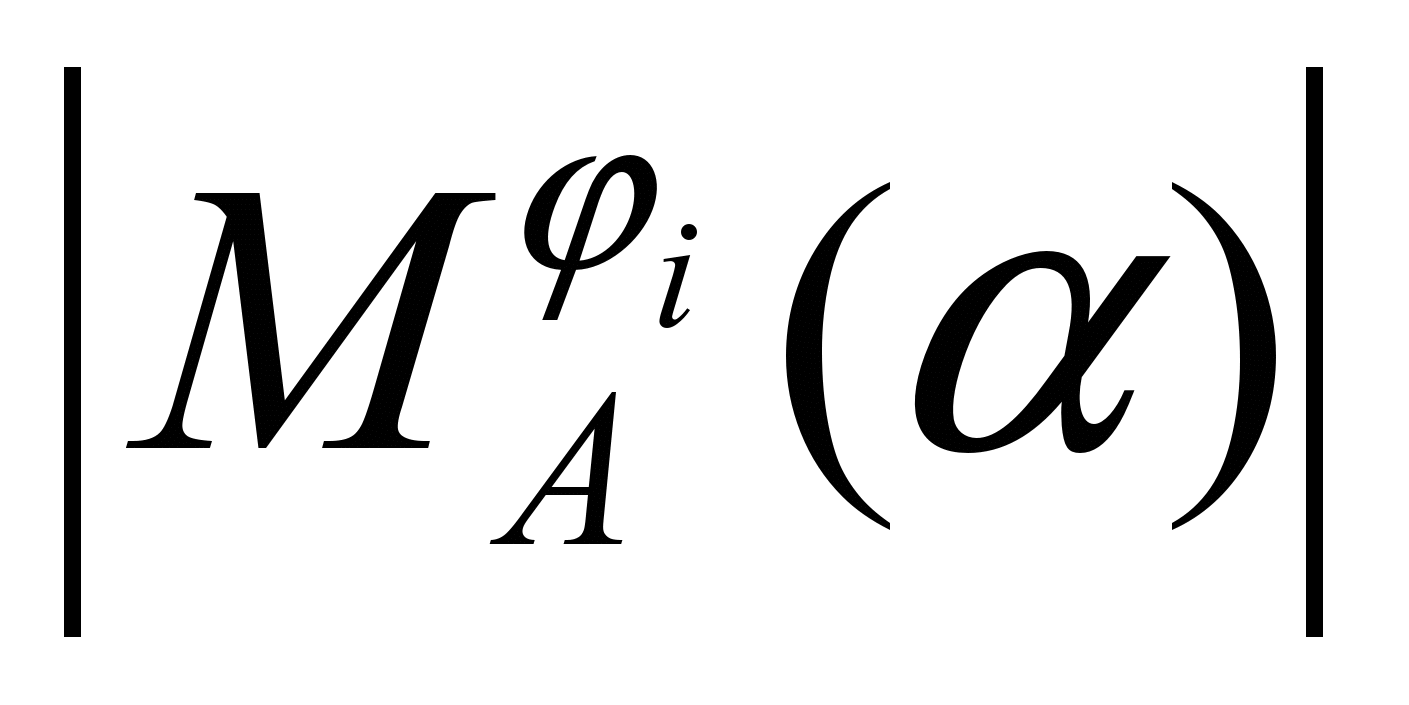может стать неприемлемо большой , т.к. 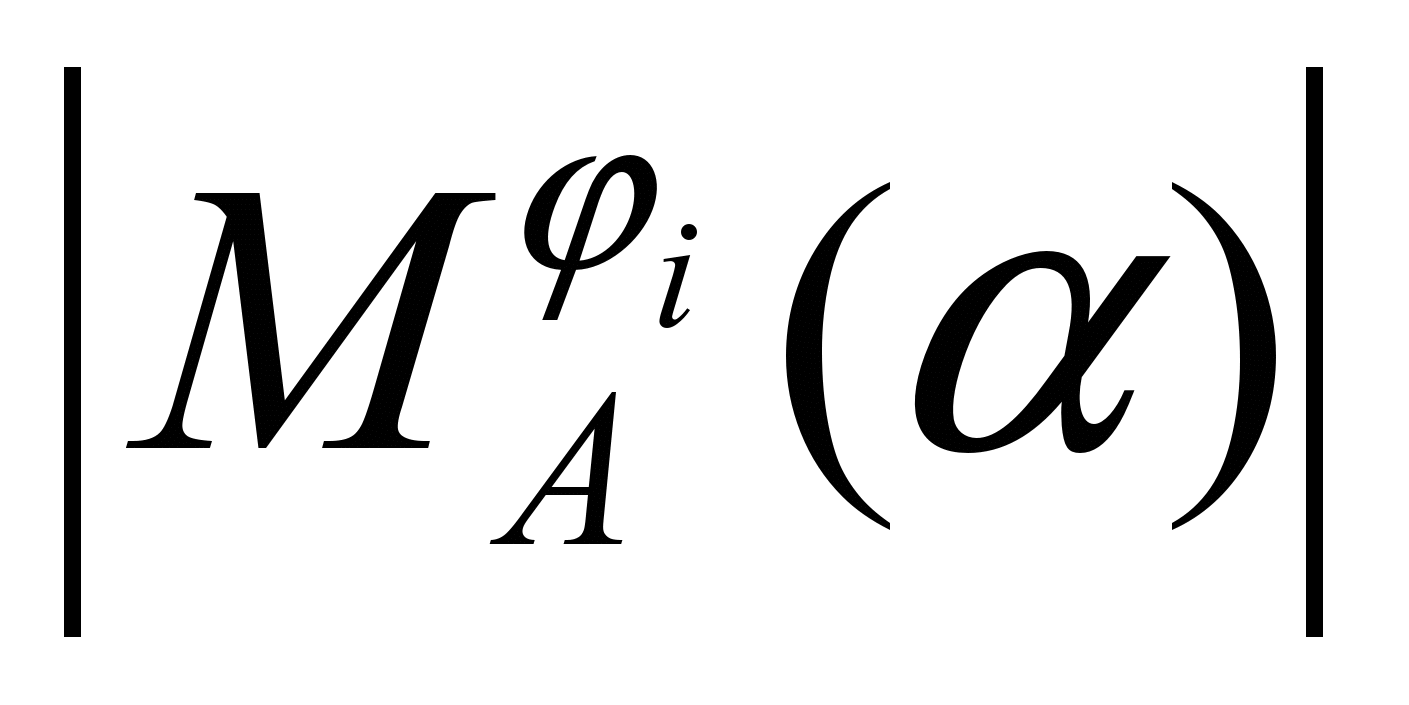пропорциональна k.

2. 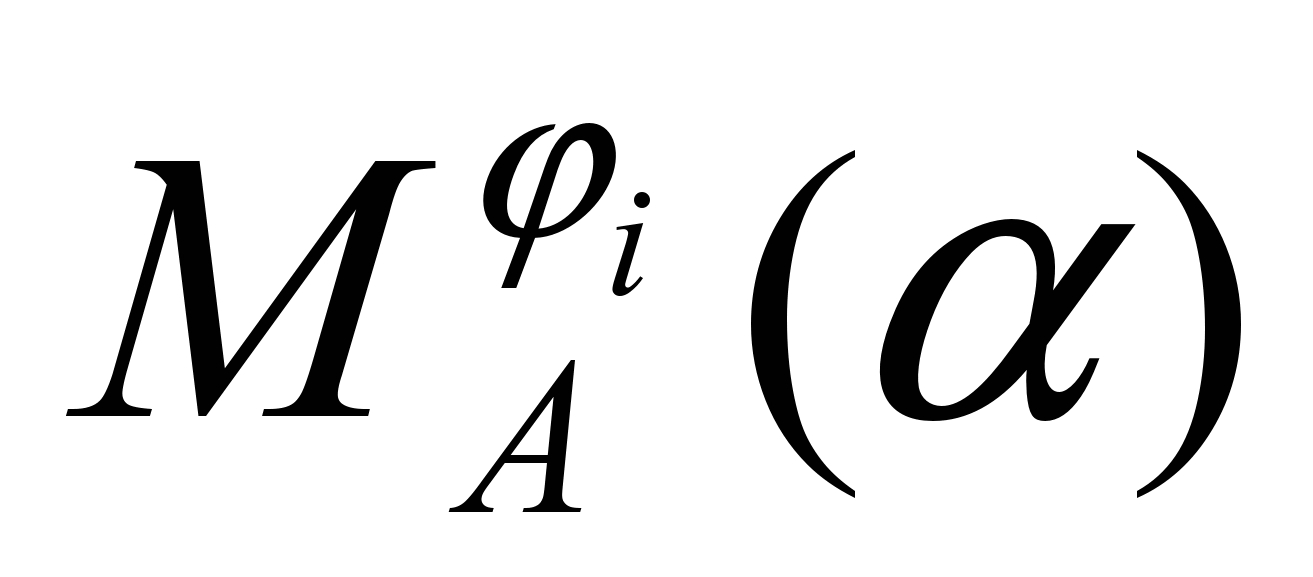является функцией от трёх переменных: А, _i,  - т.е. велик сам объём предварительных вычислений.

Однако можно упростить задачу, усилив условия, накладываемые на грамматику:

Обозначим 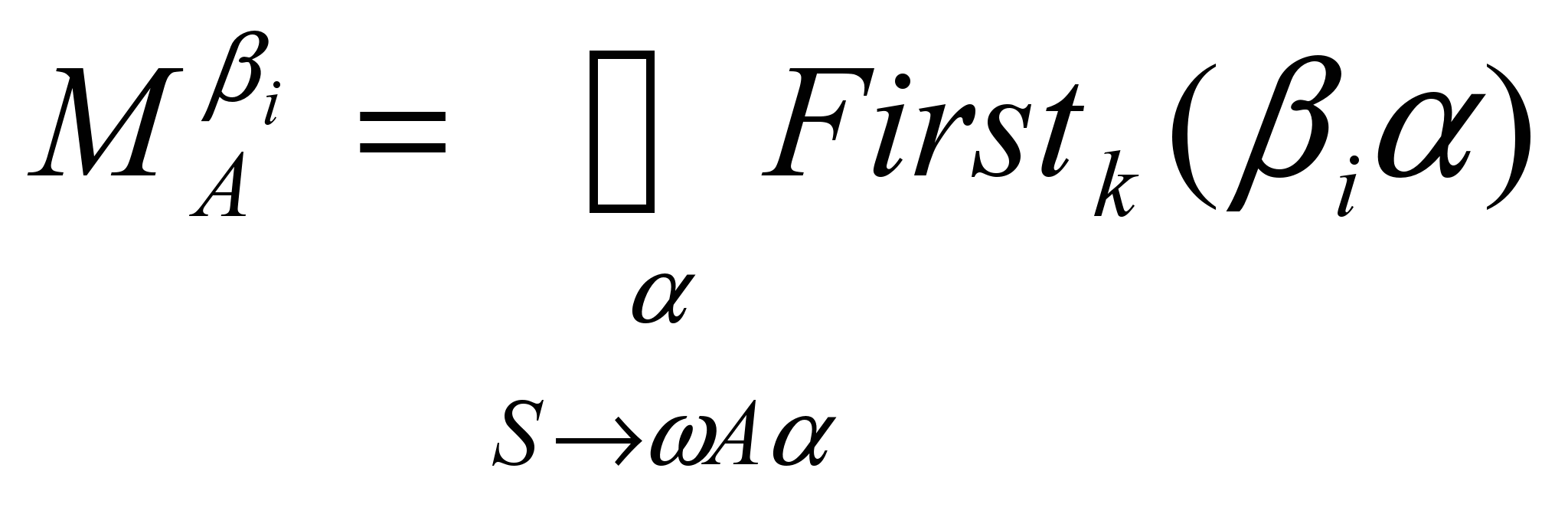и потребуем, чтобы 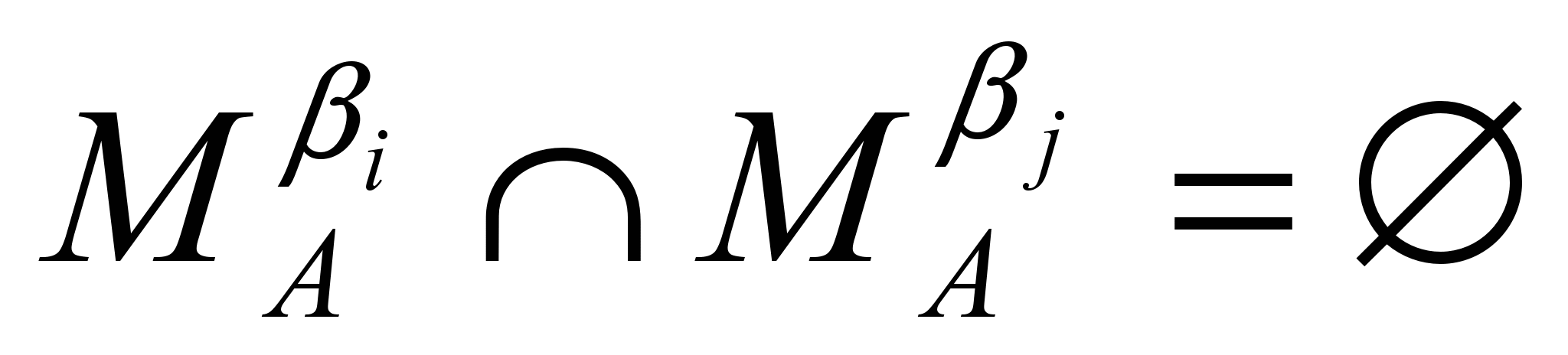при ij.

Грамматика G называется строго LL(k) грамматикой, если для любых двух левых выводов

S*₁ A ₁ ₁  ₁ *₁x

S*₂A ₂  ₂  ₂  *₂ y

AV_N, ₁, ₂, x, y  V_T*, ₁ ₂    (V_N  V_T)*, из условияFirst_k(x)=First_k(y) следует . Несложно показать, что G является строго LL(k) грамматикой  для любого AV_N из того, что AR, AR, , следует, что M_A^M_A^=.

Теорема: LL(1) грамматика всегда строго LL(1) грамматика.

Доказательство:

Предположим, что некоторая грамматика G - LL(1) грамматика, но не строго LL(1) грамматика. Тогда существуют два вывода

S*₁ A ₁ ₁  ₁ *₁x₁₁ *₁x₁y₁

S*₂A ₂  ₂  ₂  *₂ x₁₂ *₁ x₂y₂,

Такие, что First₁ (x₁y₁)= First₁(x₂y₂) &  - Условие (*).

Но т.к. G - LL(1) грамматика, то
S*₁ A ₁ ₁  ₁ *₁x₁₁ *₁x₁y₁

S*₁ A ₁ ₁  ₁ *₁x₂₁ *₁x₂y₁

и из First₁ (x₁y₁)= First₁(x₂y₁) следует, что  - Условие (**).

Покажем, что условия (*) и (**) несовместны.

Рассмотрим следующие случаи:

1. x₁, x₂ , тогда First₁(x₁y₁)=First₁(x₁), First₁(x₂y₂)=First₁(x₂), First₁(x₁ )=First₁(x₂)по условию (*) .

С другой стороны, по условию (**) First₁(x₁ )=First₁(x₂). Противоречие.

2. x₁=, x₂= приводит к неоднозначности грамматики.

3. Пусть x₁=, x₂. Тогда в условии (*)First₁(x₁y₁)=First₁(y₁)= First₁(x₂y₂)=First₁(x₂) & 

По условию (**) First₁(x₁y₁)=First₁(y₁)= First₁(x₂y₁)=First₁(x₂) & =. Противоречие.

Случай 4, x₁¹l, x₂=l разбирается аналогично случаю 3.

Из теоремы следует критерий принадлежности грамматики классу LL(1):

G – LL(1) M_A^M_A^= при  для всех AV_N, где M_A^b=


При этом если

а) ,*, , то M_A^=First₁()

b) *, M_A^=First₁()

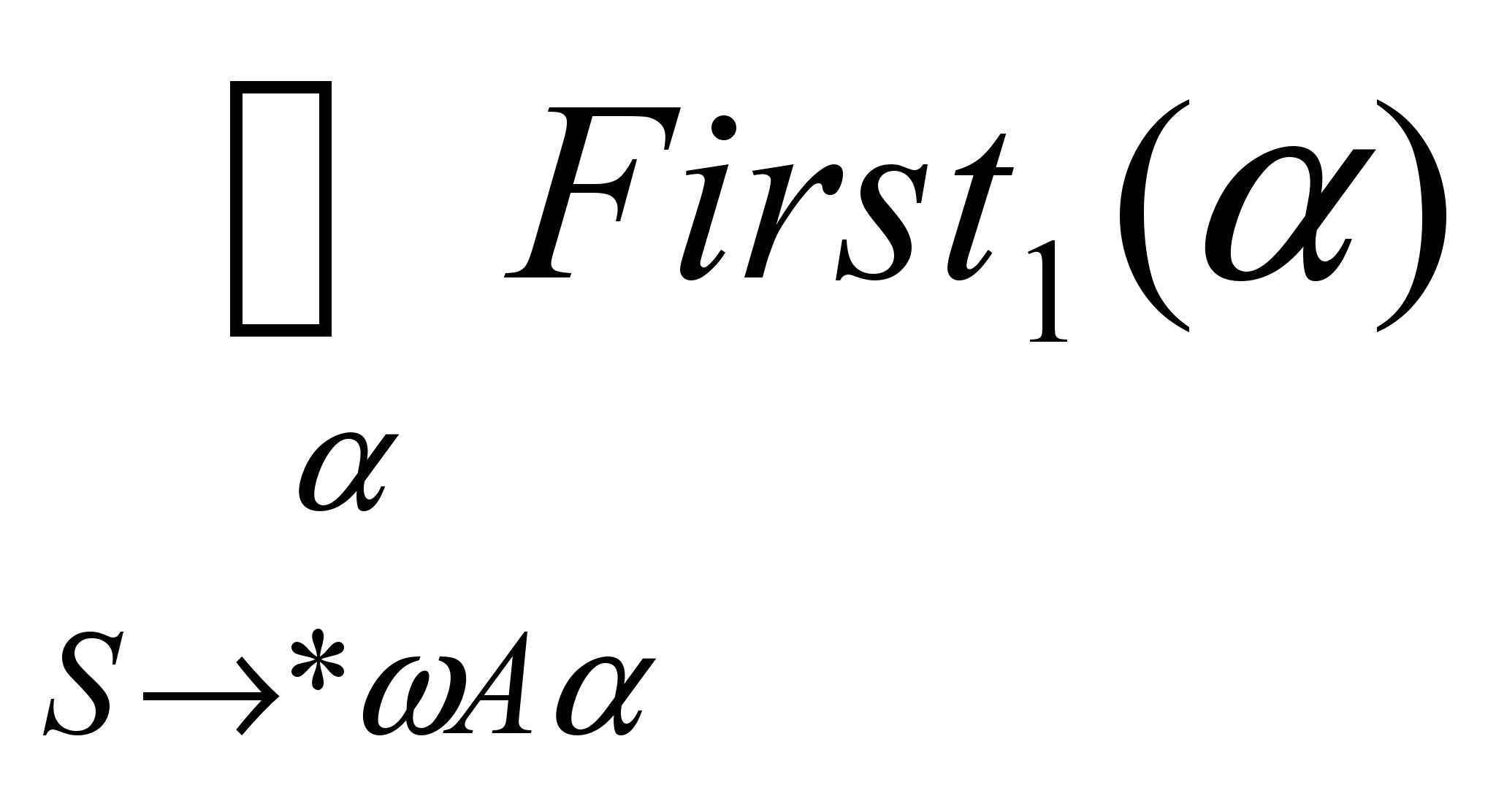
Т.К. рассматриваем пополненную грамматику, то  (First₁()=).

Определим множество Follow₁(X)={a/ S⁺Xa&aV_T}, X(V_NV_T).

Т.о. G - LL(1) грамматика  AV_N, , AR&AR&  M_A^M_A^=.

Определения и алгоритмы нахождения множеств First и Follow

1. First₁()

1. First₁()=
   
2. aV_T First₁(a)=a
   
3. First₁(A)={ First₁(x_i)/Ax₁x₂…x_nR&i=1i=m&x₁…x_m-1⁺}
   
4. First₁(x₁x₂…x_n)={ First₁(x_i)/ First₁(x₁)& i=1i=m&x₁…x_m-1⁺}
   

Например, рассмотрим грамматику:

S 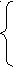 ABCCA

Aa

B  b B

CcCd

В пополненной грамматике добавляется начальной правило S’ S$.

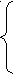S’ S

S  ABCCA

Aa

B  b B

CcCd


First₁(A)={a};

First₁(B)={b};

First₁(C)={c,d};

First₁(S)= First₁(ABC) First₁(AC)={a, b, c, d}

2. Follow₁(A)= 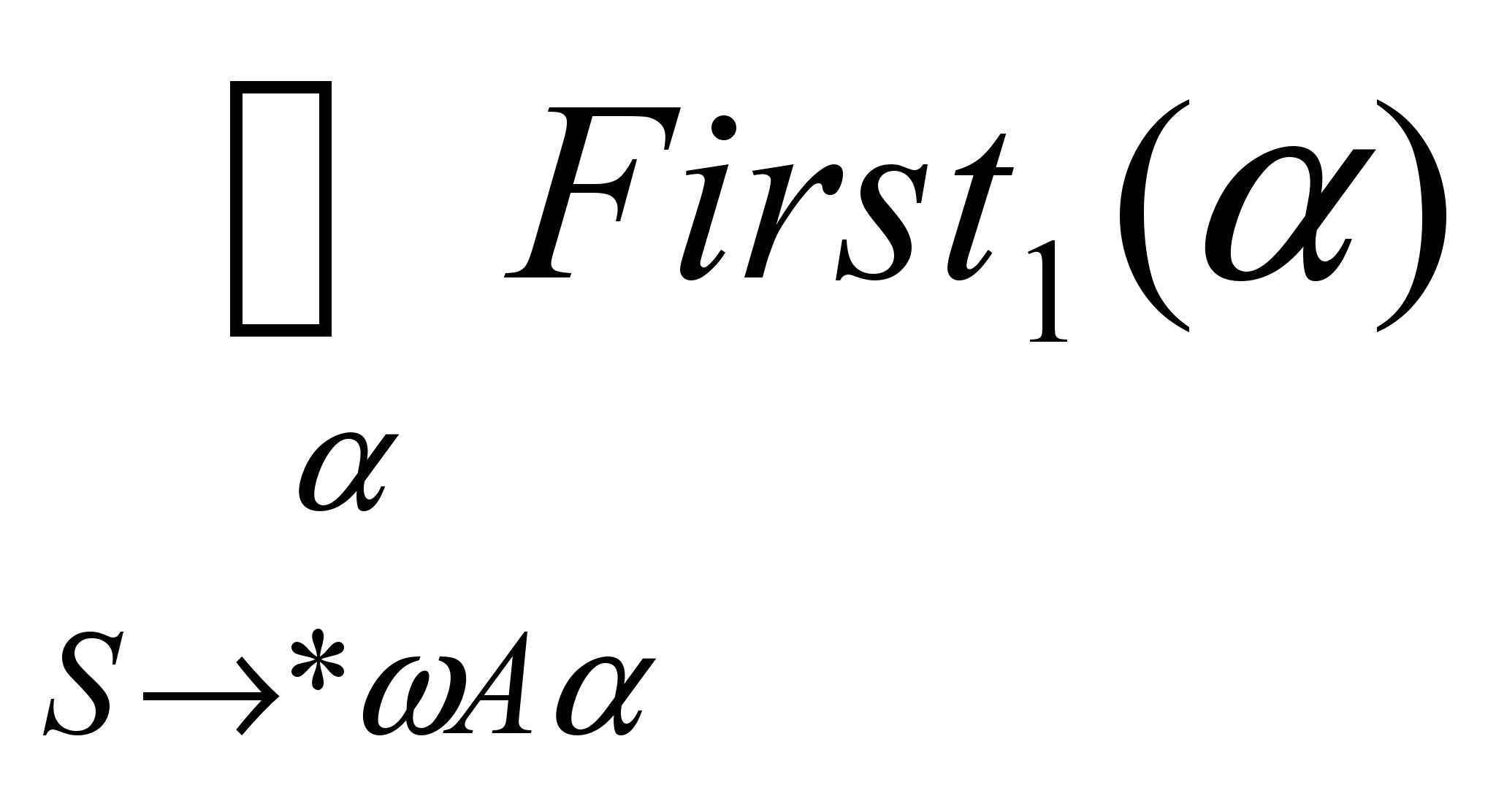={First₁()/ S * A  }
   

Рассматриваем грамматику без непроизводящих правил, тогда если S * B    A  , то First₁( ) Follow₁(A).

1. Неверно, что *, тогда First₁()=First₁().
   
2. *, тогда First₁()=First₁()First₁().
   

Поэтому Follow₁(A)={ First₁(Xm)/ B A X₁ X₂…X_nR&m=1X₁X₂…X_m*} {Follow₁(B)/B A  R &*}

Т.е. просматриваются все правые части правил, в которые входит исследуемый нетерминал.

Рассмотрим грамматику

S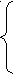’ S $

S  ABCCA

Aa

B  b B

CcCd

Здесь N_={A,B}

Follow₁(S)={$},

Follow₁(A)= First₁(B) First₁(C)  Follow₁(S)={b, c, d, $},

Follow₁(B)= First₁(C)={c,d},

Follow₁(C)= First₁(A) ) Follow₁(S)={a,$}.

Проанализируем LL(1) свойство грамматики:

M_S^ABC= First₁(A) First₁(B) First₁(C)={a, b, c, d},

M_S^CA= First₁(C)={c,d}.

Т.к. M_S^ABC M_S^CA , то грамматика не является LL(1) –грамматикой.

Восходящий анализ.

При восходящем анализе цепочка сворачивается путем применения правил в обратном порядке (дерево вывода строится снизу вверх).

Введенные строки анализируются слева направо, полученные подстроки сопоставляются в правыми частями грамматики, и при совпадении заменяются на соответствующий нетерминальный символ в левой части правила (свёртка). Цепочка, заменяемая на этот символ, называется основой.

Если свёртываемая основа выбирается случайно, то может потребоваться возврат, и число шагов построения вывода пропорционально длине цепочки.

Среди грамматик выделяется класс LR(k) грамматик - тот тип грамматик, для которых однозначно восстанавливается правый вывод (R) при чтении цепочки слева (L) направо, при подглядывании вперёд не более чем на k символов.

Алгоритм такого разбора в общем случае сложен, поэтому чаще всего рассматривается удобный подкласс ГПП (грамматики простого предшествования) – частный случай LR(k) грамматик, в которых для выделения основы используются отношения простого предшествования.

Пусть цепочка X получена G=< V_T,V_N, S, R> с помощью правого вывода:

S₁₂…._n=X (V_T)*.

Тогда при восходящем анализе будем иметь

X=_n ├ _n-1 …├ ₀ = S.

Выделим i-ый шаг вывода S*Ay (=_i-1)   y (=_i)*x y, здесь Ay текущее состояние правого вывода, A – самый правый нетерминал в выводе. Свёртка состоит в переходе от   y к aAy, (a j y├ aAy) т.е. мы должны выделить подцепочку j, которая сворачивается в нетерминал A применением правила A j в обратном порядке.

Пример разбора цепочки для грамматики с арифметикой.

Для ГПП техника выделения основы следующая:

Строится матрица отношений предшествования между символами V_TV_N. При этом между парой символов х и y может существовать не более одного отношения предшествования, обозначаемого символами <, ≗, >.

Грубо говоря, отношения предшествования отражают порядок появления символов в правом выводе.

Если a j y – текущее состояние цепочки, где j – основа, то

Между всеми смежными символами цепочки , выпол­няется отношение < или ≗ .

2. Между последним символом цепочки  и первым символом цепочки  (основы) выполняется отношение < .

3. Между смежными символами основы выполняются отношения ≗.

4. Между последним символом основы и первым символом цепочки у выполняется отношение >.

Если такое свойство отношений имеет место и для каждой пары символов определено не более одного отношения, то осно­ву легко выделить, просматривая цепочку   y слева направо до тех пор, пока впервые не встретится отношение >. Для нахождения левого конца основы надо возвращаться назад, пока впервые не встретится отношение < . Цепочка, заключенная между < и > и будет основой. Если в грамматике нет правил с одинаковыми правыми частями, то однозначно находится нетер­минал А такой, что A   , что позволяет свернуть основу, полу­чая цепочку _i-1 .

Этот процесс продолжается до тех пор, пока цепочка либо не свернется к начальному символу S, либо дальнейшие свертки окажутся невозможными.

Отношения простого предшествования с указанными свойствами могут быть определены на V_NV_T следующим образом [1]:

X < Y, если в R есть правило A  X B , и при этом B^Y;

X ≗ Y, если в R есть правило A  X Y .

Отношение > определяется на (V_NV_T)  V_T , так как непосредственно справа от основы может быть только терминальный символ.

X  > a, если в R есть правило A  X Y , и B ⁺  X, Y* a . Так как основа может совпадать с правым или левым кон­цом цепочки, то удобно заключить анализируемую цепочку в концевые маркеры $ и $ , положив для X V_NV_T, X  > $ для всех X, для которых S ^  X и X< $ для всех X, для которых S ^ X .

Грамматика G называется грамматикой простого предшествования, если она не содержит -правил, для любой пары символов из V_NV_T выполняется не более одного отношения простого предшествования и в ней нет правил с одинаковыми правыми частями.

Выполнение этих требований, очевидно, гарантирует возможность на любом шаге разбора однозначно выделить основу и произвести свертку.

Пример. Пусть множество правил грамматики: S a S S b, S c. Для заключения цепочки в маркеры вводим новый начальный символ S’и правило S’$S$. Отношения предшествования для этой грамматики приведены в табл.1.

	S	a	b	c	$
S	≗	<	≗	<
a	≗	<		<
b		>	>	>	>
c		>	>	>	>
$		<		<

Разбор цепочки $accb$.$<a<c>cb$├$<a≗S<co>b$├$<a≗S≗S≗bo>$├$S$

Вывод, соответствующий этому разбору:

S’ $ S $$ a S S b $$ a S c b $$ a c c b $
Способ построения свёртки для цепочки связан с использованием стека, куда посимвольно переносится информация из входного буфера, до тех пор, пока не встретится отношение >. Тогда к цепочке от отношения > до ближайшего слева отношения < должна применяться свёртка.

Алгоритм разбора для ГПП:

1. Анализируемая цепочка заключается в маркеры.

2. Берём очередной символ из входного буфера (слева направо). Если между верхним символом стека и первым символом входной цепочки отношение<o или ≗ , то заносим этот символ из входной цепочки в стек и возвращаемся к шагу 2, если же между верхним символом стека и первым символом входной цепочки отношение o>, то переходим к шагу 3. Если между символами нет никакого отношения предшествования, то цепочка не принадлежит языку, порождаемому грамматикой.

3. Обратное движение: из стека вынимаются символы до первого отношения <o между первым символом стека и символом цепочки во входном буфере. Если такой символ появился, то переходим к шагу 4, иначе цепочка не принадлежит языку, порождаемому грамматикой.

4. Применяем свёртку (заменяем выделенный фрагмент на левую часть правила грамматики, правая часть которого совпадает с основой) и возвращаемся к шагу 2. Если свёртка неприменима (нет такой правой части правила), то цепочка не принадлежит языку, порождаемому грамматикой.

Если в результате применения свёртки мы приходим к цепочке $ S $, то исходная цепочка принадлежит языку, порождаемому грамматикой, в противном случае цепочка не принадлежит языку, порождаемому грамматикой.

Обозначим

Head(A)={X/A⁺X} (First1(A)=Head(A) V_T),

Tail(A)= {X/A⁺  X}, тогда

X  A X B  & Y Head(B)

X  > a  A B C  & X Tail(B) & aFirst1(C).

Пример разбора цепочки aaccbbcb с использованием построенной таблицы отношений предшествования приведен в табл.2.

Таблица 2

	Отношение	Входная
Стек	предшествования	строка	Операция
$	<	aaccbcb$	сдвиг
$a	<	accbcb$	сдвиг
$aa	<	ccbcb$	сдвиг
$aac	>	cbcb$	«Свертка»
$aaS	<	cbcb$	сдвиг
$aaSc	>	bcb$	«Свертка»
$aaSS	≗	bcb$	сдвиг
$aaSSb	>	cb$	«Свертка»
$aS	<	cb$	сдвиг
$aSc	>	b$	«Свертка»
$aSS	≗	b$	сдвиг
$aSSb	>	$	«Свертка»
$S		$	«Конец»