1. Алфавит, слова, операции над словами
| Вид материала | Документы |
- Исполнительный кодекс Республики Молдова, 2184.07kb.
- Статьи 4 изложить в следующей редакции: "Статья Ответственность физических, юридических,, 41.3kb.
- Республика Молдова, 777.62kb.
- Федеральный закон, 404.04kb.
- Подготовка к операции по прорыву блокады проводилась в глубокой тайне, 18.04kb.
- Игра «Алфавит» Чтобы узнать тему нашего занятия вы должны расшифровать слова. (зашифрованные, 50.79kb.
- «День культуры и славянской письменности», 78.75kb.
- Выполнили: Фурманова Диана 3класс, 121.65kb.
- Работа со словами с непроверяемыми написаниями, 134.51kb.
- Календарно-тематический план учебная дисциплина: «Математика», 34.71kb.
1. Алфавит, слова, операции над словами
Пусть V={v1, v2,…,vn}, n1 – некоторый алфавит. Тогда любая последовательность x1x2…xk, k0, где xi V – 1 i k , слово в алфавите V, при k=0 –получается пустое слово, обозначим его . Множество всех слов алфавита V обозначается V*.
Слово X =x1…xk графически совпадает со словом Y=y1…yl, если xiV (1 i k), yjV (1 j k), l=k, и для любого i ,1 i k, xi=yi. Будем обозначать графическое совпадение слов X=Y.
Длиной слова Х (обозначается Х) будем называть число вхождений символов в слово Х. Если X =x1…xk, то Х=k . =0
Конкатенацией слов X =x1…xk и Y=y1…yl называется слово Z= XY= x1…xk y1…yl. Например, конкатенацией слов «авто» и «бус» будет слово «автобус».
Свойства конкатенации:
является единицей для конкатенации, т.е. для любого слова Х верно, что Х=Х=Х.
Операция конкатенации является ассоциативной, т.е. (XY)Z=X(YZ).
Операция конкатенации не является коммутативной, XYYX.
Для конкатенации, как и для произведения, конкатенация n одинаковых слов X обозначается Xn. Считаем, что
X0= для любого слова Х. Множество V* всех слов алфавита V является полугруппой относительно операции конкатенации.
Полугруппа – множество с заданной на нем ассоциативной бинарной операцией.
Если слово Х=Х1 Х2, то Х1 начало слова Х, а Х2 – конец слова Х.
Говорят, что слово P входит в слово Q, если существует пара слов R и S, такая, что R – первый элемент пары, S – второй элемент пары, и Q =R P S.
Легко доказать
Утверждение: Если слово P входит в слово Q, то существует некоторое слово U, такое, что P – начало U, а U - конец Q.
Следствие: Если слово P входит в слово Q, то P есть начало некоторого конца Q (или конец некоторого начала Q).
Если P есть некоторое начало (конец) Q и P Q, то P собственное начало (конец) Q.
Конкретные вхождения слова P в слово Q обозначаются RPS, где R, P,S – слова в алфавите V, V. Тогда R – левое крыло вхождения, S – правое крыло вхождения, P - основа.
Говорят, что вхождение P1 слова P в слово Q предшествует вхождению P2 слова P в это же слово, если левое крыло вхождения P1 является собственным началом левого крыла вхождения P2.
2. Языки. Операции над языками
Произвольное множество цепочек над алфавитом V, иначе любое подмножество свободной полугруппы V*, называется формальным языком над V. Поэтому язык может быть задан теми же способами, как и любое множество:
Перечислением элементов.
Ограничивающим свойством.
Через известные множества
Порождающей процедурой.
В основном будем использовать 4 способ, но начнем с третьего.
Например, для любого V множество слов четной длины является языком. Множество слов нечетной длины также является языком, но в отличие от первого — не замкнутым относительно операции конкатенации. Будем обозначать языки буквой L (с индексами или без них). Рассмотрим операции над языками.
Т.к. язык является множеством, то применимы все соответствующие операции, для которых выполняются все законы теории множеств.
В частности, L, L.
Теоретико-множественные операции
Пусть L1 и L2 - два языка над алфавитом V. Язык L называется объединением этих языков (L = L1 L2 ), если L ={x / x L1 x L2}.
Пересечением языков L1 и L2 называется язык L (L = L1 L2 ), если L ={x / x L1 & x L2}.
Дополнением языка L1 до V* называется язык L (L=V*\L1), если L={ x/ xV* & x L1}.
Специфические операции
Произведением (иначе конкатенацией) языков L1 и L2 называется язык L (L=L1L2), если L={x y/xL1 & yL2}.
Например, L1={ ac, a }, L2={ cb, b}, тогда L1L2 ={ acb, accb, ab}.
Свойства операции конкатенации:
Операция умножения языков ассоциативна:
L1 (L2 L3)= (L1 L2) L3
Операция умножения языков дистрибутивна относительно объединения
L (L1L2 ) = LL1 LL2.
(L1L2 ) L = L1L L2L
Операция умножения языков не коммутативна: L1 L2 L2 L1.
L {}= {} L = L
Однако L(L1L2 ) LL1 LL2 , в общем случае равенства нет, что легко показать, подобрав соответствующий пример.
В силу ассоциативности операции произведения, как и в случае конкатенации цепочек,
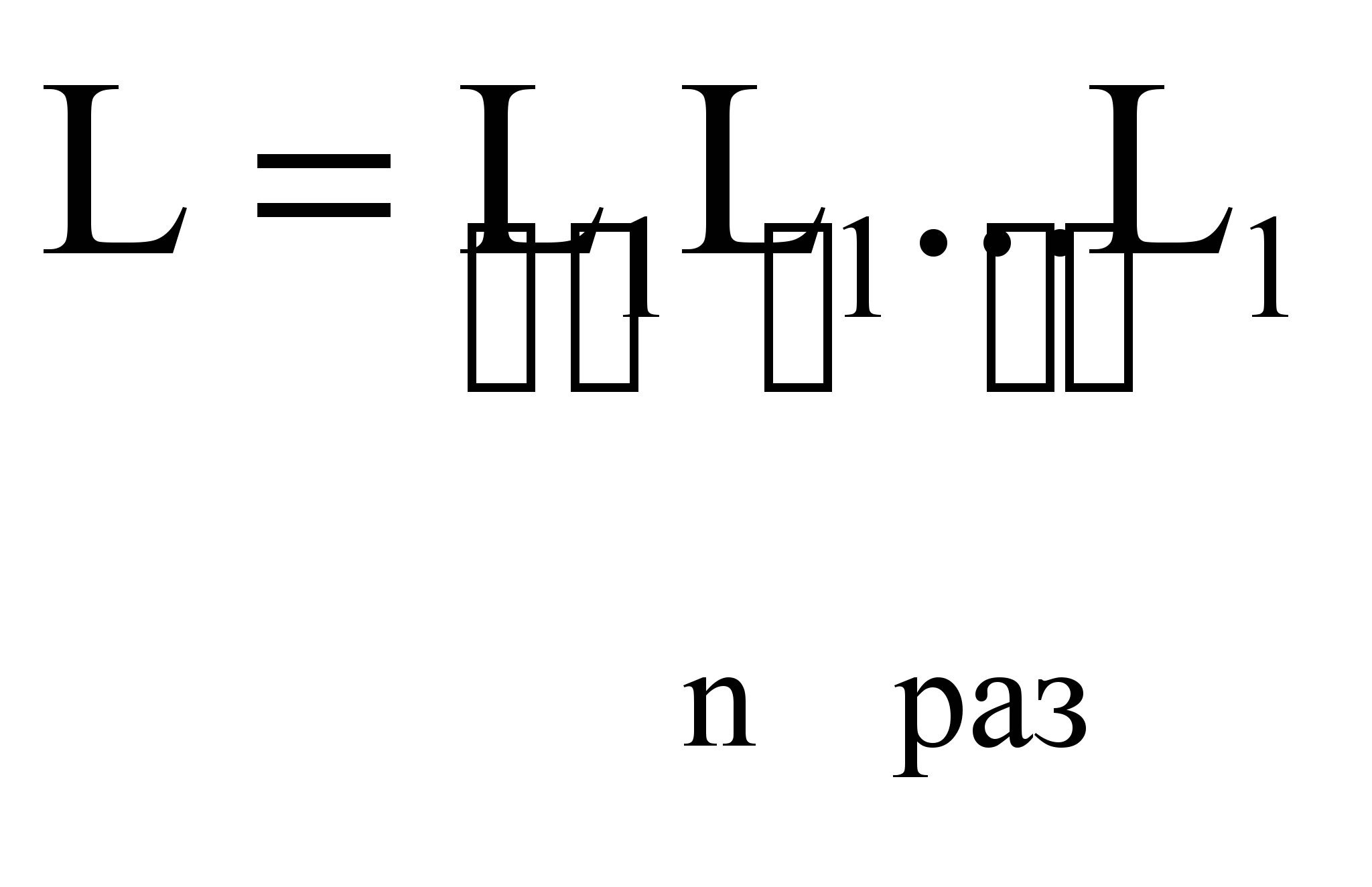
записывается как L=L1n. По определению L0={}. Отметим, что {} . так как (пустой язык) вообще не содержит никаких цепочек.
Итерацией языка L1 называется язык L (L=L1*), если
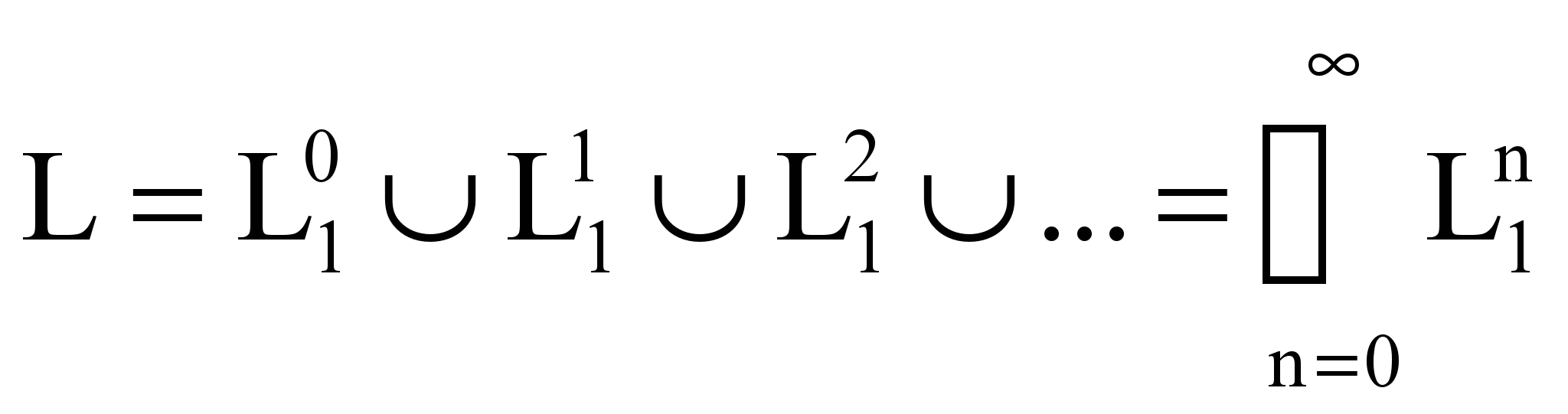 . Как нетрудно видеть, итерация алфавита V* (алфавит можно рассматривать как язык, состоящий из односимвольных слов) образует язык, состоящий из всех возможных цепочек, составленных из символов V. Это обстоятельство и объясняет, почему V* используется для обозначения всех слов над алфавитом V.
. Как нетрудно видеть, итерация алфавита V* (алфавит можно рассматривать как язык, состоящий из односимвольных слов) образует язык, состоящий из всех возможных цепочек, составленных из символов V. Это обстоятельство и объясняет, почему V* используется для обозначения всех слов над алфавитом V.Вводится также операция усеченной итерации. L называется усеченной итерацией языка L1 (L=L1+), если