1. Алфавит, слова, операции над словами

Вид материала

Документы

Содержание Порождение и распознавание цепочек. Лингвистический автомат L(A), допускаемым конечным автоматом A, называется множество допускаемых им цепочек L(A) = { x / (q

Подобный материал:

• Исполнительный кодекс Республики Молдова, 2184.07kb.
• Статьи 4 изложить в следующей редакции: "Статья Ответственность физических, юридических,, 41.3kb.
• Республика Молдова, 777.62kb.
• Федеральный закон, 404.04kb.
• Подготовка к операции по прорыву блокады проводилась в глубокой тайне, 18.04kb.
• Игра «Алфавит» Чтобы узнать тему нашего занятия вы должны расшифровать слова. (зашифрованные, 50.79kb.
• «День культуры и славянской письменности», 78.75kb.
• Выполнили: Фурманова Диана 3класс, 121.65kb.
• Работа со словами с непроверяемыми написаниями, 134.51kb.
• Календарно-тематический план учебная дисциплина: «Математика», 34.71kb.

Порождение и распознавание цепочек.

Конечный автомат (автомат Мили) S=< V_a, Q, V_b, q₀, F, G>, где

V_a={a₁,a₂,…a_m}, m1 – входной алфавит автомата,

V_b= {b₁, b₂, …, b_n}, n1 – выходной алфавит автомата,

Q= {q₀,q₁,…q_k}, k0 – внутренний алфавит (алфавит состояний),

q₀Q – начальное состояние автомата,

F - функция переходов; F: Q V_a Q,

G - функция выходов, G: Q V_a  V_b .

Автомат однозначно задает отображение V_a*  V_b* (входной цепочки в выходную).

Пример автомата:

Пусть V_a = V_b= {a, b}, Q = {A, B}, q₀=A. Функции переходов и выходов могут быть заданы в функциональной форме:

F(A, a) = A	G(A, a) = a
F(A, b) = B	G(A, b) = a
F(B, a) = A	G(B, a) = b
F(B, b) = B	G(B, b) = b

Либо в виде объединенной таблицы входов-выходов, в которой по столбцам указаны исходные состояния, во строкам – входы, в соответствующей ячейке через запятую указываются состояние, в которое переходит автомат и соответствующий выходной сигнал.

	A	B
a	A, a	A, b
b	B, a	B, b

Диаграмма (граф переходов автомата), представляющая этот автомат, изображена на рис. 3.



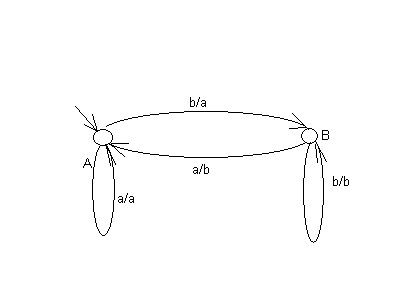
Рис. 3

Диаграмма автомата похожа на диаграмму грамматики. Отличие состоит в том, что есть некоторый выход, не выделены конечные состояния.

Если убрать выходы и ввести конечные состояния, то получится автомат, который не преобразует, а либо распознает, либо порождает цепочки – лингвистический автомат.

Лингвистический автомат – это S_L= T, q₀, F, K>,

где Q = {q₀,q₁,…q_k}, k0 – множество состояний автомата (внутренний алфавит),

V_T ={a₁,a₂,…a_m}, m1– множество терминальных символов (внешний алфавит) автомата,

q₀ – начальное состояние автомата, q₀ Q,

F: Q V_TQ функция переходов,

K Q – множество конечных(заключительных) состояний.

Рассмотрим автомат как распознающий, тогда ему соответствует следующая абстрактная модель:

Входная лента, на которой расположена анализируемая цепочка, считывающая(входная) головка и устройство управления.

На каждом шаге обозревается ровно один символ. Пара (q,a), где a - обозреваемый символ, а q - состояние автомата, называется ситуацией автомата. Если автомат находится в ситуации (q_i,a_j) и F(q_i, a_j)=q_k, то считывающая головка перемещается на один символ вправо, автомат переходит в состояние q_k. Получаемая ситуация (q_i,a_j+1) (обозревается следующий символ на ленте. Если же F(q_i, a_j) не определена, то входная цепочка не допускается автоматом.

Если в результате прочтения входной цепочки автомат окажется в заключительном состоянии, то говорим, что автомат допустил цепочку.

Более строго:

В начале работы автомат находится в состоянии q₀, на входе – цепочка a₁, a₂,…,a_n, обозревается самый левый символ цепочки ситуация (q₀, a₁) , затем переход в некоторую ситуацию (q_i, a₁),…, (q_j, a_n), и, наконец, в ситуацию (q_s, ) &q_sK. Назовём конфигурацией автомата пару H=(q, x), где q — текущее состояние автомата; x — остаток входной цепочки, самый левый символ которой обозревается входной го­ловкой. Конфигурация, очевидно, определяет и ситуацию. Говорят, что конфигурация (p, x₁) получена из конфигурации (q, x) за один такт (обозначается (q, x) ├ (p, x₁) ), если x= a x₁ и F(q, a)= p.

. Если H₀, H₁,…, H_n (n 1) - последовательность конфигураций, таких, что H_i ├ H_i+1 , i {1,…,n}, то, как и раньше, будем использовать обозначения H₀ ├ ⁺H_n или H₀ ├ * H_n если справедливо H₀ ├ ⁺H_n  H₀=H_n.

Пусть x — анализируемая цепочка. Начальная конфигу­рация имеет вид (q₀, x) заключительная – (q_s, ), q_s F. Говорят, что автомат A допустил цепочку x, если (q₀, x) ├ * (q, ) и q F (Использование отношения ├ * позволяет включить в множество допускаемых цепочек и пустую цепочку , если q₀F.

Языком L(A), допускаемым конечным автоматом A, называется множество допускаемых им цепочек

L(A) = { x / (q₀, x) ├ * (q, ) & q K}.

Диаграмма лингвистического автомата отличается от диаграммы автомата Мили выделением конечных состояний и отсутствием выходов.

Например, для лингвистического автомата S_A= 0, F, {q₁}>, функция переходов которого

F(q₀,c)=q₀,

F(q₀,a)=q₁,

F(q₁, b)= q₁,

диаграмма представлена на рис. 4.



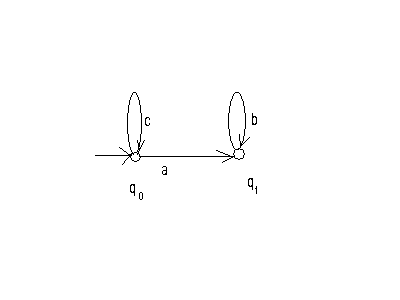
Рис.4

Язык, распознаваемый этим автоматом L(S_A)= {cⁿ a b^m, n,m0}.

Цепочка не распознается автоматом, если или нет перехода по читаемому символу, или в результате прочтения цепочки состояние, в которое перешел автомат - не конечное.

Процесс допускания цепочки соответствует движению по графу. Цепочка допущена, если существует путь из начальной вершины в заключительную, при котором последовательно выписанные метки проходимых дуг составляют анализируемую цепочку.

Граф автомата в силу тождественности его структуры с диаграммой грамматик всегда может рассматриваться как диаграмма некоторой грамматики, роль нетерминальных символов в которой будут играть метки состояний автомата. Нетрудно видеть, что грамматика, полученная по графу переходов автомата, при интерпретации последнего как ее диаграммы будет порождать тот же самый язык, который допускается автоматом. В обоих случаях язык однозначно определяется множеством путей из начальной вершины в заключительные, а множество путей совпадает, так как граф один и тот же. Таким образом, по любому конечному автомату может быть построена эквивалентная А-грамматика и, следовательно, абстрактно взятый ориентированный граф с помеченными вершинами и дугами, в котором выделена начальная и множество заключительных вершин и удовлетворяются требования однозначности отображения F, может рассматриваться и как диаграмма грамматики и как граф переходов автомата - все дело в интерпретации.

По диаграмме автомата всегда легко построить эквивалентную грамматику (автомат по грамматике строить сложнее, так как в грамматике одному символу входного алфавита может соответствовать более одного перехода см., например, рис. 2.

Правила грамматики по диаграмме автомата строится следующим образом:

Каждому состоянию автомата сопоставляем нетерминал грамматики.

Каждому переходу, соответствующему из состояния P по терминалу a в состояние Q сопоставляется правило грамматики PaQ.

Каждому конечному состоянию R сопоставляется правило R.

Начальному состоянию автомата сопоставляется начальный символ грамматики.

Например, автомату, диаграмма которого представлена на рис.4, соответствует грамматика G₁₀ с правилами

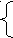S cS a A

A b A


где состоянию q₀ сопоставлен нетерминал S, а состоянию q₁ - нетериминал A.

Таким образом, состояния конечного автомата однозначно отображаются в нетерминалы грамматики.

Однако, если мы рассмотрим грамматику G₁₁ c правилами

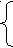S a S a A

A b Ab K

K ,

диаграмма которой представлена на рис. 5



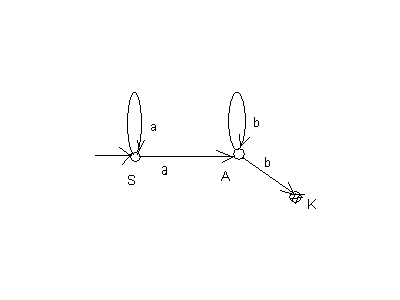
Рис.5

Однозначность нарушается неоднозначностью переходов, допускаемых в грамматиках.