1. Алфавит, слова, операции над словами

Вид материала

Документы

Содержание Детерминизация конечных автоматов A' такой, что L(A')=L(A). Автоматы с  - переходами. А = - автомат -переходами. Построим соответствующий детерминированный автомат А’=

Подобный материал:

• Исполнительный кодекс Республики Молдова, 2184.07kb.
• Статьи 4 изложить в следующей редакции: "Статья Ответственность физических, юридических,, 41.3kb.
• Республика Молдова, 777.62kb.
• Федеральный закон, 404.04kb.
• Подготовка к операции по прорыву блокады проводилась в глубокой тайне, 18.04kb.
• Игра «Алфавит» Чтобы узнать тему нашего занятия вы должны расшифровать слова. (зашифрованные, 50.79kb.
• «День культуры и славянской письменности», 78.75kb.
• Выполнили: Фурманова Диана 3класс, 121.65kb.
• Работа со словами с непроверяемыми написаниями, 134.51kb.
• Календарно-тематический план учебная дисциплина: «Математика», 34.71kb.

Детерминизация конечных автоматов

Для того, чтобы построить соответствующее таким грамматикам автоматы, можно рассматривать переходы F автомата Q  V_T в множество подмножеств Q ( т.е. в P(Q)). При этом

P(Q)=2^Q.

Будем называть недетерминированным конечным автоматом S пятерку объектов S = T, q₀, F, K>, где интерпретация Q, V_T, q₀, K такая же, как и раньше, а F – отображение Q  V_T в P(Q).

Определение цепочек, допускаемых автоматом, остается прежним, но если в детерминированном автомате последовательность конфигураций однозначно определялась заданием входной цепочки, так как из каждой конфигурации автомат мог перейти не более чем в одну конфигурацию, то в недетерминированном случае это не так. Поэтому при интерпретации определения "цепочка X допущена" как (q₀,x) ├ (q, )&qK необходимо при анализе цепочки, моделируя работу автомата, перебрать варианты выполнения тактов, чтобы найти тот (или те), которые приводят в заключительную ситуацию. В силу тех же соображений (тождественность движений по графу и при порождении цепочки, и при ее допускании) можем утверждать, что для любой грамматики G может быть построен конечный автомат A (в общем случае недетерминированный), такой, что L(G)=L(A) . Соответствия между параметрами грамматики и автомата остаются те же.

Возникает естественный вопрос о соотношении класса языков, допускаемых детерминированными и недетерминированными автоматами. Ясно, что для любого детерминированного автомата A существует недетерминированный A' допускающий тот же самый язык (достаточно в качестве A' взять А). Но верно ли обратное? Ответ на этот вопрос дает следующая теорема.

Теорема 1. Если L=L(A) для некоторого недетерминированного автомата A , то найдется конечный автомат A' такой, что L(A')=L(A).

Доказательство:

Пусть дан недетерминированный конечный автомат А = T, q₀, F, K>. Построим соответствующий детерминированный автомат А’= T, q₀’, F’, K’>

Q’ = P(Q) . При этом множество состояний 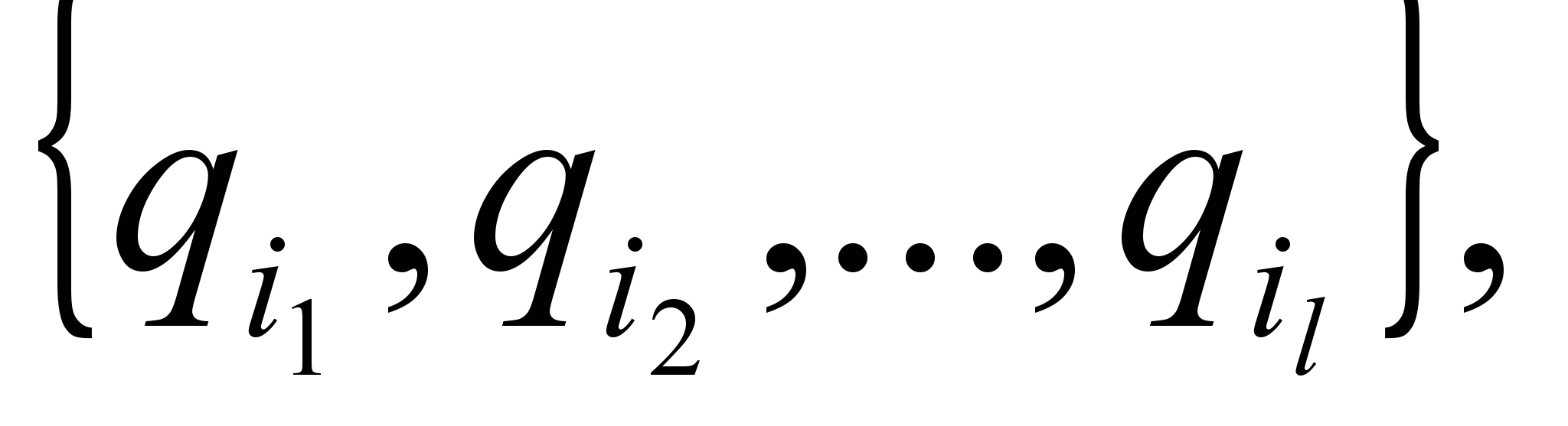будем обозначать как .

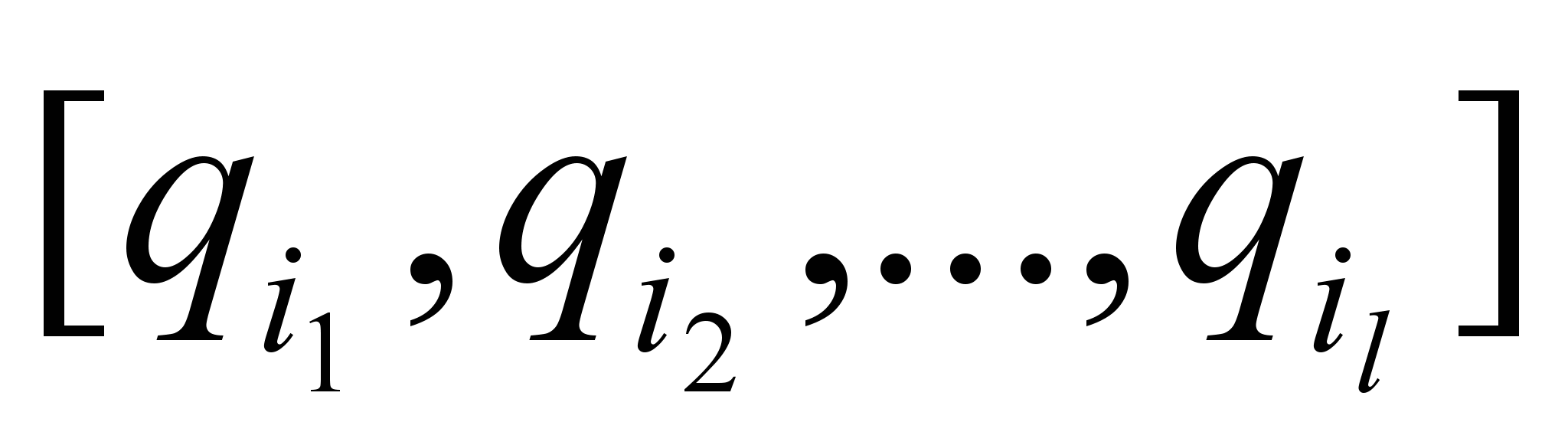q₀’=[q₀].

K’ = { 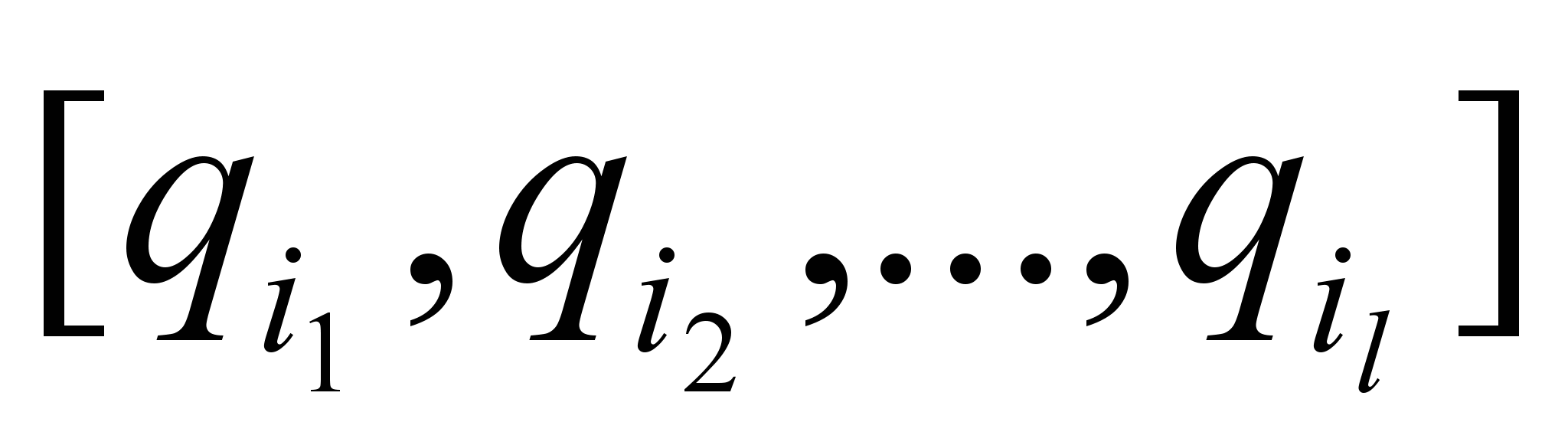/ 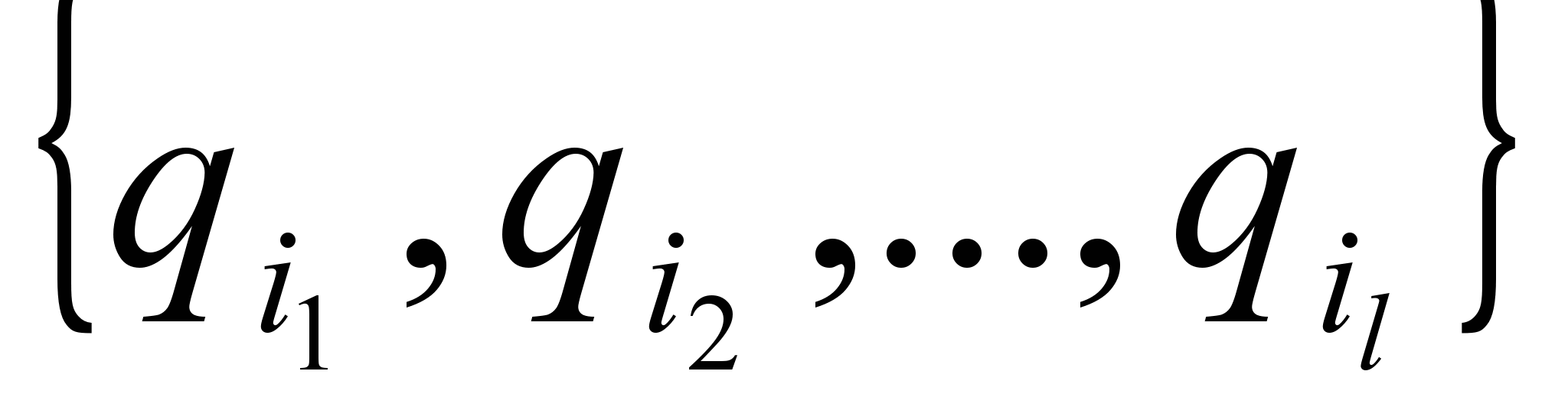K }

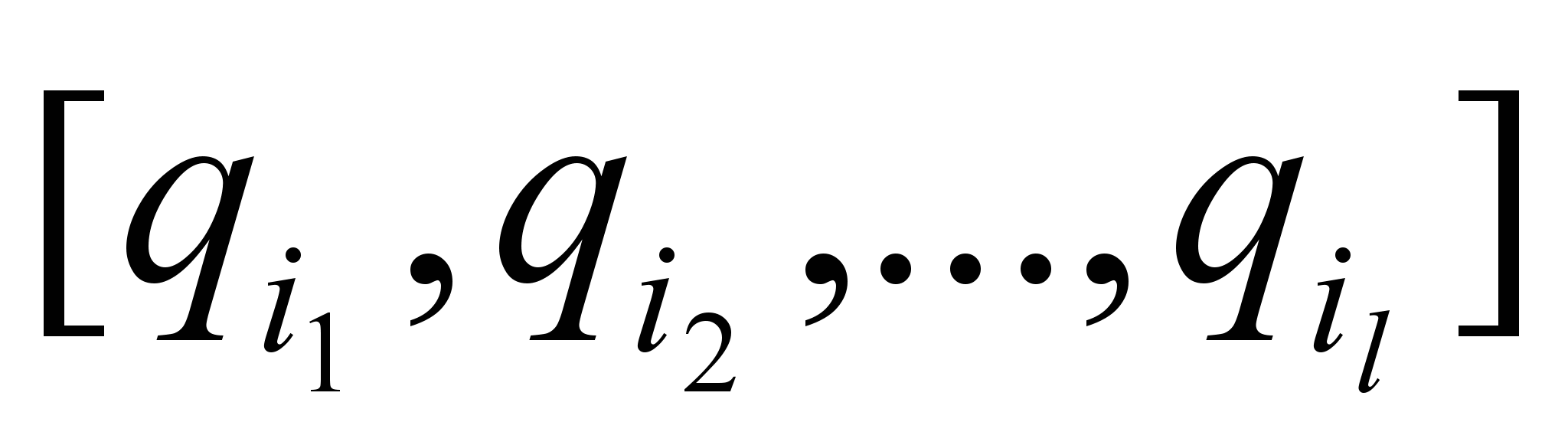F’(, a)=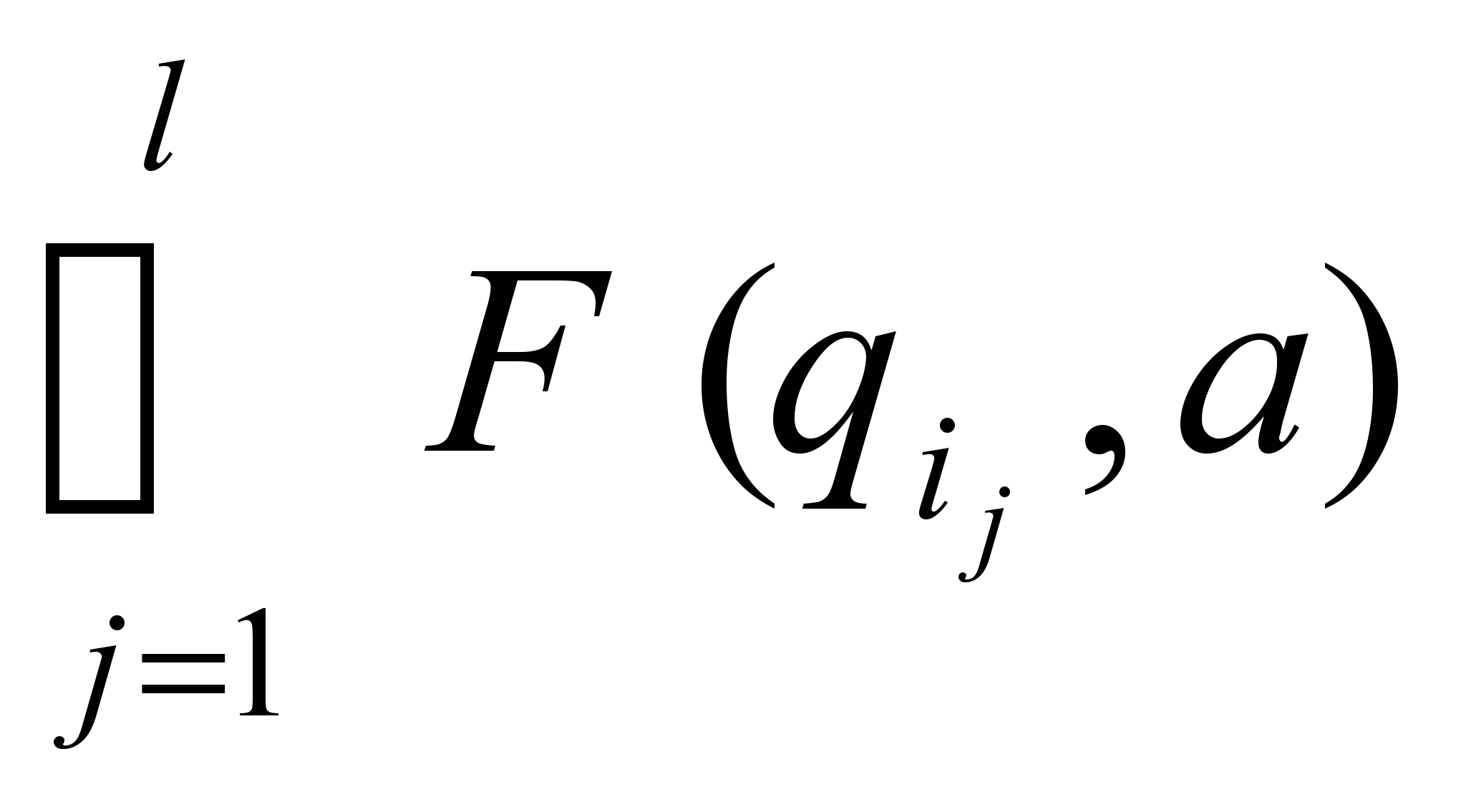

Несложно доказать методом математической индукции, что для любого I

([q₀],XY) ├ⁱ_A’(B,Y)  B={p/ (q₀, XY) ├ⁱ_A(p,Y)}

X=i.

Значит, для любой цепочки Х

([q₀],X) ├ⁱ_A’(B,)  B={p/ (q₀, X) ├ⁱ_A(p,)}

Поэтому, в случае B K’, т.е. если Х – цепочка, допускаемая детерминированным автоматом, то в исходном недетерминированном автомате существует путь из начального в конечное состояние при чтении этой цепочки, и, следовательно, L(A)=L(A’).

Т.о., сопоставляя доказанные утверждения, получаем:

Класс А-языков и класс языков, распознаваемых конечными автоматами, совпадает.

Так, например, для автомата, представленного на рис. 5, соответствующий детерминированный автомат представлен на рис. 6.



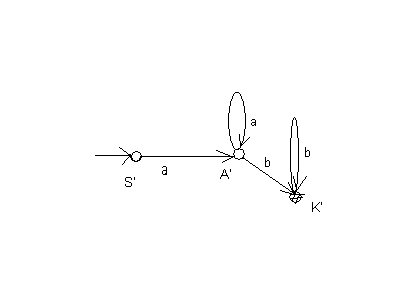
Рис.6


Здесь F(S,a)= [S,A] = A’

F([S,A], a) = [S,A]

F([S,A],b) = [A, K] = K’

F([A,K],b)= [A, K] = K’

Для автомата на рис. 7а детерминированный автомат представлен на рис.7b.




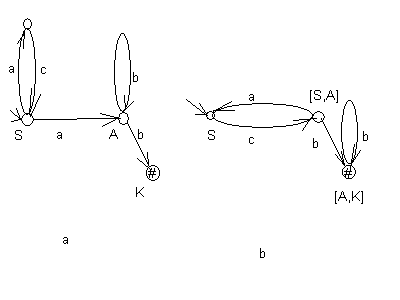
Рис.7

Алгоритм построения детерминированного автомата по недетерминированному:

Строим начальное состояние q₀’= [q₀], помечаем его как начальное.

Для каждого состояния, построенного на предыдущем шаге, строим

F(q_i’, a) для всех aV_T. Если для какого-нибудь из построенных состояний функция перехода ещё не построена, возвращаемся к шагу 2.

Помечаем как конечные все состояния q_i’= 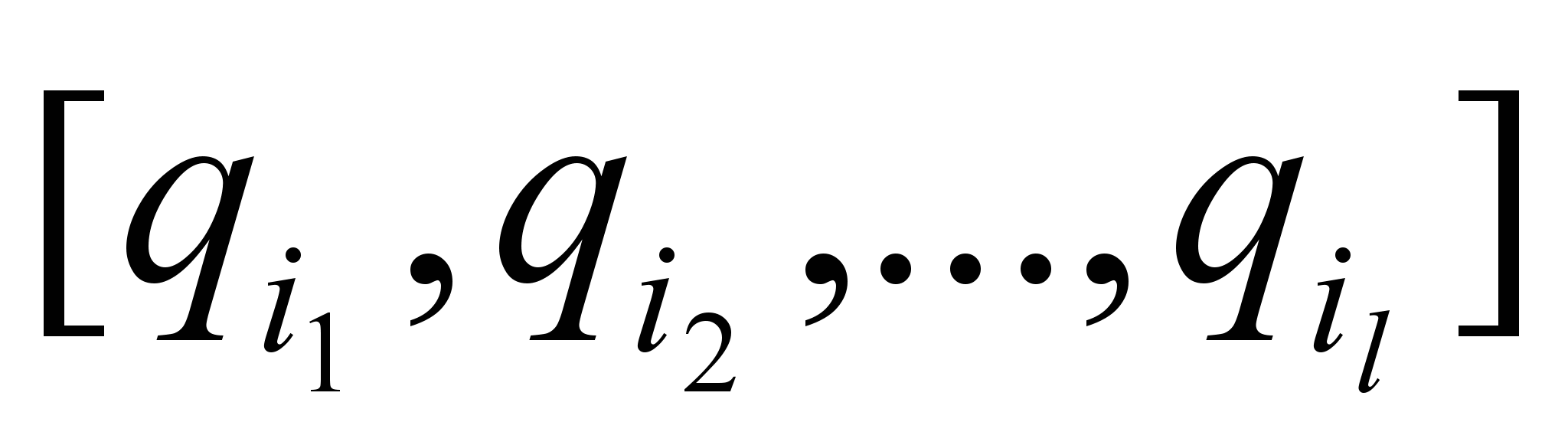/ 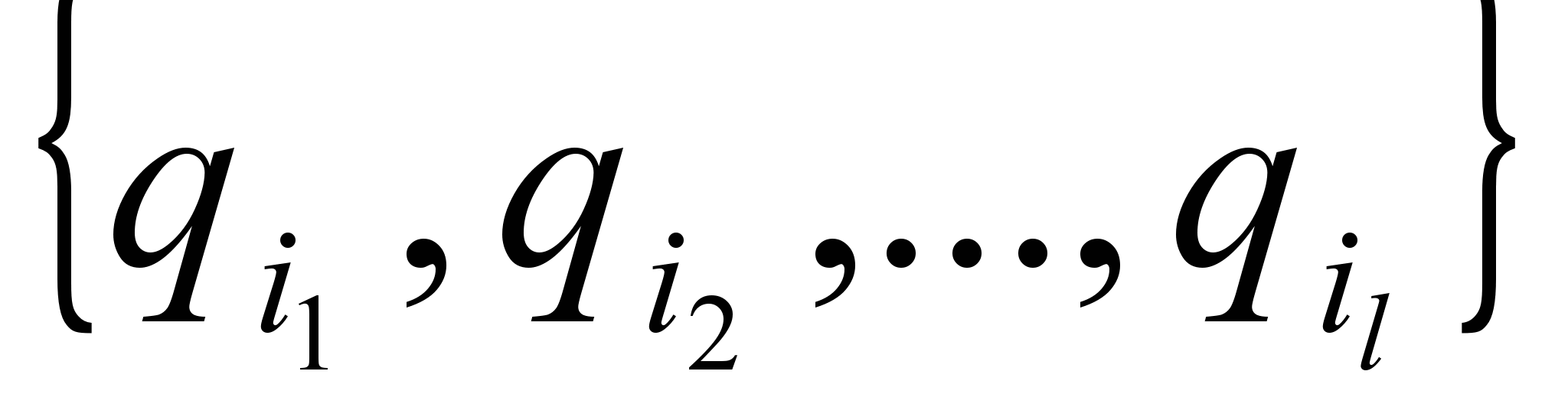 K.

Конечность процесса обеспечивается конечностью множества P(Q).

Автоматы с  - переходами.

Автоматы с  - переходами естественно возникают в различных приложениях, и позволяют представить любой автомат в виде двухполюсников с одним входом и одним выходом, а так же строить сети из таких автоматов, сохраняя в них единственный вход и единственный выход. От рассмотренных ранее автоматов они отличаются тем, что в них присутствуют переходы, осуществляемыми без чтения входной цепочки ( на диаграмме такие переходы обозначаются стрелками, помеченными символом ).




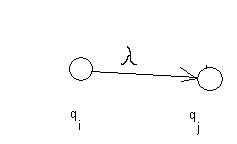
Рис. 8



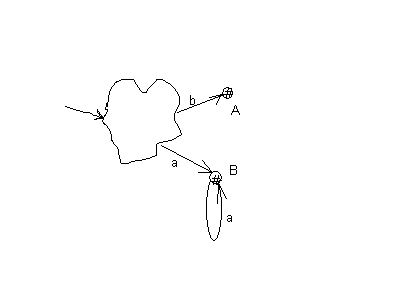
Рис.9

Например, рассмотрим автомат с двумя выходами, представленный на рис. 9. Он имеет два выхода. Если просто объединить две выходные вершины, то получившийся автомат не будет эквивалентен исходному, т.к. после построения символа b в результирующем автомате возможно будет построение символов а, что было невозможно в исходном автомате. Эквивалентный исходному автомат представлен на рис. 10.



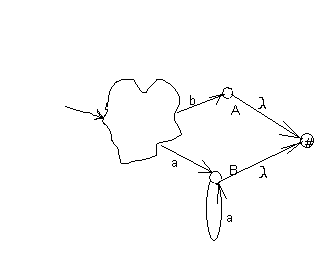
Рис.10.

Иногда в двухполюснике конечные состояния изображаются как

Очевидно, что если L – А-язык, то ему можно сопоставить двухполюсник.

Пусть языкам L₁ и L₂ сопоставлены соответствующие двухполюсники

(рис.11 а). Тогда их объединению, конкатенации и итерации языка L₁ будут, соответственно, сопоставлены двухполюсники рис. 11б, 11в, 11г



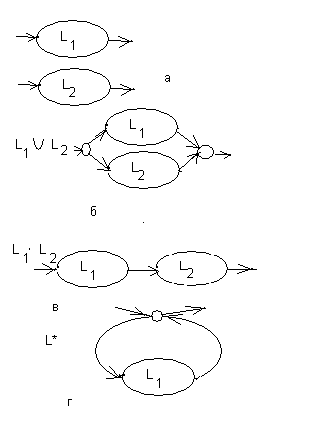
Рис.11


Т.о. доказана теорема: Класс А-языков замкнут относительно операций объединения, конкатенации и итерации.

Оптимизация автоматов с -переходами.

Если из состояния А исходит единственная дуга и это -дуга в состояние В, то вершины А и В можно слить.

Если из вершины А выходит -дуга в вершину В, являющуюся начальной вершиной некоторой дуги( не петли) или последовательности дуг, а С – конечная вершина этой дуги (последовательности дуг), и единственная дуга из С - -дуга в вершину А, то вершины А,В и С можно слить (примеры такого слияния приводятся на рис. 12 ( для одной дуги – а, б; для последовательности – в, г).



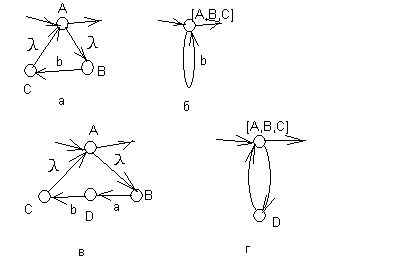
Рис.12

Теорема:

Классы языков, допускаемых детерминированными автоматами и автоматами с -переходами, совпадают.

Док-во:

Пусть автомат А = T, q₀, F, K> - автомат -переходами. Построим соответствующий детерминированный автомат А’= T, q₀’, F’, K’>, такой, что L(A)=L(A’) следующим образом.

F’(q,a)={p / (q,ax) ├⁺ (p,x)}

K’ = K {p / (q, ) ├* ( p, )& pK}

Несложно показать, с использованием математической индукции по числу символов в распознаваемой цепочке, что получаемый таким образом автомат А’ переходит при распознавании цепочки Х в конечное состояние тогда и только тогда, когда существует последовательность переходов в конечное состояние автомата А при распознавании этой же цепочки символов.

Пример. Пусть автомат представлен диаграммой на рис. 13а. Объединим по правилу 1 упрощения автоматов с -переходами состояния 4 и 5 и переобозначим состояния, как показано на рис. 13б.



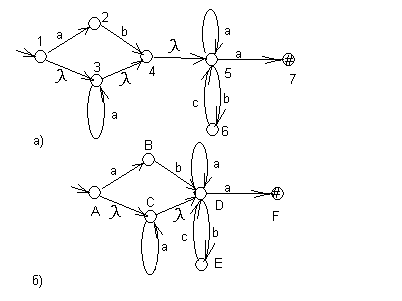
Построим функцию переходов детерминированного автомата А’.

F(A, a) = [B,C, D, F] F(A, b) = [E] F(A,c) = 	F([B, C, D, F], a) = [C,D, F], F([B, C, D, F], b) = [D, E], F([B, C, D, F], c) = ,	F([E], a) = , F([E], b) = , F([E], c) = [D],
F([C, D, F], a) = [C, D, F] F([C, D, F], b) = [E] F([C, D, F],c) = 	F([D, E], a) = [D, F] F([D, E], b) = [E] F([D, E],c) = [D]	F([D, F], a) = [D, F] F([D, F], b) = [E] F([D, F], c) = 
F([D], a) = [D, F] F([D], b) = [E] F([D], c) = 

K’ = { [B, C, D, F] , [ D, F], [C, D, F]}

Диаграмма детерминированного автомата представлена на рис. 14.



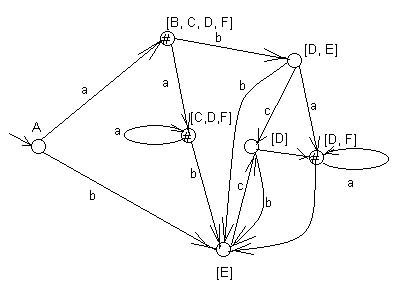
Рис.14

Тот же автомат после переобозначения состояний представлен на рис. 15.




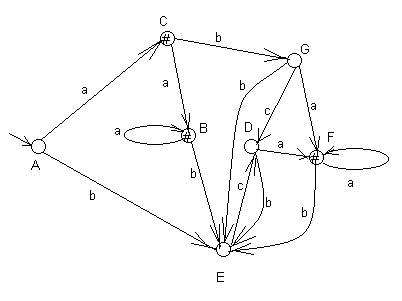
Рис.15