Geum.ru

1. Алфавит, слова, операции над словами

Вид материалаДокументы

Содержание


Разрешимые проблемы для А-грамматик
7. Нотации для задания КС-грамматик.
Подобный материал:
1   ...   4   5   6   7   8   9   10   11   ...   14

Разрешимые проблемы для А-грамматик


Теорема:

Если L – А-язык, и ZL имеет длину,  числа состояний детерминированного автомата, то Z=WXY, гдеX1и W Xi Y L для всех i0.

Доказательство: Пусть есть некоторый А-язык, и автомат ML, порождающий этот язык.

Q-{ q0,.q1,q2,…qn-1} – множество состояний автомата ML , n - число состояний автомата, q0 – начальное состояние автомата.

F(q0,Z)K т.к. ZL. Zn , поэтому qjQ , что Z=WXY, X 1, F(q0,W)= qj, F(qj,X )= qj, F(qj, Y)K. Но тогда F(q0,W XiY)K для всех i0, что требовалось доказать.

Теорема:

Проблема не пустоты для А-грамматик разрешима, т.е, если задана А-грамматика G, то существует алгоритм, позволяющий ответить на вопрос: L(G)= ?

Например, Из предыдущей теоремы, если L(G), то существует цепочка длины
Теорема:

Проблема равносильности А-грамматик разрешима. т.е., если G1 и G2 – А-грамматики, то существует алгоритм, позволяющий определить, L(G1)=L(G2)?

Док-во: В случае равенства языков минимизированные детерминированные автоматы, построенные по этим грамматикам, будут совпадать с точностью до обозначений состояний.

Теорема:

Проблема конечности языка, порождаемого А-грамматикой, разрешима.

Обозначим множество состояний, достижимых из состояния Ai =H(Ai). Тогда, если

 Ai, такое, что Ai H(q0 )& Ai H(Ai)& Aj  H(Ai )& AjK, то язык, порождаемый автоматом, бесконечен.

Интересно отметить, что подобная теорема существует для КС-грамматик:

7. Нотации для задания КС-грамматик.

  1. Математическая нотация (которую рассматривали до сих пор) – чистый синтаксис.
  2. БНФ (Бекусова нормальная форма, или форма Бекуса — Наура) есть способ записи грамматики, который широко ис­пользуется для описания синтаксиса языков программирования. В БНФ
    1. нетерминальные символы записываются как имена, за­ключенные в угловые скобки < > .
    2. Знак  записывается как :: = (читается "заменяется на").
    3. Альтернативы замены, соот­ветствующие одному и тому же нетерминалу в левой части, от­деляются друг от друга вертикальной чертой  (читается "или").
    4.  не обозначается, для того, чтобы не пропыстить эту альтернативуЮ она обычно записывается первой в конструкции выбора.

Используя БНФ, описание идентификатора как произвольной по­следовательности букв и цифр, начинающейся с буквы, можно, например, записать:

<идентификатор> ::= <буква> | <буква> <продолжение>

<продолжение> ::= < символ> | < символ> <продолжение>

<символ> ::= < буква> | <цифра>

<буква> :: = А | В | С|….| Z

<цифра> ::= 0 | 1 | ... | 9

Или:

<идентификатор> ::= <буква> <продолжение>

<продолжение> ::= | < символ> <продолжение>

<символ> ::= < буква> | <цифра>

<буква> :: = А | В | С|….| Z

<цифра> ::= 0 | 1 | ... | 9

При записи в виде грамматики G13 семантику увидеть сложнее(запись полностью соответствует последнему варианту БНФ):

S  A B

B  A B 

A  CD

C  А | В | С|….| Z

D  0 | 1 | ... | 9

Нетерминал БНФ может интерпретироваться как язык, который выводится, если рассматривать данный символ как начальный символ грамматики. БНФ может использоваться для описания синтаксиса любого языка, не только искусственного, например:

<Существительное > :: =<основа > <окончание>

<окончание > ::= окончание множественного числа окончание единственного числа…

Или:

формула исчисления высказываний::= элементарная формула(формула исчисления высказыванийбинарная операция формула исчисления высказываний) (отрицание

формула исчисления высказываний)

элементарная формула::= константапропозициональная переменная

константа::= 01

пропозициональная переменная ::=ab…z

отрицание::= N

бинарная операция ::= 

  1. Часто применяется так называемая расширенная БНФ -РБНФ в которой используются также метасимволы (,); [,]; {,}. Ведение метасимволов позволяет сделать запись более лаконичной . Синтаксис РБНФ следующий
    1. Нетерминалы записываются как последовательность символов.
    2. Терминалы( последовательности символов) заключаются в кавычки.
    3. Знак  , используемый в математической записи грамматик, обозначается как =.
    4. Альтернативы, как и в математической записи грамматик, разделяются знаком .
    5. Конструкция, заключенная в  ,  , является необязательной.
    6. Конструкция, заключенная в  ,  может повторяться произвольное число раз, от 0 (эквивалент * в регулярных выражениях).
    7. ( ) служат для факторизации, т.е. конструкция  может быть представлена в виде (). Это позволяет использовать конструкцию выбора на более глубоком уровне.

Например, идентификатор в РБНФ будет описан как:

Идентификатор = буква  буква цифра

буква = 'А’ | ‘В’ | ‘С’ |….| ‘Z’

цифра = ‘0’ | ‘1’ | ... | ‘9’

Существительное описывается как

существительное = основа ( окончание единственного числа окончание множественного числа)

Фактически, в правой части правил в РБНФ записывается некоторое регулярное выражение, в котором могут использоваться нетерминалы (т.е. расширение возможностей относительно выразительной мощности обычных регулярных выражений, т.к. обычные регулярные выражения позволяют описывать А-языки, а РБНФ – КС-языки.
  1. Синтаксическая диаграмма. Синтаксическая диаграмма – графическая форма представления РБНФ. Для каждого нетерминала рисуется своя диаграмма. Приняты следующие обозначения:
    1. Нетерминалы заключаются в прямоугольники.
    2. Терминалы заключаются в овалы.
    3. Образы нетерминалов и терминалов соединяются линиями (со стрелками или без, мы будем использовать стрелки для указания направления движения) т.о., чтобы множество путей соответствовало множеству цепочек из терминалов и нетерминалов, задаваемому РБНФ - правилами, для которых строится диаграмма.

Диаграммы для конструкции выбора и итерации представлены на рис. 22, а и б, соответственно. Скругленный прямоугольник может быть заменен как прямоугольником (в случае нетерминала), так и овалом ( в случае терминала).

Набор диаграмм для идентификатора на рис. 23.






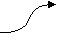
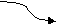
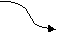
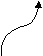
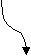
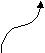
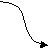
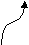
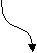
Буква

Цифра

Буква

Буква

….

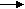
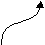
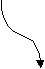
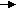
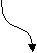
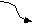
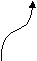
А

B


Z

Идентификатор

….

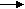
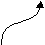
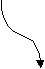
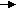
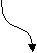
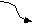
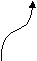
1


0

2

Цифра


а


б

Рис.22


Рис.23

В большинстве случаев существует не единственная форма представления для одних и тех же объектов.

Легко показать, что выразительная мощность РБНФ и БНФ совпадает:

Условная запись РБНФ
Условная запись БНФ для данной РБНФ

А= (12)
<А> ::=<>< 1>< ><2>

А= [ ] 
<А> ::=<>< >< >

А= { } 
<А> ::= <>

::= <> < B>