1. Алфавит, слова, операции над словами

Вид материала

Документы

Содержание 9. Преобразования грамматик.

Подобный материал:

• Исполнительный кодекс Республики Молдова, 2184.07kb.
• Статьи 4 изложить в следующей редакции: "Статья Ответственность физических, юридических,, 41.3kb.
• Республика Молдова, 777.62kb.
• Федеральный закон, 404.04kb.
• Подготовка к операции по прорыву блокады проводилась в глубокой тайне, 18.04kb.
• Игра «Алфавит» Чтобы узнать тему нашего занятия вы должны расшифровать слова. (зашифрованные, 50.79kb.
• «День культуры и славянской письменности», 78.75kb.
• Выполнили: Фурманова Диана 3класс, 121.65kb.
• Работа со словами с непроверяемыми написаниями, 134.51kb.
• Календарно-тематический план учебная дисциплина: «Математика», 34.71kb.

9. Преобразования грамматик.

В данном разделе приводятся такие преобразования грамматик, которые не выводят нас из класса эквивалентности, т.е. грамматика G₁ таким образом преобразуется в грамматику G₂, чтобы L(G₁)=L(G₂).

9.1 Устранение непроизводящих правил.

Непроизводящими правилами грамматики начинаются правила, применение которых никогда не приводит к построению терминальных цепочек.

Например, рассмотри правила для нетерминала А

АА А В А

В этом случае, появившись в цепочке, нетерминал А никогда не будет заменен терминальной цепочкой (имеется в виду, что других правил для А нет). Естественно, в реальности ситуации бывают не столь простые. Алгоритм устранения непроизводящих нетерминалов:

1. Построение множества производящих нетерминалов N_R:
   
   1. Строится множество N_R¹ = {A/ A_j,_jV_T}
      
   2. Последовательно строятся множества N_Rⁱ⁺¹={ A/ A_j,_j(N_RⁱV_T)*} до тех пор, пока получим N_Rⁱ⁺¹= N_Rⁱ или же N_Rⁱ= V_N. Тогда N_R = N_Rⁱ.
      
2. Исключаем из грамматики все правила, в правых частях которых нетерминалы из V_N\ N_R.
   
3. Исключаем из грамматики правые части правил, в которых присутствуют нетерминалы из V_N\ N_R.
   

Например, рассмотрим грамматику G с множеством правил

S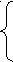 ABBC

A AAAB

B bBa

СсСd AC

Построим множество N_R. N_R¹={B,C}, N_R²={S, B, C}, N_R³= N_R²= N_R.

Преобразованная грамматика примет вид:

S BC

B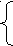 bBa

СсСd

9.2. Устранение недостижимых нетерминалов.

Недостижимыми нетерминалами называются нетерминалы, которые никогда не могут быть построены при построении вывода, начиная с начального символа грамматики. Следует отметить, что такие нетерминалы в грамматиках встречаются в основном тогда, когда исключены некоторые непроизводящие символы, т.е. недостижимым нетерминал становится чаще всего после исключения некоторых непроизводящих симовлов. Например, если в грамматике для нетерминала А правила АА А В А, и нетерминал В не встречается в других правых частях правил грамматики, то в этом случае, после устранения нетерминала А нетерминал В становится недостижимым, и, следовательно, его можно исключить из грамматики без изменения порождаемого ей языка. Построение множества недостижимых нетерминалов похоже на построение множества непроизводящих нетерминалов: мы строим множество всех достижимых нетерминалов, а затем исключаем все остальные нетерминалы грамматики. Алгоритм построения грамматики, в которой используются только достижимые нетерминалы (множество достижимых нетерминалов –D) , выглядит следующим образом:

Пусть дана грамматика G=< V_T,V_N, S, R>, строится эквивалентная грамматика без непроизводящих символов G’ =< V_T,V_N’, S, R’>.

1. Начальное значение D₀=S.
   
2. Итерационное построение множества D: D_i+1= D_i{A/BARB D_i}
   
3. Построение продолжается, до тех пор, пока D_i+1= D_i или D_i+1= V_N, в обоих случаях V_N’= D_i+1,
   

R’={ R_i / R_i=(A), A V_N’,( V_N’ V_T)*}

Построенная грамматика не содержит недостижимых нетерминалов.

Например, рассмотрим грамматику G с множеством правил

S A C B C

A AD DF

D aA  D A

F b F

B bBa

СсСd

Тогда здесь A и D непроизводящие нетерминалы, после их устранения нетерминал F становится недостижимым, поэтому нетерминалы A, D и F могут быть исключены из грамматики с сохранением языка, порождаемого грамматикой.

9.3. Устранение  - правил

Устранение  - правил связано с исключением построения цепочек, которые после преобразований превращаются в пустую цепочку. Цель такого преобразования грамматики – если в грамматике строится пустая цепочка, то она строится в результате первого шага построения. Применение любого из оставшихся правил приводит к построению непустых цепочек, более того, цепочка, построенная из каждого из нетерминала, состоит не менее чем из одного терминального символа.

Пусть дана грамматика G=< V_T,V_N, S, R>, строится эквивалентная грамматика G’ =< V_T,V_N’, S, R’>.

1. Построить множество N_ = { A / A ⁺  } - множество нетерминальных символов, из которых возможен вывод пустой цепочки. Множество N_ строится итерационно. На первом шаге строится N_⁰.
   

N_⁰ = { B / B    R}

Пусть построено N_¹, N_², ..., N_ⁱ , ( i  0). Тогда N_ⁱ⁺¹ = N_ⁱ { B / B    R &   ( N_ⁱ)* }.

Если на очередном шаге N_ⁱ⁺¹ = N_ⁱ, то искомое множество N_ найдено ( N_ = N_ⁱ ).

2. Построить R’ — множество правил эквивалентной грам­матики так, что:
   

1. Если A₀ B₁ ₁ B₂ ... B_k _k  R , k  0 и B_i  N_ для 0  i  k, но ни один символ в цепочках _j, 1  j  k не содержит символа из N_, то включить в R’ все правила вида
   

A  ₀X₁₁X₂...X_k_k

X_i либо B_i, либо  (при этом правило A   не вклю­чать; это могло бы произойти, если все _i =  ).

2. если S  N_, включить в R’ также правило S’ S где S’ - новый начальный символ.
   

Таким образом, любая КС—грамматика может быть приве­дена к виду, когда R не содержит  -правил, либо есть точно одно правило S’   и S’ не встречается в правых частях остальных правил из R. Такие грамматики будем называть неукорачивающими.

Например, пусть дана грамматика G с множеством правил




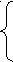
SA B BC

A aAb 

B dBc

C CCAc

N_⁰= {A, C}

N_¹= {A, C}= N_. Поскольку L(G) (S N_), правила грамматики примут вид




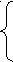
SA B B BC

A aAb ab

B dBc

C CCAca c


Б . Устранение правил А  В (цепных правил)

Применение цепных правил приводит к увеличению длины ветвей синтаксического дерева, исключение цепных правил часто приводит к большей «прозрачности» грамматики и уменьшению длины выводов, которые можно построить. Алгоритм исключения цепных правил:

1. Для каждого A V_N построить N_A = { B / A  B }, т.е. множество нетерминальных символов, выводимых из данного символа. Процедура построения следующая:

а) положить N_A⁰ ={A}.

б) пусть построены N_A⁰, N_A¹ ... N_Aⁱ . Тогда

N_Aⁱ⁺¹ = { C / B  C  R & B  N_Aⁱ }  N_A⁰.

Если на очередном шаге N_Aⁱ⁺¹ = N_Aⁱ, то положить N_A = N_Aⁱ.

2. Построить R’ (множество правил эквивалентной грамматики) так: если B    R и не является цепным правилом, то включить в R’ правила A  . для всех таких A, что

B  N_A.

Рассмотрим пример. Пусть множество правил грамматики имеет вид:

S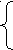T+ST

T MTM

M (S) i

Простроим для данной грамматики множества N_A

N_S ={S, T, M}

N_T = {T, M}

N_M = {M}

После преобразования грамматики она примет вид:

S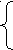T+S MT(S) i

T MT (S) i

M (S) i

В данном случае преобразование грамматики не привело к её упрощению, но построенные синтаксические деревья будут иметь меньшую глубину, и построение дерева будет происходить быстрее.

Грамматика называется неукорачивающей, если для любого правила грамматики  выполняется. Такое определение применимо как к КС-грамматикам, так и к КЗ-грамматикам. А-грамматика так же может быть неукорачивающей. Для КС и А-грамматик необходимым и достаточным условием принадлежности к классу неукорачивающих грамматик является отсутствие в них -правил.

Грамматика называется приведенной, если она неукорачивающая и не содержит непроизводящих символов.

Поэтому, если L(G), то существует приведенная грамматика G₁, такая, что L(G₁)=L(G).

В случае же L(G), существует эквивалентная грамматика с единственным укорачивающим правилом.