Учебно-методический комплекс для бакалавриата по направлению №080200 Менеджмент Москва 2011

Вид материала

Учебно-методический комплекс

Содержание Практическое занятие 9 Комплексные числа и многочлены. Практическое занятие 10 Комплексные числа и многочлены. Практическое занятие 11 Квадратичные формы. Продолжительность – 2 часа) Продолжительность – 2 часа) Продолжительность – 2 часа) Перечень Контрольных вопросов по курсу дисциплины «Линейная алгебра Формы самостоятельной работы студентов Матрицы. Определители матриц. Метод Гаусса, метод Обратной матрицы, метод Крамера решения систем линейных уравнений. Ранг матрицы. Общий метод решения системы линейных уравнений. Комплексные числа и многочлены. Квадратичные формы.

Подобный материал:

• Учебно-методический комплекс дисциплины экономическая теория (макроэкономика) по направлению, 300.76kb.
• Налоговый потенциал и налоговое планирование развития инновационных организаций Учебно-методический, 772.58kb.
• Учебно-методический комплекс дисциплины б дв1 Теория систем и системный анализ Направление, 568.62kb.
• Учебно-методический комплекс. Рабочая программа для студентов направления 080200., 490.77kb.
• Учебно-методический комплекс. Рабочая программа для студентов направления 080200., 498.73kb.
• Учебно-методический комплекс. Рабочая программа для студентов направления 080200., 1043.41kb.
• Учебно-методический комплекс. Рабочая программа для студентов направления 080200., 515.43kb.
• Учебно-методический комплекс. Рабочая программа для студентов магистерской программы, 533.44kb.
• Учебно-методический комплекс. Рабочая программа для студентов направления 080200., 1437.5kb.
• Программа учебной практики Учебно-методический комплекс для бакалавриата по направлению, 90.68kb.

Практическое занятие 9 Комплексные числа и многочлены.

(Продолжительность – 2 часа)

Вопросы для изучения

1. Понятие комплексного числа.

2. Алгебраическая, тригонометрическая, показательная формы комплексного числа.

3. Операции над комплексными числами.

Практические задания

1. Нахождение алгебраической, тригонометрической, показательной форм

комплексного числа. Графическое представление комплексного числа.

Операции над комплексными числами. Разбор и решение задач №№ 10.1.1,

10.1.5 10.1.6

2. Домашнее Задание: №№ 10.2.3 а) в), 10.2.4 а) в), 10.2.5 а) в), 10.2.6 в), 10.2.12 а) в), 10.2.15


Список источников и литературы

Основная литература

1. К.Н.Лунгу, Д.Т.Письменный, С.Н.Федин, Ю.А.Шевченко. Сборник задач по

высшей математике. 1 курс. - М.: Айрис-пресс, 2007 - с.432-441.

Дополнительная литература

1. Высшая математика для экономистов. Учебник. Под редакцией Кремера Н.Ш. -

М.: Юнити, 2006 - 497 с.

Практическое занятие 10 Комплексные числа и многочлены.

(Продолжительность – 2 часа)

Вопросы для изучения

1. Алгебраическая, тригонометрическая, показательная формы комплексного числа.

2. Операции над комплексными числами.

3. Понятие квадратичной формы.


Практические задания

1. Нахождение алгебраической, тригонометрической, показательной форм

комплексного числа. Графическое представление комплексного числа.

Операции над комплексными числами. Разбор и решение задач Домашнего

задания: №№ 10.2.3 а) в), 10.2.4 а) в), 10.2.5 а) в), 10.2.6 в), 10.2.12 а) в),

10.2.15 .

2. Разбор и решение задачи № 1 А), В), С) из Задания к Практическому занятию

№ 10.

3. Нахождение симметрической матрицы квадратичной формы.

4. Домашнее Задание: № 2 А), В), С) из Задания к Практическому занятию

№ 10:


Задание к Практическому занятию № 10

1. Комплексные числа в алгебраической форме изобразить векторами на плоскости и представить в тригонометрической форме
   

.

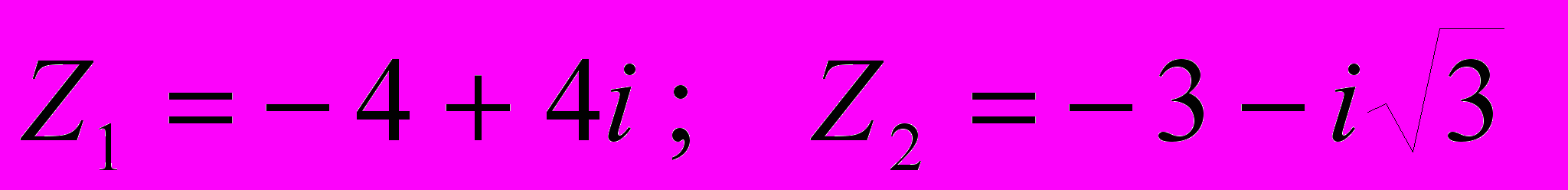А) Записать в алгебраической форме

.


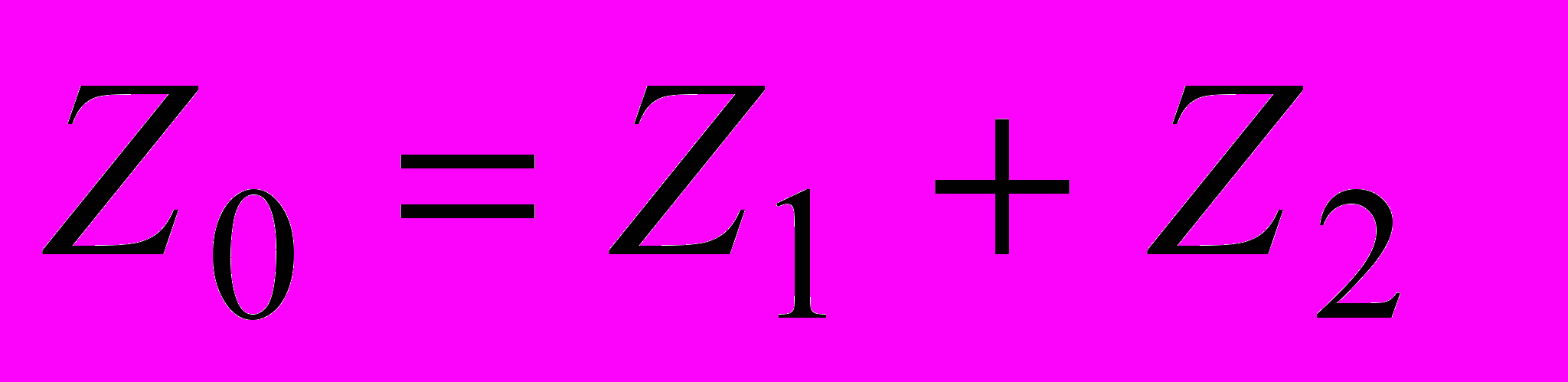В) Записать в алгебраической и тригонометрической формах



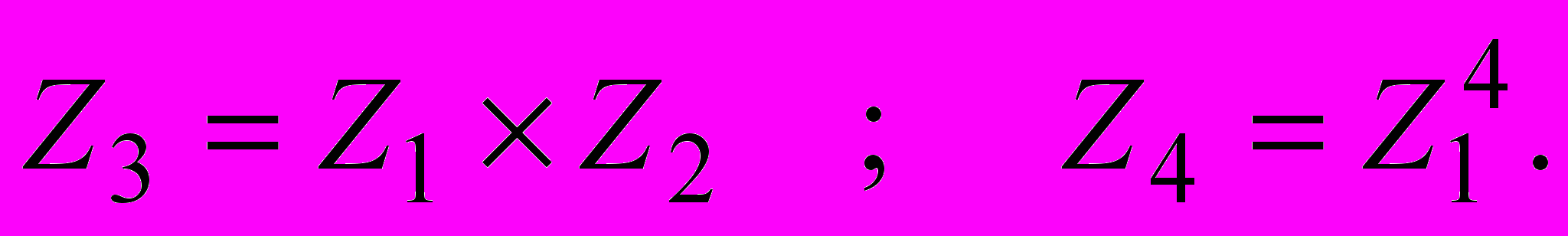
С) Записать в тригонометрической форме.




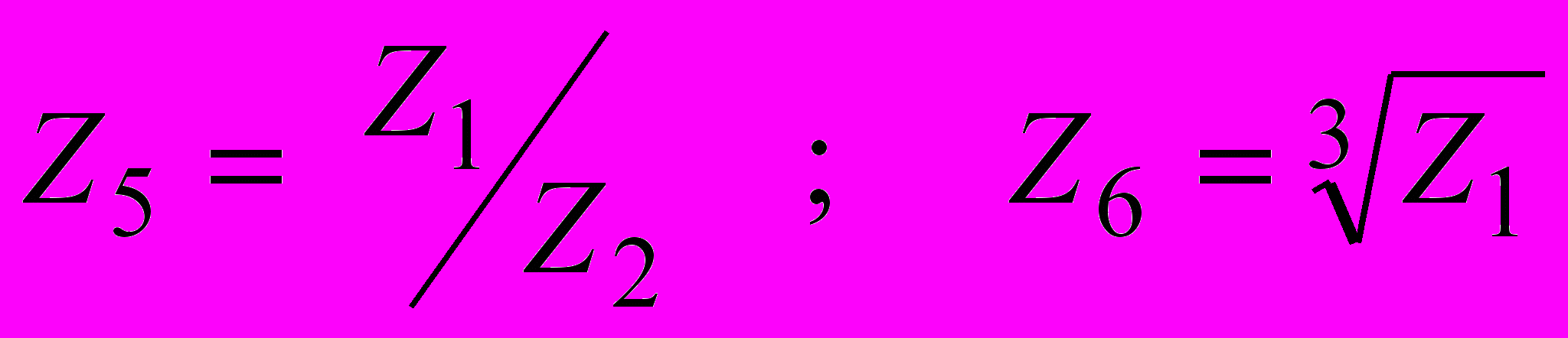
2) Комплексные числа в алгебраической форме изобразить векторами на плоскости и представить в тригонометрической форме

.

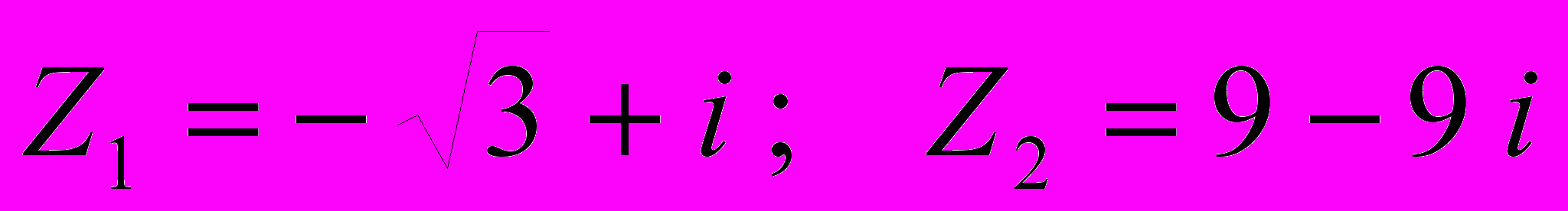А) Записать в алгебраической форме

.


В) Записать в алгебраической и тригонометрической формах



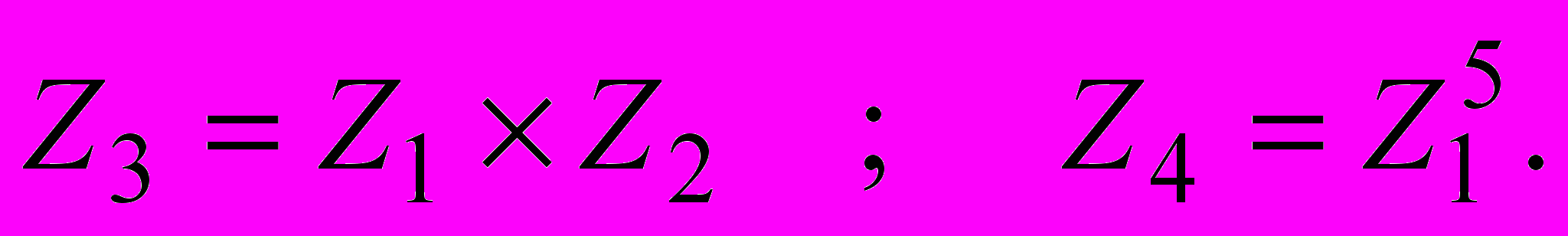
С) Записать в тригонометрической форме

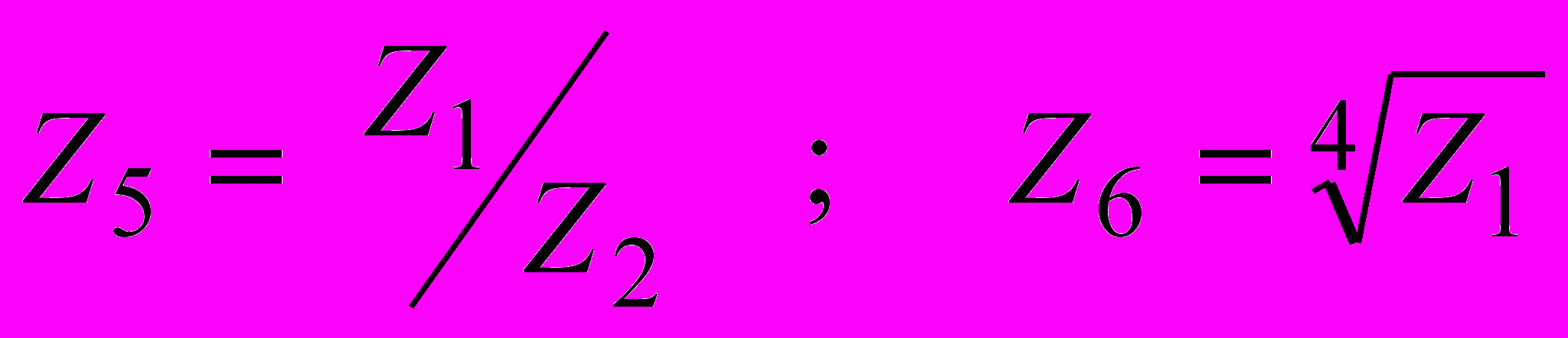
3. Записать квадратичную форму в матрично-векторном виде.
   

Выяснить, является ли квадратичная форма положительно определенной,

отрицательно определенной, неопределенной.

.

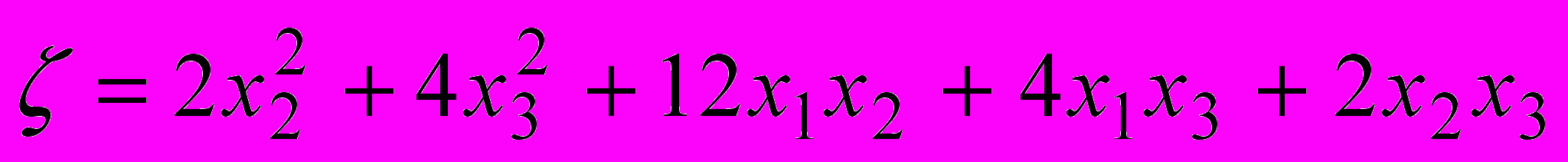3. Записать квадратичную форму в матрично-векторном виде.
   

Выяснить, является ли квадратичная форма положительно определенной,

отрицательно определенной, неопределенной.

.


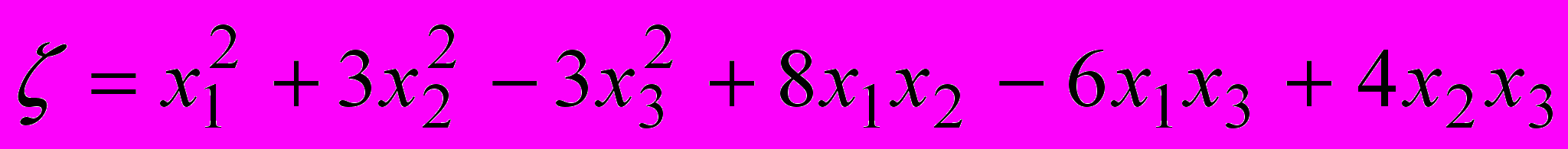Список источников и литературы

Основная литература

1. К.Н.Лунгу, Д.Т.Письменный, С.Н.Федин, Ю.А.Шевченко. Сборник задач по

высшей математике. 1 курс. - М.: Айрис-пресс, 2007 - с.432-441.

2. Высшая математика для экономистов. Учебник. Под редакцией Н.Ш.Кремера. -

М.: Юнити, 2006 - с.85-90

Дополнительная литература

1. Воеводин В.В. Линейная алгебра. Учебное пособие. – М.: Лань, 2008. – 400 с.

Практическое занятие 11 Квадратичные формы.

(Продолжительность – 2 часа)

Вопросы для изучения

1. Операции над комплексными числами.

2. Нахождение матрично-векторного вида квадратичной формы.

3. Положительная и отрицательная определенность квадратичных форм. Критерий Сильвестра.


Практические задания

1. Операции над комплексными числами. Разбор и решение задач Домашнего

задания.

2. Нахождение матрично-векторной вида квадратичной формы. Положительная и
   

отрицательная определенность квадратичных форм. Критерий Сильвестра.

Разбор и решение задачи № 3 из Задания к Практическому занятию № 10.

3. Домашнее Задание: № 4 из Задания к Практическому занятию № 10.


Список источников и литературы

Основная литература

1. К.Н.Лунгу, Д.Т.Письменный, С.Н.Федин, Ю.А.Шевченко. Сборник задач по

высшей математике. 1 курс. - М.: Айрис-пресс, 2007 - с.432-441.

2. Высшая математика для экономистов. Учебник. Под редакцией Н.Ш.Кремера. -

М.: Юнити, 2006 - с.85-90

Дополнительная литература

1. Воеводин В.В. Линейная алгебра. Учебное пособие. – М.: Лань, 2008. – 400 с.


Практическое занятие 12 Ранг матрицы. Общий метод решения системы линейных уравнений. Комплексные числа. Квадратичные формы.

(Продолжительность – 2 часа)

Вопросы для изучения

Контрольная работа №2

Матричные уравнения.

Исследование систем линейных уравнений.

Решение неопределенных систем линейных уравнений.

Операции над комплексными числами.

Квадратичные формы.


Практические задания

1. Решение индивидуального варианта Контрольной работы №2 в письменной форме.

2. Домашнее Задание: Решение невыполненных №№ Контрольной работы № 2;

решение невыполненных задач Домашнего задания к Практическим занятиям 7,

8, 9, 10, 11. Подготовка индивидуального вопроса Коллоквиума по

теоретическому материалу в письменной форме.


Список источников и литературы

Основная литература

1. К.Н.Лунгу, Д.Т.Письменный, С.Н.Федин, Ю.А.Шевченко. Сборник задач по

высшей математике. 1 курс. - М.: Айрис-пресс, 2007 - с.12-13, с.35-37, с.55-65,

с.87-90, с.432-441.

2. Высшая математика для экономистов. Учебник. Под редакцией Н.Ш.Кремера. -

М.: Юнити, 2006 - с.85-90

Дополнительная литература

1. Воеводин В.В. Линейная алгебра. Учебное пособие. – М.: Лань, 2008. – 400 с.


Практическое занятие 13 Коллоквиум по теоретическому материалу. Защита индивидуального Домашнего задания.

(Продолжительность – 2 часа)

Вопросы для изучения

1. Разбор типичных ошибок задач Контрольной работы №2.
   
2. Разбор и индивидуальное исправление ошибок в задачах Контрольной работы №2.
   
3. Коллоквиум по теоретическому материалу Лекционного курса.
   

(см. «Перечень Контрольных вопросов по курсу дисциплины «Линейная алгебра», стр. 16 ; «Перечень экспресс-тестов по лекционному материалу дисциплины «Линейная алгебра», стр. 17 .)

4. Обсуждение индивидуального Домашнего задания.


Практические задания

1. Защита индивидуального вопроса Коллоквиума по теоретическому материалу семестра в устной форме.
   
2. Защита индивидуального вопроса Тестов по теоретическому материалу семестра в устной форме.
   
3. Защита индивидуального Домашнего задания.
   

Список источников и литературы

1. К.Н.Лунгу, Д.Т.Письменный, С.Н.Федин, Ю.А.Шевченко. Сборник задач по

высшей математике. 1 курс. - М.: Айрис-пресс, 2007 - с.12-13, с.35-37, с.55-65,

с.432-441.

2. Высшая математика для экономистов. Учебник. Под редакцией Н.Ш.Кремера. -

М.: Юнити, 2006 - с.85-90


Дополнительная литература

1. Воеводин В.В. Линейная алгебра. Учебное пособие. – М.: Лань, 2008. – 400 с.


Практическое занятие 14 Коллоквиум по теоретическому материалу. Защита индивидуального Домашнего задания.

(Продолжительность – 2 часа)

Вопросы для изучения

1. Коллоквиум по теоретическому материалу Лекционного курса.

(см. « Перечень Контрольных вопросов по курсу дисциплины «Линейная алгебра», стр. 16 ; «Перечень экспресс-тестов по лекционному материалу дисциплины «Линейная алгебра», стр. 17 .)

2. Обсуждение индивидуального Домашнего задания.


Практические задания

1. Защита индивидуального вопроса Коллоквиума по теоретическому материалу

семестра в устной форме.

2. Защита индивидуального вопроса Тестов по теоретическому материалу семестра

в устной форме.

3. Защита индивидуального Домашнего задания.


Список источников и литературы

1. К.Н.Лунгу, Д.Т.Письменный, С.Н.Федин, Ю.А.Шевченко. Сборник задач по

высшей математике. 1 курс. - М.: Айрис-пресс, 2007 - с.12-13, с.35-37, с.55-65,

с.432-441.

2. Высшая математика для экономистов. Учебник. Под редакцией Н.Ш.Кремера. -

М.: Юнити, 2006 - с.85-90


Дополнительная литература

1. Воеводин В.В. Линейная алгебра. Учебное пособие. – М.: Лань, 2008. – 400 с.

4. Методические рекомендации студенту по организации самостоятельной работы


Общая трудоемкость освоения дисциплины «Линейная алгебра» составляет 3 зачетных единицы, 108 часов, из них 54 часа аудиторных занятий и 54 часа, отведенных на самостоятельную работу студента.

Самостоятельная работа студентов направлена на приобретение новых теоретических и фактических знаний, закрепление полученных навыков, - выполняется в читальном зале библиотеки и в домашних условиях, подкрепляется учебно-методическим и информационным обеспечением (учебники, учебно-методические пособия, конспекты лекций).

Индивидуальный контроль знаний может быть осуществлен на практических занятиях, которым предшествуют лекции по данной теме.

В части УМК «Тематические разделы Практических занятий» приведены Домашние задания для каждого Практического занятия, которые помогают закреплять теоретические положения курса и навыки решения типовых задач. Приведен список основной рекомендуемой литературы с указанием страниц.

В части УМК «Структура дисциплины (тематический план)» указана трудоемкость самостоятельной работы студентов по изучению соответствующих тем дисциплины «Линейная Алгебра».

№ п/п	Раздел дисциплины	Семестр	Неделя семестра	Вид работы	Самостоя-тельная работа студентов	Формы самостоятельной работы студентов (по неделям семестра)
	Трудоем-кость (в часах)
1	2	3	4		5	6
1	Системы линейных уравнений. Метод Гаусса.	2	1	Подготовка к практическому занятию № 1		Изучение лекций по теме 1. Написание Теста 1 для самоконтроля.
2	Матрицы. Операции над матрицами.	2	2	Подготовка к практическому занятию № 2	2	Изучение лекций по теме 2. Написание Теста 2 для самоконтроля. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 1 в Плане практических занятий, стр. 22-23
3	Определитель матрицы. Миноры.	2	3	Подготовка к практическому занятию № 3	2	Изучение лекций по теме 3. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 2 в Плане практических занятий, стр. 24
4	Обратные матрицы. Метод Крамера	2	4	Подготовка к практическому занятию № 4		Изучение лекций по теме 4. Написание Теста 3 для самоконтроля. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 3 в Плане практических занятий, стр. 24-25
	Обратные матрицы. Метод Крамера	2	5	Подготовка к практическому занятию № 5	2	Изучение лекций по теме 4. Написание Теста 4 пп. 1,2 для самоконтроля. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 4 в Плане практических занятий, стр. 25-26
	Матрицы. Определители матриц. Метод Гаусса, метод Обратной матрицы, метод Крамера решения систем линейных уравнений.	2	6	Подготовка к практическому занятию № 6	10	Подготовка к Контрольной работе №1. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 5 в Плане практических занятий, стр. 26-27 Составление и решение индивидуального домашнего задания.
5	Ранг матрицы.			Подготовка к практическому занятию № 7	2	Изучение лекций по теме 5. Написание Теста 4 пп. 3.4.5 для самоконтроля.
6	Общий метод решения системы линейных уравнений.			Подготовка к практическому занятию № 8	2	Изучение лекций по теме 6. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 7 в Плане практических занятий, стр. 28
7	Комплексные числа и многочлены.			Подготовка к практическому занятию № 9	2	Изучение лекций по теме 7. Написание Теста 5 пп. 1,2,3 для самоконтроля. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 8 в Плане практических занятий, стр. 29
				Подготовка к практическому занятию № 10		Изучение лекций по теме 7. Написание Теста 5 п. 4 и Теста 6 пп.1,2 для самоконтроля. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 9 в Плане практических занятий, стр. 29-30
8	Квадратичные формы.			Подготовка к практическому занятию № 11	2	Изучение лекций по теме 8. Написание Теста 6 пп.3 для самоконтроля. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 10 в Плане практических занятий, стр. 30-32
				Подготовка к практическому занятию № 12	10	Подготовка к Контрольной работе 2. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 11 в Плане практических занятий, стр. 32-33
	Коллоквиум по теоретическому материалу. Защита индивидуального Домашнего задания.	2	7	Подготовка к практическому занятию № 13	2	Изучение лекций по темам 1-8. Написание Тестов 1- 6 для самоконтроля. Выполнение домашних заданий. См. Список литературы и описание практического занятия № 12 в Плане практических занятий, стр. 33-34 Подготовка к Коллоквиуму по теоретическому материалу.
	Коллоквиум по теоретическому материалу. Защита индивидуального Домашнего задания.			Подготовка к практическому занятию № 14		Изучение лекций по темам 1-8. Написание Тестов 1- 6 для самоконтроля. Подготовка к Коллоквиуму по теоретическому материалу.
	Промежуточная аттестация	2			18	Подготовка к Зачету