Семинара- в разделах 1-4 описания и лабораторной работе №1

Вид материала

Семинар

Содержание 1.1 Свободные колебания. 1.2. Разложение Фурье. 1.3. Акустические колебания с непрерывным спектром. 1.4. Вынужденные колебания в акустических системах. В этом разделе неоднократно упоминался термин «резонанс» и мы очередной раз убедились, что любое физическое явление не может быт 1.5. Источники звука: дополнительные сведения. 2. Распространение звука. 2.1. Скорость звука. Волновое сопротивление. 2.2. Поглощение звука и ультразвука. 2.3. Эффект Доплера. 2.4. Воздействие звука и ультразвука на ткани организма. 3. Восприятие звука. 3.2. Восприятие звука: дополнительные сведения.

Подобный материал:

• Методические указания к лабораторной работе по курсу «Информатика» для студентов всех, 254.72kb.
• Методические указания к лабораторной работе по курсу «Информатика» Основы алгоритмизации, 441.82kb.
• Задание для выполнения лабораторной работы №1 средствами ms word, 50.12kb.
• Методические указания к лабораторной работе №3 по дисциплине «Периферийные устройства», 217.77kb.
• Методические указания к лабораторной работе по курсу «Механизация животноводческих, 506.22kb.
• Методические указания к лабораторной работе по курсу Компьютерный анализ электронных, 270.05kb.
• М. К. Амосова Факультет психологии Психологические проблемы современной семьи Научно-практический, 15.28kb.
• Коломенский филиал, 151.94kb.
• Методические указания к лабораторной работе по курсу «Механизация и автоматизация технологических, 316.57kb.
• Изучение полупроводникового диода Методические указания к лабораторной работе, 269.79kb.

БИОАКУСТИКА


Полезная информация по теме семинара- в разделах 1-4 описания и лабораторной работе №1.

1. Источники звука.


В принципе, источником звука может стать любое твердое тело, если возбудить в нем колебания. Например, постучать по нему.

Источники звука как устройства, специально созданные для получения звука, изобретались и совершенствовались на протяжение всей истории человечества. По-видимому, одним из первых изобретений такого рода явился барабан, и успех этой затеи легко объясним: звук, возникающий при ударе по натянутой на барабан шкуре, хорошо соответствует возможностям нашего слуха, а большая поверхность шкуры обеспечивает большую энергию колебаний, звук получается громким и слышен далеко.

Свою долгую историю имеют музыкальные инструменты, в число которых вошел, разумеется, и барабан.

Развивался голосовой аппарат человека, совершенствовались навыки его использования.

Свой путь стремительного развития прошла в двадцатом веке радиоаппаратура и электронно-акустическая техника, а также техника звукозаписи.

С точки зрения теории колебаний, во всех источниках звука имеют место колебания двух видов: свободные и вынужденные.

Рассмотрим сначала особенности свободных колебаний.


1.1 Свободные колебания.


В системе, выведенной из состояния равновесия, а затем предоставленной самой себе, устанавливаются свободные колебания некоторой строго определенной частоты ν₀, которая называется собственной частотой колебаний данной системы. Так, для математического маятника собственная частота определяется длиной нити и ускорением свободного падения тел в данной местности:



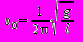
Более сложные системы имеют не одно, а несколько значений собственной частоты: ₁, ₂, ₃,… Применительно к источникам звука это следует понимать так: подобная система, выведенная из состояния равновесия, начинает звучать сразу на всех собственных частотах ₁, ₂, ₃,… Возникает сложное колебательное движение как сумма простых синусоидальных колебаний.

Примером такой системы является струна. Каждому натяжению струны соответствует свой ряд значений собственной частоты колебаний ₁, ₂, ₃,... .

Аналогично, ряд значений собственной частоты колебаний характерен для любого натяжения голосовых связок.

Наименьшая частота ₁ из этого ряда называется частотой основного тона, или просто тоном. Остальные частоты называются обертонами, и они связаны с основным тоном следующим образом: _{2 =} 2₁; _{3 =} 3₁; и т.д. Значения собственных частот часто называют так же «первая гармоника», «вторая гармоника», и т.д.

Распределение общей энергии сложного колебания по различным гармоникам может быть самым разнообразным. Диаграмма, показывающая зависимость амплитуды А каждой гармоники от ее частоты называется спектром колебаний, и имеет следующий вид:


А













₁ ₂ ₃ ₄ ₅  рис. 1


Спектр данного вида называется линейчатым.

Информация о фазах колебаний в каждой гармонике на таких диаграммах не представлена. Да она, как оказалось, и не очень нужна. Как доказал Георг Симон Ом, наше восприятие сложного звука не зависит от разности фаз в гармониках.

А вот как обстоят дела со свободными колебаниями в камертоне. Он применяется для настойки музыкальных инструментов, а так же и для «настройки» хора. Представляет собой U – образный стальной стержень прямоугольного поперечного сечения. Имеет ножку, за которую его можно держать. Начинает звучать, если его обо что-нибудь ударить. Является источником стандартного настроечного звука с частотой 440 Гц; высшие гармоники от него не требуются; более того, они не желательны. Однако, аппаратура для измерения энергии колебаний на различных частотах показала, что при ударе по камертону возникает несколько обертонов, но в этом устройстве они очень быстро затухают, оставляя лишь колебания основного тона, что от камертона и требуется.

Воздушные столбы, ограниченные стенками, так же являются обладателями своего ряда собственных частот. Их собственные частоты – это частоты таких волн, для которых длина волны укладывается в длину воздушного столба целое число раз.

П
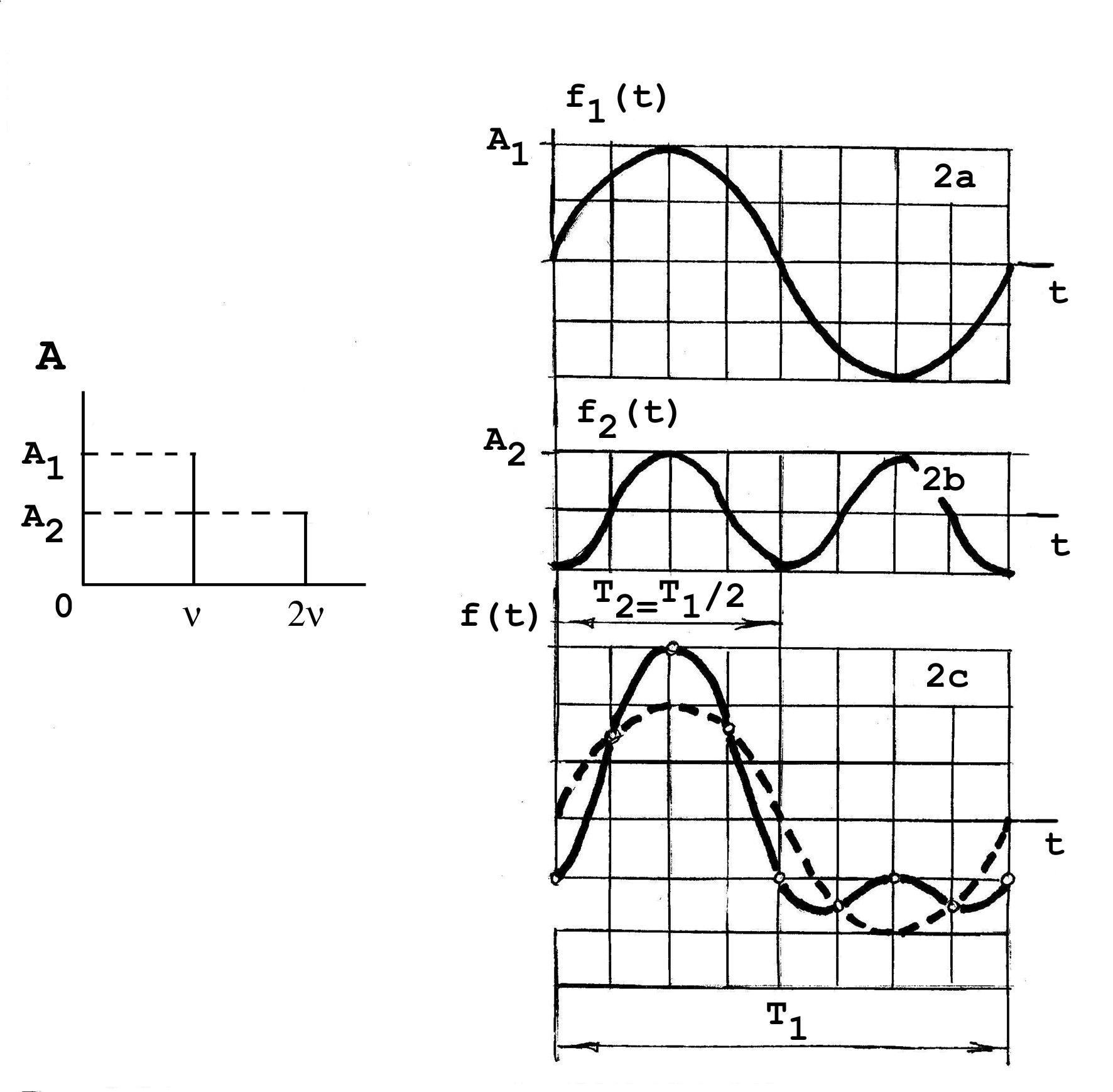
роследим графически, как из двух простых колебаний получается сложное колебательное движение. На рис.2 слева представлен линейчатый спектр, имеющий гармоники  и 2. Пусть амплитуды колебаний в этих гармониках равны, соответственно, А₁ = 2 см и А₂ = 1 см. Если на вход осциллографа подавать поочередно колебания частоты  и 2, то мы вправе рассчитывать на получение на экране картинок (2а), а затем (2b). Сплошную кривую на графике (2с) можно рассматривать как прогноз: что должен показать осциллограф, если на его вход подать обе гармоники одновременно. Сплошная кривая получена простым суммированием ординат двух предыдущих графиков. Отчетливые точки на сплошной кривой соответствуют тем стадиям колебаний, когда суммирование ординат предельно упрощается. Мы получили картину сложных колебаний в пределах одного периода Т, который соответствует частоте  основного

Рис. 2


тона: Т = 1/. Мы шли от простых гармонических колебаний к сложной сумме.

Подавая на вход осциллографа электрический сигнал от микрофона, «озвученного» каким-нибудь музыкальным звуком, мы получим на экране периодические кривые типа 2с, но более сложные в связи с большим числом гармоник.

Оказалось возможным математическое решение обратной задачи: сложное колебание представить в виде суммы простых гармоник с любой требуемой точностью.

1.2. Разложение Фурье.


Математическое представление сложных периодических колебаний в виде суммы простых гармоник называется разложением в ряд Фурье, любая периодическая функция времени f (t), имеющая период Т, может быть представлена в виде суммы простых гармоник следующего вида:

f (t) = A₀ + (A₁ сos ωt + B₁ sin ωt) + (A₂ cos 2ωt + B₂ sin 2ωt) +… (1)

Здесь ω = 2π/Т – величина, называемая циклической частотой.

Решить эту задачу для какой-нибудь конкретной функции f (t) – это значит найти для этой функции числовые значения коэффициентов (А₀, А₁, А₂…) и (В₁, В₂…).

В математике функциональный ряд – это, например, то, что записано в правой части формулы (1) с неограниченно большим (стремящимся к бесконечности) числом слагаемых. На практике этот бесконечный хвост слагаемых в правой части рано или поздно обрубают, и то, что остается, называется уже не рядом Фурье, а суммой Фурье. Если оказывается, что график суммы Фурье и график исходной функции f (t) отличаются слишком заметно, то сумму Фурье надо удлинить, вычислив еще пару коэффициентов А_k, В_k в дополнительное слагаемое (А_к cos kωt + B_k sin kωt). Действуя в таком духе, можно получить для любой функции f (t) приближенное математическое описание в виде суммы Фурье с любой желаемой точностью. Правда, полученная формула может оказаться громоздкой, но в наш компьютерный век эта беда – не беда.

Весьма существенное обстоятельство: при вычислении дополнительных коэффициентов (А_k, В_k) не требуется пересмотра ранее вычисленных коэффициентов.

В этом обзоре мы обходим стороной вопрос о том, как следует вычислять коэффициенты разложения (А_k, В_k). Отметим лишь, что они вычисляются интегрированием. Что и как нужно интегрировать, можно выяснить в справочной и специальной литературе.

Разложение Фурье было предложено еще в начале 19 века, и с тех пор широко применяется. По этой причине разложение Фурье фигурирует и в учебных программах медицинских вузов. Этот мощный метод дает возможность представить любой сложный процесс в виде суммы гармоник различной амплитуды. Легко обходится даже требование о периодичности исходной функции f(t). А громоздкие процедуры по вычислению коэффициентов (А_k, В_k) в нынешние времена легко решаются обращением к соответствующей стандартной компьютерной программе.

Однако есть в этом деле одна тонкость, которая нам представляется важной: метод Фурье может давать описание в виде суммы гармоник, которых в реальном процессе может и не быть.

Например, на столбе висит фонарь, и он периодически то включается, то выключается. Получается, что освещенность под фонарем – это функция f (t) следующего вида:


f(t)






⁰ t рис.3


Для этой функции можно получить разложение Фурье, и график полученной формулы может совпадать с графиком рис.3 с любой требуемой точностью, но метод Фурье здесь будет работать чисто формально. Интерпретировать гармоники такого формального разложения Фурье как совокупность неких реальных колебаний было бы совершенно некорректно.

Другое дело – акустические колебания: сложный звук допускает разложение Фурье в виде (1), при этом гармоники разложения соответствуют реальным физическим процессам. Так, если частота основного тона струны ₁ = 440 Гц, то при этом действительно возникают (экспериментально подтверждаются) гармоники с частотами ₂ = 2₁ = 880 Гц, ₃ = 3₁ = 1320 Гц, и т.д., потому что струна звучит как единое целое (440 Гц), но так же излучает дополнительный звук двумя половинами своей длины (880 Гц), и т.д. Потому что вдоль струны устанавливаются так называемые «стоячие волны», узлы которых разделяют струну на автономно и совместно звучащие участки.


1.3. Акустические колебания с непрерывным спектром.


Звуковые колебания с непрерывным спектром относятся к категории шумов. А у шумов – устойчивая репутация посторонних, ненужных звуков, от которых следует избавиться. Но это верно лишь отчасти. Произнося согласные, мы издаем звуки с непрерывным частотным спектром. Звучание духовых музыкальных инструментов инициируется шумовыми акустическими колебаниями, создаваемыми с помощью губ музыканта или специального язычка. Скрипка звучит благодаря скрипу (шуму), возникающему при трении смычка о струну.

Если амплитуда колебаний в шуме на всех частотах в среднем одинакова, то такой шум называется белым. Произнося звук «Ф», мы создаем что-то близкое к белому шуму.

Вопросы на засыпку:

• В чем отличие чуть слышимого белого шума от белого шума, который мешает жить и работать?
  
• В различных отраслях науки и техники есть проблема, которую можно обозначить так: «соотношение сигнал – шум». Как Вы понимаете сущность этой проблемы (на тех или иных частных примерах)? Что может мешать простому решению: шум отрезать, а сигнал оставить?
  

Энергия колебаний может распределяться по частотам шума неравномерно. Например, акустический спектр при произнесении звука «С» примерно такой:


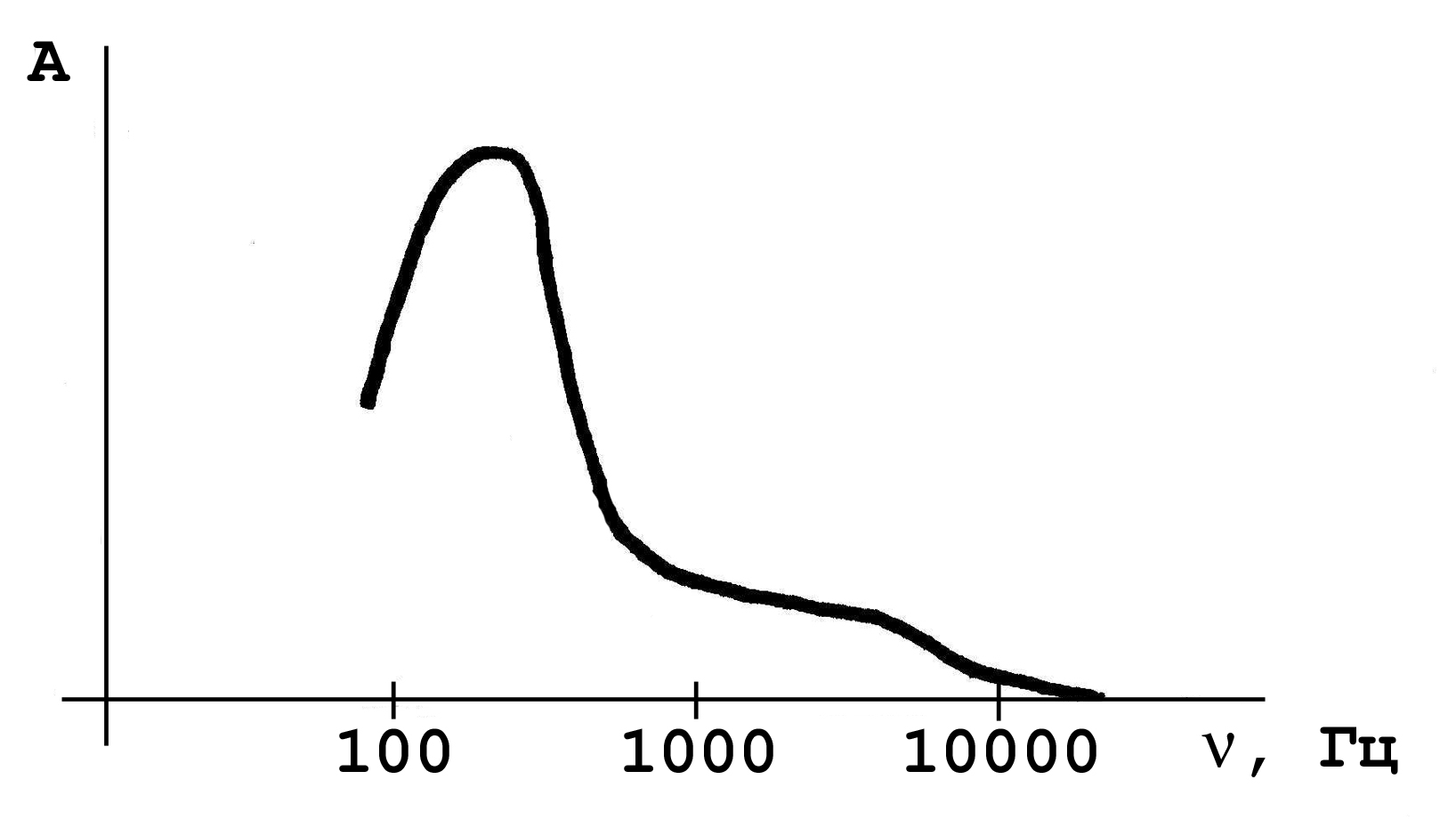
рис.4


Шумы как нежелательное явление, с которым приходится бороться, подразделяются на низкочастотные, среднечастотные и высокочастотные. Эти названия следует понимать так: в шуме представлены все частоты колебаний, но преобладают (имеют повышенную амплитуду) колебания низких, средних или высоких частот. Особо зловредными считаются высокочастотные шумы. Специфика их воздействия – в том, что спустя какое-то время мы их почти не замечаем, но эта защитная реакция организма не отменяет угнетающего действия такого шума на нервную систему, и угнетенное состояние постепенно усугубляется. А вот если кто-то пойдет и выключит источник такого шума, мы чувствуем резкое облегчение, и произносим что-то типа «Ах, как хорошо!» Стало быть, до этого было ах как плохо, но мы этого не замечали или почти не замечали. Шум может замедлять мыслительные процессы, увеличивать время реакции.

Однако же и «гробовая тишина» – тоже не подарок. Испытания космонавтов в сурдокамере не считаются ими самым легким тестом. Выезжая «на природу», мы оказываемся вдали от шума городского, но в атмосфере слабых природных шумов листвы, воды и т.п., оказывающих весьма благотворное действие.

Вопрос на засыпку: в чем особенности шума листвы в сравнении, например, с каким-нибудь техногенным шумом такого же уровня громкости? И заодно попытайтесь объяснить, почему мы смотрим на пламя костра как зачарованные?

Обсудим вопрос о звуках с непрерывным спектром на частном примере произнесения звука «С». Здесь физическая картина событий такова: выдыхая воздух, мы с помощью языка, зубов, губ создаем на его пути преграды с достаточно резкими геометрическими формами. При обтекании таких преград течение воздушного потока становится турбулентным, т.е. вихревым. Появление вихрей становится неизбежным, если велики отличия в скорости смежных слоев потока, в данном случае газового.

Что такое турбулентный вихрь? Это временный коллектив частиц, в котором происходит вращательное движение. Местные колебания давления в потоке возникают в связи с взаимодействием вихрей друг с другом, а так же на стадиях их возникновения и исчезновения. Хаотичная система возникающих и исчезающих вихрей различного масштаба приводит к разнообразным местным пульсациям давления в объеме потока, которым соответствует сложный звук с непрерывным спектром.

Наличие максимума в непрерывном спектре рис.4 говорит о том, что при произнесении звука «С» в системе возникающих вихрей преобладают сравнительно крупные вихри, «работающие» на сравнительно низких частотах.


1.4. Вынужденные колебания в акустических системах.


Если между двумя деревьями натянуть проволоку, то можно убедиться, что как бы она ни была натянута, мы получаем очень слабый, можно сказать, никудышный источник звука. Это объясняется двумя обстоятельствами. Во-первых, у проволоки, как и у любой струны, мала площадь поверхности: это Вам не барабан. Во-вторых, если струна или проволока, отклоняясь при колебаниях, одной своей стороной теснит воздух и создает зону сжатия, то противоположная сторона создает зону разрежения; возникают две волны, в которых колебания – в противофазах. Такие две волны при интерференции ослабляют друг друга почти до нуля практически во всем окружающем пространстве.

Наши голосовые связки сами по себе тоже очень слабый источник звука по тем же двум причинам. К тому же они находятся где-то в глубине нашего «Я».

Струна звучит, когда она – часть музыкального инструмента. При этом излучателями звука являются поверхности корпуса и воздух, заполняющий полости инструмента. Свободные колебания с линейчатым спектром, возникающие в струне если ее, например, ущипнуть, передаются корпусу. Колебания корпуса – это вынужденные колебания под воздействием переменной силы натяжения колеблющейся струны. Ну, а колебания воздуха в полостях инструмента – это вынужденные колебания, вызванные колебаниями в корпусе.

А теперь рассмотрим технологию произнесения гласных звуков. В голосовом аппарате связки, натяжение которых – в подчинении центральной нервной системы, начинают совершать колебания при нашем выдохе. Их выводят из состояния равновесия турбулентные вихри с непрерывным акустическим спектром, но благодаря явлению резонанса, в связках возбуждаются колебания на их собственных частотах ₁,₂,… Эти красивые, но слабые звуки усиливаются опять-таки благодаря резонансу: резонирует воздух в полостях носоглотки. Через открытый рот выдыхаемый воздух, в котором возбуждены акустические колебания, сообщается с внешней воздушной средой, в которой возникают воздушные волны, достигающие ушей слушателя.

При шепоте голосовые связки расслабляются и бездействуют; частота произносимых звуков определяется в этом случае колебаниями воздуха на других препятствиях и резонансными частотами носоглотки.

При произнесении согласных связки не работают (например, «К» и «П») или работают вполсилы («М» и «Н»). Звуки с непрерывным спектром возникают в результате возникновения турбулентных вихрей на преградах, создаваемых на пути выдыхаемого воздуха языком, губами, зубами.

Мужской голос обычно ниже женского, так как у мужчин голосовые связки толще, длиннее и набор собственных частот их колебаний смещен в сторону низких частот. Голос мальчиков «ломается» в период их быстрого роста, когда гортань увеличивается и голосовые связки из детских – тонких и коротких – превращаются в мужские. Происходят изменения и в системе управления этим акустическим аппаратом. Но эти изменения могут отставать от текущих потребностей. В итоге приходится слышать то, что приходится слышать.

В духовых музыкальных инструментах технология получения звука такова: первичный звук создается с помощью губ музыканта или специального язычка и имеет непрерывный спектр. Из этого спектра получают развитие те частоты, которые совпадают с собственными частотами столба воздуха в полостях инструмента. На этих же частотах вынуждены совершать колебания стенки инструмента.

Если в ударных музыкальных инструментах звук появляется сразу и в готовом виде, то в остальных музыкальных инструментах и в нашем голосовом аппарате звук вызревает, проходя определенные стадии развития.

Как в голосовом аппарате, так и в музыкальных инструментах нет ничего лишнего и нет ничего такого, что можно бы радикально менять. Медленная эволюция голосового аппарата человека, похоже, благополучно завершилась. Эволюция музыкальных инструментов продолжается, но происходит очень медленно и осторожно. Изготовление элитных музыкальных инструментов было и остается в большей степени искусством, чем технологией.

Появляются ли новые музыкальные инструменты? Да, появляются. Например, саксофон – дитя двадцатого века. Инструмент, блестящий во всех отношениях, это инструмент новый, а не усовершенствованный старый.

Вообще, двадцатый век оказался очень щедрым на изобретения и открытия, и в частности в том, что касается звука. Возникли следующие новые направления:

• Техника преобразования звуковых колебаний в электрические и передачи звука на расстояние, сначала по проводам (телефон), а потом и без проводов (радиотехника).
  
• Техника звукозаписи и воспроизведения записей со сменой поколений звуконосителей: восковые валики, виниловые диски, магнитная лента, лазерные диски.
  
• Техника электронных синтезаторов звука.
  

Любое из подобных устройств (кроме устройств, работающих только на запись) имеет на выходе преобразователь электрических колебаний в звук. Остановимся кратко на особенностях таких источников звука.

Преобразования электрических колебаний в звуковые в электродинамических громкоговорителях (динамиках) происходит следующим образом. Электрический ток звуковых частот, усиленный до необходимых значений амплитуды с помощью усилителя, пропускается по виткам легкой катушки, находящейся в мощном магнитном поле постоянного магнита. Катушка соединена с мембраной или ее усовершенствованным аналогом – диффузором. На катушку с переменным током действует переменная сила Ампера, которая и является причиной вынужденных колебаний диффузора. Фактическим источником звука является диффузор.

Не будь явления резонанса, эта система работала бы безупречно: частота звуковых колебаний диффузора определялась бы частотой тока, протекающего по катушке, а амплитуда звуковых волн – амплитудными значениями тока.

Правда, при колебаниях диффузора, как и в случае со струной, возникают две волны. Волна, возбужденная задней, тыльной стороной диффузора, может ослаблять волну, излучаемую его передней поверхностью. Чтобы этого не происходило, можно было бы создать условия для поглощения колебаний «задней» волны, но нашелся более элегантный выход из положения: динамик помещают в корпус, с тем, чтобы «задняя» волна диффузора, отразившись от стенки корпуса, вернулась на диффузор. Глубина корпуса выбирается такой, чтобы фаза колебаний отраженной волны и фаза колебаний диффузора совпадали. «Задняя» волна, через явление акустического резонанса, из противника становится союзником.

Теперь посмотрим, какие неприятности возникают в этой системе в связи с явлением резонанса. Прежде всего, диффузор с закрепленной на нем катушкой имеет некоторую собственную частоту колебаний ₀. Она определяется массой этой системы, ее размерами, жесткостью материала. Чем крупнее диффузор, тем меньше его собственная частота ₀. Диффузор при своей работе совершает вынужденные колебания, отдавая предпочтение тем из них, частота которых равна или близка к ₀. Если спектр электрических колебаний в катушке динамика считать сценарием будущего звучания диффузора, то резонанс приводит к большим отступлениям от этого сценария в некотором диапазоне частот в окрестностях его собственной частоты колебаний ₀. Диффузор искажает спектр воспроизводимых частот, и эти искажения называются резонансными искажениями.

Резонансные искажения будут менее ощутимы, если собственная частота диффузора будет смещена к границам диапазона слышимых звуков 16 Гц – 20 кГц, поскольку чем ближе любая из этих границ, тем ниже острота нашего слуха. Но диффузор с низкой частотой ₀ – это диффузор больших размеров, а такие диффузоры плохо справляются с высокочастотными колебаниями. А маленький диффузор хорошо работает на высоких частотах, но плохо – на низких.

Недостатки крупных динамиков можно скомпенсировать достоинствами мелких, если они будут работать совместно по принципу разделения труда. В современных акустических колонках мы видим диффузоры разного калибра. Крупный диффузор работает на низких частотах, среднего размера – на средних, и один-два маленьких – на высоких частотах. Однако следует отдавать себе отчет, что эта мера снижает остроту проблемы резонансных искажений, но не снимает ее полностью.

Акустические колонки изначально задуманы как источники звука повышенного качества, а от динамика в составе кухонного репродуктора никто не ждет акустических изысков. Так вот, даже обсуждая качество звука элитных акустических колонок, мы должны вспомнить, что не диффузорами едино жива колонка. Есть в любой из них два важных элемента, тоже имеющих свои собственные частоты колебаний в слышимом диапазоне, и значит, готовых внести свой вклад в резонансные искажения. Речь идет о корпусе колонки и о воздухе, ее заполняющем.

Не будем погружаться в специфику этих дополнительных проблем. Ограничимся констатацией мнения специалистов, что эти проблемы могут быть сняты, если объем колонок будет не менее трехсот литров.

Что мы получаем, если хотим иметь акустическую колонку как источник звука, работающий без искажений? А получаем мы громоздкое сооружение, врожденные недостатки которого упорно не удается устранить.

Конечно, такой сундук или шкаф можно отделать ценными породами древесины, но все же складывается ощущение если не тупика, то кризисной ситуации.

Попробуйте высказать свои соображения по такому вопросу: что можно поручить компьютеру для минимизации искажений, возникающих при работе источников звука?

Может ли быть альтернатива динамикам, ставшим уже классическими? Вероятно, да. Появлялись сообщения о разработке плазменных «громкоговорителей» (название – то какое!)

Их возможный принцип действия: электрический разряд в воздухе, созданный высокочастотными колебаниями электрического напряжения, на которые наложены модулирующие электрические колебания звуковой частоты. Высокочастотная компонента должна создавать в ходе электрического разряда высокоионизированное состояние, которое в физике называется плазмой. Звуковая компонента электрических колебаний должна создавать в этой плазме колебания давления, которые мы и называем звуком.


Автор этих строк случайно имел возможность убедиться в жизнеспособности этого принципа. Однажды на радиостанции города Петропавловска-на-Камчатке произошла электрическая утечка с кабеля, идущего от радиопередатчика на мачту к передающей антенне. Возник слабо светящийся электрический разряд между кабелем и кем-то забытым ломом. Этот светящийся разряд заговорил чистым человеческим голосом: «Передаем последние известия». Все кинулись выдергивать лом из земли, потому что пока длился этот разряд, радиостанция вряд ли работала по прямому назначению.

В этом разделе неоднократно упоминался термин «резонанс» и мы очередной раз убедились, что любое физическое явление не может быть чисто полезным или чисто вредным.

Резонанс – явление, над которым стоит лишний раз задуматься. На примере простых качелей, которые резонансно раскачиваются благодаря Вашим своевременным подталкиваниям, объясните причины неуклонного роста амплитуды колебаний. Что ограничивает этот рост? И почему толчки, такие же по затратам Вашей энергии, но несвоевременные, приводят к колебаниям гораздо меньшего размаха.


1.5. Источники звука: дополнительные сведения.


В этом разделе Вы найдете объяснение звуковых эффектов, возникающих в ряде частных ситуаций.

• РАСКАТЫ ГРОМА. Электрический разряд молнии вызывает сильное нагревание и резкое расширение воздуха. Возникает цилиндрическая ударная волна, которая и служит основным источником грома. Длительное звучание грома – рокот и раскаты – обусловлено отражением звука от окружающих объектов.
  

• Если над нами пролетел сверхзвуковой самолет, и высота его полета не слишком велика, то в некоторый момент мы слышим громоподобный звук. Это означает, что коническая ударная волна, вершина которой – перед носовой точкой самолета, соприкоснулась с поверхностью земли в том месте, где мы находимся. Те, кто находятся дальше по ходу самолета, услышат то же самое, но несколько позже.
  

• ЖУРЧАНИЕ РУЧЕЙКА. Одна из причин – образование пузырьков в быстро текущей воде. Возникновение пузырьков сопровождается слабыми звуками. Более громкие звуки вызваны колебаниями объема пузырьков и их «схлопываниями», т.е. исчезновением. Ну, а возникают пузырьки благодаря турбулентным вихрям в водяном потоке.
  
• ЗАВЫВАНИЯ ВЕТРА. Могут возникать на висящих проводах, голых ветвях деревьев, на углах крыш и других заостренных предметах. При обтекании провода или ветки дерева воздушный поток становится неустойчивым, турбулентным. Колебания воздуха, которые мы воспринимаем как звук, создаются этими вихрями. Возникающие звуки, распространяясь, в частности, против воздушного потока, делают его еще более неустойчивым. Ветки или провод при этом часто совершают колебания, перпендикулярные потоку, но эти колебания для возникновения звука не обязательны.
  

Если ветер обтекает препятствие с резкими кромками, то «поют» не только вихри, но и кромки препятствия.

Вихри, возникающие на кромках выступающих печных труб, могут возбуждать колебания воздуха в столбе дымохода на его собственных частотах. При длинном дымоходе собственная частота может быть ниже 16 Гц; это будет инфразвук, неслышимый, но способный влиять на настроение.

Говорят, что иногда печники, не довольные оплатой их труда, в отместку вмуровывают в дымоходы резонаторы в виде пустых бутылок. Вот тогда возникают слышимые звуки.

При сильном ветре провода могут совершать вынужденные колебания не отельными участками, а как единое целое, от опоры до опоры. Если при этом провод оборвется, то ответственность за это следует возложить на явление резонанса.

• ТРЕСК СУСТАВОВ – звук, обусловленный образованием крохотных газовых пузырьков в синовиальной жидкости, смазывающей сустав. Пузырьки возникают, когда давление в жидкости резко уменьшается при растяжении суставов. Требуется подождать несколько минут, прежде чем повторить этот сомнительный номер на «бис»: газ должен успеть снова раствориться в жидкости.
  
• РЫЧАЩИЕ ТРУБЫ. Трубы начинают рычать, если в них что-нибудь не в порядке. Обычно источником неприятного звука являются изношенные детали кранов, которые начинают вибрировать в турбулентных вихрях водяного потока. А вихри, возникнув, делают поток воды все более неустойчивым. Основным излучателем звука при этом являются стенки трубы, совершающие вынужденные колебания.
  

Если разболтанная прокладка резко встает на место и перекрывает водный поток, возникает гидравлический удар, звук которого хорошо прослушивается на нескольких этажах. Энергия этого удара – это кинетическая энергия mV²/2 всей массы m воды в трубе. При резкой остановке потока, эта кинетическая энергия должна перейти в какой-нибудь другой вид энергии.

Чем чаще гидравлические удары, тем ближе тот день и час, когда старенькая водопроводная труба не выдержит всего этого безобразия и лопнет.

• ШУМЫ ЧАЙНИКА. Спустя некоторое время после того, как чайник поставлен на огонь, на горячем дне чайника возникают пузырьки. Их содержимое – в основном горячий насыщенный водяной пар. Образование первых пузырьков сопровождается легким щелчком, а сообща они создают шипение. При дальнейшем нагревании пузырьки отделяются от дна и начинают всплывать, но оказавшись в еще холодных слоях воды, «схлопываются», прекращая свое существование. При этом возникает более громкий коллективный звук. Когда же вся вода в чайнике достаточно прогрета, пузырьки, всплывая, достигают поверхностного слоя и там раскрываются. Возникает «белый шум», белый – потому что беловатым от всплывающих пузырьков выглядит поверхностный слой воды. Чуть позже шум становится плещущим: вода на поверхности ходит ходуном.
  

Чайные гурманы утверждают, что заваривать чай следует водой, нагретой до «белого шума». Более того, якобы требуется первый «белый шум», а если кипяток остыл и его подогрели до «белого шума» повторно, то это уже совсем не то, что надо для заварки. Такую воду надо вылить (а чайник - выкинуть)

• ШУМ МОРСКОЙ РАКОВИНЫ – звуки, которые мы слышим, прижимая к уху пустую морскую раковину, имеют следующее происхождение. Легкое движение воздуха вблизи устья раковины или окружающие звуки возбуждают в воздушной полости раковины резонансные колебания на ее собственных частотах. Плавное возбуждение и затухание таких колебаний создает у слушателя иллюзию звуков океанского прибоя.
  
• ЩЕЛКАНЬЕ КНУТА. Резкий звук, возникающий при резком взмахе кнута, допускает двоякое объяснение. Возможно, в конце распрямления кнута вся его начальная кинетическая энергия достается самому кончику, и он создает ударную волну. Но может быть и так: энергичный кончик ударяет о какую-то соседнюю часть кнута (вдова сама себя высекла?)
  
• «РВАЧЕСТВО». Звук, возникающий при разрывании тканей – это последовательность звуков, возникающих, когда волокна ткани рвутся одно за другим. А когда мы рвем бумагу, развивается процесс ее разрушения по месту разрыва, и звуковые колебания совершают отдельные участки образующихся кромок.
  
• ТИШИНА ПОСЛЕ СНЕГОПАДА. Даже в большом городе сразу после снегопада устанавливается глубокая тишина. Если проезжает транспорт, его звуки на удивление деликатно тихие. Эта тишина – временная, и объясняется тем, что свежевыпавший снег еще не успел слежаться; его поверхностный слой – снежинки, между которыми много воздуха. Такие структуры хорошо поглощают звук и практически его не отражают.
  

Пройдет немного времени, снег слежится и очарование исчезнет.

Неплохо бы для наружных поверхностей зданий иметь отделочные материалы с акустическими свойствами свежевыпавшего снега.

• В инженерной практике борьбы с шумами нашли применение щиты, пакеты и т.п., в которых слои материала, хорошо поглощающего звук, чередуются со слоями жесткими, плохо поглощающими, но хорошо отражающими звук. Благодаря отражениям от жестких прослоек, звук вынужден возвращаться в ранее пройденные слои хороших поглотителей. Общий итог таков, как будто звук прошел сквозь этот слоеный пирог не один, а несколько раз, и как это он не поглотился полностью, до сих пор не понятно.
  

2. Распространение звука.


В этом разделе обсуждаются звуковые волны в той стадии, когда они ушли от источника звука, но еще не достигли наших ушей или регистрирующей аппаратуры.


2.1. Скорость звука. Волновое сопротивление.


Скорость звука в воздухе при нормальных условиях (0˚С; 760 мм рт. ст.) V = 331,5 м/с. Этот экспериментальный результат находится в хорошем согласии с теоретической формулой для газов:

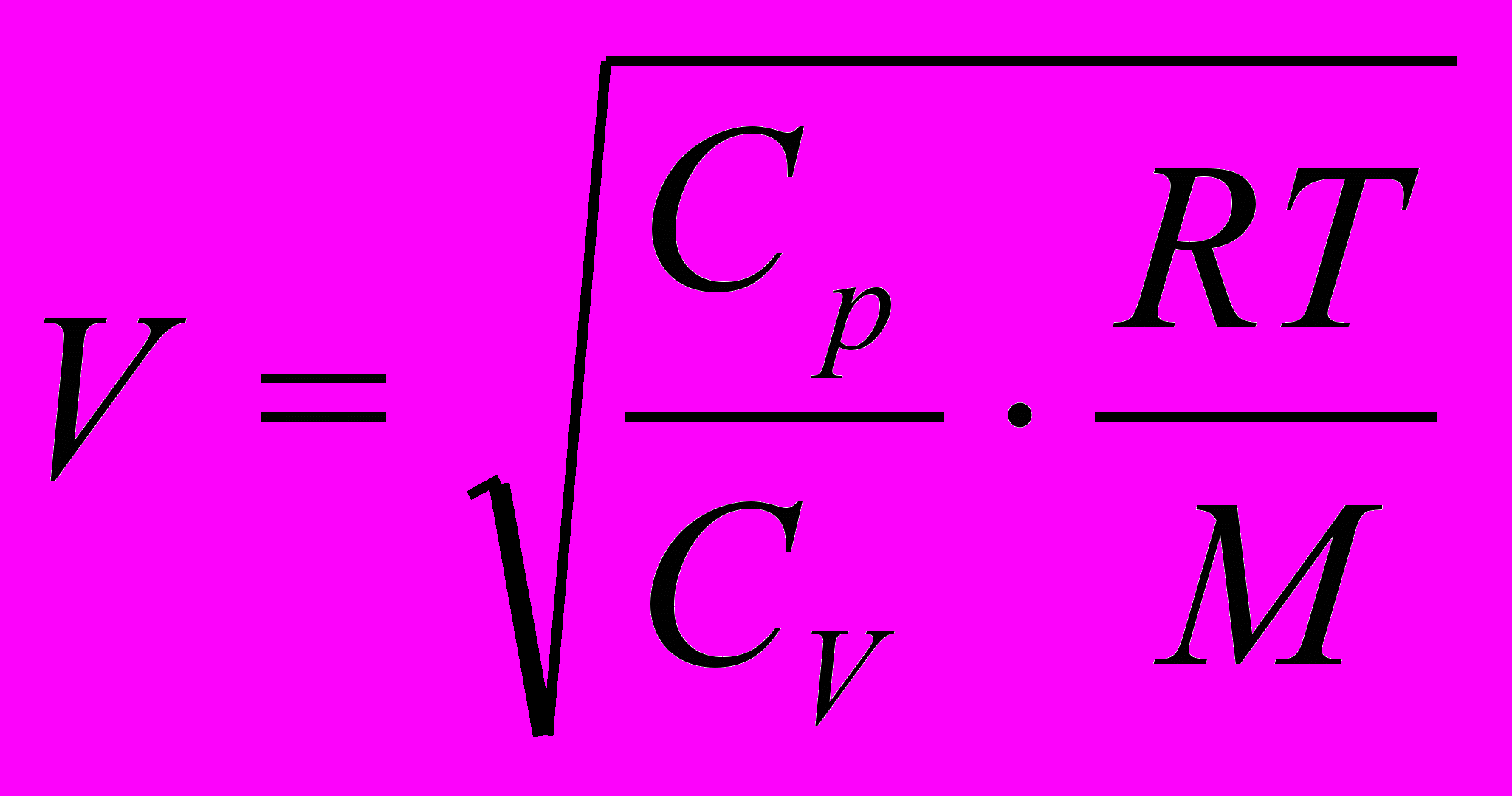(2)

Здесь R = 8,31 Дж/моль – универсальная газовая постоянная; М – молярная масса газа; Т – абсолютная температура газа (Т = 273 + t˚С); С_р; С_v – значения теплоемкостей газа при постоянном давлении и при постоянном объеме. Для двухатомных газов С_р/С_v = 1.4; для одноатомных – 1,67.

Приведенная формула показывает, что скорость звука в газах – величина, зависящая от температуры, хотя и не сильно. Так, если температура повысится от Т₁ = 0˚С = 273К до Т₂ = 20˚С = 293К, то есть возрастет в Т₂/Т₁ = 1,073 раза, то скорость звука возрастет в 1,036 раза и составит V = 343,4 м/с. При понижении температуры до t = -20˚С скорость звука уменьшится до 324 м/с. Колебания скорости звука составили ±3,3%. Это не много, но некоторые последствия непостоянства скорости звука в воздухе мы обсудим чуть позже. А пока обратимся еще раз к формуле (2). Из нее следует, что скорость звука зависит так же и от молярной массы газа. Для легких газов скорость звука значительно больше, чем для воздуха. Так, для водорода (двухатомные молекулы; М = 2 г/моль) V = 1265 м/с. Для гелия она составляет 897 м/с. Приведем пример ситуации, когда эти обстоятельства становятся существенными. При погружениях на большую глубину экипаж батискафа вынужден работать в условиях высокого давления газовой смеси, заполняющей батискаф. Это необходимо чтобы батискаф не был раздавлен забортной водой. Вместо воздуха применяют дыхательную смесь, в которой азот заменен гелием. Эта мера оказалась необходимой в связи с тем, что при повышении давления увеличивается количество азота, растворенного в крови, и он начинает оказывать наркотическое действие.

Скорость звука в такой газовой смеси гораздо больше, чем в воздушной; пропорционально возрастают и значения длин звуковых волн. Это приводит к большим изменениям акустических свойств полостей голосового аппарата. Голос взрослого мужчины становится похож на голоса персонажей из детских мультфильмов: пропадают низкочастотные компоненты.

Попробуйте объяснить, почему они пропадают.

Скорость звука V и плотность среды ρ образуют комплекс ρV, который называется волновым сопротивлением.

Особенно велико волновое сопротивление металлов: у них велики оба сомножителя. Так, у стали V = 5100 м/с; ρ = 7,8 · 10³ кг/м³, в то время как у воздуха V = 332 м/с; ρ = 1,29 кг/м³.

Казалось бы, если в металлах звук с такой скоростью распространяется, то их сопротивление распространению звука должно быть малым. Ан нет, все правильно: источник звука, «работающий на металл», должен за одну секунду «озвучить» участок протяженностью 5 км, раскачав в нем вещество большой плотности. Среда с большим волновым сопротивлением предъявляет к источнику звука большие энергетические требования.

Значения волнового сопротивления двух сред, следующих одна за другой по ходу волнового луча, определяют коэффициент отражения звука на границе раздела этих сред:

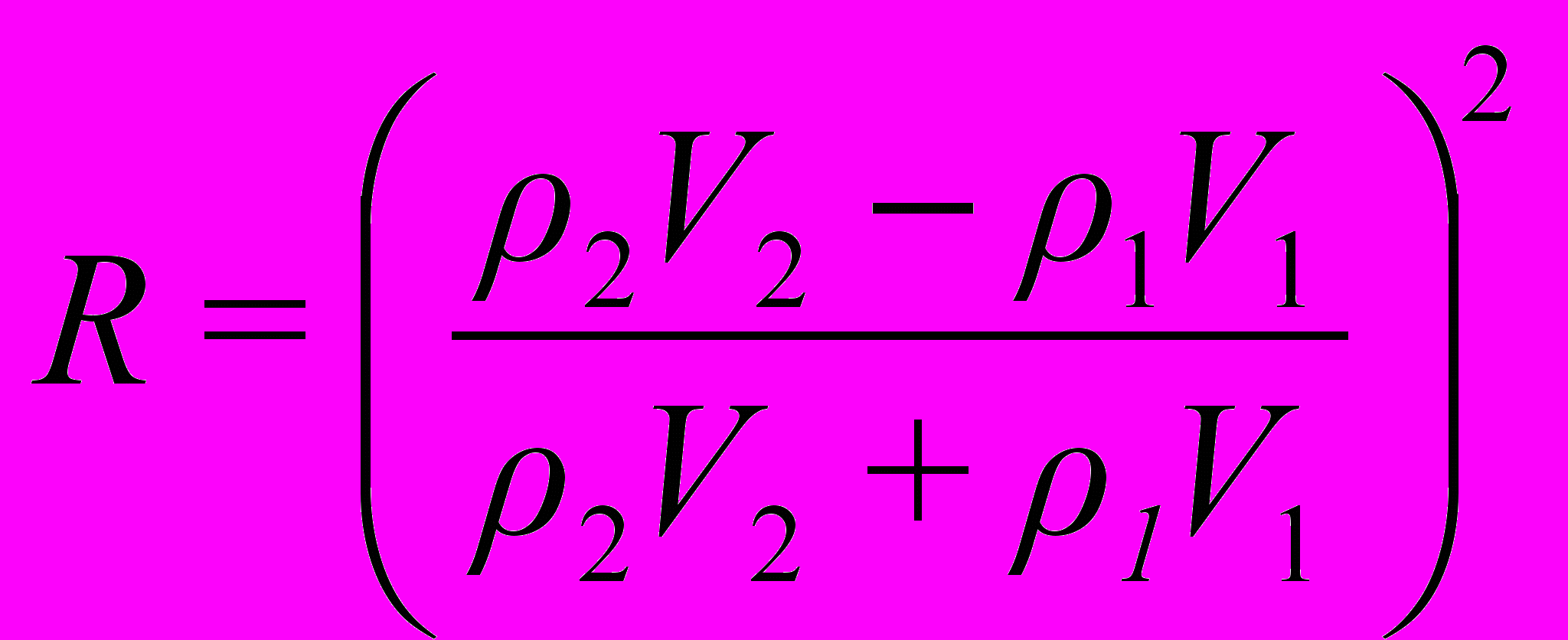(3)

Эта формула справедлива для нормального падения, то есть когда луч перпендикулярен поверхности раздела сред.

Коэффициент отражения показывает, какая часть энергии, т.е. интенсивности падающей волны, приходится на волну отраженную. Величина D = 1 – R дает для тех же условий отношение интенсивности луча, уходящего во вторую среду, к интенсивности падающего луча.

Формуле (3) соответствуют следующие значения коэффициента отражения:


Таблица 1

Среды по ходу луча	R, %	D, %
Воздух – вода или мягкие ткани Кровь – мышца Кровь – печень Мышца - кость	99.9 1.5 2.7 57.9	0,01 98,5 97,3 42,1

Коэффициент отражения не зависит от частоты, а следовательно данные приведенной таблицы справедливы как для звука, так и для ультразвука.

Принимая во внимание первую строку таблицы, при ультразвуковых исследованиях место контакта излучающей ультразвук головки с телом пациента тщательно смазывают жидкостью (вазелиновое масло, глицерин и т.п.). Даже тончайшая воздушная прослойка должна быть исключена.

Из той же строки следует, что рыбаки распугивают рыбу не своими разговорами, а своими телодвижениями.

Вопросы на засыпку:

1. Как изменится коэффициент отражения при обратном ходе акустического луча?

2. Аппаратура для ультразвуковых исследований (УЗИ) существует в двух вариантах технического исполнения: «на отражение» и «на просвет». С учетом табл.1 и Вашего ответа на предыдущий вопрос, постарайтесь ответить, как проявляют себя при обследованиях «на отражение» и «на просвет» воздушные полости внутри организма?

На границах раздела двух сред волновое сопротивление меняется резко, скачком от ρ₁v₁ до ρ₂v₂. Но в некоторых случаях оно меняется плавно и постепенно. Пример тому – атмосферный воздух: летом его температура выше у поверхности прогретой земли, а с ростом высоты понижается; зимой – бывает и наоборот. Скорость звука в более нагретых слоях воздуха больше, чем в холодных, из-за этого фронт волны и акустические лучи – перпендикуляры к фронту – разворачиваются в сторону более холодных слоев воздуха. По этим причинам мы не слышим грома когда видим зарницы – отдаленные грозовые разряды: если разряды удалены от нас дальше, чем на 25 км, то мы не слышим грома не потому, что он слаб, а потому, что звуковые лучи, отклоняясь вверх, не достигают наших ушей. Зимой встречаются обратные ситуации: когда звуковые лучи, искривляясь, огибают Землю, то становятся слышны звуки от очень удаленных объектов.

Существует гипотеза, согласно которой Наполеон проиграл битву при Ватерлоо именно из-за фокусов с распространением звука. Маршал, командовавший резервом наполеоновской армии, не услышал звуков начавшегося сражения и не вступил в бой. В тот день искривленные акустические лучи образовали глухую зону в том месте, где стояли войска подкрепления...

Световые лучи в неоднородной атмосфере ведут себя сходным образом; пример тому – миражи в пустыне.


2.2. Поглощение звука и ультразвука.


При распространении звука всегда имеет место необратимый переход звуковой энергии, т.е. механической энергии упорядоченных колебаний частиц, в теплоту. Интенсивность звука уменьшается в связи с этим по закону:

I = I₀e^-γx (4)


Здесь I₀ – интенсивность звука в точке x = 0; γ – коэффициент затухания звука. Величина этого коэффициента определяется тем, насколько велики в данной среде потери энергии двух видов: потери на преодоление сил вязкого трения и потери на теплопроводность. Второй вид потерь имеет следующую специфику. В зонах сжатия звуковых волн повышению давления соответствует и некоторый рост температуры. Тепловая энергия, передаваемая от таких областей к смежным более холодным, обратно, в энергию колебаний, уже не возвращается. Оба этих вида потерь, а значит и коэффициент γ в целом, сильно зависят от частоты колебаний:


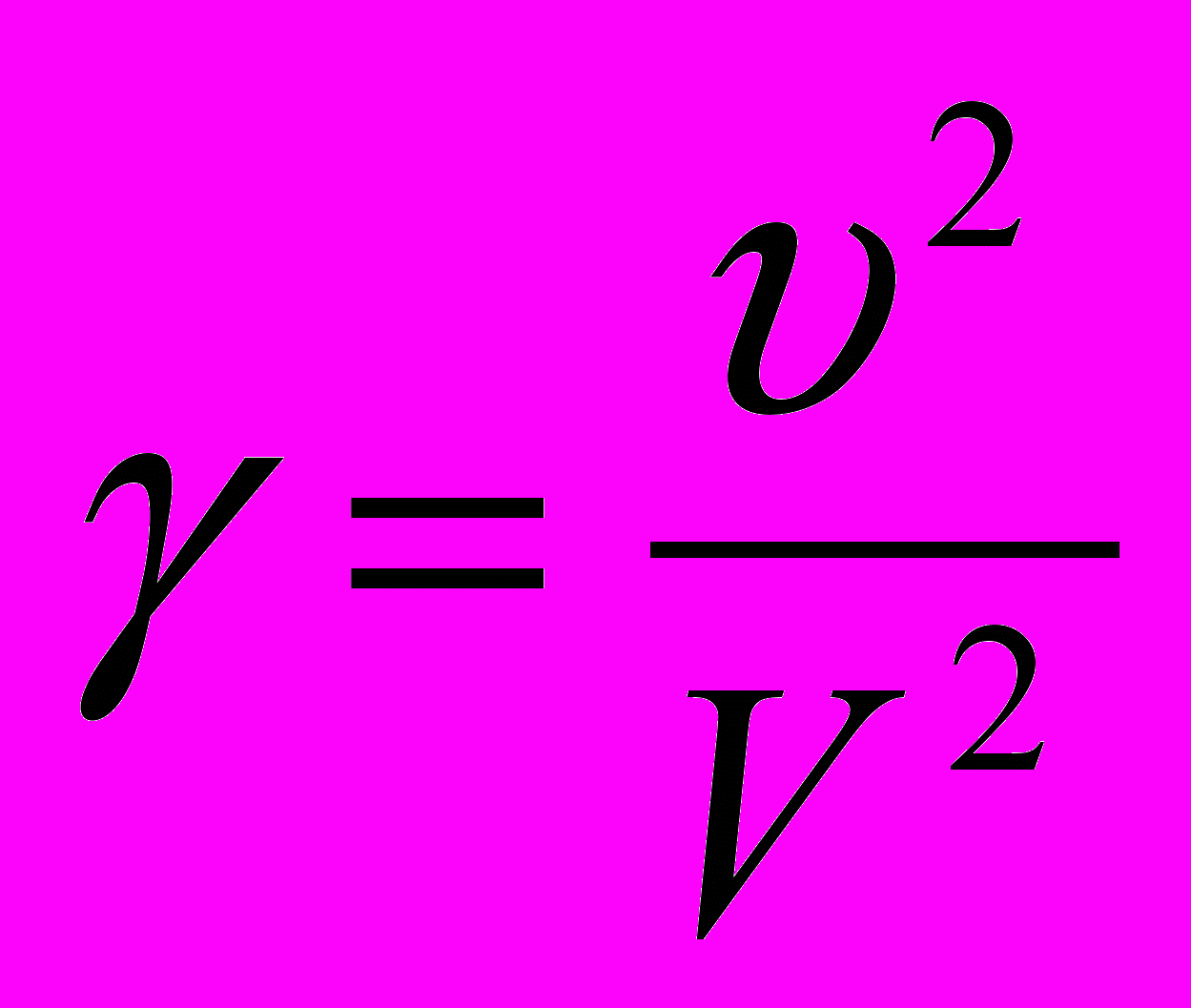(5)


Здесь  - частота звуковых колебаний; V – скорость звука.

Отсюда следует, что чем больше частота колебаний, тем быстрее они затухают. Чем дальше мы от источника звука, тем больше в слышимых звуках преобладание низких частот: высокие поглощаются, не дойдя до нас. А сквозь стенки от соседей нам слышны только уханья басов.

Из (5) следует так же, что ультразвук – это колебания, затухающие гораздо быстрее, чем слышимый звук. Но при этом даже небольшие отличия в величине акустического сопротивления тканей (куда входит и скорость звука) способны сделать эти ткани заметными при ультразвуковом просвечивании.

Вопрос на засыпку: уравнения, подобные уравнению (4) обсуждаются в работе № 25 в связи с поглощением света, в работе № 43 в связи с ослаблением потока β-излучения, в работе №48 в связи с радиоактивным распадом. Что в этих разнохарактерных процессах такое общее, что их математические описания оказываются одинаковыми?


2.3. Эффект Доплера.


Эффект Доплера возникает в тех случаях, когда источник звука и приемник звука движутся по отношению друг к другу, сближаясь или удаляясь, и состоит в том, что в этих обстоятельствах частота колебаний, регистрируемых наблюдателем, отличается от частоты колебаний, создаваемых источником звука.

Неизбежность возникновения этого эффекта, качественные особенности (какая частота будет больше, а какая – меньше), а при желании и точное количественное описание эффекта можно проиллюстрировать с помощью следующей модели ситуации.

Сначала без всяких моделей представьте себе, что источник звука с частотой колебаний  находится слева от Вас, и его акустический луч идет мимо Вас слева направо. В том месте, где Вы находитесь, в какой-то момент времени возникла зона сжатия. Далее, за интервал, равный периоду колебаний источника Т, в том месте, где Вы находитесь, зона сжатия успеет рассосаться, смениться зоной разрежения, и опять возникнуть. Итак, Вы – неподвижны, а там, где Вы находитесь, возникает зона сжатия с периодичностью Т работающего источника.

А теперь начинаем моделировать ситуацию: мимо Вас проносят со скоростью V, равной скорости звука, забор, так что когда возле Вас оказывается рейка, то это символизирует зону сжатия, а когда просвет между рейками – зону разрежения. Рейки перед Вашими глазами будут появляться, сменяя друг друга за интервалы времени Т, то есть мелькать с частотой  = 1/Т.

А теперь – внимание: начинается эффект Доплера. Если Вы побежите влево, в сторону источника, рейки начнут мелькать перед Вашими глазами чаще, с частотой ΄>. Фактом своего движения Вы сокращаете длительность ожидания встречи с очередной рейкой.

Если же Вы побежите вправо, то чем быстрее Вы побежите, тем меньше будет частота мельканий реек ″, а при скорости Вашего бега, равной скорости забора (т.е. скорости звука) частота мельканий станет ″ = 0: Вы поравняетесь с какой-то рейкой и она будет оставаться около Вас, не опережая Вас и не отставая.

Количественный анализ эффекта Доплера можно легко и убедительно провести с помощью рассмотренной модели. Приведем результаты анализа в готовом виде.

1. Если наблюдатель движется со скоростью U в сторону неподвижного источника звука, то частота колебаний, регистрируемых им:

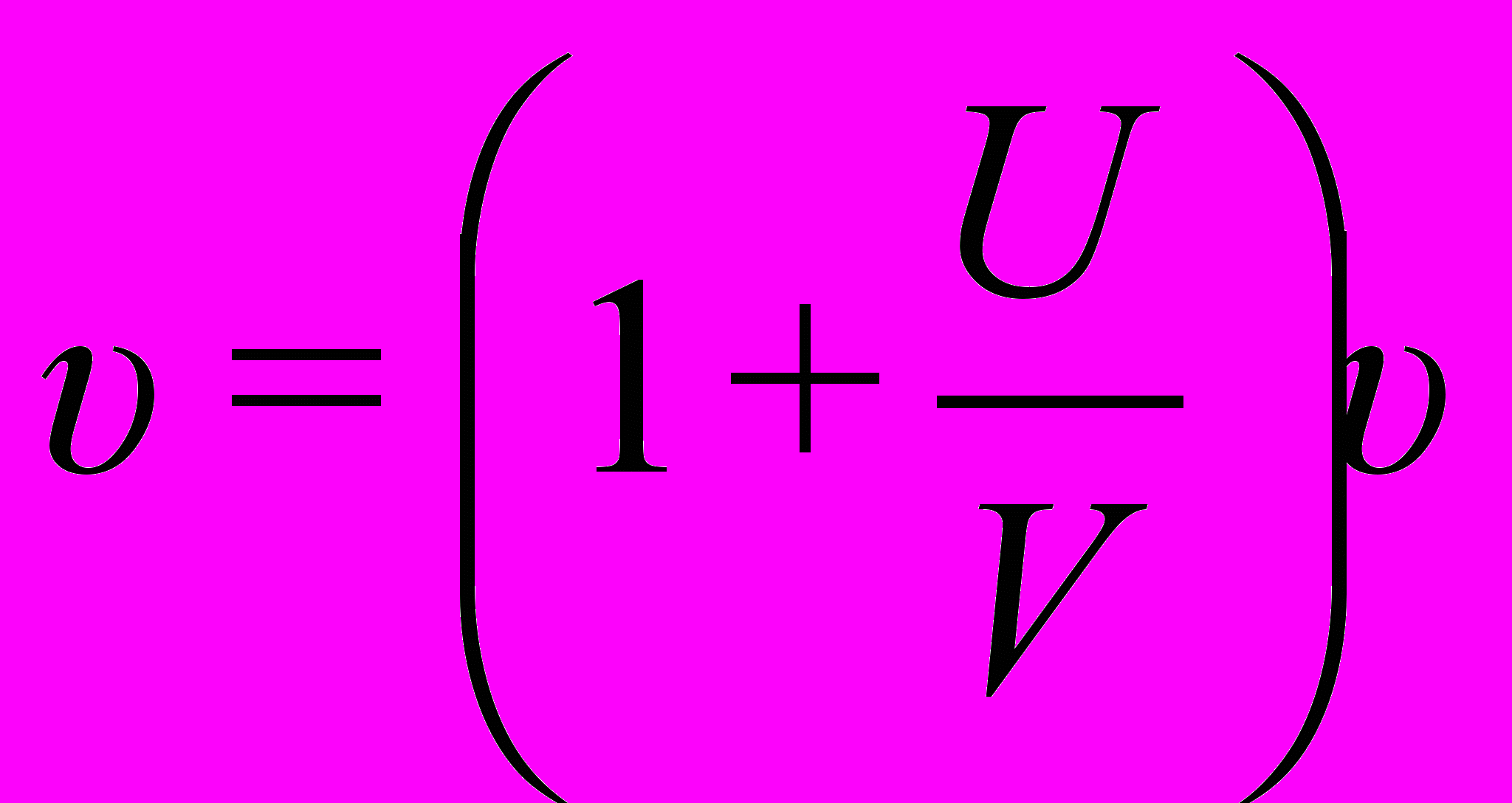(^/ ) (6)

В этой формуле ничего не изменится, если вместо движения наблюдателя в сторону источника будет движение источника в сторону наблюдателя. Важен факт их сближения.

2. Если наблюдатель удаляется от источника (или источник – от наблюдателя), то частота колебаний, регистрируемых наблюдателем, будет:

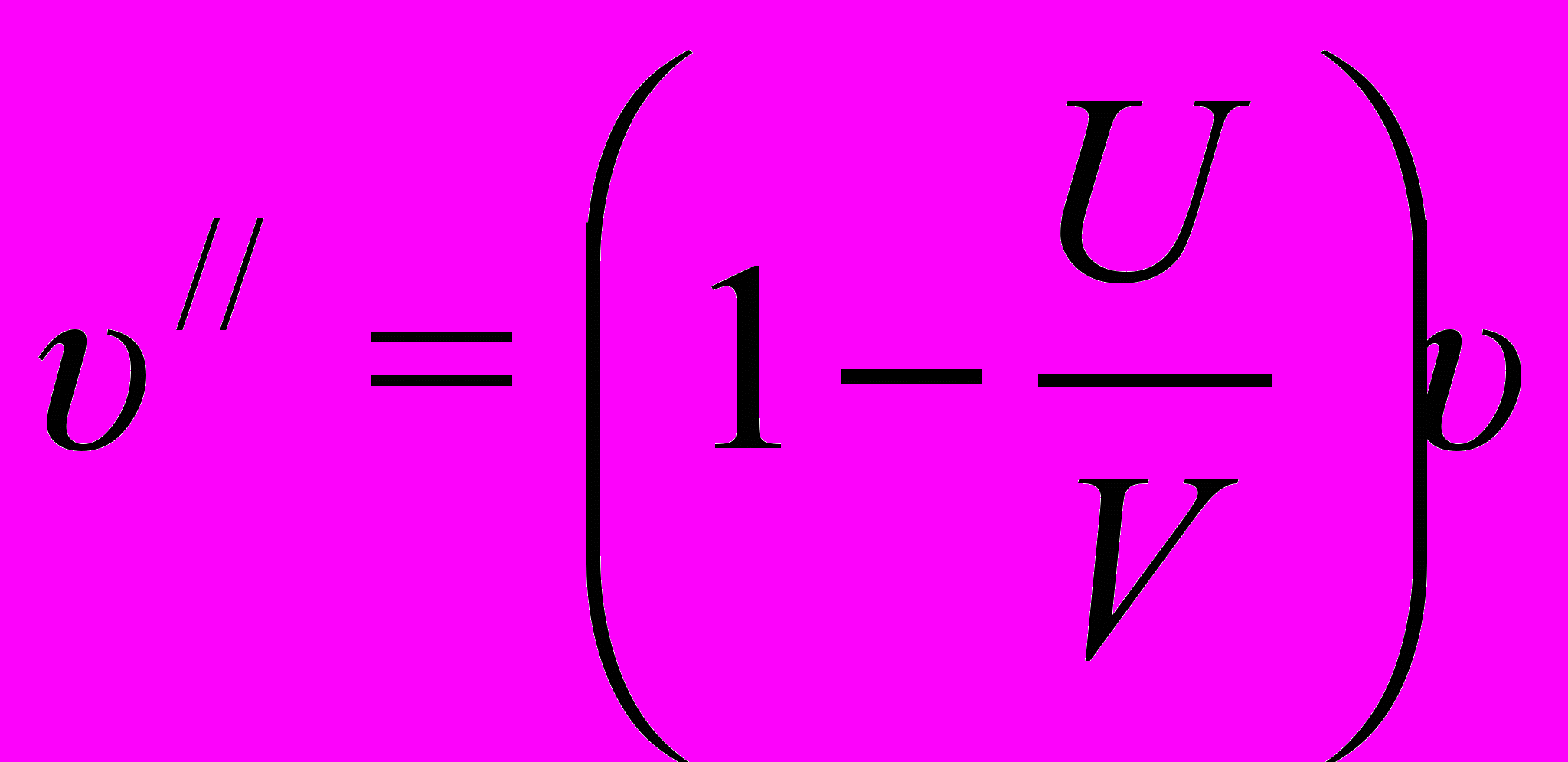(^// ) (7)

Уравнения получены в предположении, что все события развиваются вдоль одной прямой.

Приведем пример ситуации, в которой проявляется эффект Доплера. Вы стоите на обочине шоссе, а мимо Вас на неизменных оборотах мотора (и на неизменной частоте ν производимого им звука) проезжает автомобиль. Пока он к Вам приближается, Вы слышите звук его мотора ΄ более высокий, чем , а как только он проехал мимо Вас, звук мотора становится низким, басовитым: ″  . Вы даже можете подумать о водителе что-нибудь лестное: что он нажал на педаль газа только после того, как проехал мимо Вас...

В качестве примера практического медицинского применения эффекта Доплера рассмотрим способ измерения скорости кровотока, основанный на этом эффекте. Используются компактные источники ультразвуковых колебаний, которые «по совместительству» являются и приемниками отраженных ультразвуковых волн. Такой источник прижимается к кровеносному сосуду и работает в режиме излучение – прием – излучение – и т.д. Частота излучаемого ультразвука  строго постоянна. Она равна собственной частоте колебаний пьезоэлектрического кристалла – основного элемента ультразвуковой головки. Импульс ультразвукового излучения отражается от эритроцитов и они становятся движущимися источниками ультразвука, а неподвижная ультразвуковая головка его регистрирует. Чем больше скорость кровотока, тем больше, через эффект Доплера, отличаются частоты излученного () и отраженного ультразвука ΄ или ″. Скорость кровотока U становится единственной неизвестной в уравнениях (6) и (7).

Эффект Доплера наблюдается и при распространении световых волн. Если источник и приемник света движутся по отношению друг к другу, то чем больше скорость этого относительного движения, тем больше отличаются друг от друга значения излучаемой частоты  и регистрируемой наблюдателем частоты ΄ или ″. Эффект Допплера дал астрономам основной, а очень часто – единственный метод измерения расстояний до дальних и сверхдальних объектов во Вселенной. Кратко поясним эту ситуацию.

Считается общепринятой концепция равномерно расширяющейся вселенной. Это означает, что расстояния между всеми ее объектами увеличиваются, и чем дальше объекты друг от друга, тем больше скорость их разбегания. Разбегание связывают не со свойствами самого пространства, а с теми процессами, которые в нем происходили и происходят (был Большой Взрыв, «осколки» разлетаются все дальше несмотря на действие закона всемирного тяготения). На расстояниях в масштабах нашей Солнечной Системы это разбегание еще не ощутимо, но чем дальше от нас какая-то галактика, тем больше ее скорость удаления от нас. Законы светового излучения звезд хорошо изучены, и считается, что они одинаковы повсеместно. Поэтому если звезды или их скопление – галактика – удаляются от нас, то все характерные и надежно изученные особенности в спектре их излучения смещаются, следуя Допплеру, в сторону меньших значений частоты (больших значений длин волн). Имеет место так называемое «красное смещение» в регистрируемых оптических спектрах. По величине «красного смещения» частот вычисляется скорость удаления этого объекта от нас, и эта скорость пересчитывается на расстояние до него.

Не следует думать, что при этом наша Земля – Пуп Вселенной, от которого все разбегается во всех направлениях. Растут, в связи с расширением Вселенной, расстояния между любыми двумя объектами.

В изложенной концепции можно найти спорные моменты, но ничего лучшего пока не придумали, а если и придумали, то еще не доказали.


2.4. Воздействие звука и ультразвука на ткани организма.


Механические колебания звуковых частот, возбуждаемых с помощью вибраторов, работающих в контакте с кожным покровом, оказывают массирующее действие, способствуют улучшению местного кровообращения.

Напомним, что возбуждение таких колебаний в тканях организма от излучателей, работающих в воздушной среде, практически невозможно: вспомните, каков коэффициент отражения звука на границе воздух – ткани (раздел 2.1).

Массирующее действие колебаний в тканях на ультразвуковых частотах имеет свою специфику. Размеры массируемых областей соизмеримы с длиной волны, а она для ультразвука весьма мала. Так, при V = 1200 м/с и  = 1,2 МГц

 = v = v/ = 1200/1,210⁶ = 10^-3м = 1мм

Такой массаж можно назвать микромассажем. Ему способствует и легкое тепловое воздействие: ведь на таких частотах коэффициент затухания велик и потери для ультразвука оборачиваются полезным приобретением для тканей.

Однако чем больше амплитуда ультразвуковых колебаний в тканях, тем внимательнее следует относиться к ситуациям, которые складываются в них в масштабах любого участка протяженностью λ. Дело в том, что в пределах таких отрезков сосуществуют зона сжатия и зона разрежения. Расстояние вдоль луча между точками с максимальным сжатием и максимальным разрежением равно λ/2. Чем больше интенсивность ультразвука, тем больше перепад давления на единицу длины, называемый градиентом давления. Так, для ультразвука на частоте 1,2 МГц при интенсивности 100 Вт/м² возникает градиент давления порядка 5 атм/см. Здесь 1 атм = 10⁵ Па = 760 мм рт. ст. – атмосферное давление.

Большие градиенты давления могут представлять угрозу для клеток. Пороговые значения градиентов, допустимые для тканей, еще не названы. Можно лишь констатировать, что первоначальная эйфория по поводу УЗИ как абсолютно безопасной замены для рентгеновского обследования, прошла. Начинает действовать концепция такого рода: поскольку в ходе естественных процессов организма ультразвук не появляется, то к ультразвуку, привнесенному в организм извне, следует относиться с разумной осторожностью. Воздействия ультразвука на организм, в том числе и самые благотворные, пока что изучены недостаточно.

Пример практического применения разрушительного действия ультразвука большой интенсивности – ультразвуковой скальпель. Он рассекает как мягкие, так и костные ткани. В отличие от лазерного, не создает запаха паленого.

Разрушительные действия больших градиентов давления в ультразвуке большой интенсивности можно использовать для подавления и разрушения клеток злокачественных опухолей.

Если интенсивность ультразвука в жидкости превосходит некоторый пороговый уровень, в ней появляется еще один фактор разрушительного действия – явление кавитации. Для воды такой пороговый уровень: I = 5·10³ Вт/м² = 5 кВт/м². Диагностическая ультразвуковая аппаратура использует гораздо более скромные значения интенсивности, при которых кавитация невозможно. Но кавитация нашла применение в некоторых смежных с медициной областях, она может пригодиться и в медицине. Поэтому кратко остановимся на сущности этого явления.

Cavity (лат.) – пустота. Кавитация – явление возникновения в жидкости пустот в виде пузырьков, заполненных газом или насыщенным паром, в условиях, когда в жидкости возникает пониженное давление. В отличие от газов, жидкости при пониженном давлении расширяться не умеют и разрываются. Кавитационные пузырьки – последствия таких разрывов.

Кавитационные пузырьки, возникнув в зонах пониженного акустического давления, оказываются, спустя полпериода колебаний, в зоне давления повышенного, и вот тут-то и способны проявиться их разрушительные способности. Схлопывание пузырька – это его сокращение до нулевых размеров (заполняющий его насыщенный пар опять становится жидкостью). При этом происходит сближение его диаметрально противоположных поверхностей с очень большой, и все возрастающей скоростью. Это заканчивается гидравлическим ударом – резким всплеском давления, который способен разрушить не только клетки или микроорганизмы, но и металлы. Есть даже способ контроля кавитации по количеству дырочек, возникающих в металлической фольге за одно погружение в жидкость.

Примеры практического применения ультразвука больших интенсивностей: сверхтонкое дробление вещества, образование эмульсий несмешивающихся жидкостей (например, ртути и воды), расщепление высокополимерных молекул.


3. Восприятие звука.


В этом разделе обсуждается психофизический аспект акустики.


3.1. Закон Вебера-Фехнера.


Э. Вебер сумел понять, как человек приспособился к условиям, в которых внешнее воздействие может меняться в широчайшем диапазоне, от сверхмалых до сверхбольших значений показателя интенсивности. Свое понимание этого приспособительного механизма он сформулировал в виде закона, согласно которому ощущение растет в арифметической прогрессии (т.е. на одинаковую величину), если интенсивность вызвавшего его раздражителя – в геометрической прогрессии (т.е. в одинаковое число раз).

Г. Фехнер выразил эту закономерность языком логарифмической функции: если ряд значений интенсивности образует геометрическую прогрессию (например, 10; 100; 1000;...), то нашим ощущениям соответствуют логарифмы членов этой прогрессии (в нашем примере – 1, 2, 3...)

Во введении к работе №1 логарифмическая децибельная шкала интенсивностей звука была введена из соображений математической целесообразности. Теперь же мы можем констатировать, что децибельная шкала соответствует специфике наших ощущений, отраженной в законе Вебера-Фехнера. А тот, кто изобрел логарифмы, поступил очень разумно.

Закону Вебера-Фехнера соответствуют наши ощущения как звуковых, так и в сфере световых ощущений. Ведь наше зрение тоже функционирует в широчайшем диапазоне: от единичных квантов на колбочку или палочку до громадных световых потоков в солнечный день.

Можно высказать сожаление, что логарифмическая шкала, подобная децибельной, не вошла в обиход фотометрических измерений. Плата за это – громоздкая и невнятная система сложившихся фотометрических характеристик.

А вот в области тактильных ощущений диапазон внешних воздействий, от «чуть-чуть» до болевого ощущения, гораздо уже, и приспособительные логарифмические реакции на уровне ощущений не потребовались.


3.2. Восприятие звука: дополнительные сведения.

• БИНАУРАЛЬНЫЙ ЭФФЕКТ. Под этим названием скрывается наша способность определять направление прихода звуковых волн. Лучше всего это удается, когда звуки или шумы имеют резкое начало или обладают повторяющимися характерными особенностями. Решающим фактором является разность во времени появления звукового ощущения в левом и правом ухе. Мы уверенно различаем запаздывания по времени до 10^-4 с; для звука на частоте 1000 Гц это составляет 0,1 периода колебаний. Этим данным и тому факту, что расстояние между ушами – около 20 см, соответствует точность определения направлений Δφ = ± 10˚ (на частоте 1000 Гц)
  
• «РАЗНОСТНЫЕ ТОНЫ». При большой интенсивности звука мы можем слышать то, чего нет. Наряду с ощущениями, соответствующими реально действующим частотам ₁ и ₂ мы начинаем слышать разностные тоны (₁ - ₂) и комбинированные тоны (₁ + ₂) или (2₁ - ₂). Благодаря этим причудам восприятия, мы из плохонького динамика в наушниках слышим низкие частоты, на воспроизведение которых он не способен.
  
• Стереофоническое звучание технически обеспечивается от двух акустических колонок, каждая из которых воспроизводит звук, специально для нее записанный. Звуки от двух колонок накладываются друг на друга, создавая в нашем восприятии иллюзию «живого» звучания группы музыкальных инструментов, группы участников разговора, и т.п.
  

Менее известно, что получая монофонический звук от одной колонки, мы и его воспринимаем как стереофонический; кто-то в большей степени, кто-то – в меньшей. Мы подсознательно достраиваем то, что есть, до того, что хотелось бы.

• Колебания одной гармоники мы воспринимаем как определенный тон. Каждый тон имеет некоторую высоту. Высота тона – это качество ощущения, и как таковое физическому измерению не доступно. Наше ощущение высоты тона зависит от частоты волн, но в некоторой степени и от их интенсивности.
  
• На несинусоидальные колебания мы реагируем ощущением сложного звука, обладающего тембром. Наше ощущение тембра соответствует линейчатому спектру источника звука и распределению энергии по линиям. При этом изменение частоты основного тона не меняет наших ощущений тембра. Мы различаем голоса людей и музыкальные инструменты по их тембру.
  

Свойства акустического спектра как категории физической, определяют наши ощущения тембра как категории психофизической, физическим измерениям не доступной.

• Если звук, произнесенный в помещении, затухает быстро, он воспринимается как приглушенный, как бы не до конца расслышанный. Если же произнесенный звук, многократно отражаясь, долго не затухает, то помещения с таким звучанием мы называем гулкими. «Приглушенность», «гулкость» – оценки психофизические. Им соответствует измеряемая физическая величина – время реверберации, под которым понимается время, за которое затухающий звук уменьшает свою интенсивность в 10⁶ раз. В хороших концертных залах время реверберации на средних частотах – 1-2 секунды. Для достижения оптимального времени реверберации стены и перекрытия отделываются элементами, сочетающими свойства декоративные со свойствами поглотителей или отражателей звука.
  

В состав современных электронных музыкальных комплексов входят отдельными блоками ревербераторы – устройства, с помощью которых «длительность послезвучания» может меняться по усмотрению исполнителей.


Контрольные вопросы.


1. Свободные колебания. Линейчатый акустический спектр.

2. Сложный звук как сумма колебаний. Понятие о разложении Фурье.

3. Акустические колебания с непрерывным спектром. Шумы. Звуки речи.

4. Вынужденные колебания и резонанс. Их роль в акустике.

5. Скорость звука. Волновое сопротивление.

6. Поглощение звука и ультразвука. Борьба с шумами.

7. Эффект Доплера. Его применение в медицине.

8. Воздействие звука и ультразвука на ткани и органы.

9. Восприятие звука. Закон Вебера-Фехнера.

10. Физические и психофизические характеристики звука.