Программа вступительных испытаний для лиц, поступающих в магистратуру на направление «050200. 68 Физико-математическое образование», магистерская программа «Математическое образование»
| Вид материала | Программа |
- Программа вступительных испытаний для лиц, поступающих на направление подготовки 050100., 78.45kb.
- Программа вступительного экзамена в магистратуру по направлению 050200 «Физико-математическое, 500.22kb.
- Программа вступительных испытаний в магистратуру по направлению 050100. 68 Педагогическое, 226.87kb.
- Программа вступительного испытания по дисциплине Физика с теорией и методикой обучения, 388.78kb.
- Программа вступительного экзамена в магистратуру направление подготовки, 274.96kb.
- Программа вступительных испытаний для лиц, поступающих на направление подготовки 030900., 422.7kb.
- Программа вступительного экзамена в магистратуру по направлению подготовки 050100 «Физико, 86.06kb.
- Программа вступительных испытаний для лиц, поступающих на направление подготовки 050100., 103.16kb.
- Программа вступительных испытаний в магистратуру по направлению 050100 «Педагогическое, 212.58kb.
- Учебное пособие для студентов высших учебных заведений, обучающихся по направлению, 1100.02kb.
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
"Хакасский государственный университет им. Н.Ф. Катанова"
ИНСТИТУТ ЕСТЕСТВЕННЫХ НАУК И МАТЕМАТИКИ
Кафедра математики и МПМ
Утверждаю
Председатель приемной комиссии
Ректор ХГУ им. Н.Ф. Катанова
Профессор Г.С. Сурвилло
«____» _________________2009 г.
Программа
вступительных испытаний для лиц, поступающих в магистратуру
на направление «050200.68 Физико-математическое образование», магистерская программа «Математическое образование»
Абакан 2008
Вступительные экзамены по математике в магистратуру по направлению 050200.68 Физико-математическое образование ХГУ им. Н.Ф. Катанова проходят в форме письменного тестирования на двух уровнях.
Объем знаний и степень владения материалом определяется общей программой по математике в соответствии со стандартом направления подготовки 050200.62 Физико-математическое образование (профиль Математики). Данная программа полностью соответствует содержанию курса математики в вузе.
На экзамене по математике поступающий в ХГУ им. Н.Ф. Катанова должен показать:
а) четкое знание математических определений и теории, предусмотренных программой;
б) умение точно и сжато выражать математическую мысль в устном и письменном изложении, использовать соответствующую символику;
в) уверенное владение математическими знаниями и навыками, предусмотренными программой, умение применять их при решении задач.
Для лиц, имеющих непрофильное образование
Данный уровень вступительных испытаний определен для лиц, не имеющих базового математического образования.
Форма заданий вступительного экзамена – тестовые задания по основным математическим дисциплинам: алгебра, теория чисел и числовые системы, геометрия, математический анализ, теория функций одного переменного, теория функции комплексного переменного, дифференциальные уравнения и уравнения с частными производными.
В одном варианте предлагается 20 заданий. На решение задач данного контрольного мероприятия отводится 120 минут (без перерыва).
Критерии оценивания: 10-13 заданий – 51-68 баллов, 14-17 заданий – 69-84 баллов, 18-20 заданий – 85-100 баллов.
Для лиц, имеющих профильное образование
Данный уровень вступительных испытаний определен для лиц, имеющих базовое математическое образование и успешно преодолевших вступительные испытания для лиц, имеющих непрофильное образование.
Форма заданий вступительного экзамена – тестовые задания. В одном варианте предлагается 20 заданий. На решение задач данного контрольного мероприятия отводится 120 минут (без перерыва).
Критерии оценивания: 10-13 заданий – 51-68 баллов, 14-17 заданий – 69-84 баллов, 18-20 заданий – 85-100 баллов.
Программа вступительных испытаний по математике на первом уровне состоит из трех разделов. Раздел 1.1 представляет собой перечень основных математических понятий и фактов, которыми должен владеть поступающий (уметь правильно их использовать при решении задач, ссылаться при доказательстве теорем). В разделе 1.2 указаны теоремы, которые надо уметь доказывать (для поступающих на специальность «математика»). В разделе 1.3 перечислены основные математические умения и навыки, которыми должен владеть экзаменуемый.
В соответствии со стандартом направления подготовки 050200.62 Физико-математическое образование (профиль Математики), абитуриент должен:
знать:
- основы общих и специальных теоретических дисциплин в объеме, необходимом для решения типовых задач профессиональной деятельности,
- школьные программы и учебники;
- средства обучения и их дидактические возможности;
- требования к оснащению и оборудованию учебных кабинетов и подсобных помещений;
- средства обучения и их дидактические возможности;
- санитарные правила и нормы, правила техники безопасности и противопожарной защиты.
Структура и содержание вступительного экзамена на первом уровне
1. Экзамен имеет целью проверить уровень знаний и умений абитуриентов по математическим дисциплинам, практических навыков в процессе решения задач, а также профессиональный уровень их подготовки.
2. Дисциплины образовательной программы, обеспечивающие получение соответствующей подготовки абитуриента, проверяемой в процессе экзамена: математический анализ, теория функций действительного переменного, теория функций комплексного переменного, дифференциальные уравнения и уравнения с частными производными; алгебра, теория чисел и числовые системы, геометрия
3. Перечень вопросов, выносимых для проверки на вступительном экзамене
3.1. Математический анализ, теория функций действительного переменного, теория функций комплексного переменного, дифференциальные уравнения и уравнения с частными производными
1. Отображения множеств (функции). Предел и непрерывность функции в точке. Раскрыть понятие отображения и понятие действительной функции действительной переменной. Привести примеры. Сформулировать различные определения предела функции в точке и непрерывности в точке. Доказать, что данное число является пределом функции в заданной точке (пример подобрать самостоятельно). Доказать эквивалентность определения предела по Коши и по Гейне.
2. Основные свойства непрерывных функций на отрезке. Дать определение функции, непрерывной на отрезке. Сформулировать теоремы о свойствах функции, непрерывной на отрезке: теорему об обращении функции в нуль, теорему о промежуточном значении, теорему о достижении наибольшего и наименьшего значений, теорему о существовании обратной функции. Указать, где используются эти свойства в школьном курсе математики. Раскрыть геометрический смысл каждой из этих теорем. Доказать одну из них.
3. Предел числовой последовательности. Существование точной верхней границы ограниченного сверху множества. Теорема о пределе монотонной последовательности. Дать определение предела числовой последовательности и раскрыть геометрический смысл этого понятия. Привести примеры сходящихся и расходящихся последовательностей. Сформулировать теорему о единственности предела. Дать определение ограниченного множества и сформулировать предложение о существовании точной верхней границы. Сформулировать и доказать теорему о пределе монотонной последовательности. Ввести число е.
4. Теорема Больцано-Вейерштрасса. Необходимый и достаточный признак сходимости последовательности. Сформулировать теорему об ограниченности сходящейся последовательности. Привести пример, показывающий, что обратное утверждение не имеет места. Сформулировать и доказать теорему Больцано-Вейерштрасса об ограниченных последовательностях. Сформулировать необходимый и достаточный признак сходимости последовательности (критерий Коши).
5. Степенная функция с натуральным, целым, рациональным и действительным показателем. Дать определения степени с натуральным, целым, рациональным и действительным показателем. Ввести понятие степенной функции, сформулировать ее основные свойства (непрерывность, монотонность, существование экстремумов, выпуклость, наличие асимптот и др.) и раскрыть их геометрический смысл. Некоторые из этих свойств доказать (можно пользоваться аппаратом дифференциального исчисления).
6. Показательная функция. Ее основные свойства. Разложение в степенной ряд. Определить показательную функцию. Сформулировать основные свойства (непрерывность, монотонность, отсутствие экстремумов, выпуклость, наличие асимптот, область значений и др.) и раскрыть их геометрический смысл. Некоторые из этих свойств доказать (можно пользоваться аппаратом дифференциального исчисления). Разложить функцию в степенной ряд.
- Показательная функция комплексной переменной. Формулы Эйлера. Определить показательную функцию комплексной переменной. Сформулировать ее основные свойства. Особое внимание обратить на отличие свойств показательной функции комплексной переменной. Вывести формулы Эйлера.
- Логарифмическая функция, ее основные свойства. Разложение в степенной ряд. Логарифмическая функция комплексной переменной. Дать определение логарифмической функции действительного аргумента, как функции, обратной показательной. Сформулировать основные свойства этой функции (монотонность, отсутствие экстремумов, выпуклость, наличие асимптот, область значений и др.) и раскрыть их геометрический смысл. Доказать некоторые из этих свойств (при этом можно пользоваться аппаратом дифференциального исчисления). Разложить логарифмическую функцию в степенной ряд. Дать определение логарифмической функции комплексной переменной. Вывести формулу для ее вычисления. Вывести формулы для логарифма произведения и частного комплексных чисел
- Тригонометрические функции, их основные свойства. Разложение синуса и косинуса в степенной ряд. Дать определение тригонометрических функций: синуса, косинуса и тангенса. Сформулировать основные свойства этих функций (периодичность, непрерывность, монотонность, наличие асимптот, область значений и др.) и раскрыть их геометрический смысл. Доказать некоторые из этих свойств (при этом можно пользоваться аппаратом дифференциального исчисления). Разложить синус и косинус в степенной ряд.
- Тригонометрические функции в комплексной области. Дать определения синуса, косинуса и тангенса в комплексной области. Сформулировать их основные свойства. Указать, какие из них отличны от аналогических свойств этих функций в действительной области. Доказать некоторые из этих свойств.
11. Дифференцируемые функции одной и нескольких переменных. Геометрический и механический смысл производной. Правила дифференцирования. Дать понятие дифференцируемой функции одной переменной и ее производной. Установить механический и геометрический смысл производной. Дать определение дифференцируемости функции нескольких переменных и частной производной. Сформулировать правила дифференцирования суммы, произведения, частного, сложной функции и обратной функции одной переменной. Доказать хотя бы одно из этих свойств.
12. Теорема Лагранжа. Условия постоянства и монотонности функции на промежутке. Выпуклые кривые. Сформулировать и доказать теорему Лагранжа. Раскрыть ее геометрический смысл. Так как доказательство теоремы Лагранжа опирается на теорему Ролля, то обязательно знать содержание этой теоремы. Сформулировать теорему о необходимом и достаточном условии постоянства функции и теорему о достаточном условии строгой монотонности функции на промежутке. Показать, что условие это не является необходимым. Дать понятие кривой, выпуклой на промежутке. Сформулировать теорему об условии выпуклости кривой.
13. Экстремумы и точки перегиба. Дать определения максимума и минимума функции одной переменной, а также точек минимума и максимума. Раскрыть геометрический смысл этих понятий. Сформулировать и доказать теорему о необходимом условии экстремума. Показать, что это условие не является достаточным. Сформулировать достаточное условие экстремума: по характеру изменения знака первой производной и по знаку второй производной. Один из этих признаков доказать. Привести пример на отыскание экстремума. Ввести понятие точки перегиба кривой. Сформулировать правило отыскание точек перегиба. /
14. Первообразная и неопределенный интеграл. Интегрирование по частям и подстановкой. Ввести понятие первообразной функции. Привести примеры. Знать, что всякая непрерывная в данном промежутке функция имеет первообразную. Описать множество всех первообразных данной функции. Доказать, что если функция имеет первообразную, то это множество состоит из тех и только тех функций, которые отличаются от данной первообразной на постоянное слагаемое. Ввести понятие неопределенного интеграла. Раскрыть связь между операциями интегрирования и дифференцирования. Сформулировать простейшие правила интегрирования. Привести примеры интегрирования по частям.
15. Определенный интеграл и его свойства. Интегрируемость непрерывной функции. Дать определение определенного интеграла через интегральные суммы и через приращение первообразной. Какой из этих подходов предпочтительней в средней школе? Установить их геометрический смысл. Сформулировать необходимое условие существования определенного интеграла и его основные свойства. Ввести понятие сумм Дарбу и перечислить их основные свойства. Сформулировать необходимое и достаточное условия интегрируемости функции (с использованием сумм Дарбу). Знать определение равномерной непрерывности и формулировку теоремы Кантора. Доказать, что всякая непрерывная на отрезке функция интегрируема на нем.
16. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Рассмотреть определенный интеграл с переменным верхним пределом интегрирования. Доказать, что если подынтегральная функция непрерывна, то производная по верхнему пределу равна подынтегральной функции. Вывести формулу Ньютона-Лейбница. Показать на примере применение этой формулы.
17. Понятие квадрируемой фигуры и ее площади. Вычисление площади с помощью определенного интеграла. Ввести понятие квадрируемой фигуры. Сформулировать признак квадрируемости. Доказать квадрируемость криволинейной трапеции, ограниченной сверху графиком непрерывной функции. Обосновать вычисление ее площади с помощью определенного интеграла. Рассмотреть более общий случай, когда криволинейная трапеция ограничена снизу и сверху графиками непрерывных функций. Привести примеры.
- Вычисление объема и площади поверхности тела вращения с помощью определенного интеграла. Ввести понятие кубируемого тела. Сформулировать необходимое и достаточное условие кубируемости тела. Доказать, что тело, полученное вращением криволинейной трапеции, ограниченной сверху графиком непрерывной функции, вокруг основания, - кубируемо. Обосновать вычисление его объема с помощью определенного интеграла. Привести пример на вычисление объема тела вращения. Не вводя общего понятия кривой поверхности, считая поэтому площадь поверхности вращения существующей, показать на примере, как она вычисляется.
- Понятие спрямляемой кривой и ее длины. Вычислению длины кривой с помощью определенного интеграла. Ввести понятие спрямляемой дуги кривой и ее длины. Вывести формулу для вычисления длины дуги. Привести примеры..
- Числовые ряды. Признаки сходимости положительных рядов. Ввести понятие числового ряда и его суммы. Сформулировать необходимое условие сходимости числового ряда, а также признак сравнения положительных рядов. Доказать признак сходимости Даламбера. Сформулировать интегральный признак сходимости.
- Знакочередующиеся ряды. Абсолютно и условно сходящиеся ряды. Ввести понятие знакочередующегося ряда. Доказать теорему Лейбница. Ввести понятия абсолютно и условно сходящихся рядов. Привести примеры. Сформулировать свойства абсолютно сходящихся рядов (сочетательное, переместительное). Сформулировать теорему Римана для условно сходящихся рядов.
- Формула и ряд Тейлора. Биномиальный ряд. Ввести понятие формулы Тейлора и ее остаточного члена. Раскрыть смысл разложения функции в степенной ряд. Сформулировать необходимое и достаточное условия разложимости функции в степенной ряд (ряд Тейлора). Вывести ряд Тейлора для функции (x + a)α и найти радиус его сходимости. Формула бинома Ньютона.
- Обыкновенные дифференциальные уравнения первого порядка. Уравнения с разделяющимися переменными. Линейные уравнения. Ввести понятия дифференциального уравнения первого порядка, его решения, общего решения и частного решения, удовлетворяющего заданным начальным условиям. Дать этим понятиям геометрическое истолкование. Сформулировать теорему о существовании и единственности решения дифференциального уравнения первого порядка. Записать общий вид дифференциального уравнения с разделяющимися переменными и рассказать об общем методе его решения. Привести пример. Ввести понятие линейного дифференциального уравнения первого порядка и рассказать о методах его решения. Привести пример.
- Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Ввести понятия линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами и его характеристического уравнения. Рассмотреть различные случаи решения дифференциального уравнения в зависимости от особенностей корней характеристического уравнения. Привести примеры.
3.2. Алгебра, теория чисел и числовые системы
- Группа. Примеры групп. Простейшие свойства групп. Подгруппы. Гомоморфизмы и изоморфизмы групп. Группа, примеры групп. Единственность единичного элемента. Единственность элемента, обратного данному. Подгруппа, примеры подгрупп, признак подгруппы. Гомоморфное и изоморфное отображения одной группы в другую, примеры. Свойства гомоморфного и изоморфного отображений группы.
- Кольцо. Примеры колец. Простейшие свойства кольца. Подкольцо. Гомоморфизмы и изоморфизмы колец. Кольцо, примеры колец. Простейшие свойства: умножение на нулевой элемент, на разность элементов, правила знаков. Подкольцо, примеры подколец, признак подкольца. Гомоморфное и изоморфное отображения одного кольца в другое, примеры. Свойства гомоморфного отображения кольца.
- Теорема о делении с остатком. Наибольший общий делитель и наименьшее общее кратное двух чисел в кольце целых чисел. Ввести понятие делимости чисел. Сформулировать простейшие свойства делимости. Сформулировать и доказать теорему о делении с остатком. Дать определения НОД и НОК двух чисел. Рассмотреть алгоритм Евклида нахождения наибольшего общего делителя. Установить формулу, связывающую НОД и НОК.
- Поле. Простейшие свойства поля. Поле комплексных чисел. Поле, примеры полей. Существование и единственность нуля, единицы, элемента, противоположного данному, элемента, обратного ненулевому. Отсутствие делителей нуля. Поле комплексных чисел. Алгебраическая форма комплексного числа, ее единственность, действия над комплексными числами в алгебраической форме.
- Тригонометрическая форма комплексного числа. Геометрическое представление комплексных чисел и операций над ними. Тригонометрическая форма комплексного числа. Умножение и деление комплексных чисел в тригонометрической форме. Геометрическое представление комплексных чисел и операций над ними.
- Векторное пространство. Примеры и простейшие свойства векторных пространств. Линейная зависимость и независимость системы векторов. Базис и ранг конечной системы векторов. Векторное пространство над полем, примеры, свойства. Линейно зависимые и линейно независимые системы векторов. Базис конечной системы векторов, его существование. Доказать, что любые два базиса конечной системы векторов состоят из одинакового числа векторов. Ранг конечной системы векторов.
- Равносильные системы линейных уравнений. Критерий совместности системы линейных уравнений. Решение системы линейных уравнений методом последовательного исключения неизвестных. Система линейных уравнений. Решение системы. Равносильные системы. Элементарные преобразования систем. Критерий совместности систем линейных уравнений /с доказательством/. Критерий определенности. Решение системы линейных уравнений методом последовательного исключения неизвестных методом Гаусса (на примере).
- Конечномерное векторное пространство. Базис и размерность. Подпространства. Изоморфизм векторных пространств. Конечномерное векторное пространство над полем. Примеры. Базис векторного пространства. Доказать, что любые два базиса конечномерного векторного пространства состоят из одинакового числа векторов. Размерность конечномерного векторного пространства. Подпространства. Изоморфизм векторных пространств. Теорема об изоморфизме конечномерных векторных пространств.
- Простые числа. Бесконечность множества простых чисел. Каноническое разложение составного числа и его единственность. Простые и составные натуральные числа. Теорема Евклида о бесконечности множества простых чисел. Основная теорема арифметики. Каноническая форма натурального числа.
- Основные свойства сравнений. Полная и приведенная системы вычетов. Теоремы Эйлера и Ферма. Числовые сравнения, основные свойства (2-3 свойства с доказательством). Классы чисел, взаимно простых с модулем. Приведенная система вычетов, пример. Теоремы Эйлера и Ферма.
- Обращение обыкновенной дроби в десятичную и определение длины периода десятичной дроби. Доказать, что правильная положительная обыкновенная дробь, знаменатель которой не делится ни на 2, ни на 5, обращается в чисто периодическую дробь, число цифр в периоде которой совпадает с показателем 10 по модулю знаменателя. Используя это, доказать, что каждая обыкновенная дробь может быть обращена в периодическую десятичную дробь.
- Многочлены над полем. Наибольший общий делитель двух многочленов и алгоритм Евклида. Многочлены над полем и операции над ними. Кольцо многочленов. Отношение делимости в кольце многочленов. НОД двух многочленов и алгоритм Евклида.
- Разложение многочлена в произведение неприводимых множителей и его единственность. Неприводимые многочлены над данным полем. Примеры. Свойства неприводимых многочленов (два-три доказать). Разложение многочлена в произведение неприводимых множителей и его единственность.
- Строение простого алгебраического расширения поля. Освобождение от алгебраической иррациональности в знаменателе дроби. Дать определение простого алгебраического расширения поля. Сформулировать и доказать теорему о строении простого алгебраического расширения поля. Привести пример использования этой теоремы в элементарной математике.
- Аксиоматическая теория натуральных чисел. Сложение и умножение натуральных чисел. Роль аксиом индукции в арифметике. Содержательная аксиоматическая теория натуральных чисел
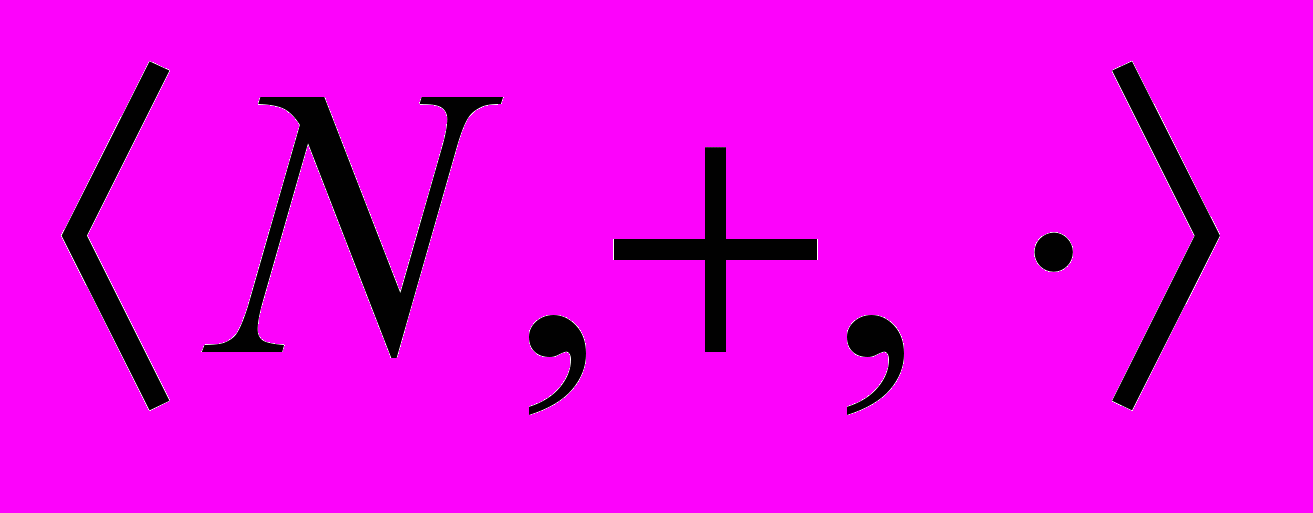. Свойства сложения и умножения натуральных чисел. Полукольцо натуральных чисел. Независимость аксиомы индукции. Роль аксиомы индукции в обосновании теории неравенств, теории делимости и свойств арифметических действий.
- Аксиоматическая теория целых чисел. Построение модели. Аксиоматическая теория целых чисел. Кольцо целых чисел
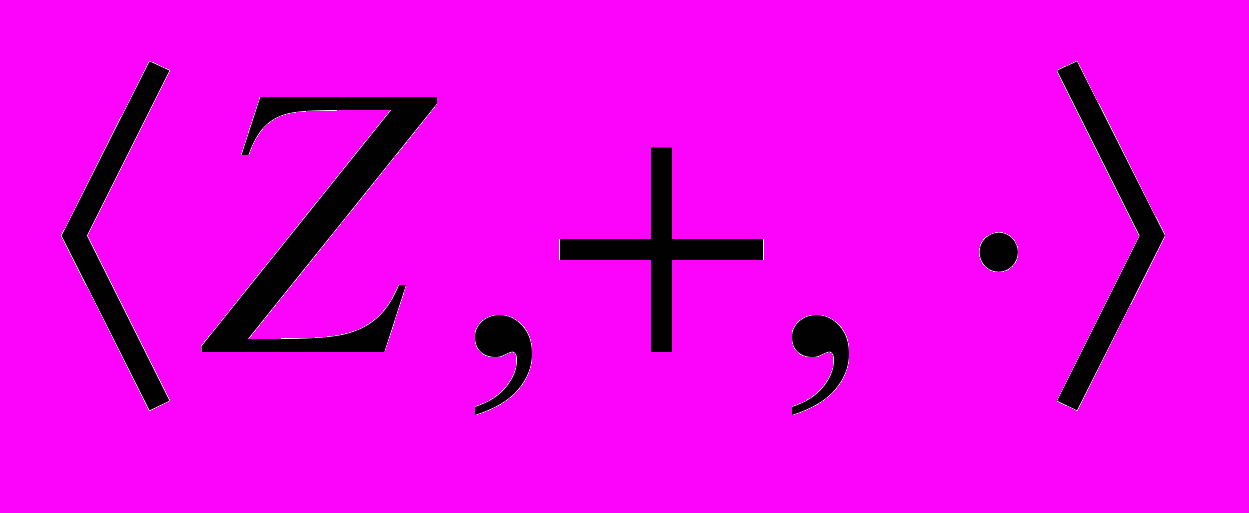. Категоричность системы целых чисел.
- Аксиоматическая теория действительных чисел. Построение модели. Свойства действительных чисел. Теорема о существовании корня. Первичные термины и аксиомы системы действительных чисел
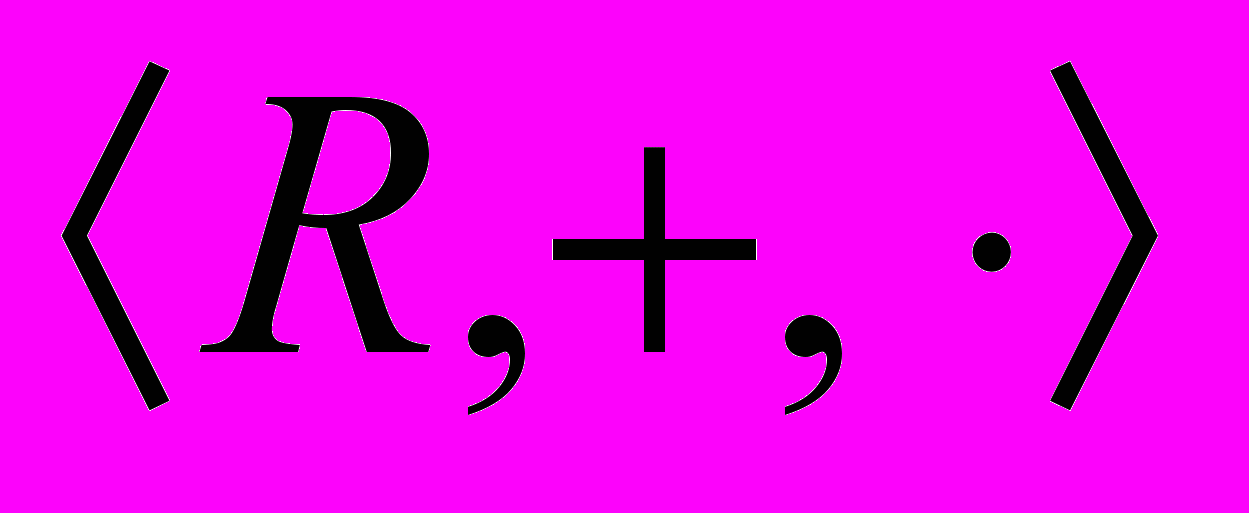- линейно и архимедовски упорядоченное поле, всякая фундаментальная последовательность которого сходится. Свойства действительных чисел. Теорема о существовании корня.
3.3. Геометрия
- Векторы на плоскости и в пространстве. Линейная зависимость векторов. Определение линейно зависимой и линейно независимой системы векторов. Базис и координаты вектора в нем. Признаки линейной независимости векторов на плоскости и в пространстве. Теорема о единственности разложения вектора по базису.
- Скалярное произведение векторов. Определение и свойства скалярного произведения. Вычисление его в координатах. Вычисление длин и углов с помощью скалярного произведения.
- Векторное произведение векторов. Определение и свойства векторного произведения. Вычисление его в координатах. Вычисление площади параллелограмма с помощью векторного произведения.
- Смешанное произведение векторов. Определение и свойства смешанного произведения. Вычисление его в координатах. Вычисление объемов параллелепипеда и тетраэдра с помощью смешанного произведения. Признак компланарности трех векторов.
- Плоскость в пространстве. Взаимное расположение двух плоскостей. Различные виды уравнений плоскости. Вектор нормали плоскости, заданной в прямоугольной системе координат. Угол между двумя плоскостями. .
- Прямая в пространстве, Взаимное расположение двух прямых, прямой и плоскости. Различные виды уравнений прямой в пространстве. Угол между двумя прямыми. Взаимное расположение двух прямых (пересекающиеся, параллельные, скрещивающиеся прямые). Угол между прямой и плоскостью. Нахождение точки пересечения прямой и плоскости.
- Эллипс, гипербола, парабола. Определения эллипса, гиперболы, параболы. Вывести каноническое уравнение одной из этих линий. Исследование формы гиперболы по ее каноническому уравнению. Оптические свойства этих кривых.
- Движение плоскости. Классификация движений. Определение и аналитическая запись движения плоскости. Связь движения с изометрией. Классификация движений.
- Проективная плоскость. Принцип двойственности. Расширенная аффинная плоскость. Основные свойства принадлежности точек и прямых на расширенной плоскости. Проективная плоскость. Система координат в ней. Уравнение проективной прямой. Принцип двойственности.
- Теорема Эйлера для выпуклых многогранников. Правильные многогранники. Доказать теорему Эйлера: В-Р+Г=2. Доказать существование 5 различных правильных многогранников.
- Аксиоматика Вейля. Непротиворечивость аксиоматики Вейля. Аксиомы Вейля. Непротиворечивость системы аксиом Вейля. .
- Определения основных геометрических понятий в аксиоматике Вейля. Определения в этой системе прямых, плоскостей, длины, угла. Привести пример доказательства какой-либо теоремы.
- Изображение плоских фигур в параллельной проекции. Параллельное проектирование, его свойства. Определение изображения фигуры. Теорема об изображении треугольника. Примеры построения изображения плоских фигур. Построение эллипса по изображению сопряженных диаметров.
- Изображение пространственных фигур в параллельной проекции. Определение изображения фигуры. Теорема Польке – Шварца. Полнота чертежа. Примеры решения позиционных задач. Построение сечений многогранников. Изображение сферы.
- Геометрия Лобачевского. Аксиомы планиметрии Лобачевского. Параллельные прямые в геометрии Лобачевского. Непротиворечивость геометрии Лобачевского. Основные факты геометрии Лобачевского.
Литература
- Александров, П.С. Курс аналитической геометрии и линейной алгебры [Текст] / П.С. Александров - М.: Наука, 1979.
- Базылев, В.Т. Геометрия I [Текст] / В.Т. Базылев - М.: Просвещение, 1974.
- Варапаховский, Ф.Я. , Солодовников, А.С. Алгебра [Текст] / Ф.Я.Варапаховский, А.С. Солодовников - МГЗПИ, 1981.
- Варапаховский, Ф.Я., Солодовников, А.С., Стеллецкий, И.В. Алгебра. Группы, кольца и поля. Векторы и евклидовы пространства. [Текст] / Ф.Я.Варапаховский, А.С. Солодовников, И.В. Стеллецкий – М.: МГЗПИ, 1978.
- Виленкин, Н.Я., Балк, М.Г., Петров, В.А. Мощность. Метрика. Интеграл. [Текст] / Н.Я. Виленкин, М.Г.Балк, В.А. Петров - М.: Просвещение. 1980.
- Винберг, Э.Б. Алгебра многочленов. [Текст] / Э.Б. Винберг - М.: Просвещение, 1980.
- Завало, С.Т. Алгебра и теория чисел. Ч. 1. [Текст] / С.Т. Завало – Киев: Высшая школа, 1977.
- Маркушевич, А.И., Маркушевич, Л.А. Введение в теорию аналитических функций. [Текст] / А.И. Маркушевич, Л.А.Маркушевич - М.: Просвещение. 1977.
- Певзнер, С.Л.Проективная геометрия. [Текст] / С.Л. Певзнер - М.: Просвещение, 1980.
- Трайнин, Я.Л. Основания геометрии. [Текст] / Я.Л. Трайнин - М.: Учпедгиз, 1961.
- Уваренков,И.М. Курс математического анализа. [Текст] / И.М.Уваренков - М.: Просвещение. т. 1. 1966, т.2 . 1976.
Программа второго уровня ориентировано на выпускников, имеющих квалификацию учитель математики, бакалавр Физико-математического образования, готовящихся к поступлению в вуз, на преподавателей, ведущих занятия в школах, лицеях, колледжах.
Программа по математике для поступающих в высшие учебные заведения в 2009 году состоит из трех разделов. Первый из них представляет собой перечень основных математических понятия и фактов, которыми должен владеть поступающий (уметь правильно их использовать при решении задач, ссылаться при доказательстве теорем). Во втором разделе указаны теоремы, которые надо уметь доказывать. Содержание теоретической части экзаменов должно черпаться из этого раздела. В третьем разделе перечислены основные математические умения и навыки, которыми должен владеть экзаменуемый.
Примерные вопросы вступительных испытаний в магистратуру по направлению 050200.68 Физико-математическое образование в 2009 году
I. Общая методика обучения математике
1. Предмет методики обучения математике (содержание, цели и задачи).
2. Цели изучения математики в средней школе. Значение школьного курса математики в общем образовании. Формирование научного мировоззрения, воспитание учащихся в процессе изучения математики. Связь изучения математики с жизнедеятельностью человека.
3. Анализ программ по математике для 1-11 классов. Проблема преемственности в обучении математике. Вопросы реализации межпредметных и внутрипредметных связей в обучении математике.
4. Требования, предъявляемые к современному учебнику математики.
5. Принципы дидактики в обучении математике.
6. Методы обучения математике.
7. Методы научного познания: индукции и дедукции, анализа и синтеза.
8. Лабораторные и практические работы по математике, экскурсии.
9. Методика формирования математических понятий, аксиом, теорем. Логическая структура определений и теорем. Необходимые и достаточные условия. Доказательства.
10. Роль задач в обучении математике. Обучение общим методам решения задач.
11. Дидактические требования к уроку математики. Подготовка учителя к уроку. Наглядные пособия и технические средства обучения. Кабинет математики.
12. Формы и методы проверки знаний, умений и навыков учащихся. Организация самостоятельной работы учащихся. Дифференцированный и индивидуальный подход при обучении математике.
13. Специфика работы учителя в школах, классах с углубленным изучением математики. Цели, содержание факультативных занятий по математике.
14. Проблема профессиональной ориентации учащихся в учебно-воспитательной работе учителя математики.
II. Специальная (частная) методика
- Методика изучения числовых систем. Натуральные числа и действия над ними. Обыкновенные и десятичные дроби, положительные и отрицательные числа. Арифметические действия над положительными и отрицательными числами. Рациональные числа. Действительные и комплексные числа.
- Уравнения, неравенства и их системы в школьном курсе математики. Решение задач на составление уравнений.
- Алгебраические выражения. Изучение тождественных преобразований на различных этапах обучения.
- Обучение приближенным вычислениям. Ознакомление учащихся с калькулятором.
- Изучение функций. Методика введения понятия функции. Функциональная пропедевтика в 5-6 классах. Изучение элементарных функций: линейной, квадратичной, степенной, показательной, логарифмической, тригонометрической.
- Числовые последовательности и прогрессии в школьном курсе математики.
- Понятие предела и непрерывности функции. Производная и ее приложение.
- Методика изучения первообразной и интеграла. Простейшие дифференциальные уравнения в школьном курсе математики.
- Логическое строение школьного курса в геометрии.
- Методика изучения элементов геометрии в 5-6 классах.
- Первые уроки систематического курса геометрии. Доказательство первых теорем.
- Методика изучения геометрических построений в 7-9 классах.
- Методика изучения тем: «Равенство фигур», « Многоугольники», «Геометрические преобразования», «Параллельность», «Векторы на плоскости и в пространстве», «Метрические соотношения в треугольнике», «Вписанные и описанные многоугольники».
- Методика изучения систематического курса в стереометрии. Задачи на построение в курсе стереометрии. Изучение многогранников и тел вращения.
- Применение координат и векторов к доказательству теорем и решению задач.
- Методика изучения длин, площадей, объемов школьном курсе геометрии.
Литература
- Программа средней школы. Математика. – М.: Просвещение, 1984-1996 гг.
- Методика преподавания математики в средней школе: Общая методика. – М.: Просвещение, 1980 г.
- Метельский Н.В. Дидактика математики. [Текст] / Н.В. Метельский – Минск: издательства БГУ им. В.И. Ленина, 1982 г.
- Столяр, А.А. Педагогика математики. [Текст] / А.А. Столяр – Минск: Высшая школа, 1974 г.
- Методика преподавания математики в средней школе: Общая методика. Учебное пособие для студентов педагогических институтов по специальности 2104 «Математика» и 2105 «Физика» [Текст] / А.Я. Блох, Е.С. Канин, Н.Г. Калина и др. Сост. Р.С. Черкасов, А.А. Столяр. – М.: Просвещение, 1985 г.
- Методика преподавания математики в средней школе: Частная методика. Учебное пособие для студентов педагогических институтов по физико-математическим специальностям [Текст] / А.Я. Блох, В.А. Гусев и др., Сост В.И. Мишин. – М.: Просвещение, 1987 г.
- Демидов, В.П., Саранцев, Г.И. Методика преподавания математики. [Текст] / В.П. Демидов, Г.И. Саранцев - Мордовский государственный университет им. Н.П. Огарева, 1976 г.
- Программа факультативных курсов для средней школы.
- Учебные пособия по факультативным курсам для средней школы.
- Журналы «Математика в школе», «Квант». Газета «Математика».
- Учебники и учебные пособия по математике для 5-6, 7-9, 10-11 классов.
- Серия книг «Библиотека учителя математики».
Программа утверждена на заседании
Ученого совета Института естественных наук и математики
ГОУ ВПО «Хакасский государственный университет им. Н.Ф. Катанова»
протокол № __ от «__» ___________ 2009г.
Председатель Ученого совета ИЕНиМ ______________ И.В. Карпухина