Программа вступительного экзамена в магистратуру направление подготовки

Вид материала

Программа

Содержание 2011 Пояснительная записка 050200.68 - Физико-математическое образование Критерии оценивания 050200.68 - Физико-математическое образование Содержание программы Алгебра и теория чисел 4. Технологии и методики обучения математике

Подобный материал:

• Программа вступительного экзамена в магистратуру направление подготовки, 173.18kb.
• Программа вступительного экзамена в магистратуру по специальности «Статистика», 133.32kb.
• Программа комплексного вступительного экзамена в магистратуру по специальности 6М020300, 604.91kb.
• Программа вступительного экзамена в магистратуру по направлению, 321.1kb.
• Программа вступительного экзамена в магистратуру по направлению, 376.66kb.
• Программа вступительного экзамена в магистратуру по направлению, 664.35kb.
• Программа вступительного экзамена в магистратуру по направлению, 444.52kb.
• Программа вступительного собеседования в магистратуру Направление подготовки 520300, 711.31kb.
• Программа комплексного вступительного экзамена в магистратуру по специальности 6М060700-Биология, 523.49kb.
• Программа вступительного экзамена в магистратуру перечень примерных вопросов вступительного, 510.66kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НИЖНЕВАРТОВСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ


«Утверждаю»

Ректор____________Горлов С.И.

«___»_______________20____ г.


ПРОГРАММА

ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА В МАГИСТРАТУРУ

Направление подготовки

050200.68 «Физико-математическое образование»

Магистерская программа

«Математическое образование»


2011

Пояснительная записка


На обучение в магистратуру направления 050200.68 - Физико-математическое образование принимаются лица, имеющие документ государственного образца о высшем образовании бакалавра или специалиста. Обучение ведется по очной форме.

Для всех поступающих в магистратуру проводятся следующие вступительные испытания в объеме требований, предъявляемых Федеральным агентством по образованию к подготовке бакалавров по направлению 050200.62 - Физико-математическое образование:

- письменный экзамен по математике в форме тестовых заданий.

Цель экзамена – отобрать наиболее подготовленных абитуриентов для обучения в магистратуре по направлению 050200.68 - Физико-математическое образование.

Форма заданий вступительного экзамена – тестовые задания. В одном варианте предлагается 20 заданий. На решение задач данного контрольного мероприятия отводится 120 минут (без перерыва).

Критерии оценивания: 10-13 заданий – 51-68 баллов, 14-17 заданий – 69-84 баллов, 18-20 заданий – 85-100 баллов.

Вопросы для ответов представлены на специальном тестовом бланке. Во время экзамена абитуриентам запрещается пользоваться мобильными телефонами и любым другим электронным оборудованием.

 В соответствии со стандартом направления подготовки 050200.68 Физико-математическое образование, абитуриент должен:

знать:

- основы общих и специальных теоретических дисциплин в объеме, необходимом для решения типовых задач профессиональной деятельности,

- школьные программы и учебники;

- средства обучения и их дидактические возможности;

- требования к оснащению и оборудованию учебных кабинетов и подсобных помещений;

- средства обучения и их дидактические возможности;

- санитарные правила и нормы, правила техники безопасности и противопожарной защиты.


Программа вступительного экзамена по математике в магистратуру направления 050200.68 - Физико-математическое образование разработана в соответствии с Федеральным Государственным образовательным стандартом высшего профессионального образования и включает следующие разделы:

• Математический анализ;
  
• Алгебра и теория чисел;
  
• Геометрия;
  
• Технологии и методики обучения математике.
  

СОДЕРЖАНИЕ ПРОГРАММЫ

1. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
   

Экзаменующиеся должны владеть основными понятиями теории мно­жеств, метрического пространства, предела, непрерывности, произ­водной и дифференциала, первообразной и неопределенного интегра­ла, определенного интеграла, сходимости рядов, дифференциальных уравнений; владеть техникой дифференцирования и интегрирования, решать простейшие дифференциальные уравнения; знать основные свойства элементарных аналитических функций.

1. Мощность множества. Счетные множества и их свойства. Счетность множества рациональных чисел. Несчетность множества действи­тельных чисел.

Содержание. Взаимнооднозначное соответствие, равномощные (эк­вивалентные) множества. Мощность. Примеры. Счетные множества и их свойства. Счетность множества рациональных чисел. Несчетность отрезка [0,1]. Несчетность множества действительных чисел. Сравнение мощностей. Примеры.

Литература. [3], с. 13-32; [4], с. 17-31; [5], с. 14-23.

2. Отображение множеств (функции). Предел и непрерывность
функции в точке. Основные свойства непрерывных функций на отрез­ке.

Содержание. Определение отображения множеств (функции). Область определения функции, область изменения функции. График функции. Важнейшие классы функций. Аналитический, графический и табличный способы задания функции. Примеры. Определение предела функции по Коши и по Гейне, их эквивалентность. Примеры, различные опреде­ления непрерывности функции в точке. Примеры, основные свойства функций, непрерывных на отрезке: теоремы об ограниченности функ­ции и о достижении наибольшего и наименьшего значений функции на отрезке.

Литература. [5], с. 24-25; [10], с. 37-68, 146-158, 194-209; [12], с 37-46, 68-76, 117-123, 133-136; [1], с. 27-44, 91-102, 114-I29, 132-134.

3. Предел числовой последовательности. Необходи­мый и достаточный признак сходимости последовательности.

Содержание. Определение предела числовой последовательности. Принцип стягивающихся отрезков. Верхняя грань. Существование верхней грани ограниченного сверху множества. Теорема о пределе монотонно* последовательности. Теорема Больцано-Вейерштрасса. Не­обходимый и достаточный признак сходимости последовательности (критерий Коши).

Литература. [1] , с. 60-65, 82-83, 87-90, 220-222; [10], с. 104-112, 137-142, 144-145; [12], с. 59-62, 92-98, 104-108.

4. Определение и свойства степени. Степенная функция. Степень
в комплексной области.

Содержание. Определение и свойства степени с целым показате­лем. Существование корня с натуральным показателем. Определение и свойства степени с рациональным показателем. Определение, су­ществование и свойства степени с иррациональным показателем. Степенная функция. График. Степень в комплексной области.

Литература, [1] , с. 46-49, 121, 135-139, 141; [10], с. 76-82, 233-234; [8], с. 16-17; [15], с. 8-12, 76-77; [6], с. 15-17, 62-65, 109-114, 123-126; [9], с. 171-178; [2], с. 302-305.

5. Показательная функция, ее основные свойства. Разложение
показательной функции в степенной ряд. Показательная функция
комплексной переменной. Формулы Эйлера.

Содержание. Показательная функция и ее основные свойства (область определения, четность и нечетность, периодичность, моно­тонность, непрерывность, множества значений, график). Разложение функции у = е^х в степенной ряд. Показательная функция компле­ксной переменной, свойства.

Литература, [1], с. 140; [2], с. 289-293, 352-353; [10], с. 223-230; [11] , С. 80; [l3], с. 52; [6], с. 90-95 [8], с. 42-43; [15], с. 68-72.

6. Логарифмическая функция, ее основные свойства. Разложение в степенной ряд. Логарифмическая функция комплексной переменной.

Содержание. Существование логарифмов. Логарифмическая функция и ее свойства. График. Разложение функции 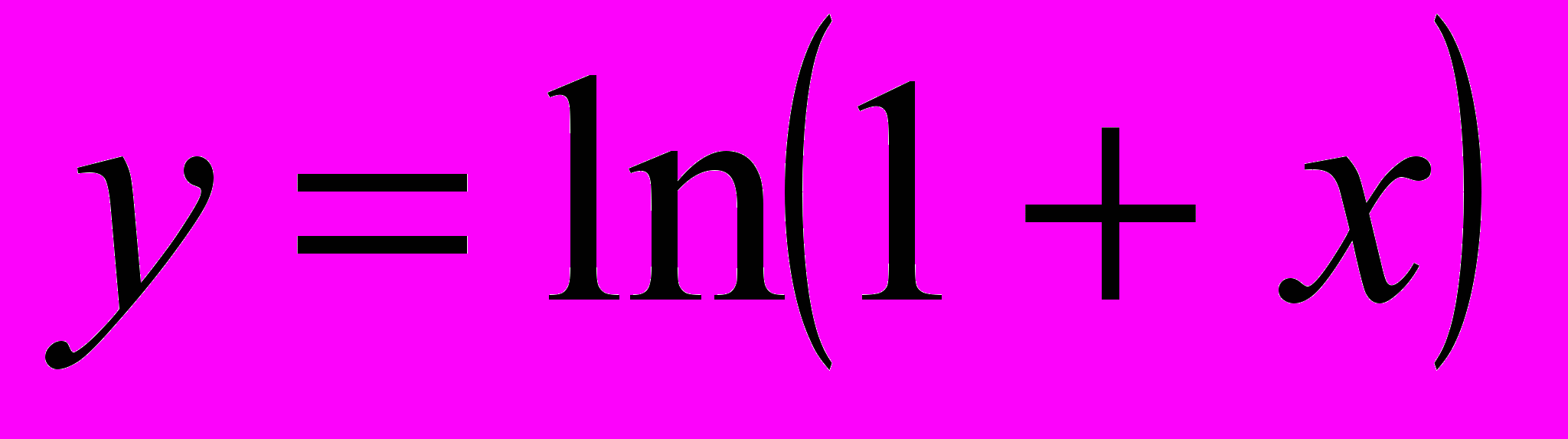в степен­ной ряд. Логарифмическая функция комплексной переменной и ее свойства. Примеры. Интегральное определение логарифмической функ­ции.

Литература. [1], с. 141; [10], с. 231-232; [2],с. 255-257, 299-302; [11], с. 82; [13], с. 56-57; [6] , с. 118-123; [8], с. 45-46, 99-100; [9], С. 160-169; [12], с. 73-74.

7. Тригонометрические функции, их основные свойства. Разложение синуса и косинуса в степенной ряд. Синус и косинус в комплексной области.

Содержание. Тригонометрические функции, их основные свойства (область определения, четность и нечетность, периодичность, про­межутки монотонности, непрерывность, множества значений, график). Разложение синуса и косинуса в степенной ряд. Синус и косинус в комплексной области, свойства.

Литература. [1], с. 50; [2], с. 253-254, 289-291, 293-296; [10], с.235; [11], с. 80; [6], с. 97-102; [8], с. 76-78, 80, 83-85; [9], с. 43-45; [15], с 68-72.

8. Дифференцируемые функции одной действительной переменной.
Геометрический и механический смысл производной. Правила диффе­ренцирования.

Содержание. Дифференцируемость и производная функции одной пе­ременной. Геометрический и механический смысл производной. Произ­водная суммы, произведения и частного двух функций. Производные сложной и обратной функций. Примеры.

Литература, [1], с. 150-171, 178-184; [10], с. 242-276, 285-289; [12], с. 140-156, 161-166.

9. Теорема Лагранжа. Условия постоянства, монотонности и вы­
пуклости функции на промежутке, экстремумы и точки перегиба.

Содержание. Теорема Лагранжа. Геометрический смысл теоремы Лагранжа. Применение теоремы Лагранжа при исследовании функции на монотонность. Максимум и минимум функции. Достаточные условия экстремума. Выпуклость и вогнутость. Достаточное условие выпук­лости и вогнутости. Точки перегиба.

Литература. [1], с. 195-196, 211-229; [10], с. 296-299, 338-343, 352-361, 381-387; [12], с. 180-181, 195-202, 403- 405.

10. Первообразная и неопределенный интеграл. Интегрирование
подстановкой и по частям.

Содержание. Первообразная. Связь между первообразными одной и той же функции. Неопределенный интеграл, основные свойства неопре­деленного интеграла. Интегрирование подстановкой и по частям. При­меры.

Литература, [1], с. 254-276; [10], 403-435; [12], с. 279-296.

11. Определенный интеграл. Интегрируемость непрерывной функции. Формула Ньютона-Лейбница.

Содержание. Задачи, приводящие к понятию определенного инте­грала, определение определенного интеграла. Верхняя и нижняя сум­мы ограниченной функции. Необходимое и достаточное условие инте­грируемости. Интегрируемость непрерывной функции. Определенный интеграл с переменным верхним пределом. Существование первообраз­ной для непрерывной функции. Формула Ньютона-Лейбница.

Литература. [1] , с. 301-327, 336-343; [10] , с. 468-502, 517-530; [12], с. 320-327, 340-341, 345-349.

12. Площадь плоской фигуры и длины дуги. Приложения определен­ного интеграла к вычислению площади плоской фигуры, объема тела
вращения.

Содержание. Понятие квадриремой фигуры и ее площади. Достаточ­ные условия квадрируемости. Вычисление площади в декартовых и по­лярных координатах. Понятие тела вращения и его объема. Объем тела с заданным поперечным сечением. Вычисление объема тела вращения.

13. Приложения определенного интеграла к вычислению длины дуги и площади поверхности вращения.

Содержание.

Понятие спрямляемой дуги и ее длины. Вычисле­ние длины дуги. Понятие поверхности вращения и ее площади. Вычисление площади по­верхности вращения. Примеры.

Литература. [l], с. 345-376; [10], с. 555-580,588-605; [l2],
с. 354-356, 357-378, 382-383.

14.Числовые ряды. Признаки сходимости: Коши, Даламбера и интегральный.

Абсолютно и условно сходящиеся ряды.

Содержание. Определение ряда. Сходящиеся и расходящиеся ряды. Необходимое условие сходимости. Положительный ряд. Признаки схо­димости положительного ряда: Даламбера и интегральный (не в пре­дельной и в предельной формах). Абсолютно и условно сходящиеся чередующегося ряда.

Литература. [2], с. 185-190, 196-197, 202-203, 209-219; [11], с. 3-8, 11-15, 21-24, 27-29, 31-37; [13], с. 11-15,21-24, 26-28, 30-34.

15. Функциональные последовательности и ряды. Равномерная сходимость. Степенные ряды в комплексной области. Круг сходимости.

Содержание. Функциональная последовательность и функциональ­ный ряд. Область сходимости. Равномерная сходимость. Признак равномерной и абсолютной сходимости функционального ряда (Приз­нак Вейерштрасса). Сте­сненные ряды комплексной области. Теорема Абеля. Круг сходимос­ти.

Литература. [2], о. 224-234, 279-282; [11], с. 46-64; [13], с. 68-85; [6], с 135-137; [8], с. 64-69; [93], с. 94-96; [12], с. 61-65.

16. Формула и ряд Тейлора. Биномиальный ряд.

Содержание. Формула Тейлора с остаточным членом в формах Ла­гранжа и Коши. Ряд Тейлора. Биномиальный ряд.

Литература. [1],, с. 205-207; [2], с. 247-249, 258-262; с. .303-311; [2], с. 71-79, 82-86.

17. Метрические пространства. Открытые и замкнутые множества.
Полные метрические пространства. Теорема Банаха о сжимающем ото­бражении к ее приложение.

Содержание. Метрическое и нормированное пространства. Приме­ры. Открытые и замкнутые множества. Фундаментальная последователь­ность. Понятие полного пространства. Банахово пространство. При­меры полных метрических пространств: 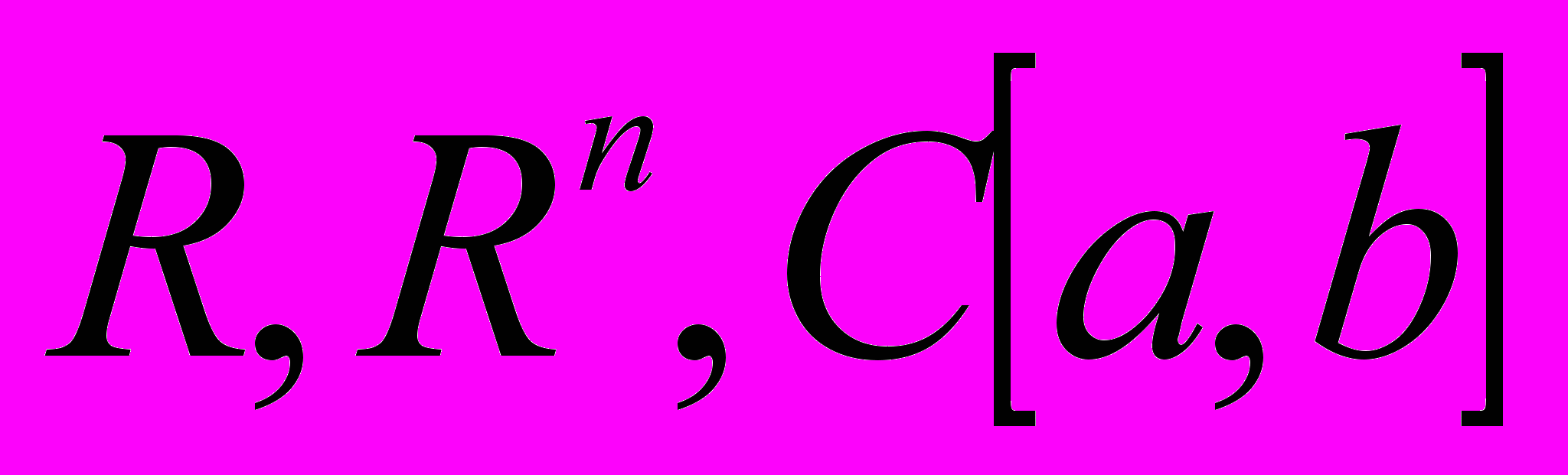. Теорема о полноте всякой замкнутой части полного пространства. В качестве примера показать, что 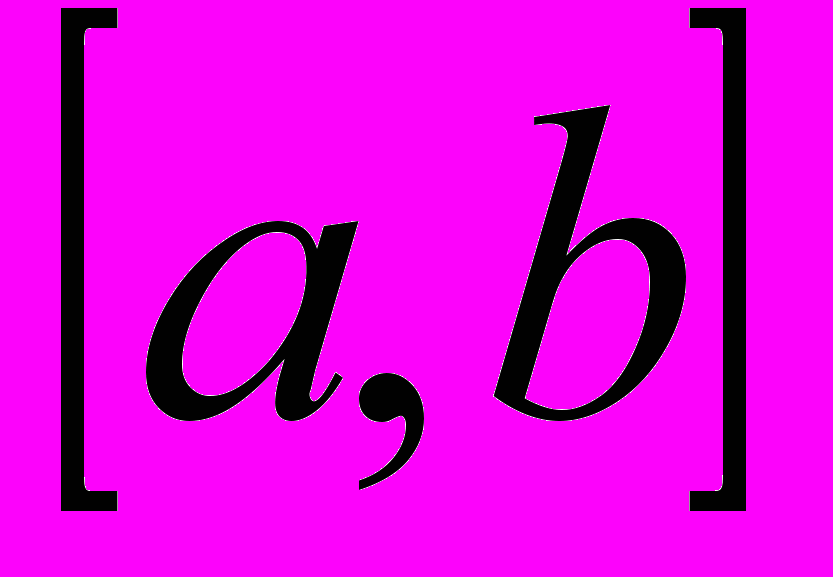- полное пространство.

Литература. [4], с. 39-49, 60-72, 74-78; [5], с. 46-57, 58-67, 72-79, 138-140; [16] , с. 24-33, 30-51, 67-71, 82-88.

18. Обыкновенные дифференциальные уравнения первого порядка.
Уравнения с разделяющимися переменными. Линейные уравнения.

Содержание. Понятие дифференциального уравнения. Основные по­нятия (обыкновенное дифференциальное уравнение, порядок, общее и частные решения дифференциальных уравнений первого порядка, на­чальные условия, интегральная кривая). Уравнения с разделяющимися переменными. Линейные уравнения (однородные и неоднородные) пер­вого порядка. Отыскание общих решений линейных уравнений первого порядка.

Литература. [2], с. 317-319, 326-327, 334-339, 345-349; [11], с. 364-368, 372-384, 392-398; [7], с. 7-12, 15-17.

19. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами, их применение к изучению свободных и вынужденных колебаний.

Содержание. Однородные и неоднородные линейные уравнения вто­рого порядка с постоянными коэффициентами и отыскание их общих решений, математическая модель свободных и вынужденных колебаний. Резонанс.

Литература. [2], с. 378-400; [11], с. 454-467.

20.Производная функции комплексной переменной. Условия дифференцируемости. Понятие аналитической функции. Производные

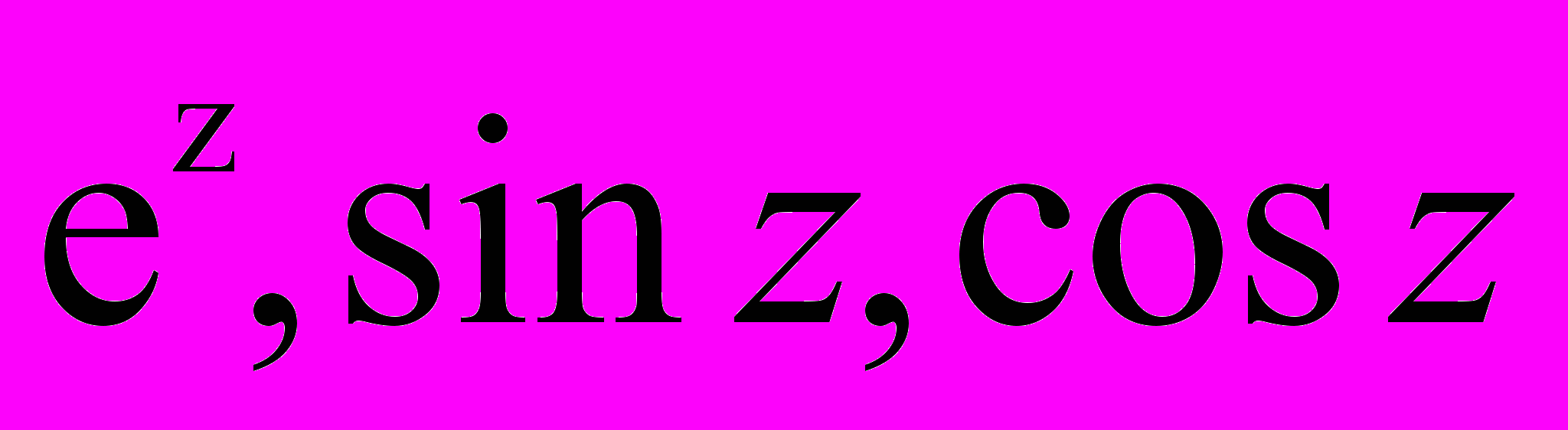
Содержание. Понятие производной функции комплексной переменной.

Дифференцируемая функция. Необходимое и достаточное условие диф­ференцируемости. Понятие аналитической функции.

Литература. [2], с. 282-288; [6], с. 32-39; [8], с 31-33; [15], с. 30-35, 38-33.


ЛИТЕРАТУРА

1. Бохан К.А., Егорова И.А., Ладенов К.В. Курс математичес­кого анализа. - Минск: Интеграл, 2004. - т.1.
   
2. Бохан К.А., Егорова И.А., Лащенов К.В. Курс математического анализа. - Минск: Интеграл, 2004. - т.2.
   
3. Натансон И.Г. Теория функций вещественной переменной. - М., 2008.
   
4. Вулих Б.З. Краткий курс теории функций вещественной переменной. - М., 2007.
   
5. Колмогоров А.Н., Фомин СВ. Элементы теории функций и
   функционального анализа. - М., 2008.
   
6. Маркушевич А.И. Краткий курс теории аналитических функций. - М.: Наука, 1966.; Электронный ресурс: ссылка скрыта
   
7. Понтрягин И.С. Обыкновенные дифференциальные уравнения. - М., 2009.
   
8. Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. - М.: Наука, 1967.; Электронный ресурс:
   

ссылка скрыта

9. Сидоров Ю.Б., Федорюк М.В., Шабунин М.И. Лекции по теории
   функций комплексного переменного. - М.: Наука, 1976.
   

10. Уваренков И.М., Маллер М.З. Курс математического анализа.
    - М.: Просвещение, 1966. -T.I.
    
11. Уваренков И.М., Маллер м.8. Курс математического анализа. - М.: Просвещение, 1976. - т.2.
    
12. Фихтенгольц Г.М. Основы математического анализа Часть 1. – СПб.: Издательство «Лань», 2005. – 448 с.
    
13. Фихтенгольц Г.М. Основы математического анализа. Часть 2. – СПб.: Издательство «Лань», 2005. – 464 с.
    
14. Данилина И.И., Дубровская И.С.Кваша О.П., Смирнов Б.Л.,
    Феклисов Г.Н. Численные методы. - М.: Высшая школа, 1976.
    
15. Хапланов М.Г. Теория функций комплексного переменного.
    - М.: Просвещение, 1965.
    

16. Виленкин Н.Я., Балк М.Н., Петров В.А. Математический анализ. Мощность. Метрика. Интеграл. - М.: Просвещение, 1980.

2. АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ
   

Экзаменующиеся должны владеть основными понятиями алгебры (груша, кольцо, поле, векторное пространство, линейная алгебра) и теории чисел (система натуральных чисел, простые числа, дели­мость, сравнения и их приложения), иметь отчетливое представление об основных числовых системах и их построении, владеть навыками решения систем линейных уравнений.

1. Бинарные отношения. Отношение эквивалентности и разбиение
на классы, фактор-множество.

Содержание. Декартово произведение двух множеств. Бинарные от­ношения. Типы бинарных отношений. Примеры бинарных отношений. От­ношение эквивалентности. Классы эквивалентности, фактор-множест­во; примеры. Отношение порядка.

Литература. [1], гл. 2, §§ 2,4; [5], §§ 5,6.

2. Группа. Примеры групп, простейшие свойства группы. Подгруппы. Гомоморфизмы и изоморфизмы групп.

Содержание. Определение группы. Порядок группы. Порядок эле­мента группы. Абелевы группы. Простейшие свойства группы. Под­группа группы. Примеры групп и их подгрупп. Гомоморфизм и изо­морфизм групп; примеры. Теорема о гомоморфизме (без доказатель­ства).

Литература. [1], гл. 3, § 3, гл. 4, §§ 1-4; [2], §§ 63-65; [5], гл. 4, §§ 1-3; [6], гл.10, §§ 1-3;[7], гл. 2, § 3.

3. Кольцо. Примеры колец. Простейшие свойства кольца. Гомоморфизмы и изоморфизмы колец.

Содержание. Определение кольца, примеры колец. Простейшие свойства колец. Гомоморфизм и изоморфизм колец; примеры.

Литература. [1], гл. 3, § 4; [21], §§ 43, 44, 46; [5], гл. 4, § 4; [6], гл. 1, § 3; [7], гл. 2, § 4.

4. Система натуральных чисел. Принцип математической индукции.

Содержание. Аксиомы системы натуральных чисел. Принцип мате­матической индукции. Примеры доказательства методом математичес­кой индукции.

Литература. [I], гл. 4, §§ 1-3; [5], гл. I, § 7.

5. Кольцо целых чисел. Теорема о делении с остатком.

Содержание. Необходимость расширения системы натуральных чи­сел, определение системы целых чисел. Аксиомы системы целых чи­сел. Делимость целых чисел, свойства делимости. Теорема о дели­мости с остатком.

Литература. [1], гл. 4, § 4; [4], гл. I, § I; [6], гл. I, § I.

6. Наибольший общий делитель и наименьшее общее кратное двух
чисел.

Содержание. НОД двух целых чисел. Свойства НОДа. Вычисление НОДа с помощью разложения данных чисел на простые множители и с помощью алгоритма Евклида. НОК двух целых чисел. Вычисление НОК.

Литература. [I], гл. II, §§ 2, 3; [3], гл.3; [4], гл. I, §§ 2,3; [5], гл. I, § 8; [6], гл. I, § I.

7. Поле. Простейшие свойства поля. Поле рациональных чисел.
Примеры полей.

Содержание. Определение поля. Примеры полей. Простейшие свой­ства полей. Необходимость расширения системы целых чисел. Опреде­ление системы рациональных чисел. Аксиомы системы рациональных чисел.

Литература. [I], гл. 4, § 5; [2], §45,50; [5], гл. 4, §4 гл. 5, § 4; [6], гл. 1, §1; [7], гл.2, §4.

8. Упорядоченное поле. Система действительных чисел.

Содержание. Определение бинарного отношения порядка; типы по­рядка, определение упорядоченного поля, необходимость расширения системы рациональных чисел. Определение системы действительных чисел. Аксиомы системы действительных чисел.

Литература. [I], гл. 2, § 5; гл. 4, § 6.

9. Поле комплексных чисел. Геометрическое представление ком­плексных чисел и операции над ними.

Содержание. Необходимость расширения системы действительных чисел. Определение комплексных чисел. Поле комплексных чисел. Геометрическое представление комплексных чисел и операции над ними.

Литература. [I] , гл. 4, § 7; [2], §§ 17 , 18 ; [5], гл. 5, § I ; [6], гл. 2, §§ 1-3.

10. Тригонометрическая форма комплексного числа.

Содержание. Тригонометрическая форма комплексного числа. Фор­мула Муавра.

Литература, [1], гл. 4, § 8 ; [2], §§ 17-19 ; [5], гл. 5, § I.

11. Следствие системы линейных уравнений. Равносильные систе­мы линейных уравнений. Решение системы линейных уравнений мето­дом последовательного исключения переменных. Критерий совместнос­ти системы линейных уравнений.

Содержание. Определение системы линейных уравнений (СЛУ), ее решения. Совместная и несовместная, определенная и неопределен­ная СЛУ. Матрица СЛУ. Решение СЛУ методом последовательного ис­ключения переменных (способ Гаусса). Критерий совместности СЛУ (теоремы Кронекера-Капелли без доказательства).

Литература, [1], гл.5, §§ 2 , 3; [2], §§ 11 ,12; [5], гл.I, § 3; гл. 2, §§ 2 , 4; гл. 4, § 4.

12. Векторное пространство. Примеры и простейшие свойства век­торных пространств.

Содержание. Определение векторного пространства (линейного). Примеры векторных пространств. Арифметическое n-мерное вектор­ное пространство. Простейшие свойства векторных пространств.

Литература. [1], гл. 5, § I; гл. 7, § I; [2], §§ 8 , 29; [5], гл. 2, § I.

13. Линейная зависимость и независимость системы векторов. Базис и размерность конечномерного векторного пространства.

Содержание. Определение линейной зависимости и независимости системы векторов; простейшие свойства таких систем. Определение базиса и размерности векторного пространства; число базисов. Единственность представления любого вектора через векторы бази­са. Координаты вектора; свойства координат. Примеры векторных пространств с указанием их базисов.

Литература. [I], гл. 5, § I; [2], §9; [5], гл. 2, § I; [6], гл. 4, § 3.

14. Подпространства. Линейные многообразия. Изоморфизмы век­
торных пространств.

Содержание. Определение подпространства. Примеры подпростран­ств. Линейное многообразие. Линейное многообразие решений неодно­родной системы линейных уравнений. Изоморфизмы векторных прос­транств.

Литература. [I], гл. 7, §§ 2-4 ; [2], § 30 ; [5], гл. 2,§§ I , 4 ; [6], гл. 12, §§1,2.

15. Простые числа. Бесконечность множества простых чисел. Ка­ноническое разложение составного числа и его единственность.

Содержание. Определение простого числа. Бесконечность множес­тва простых чисел. Решето Эратосфена. Теорема о разложении любо­го числа на простые множители. Каноническое разложение числа.

Литература. [I], гл. II, § I; [3], гл. 2 ; [4] гл. I,§§ 5,6 ; [5], гл. I, §8.

16. Основные свойства сравнений. Полная и приведенная системы вычетов. Теоремы Эйлера и Ферма.

Содержание. Определение сравнения двух целых чисел по данно­му модулю 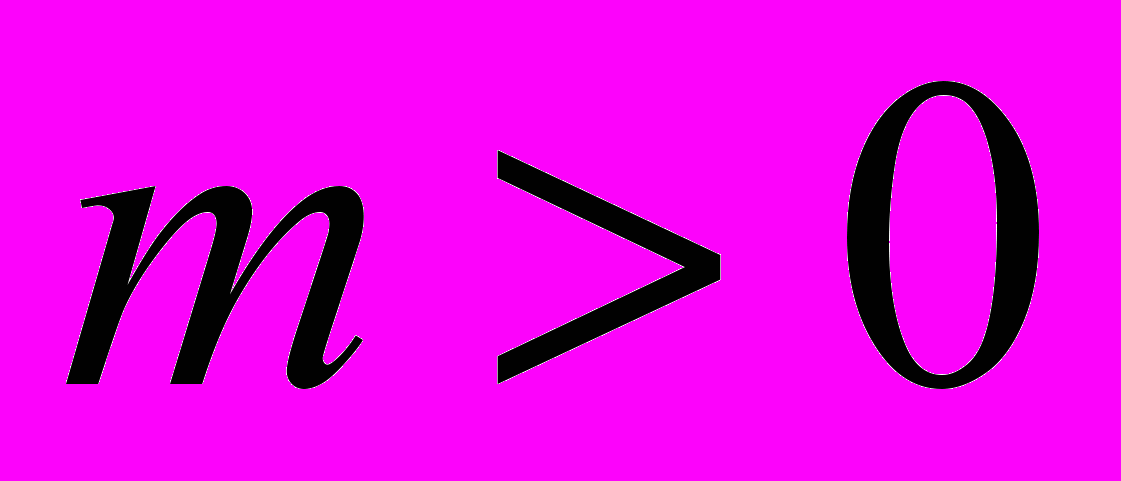. Основные свойства сравнений. Разбиение целых чисел на классы по данному модулю. Полная и приведенная системы вычетов. Определение функции Эйлера 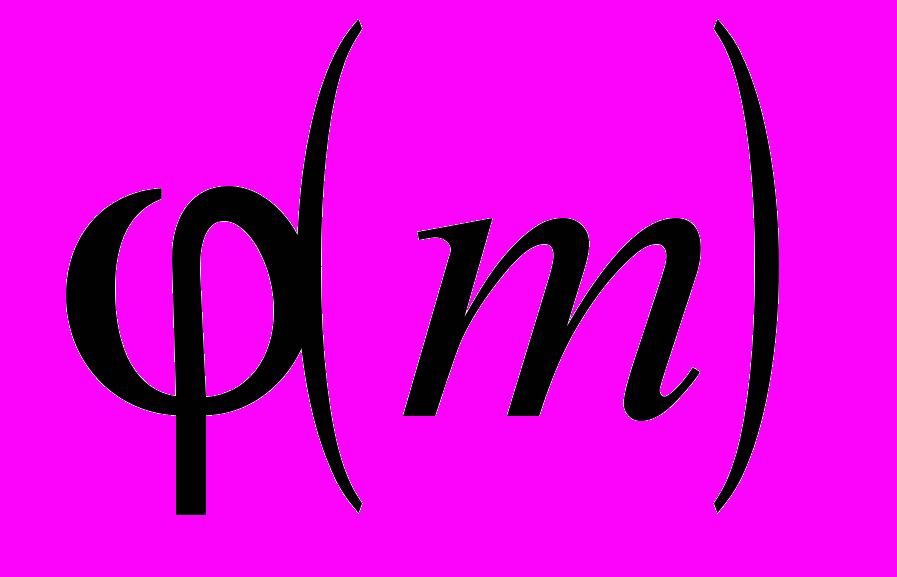. Теорема Ферма; тео­рема Эйлера.

Литература, [1], гл. 12, §§ 1-3; [3], гл. 7-11; [4], гл. 2, § 41; гл. 3; [6], гл. I, § 2.

17. Линейные сравнения с одной переменной.

Содержание. Понятие сравнения с неизвестным числом. Линейные сравнения. Понятие решения и числа решений. Равносильные сравне­ния. Условие разрешимости линейного сравнения. Способы решения линейных сравнений.

Литература, [1] , гл. 12, §§ 1,4 ; [3] гл. 13,12,23 ; [4], гл. 4, § I ; [6], гл. I, § 2.

18. Приложения теории сравнений к выводу признаков делимости.

Содержание. Приложение теории сравнений для вывода признаков делимости на 3 и 9. Способ Паскаля вывода признаков делимости.

Признаки делимости на 2, 4, 5, 6, 8, 10.

Литература. [3], гл. 23; [4], гл. 4, § 2.

19. Полиномы над полем. Наибольший общий делитель двух поли­
номов и алгоритмы Евклида. Разложение полинома в произведение
неприводимых множителей и его единственность.

Содержание. Понятие полинома над полем. Кольцо полиномов как область целостности. Делимость полиномов, свойства делимости. Теорема о делении с остатком. Определение НОД двух полиномов. Вычисление НОД двух полиномов с помощью алгоритма Евклида. Опре­деления приводимых и неприводимых над данным полем полиномов. Те­орема о разложении полинома в произведение неприводимых полиномов Вопрос о приводимости полиномов над полями .

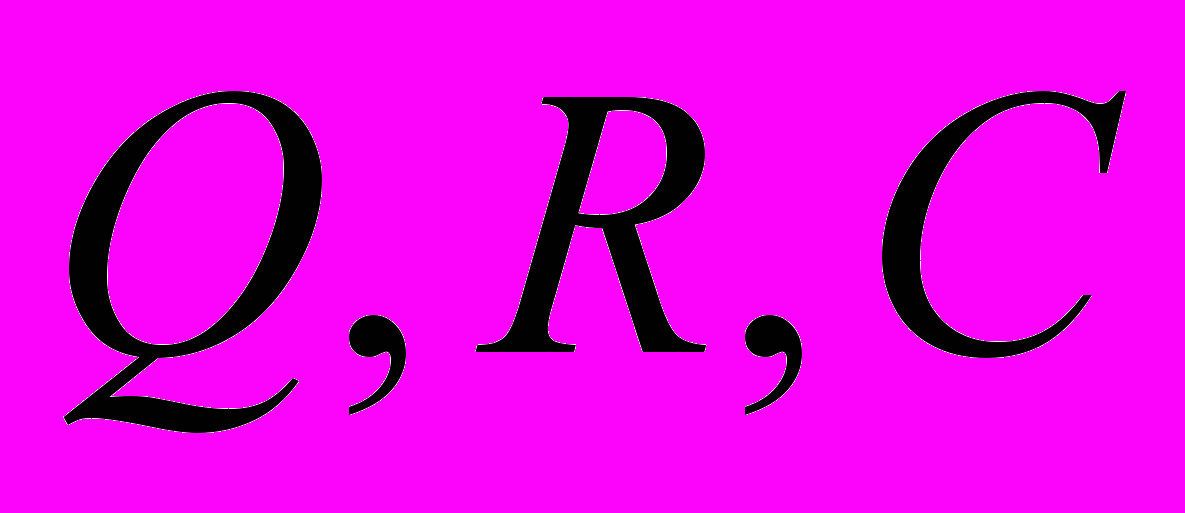Литература. [I], гл. 14, §§ 1-4 ; [2], §§ 20-22, 47, 48 ; [5], гл. 5, § 2 [6], гл. 3, § I; гл. 6, § I.

20. Алгебраическая замкнутость поля комплексных чисел. Сопряженность мнимых корней полинома с действительными коэффициентами.
Неприводимые над полем действительных чисел полиномы.

Содержание. Понятие алгебраической замкнутости поля. Алгебраи­ческая замкнутость поля комплексных чисел. Основная теорема ал­гебры: любой полином с комплексными коэффициентами степени 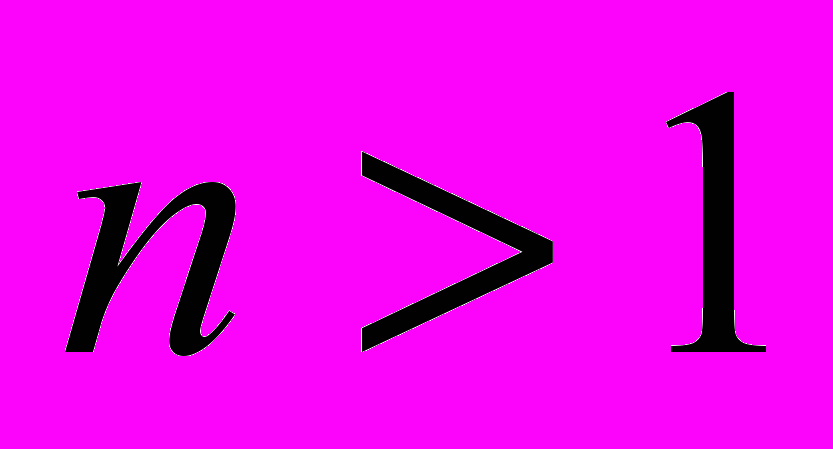имеет по меньшей мере один комплексный корень). Сопряженность мнимых корней полинома с действительными коэффициентами. Неприво­димость над полем действительных чисел полиномов степени I и 2.

Литература. [I], гл. 16, §§ 1,2; [2], §§ 23, 24, 55; [5],гл. 6, §§ I, 3; [6], гл. 9, § I.


2.2. ЛИТЕРАТУРА

1. Куликов Л.Я. Алгебра и теория чисел. - М.: Просвещение, 1979.; Электронный ресурс: ссылка скрыта
   
2. Курош А.Г. Курс высшей алгебры. - М., 2008.
   
3. Бухштаб А.А. Теория чисел. - М.: Просвещение, 1966.; Электронный ресурс:
   

ссылка скрыта

4. Виноградов И.М. Основы теории чисел. - М.: ФМЛ, 2007.
   
5. Кострикин А.И. Введение в алгебру. - М.: ФМЛ, 2004.
   
6. Фадеев Д.К. Лекции по алгебре. - М., 2008.
   
7. Скорняков Л.А. Элементы алгебры. - М.: Наука, 1983. Электронный ресурс:
   

ссылка скрыта


3. ГЕОМЕТРИЯ


Экзаменующиеся должны знать аксиоматический метод построения геометрии, иметь ясное представление о различных группах преобра­зований плоскости и уметь пользоваться этими преобразованиями при решении задач на построение и доказательство, владеть векторным и координатным методами при изучении геометрии на плоскости и в пространстве, знать основы теории изображений плоских и простран­ственных фигур (в параллельной проекции).


1. Скалярное произведение векторов. Приложения к решению задач.

Содержание. Определение скалярного произведения двух векторов, его свойства, выражение в координатах. Приложения к вычислению расстояния между двумя точками, угла между двумя векторами.

Литература. [I (§§ 9, 10); 5].

2. Векторное произведение векторов. Приложения к решению задач.

Содержание. Определение векторного произведения двух векторов, его свойства, выражение в координатах. Приложения к вычислению площади треугольника и параллелограмма.

Литература. [I (§§ 56, 58); 5].

3.Смешанное произведение векторов. Приложения к решению задач.

Содержание. Определение смешанного произведения трех векторов, его свойства, выражение в координатах, условие компланарности трех векторов. Приложения к вычислению объема параллелепипеда, тетра­эдра.

Литература. [I (§§ 55, 58); 5].

4.Группа движений (перемещений) плоскости.

Содержание. Определение движения. Свойства движений. Группа движений.

Литература. [I (§§ 41, 43)].

5. Аналитическое задание движений плоскости. Приложения движе­ний к решению задач.

Содержание. Вывод формулы движений. Примеры решения задач.

Литература. [I (§§ 42, 51)].

6.Группа преобразований подобия плоскости и ее подгруппы.
Приложения преобразований подобия к решению задач.

Содержание. Определение подобия. Гомотетия, ее свойства. Подо­бие как произведение гомотетии и движения. Свойства подобия, его аналитическое задание. Подгруппы группы преобразований подобия. Предмет евклидовой геометрии. Примеры решения задач с помощью пре­образований подобия.

Литература. [I (§§ 46, 47)].

7.Взаимное расположение двух плоскостей, прямой и плоскости,
двух прямых в пространстве (в аналитическом изложении).

Содержание. Взаимное расположение двух плоскостей, заданных общими уравнениями. Нахождение точки пересечения прямой, заданной параметрически, и плоскости, их взаимное расположение. Взаимное расположение двух прямых, заданных каноническими уравнениями.

Литература. [I (§§ 61, 64); 5].

8. Проективная плоскость и ее модели.
   

Содержание. Определение проективной плоскости. Модели проек­тивной плоскости: связка прямых, расширенная плоскость.

Литература. [2 (§§ 2, 4)].

9.Группа проективных преобразований. Приложения к решению
задач.

Содержание. Определение проективного преобразования, его свой­ства, аналитическое задание. Группа проективных преобразований. Проективные свойства, предмет проективной геометрии. Примеры ре­шения задач с помощью проективной геометрии.

Литература. [2(§§ 11, 12, 25)].

10. Изображения плоских и пространственных фигур в параллель­ной проекции. Позиционные задачи.

Содержание. Параллельное проектирование, его свойства (без доказательства). Примеры изображения некоторых фигур в параллель­ной проекции. Позиционные задачи.

Литература. [2 (§§ 26-29); 3, гл. 19 (§§ 5-7)].

11. Измерение отрезков.

Содержание. Понятие измерения отрезка. Доказательство теоремы существования. Формулировка теоремы единственности.

Литература. [2 (§§ 86, 87); 3, гл. 18 (§§ I, 2)].

12. Многоугольники. Площадь многоугольника, теорема существования и единственности.

Содержание. Определение многоугольника. Определение площади многоугольника. Площадь прямоугольника, трапеции, треугольника, параллелограмма. Теорема существования и единственности.

Литература. [2 (§§ 88, 89); 3, гл. 18 (§§ 2, 3)].

13. Выпуклые многогранники. Теорема Эйлера для выпуклых многогранников.

Содержание. Определение выпуклого многогранника. Доказатель­ство теоремы Эйлера для выпуклых многогранников.

Литература. [3, гл. 20 (§§ 6, 7); 2 (§ 45)].

14. Правильные многогранники. Пять типов правильных многогранни­ков.

Содержание, доказательство и реализации пяти типов правильных

многогранников.

Литература. [3, гл. 20 (§ 9); 2 (§ 46)].


3.2. ЛИТЕРАТУРА

1. Атанасян Л.С., Базылев В.Т. Геометрия. - М.: Просвещение, 1986. - ч. I.
   
2. Атанасян Л.С., Базылев В.Т. Геометрия. - М.: Просвещение, 1987. - ч. 2.
   
3. Погорелов А.В. Геометрия. - М.: Наука, 1983.
   
4. Аргунов Б.И. Преобразования плоскости. - М.: Просвещение, 1976.
   
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. 1: Учеб. пособие для вузов. – М.: Высш. шк. – 6-е изд., 2006. - 304с.
   

4. ТЕХНОЛОГИИ И МЕТОДИКИ ОБУЧЕНИЯ МАТЕМАТИКЕ


Экзаменующиеся должны:

• владеть основными понятиями дисциплины «Технологии и методики обучения математике»;
  
• знать принципы дидактики в обучении математики, методы научного познания в обучении математики, основные методики обучения математике;
  
• разделять урочные, внеурочные, традиционные, современные, групповые, индивидуальные, дифференцированные и другие технологии обучения;
  
• проявлять компетентность в применении общих методик в специальных методиках (методика обучения математике в 5-6 классах, алгебре, геометрии (раздел планиметрия)).
  

1. Предмет технологии и методики преподавания математики. Цели, принципы, методы и технологии, формы и средства обучения математике. Планирование работы учителя.

Содержание. Обучающая, развивающая и воспитательная цели обучения. Принципы дидактики в обучении математике. Технологии и методики обучения математике (урочные, внеурочные, традиционные, современные, групповые, индивидуальные, дифференцированные и др.). Эмпирически, логические и математические методы научного познания в обучении математике. Математические понятия (содержание, объем, классификация, ошибки в определениях) и методика их изучения в школе. Методика изучения теорем и их доказательств. Методика обучения учащихся решению математических задач. Современные средства контроля и оценивания результатов достижения обучения школьников. Формы организации обучения: уроки и их классификации; факультативные и элективные курсы. Возможные технологии и методики построения уроков, ориентированных на развитие ключевых компетентностей. Календарно-тематическое и поурочное планирование работы учителя.

Литература. [6], [8], [9], [10].

2. Методика изучения числовых систем. Методика изучения тождественных преобразований. Методика изучения уравнений и неравенств. Методика изучения функций.

Содержание. Различные подходы к изучению тем. Методика изучения натуральных чисел. Методика изучения дробных чисел. Методика изучения отрицательных, иррациональных и комплексных чисел. Алгоритмы выполнения арифметических действий. Целенаправленность тождественных преобразований. Реализация принципа сознательности при изучении тождественных преобразований. Ошибки учащихся и их исправления. Методика введения понятия тождества. Методика выполнения тождественных преобразований различных классификаций. Различные типы уравнений и неравенств. Решение задач на составление уравнений. Системы уравнений в школьном курсе математики. Методика введения понятия функция. Методическая схема изучения функции. Методика изучения общефункциональных понятий. Методика изучения линейной функции. Методика изучения квадратичной функции. Методика изучения числовых последовательностей.

Литература. [4], [7].

3. Современные тенденции совершенствования учебников геометрии. Выделение геометрических линий, их классификация, цели изучения, различные подходы.

Содержание. Различные подходы к изучению тем. Методика изучения геометрического материала в 5-6 классах. Методика изучения аксиом планиметрии. Методика изучения треугольников, многоугольников. Методика изучения величин измерения в планиметрии. Методика изучения взаимного расположения на плоскости. Методика изучения геометрических построений. Методика изучения преобразования фигур, координат и векторов.

Литература. [1], [2], [3], [5].


4.2. ЛИТЕРАТУРА

1. Вернер А.Л. Геометрия: книга для учителя: методич. рекомендации к учебнику 7-9 классов. – М.: Просвещение, 2005.
   
2. Геометрия. 7-11 классы: программно-метод. материалы / [авт.-сост.: И. М. Смирнова, В. А. Смирнов]. - М.: Мнемозина, 2007.
   
3. Гусев В.А., Орлов В.В. и др. Методика обучения геометрии: Учеб. пособие для студ. высш. пед. учеб. заведений. – М.: Издательский центр «Академия», 2005.
   
4. Дорофеев, Георгий Владимирович. Математика : Сборник заданий для проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы: 11 класс/ Г. В. Дорофеев, Г. К. Муравин, Е. А. Седова. - 7-е изд., стер. - М.: Дрофа, 2005.
   
5. Каганов Э.Д. Решение задач повышенной сложности: Алгебра. Элементарные функции: сборник задач – М.: АРКТИ, 2005.
   
6. Манвелов С.Г. Конструирование современного урока математики : книга для учителя. - М.: Просвещение, 2005.
   
7. Проблемы целеполагания в учебном процессе: сб. науч. тр. / Федер. агентство по образованию, Департамент образования и науки Ханты-Манс. авт. окр.-Югры, Нижневарт. гос. гуманит. ун-т, Науч.-исслед. лаб. прикладной дидактики; отв. ред. А. В. Абрамов. - Нижневартовск: Изд-во Нижневартовского государственного гуманитарного университета, 2007.
   
8. Фокин Ю.Г. Теория и технология обучения: деятельностный подход: учеб. пособие для студентов вузов – М.: Академия, 2006.
   
9. Фридман Л.М. Психолого-педагогические основы обучения математике в школе: методические указания / Л. М. Фридман, 2005.
   
10. Щуркова Н.Е. Педагогическая технология: учеб. пособие для студентов вузов – Изд. 2-е, доп. – М.: Педагогическое общество России, 2005.