Geum.ru

Методическое объединение учителей математики и физики Учебная программа По дисциплине Математика Нестандартный задания курса алгебры и начала анализа 10 класс

Вид материалаПрограмма

Содержание


Цель курса
Учебный план
Содержание программы.
Общие методические рекомендации.
Подобный материал:
Методическое объединение учителей математики и физики


Учебная программа


По дисциплине Математика


Нестандартный задания курса алгебры и начала анализа 10 класс


Факультативный курс по математике

для 10 класса на 34 часов

Морозовой М.А.


Волжск

2011


Пояснительная записка


Данный факультативный курс рассчитан на одаренных детей, склонных к математике. Он направлен на расширение знаний учащихся, повышения уровня математической подготовки через решение различных задач.

Навыки в решении всех типов уравнений и неравенств, построение графиков элементарных функций полезны ученикам, принимающим участие в конкурсах и олимпиадах. Они помогут подготовиться к сдаче ЕГЭ и будут полезны при поступлении в высшие учебные заведения.

Материал данного курса содержит нестандартные методы, которые позволяют решить задания. Он может использоваться учителем как на уроках математики, так и на факультативах и дополнительных занятиях.

Программу можно использовать в 10-11классах с любой степенью подготовленности. Она способствует развитию познавательных интересов, мышления учащихся, для чего предложены разно-уровневые задания.

Данный курс предусматривает не только обеспечение прочного и сознательного овладения учащимися математическими знаниями и умениями, формирование устойчивого интереса к предмету, но и выявление и развитие математических способностей, способствует выбору профиля дальнейшего обучения и ориентации на профессии, связанные с математикой.

Цель курса:

помочь выяснить степень интереса к математике и оценить возможности овладения ею для дальнейшей перспективы.

Задачи курса:

научить учащихся преобразовывать рациональные выражения,

научить учащихся решать все типы уравнений и неравенств;

научить строить графики элементарных функций;

выработать достаточные навыки и умения по выполнению заданий к решению текстовых задач.

Учебный план


Данный курс рассчитан на 34 часа, предлагает комплексное и четкое изложение теории вопроса, решение типовых задач, зачетную работу.


Учебно-тематическое планирование

№

п/п
Тема
Количество часов
Лекции
Практическая работа

1
Понятие модуль
1
0,5
0,5

2
Решение уравнений, содержащих модуль
2
0,5
1,5

3
Решение неравенств, содержащих модуль
2
0,5
1,5

4
Построение графиков, содержащих модуль
2
0,5
1,5

5
Решение рациональных уравнений и неравенств.
5
0,5
4,5

6
Решение логарифмических уравнений и неравенств.
5
1
4

7
Текстовые задачи.
3
0,5
2,5

8
Элементы теории вероятностей
8
2,5
5,5

9
Тригонометрические функции
4



4

10
Зачетная работа
2








Содержание программы.

Тема 1. Понятие модуля (1 ч).

Понятие модуля. Общие сведения: определение, свойства модуля, геометрический смысл. Преобразование выражений, содержащих модуль.

Методы обучения: лекция, объяснение, выполнение тренировочных упражнений.

Формы контроля: проверка самостоятельно решенных заданий.

Тема 2. Решение уравнений, содержащих модуль (2ч).

Решение уравнений вид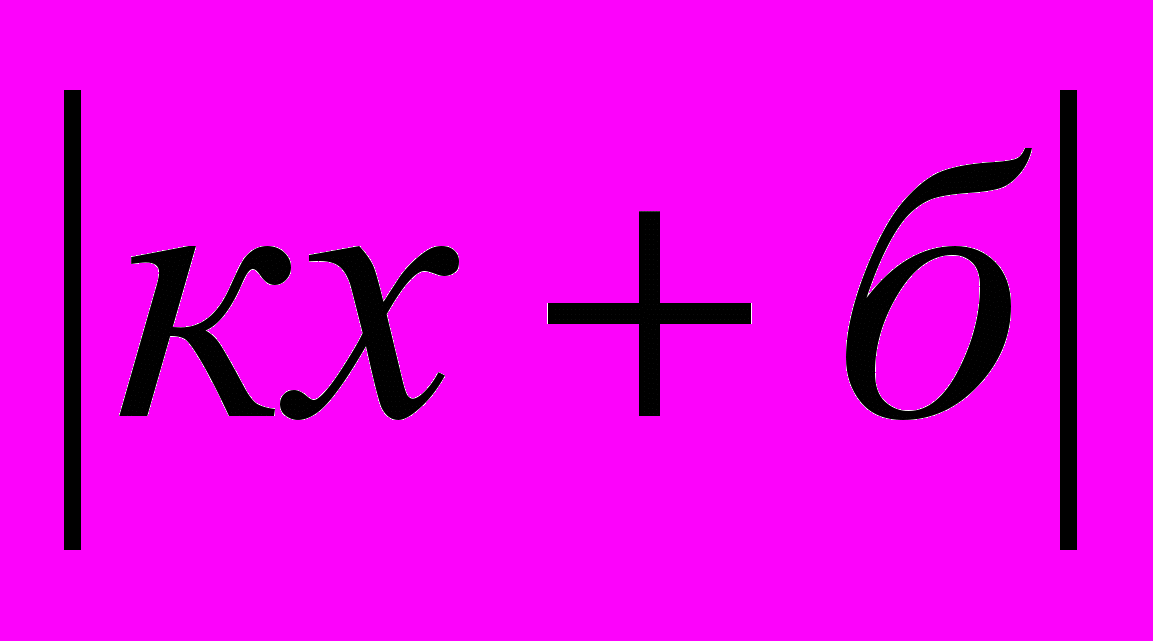а: =а; 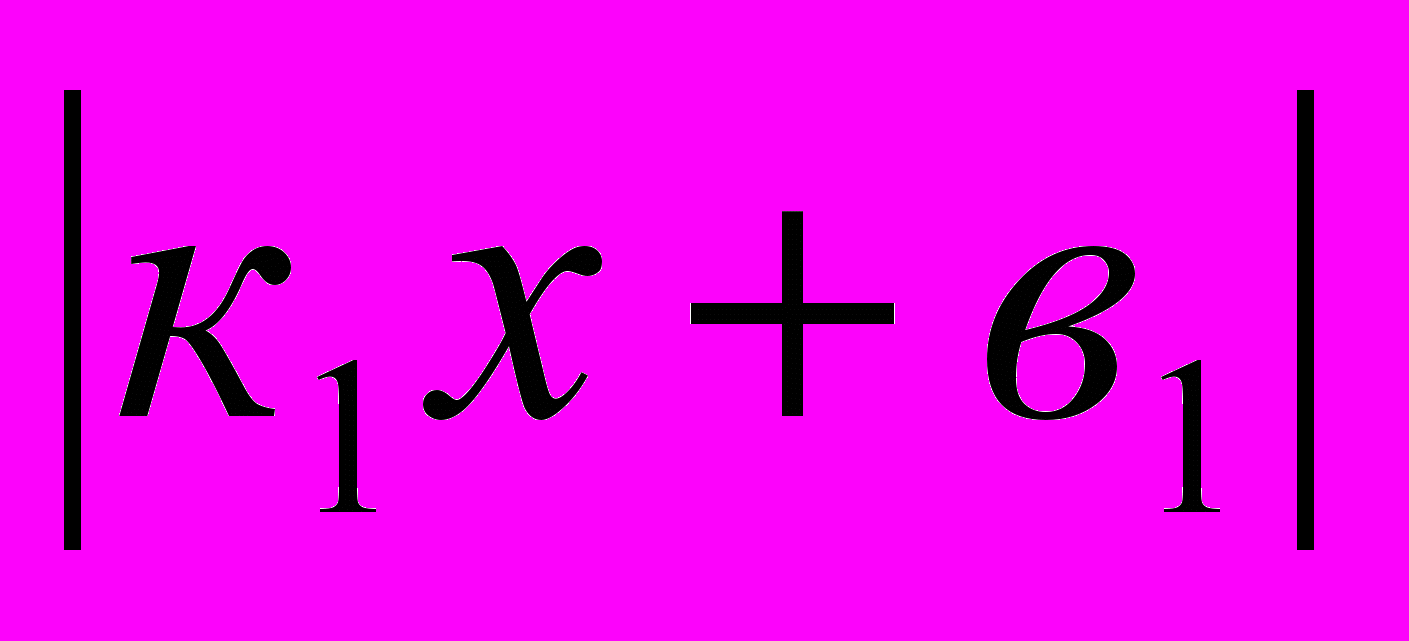=к2х+в2; 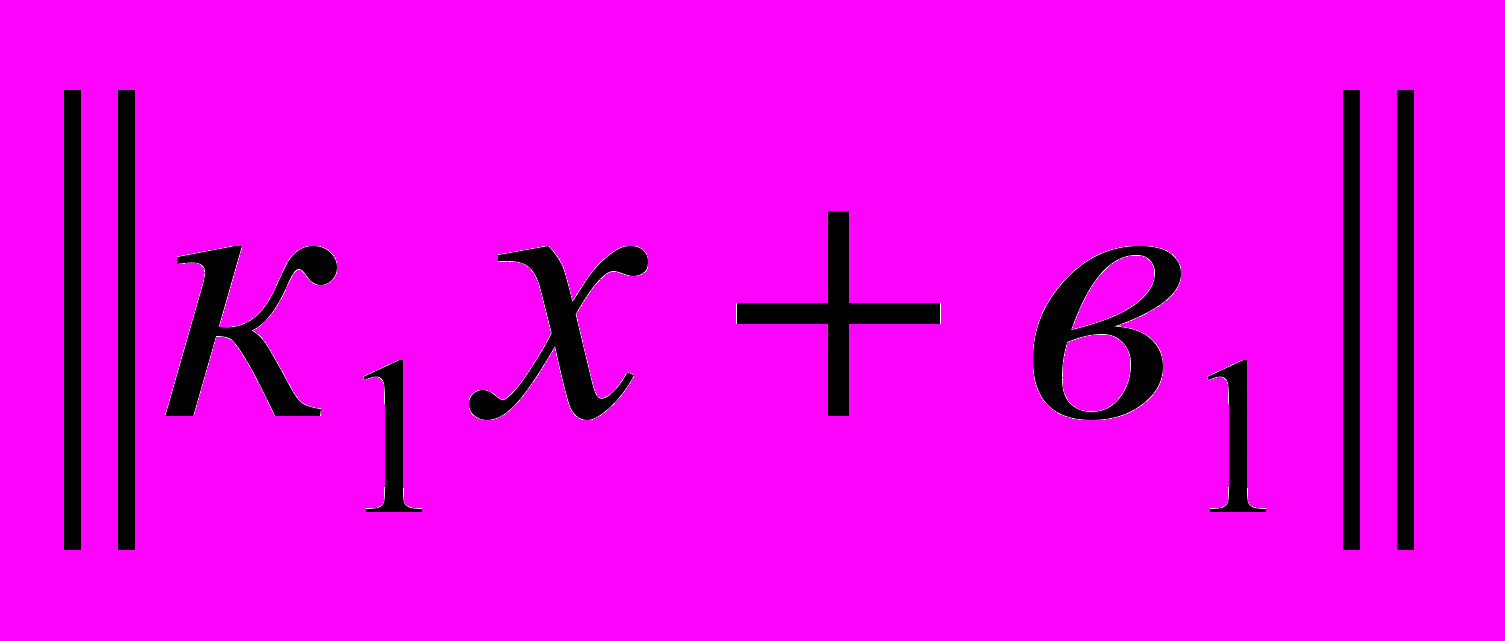= к2х+в2 ; ; ;

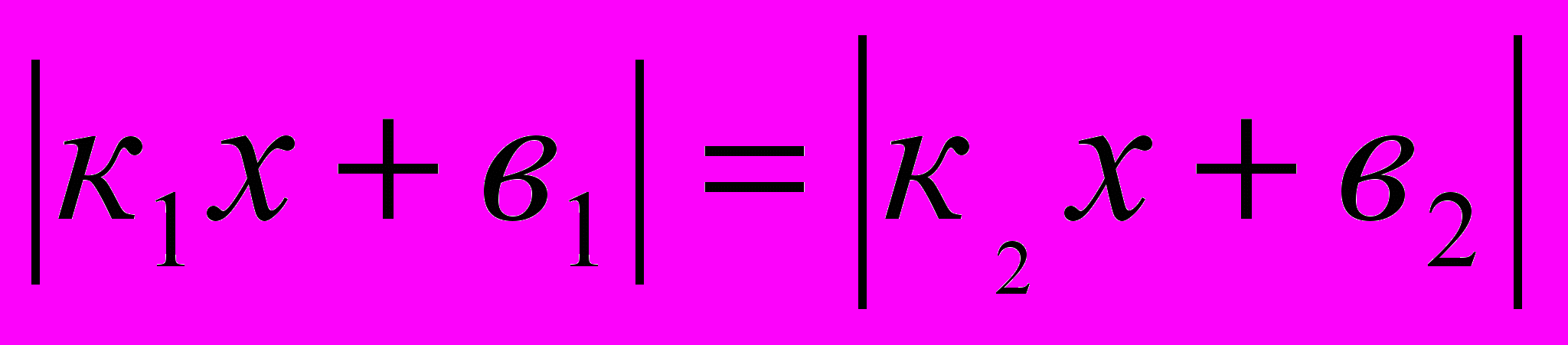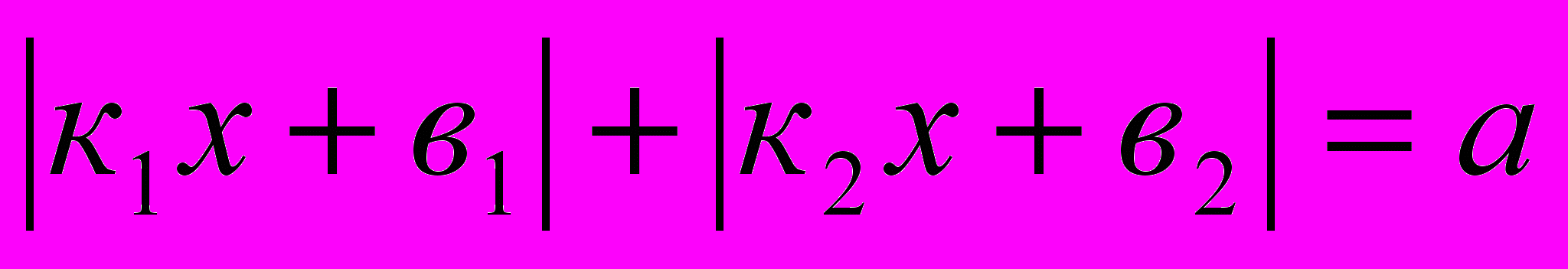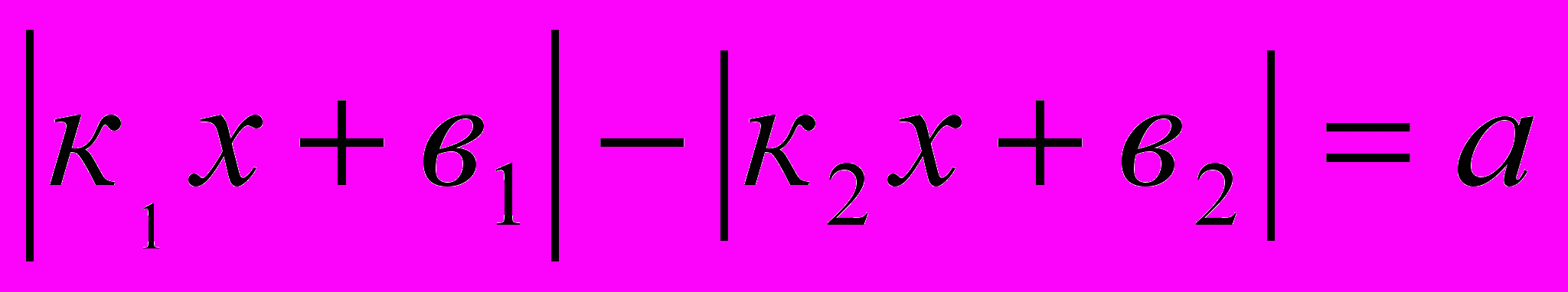
Методы обучения: объяснение, беседа, выполнение тренировочных упражнений.

Формы контроля: проверка самостоятельных заданий.

Тема 3. Решение неравенств, содержащих модуль (2ч).

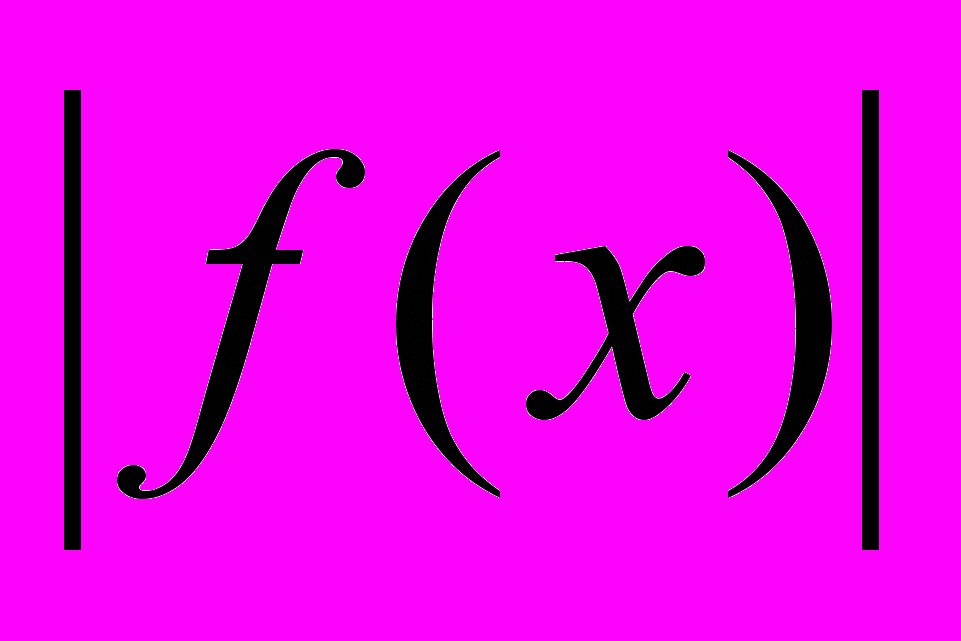
Решение неравенств вида: а; ; ; .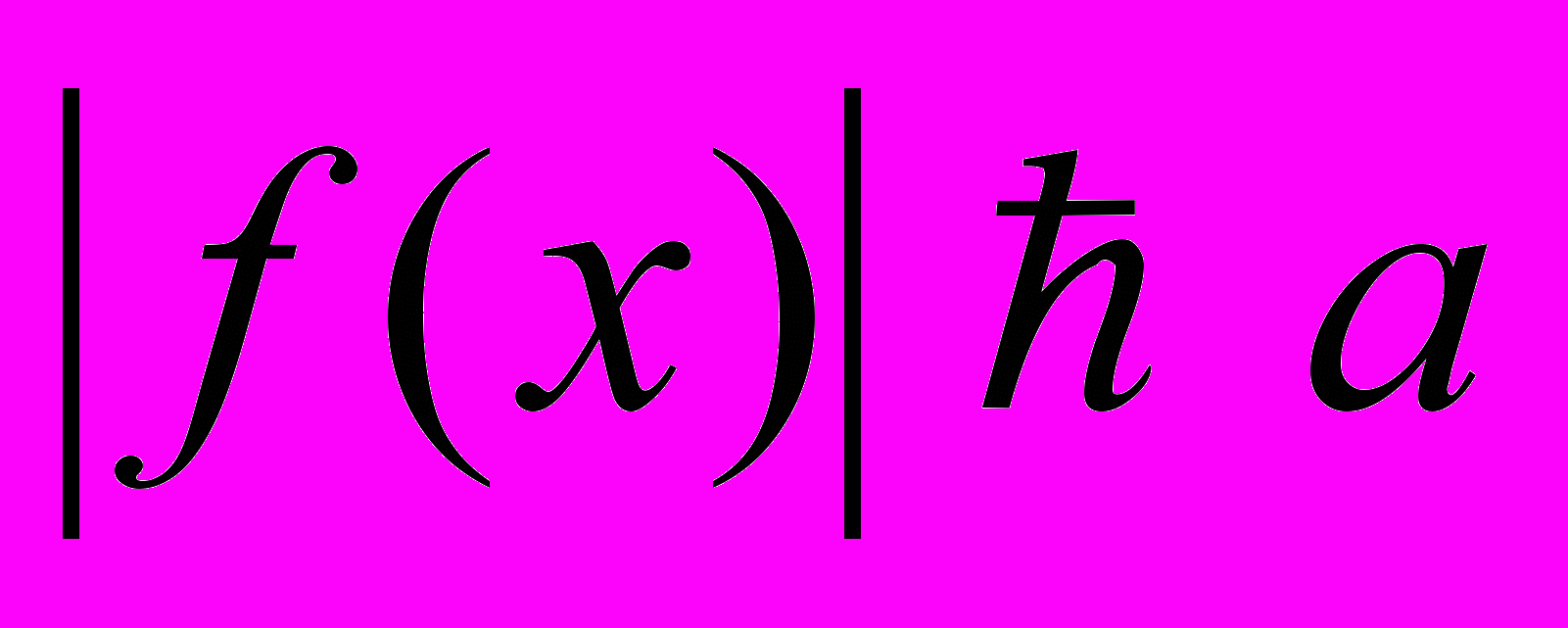

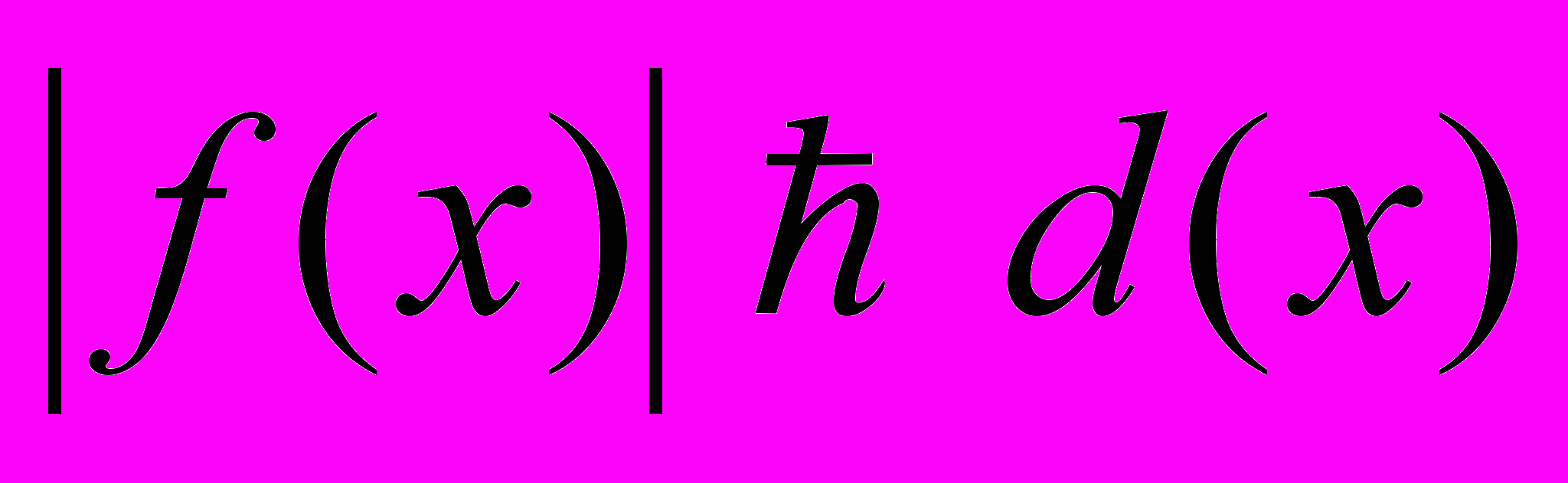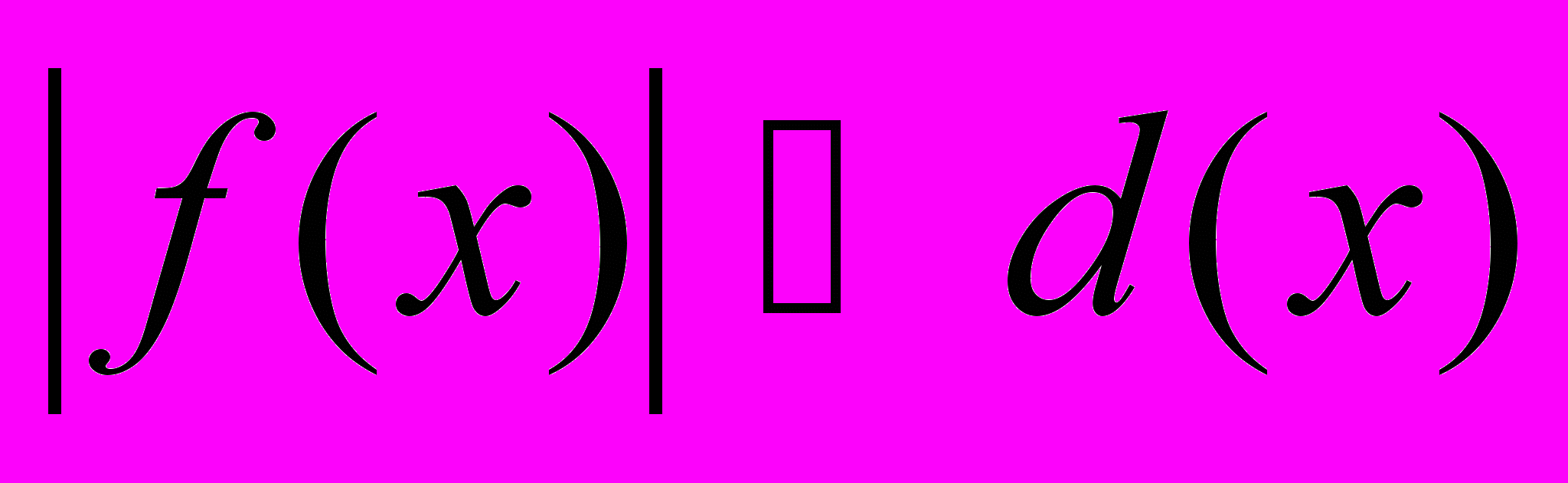Методы обучения: объяснение, беседа, выполнение тренировочных упражнений.

Формы контроля: проверка самостоятельно решенных заданий.

Тема 4. Построение графиков функций, содержащих модуль (2ч).

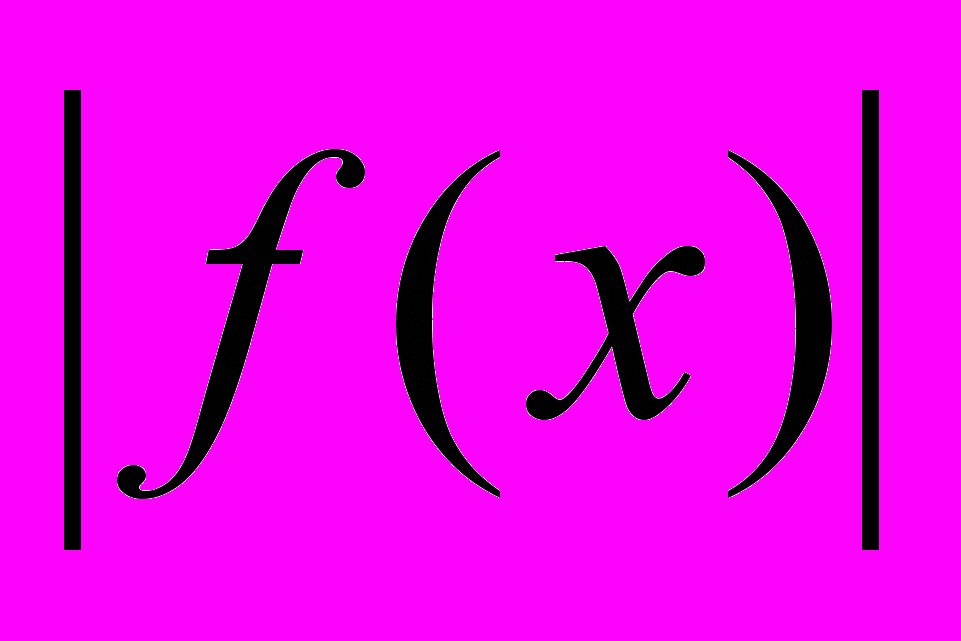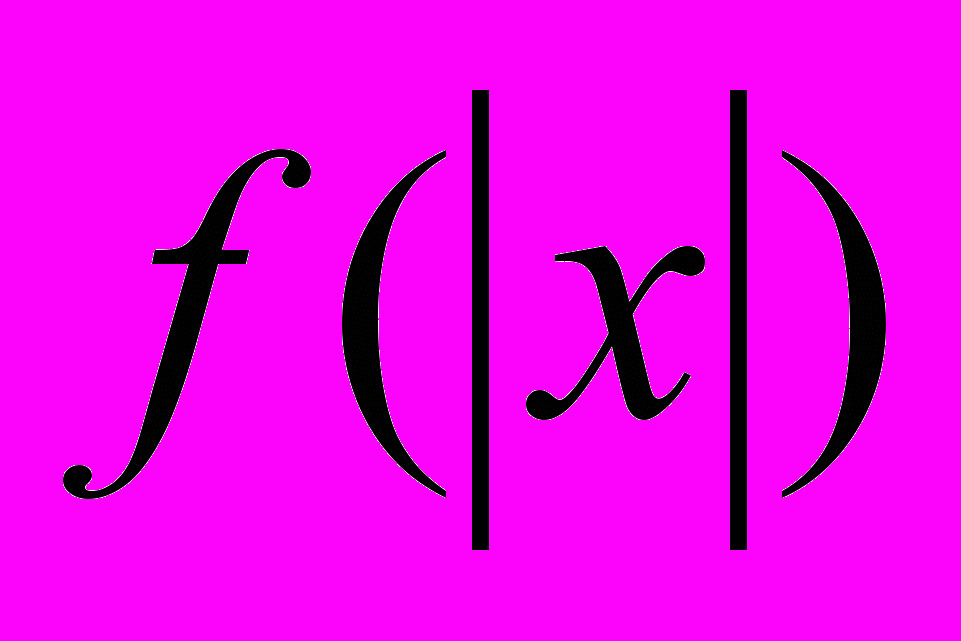Построение графиков функций: y=, y=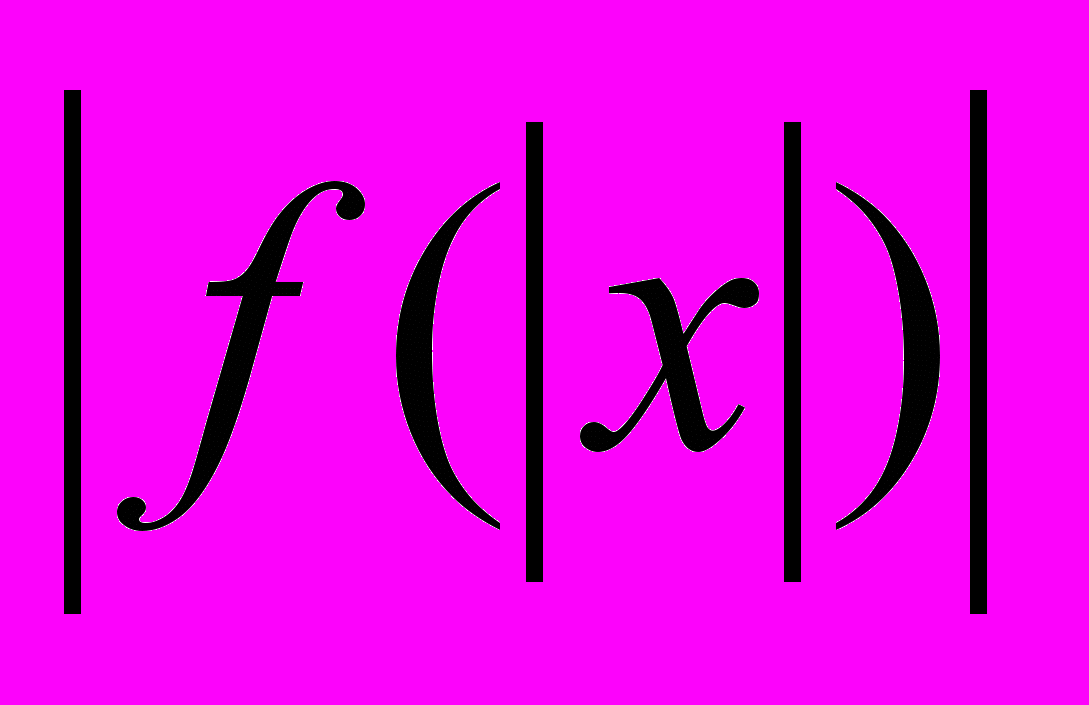, y=, y=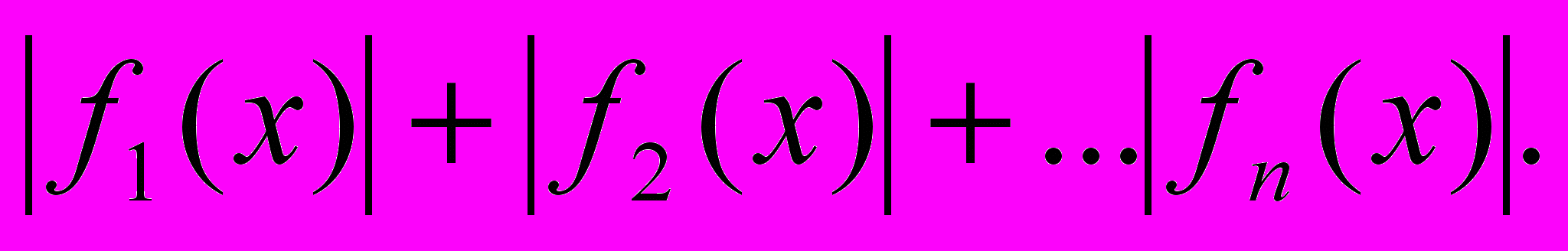

Методы обучения: объяснение, беседа, выполнение тренировочных заданий.

Формы контроля: проверка самостоятельно построенных графиков.

Тема 5. Решение рациональных уравнений и неравенств (8ч).

Решение уравнений в целых числах. Алгоритм Евклида. Теорема Безу. Решение симметрических уравнений. Решение однородных уравнений. Решение уравнений с параметром. Рациональные неравенства. Система рациональных неравенств.

Методы обучения: лекция, объяснение, беседа, выполнение тренировочных упражнений.

Формы контроля: проверка самостоятельной работы.

Тема 6. Решение логарифмических уравнений и неравенств (5ч).

Решение логарифмических уравнений, показательных уравнений, а также неравенств (из разделаС1;С2 ЕГЭ).

Методы обучения: объяснение, беседа, выполнение тренировочных упражнений.

Формы контроля: проверка самостоятельно решенных заданий.

Тема 7. Текстовые задачи (3ч).

Задачи на проценты, сплавы, смеси. Задачи на движение. Задачи на производительность, работу.

Методы обучения: объяснение, беседа, выполнение тренировочных упражнений.

Формы контроля: проверка самостоятельно решенных заданий.

Тема 8. Элементы теории вероятностей (8ч).

Случайные события. Вероятность. Теория сложения. Независимые случайные события. Формула умножения

Методы обучения: лекция, беседа, объяснение, выполнение тренировочных заданий.

Формы контроля: проверка решенных заданий в группах.

Тема 9. Тригонометрические функции (4ч).

Тригонометрические функции двойного, тройного аргумента. Тригонометрические функции половинного аргумента. Основные методы решения тригонометрических уравнений и неравенств.

Тема 10. Зачет (2ч).


Общие методические рекомендации.


Данный факультативный курс «Нестандартные задания курса алгебры и начала анализа 10 класс» дает примерный объем знаний, умений и навыков, которыми должны овладевать школьники склонные к математике. Следует отметить, что требования к знаниям и умениям не должны быть завышены. Чрезмерность требований может привести к угасанию интереса из-за перегрузки.

Особое внимание следует обратить решению рациональных уравнений и неравенств, логарифмическим уравнениям и неравенствам, показательным уравнениям и неравенствам, а также решению уравнений с параметром. Навык решения данных тем надо довести до автоматизма, так как они часто встречаются в заданиях ЕГЭ.

Домашние задания являются обязательными для всех. Активным учащимся можно давать задания творческого характера.

Самостоятельные и проверочные работы можно давать дифференцировано.

В результате изучения курса учащиеся должны уметь:

применять изученные алгоритмы для решения соответствующих заданий;

решать уравнения и неравенства, содержащие модуль;

решать уравнения и неравенства высших степеней;

строить графики элементарных функций;

решать текстовые задачи;

решать задачи на применение теории вероятностей;

применять основные методы решения тригонометрических уравнений и неравенств.


Литература для учителя:


1. Галицкий М.Л. и др. Углубленное изучение алгебры и математического анализа. М. Просвещение, 1997.-243с.


2. Карп А.П. Сборник задач по алгебре и началам анализа. М. Просвещение, 1995.-176с.


3. Сканави М.И. Сборник задач по математике «Оникс 21 век» «Мир и образование», 2003.-324с.


4. Шарыгин И. Ф. Факультативный курс математики. Решение задач. М. Просвещение, 1989.-157с.


5. Шамшин В.М. Тематические тесты для подготовки к ЕГЭ по математике. М. Феникс, 2004.-315с.


6. Рурукин А.Н. Пособие для интенсивной подготовки к выпускному, вступительному экзаменам и ЕГЭ по математике. –М.:ВАКО,2004.-248с.-(Интенсив).


Литература для учащихся:


1. Галицкий М.Л. и др. Углубленное изучение алгебры и математического анализа. М. Просвещение, 1997.-243с.


2. Карп А.П. Сборник задач по алгебре и началам анализа. М. Просвещение, 1995.-176с.


3. Сканави М.И. Сборник задач по математике «Оникс 21 век» «Мир и образование», 2003.-324с.


4. Шарыгин И. Ф. Факультативный курс математики. Решение задач. М. Просвещение, 1989.-157с.


5. Шамшин В.М. Тематические тесты для подготовки к ЕГЭ по математике. М. Феникс, 2004.-315с.


6. Рурукин А.Н. Пособие для интенсивной подготовки к выпускному, вступительному экзаменам и ЕГЭ по математике. –М.:ВАКО,2004.-248с.-(Интенсив).