Специальная (частная) методика алгебры, алгебры и начал анализа

Вид материала

Образовательный стандарт

Содержание Q+, то есть раскрываем вторую методическую задачу – показать целесообразность изучения операций на множестве Q Таблица Вопросы для самопроверки Тема 1. Тождественные преобразования в курсе математики средней школы.

Подобный материал:

• «Формирование понимания практической значимости алгебры и начал анализа учащихся, 133.22kb.
• Некоммутативная геометрия, 36.84kb.
• Примерное поурочное планирование общеобразовательного курса алгебры и начал анализа, 77.08kb.
• Тематическое планирование уроков алгебры и начал анализа 10 класс, 279.38kb.
• Рабочая программа «Практикум по алгебре» в 10 а классе, 70.39kb.
• Реферат по теме «Зарождение современных компьютерных роботов.», 91.85kb.
• Функции алгебры логики, 47.25kb.
• Программа школы-конференции «алгебры ли, алгебраические группы и теория, 53.74kb.
• Урок алгебры и начал анализа в 11 классе. Тема: «Первообразная и интеграл», 73.08kb.
• Султанов Адгам Яхиевич кандидат физ мат наук, доцент, отличник народного образования,, 70.81kb.

Раздел. Специальная (частная) методика алгебры, алгебры и начал анализа


Государственный образовательный стандарт полной средней школы определяет основные задачи курса алгебры (7-9 класс) и курса алгебры и начал анализа (10-11 класс):

«1. развитие представлений о числе и роли вычислений в практике; формирование практических навыков вычислений и вычислительной культуры;

2. формирование формально-оперативных алгебраических умений и применение их к решению математических и внематематических задач;
   
3. изучение элементарных функций и использование графических представлений для описания и анализа реальных зависимостей;
   
4. ознакомление с элементами дифференциального и интегрального исчисления как аппаратом исследования функций и решения прикладных задач;
   
5. формирование представлений обучаемых понятиях и методах как важнейших средств математического моделирования реальных процессов и явлений, о математике как элементе человеческой культуры, о ее применении в практике и научном познании;
   
6. развитие интеллектуальных и речевых умений».
   

При любом изменении содержания школьного математического образования в нем должно оставаться «ядро» из тех тем, без которых учащиеся не смогут получить представление о математике и ее методах. Совокупность таких тем составляет содержательно-методических линий школьного курса математики. Эти темы также выделяются стандартом математического образования.

В курсе алгебры, алгебры и начал анализа к ним относятся: «Числа и вычисления», «Выражения и их преобразования», «Уравнения и неравенства», «Функции».

Эти темы остаются неизменными а «изменяются» темы так называемой стохастической линии. Они могут вводится в содержание школьного курса или исключаться из нее. Это зависит от потребностей и динамично меняющихся условий современного общества.

Исходя из выше сказанного, в курсе лекций по теории и методике обучения математике раскрываются именно основные содержательные линии школьного курса математики.

Содержание выделенных линий курса невозможно изучить в пределах одного класса, одной темы, так как их изучение должно пройти несколько этапов:

• пропедевтический;
  
• изучение основного содержания;
  
• углубление, обобщение и систематизация изученного.
  

При чтении лекций по основным содержательным линиям реализуется схема:

1. проводится логико-математический анализ изучаемого материала;
   
2. определяется место данного математического содержания в школьной программе и учебниках;
   
3. определяются цели и задачи каждой содержательной линии;
   
4. выделяются основные типы математических задач и обобщенные приемы их решения;
   
5. рассматриваются методы и приемы обучения, которые можно использовать для изучения отдельных тем или разделов данной содержательно-методической линии.
   

Рабочая программа включает следующие лекции:

Лекция 1-2. Развитие понятия числа в школьном курсе математики.

Лекция 3-4. Линия уравнений и неравенств в школьном курсе математики.

Лекция 5-6. Функциональная линия в курсе математики основной школы.

Лекция 7. Функциональная линия в курсе средней школы: изучение тригонометрических функций, показательной, логарифмической и степенной функций.

Лекция 8. Изучение предела и непрерывности функции в точке в школьном курсе.

Лекция 9-10. Методика изучения производной и ее приложений в курсе алгебры и начал анализа.

Лекция 11-12. Интеграл и его приложения в школьном курсе.

Часть вопросов предлагается для самостоятельного изучения, а именно:

1. Тождественные преобразования выражений.
   
2. Тригонометрические функции и методика их изучения.
   

Лекция 1-2. Развитие понятия числа в школьном курсе математики.

План лекции:

1. Изучение числовых систем в школьном курсе математики, место темы в программе.
   
2. Методика изучения натуральных и дробных чисел.
   
3. Методика изучения рациональных чисел.
   
4. Некоторые вопросы изучения действительных чисел в курсе средней школы.
   

Содержание лекции

1. Дается краткий логико-математический анализ линии числа в школьном курсе. Особое внимание уделено сравнению последовательностей расширения понятия числа в научных курсах и в историческом аспекте. Исходя из целей изучения числовых систем в школьном курсе обосновывается использование одной из последовательностей в школе расширения понятия числа. Далее подробно анализируется программа с 1 по 11 классы. На примерах изучения конкретных числовых множеств показываются два пути введения нового числового множества.
   

Вводится общая методическая схема, используемая на любом этапе расширения понятия числа и показываются основные условия, влияющие на ее использование на разных возрастных этапах.

2. Рассмотрение второго вопроса начинается с обзора знаний, умений и навыков с которыми в 5 класс приходят ученики после начальной школы. Затем выделяются сведения из раздела «Натуральные числа», которые необходимо переосмыслить и обобщить в курсе 5 класса и более подробно рассматривается методика изучения вопросов «новых» для учащихся, относящихся к теме «Делимость натуральных чисел, а именно понятий делителя и кратного числа, НОК, НОД, признаков делимости чисел. Уделяется внимание практическим приложениям изучаемых вопросов. Заканчивая с учениками изучение натуральных чисел, учитель должен до четкого их понимания довести тот факт, что на множестве натуральных чисел (N) всегда выполнимы операции сравнения, сложения и умножения и они подчиняются определенным законам.
   

В курсе 5 класса ученики встречаются с первым расширением понятия числа. Следуя исторической схеме, множество натуральных чисел расширяется до множества положительных рациональных чисел, то есть появляются дробные числа (для краткости – дроби).

Необходимо показать студентам, что в пропедевтическом плане знакомство с дробными числами произошло в начальной школе. Выделяются же сведения о дробях, которые им известны.

Далее, используя метод целесообразных задач, решается одна методическая задача – показывается целесообразность расширения множества натуральных чисел. В отличии от начальной школы этот процесс связывается с невозможностью решения уравнения типа (или невыполнимостью операции деления) на множестве натуральных чисел.

Затем рассматриваются возможные последовательности изучения обыкновенных и десятичных дробей, анализируются школьные учебники.

После введения понятия дробного числа переходим к методике изучения операций на множестве ^ Q₊, то есть раскрываем вторую методическую задачу – показать целесообразность изучения операций на множестве Q₊ и ввести их. С введением операций сложения, вычитания, умножения и деления связано и изучение законов арифметических действий.

3. Рассмотрение третьего вопроса лекций начинается с введения отрицательного числа. Целесообразность его введения можно показать двумя путями: формально-логическим (связать с невыполнимостью операции вычитания на множестве N) или реально-конкретным (рассматриваются величины, изменение которых проходит в двух противоположных направлениях.
   

Методика обучения – метод целесообразных задач. Затем показывается методика изучения операций на множестве Q и рассматриваются все законы арифметических действий.

4. Изучение множества действительных чисел начинается в курсе 8 класса с повторения всех сведений о рациональных числах, затем рассматривают две задачи: задачу, связанную с извлечением квадратного корня (х²=а), или задачу, связанную с измерением отрезков, выделяя случай несоизмеримости длины отрезка с выбранной единицей измерения. Эти задачи приводят к появлению иррационального числа.
   

Далее отмечается, что строгая теория действительного числа в школьном курсе недоступна учащимся, поэтому изложение материала идет индуктивно, опираясь на предшествующие знания.

Заканчивая, среднюю школу, ученик должен уметь охарактеризовать известные ему числовые множества:

N – бесконечное упорядоченное, дискретное с начальным элементом и без конечного элемента. Замкнутое относительно операций сложения и умножения;

Z – бесконечное, упорядоченное, дискретное, без начального и конечного элементов. Замкнутое относительно операций сложения, вычитания, умножения;

Q – бесконечное, упорядоченное, без начального и конечного элементов, всюду плотное. Замкнутое относительно операций сложения, вычитания, умножения, деления;

R - бесконечное, упорядоченное, без начального и конечного элементов, плотное, непрерывное.

Закончить лекцию необходимо краткими сведениями об изучении комплексных чисел.

Вопросы для самопроверки:

1. Что вы понимаете под расширением понятия числа?
   
2. Цели изучения чисел и вычислений в школьном курсе?
   
3. Распределение материала по классам. В чем различие в учебниках разных авторов?
   
4. В чем суть основных методических задач на каждом этапе расширения понятия числа?
   
5. Перечислите сведения известные учащимся из курса начальной школы о числах и операциях над ними.
   
6. В чем заключается преемственность в методике изучения натуральных и дробных чисел между начальной школой и 5-6 классами?
   
7. Что вы можете сказать о порядке изучения обыкновенных и десятичных дробей?
   
8. Охарактеризуйте 2 подхода к введению отрицательного числа.
   
9. В чем заключается суть метода целесообразных задач? Показать его реализацию на примере введения любой операции на множестве целых чисел.
   
10. Основные подходы к введению иррационального числа?
    
11. Почему в школьном курсе нельзя дать строгую теорию действительного числа?
    
12. Где, когда и как в школьном курсе проходит знакомство с комплексными числами?
    

Лекция 3-4. Линия уравнений и неравенств в школьном курсе математики.

План лекции:

1. Цели изучения уравнений и неравенств в школьном курсе. Место темы в программе.
   
2. Логико-математический анализ основного понятийного аппарата темы. Различные трактовки понятия уравнения и неравенства в школьных учебниках.
   
3. Основные этапы в изучении уравнений и неравенств.
   
4. Методика изучения уравнений и неравенств в 5-6 классах.
   
5. Методика изучения уравнений, неравенств и их систем в 7-9 классах.
   
6. Изучения вопросов равносильности уравнений, неравенств и их систем в школьном курсе математики.
   
7. Изучение уравнений, неравенств и их систем в старших классах (обзор материала).
   
8. Решение текстовых задач в курсе алгебры 7-9 классов (самостоятельное изучение по книге «Методика преподавания математики в средней школе. Частные методики. /Составитель Мишин В.И.: М.: Просвещение, 1987 г. Стр. 137-151)
   

Содержание лекции:

1. Материал линии уравнений и неравенств составляет значительную часть школьного курса математики. Это определяет и цели их изучения:
   

1. через них проходит ознакомление учащихся с основами наук;
   
2. их решение способствует развитию логического мышления, формирует и закрепляет вычислительные навыки;
   
3. они находят широкое применение при изучении многих тем школьного курса математики;
   
4. они позволяют реализовать межпредметные связи;
   
5. уравнения и неравенства позволяют закрепить, углубить и повторить пройденный материал. Используются при решении практических задач.
   

В изучении линии уравнений и неравенств можно выделить три основных направления ее развертывания в школьном курсе математики:

1. прикладная направленность – раскрывается при изучении алгебраического метода решения текстовых задач.
   
2. теоретико-математическая – раскрывается в двух аспектах:
   

а) в изучении наиболее важных классов уравнений, неравенств и их систем,

б) в изучении обобщенных приемов и методов решений.

Распределение изучения по классам определяется тематическим планированием и выбранным учебником.

2. Основной понятийный аппарат этой содержательной линии: понятие уравнения, неравенства, равносильность уравнений и неравенств, определение частных видов уравнений и неравенств.
   

Далее рассматриваются различные трактовки понятия уравнения и неравенства в научных курсах и как это влияло и влияет на их определения в школьных учебниках. Дается краткая историческая справка и останавливаемся на трактовке основных понятий в действующих учебниках.

3. Подробно изложены основные направления в изучении уравнений и неравенств на этапах:
   

1. пропедевтическом (начальная школа и курс математики 5-6 классов),
   
2. основном (курс алгебры 7-9 классов),
   
3. завершающем (курс алгебры и начал анализа 10-11 классов).
   

Выделяются типы уравнений и неравенств на каждом этапе, показывается на какие теоретические сведения опираются на каждом из этих этапов.

4. Начинаем с повторения сведений из курса начальной школы, затем, используя игровые ситуации, метод целесообразных задач, подводим к определению понятия уравнения и соответствующих понятий. По мере появления отрицательных чисел в неявном виде начинаем использовать равносильные преобразования при решении уравнений. Решаются линейные уравнения с одной переменной.
   
5. На основном этапе вводятся соответствующие термины: линейное уравнение с одной переменной, с двумя переменными и их системы. Рассматриваются приемы по созданию проблемных ситуаций на уроках при введении квадратных уравнений, рациональных уравнений, дробно-рациональных уравнений. По аналогии рассматриваются решение неравенств, начиная с 8 класса. Как итог рассматриваются суть алгебраического метода решения уравнений и неравенств и графического метода. При первом подходе, равносильные преобразования уравнений и неравенств к простейшим можно разделить на две группы:
   

1. общие для всех видов уравнений и неравенств – следствия из теорем о равносильности,
   
2. специальные, основанные на свойствах функций f(х) и g(х), если уравнение записано как f(х) = g(х).
   

Следовательно необходимо рассмотреть вопросы равносильности уравнений и неравенств.

6. К рассмотрению понятий равносильности уравнений и неравенств и их систем подходим по разному. Это зависит от определений уравнений и неравенств в школьном курсе. Если уравнение определялось как предложение с переменной, то и равносильность так же определялась через это родовое понятие. В действующих учебниках уравнения называются равносильными, если они имеют одни и те же корни (аналогично неравенства). Далее формулируются три основных теоремы, позволяющие перейти от уравнения к равносильному и показывается как их смысл в школьных учебниках раскрывается через свойства равенств и неравенств. Используются конкретно-индуктивный путь изучения многих вопросов и метод целесообразных задач. Функциональный подход к обоснованию решения уравнений и неравенств рассматривается в 10-11 классах при решении иррациональных, показательных, логарифмических и тригонометрических уравнений.
   
7. В этой лекции более подробно рассматривается методика изучения иррациональных уравнений и их систем, даются основные методы решения. Подробнее останавливаются на решении уравнений степени выше второй, отрабатываются метод интегралов. Изучение показательных, логарифмических и тригонометрических уравнений и неравенств более подробно рассматривается при изучении соответствующих функций. Закончить лекцию можно таблицей классификации уравнений и неравенств в связи с классификацией выражений и классификацией функций.
   

^ Таблица




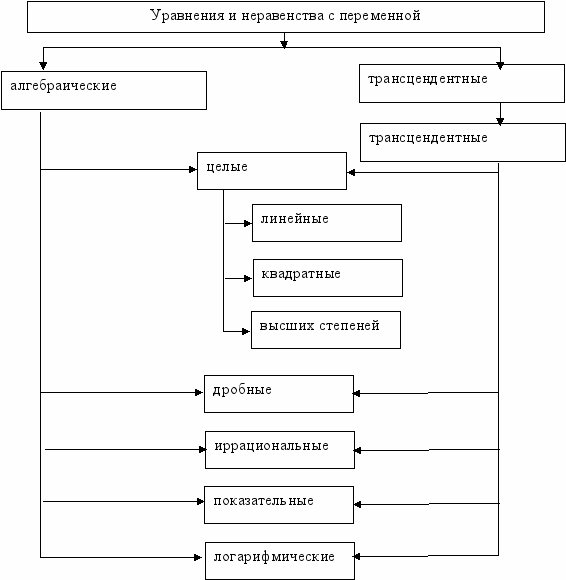
Вопросы для самопроверки:

1. Раскрыть цели изучения уравнений и неравенств в средней школе.
   
2. Что влияло на подходы в определении уравнений и неравенств в школьных учебниках?
   
3. Какие этапы можно выделить в изучении уравнений и неравенств?
   
4. Что лежит в основе решения уравнений в начальной школе и в 5 классе? В 6 классе?
   
5. Как определяется понятие уравнения в 5 классе и в 7 классе?
   
6. Какие виды уравнений изучаются в алгебре 7-9 классов? В 10-11 классах?
   
7. Что общего в методике изучения линейных уравнений и квадратных уравнений.
   
8. Перечислите свойства числовых неравенств, изучаемых в 8 классе?
   
9. Как можно создать проблемную ситуацию при введении способа решения линейного уравнения с двумя переменными?
   
10. Какие способы решения систем уравнений изучаются в школе?
    
11. Какие подходы Вы можете изложить при рассмотрении равносильности уравнений и неравенств в 5-9 классах и в 10-11 классах?
    
12. Почему метод интервалов изучается после изучения квадратичной функции?
    
13. В чем отличие графического способа решения неравенств от графической иллюстрации решения неравенств и их систем?
    
14. Что лежит в основе решения дробно-рациональных уравнений в школе?
    
15. Почему решение показательных, логарифмических и тригонометрических уравнений и неравенств в основном рассматривают в 10-11 классах?
    

Лекция 5-6. Функциональная линия в курсе математики основной школы.

План лекции:

1. Логико-математический анализ функциональной линии.
   
2. Место функций в программе. Этапы в изучении функций в средней школе.
   
3. Функциональная пропедевтика в 5-6 классах.
   
4. Методика введения понятия функций в 7 классе. Область определения и область значения функций.
   
5. Изучение элементарных функций: линейной, квадратичной, степенной в 7-9 классах.
   

Содержание лекции:

1. Основным понятием функциональной линии является понятие функции, которое Ф. Клейн считал центральным понятием всей математики. Затем остановиться на различных подходах к определению функции и связать их с «изменением» этого определения в курсе математики средней школы. С понятием функции связана система понятий: область определения, область значения, графика функции и других. Уже к XVII веку были достаточно хорошо изучены так называемые элементарные функции – класс функций, включающий в себя многочлены и рациональные функции, показательные, логарифмические и тригонометрические функции.
   

Их изучением и занимаются в школьном курсе математики.

2. Охарактеризовать цели изучения функций в школе. Выделяют следующие этапы в изучении функций:
   

1. пропедевтический (5-6 классы),
   
2. основной – изучения понятия функции и изучение элементарных функций, когда исследование проводится элементарными средствами (7-10 классы),
   
3. завершающий – исследование функций проводится с помощью производной (10-11 классы).
   

Распределение по классам дает тематическое планирование программы и соответствующий учебник, выбранный учителем.

3. Подготовительная работа на первом этапе заключается в рассмотрении зависимостей величин и результатов действий от изменения компонентов. Этот материал входит во все темы 5-6 классов, где рассматриваются выражения, содержащие буквы.
   

Рассматривается прямоугольная система координат, координаты точки, примеры графиков.

4. В курсе 7 класса вводят через систему целесообразных задач основной понятийный аппарат и способы задания функций. В 8 и 9 классах при рассмотрении конкретных функций вводят понятия, связанные с исследованием функции: возрастание, убывание и так далее. В курсе 9 класса, а затем в 10 классе уточняется понятие числовой функции.
   
5. Изучение линейной функции у=кх+b и функции у=х² проходит по единому плану: рассматриваются конкретные задачи, подводящие к функциональной зависимости, выраженной определенной формулой (мотивация) и вводят определение. По точкам строят график этой функции и из графика получают свойства функции. Заканчивается изучение решением практических задач на применение свойств изучаемой функции. Подробно остановиться на изучении функции у=кх+b, затем рассмотреть частный случай у=кх+b и сравнивая зависимости у=кх+b и 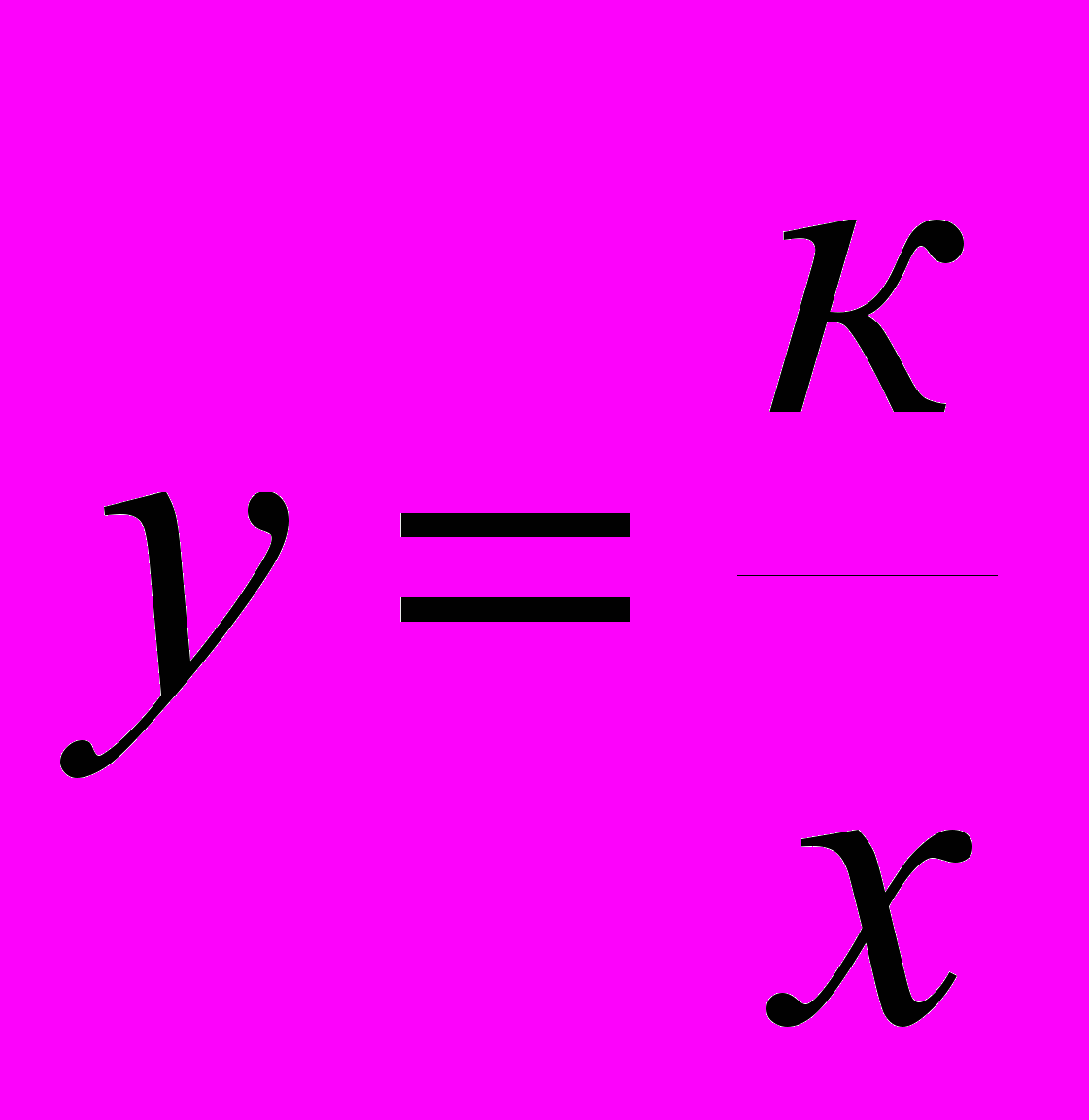рассмотреть функцию .
   

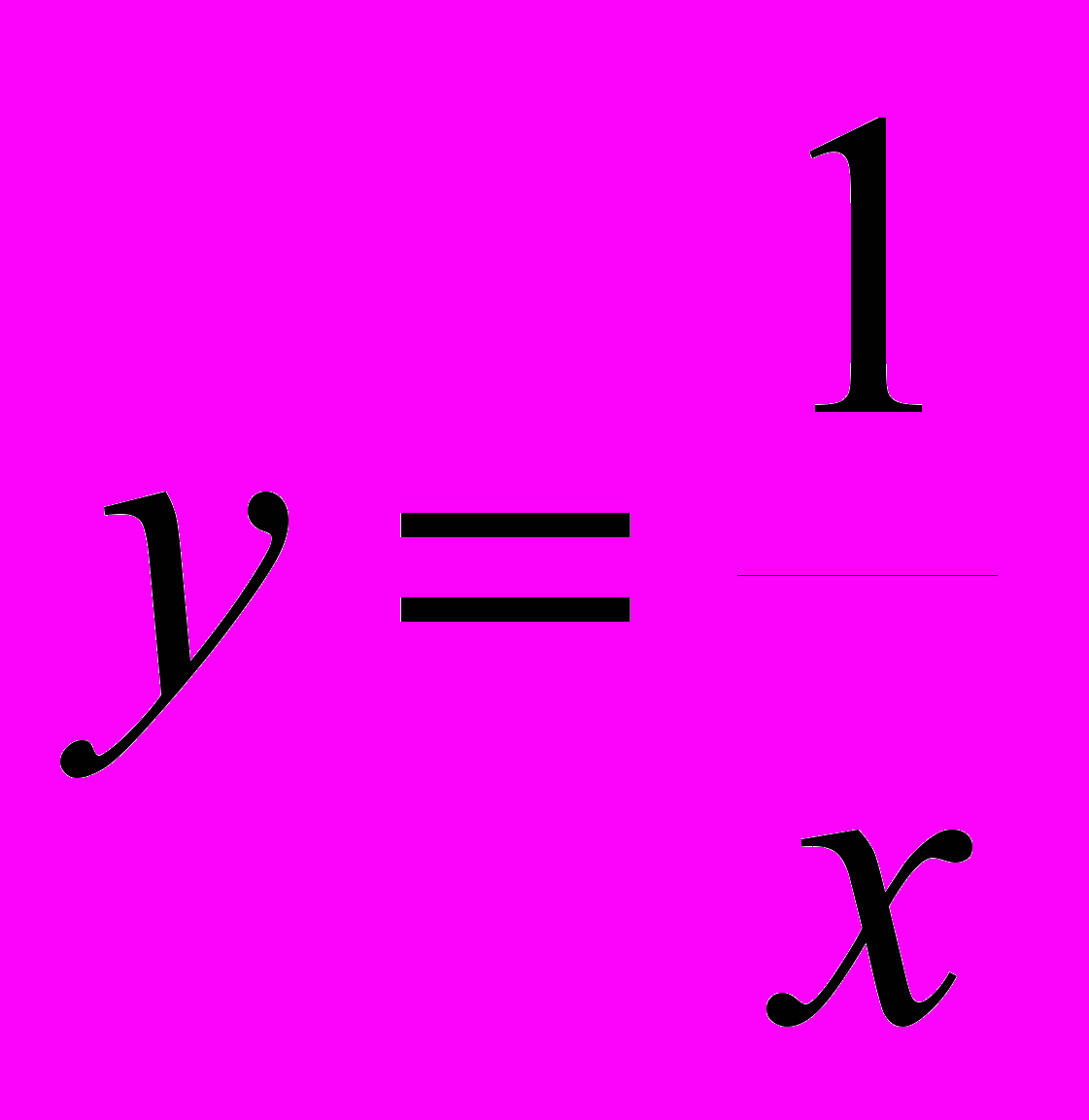По аналогии на практическом занятии рассмотреть изучение функций у=ах².

6. Функцию ().
   

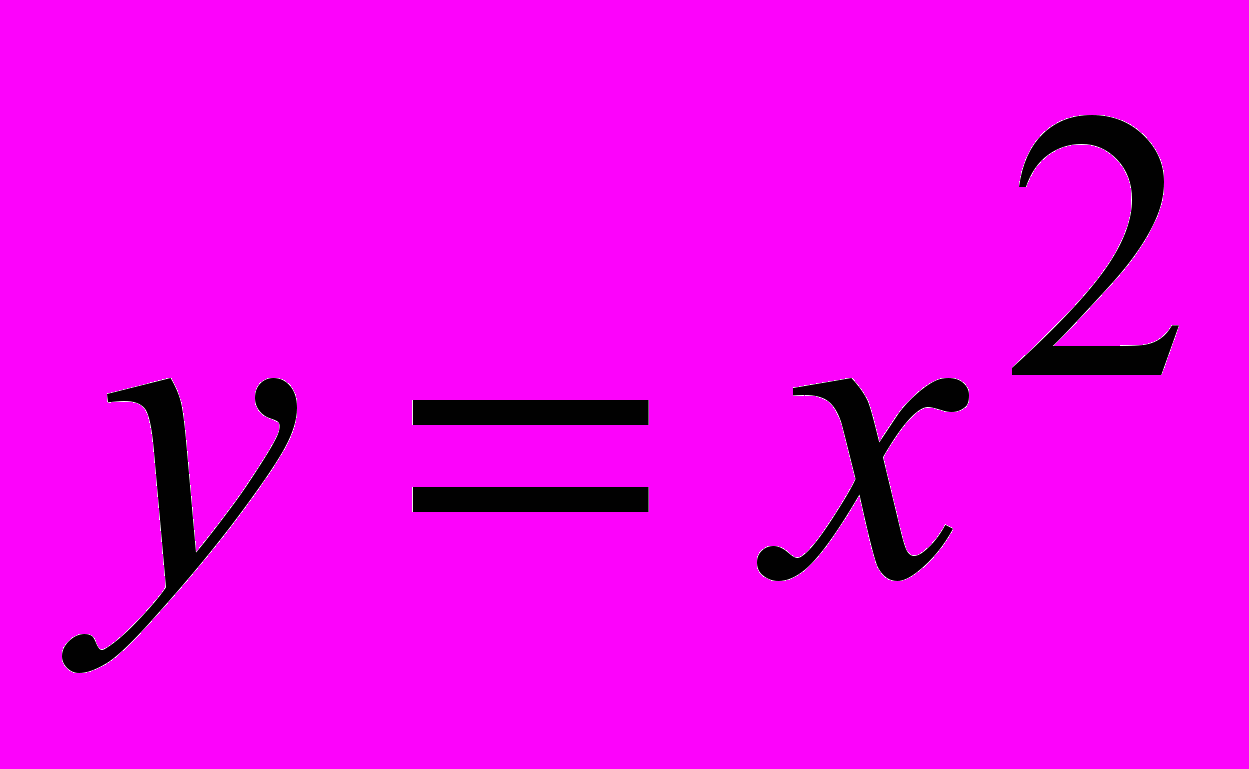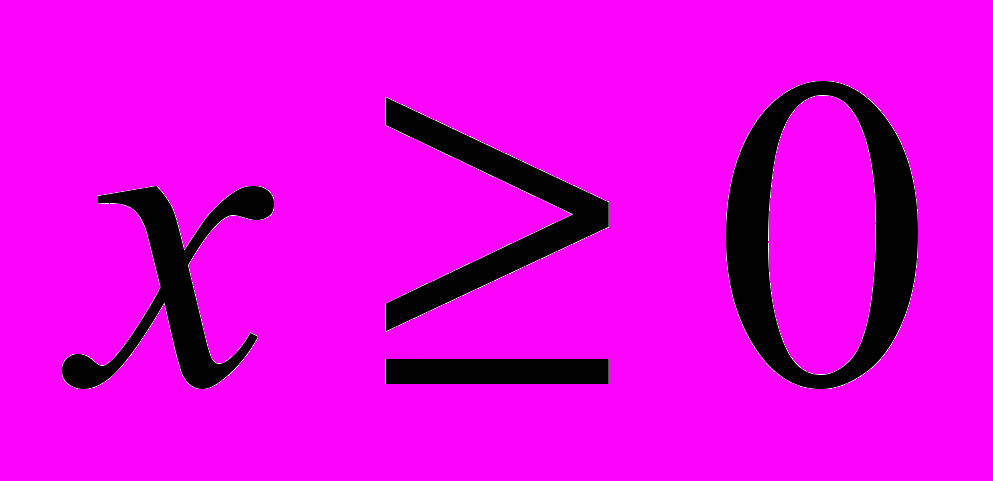В курсе 9 класса обобщаются все сведения об изученных функциях, дается, через их рассмотрение, схема исследования функции элементарными способами.

Изучение показательных, логарифмических и тригонометрических функций отнесено к курсу «Алгебры и начал анализа». Этому посвящены следующие лекции.

Вопросы для самопроверки:

1. Перечислите цели изучения функций в средней школе?
   
2. В чем сходство и различие в «традиционном» и «современном» подходе к понятию функции?
   
3. Какие видоизменения претерпело понятие функции в школе? Дайте определение функции в школе? Дайте определение этого понятия в действующих учебниках.
   
4. Охарактеризуйте три основных этапа в изучении функций.
   
5. Что общего в подходе к изучению функций 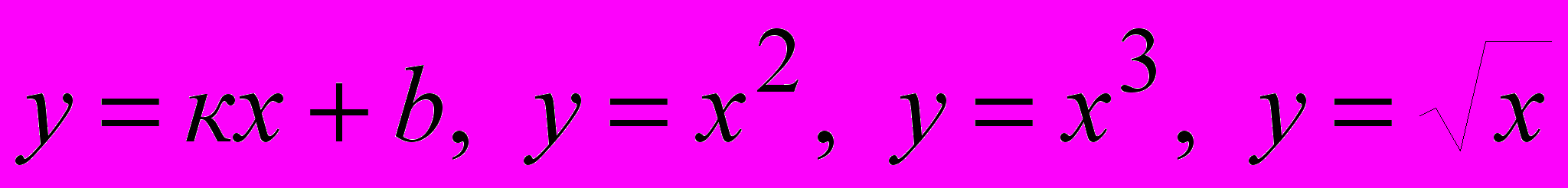в основной школе?
   
6. Почему курс алгебры 9 класса можно считать одним из значимых этапов в изучении функций?
   
7. Почему функциональная линия в школьном курсе «связывает», объединяет другие основные линии школьного курса?
   
8. В чем заключается необходимость III этапа в изучении функций?
   
9. Какие функции изучаются в курсе алгебры и начал анализа?
   
10. В чем Вы видите реализацию межпредметных связей при изучении функций?
    

Лекция 7. Методика изучения показательной и логарифмической функции.

План.

1. Роль и место показательной и логарифмической функции в школьном курсе.
   
2. Различные подходы к изучению показательной функции.
   
3. Методика изучения логарифмической функции.
   
4. Решение показательных и логарифмических уравнений и неравенств и их систем в школьном курсе.
   

Содержание лекции

1. В последнее время школьный курс алгебры и начал анализа обычно завершается главой «Показательная и логарифмическая функции».
   

Основная цель ее изучения – привести в систему и обобщить сведения о степени, ознакомить с показательной, логарифмической и степенной функциями и их свойствами; научить решать несложные показательные и логарифмические уравнения и их системы. Одной из важнейших задач курса математики старших классов является развитие и в некотором смысле завершение всех основных линий, составляющих основу школьного математического образования, в том числе систематизация и углубление знаний о функции. В этом аспекте и следует рассматривать изучение показательной и логарифмической функций в 11 классе.

На примере показательной функции можно развить представление о функциях как о модели процессов и закономерных связей явлений.

Изучение показательной функции происходит в 11 классе (пропедевтика – изучение геометрической прогрессии, функция у=2^х ), когда учащиеся владеют значительно большим аппаратом исследования функций, чем при первом знакомстве. Это дает возможность развивать формально-оперативные навыки.

При изучении темы создаются благоприятные условия для работы над повышением логической грамотности. Определенные сложности возникают при изучении логарифмической функции без пропедевтики.

2. В методической литературе можно выделить следующие подходы к введению показательной функции:
   

1 подход: В этом варианте изложения, внимание учащихся обращается на то, что функция может быть задана перечислением характеристических свойств. Для учащихся он непривычен, так как обычно все функции задавались обычно «оперативно», указывались операции, которые нужно было провести над значением аргумента, чтобы получить соответствующее значение функции. То есть обычно идут от правила вычисления значений функций по заданному значению аргумента к свойствам этой функции. При изучении показательной функции появляется возможность показать обратную связь: свойства функции могут определять способ вычисления ее значений.

При 2 подходе к определению показательной функции акцентируется внимание учащихся на понятии функции как математической модели различных явлений. В отличии от процессов, описываемых линейной функцией, в которых за равные промежутки времени значение переменной величины изменяется на одно и то же число, существует другой класс явлений, у которых при изменении значений некоторой величины на одно и то же число значение другой величины увеличивается или уменьшается не на одно и то же число, а в одном и том же отношении.

Другими словами, скорость роста линейной функции постоянна, квадратичной – линейна и вообще скорость роста (производная) степенной функции, являясь линейной степенью, растет медленнее, чем сама функция. Скорость же роста показательной функции пропорциональна самой функции. Необходимость изучения таких функций возникла с обнаружением таких законов естествознания как: законы разложения, законы радиоактивного излучения, законы движения в тормозящей среде и т.д.

При этом подходе целесообразно рассмотреть перед введением показательной функции практические задачи.

3 подход реализован в действующих школьных учебниках (под редакцией А.Н. Колмогорова и в учебнике М.И. Башмакова).

Введение показательной функции связывают с обобщением понятия степени до степени с вещественным показателем.

3. Изучение логарифмической функции необходимо начинать с определения логарифма. Доказывается формула перехода от одного основания логарифма к другому основанию. Используя доказанные свойства, необходимо сформировать у учащихся достаточно твердые умения и навыки логарифмирования выражений и потенцирования. После этого можно вводить понятие логарифмической функции.
   

Далее рассматривают основные свойства логарифмической функции. Возможен вариант изучения свойств логарифмической функции как функции, обратной показательной. Но от этого варианта в действующих учебниках в последнее время отказались. А понятие об обратной функции изучается как необязательный материал.

В конце раздела рассматривают производную показательной функции, число е и производную логарифмической функции. Завершается изучение школьного курса алгебры и начал анализа рассмотрением степенной функции и ознакомлением учащихся с понятием дифференциальных уравнений.

Свойства показательной и логарифмической функций широко используются при решении показательных и логарифмических уравнений и неравенств.

4. В учебнике М.И. Башмакова общая идея при решении показательных уравнений сформулирована в виде теоремы. Далее рассматриваются основные подходы (эвристические приемы), используемые при решении показательных уравнений: введение новой переменной, выражение показательных функций друг через друга с использованием свойств степеней, использование свойства монотонности функций и др.

Можно выделить следующие основные эвристические приемы, используемые при решении логарифмических уравнений: замена переменной, использование свойств логарифмов и логарифмических тождеств для упрощения выражений в обеих частях уравнения, логарифмирование обеих частей уравнения, графический метод и др.


Лекция 8. Методика изучения предела и непрерывности функции в школьном курсе «Алгебры и начал анализа».


План.

1. Цели и задачи изучения вопросов начал анализа. Исторический аспект изучения этих вопросов в школе.
   
2. Обзор школьной программы по алгебре и началам анализа.
   
3. Методика введения и изучения понятия предела функции в точке.
   
4. Методика изучения непрерывности функции в точке и применения непрерывности.
   

Содержание лекции

1. Изучение начал анализа в школе значительно обогащает идейное содержание, расширяет прикладную направленность школьного курса математики. Основная задача изучения вопросов дифференциального и интегрального исчисления – подготовить необходимый аппарат для исследования функций и построения их графиков; для изучения физики (скорость, ускорение, колебания и т.д.) и геометрии (площади поверхностей и объем геометрических тел).
   
2. После корректировок и изменений программ в настоящее время в школьном курсе математики (10-11 классов) остались следующие вопросы начал анализа: 10 класс – «Производная», «Применение производной»; 11 класс – «Первообразная и интеграл».
   

Исследованиями установлено, что ознакомление учащихся с четкими формальными определениями понятий еще не гарантирует усвоения этих понятий. Такие сложные понятия «предел функции в точке», «непрерывность», «производная», «интеграл» трудно усваиваются учениками, поэтому их нужно сделать для учащихся интуитивно ясными и затем дать им определения.

3. Понятие предела функции и непрерывности относятся к числу самых сложных для усвоения в школьном курсе. Возможны два варианта в последовательности изложения:
   

1. Определяется непрерывность функции в точке (используя сведения о приближенных вычислениях).
   
2. Вводят предел, затем на его основе – непрерывность функции в точке.
   

В действующей школьной программе принят второй порядок изложения.

Существует два варианта изложения вопросов о пределе функции в точке:

1. на языке ε – δ (на языке последовательности);
   
2. приближенное вычисление (заданная через точность).
   

Формирование понятия функции, непрерывной в точке, рекомендуется проводить вслед за изучением понятия предела функции в точке по следующим причинам:

1. оба определения имеют одинаковую логическую структуру, непосредственное определение их вслед друг за другом улучшает усвоение обоих понятий;
   
2. при изучении предела функции в точке строилось достаточное число графиков непрерывных и разрывных функций, которое можно использовать и при формировании понятия непрерывной функции в точке.
   
3. Понятие предела сразу же находит применение при решении вопроса о непрерывной функции в точке.
   

Лекция 9-10. Методика изучения производной и ее приложений.

План.

1. Пропедевтика понятия производной.
   
2. Методика введения понятия производной.
   
3. Приложения производной.
   

Содержание лекции

1. Приступая к изучению понятия производной, целесообразно:
   

а) повторить все вопросы, связанные с линейной функцией и элементарными функциями, так как основная идея дифференциального исчисления – представление о функции как о линейной в достаточно малой окрестности некоторой точки; б) отработать такие понятия как приращение функции и приращение аргумента. Это понятие иллюстрируется с помощью графиков функций; в) важно не просто ввести понятие приращения, но выработать у учащихся твердые навыки в их нахождении, с этой целью можно предложить учащимся ряд задач по нарастанию трудности; г) выяснить геометрический смысл отношение приращения функции к приращению аргумента, ввести понятие касательной к кривой как предельного положения секущей. После того как эти понятия отработаны. Переходят к введению понятия производной.

2. В предыдущих учебных пособиях введение этого понятия начинали с решения задач физического содержания и необоснованно отрывали геометрический смысл от производной. Лучший вариант – это рассмотреть задачу о мгновенной скорости, о геометрическом смысле производной именно на этапе введения производной. Затем, на следующем уровне, обобщая способы решения этих задач, обратим внимание на то, что этим способом решается ряд других задач в физике, технике: о теплоемкости тела при данной температуре, о мгновенной величине силы тока в данный момент времени и др.
   

Введение понятия производной необходимо связать с основной проблемой дифференциального исчисления – проблемой исследования процесса изменения функции.

Также необходимо знание правил, позволяющих этот процесс облегчить. В виде теорем рассматриваются производная суммы двух функций, производная, частного и степенной функции (последняя – без доказательства.

3. Вопросы приложения производной в школе оправдано лишь в том случае, если оно применяется. Основные направления применения: к решению задач на отыскание наименьшего и наибольшего значения функции на интервале, к исследованию функций, к решению физических задач, к приближенным вычислениям, к построению касательной.
   

Перед введением геометрического смысла производной необходимо повторить материал: линейная функция, ее угловой коэффициент, понятие производной, рассмотренные ранее задачи о мгновенной скорости, о касательной к графику функции. Эти задачи позволяют убедится в значимости нового понятия – производной, а перед рассмотрением ее геометрического смысла – выполняют и новую дидактическую функцию – являются средством подготовки учащихся к новому осознанию понятия производная.

Методика изучения применения производной к исследованию функций.

Этот раздел имеет большое значение для многих классов функций, реализует межпредметные связи. Но он вызывает и ряд трудностей. Необходимо выбрать минимум материала. В различных учебниках имеются различные подходы к изложению этого материала, но стремление единое – найти приемы изложения, которые сводили бы недосказанные факты к минимуму. Таким материалом, в частности, является теорема Лагранжа.

Изложение вопросов связанных с исследованием функции на экстремум обычно начинают с доказательства достаточных признаков возрастания и убывания функций, затем теоремы Ферма (необходимое условие существования экстремума), затем достаточные условия существования экстремума, общая схема исследования функций и задачи на наибольшее и наименьшее значения функции на интервале.

Перед изучением этих вопросов целесообразно повторить понятие возрастающей и убывающей функций, определение производной, ее геометрический смысл, понятие касательной, угловой коэффициент, условие параллельности прямых, графики известных функций.

Кроме того, ученик должен иметь представление о непрерывных функциях.


Лекция 10. Изучение первообразной и интеграла в школьном курсе математики.

План.

1. О месте этой темы в школьном курсе математики.
   
2. Различные подходы к изложению теории интегралов в школе.
   
3. Методика введения понятий первообразная и интеграла.
   
4. Применение интегралов к решению задач.
   

Содержание лекции

Начальные сведения об интегральном исчислении вводятся в 11 классе в курсе алгебры и начал анализа» в теме «Первообразная и интеграл».

1. Роль этой темы: Вместе с дифференциальным исчислением интегральное делает школьный курс логически стройным, шире, и глубже раскрывает значение математики для изучения других наук, способствует формированию у школьников диалектико-материалистического мировоззрения, облегчает изучение некоторых вопросов физики, геометрии.

Интегральное исчисление повышает научный уровень всего курса, помогает привести его по возможности в соответствие с современным состоянием науки, повышает математическую культуру выпускников школы.

Цель изучения данной темы – познакомить учащихся с интегрированием как операцией, обратной дифференцированию, показать применение интеграла к решению геометрических задач.

Данная тема включает в себя следующие вопросы: первообразная, основное свойство первообразной, три правила нахождения первообразных, площадь криволинейной трапеции, интеграл, формула Ньютона – Лейбница, применение интеграла.

2. В учебно-методической литературе наметились два основных способа построении теории интегралов:

I подход. На основе решения конкретных задач вводятся понятия интегральной суммы и определенного интеграла, рассматриваются некоторые его свойства и теорема существования. Далее доказывается, что производная определенного интеграла с переменным верхним пределом равна значению подинтегральной функции от верхнего предела. Вводится понятие первообразной, неопределенного интеграла и получают формулу Ньютона-Лейбница для вычисления определенного интеграла. Заканчивают изложение применением интегрального исчисления к решению задач.

II подход. Сначала вводят понятие первообразной функции, неопределенного интеграла, изучаются его свойства и теоремы существования (без доказательства), устанавливают связь первообразной с площадью под графиком функции. Затем вводят понятие определенного интеграла (или как предела интегральных сумм, или как приращения первообразной), в конце – применение интеграла.

Школьный вариант расположен между ними, но ближе ко II подходу.

Достоинства I подхода – всестороннее выяснение идейного смысла определенного интеграла. Вначале изучения интегрального исчисления при решении различных задач учащиеся овладевают искусством перехода от равномерных процессов к неравномерным, составлением интегральных сумм, перехода от нее к интегралу.

Недостатки: Неоправданно большой разрыв во времени между введением понятия интеграла и его вычислением. Учащиеся сначала изучают задачи, приводящие к понятию интеграла, его свойства, только в конце темы занимаются непосредственным интегрированием. Это приводит к тому, что у них теряется интерес к изучению теории, а это влияет на отработку навыков решения задач.

Достоинства II подхода: 1) Ранее ознакомление школьников с основной задачей интегрального исчисления – нахождением по данной функции f (х) ее первообразной F(х) и овладение аппаратом для решения. 2) Обеспечение возможности вычислять интегралы, следовательно, прививать им навыки интегрирования в ходе изучения темы. 3) Результатом является лучшая подготовленность к решению задач геометрии и физики.

Недостатки: Определение определенного интеграла как приращения первообразной не позволяет полно раскрыть идейную сторону.

3. Перед изучением темы в 11 классе необходимо повторить предел функции, непрерывность и производную, физический и геометрический смысл производной. Целесообразно обратиться к таблице, в которой записаны функции и их производные, чтобы воспользоваться ею для отыскания функции, производная которой задана. Изучение новой темы можно начать с решения конкретных задач, в которых показывается, что произвольная постоянная имеет реальный смысл, учащиеся подводятся к определению первообразной, заполняется таблица первообразных. На первых порах правильность решения проверяется дифференцированием. Затем изучают основное свойство первообразной. Рассматриваются три правила нахождения первообразных, которые легко доказываются, опираясь на определение первообразной.

Следующим важным вопросом в данной теме является понятие криволинейной трапеции и нахождение ее площади. Перед его рассмотрением необходимо вспомнить все о площадях из геометрии и поставить проблему, как можно найти площадь произвольной фигуры Ф. Этот вопрос решается двояко: 1. Доказывается теорема о площади криволинейной трапеции: сначала вводится функция, затем доказывается, что она является первообразной. 2) Второй подход к нахождению площади криволинейной трапеции, образованный графиком непрерывной и неотрицательной функции и прямыми.

4. Применение интегралов рассматриваются при решении задач: на нахождение площади плоской фигуры; на вычисление пройденного пути за данный промежуток времени, на нахождение силы давления жидкости, работы переменной силы, на нахождение объемов тел.

Наиболее трудным является вопрос об объеме пирамиды. Возможны различные варианты: 1) по учебнику А.В. Погорелова сначала доказываем равновеликость треугольных пирамид с равновеликими основаниями и равными высотами, затем доказываем, что наклонная треугольная призма состоит из трех равновеликих пирамид. В учебнике Киселева А.П. подход аналогичен «Погореловскому» но при этом еще показывается, что за объем пирамиды принимается число, которое больше суммы объемов входящих призм и меньше суммы объемов выходящих призм. В учебном пособии Н.А. Глаголева – находится предел последовательности сумм объемов входящих призм при бесконечном возрастании их числа, этот предел и принимают за объем пирамиды. 2) изложение этого вопроса с использованием интегрального исчисления. Этот подход можно использовать и при выводе объема пирамиды, считая, что объем пирамиды существует и нужно доказать, что он является первообразной для функции S(х). Методическая особенность такого подхода состоит в том, что вывод объема пирамиды является базовым доказательством, оно обслуживает и объемы фигур вращения.


Как указывалось выше, ряд тем вынесено на самостоятельное изучение. Для ориентации студентов дается подробный план их изучения.


^ Тема 1. Тождественные преобразования в курсе математики средней школы.

План изучения:

1. Тождественные преобразования выражений – одна из основных линий школьного курса математики. Цели их изучения.
   
2. Основной понятийный аппарат. Логико-математический анализ.
   
3. Место выражений и их преобразований в школьной программе.
   
4. Методические особенности изучения преобразований числовых выражений в 5-6 классах.
   
5. Пропедевтика изучения алгебраических целых выражений в 5-6 классах.
   
6. Методика введения основных понятий в алгебре 7 класса.
   
7. Методика изучения преобразований целых алгебраических выражений. Что лежит в их основе?
   
8. Методика изучения преобразований дробно-рациональных выражений.
   
9. Изучение преобразований выражений, содержащих радикалы. На чем основаны эти преобразования?
   
10. Методика изучения преобразований выражений, содержащих тригонометрические функции.
    
11. Методика изучения преобразований выражений, содержащих логарифмы.
    
12. Основные типы упражнений при изучении преобразований алгебраических выражений.
    
13. Привести примеры использования тождественных преобразований выражений при решении уравнений, неравенств, при изучении функций.
    

Тема 2. Тригонометрические функции и методика их изучения.

1. Логико-математический анализ основных понятий.
   
2. Цели изучения тригонометрических функций в средней школе. Роль и место в школьной программе.
   
3. Сравнительный анализ действующих школьных учебников.
   
4. Различные подходы в изучении тригонометрических функций.
   
5. Методика изучения основных понятий в курсе геометрии.
   
6. Изучение тригонометрических функций в курсе 9 класса алгебры.
   
7. Методика изучения тригонометрических функций и их свойств в курсе алгебры и начал анализа в 10 классе.
   
8. Применение свойств тригонометрических функций к решению тригонометрических уравнений и неравенств.