Курс лекций Рекомендовано редакционно-издательским советом Орелгту в качестве учебного пособия Орел 2005
| Вид материала | Курс лекций |
- Конспект лекций Рекомендовано в качестве учебного пособия Редакционно-издательским, 1023.31kb.
- Прокурор в уголовном процессе, 2839.04kb.
- Нефтяное товароведение, 1449.59kb.
- А. С. Калмыкова Главный внештатный детский инфекционист, 1294.52kb.
- Учебное пособие Рекомендовано в качестве учебного пособия Редакционно-издательским, 2331.42kb.
- Рекомендовано в качестве конспекта лекций Редакционно-издательским советом Томского, 1088.59kb.
- И. З. Шарипов материаловедение рекомендовано редакционно-издательским советом угату, 1223.16kb.
- Пособие подготовлено на кафедре экономической теории © Новосибирский государственный, 754.49kb.
- А. В. Терентьев менеджмент организации курсовое и диплом, 2230.76kb.
- Методические указания к курсовому и дипломному проектированию Москва 2007, 873.19kb.
5.2 Категорические суждения
Категорическими называют суждения, у которых точно выяснено их качество и количество.
По этим двум признакам (качество и количество) проводят классификацию категорических суждений, выделяя общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные. Единичные и общие суждения объединяют в одну группу, так как и в одном, и в другом случае предикат высказывается обо всем объеме субъекта.
Общеутвердительные суждения обозначаются буквой А.
Их каноническая форма: Все S есть Р.
На языке логики предикатов общеутвердительное суждение запишется следующим образом: x(S(x)P(x)).
Отметим, что это суждение истинно при определенных отношениях между понятиями S и Р (рис. 11).
Пример. «Все люди есть существа, имеющие преступные наклонности».
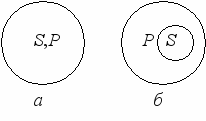
Рис. 11. Возможные отношения между субъектом и предикатом
истинного общеутвердительного суждения
Общеотрицательные суждения обозначаются буквой Е.
Каноническая форма: Ни одно S не есть Р.
Запись на языке логики предикатов: x(S(x)P(x)).
Общеотрицательное суждение истинно при отношениях между понятиями S и Р, показанных на рис. 12.
Пример. «Ни один человек не есть существо, имеющее преступные наклонности».
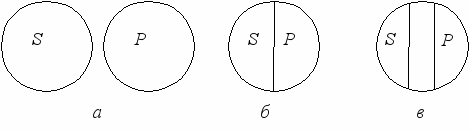
Рис. 12. Возможные отношения между субъектом и предикатом
истинного общеотрицательного суждения
Частноутвердительные суждения обозначаются буквой I.
Каноническая форма: Некоторые S есть Р.
Запись на языке логики предикатов: x(S(x) P(x)).
Частноутвердительное суждение истинно при отношениях между понятиями S и Р, показанных на рис. 13.
Пример. «Некоторые люди есть существа, имеющие преступные наклонности».
Частноотрицательные суждения обозначаются буквой О.
Каноническая форма: Некоторые S не есть Р.
Запись на языке логики предикатов: x(S(x) P(x)).
Частноотрицательное суждение также истинно только при определенных отношениях между понятиями S и Р (рис. 14).
Пример. «Некоторые люди не есть существа, имеющие преступные наклонности».
Буквенные обозначения категорических суждений – это гласные буквы латинских слов affirmo - утверждаю и nego - отрицаю.
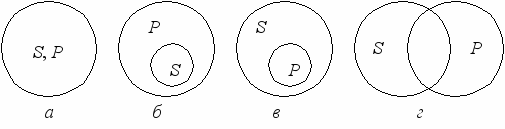
Рис. 13. Возможные отношения между субъектом и предикатом
истинного частноутвердительного суждения
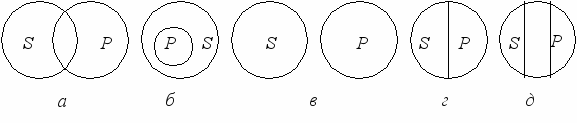
Рис. 14. Возможные отношения между субъектом и предикатом
истинного частноотрицательного суждения
5.3 Распределенность терминов в категорических суждениях
Формы категорических суждений выражают четыре типа отношений между классами, которые представляют общие имена S и Р:
- в общеутвердительных суждениях утверждается, что каждый предмет класса S тождественен каким-то предметам Р;
- в частноутвердительных суждениях утверждается то же самое о некоторых предметах S (причем, говоря о некоторых, не исключают, что и все);
- в общеотрицательных суждениях, наоборот, утверждается, что ни один предмет класса S не совпадает ни с одним предметом Р, т.е. не тождественен никакому из этих предметов;
- в частноотрицательных суждениях то же самое утверждается о части (возможно, совпадающей со всем классом) предметов S.
Информация о тождестве или различии терминов категорического суждения – субъекта и предиката – выражается в понятии их распределенности. Термин категорического суждения называется распределенным, если он рассматривается в данном суждении во всем объеме, т.е. он полностью включается в объем другого термина или полностью исключается из него. Другими словами, распределенность или нераспределенность термина категорического суждения – его субъекта или предиката – указывает на то, имеем ли мы в данном суждении информацию обо всех или не обо всех предметах класса, представителем которого является данный термин (как общий знак предметов этого класса).
Распределенность терминов обозначается знаками «+» и «-»: S+, P+ – распределенные термины; S-, P- – нераспределенные термины.
Существует правило распределенности терминов в категорических суждениях: субъекты распределены в общих и не распределены в частных суждениях; предикаты распределены в отрицательных и не распределены в утвердительных суждениях. Содержание этого правила можно представить в виде таблицы (табл. 1).
Таблица 1
Распределенность терминов категорического суждения
| | A | E | I | O |
| Субъект (S) | + | + | | |
| Предикат (P) | (+) | + | (+) | + |
Пример. «Все киты (S+) – млекопитающие (Р-)»; «Ни одна рыба (S+) не есть кит (Р-)»; «Некоторые студенты (S-) – отличники (Р-)»; «Некоторые дети (S-) – не школьники (Р+)»; «Некоторые цветы (S-) – фиалки (Р+)».
