Курс лекций Рекомендовано редакционно-издательским советом Орелгту в качестве учебного пособия Орел 2005
| Вид материала | Курс лекций |
- Конспект лекций Рекомендовано в качестве учебного пособия Редакционно-издательским, 1023.31kb.
- Прокурор в уголовном процессе, 2839.04kb.
- Нефтяное товароведение, 1449.59kb.
- А. С. Калмыкова Главный внештатный детский инфекционист, 1294.52kb.
- Учебное пособие Рекомендовано в качестве учебного пособия Редакционно-издательским, 2331.42kb.
- Рекомендовано в качестве конспекта лекций Редакционно-издательским советом Томского, 1088.59kb.
- И. З. Шарипов материаловедение рекомендовано редакционно-издательским советом угату, 1223.16kb.
- Пособие подготовлено на кафедре экономической теории © Новосибирский государственный, 754.49kb.
- А. В. Терентьев менеджмент организации курсовое и диплом, 2230.76kb.
- Методические указания к курсовому и дипломному проектированию Москва 2007, 873.19kb.
4.5 Отношение между понятиями. Совместимые и несовместимые понятия
Объективные отношения между самими предметами находят свое отражение в отношениях между понятиями. Все многообразие этих отношений также можно классифицировать на основе содержания и объема понятий.
Сравнимые и несравнимые понятия. Сравнимыми называют понятия, в содержании которых имеется хотя бы один общий признак. Почти все понятия являются сравнимыми. В данном случае опровергается известная пословица «Нельзя сравнивать Божий дар с яичницей». С точки зрения логики, это также сравнимые понятия, так как о них, по крайней мере, можно сказать, что и то, и другое – предмет. Это и будет их общий признак. Несравнимыми называют понятия, в содержании которых нет ни одного общего признака. Некоторые авторы в качестве примера несравнимых понятий приводят понятия «предмет» и «свойство». Сравнимые понятия могут быть совместимыми или несовместимыми.
Совместимые и несовместимые понятия. Понятия называются совместимыми, если их объемы имеют хотя бы один общий элемент. Несовместимые – это понятия, в объемах которых нет ни одного общего элемента. Обычно отношения между понятиями изображают с помощью так называемых кругов Эйлера (рис. 2, 3).
Виды совместимых понятий. Совместимые понятия могут быть равнозначными (тождественными), перекрещивающимися, а также подчиненным и подчиняющим.
Равнозначные (тождественные) - это понятия, объемы которых полностью совпадают (рис. 2, а).
Пример. А – понятие «автор романа «Анна Каренина»»; В – понятие «автор романа «Война и мир»».
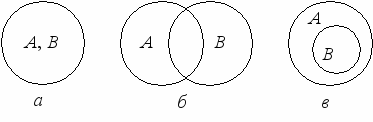
Рис. 2. Виды совместимых понятий
Перекрещивающиеся - это понятия, объемы которых частично совпадают (рис. 2, б).
Пример. А – понятие «студент»; В – понятие «спортсмен».
Подчиняющее и подчиненное понятия. Объем подчиненного понятия полностью входит в объем подчиняющего, не исчерпывая его (рис. 2, в).
Пример. А – понятие «деревья»; В – понятие «береза».
Виды несовместимых понятий. Несовместимые понятия бывают соподчиненными, противоположными (контрарными) и противоречащими (контрадикторными).
Соподчиненные – это понятия, объемы которых различны и входят в объем общего для них понятия, не исчерпывая его (рис. 3, а).
Пример. А – понятие «фиалка»; В – понятие «роза»; С – понятие «цветы».
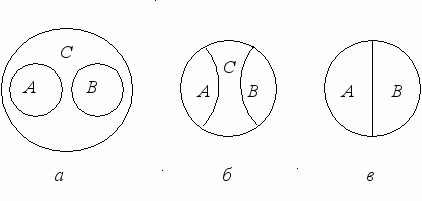
Рис. 3. Виды несовместимых понятий
Противоположными (контрарными) понятиями являются такие, которые соподчинены третьему понятию и представляют собой крайние степени выраженности некоторого качества. Можно сказать, что их объемы занимают полярные места в объеме общего для них понятия (рис. 3, б).
Пример. А – «черный»; В – «белый»; С – «цвет».
Противоречивые (контрадикторные) понятия подчиняются общему для них понятию, и при этом в общем понятии не существует такого элемента, который не был бы элементом одного из этих понятий. Их объемы делят объем общего для них понятия на две части (рис. 3, в).
Пример. А – «монархия»; В – «республика». Общим для этих понятий является понятие «форма правления». Причем «монархия» и «республика» – несовместимые формы правления, и в то же время других форм правления не существует.
С помощью кругов Эйлера можно получать достаточно сложные схемы. Например, можно изобразить отношение между понятиями А – «студент», В – «спортсмен», С – «мастер спорта», D – «кандидат в мастера спорта» (рис. 4).
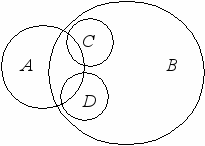
Рис. 4. Отношение между понятиями «студент» (А), «спортсмен» (В), «мастер спорта» (С), «кандидат в мастера спорта» (D)
Изучение отношений между понятиями имеет огромное значение для правильного употребления понятий в устной и письменной речи. И наоборот, незнание этих отношений способно повлечь за собой искаженное отражение действительности – отношений между самими вещами.
4.6 Основные операции с объемами понятий
Основные операции с объемами и содержаниями понятий составляют часть так называемой теории множеств. К операциям с объемами понятий относятся пересечение, объединение, дополнение и вычитание.
Пересечение. С использованием языка логики предикатов операция пересечения запишется следующим образом:
WxP(x)WxQ(x),
где W – оператор образования множества из понятия (оператор выделения объема понятия из самого понятия). W указывает на то, что речь идет именно об объемах понятий; – знак пересечения.
Если мы ищем пересечение, то для разных видов совместимых и несовместимых понятий результаты пересечений их объемов будут разными (рис. 5).
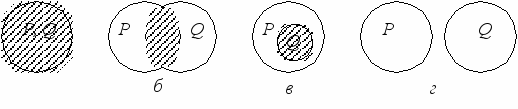
а
Рис. 5. Пересечение: а – тождественные понятия; б – перекрещивающиеся понятия; в – подчиненное и подчиняющее понятия; г – несовместимые (соподчиненные) понятия
Объединение. Операция объединения запишется так:
WxP(x)WxQ(x),
где – знак объединения.
Объединение объемов понятий также может иметь различные варианты (рис. 6).
Дополнение. Дополнением объема понятия хР(х) до универсума области возможных значений переменной х называется множество тех элементов этого универсума, которые не принадлежат понятию хР(х) (рис. 7). Записывается дополнение следующим образом:
WxP(x)
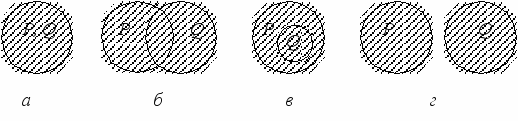
Рис. 6. Объединение: а – тождественные понятия; б – перекрещивающиеся понятия; в – подчиненное и подчиняющее понятия; г – несовместимые (соподчиненные) понятия
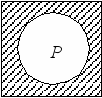
Рис. 7. Дополнение
Вычитание. Формула вычитания имеет следующий вид:
WxP(x)\WxQ(x),
где \ – знак вычитания объема одного понятия из объема другого.
Вычитание объемов понятий имеет разные варианты (рис. 8).
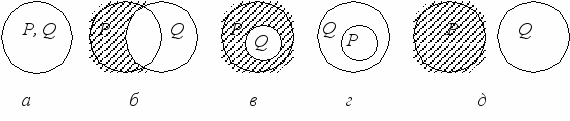
Рис. 8. Вычитание: а – тождественные понятия; б – перекрещивающиеся понятия; в, г – подчиненное и подчиняющее понятия; д – несовместимые (соподчиненные) понятия
