Geum.ru

Курс лекций Рекомендовано редакционно-издательским советом Орелгту в качестве учебного пособия Орел 2005

Вид материалаКурс лекций

Содержание


5.7 Отношение между сложными суждениями
Пример. Рассмотрим суждения p
Пример. Суждения (p
Пример. Частично совместимыми будут суждения (p
Пример. В отношении логического следования находятся суждения p
Пример. Отношение противоречия имеет место между суждениями p
Пример. Противоположными являются суждения p
Подобный материал:
1   ...   17   18   19   20   21   22   23   24   ...   47

5.7 Отношение между сложными суждениями



Сложные суждения вступают в отношения, подобные отношениям между категорическими суждениями, правда, с некоторыми отличиями.

Как и категорические, сложные суждения могут быть сравнимыми и несравнимыми.

Сложные суждения называются несравнимыми, если в совместно построенной для них таблице истинности среди сочетаний их истинностных значений встречаются все возможные комбинации: (И И), (И Л), (Л И), (Л Л).

Пример. Рассмотрим суждения p  q и pr. Построим для них совместную таблицу истинности:


p
q
r
q
p  q
p
pr

И
И
И
Л
И
Л
Л

И
И
Л
Л
И
Л
Л

И
Л
И
И
И
Л
Л

И
Л
Л
И
И
Л
Л

Л
И
И
Л
Л
И
И

Л
И
Л
Л
Л
И
Л

Л
Л
И
И
И
И
И

Л
Л
Л
И
И
И
Л

Сравнивая в выделенных столбцах значения истинности по строкам, видим, что в таблице встречаются все возможные комбинации истинностных значений. Значит, суждения p  q и pr являются несравнимыми.

Сложные суждения называются сравнимыми, если в совместной таблице истинности среди сочетаний их истинностных значений отсутствует хотя бы одна возможная комбинация.

Пример. Суждения pq и pq сравнимы. Проверим это с помощью совместной таблицы истинности:

p
q
pq
pq

И
И
И
И

И
Л
Л
Л

Л
И
И
Л

Л
Л
И
Л

В строках выделенных столбцов отсутствует комбинация (Л И), что и свидетельствует о совместимости суждений.

Среди сложных сравнимых суждений различают совместимые и несовместимые.

Совместимыми называются суждения, одновременно истинные или принимающие во всех строках таблицы одни и те же значения. Несовместимыми считаются сложные суждения, которые не являются одновременно истинными и не принимают во всех строках таблицы истинности одни и те же значения.

Отношение совместимости имеет несколько разновидностей: эквивалентность, частичная совместимость и логическое следование (подчинение).

Эквивалентными называются суждения, которые принимают одно и то же значение во всех строках построенной для них совместно таблицы истинности.

Пример. Суждения (pq) и p  q являются эквивалентными:

p
q
p
q
pq
(pq)
p  q

И
И
Л
Л
И
Л
Л

И
Л
Л
И
Л
И
И

Л
И
И
Л
Л
И
И

Л
Л
И
И
Л
И
И


Все логически истинные и логически ложные суждения эквивалентны друг другу.

Суждения частично совместимы, если в построенной для них совместно таблице истинности не встречается комбинация значений (Л Л), но встречаются все остальные возможные комбинации их значений. Главная черта частично совместимых суждений – они не могут быть одновременно ложными.

Пример. Частично совместимыми будут суждения (pq) и pq:

p
q
pq
(pq)
pq

И
И
И
Л
И

И
Л
Л
И
И

Л
И
Л
И
И

Л
Л
Л
И
Л


Эти суждения находятся в отношении частичной совместимости, так как они могут быть вместе истинными, но не могут быть вместе ложными.

Суждения находятся в отношении логического следования, если не может быть так, чтобы первое суждение было истинно, а второе – ложно. Отношение логического следования в логике самое важное. Для его обозначения введен специальный знак «╞ ».

Пример. В отношении логического следования находятся суждения p  q и pq:

p
q
p
pq
pq

И
И
Л
Л
И

И
Л
Л
Л
И

Л
И
И
И
И

Л
Л
И
Л
Л


Отношение несовместимости сводится к двум типам: противоречию и противоположности.

Суждения находятся в отношении противоречия, если они не могут быть ни вместе истинными, ни вместе ложными.

Пример. Отношение противоречия имеет место между суждениями p  q и p  q:

p
q
p
q
pq
p  q

И
И
Л
Л
И
Л

И
Л
Л
И
Л
И

Л
И
И
Л
Л
И

Л
Л
И
И
Л
И


Суждения находятся в отношении противоположности, если в построенной для них совместно таблице истинности не встречается комбинация значений (И И), но встречаются все остальные возможные комбинации. Эти суждения могут быть вместе ложными, но не могут быть вместе истинными.

Пример. Противоположными являются суждения pq и p  q:

p
q
p
q
pq
p  q

И
И
Л
Л
И
Л

И
Л
Л
И
Л
Л

Л
И
И
Л
Л
Л

Л
Л
И
И
Л
И


Классификация отношений между сложными суждениями может быть представлена в виде схемы (рис. 17).





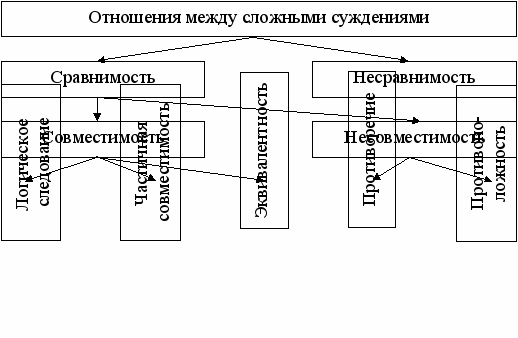
Рис. 17. Отношение между сложными суждениями


Знание отношений между сложными суждениями, как и между простыми, помогает правильно сочетать их в рассуждениях, избегать собственных ошибок и находить ошибки у оппонентов.