Инновационные элементы в организации сессионного экзамена в вузе

Вид материала

Реферат

Содержание Ключевые слова Содержание подхода

Подобный материал:

• Методика обучения второму иностранному языку в вузе. Инновационные образовательные, 50.99kb.
• Единый государственный экзамен по русскому языку цель экзамена: объективная оценка, 80.48kb.
• Программа вступительного экзамена для поступающих в докторантуру Phd специальность, 121.51kb.
• Программа вступительного экзамена в магистратуру элементы теории погрешностей, 51.03kb.
• Темы курсовых работ сущностный подход к планированию, организации и реализации процесса, 36.03kb.
• Xiv межрегиональная межвузовская учебно-методическая конференция «Инновационные методы, 899.22kb.
• Программа государственного выпускного экзамена специальность 030501. 65 (021100) «Юриспруденция», 387.86kb.
• Программа итогового государственного междисциплинарного экзамена Специальность 080507., 329.85kb.
• Программа итогового государственного междисциплинарного экзамена Специальность 080507., 352.28kb.
• Классификация элементов вычислительных средств, 641.33kb.

Инновационные элементы в организации сессионного экзамена в вузе

Бодряков В. Ю., заведующий кафедрой, д.ф.-м.н., доцент.
Фомина Н.Г., старший преподаватель

Кафедра математического анализа математического факультета Уральского государственного педагогического университета (УрГПУ), Екатеринбург

Bodryakov_VYu@e1.ru

Аннотация. В работе предлагается содержащий инновационные элементы подход к организации традиционного сессионного экзамена в вузе. Новым является структура и содержание экзаменационного билета (комплекта), которые выстроены в соответствии со структурой и содержанием дидактических единиц ГОС ВПО. Итоги практической реализации предложенного подхода обсуждаются на примере экзамена по математическому анализу, сдававшемуся студентами 2 курса математического факультета УрГПУ в зимнюю сессию 2008-2009 уч.г. Анализируются проблемы и перспективы подхода, предлагаются конкретные способы педагогической коррекции выявленных несоответствий.

Ключевые слова: высшее профессиональное образование, государственный образовательный стандарт, качество образования, инновации в образовании экзаменационная сессия, дидактические единицы, педагогическая коррекция.

Введение

Несомненно, что вопросы повышения качества образования, являющиеся приоритетными для любого общества, становятся особенно значимыми для постиндустриального общества, которое формируется в мире и, в частности, в России [1]. Важнейшим элементом повышения качества является его постоянное измерение, сопоставление с установленными требованиями и внесение необходимых корректив, т.е., фактически, обеспечение непрерывного мониторинга качества работы системы. Сказанное в полной мере относится и к образовательным системам, принципиальной отличительной особенностью которых является наличие и выраженное влияние человеческого фактора [2 – 4]. Заметим, что контроль качества учебного процесса, прежде всего уровня профессиональной обученности студентов, является одним из основных элементов технологического подхода в обучении (ТПО) [5].

Одной из острейших в России стала проблема повышения качества образования. Как отмечено в [6], до 60% медалистов школ не подтверждают свои отличные знания при поступлении в вузы страны. Сказанное справедливо как по отношению к качеству общего образования в целом, так и, в особенности, к качеству школьного математического образования [7]. Так, по итогам сдачи ЕГЭ по математике неудовлетворительные оценки в 2008 г. получили почти 25% выпускников школ [8]. И это при «сверхдемократичном» подходе к оцениванию уровня знаний (отметка «три» ставилась уже за набранные 25 баллов из 100)! О необходимости повышения качества математического образования говорят исследователи и педагоги не только в России, но и за рубежом. В частности, в США принята национальная программа «Ни один ребенок не будет оставлен», требующая, чтобы в каждом штате каждая общественная школа располагала высококвалифицированными учителями математики [9]. Допущенное в последние годы снижение уровня математической подготовки школьников резко затрудняет получение высшего профессионального образования по самому широкому кругу специальностей, прежде всего в естественно-научной, технической и экономической областях. Конечно, обозначенные проблемы комплексны, но ясно, что одним из определяющих факторов является слабая подготовка самих учителей математики, – в прошлом выпускников педагогических вузов. Без надежного решения задачи качественной математической подготовки студентов-математиков педвузов не приходится ожидать хороших и надежно воспроизводимых результатов от их учеников. Приоритетное повышение качества образования студентов педагогических вузов, в частности, учителей математики, является на современном этапе одной из важнейших и безотлагательных задач. Заметим, вместе с тем, что необходимо одновременно принимать действенные меры по повышению социального и материального статуса учителя, улучшать условия его работы, создавать дополнительные возможности для его самообразования и повышения квалификации.

Как известно, весьма важную роль в технологическом подходе в обучении математике играет систематическое и адекватное оценивание текущего уровня знаний студентов [5, 10], достаточно глубокий статистический анализ полученных результатов и сопоставление их с запланированными педагогическими целями, выработка и осуществление педагогических мероприятий для коррекции выявленных несоответствий [11-14]. Важно, чтобы оценка была объективной и осуществлялась на основании количественно измеренного уровня знаний учащихся по заранее определенным критериям, а способ ее формирования был прозрачным и понятным студентам.

Традиционными мероприятиями для контроля качества образования студентов являются проводимые дважды в год экзаменационные сессии. В межсессионный период проводится текущий контроль знаний, включая «срезы остаточных знаний», независимое Интернет – тестирование и др. Кажется, что ничего нового в эти привычные традиционные формы контроля знаний привнести уже нельзя. Вместе с тем, любому практикующему преподавателю известно, что хорошие и даже отличные экзаменационные отметки далеко не всегда соответствует наличию крепких уверенных знаний по изученным курсам. Это объективно и отчетливо показывают «срезы остаточных знаний» по математике [12]. Таким образом, традиционные формы контроля знаний уже в силу их привычности не всегда дают объективную картину действительного положения дел. Не вызывает сомнений необходимость внесения новых элементов в стиль проведения традиционных контрольных мероприятий в направлении повышения их объективности, технологичности и открытости. В настоящей работе, в развитие идей ранее опубликованных исследований [11-18], мы внесли инновационные элементы в традиционную технологию проведения вузовского сессионного экзамена, структурировав экзаменационные задания в точном согласно требованиям ГОС ВПО. В качестве примера проанализированы итоги сдачи по новой схеме экзамена по математическому анализу (МА) студентами - математиками 2-го курса УрГПУ (зимняя сессия 2008-2009 уч.г.).


Содержание подхода

Новым в технологии проведения сессионного экзамена по ВМ является формирование экзаменационных билетов, состоящих из теоретических и практических заданий, охватывающих по возможности наиболее полно весь изученный курс. При этом билеты структурированы в соответствии с содержанием ГОС ВПО. А именно, экзаменационные билеты разбиты на несколько блоков по числу дидактических единиц (ДЕ) ГОС. Каждый блок, в зависимости от числа ДЕ и желаемой глубины проверки знаний может содержать различное число заданий. Предпочтительно, чтобы все экзаменационные задания имели приблизительно равный уровень сложности. Это удобно для последующей статистической обработки результатов экзамена, но не является обязательным. Экзамен удобнее проводить в письменной форме, хотя возможна и устная форма. В последнем случае, студент является соучастником всех этапов процесса формирования итоговой оценки, что особенно важно в педагогическом вузе при подготовке будущих учителей. Итоговая оценка в традиционном регламентированном формате «2»-«3»-«4»-«5» определяется путем перевода из набранной суммы баллов, например, с помощью табл. 1.

Таблица 1

Таблица перевода числа k набранных баллов в экзаменационную оценку

Баллы	0  k  4⅓	4⅔  k  6⅓	6⅔  k  8⅓	8⅔  k  10
Оценка	Неудовл.	Удовл.	Хорошо	Отлично

Принципиально важным инновационным элементом здесь является то, что по каждой ДЕ студент должен набрать определенное заранее установленное экзаменатором число баллов (как правило, не менее 50%). Если это условие не выполнено хотя бы по одной ДЕ, студент получает «неуд.» независимо от набранной общей суммы баллов. Верно решенной задаче приписывался 1 балл; если решение задачи имело небольшие недочеты (описки, неточности, негрубые ошибки в арифметических вычислениях) ему приписывалось 2/3 балла; если решение имело существенные ошибки, но при этом логика рассуждений была верна, решению приписывалось 1/3 балла; и если задача была решена с грубыми ошибками или не решалась совсем, ей приписывалось 0 баллов. Таким образом, сумма набранных баллов изменялась от 0 до 10. Преимущества такого подхода к организации экзамена очевидны. Экзаменационное задание построено в точном соответствии со структурой и содержанием ДЕ ГОС ВПО; ясны критерии оценки и прозрачна сама процедура оценивания; студенту, получившему низкий балл, понятно, какие именно разделы курса он должен дополнительно проработать. Очевидна большая объективность данной формы проведения экзамена по сравнению с традиционной. Добавим, что по аналогичному принципу построено независимое Интернет-тестирование знаний студентов, проводимое ФИПО [19].

В качестве примера конкретного применения развитого подхода к организации проверки знаний проанализируем итоги сдачи студентами 2-го курса МФ УрГПУ письменного экзамена по математическому анализу (МА) в период зимней экзаменационной сессии 2008-2009 уч.г. Студенты экзаменовались по разделу 3 «Интегральное исчисление». К экзамену по МА было допущено 49 студентов (из 51), в т.ч. в группе М-201: 18 чел., М-202: 15 чел.; М-203: 16 чел. Студент получал экзаменационное задание в виде экзаменационного комплекта, который содержал собственно билет, а также подколотую к нему степлером бумагу для черновых и чистовых записей. На рабочем столе не нужно было иметь ничего кроме экзаменационного комплекта и пишущего средства. Экзаменационный процесс мог легко контролироваться. Каждый экзаменационный билет (всего было разработано 6 вариантов) был структурно разделен на четыре части по числу ДЕ и содержал 10 теоретических и практических заданий, охватывающих основные разделы учебного курса (см. образец билета в прил. А). За многолетнюю экзаменационную практику на МФ УрГПУ подобный формат сессионного контроля знаний применен впервые, поэтому студентам для решения заданий было отведено несколько большее время, чем предварительно планировалось (2 астрономических, а не учебных часа). После завершения подготовки студент сдавал работу и ожидал результатов ее проверки преподавателем. По завершении проверки со студентами проводились индивидуальные собеседования для указания основных недочетов. Экзамены по МА для трех групп 2 курса прошли в течение шести дней в последовательности: М-201, М-203, М-202. Через 10 дней после официального завершения сессии была назначена общая пересдача для студентов, получивших неудовлетворительные оценки. Итоги сдачи экзамена по МА в сессионный период и первой пересдачи отражены на рис. 1 – рис. 4.




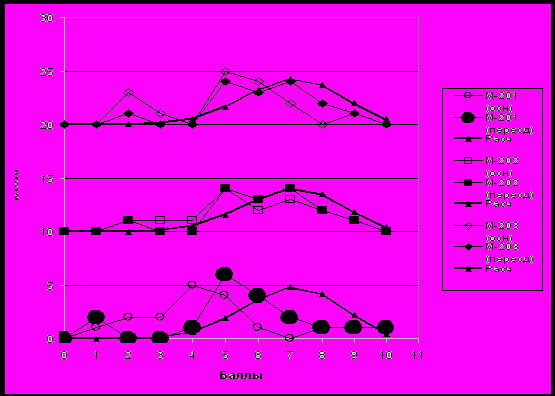
Рис. 1. Частотная диаграмма распределения числа набранных баллов студентов 2 курса МФ по итогам сессионной проверки знаний по МА (зимняя сессия 2008-2009 уч.г.) в сопоставлении с расчетом по ВСМ-10 [16, 17]. Каждое распределение смещено относительно соседнего на 5 ед. по вертикальной оси.




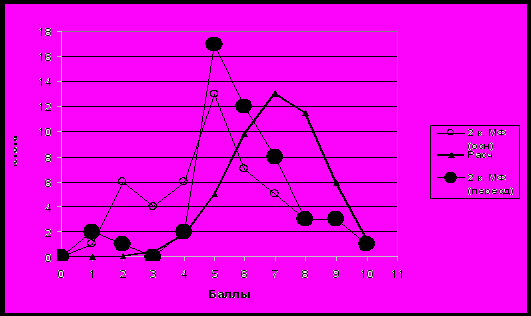
Рис. 2. То же, что рис. 1 в целом по 2-му курсу МФ.



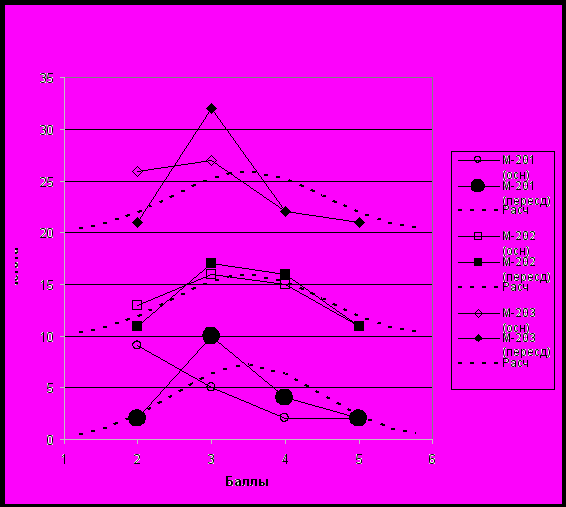
Рис. 3 Частотная диаграмма распределения итоговых оценок студентов 2 курса МФ по итогам сессионной проверки знаний по МА (зимняя сессия 2008-2009 уч.г.) в сопоставлении с кривой опорного нормального распределения N(3,5; 1,0) (пунктир).




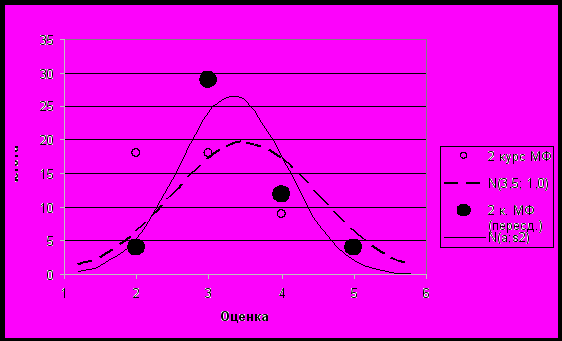
Рис. 4 То же, что рис. 3 в целом по 2-му курсу МФ. Сплошная кривая – эмпирическая нормальная кривая.

Из рис. 1 – рис. 4 видно, что наихудшие результаты сдачи экзамена в сессионный период показали студенты группы М-201, сдававшие экзамен первыми; наилучшие – студенты группы М-202, сдававшие последними. Промежуточные итоги – у группы М-203. С учетом того, что в течение предшествующего семестра студенты всего курса в целом показывали приблизительно одинаковые учебные результаты, наблюдаемую закономерность можно объяснить непривычностью для студентов нового стиля проведения экзамена и адаптационными явлениями, которые завершились достаточно быстро. Уже при первой пересдаче экзамена по МА студенты групп М-201 и М-203 существенно улучшили свои результаты: количество неудовлетворительных оценок уменьшилось в несколько раз (за счет увеличения количества хороших и, преимущественно, удовлетворительных оценок). Количество отличных оценок в результате пересдачи не изменилось, т.е. новый формат проведения экзамена не обескуражил сильных студентов. При пересдаче каждый студент получил новый, еще не решавшийся им, вариант экзаменационного билета.

Сопоставление эмпирических распределений с расчетным биномиальным распределением [20], согласно вероятностно-статистической модели (ВСМ-10) оценки знаний учащихся по 10-балльной шкале [16, 17] для биномиальной вероятности успеха p = 0,7, характерной для посредственного студента, выявляет наличие пробелов в знаниях студентов. Во всех случаях эмпирические распределения на 1 – 2 балла смещены влево относительно модельных (рис. 1, рис. 2). С другой стороны, итоговое курсовое распределение баллов (рис. 2) является достаточно узким и компактным, что в целом означает однородность студенческого коллектива по уровню усвоения материала и, следовательно, возможность эффективного управления педагогическим процессом с целью повышения коллективного уровня профессиональной обученности студентов 2 курса МФ. К сожалению, и после пересдачи экзамена на 2-м курсе МФ выделяется группа очень слабых студентов, набравших менее 4-х баллов из 10 (4 чел.). По-видимому, для них продолжение учебы на МФ проблематично.

Наибольшей по численности (см. рис. 3, рис. 4) является группа студентов с удовлетворительными оценками после пересдачи экзамена («группа риска»). В данном случае неудовлетворительные оценки после сдачи основного экзамена удалось исправить, но лишь формально ситуацию можно признать удовлетворительной. Пребывание студента в «группе риска» чревато возникновением проблем при дальнейшем усложнении курса высшей математики и требует коррекции. Сравнение эмпирических распределений оценок в нормативном формате «2-3-4-5» с нормальными кривыми опорного распределения [11-17] позволяет указать на имеющиеся учебные проблемы в группах М-201 и М-203, тогда как в М-202 ситуация в целом удовлетворительна. «Группа риска» студентов нуждаются в учебной и психолого - педагогической поддержке. Учебная поддержка для таких учащихся может заключаться в проведении дополнительных консультаций по дисциплине, индивидуальный подход, помощь старшекурсников. Психолого – педагогическая поддержка может заключаться в проведении адаптационных тренингов, создании ситуации успеха, системной работе преподавателей математических дисциплин по формированию элементов профессиональной структуры интеллекта студентов – математиков [20]. Добавим, что нормальное распределение, аппроксимирующее эмпирическое распределение оценок по всему 2-му курсу МФ (рис. 4) достаточно близко к опорному, но имеет несколько меньшее среднее значение a = 3,33 (против a = 3,5) и меньшее СКО  = 0,74 (против  = 1,0). Эти данные подтверждают выводы работ [11-17] и др. об адекватности применения нормального распределения N(3,5; 1,0) в качестве базового (опорного).

Важно убедиться, что все шесть вариантов экзаменационных билетов приблизительно равноценны по сложности и все три студенческих группы находились в равноценных экзаменационных условиях. Одним из способов решения вопроса является сопоставление распределений набранных баллов для каждого из шести вариантов (рис. 5). Из рис. 5 отчетливо видно, что для каждого из шести вариантов распределения в значительной мере пересекаются без выраженного смещения одного распределения относительно другого. Т.о., в целом варианты экзаменационных билетов имеют одинаковый уровень сложности, что позволяет экзаменационные итоги считать адекватными. Аналогичные экзаменационные билеты могут быть применены в будущем.

Проведенный анализ «внешних» количественных показателей качества учебного процесса необходимо дополнить анализом «внутренних» причин наблюдаемых результатов. Такой анализ показывает, что наиболее проблемными для студентов являются дидактические единицы ДЕ-2 «Определенный интеграл. Формула Ньютона – Лейбница» и ДЕ-3 «Понятие квадрируемой фигуры, кубируемого тела, спрямляемой кривой». Если слабое раскрытие ДЕ-3 можно объяснить довольно высокой степенью абстрактности и сложностью материала, к тому же, излагавшемуся в конце учебного семестра, то слабое раскрытие материала ДЕ-2, во многом основанного на школьном курсе «Алгебра и начала анализа», является следствием недостаточности школьной подготовки студентов. К сожалению, эти пробелы не были устранены на факультативных занятиях, специально организуемых для этой цели на факультете. Добавим здесь, что в экзаменационных работах самых слабых студентов – кандидатов на отчисление (4 чел.) не зачтено от трех до четырех ДЕ, т.е. их неудовлетворительные результаты не вызывают никаких сомнений.



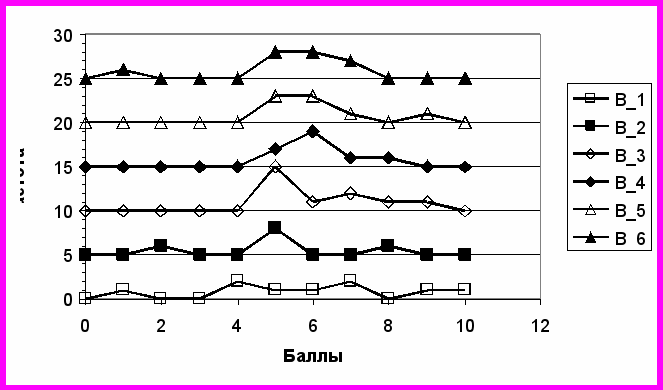
Рис. 5 Повариантная частотная диаграмма распределения набранных баллов для студентов 2 курса МФ по итогам экзамена по МА (зимняя сессия 2008-2009 уч.г.). Каждое распределение смещено относительно соседнего на 5 ед. по вертикальной оси.


Заключение

В работе предлагается содержащий инновационные элементы подход к организации сессионного экзамена в вузе. Новым является структура и содержание экзаменационного билета, который выстроен в соответствии со структурой и содержанием дидактических единиц ГОС ВПО. Итоги практической реализации предложенного подхода обсуждаются на примере экзамена по математическому анализу, сдававшемуся студентами 2 курса (49 чел.) МФ УрГПУ в зимнюю сессию 2008-2009 уч.г. Статистический анализ итогов проверки знаний студентов позволил дать объективную оценку состояния и уровня образовательного процесса на факультете, выявить проблемы качества и выработать конкретные рекомендации для всех его участников по устранению несоответствий. Проведенный в середине следующего весеннего семестра опрос мнений студентов (в виде анонимных кратких эссе, где студентам было предложено в свободной форме) подтвердил преимущества развитого подхода к организации экзамена. Экзаменационное задание построено в точном соответствии со структурой и содержанием ДЕ ГОС ВПО; ясны критерии оценки и прозрачна сама процедура оценивания; студенту, получившему низкий балл, понятно, какие именно разделы курса он должен дополнительно проработать. Очевидна большая объективность данной формы проведения экзамена по сравнению с традиционной. Описанная схема анализа количественных показателей качества учебного процесса может быть с успехом использована и на других кафедрах, факультетах, вузах.

Приложение A

ГОУ ВПО Уральский государственный университет

Математический факультет

Кафедра математического анализа

Учебная дисциплина: «Математический анализ». Раздел: «Интегральное исчисление». Семестр: 3


Дата экзамена: «___» января 2009 г. Студент: ___________________ Группа: М -____

ДЕ	ДЕ - 1		ДЕ - 2				ДЕ - 3		ДЕ – 4
Задание	1.1	1.2	2.1	2.2	2.3	2.4	3.1	3.2	4.1	4.2
Баллы

Общая сумма баллов: ______. Итоговая оценка: ____________. Экзаменатор: ___________


Вариант 1

ДЕ-1: Неопределенный интеграл и основные методы интегрирования.

1.1 Вычислить интеграл .

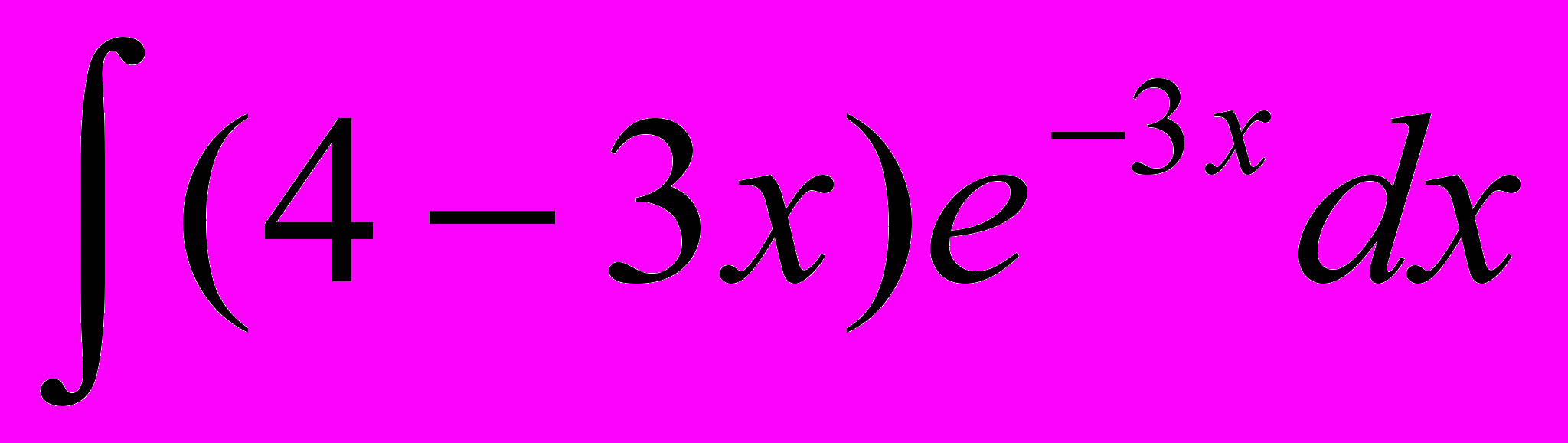1.2 Найти .

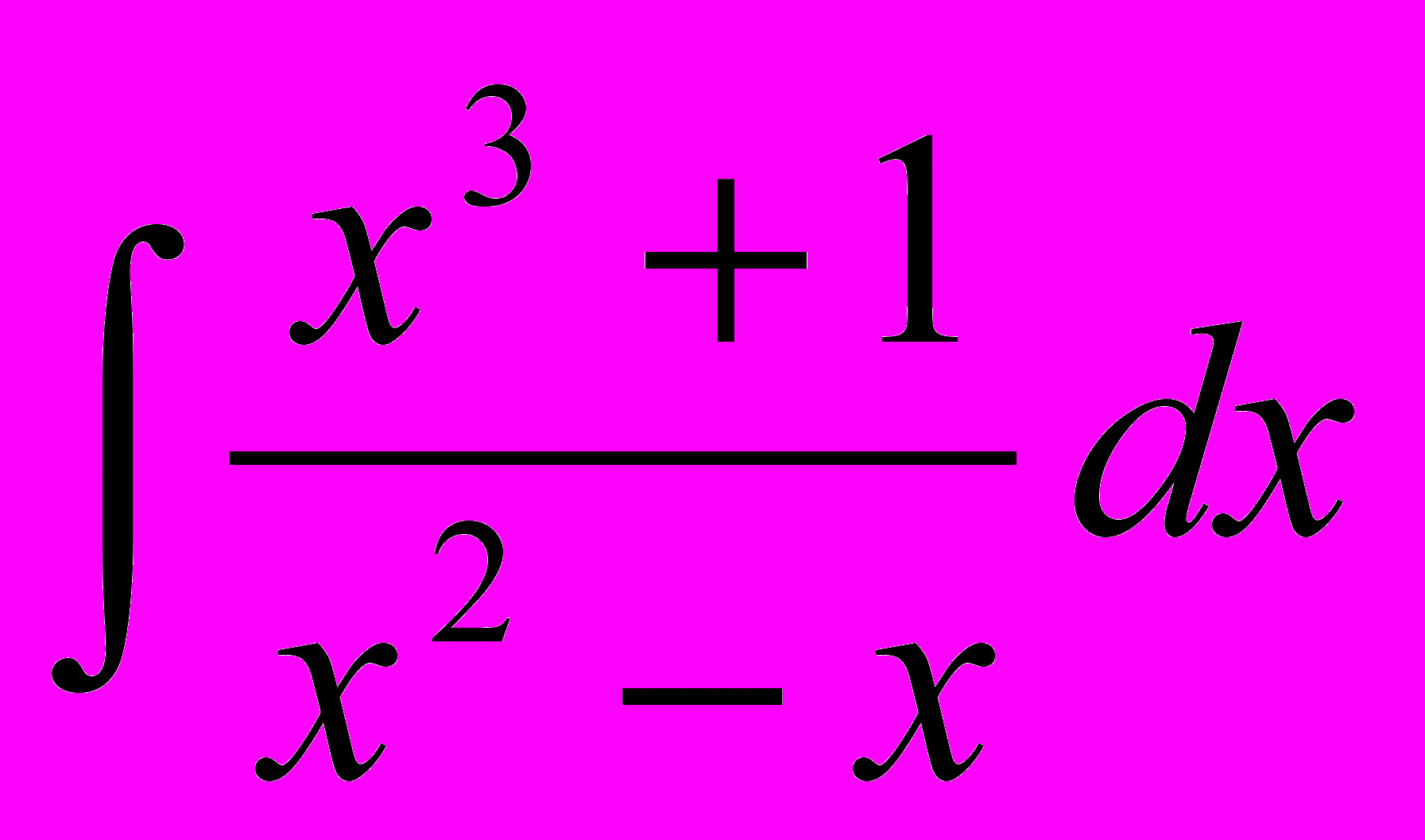ДЕ-2. Определенный интеграл. Формула Ньютона – Лейбница.

2.1 Дать описание способа построения интегральной суммы.

2.2 Указать и доказать основные свойства определенных интегралов, выражаемые равенствами.

2.3 Вычислить интеграл .

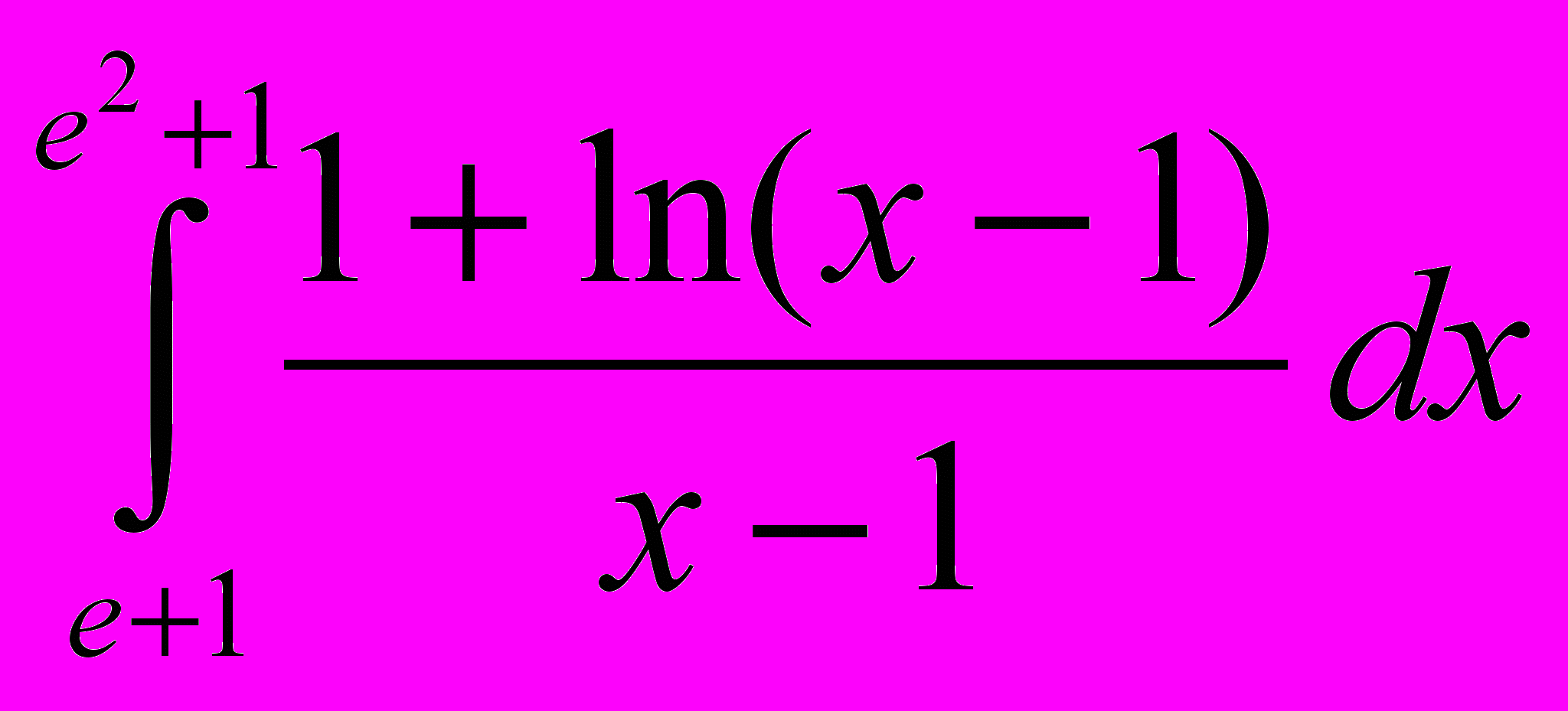2.4 Найти .

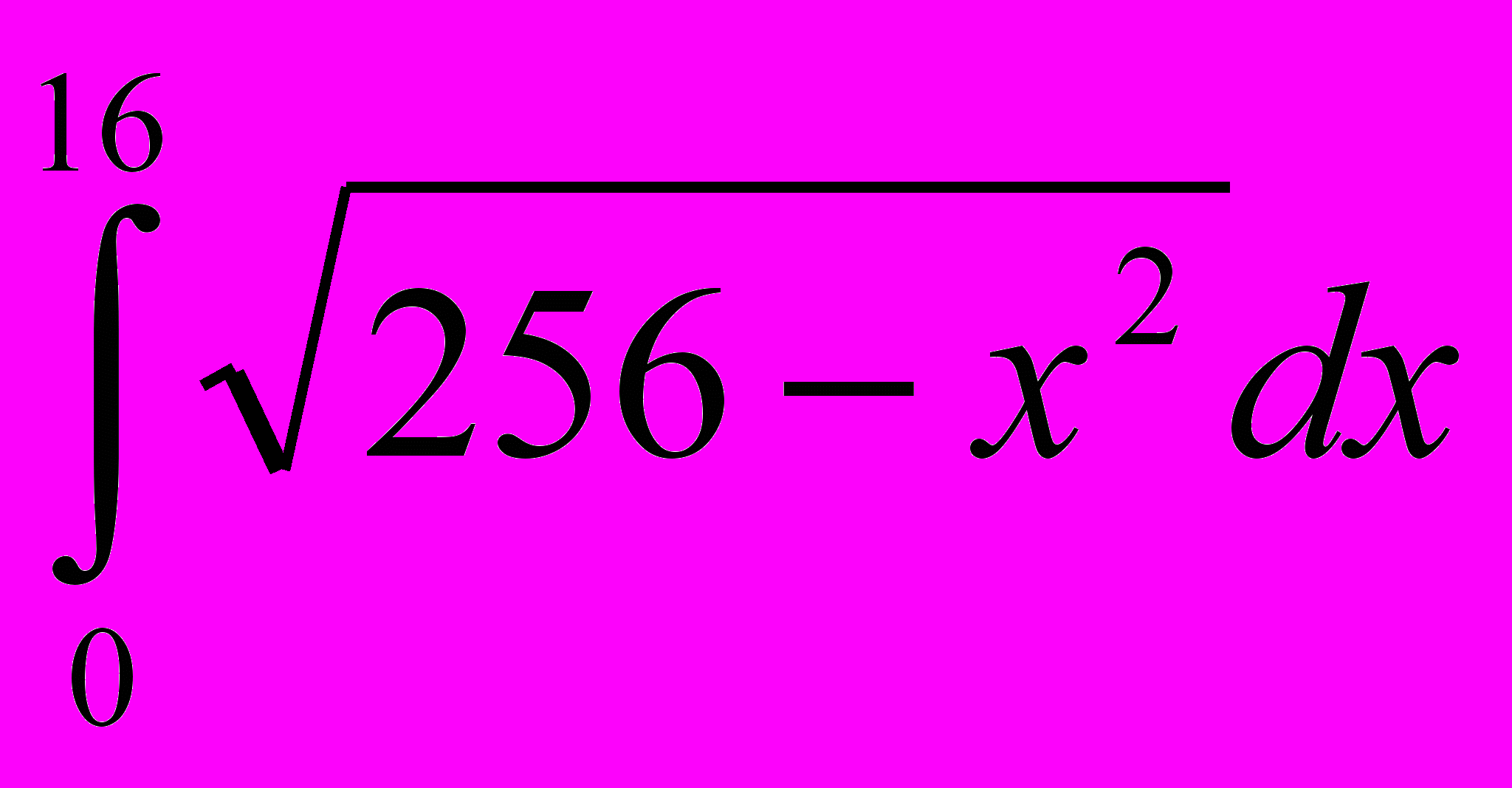ДЕ-3. Понятие квадрируемой фигуры, кубируемого тела, спрямляемой кривой.

3.1 Сформулировать и доказать теорему о необходимом и достаточном условии существования площади плоской фигуры.

3.2 Вычислить длину дуги кривой, заданной в прямоугольной системе координат: y = ln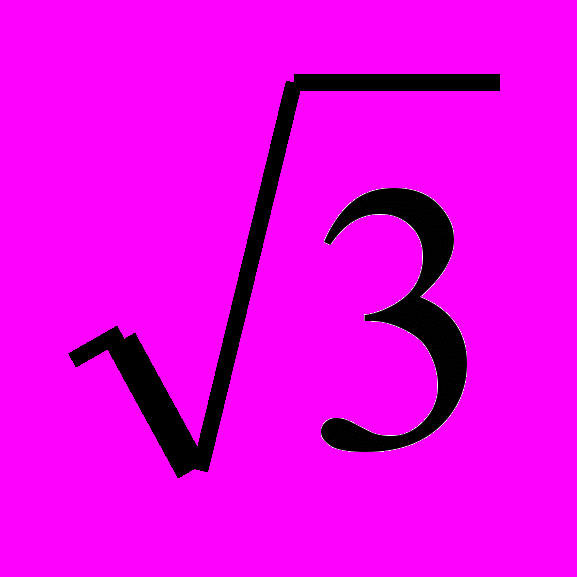x,  x  .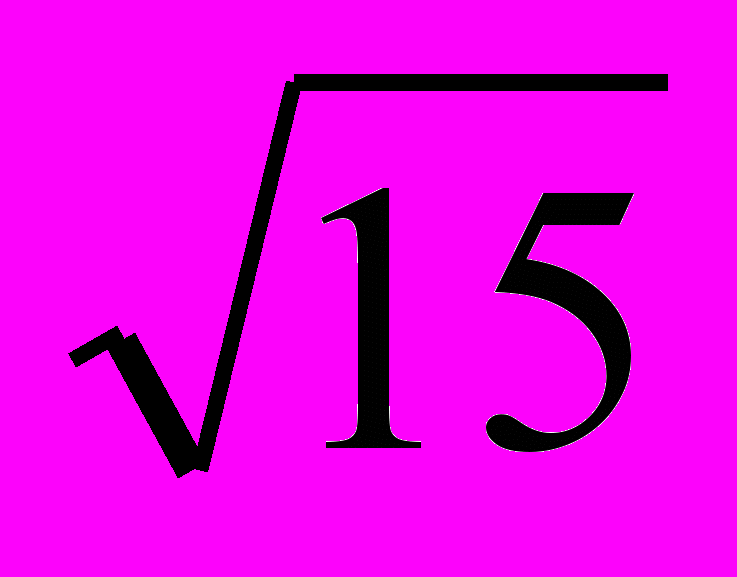

ДЕ-4. Несобственные интегралы.

4.1 Сформулировать определение понятия: несобственный интеграл I рода.

4.2 Вычислить интеграл .


Зав. кафедрой математического анализа

д.ф-м-н


П р и м е ч а н и я

1. Каждое задание оценивается по четырехбалльной шкале: «0» - задание не решено; «1/3» - решение задания намечено, но существенные для решения результаты не получены; «2/3» - получены существенные для решения результаты, но окончательное решение не получено; «1» - решение получено полностью.

2. Экзаменационная работа согласно ГОС ВПО содержит четыре дидактических единицы (ДЕ). Для зачета каждой ДЕ необходимо в ней набрать не менее половины от максимально возможного для нее числа баллов.

3. Для получения положительной оценки необходимо получить зачет всех четырех ДЕ.

4. Набранная общая сумма баллов переводится в экзаменационную оценку с помощью переводной таблицы (при условии зачета всех ДЕ).

5. Решение каждого задания следует завершать словом «Ответ: …», а результаты интегрирования проверять дифференцированием.

Список литературы

1. Шишов С.Е. Качество общего образования в постиндустриальном обществе.// Стандарты и мониторинг в образовании. 2008. № 5. С. 52-56.
   
2. Бордовский Г.А., Трапицын С.Ю., Граничина О.А. Мониторинг качества педагогического образования: состояние и проблемы.// Стандарты и мониторинг в образовании. 2008. № 6. С. 38-34.
   
3. Шаталов А.А., Афанасьев В.В., Афанасьева И.В., Гвоздева Е.А., Пичугина А.М. Мониторинг и диагностика качества образования. М.: НИИ школьных технологий, 2008. 322 С.
   
4. Шаталов А.А., Афанасьев В.В., Афанасьева И.В., Гвоздева Е.А., Пичугина А.М. Психолого-педагогическая диагностика качества образовательного процесса. М.: НИИ школьных технологий, 2008. 134 С.
   
5. Селевко Г.К. Энциклопедия образовательных технологий. В 2-х т. Т. 2. М.: НИИ школьных технологий, 2006. 816 С.
   
6. Поташник М.М. Требования к современному уроку: методическое пособие. М.: Центр педагогического образования, 2008. 272 C.
   
7. Попов Н.И. Мониторинг качества подготовки специалистов - математиков в рамках университетского образования.// Стандарты и мониторинг в образовании. 2008. № 6. С.35-36.
   
8. Портал ЕГЭ - ege.ru; www.ege.edu.ru.
   
9. Ховермилл Дж., Крайтес Т. Интегрирование содержания, педагогики и рефлексивной практики: новые инновационные курсы дистанционного обучения и программы для учителей математики.// Дистанционное и виртуальное обучение. 2008. № 12. С.65-67.
   
10. Медведенко Н.В., Рубцова С.Ю. Оценка и ее взаимосвязь с контролем, измерением и диагностикой в управлении качеством образования.// Стандарты и мониторинг в образовании. 2008. № 2. С. 19-22.
    
11. Бодряков В.Ю., Торопов А.П., Фомина Н.Г. Статистические методы исследования и оценки результатов экзаменационной сессии в вузе.// Сборник научных статей «Математика в образовании». Вып. 4. – Чебоксары: ЧувГУ, 2008, С.18-21.
    
12. Бодряков В.Ю., Торопов А.П., Фомина Н.Г. Оценка остаточных знаний по математическому анализу студентов математического факультета педагогического университета. // Сборник научных трудов 3-ей Международной заочной научно - практической конференции «Актуальные вопросы преподавания математики и информатики». – Биробиджан: Изд-во ДВГСГА, 2008, С.8-11.
    
13. Бодряков В.Ю., Торопов А.П., Фомина Н.Г. Динамика успеваемости студентов – математиков при обучении в УрГПУ в период поступления 2001 – выпуска 2006 г.// Качество. Инновации. Образование. 2008. №8. С.20-26.
    
14. Бодряков В.Ю., Торопов А.П., Фомина Н.Г. Анализ успеваемости студентов - математиков. // Alma mater. 2008. № 9. С.47-51.
    
15. Бодряков В.Ю., Фомина Н.Г. Инновационный подход к реорганизации традиционного экзамена в вузе с применением переносного персонального компьютера.// Сборник научных статей «Математический вестник педвузов и университетов Волго-Вятского региона». Вып. 10. – Киров: ВятГГУ, 2008, С.136-139.
    
16. Бодряков В.Ю., Фомина Н.Г. Простая вероятностно-статистическая модель количественной оценки знаний учащихся.// Alma mater. 2008. № 7. С. 55-61.
    
17. Бодряков В.Ю., Фомина Н.Г. Вероятностно-статистическая модель равно- и неравновзвешенного подходов к количественному оцениванию знаний учащихся.// Качество. Инновации. Образование. 2008. № 10. С. 12-16.
    
18. Бодряков В.Ю., Жаворонков В.Д., Фомина Н.Г. Инновационные элементы в проведении сессионного экзамена по высшей математике с учетом содержания ГОС ВПО.// Тезисы доклада на V Региональной научно-практической конференции «Колмогоровские чтения». – Владикавказ: СОГУ, 12-16 февраля, 2009 г.
    
19. Росаккредагентство. - fepo.ru.
    
20. Гмурман В.Е.. Теория вероятностей и математическая статистика. М.: Высшее образование, 2006. 479 С.
    
21. Бодряков В.Ю., Фомина Н.Г. Системный подход к формированию элементов профессиональной структуры интеллекта студентов - математиков.// Сборник научных статей «Математический вестник педвузов и университетов Волго - Вятского региона». Вып. 10. – Киров: Изд-во ВятГГУ, 2008, С.140-143.