Geum.ru

Рабочая программа дисциплины математика для специальности 190604

Вид материалаРабочая программа

Содержание


Цель дисциплины
Реализация общих компетенций
Распределение учебных часов
Максимальная учебная нагрузка
Самостоятель-ная работа
ТЕМА 4. Дифференциальные уравнения в частных производных
Итого по модулю
ТЕМА 5. Математическое ожидание и дисперсия случайной величины
Тема 3. Численное решение дифференциальных уравнений
Итого по модулю
Содержание курса
Входной контроль
Информационный блок
ТЕМА 2. Дифференциальное и интегральное исчисление
ТЕМА 3. Обыкновенные дифференциальные уравнения
ТЕМА 4. Дифференциальные уравнения в частных производных
Входной контроль
ТЕМА 3. Вероятность события, теоремы сложения и умножения
ТЕМА 4. Случайная величина, её функция распределения
ТЕМА 5. Математическое ожидание и дисперсия случайной величины
...
Полное содержание
Подобный материал:
Федеральное государственное образовательное учреждение

Среднего профессионального образования

«ОМСКИЙ АВТОТРАНСПОРТНЫЙ КОЛЛЕДЖ»


РАБОЧАЯ ПРОГРАММА


Дисциплины МАТЕМАТИКА

для специальности 190604

«Техническое обслуживание и ремонт

(код и наименование специальности)

автомобильного транспорта


Омск, 2009 г.

Модульная Рабочая программа по дисциплине

«МАТЕМАТИКА»


Рабочая программа по дисциплине «Математика» разработана для студентов специальности 190604 «Техническое обслуживание и ремонт автомобильного транспорта».

Учебная дисциплина «Математика» формирует базовые знания для освоения общепрофессиональных и специальных дисциплин. Программа направлена на получение багажа знаний, необходимых для формирования общих и профессиональных компетентностей.

Цель дисциплины:
  • формирование у студентов знаний и умений в области математики, необходимых для будущей трудовой деятельности по специальности 190604 «Техническое обслуживание и ремонт автомобильного транспорта».

В ходе дисциплины студенты будут:
  • иметь представление о роли и месте математики в современном мире, общности ее понятий и представлений;
  • знать основные понятия и методы математического анализа, дискретной математики, теории вероятности и математической статистики; основные численные методы решения прикладных задач;
  • уметь решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления; решать простейшие дифференциальные уравнения в частных производных; находить значения функций с помощью ряда Маклорена; решать простейшие задачи, используя элементы теории вероятности; находить функцию распределения случайной величины; использовать метод Эйлера для численного решения дифференциальных уравнений; находить аналитическое выражение производной по табличным данным; решать обыкновенные дифференциальные уравнения;
  • иметь опыт применять известные методы и способы решения задач, анализировать полученные результаты; решать типовые и творческие задания; работы с учебной документацией; систематизации информации.

Данная рабочая программа рассчитана на 45ч. аудиторных занятий, в том числе 20ч. отводится на практические занятия. Максимальная учебная нагрузка студентов составляет 61ч., из них 16ч. отводится на самостоятельную работу.

Программа реализует модульный подход в обучении и включает 4 модуля.

Модуль 1. Математический анализ

ТЕМА 1. Ряды

ТЕМА 2. Дифференциальное и интегральное исчисление

ТЕМА 3. Обыкновенные дифференциальные уравнения

ТЕМА 4. Дифференциальные уравнения в частных производных

Модуль 2. Основы дискретной математики, теории вероятности и математической статистики

ТЕМА 1. Множества и отношения. Операции над множествами. Свойства отношений

ТЕМА 2. Графы. Основные понятия теории графов

ТЕМА 3. Вероятность события, теоремы сложения и умножения

ТЕМА 4. Случайная величина, её функция распределения

ТЕМА 5. Математическое ожидание и дисперсия случайной величины

Модуль 3. Основные численные методы

ТЕМА 1. Численное интегрирование

ТЕМА 2. Численное дифференцирование. Численное решение дифференциальных уравнений

Тема 3.Численное решение дифференциальных уравнений

Модуль 4. Комплексный экзамен

Целью и формами реализации программы является переход на модульно-компетентностную основу подготовки специалиста, которая реализуется в дисциплине «Математика» через формирование общих компетенций:

ОК 1. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 2. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 3. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 4. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

Форма контроля знаний – модульный рейтинг по завершении работы по каждому модулю, по окончании курса – зачет, форма зачета – итоговые задания в тестовой форме, итоговые практические задания.


Составитель: О.В. Романова

Рецензенты:

РЕАЛИЗАЦИЯ ОБЩИХ КОМПЕТЕНЦИЙ

Набор и перечень общих компетенций
Практический опыт
Уметь
Знать

ОК 1. Организовывать собственную деятельность, производить выбор типовых методов и способов выполнения профессиональных задач, оценивать их эффективность и качество

Применять известные методы и способы решения задач, анализировать полученные результаты
Вычисление производных функций при заданных значениях аргумента.
  • Определение производной, ее геометрический смысл
  • Таблицу производных

Вычисление площадей плоских фигур
  • Понятия неопределенного и определенного интеграла
  • Основные методы интегрирования
  • Формулы интегрирования
  • Формулу Ньютона-Лейбница

Определение сходимости функциональных и числовых рядов
  • Определения функционального и числового рядов
  • Необходимые и достаточные признаки сходимости рядов
  • Признак Даламбера

Вычисление интегралов по формулам прямоугольников, трапеций и формуле Симпсона.
  • Способы представления функции в виде прямоугольника и трапеции
  • Формулу Симпсона

ОК 2. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность
Решать типовые и творческие задания
Исследовать функцию с помощью производной и построить график
  • Алгоритм исследования функции
  • Признаки экстремума функции
  • Признаки монотонности функции

Составление и решение дифференциального уравнения на простейшие задачи
  • Типы задач, приводящие к дифференциальным уравнениям
  • Определение дифференциального уравнения
  • Определения общего и частного решения дифференциального уравнения и их геометрические интерпретации
  • Методы решения обыкновенных дифференциальных уравнений с разделяющимися переменными и дифференциальных уравнений второго порядка с постоянными коэффициентами

Решение простейших задач на определение вероятности
  • Понятия: события, частота и вероятность появления события, совместные и несовместные события, полная вероятность
  • Теорема сложения вероятностей
  • Теорема умножения вероятностей

ОК 3. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития

Работа с учебной документацией
Выбирать нужные методы и способы для решения поставленных задач
  • Основные формулы по курсу «Математика»
  • Основные методы и способы решения типичных заданий
  • Вычисление погрешностей найденного решения

Составление алгоритма решения дифференциального уравнения второго порядка с постоянными коэффициентами
  • Определение дифференциального уравнения второго порядка с постоянными коэффициентами
  • Формулы общего решения
  • Правило нахождения частного решения дифференциального уравнения

ОК 4. Ориентироваться в условиях частой смены технологий в профессиональной деятельности
Систематизация информации
Применение графов для представления информации
  • Определение графов и его элементов
  • Виды графов и операции над ними

Составление и использование закона распределения случайной величины
  • Понятие закона распределения случайной величины
  • Определение математического ожидания, дисперсии дискретной случайной величины
  • Среднее квадратичное отклонение случайной величины

РАСПРЕДЕЛЕНИЕ УЧЕБНЫХ ЧАСОВ

Наименование модуля
Количество часов

Максимальная учебная нагрузка
Всего
На занятиях
Лабораторно-практические занятия
Самостоятель-ная работа

1
2
3
4
5
6

Модуль 1. Математический анализ: ОК 3, ОК4.

ТЕМА 1. Ряды
11
9
3
6
2

ТЕМА 2. Дифференциальное и интегральное исчисление
16
10
2
8
6

ТЕМА 3. Обыкновенные дифференциальные уравнения
6
4
2
2
2

ТЕМА 4. Дифференциальные уравнения в частных производных

4
4
2
2



Итого по модулю
37
27
9
18
10

Модуль 2. Основы дискретной математики, теории вероятности и математической статистики: ОК 1, ОК 2.

ТЕМА 1. Множества и отношения. Операции над множествами. Свойства отношений
2
2
2






ТЕМА 2. Графы. Основные понятия теории графов
3
2
2



1

ТЕМА 3. Вероятность события, теоремы сложения и умножения
6
4
2
2
2

ТЕМА 4. Случайная величина, её функция распределения
3
2
2



1

ТЕМА 5. Математическое ожидание и дисперсия случайной величины
2
2
2






Итого по модулю
16
12
10
2
4

Модуль 3. Основные численные методы: ОК 1, ОК 2.

ТЕМА 1. Численное интегрирование
4
2
2



2

ТЕМА 2. Численное дифференцирование. Численное решение дифференциальных уравнений
2
2
2






Тема 3. Численное решение дифференциальных уравнений
4
4
4






Итого по модулю
8
6
4



2

Модуль 4. Комплексный экзамен















ИТОГО
61
45
25
20
16


СОДЕРЖАНИЕ КУРСА


Модуль 1. Математический анализ

Цели:
  • иметь представление о роли математике при изучении общепрофессиональных и специальных дисциплин в профессиональной деятельности;
  • знать определение числовой последовательности, предела последовательности; предел функции в точке, непрерывность функции; первый и второй замечательные пределы; определение числового ряда, суммы ряда; необходимый и достаточный признаки сходимости рядов, признак Даламбера; определение производной, ее физический и геометрический смысл; таблицу производных; формулы производных суммы, произведения, частного функций; основные методы интегрирования; формулы интегрирования; формулу Ньютона-Лейбница; определения частной производной; свойства определенного и неопределенного интегралов; типы задач, приводящих к дифференциальным уравнениям; определение дифференциального уравнения; определение общего и частного решения дифференциальных уравнений, их геометрической интерпретации; методы решения дифференциальных уравнений с разделяющимися переменными, дифференциальных уравнений первого порядка, дифференциальных уравнений второго порядка с постоянными коэффициентами; методы решения простейших дифференциальных уравнений в частных производных;
  • уметь определять сходимость числового ряда по признаку Даламбера; вычислять производные при заданном значении аргумента; исследовать функцию с помощью производной и строить графики; интегрировать простейшие определенные интегралы; вычислять площади плоских фигур; находить частные производные различных порядков; составлять дифференциальные уравнения на простейших задачах; решать дифференциальные уравнения с разделяющимися переменными; решать однородные дифференциальные уравнения первого порядка; решать однородные линейные уравнения второго порядка с постоянными коэффициентами; решать простейшие дифференциальные уравнения в частных производных;
  • иметь опыт применять известные методы и способы решения задач, анализировать полученные результаты.

Входной контроль

Мозговой штурм по теме «Основные математические формулы за курс средней школы. Связь математики с общепрофессиональными и специальными дисциплинами»

Информационный блок

ТЕМА 1. Ряды

Числовая последовательность, предел последовательности. Числовой ряд, сумма ряда. Необходимый и достаточный признак сходимости ряда.

ТЕМА 2. Дифференциальное и интегральное исчисление

Производная, геометрический смысл производной. Исследование функции. Неопределенный интеграл. Непосредственное интегрирование. Замена переменной. Определенный интеграл. Вычисление определенного интеграла. Геометрический смысл определенного интеграла. Приложение определенного интеграла к решению прикладных задач. Частные производные.

ТЕМА 3. Обыкновенные дифференциальные уравнения

Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

ТЕМА 4. Дифференциальные уравнения в частных производных

Решение дифференциальных уравнений в частных производных.

Практическая работа
  1. Вычисление предела функции в точке. Применение замечательных пределов.
  2. Исследование функции на непрерывность в точке.
  3. Исследование рядов на сходимость с помощью необходимого и достаточного условия сходимости , признака Даламбера.
  4. Производная, ее физический и геометрический смысл. Производная сложной функции. Нахождение производной.
  5. Исследование функции с помощью производной.
  6. Неопределенный интеграл, его свойства. Методы интегрирования. Вычисление неопределенного интеграла.
  7. Определенный интеграл. Формула Ньютона-Лейбница. Вычисление определенного интеграла.
  8. Решение дифференциальных уравнений II порядка с постоянными коэффициентами.
  9. Решение дифференциальных уравнений в частных производных.

Самостоятельная работа

Практические задания:
  1. Исследование функции с помощью производной и построение графика.
  2. Вычисление производных функций при заданных значения аргумента.
  3. Вычисление площадей плоских фигур.
  4. Определение сходимости функциональных и числовых рядов.
  5. Найти дифференциал функции.
  6. Решение задач с практическим содержанием.
  7. Составление и решение дифференциального уравнения на простейшие задачи.
  8. Составление алгоритма решения дифференциального уравнения второго порядка с постоянными коэффициентами.

Примерные темы рефератов:
  1. Роль математики в подготовке специалиста специальности 190604 «Техническое обслуживание и ремонт автомобильного транспорта».
  2. История развития дифференциального исчисления.

Подготовить сообщение «Приложение рядов (при обращении десятичных дробей в обыкновенную)»

Выходной контроль
  1. Задания в тестовой форме.
  2. Рефераты.


Модуль 2. Основы дискретной математики, теории вероятности и математической статистики

Цели:
  • иметь представление о способах задания множеств; о диаграммах Эйлера; о связи понятия графа и понятия отношения;
  • знать определения множества и отношения; операции и свойства операций над множествами; свойства отношений; определение графов и его элементов; виды графов и операции над ними; понятия: событие, частота и вероятность появления события, совместные и несовместные события, полная вероятность; теорему сложения вероятностей; теорему умножения вероятностей; способы задания случайной величины; определение непрерывной и дискретной случайных величин; закон распределения случайной величины; определение математического ожидания, дисперсия случайной величины; среднее квадратичное отклонение случайной величины;
  • уметь находить вероятность в простейших задачах, используя классическое определение вероятности; решать задачи с применением теоремы сложения вероятностей для несовместных событий; строить ряд распределения случайной величины; находить функцию распределения; находить математическое ожидание и дисперсию случайной величины по заданному закону её распределения; находить среднее квадратичное отклонение случайной величины;
  • иметь опыт решения типичных и творческих заданий; систематизации информации.

Входной контроль

Задания в тестовой форме по теме «Первичные понятия математики».

Информационный блок

ТЕМА 1. Множества и отношения. Операции над множествами. Свойства отношений

Элементы множества. Задание множеств. Операции над множествами. Отношения. Свойства отношений.

ТЕМА 2. Графы. Основные понятия теории графов

Графы. Основные определения. Элементы графов. Виды графов и операции над ними.

ТЕМА 3. Вероятность события, теоремы сложения и умножения

Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятности. Теорема сложения вероятностей. Теорема умножения вероятностей.

ТЕМА 4. Случайная величина, её функция распределения

Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения случайной величины.

ТЕМА 5. Математическое ожидание и дисперсия случайной величины

Математическое ожидание дискретной случайной величины. Дисперсия случайной величины. Среднее квадратичное отклонение случайной величины.

Практическая работа

1. Элементы комбинаторики. Решение задач по комбинаторике.

Самостоятельная работа
  1. Поиск дополнительной информации в современных поисковых системах (Internet).
  2. Составить условие и построить закон распределения случайной величины.
  3. Решение простейших задач на определение вероятности.
  4. Применение графов для представления информации.
  5. Составление и использование закона распределения случайной величины.

Выходной контроль
  1. Задания в тестовой форме.
  2. Представление материалов самостоятельной работы.


Модуль 3. Основные численные методы

Цели:
  • знать способы представления функции в виде прямоугольника и трапеции; формулу Симпсона; выражения для определения предельных абсолютных погрешностей; гентерполяционные формулы Ньютона; таблицу конечных разностей; метод Эйлера для решения задачи Коши;
  • уметь вычислять интегралы по формулам прямоугольников и трапеций и по формуле Симпсона; по табличным данным находить аналитическое выражение производной; Находить значение функции, определяемое заданным дифференциальным уравнением и начальными условиями с использованием метода Эйлера;
  • иметь опыт применения известных методов и способов решения задач, анализировать полученные результаты.

Входной контроль

Задания в тестовой форме по теме «Вычисление определенного интеграла. Нахождение значения производной в точке».

Информационный блок

ТЕМА 1. Численное интегрирование

Формулы прямоугольников. Формулы трапеций. Формула Симпсона. Абсолютная погрешность при численном интегрировании.

ТЕМА 2. Численное дифференцирование.

Численное дифференцирование. Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона. Погрешность в определении производной. Построение интегральной кривой. Метод Эйлера.

ТЕМА 3. Численное решение дифференциальных уравнений

Самостоятельная работа

Вычисление определенного интеграла по формулам прямоугольников, трапеций и формуле Симпсона.

Выходной контроль

Задания в тестовой форме.

Отчет по самостоятельной работе.

Модуль 4. Комплексный экзамен

Цели:

Проверка знаний и умений студентов по дисциплине «Математика».

Контроль
  1. Итоговые задания в тестовой форме.
  2. Итоговые практические задания.

УЧЕТ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТА, НАЦЕЛЕННОЙ НА ФОРМИРОВАНИЕ ОБЩИХ КОМПЕТЕНЦИЙ

Компетенции
Тема занятия
Вид СРС (работа по формированию компетенций)
Время (ч)

ОК 1
ТЕМА 1. Ряды
Определение сходимости функциональных и числовых рядов
2

ТЕМА 2. Дифференциальное и интегральное исчисление
Вычисление производных функций при заданных значения аргумента

Вычисление площадей плоских фигур

2


2

ТЕМА 1. Численное интегрирование
Вычисление интегралов по формулам прямоугольников, трапеций и формуле Симпсона
2

ОК 2
ТЕМА 2. Дифференциальное и интегральное исчисление
Исследование функции с помощью производной и построение графика
2

ТЕМА 3. Обыкновенные дифференциальные уравнения
Составление и решение дифференциального уравнения на простейшие задачи
1

ТЕМА 3. Вероятность события, теоремы сложения и умножения
Решение простейших задач на определение вероятности
2

ОК 3
ТЕМА 3. Обыкновенные дифференциальные уравнения
Составление алгоритма решения дифференциального уравнения второго порядка с постоянными коэффициентами
1

ОК 4
ТЕМА 2. Графы. Основные понятия теории графов
Применение графов для представления информации
1

ТЕМА 4. Случайная величина, её функция распределения
Составление и использование закона распределения случайной величины
1

Итого
16


РУБЕЖНЫЙ КОНТРОЛЬ

№ и название модуля
Вид, форма контроля
Время (ч)

Модуль 1. Математический анализ
  1. Задания в тестовой форме.
  2. Рефераты.
2

Модуль 2. Основы дискретной математики, теории вероятности и математической статистики
  1. Задания в тестовой форме.
  2. Представление материалов самостоятельной работы.
2

Модуль 3. Основные численные методы
  1. Задания в тестовой форме.
  2. Отчет по самостоятельной работе.
3

Модуль 4. Комплексный экзамен
  1. Итоговые задания в тестовой форме.
  2. Итоговые практические задания.
3


МОДУЛЬНО-РЕЙТИНГОВАЯ КАРТА ДИСЦИПЛИНЫ

Наименование модуля, виды работ и формы контроля
Рейтинг-баллы

минимум
максимум

Модуль 1
15
24
  1. Работа на занятиях
6
9
  1. Практическая работа
1
3
  1. Задания в тестовой форме
6
9
  1. Реферат
2
3

Модуль 2
15
24
  1. Входной контроль
2
3
  1. Работа на занятиях
6
9
  1. Задания в тестовой форме
4
7
  1. Самостоятельная работа
3
5

Модуль 3
29
46
  1. Входной контроль
2
3
  1. Работа на занятиях
16
24
  1. Самостоятельная работа
5
10
  1. Задания в тестовой форме
6
9

Итоговый модуль (зачет)
18
30
  1. Итоговые задания в тестовой форме
9
15
  1. Итоговые практические задания
9
15

Дисциплинарный рейтинг:
77
124

Шкала перевода дисциплинарного рейтинга в академические оценки

Дисциплинарный рейтинг
Академическая оценка

62 - 74 %
3 (удовлетворительно)

75 - 87%
4 (хорошо)

88 - 100 %
5 (отлично)


РЕЙТИНГ-КАРТА СТУДЕНТА

Наименование модуля, виды работы и формы контроля
Рейтинг-баллы
Сроки сдачи освоенных элементов модуля
Рейтинг-баллы, набранные студентом
Подпись преподавателя

минимум
максимум

Модуль 1
15
24








  1. Работа на занятиях
6
9








  1. Практическая работа
1
3








  1. Задания в тестовой форме
6
9








  1. Реферат
2
3









Модуль 2
15
24








  1. Входной контроль
2
3








  1. Работа на занятиях
6
9








  1. Задания в тестовой форме
4
7








  1. Самостоятельная работа
3
5









Модуль 3
29
46








  1. Входной контроль
2
3








  1. Работа на занятиях
16
24








  1. Самостоятельная работа
5
10








  1. Задания в тестовой форме
6
9









Итоговый модуль (зачет)
18
30








  1. Итоговые задания в тестовой форме
9
15








  1. Итоговые практические задания
9
15









Дисциплинарный рейтинг:
77
124



Шкала перевода дисциплинарного рейтинга в академические оценки

Дисциплинарный рейтинг
Академическая оценка

62 - 74 %
3 (удовлетворительно)

75 - 87%
4 (хорошо)

88 - 100 %
5 (отлично)

ВОПРОСЫ К ЭКЗАМЕНУ ПО МАТЕМАТИКЕ

для специальности

190604 «Техническое обслуживание и ремонт автомобильного транспорта»

  1. Последовательность, способы задания (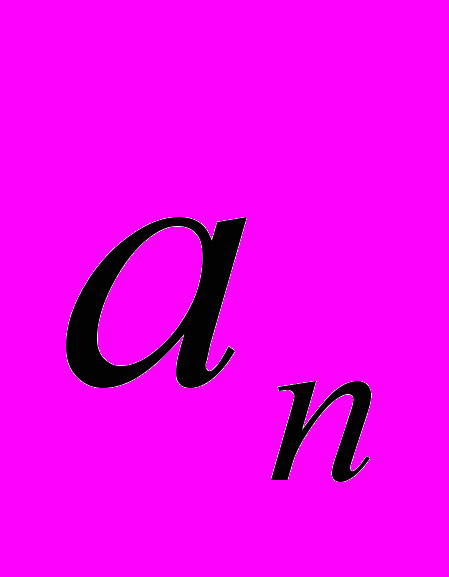). Предел последовательности. Свойства пределов.
  2. Предел функции в точке. Теоремы о пределах.
  3. Непрерывность функции в точке и на промежутке.
  4. Замечательные пределы (I и II).
  5. Понятие числового ряда, суммы ряда, сходимость ряда.
  6. Необходимое и достаточные условия сходимости ряда. Признак Даламбера.
  7. Производная, ее физический и геометрический смысл.
  8. Формулы дифференцирования.
  9. Производная суммы, произведения, частного.
  10. Производная сложной функции.
  11. Признаки возрастания и убывания функции (необходимое и достаточное условия). Правило нахождения интервалов монотонности.
  12. Экстремумы функции. Необходимое и достаточные условия существования экстремума.
  13. Правило нахождения экстремума (I-ое).
  14. Исследование функции на выпуклость графика, точку перегиба. Правило нахождение интервалов выпуклости графика и нахождение точки перегиба.
  15. Функции нескольких переменных. Частные производные. Полный дифференциал функции.
  16. Неопределенный интеграл и его свойства. Основные формулы интегрирования.
  17. Определенный интеграл и его геометрический смысл.
  18. Формула Ньютона-Лейбница. Вычисление определенного интеграла и его приложения.
  19. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения. Основные понятия и определения.
  20. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения.
  21. Однородные дифференциальные уравнения II порядка с постоянными коэффициентами.
  22. Предмет теории вероятностей. Случайные события. Виды случайных событий.
  23. Частота и вероятность события, классическое определение вероятности.
  24. Элементы комбинаторики. Размещения, сочетания, перестановки и формулы их числа.
  25. Теоремы сложения вероятностей.
  26. Теоремы умножения вероятностей.
  27. Формула полной вероятности.
  28. Дискретная случайная величина и ее закон распределения.
  29. Математическое ожидание и дисперсия случайной величины.


Литература

Основная
  1. Белявский С.С. Высшая математика. Решение задач / С.С. Белявский, Н.А. Широкова. – Минск: Высшая школа, 2004.
  2. Богомолов Н.В. Практические занятия по математике / Н.В. Богомолов. – М.: Высшая школа, 1990.
  3. Валуцэ И.И. Математика для техникумов / И.И. Валуцэ, Г.Д. Дилигун. – М.: Наука, 1990.
  4. Дадаян А.А. Сборник задач по математике / А.А. Дадаян. – М.: Инфра-М, 2005.
  5. Колягин Ю.М. Математика: учебное пособие: в 2 кн. / Ю.М. Колягин, Г.Л. Луканкин, Г.Н. Яковлев. – М.: ООО «Издательство Новая Волна», 2004.
  6. Лисичкин В.Т. Математика: учебное пособие / В.Т. Лисичкин, И.Л. Соловейчик. – М.: ABF, 1995.
  7. Омельченко В.П. Математика: учебное пособие / В.П. Омельченко, Э.В. Курбатова. – Ростов-н/: Феникс, 2007.
  8. Пехлецкий И.Д. Математика / И.Д. Пехлецкий. – М.: Издательский центр «Академия», 2002.
  9. Сборник задач по высшей математике для экономистов: учебное пособие / Под ред. В.И. Ермакова. – М.: Инфра-М, 2006.


Дополнительная
  1. Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов. – М.: Наука, 1990
  2. Бутузов В.Ф., Крутицкая Н.И. Математический анализ в вопросах и задачах. – М.: Физматлит, 2000
  3. Выготский М.Я. Справочник по высшей математике. – М.: Росткнига, 2001
  4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 1 и 2. – М.: Высшая школа, 1999
  5. Ерусалимский Я.М. Дискретная математика. – М.: Вузовская книга, 2001
  6. Калинина В.Н., Панкин В.Ф. Математическая статистика. – М.: Высшая школа, 2001
  7. Натансон И.П. Краткий курс высшей математики. – С-Пб.: Лань, 2001
  8. Щипачев В.С. Задачи по высшей математике. – М.: Высшая школа, 1997
  9. Щипачев В.С. Основы высшей математики. – М.: Высшая школа, 2001


Средства обучения:


1. Учебники и учебные пособия.

2. Плакаты.

3. Дидактический материал по всем разделам курса «Математика»:

4. Тестовые задания для контроля знаний

5. Контрольные работы.

6. Справочная литература.

7. Средства ТСО, Интернет.