Рабочая программа дисциплины

Вид материала

Рабочая программа

Содержание Российской Федерации» В.М. Гончаренко Рекомендовано Ученым советом факультета «Математические ?? В.М. Гончаренко Учебное издание Задача дисциплины 2. Место дисциплины в структуре ООП 3. Требования к результатам освоения дисциплины 4. Объём дисциплины и виды учебной работы Вид учебной работы 5. Содержание дисциплины Решение общей задачи линейного программирования. 5.2. Разделы дисциплины и виды занятий 5.3. Разделы дисциплины и междисциплинарные связи с обеспечиваемыми дисциплинами 6. Практические (семинарские) занятия 7. Самостоятельная работа 8. Контрольные вопросы и системы оценивания Уровень требований и критерии оценок М.: юнити, 2008. Линейные модели в экономике ... Полное содержание

Подобный материал:

• Рабочая программа учебной дисциплины ф тпу 1 -21/01, 102.93kb.
• Рабочая программа, программа дисциплины по дисциплине Культура Китая Аббревиатура специальности, 300.02kb.
• Рабочая программа, программа дисциплины история российско-китайских отношений аббревиатура, 505.79kb.
• Рабочая учебная программа (Syllabus) дисциплины Наименование дисциплины: социальная, 372.74kb.
• Рабочая программа дисциплины Культурология опд. 00 Общепрофессиональные дисциплины, 478.45kb.
• Рабочая программа дисциплины «уголовное право» рабочая программа дисциплины, 543.84kb.
• Рабочая программа учебной дисциплины: рабочая программа дисциплины «криминология», 325.75kb.
• Рабочая программа учебной дисциплины: рабочая программа дисциплины «юридическая психология», 239.82kb.
• Рабочая программа дисциплины, 286.45kb.
• Рабочая программа дисциплины, 206.05kb.

Федеральное государственное образовательное бюджетное учреждение

высшего профессионального образования


«ФинансовЫЙ УНИВЕРСИТЕТ при Правительстве

Российской Федерации»


Кафедра «Прикладная математика»


В.М. Гончаренко


Исследование операций


Рабочая программа дисциплины


Для подготовки бакалавров направления 010400.62 «Прикладная

математика и информатика» по профилю «Математическое и

информационное обеспечение экономической деятельности»


Москва 2010


Федеральное государственное образовательное бюджетное учреждение

высшего профессионального образования


«ФинансовЫЙ УНИВЕРСИТЕТ при Правительстве

Российской Федерации»


Кафедра «Прикладная математика»


утверждаю

Ректор

__________ М.А. Эскиндаров

_______ ___________ 2010 г.


В.М. Гончаренко


Исследование операций


Рабочая программа дисциплины


Для подготовки бакалавров направления 010400.62 «Прикладная

математика и информатика» по профилю «Математическое и

информационное обеспечение экономической деятельности»


Рекомендовано Ученым советом факультета «Математические

методы и анализ рисков», протокол № 6 от 25 мая 2010 г.


Одобрено кафедрой «Прикладная математика», протокол № 12 от

19 мая 2010 г.


Москва 2010



УДК ?

ББК ?

Рецензент: В.В. Киселев, доцент кафедры «Прикладная математика»

?? В.М. Гончаренко

«Исследование операций». Программа дисциплины для студентов, обучающихся по направлению «Прикладная математика» (программа подготовки бакалавров) – очная форма обучения.– М.: ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», кафедра «Прикладная математика», 2010. - с.


Дисциплина «Исследование операций» является дисциплиной вариативной части цикла «Математика» дисциплин ФГОС ВПО по направлению 010400.62 «Прикладная математика и информатика». Программа содержит: программу дисциплины; рабочий план изучения дисциплины; тематику и планы лекций, тематику практических и самостоятельных занятий с указанием технологии их проведения; формы контроля за их выполнением.

УДК ?

ББК ?

Учебное издание

Василий Михайлович Гончаренко


Исследование операций


Рабочая программа дисциплины


Компьютерный набор, верстка: В.М. Гончаренко.

Формат 60х90/16. Гарнитура Times New Roman

Усл.п.л.1,1. Изд. № -2010. Тираж ___ экз.


Отпечатано в ФГОУ ВПО «Финансовый университет при

Правительстве Российской Федерации»

 В.М. Гончаренко, 2010

 ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», 2010





Содержание

1. Цели и задачи дисциплины . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
   
2. Место дисциплины в структуре ООП . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
   
3. Требования к результатам освоения дисциплины . . . . . . . . . . . . . . . . . . 5
   
4. Объем дисциплины и виды учебной работы . . . . . . . . . . . . . . . . . . . . . . 7
   
5. Содержание дисциплины
   

5.1 Содержание разделов дисциплины . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

5.2 Разделы дисциплины и междисциплинарные связи . . . . . . . . . . . . . 10

5.3 Разделы дисциплины и виды занятий . . . . . . . . . . . . . . . . . . . . . . . . 11

6. Практические (семинарские) занятия . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
   
7. Самостоятельная работа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
   
8. Контрольные вопросы и системы оценивания. . . . . …………………… 13
   
9. Учебно-методическое и информационное обеспечение дисциплины ... 17
   
10. Приложение. Учебно-методическая карта дисциплины . . . . . . . . . . . 19
    

1. Цели и задачи дисциплины

Цель дисциплины –

1. Получение базовых знаний и формирование основных навыков по линейному программированию и теории двойственности, необходимых для решения задач, возникающих в практической экономической деятельности.

2. Развитие понятийной теоретической базы и формирование уровня практической подготовки, необходимых для понимания основных методов исследования операций и их применения в экономике.

Задача дисциплины –

В результате изучения дисциплины «Исследование операций» студенты должны владеть основными математическими понятиями дисциплины; уметь использовать математический аппарат для решения теоретических и прикладных задач экономики; уметь решать типовые задачи и иметь навыки работы со специальной математической литературой.


2. Место дисциплины в структуре ООП


Дисциплина «Исследование операций» является дисциплиной вариативной части математического цикла Федеральных государственных образовательных стандартов высшего профессионального образования (ФГОС ВПО) по направлению 010400.62 «Прикладная математика и информатика» (бакалавриат).

Изучение дисциплины «Исследование операций» основывается на базе знаний, полученных студентами в ходе освоения дисциплин «Линейная алгебра» и «Математический анализ» того же блока.

Дисциплина «Исследование операций» изучается на первом году обучения, закладывает фундамент для понимания основных методов решения задач оптимизации и эконометрического прогнозирования и является базовым теоретическим и практическим основанием для многих последующих математических и финансово-экономических дисциплин подготовки бакалавров по направлению «Прикладная математика и информатика».


3. Требования к результатам освоения дисциплины


В совокупности с другими дисциплинами базовой и вариативной части математического цикла ФГОС ВПО дисциплина «Исследование операций» обеспечивает инструментарий формирования следующих общих и профессиональных компетенций бакалавра экономики:

• владение культурой мышления, умение аргументировано и ясно строить устную и письменную речь (ОК-1);
  
• способность к интеллектуальному, культурному и профессиональному саморазвитию, стремление к повышению свей квалификации и мастерства (ОК-2);
  
• способность осознавать социальную значимость своей профессии, обладание высокой мотивацией к выполнению профессиональной деятельности (ОК-9);
  
• демонстрация общенаучных базовых знаний естественных наук, математики и информатики, понимание основных научных фактов, концепций, принципов теорий, связанных с прикладной математикой (ОК-10);
  
• умение использовать навыки поиска и работы с информацией из различных источников, включая сетевые ресурсы сети Интернет, для решения профессиональных и социальных задач (ОК-15);
  
• умение приобретать новые научные и профессиональные знания, используя современные и информационные технологии (ОК-16);
  
• способность собирать, обрабатывать и интерпретировать данные современных научных исследований, необходимые для формирования выводов по соответствующим научным, профессиональным, социальным и этическим проблемам (ПК-1);
  
• способность понимать и применять в исследовательской и прикладной деятельности современный математический аппарат (ПК-2);
  
• способность в составе научно-исследовательского и производственного коллектива решать задачи профессиональной деятельности (в соответствии с профилем подготовки) (ПК-4);
  
• способность критически переосмысливать накопленный опыт, изменять при необходимости вид и характер своей профессиональной деятельности (ПК-5);
  
• способность осуществлять целенаправленный поиск информации о новейших научных и технологических достижениях в сети Интернет и из других источников (ПК-6);
  
• знание и следование в жизни кодексу профессиональной этики (ПК-7);
  
• способность формировать суждения о значении и последствиях своей профессиональной деятельности с учетом социальных, профессиональных и этических позиций (ПК-8);
  
• понимание сущности и значения информации в развитии современного общества; владение основными методами, способами и средствами получения, хранения, переработки информации (ПК-9);
  
• способность решать задачи производственной и технологической деятельности на профессиональном уровне (ПК-10);
  
• способность составлять и контролировать план выполняемой работы, планировать необходимые для выполнения работы ресурсы, оценивать результаты собственной работы (ПК-12);
  

В результате освоения содержания дисциплины «Исследование операций» студент должен:

знать

- основы теории линейного программирования и теории двойственности, необходимые для решения математических и финансово-экономических задач;

уметь

- применять методы исследования операций для решения экономических задач;

владеть

- навыками применения современного математического инструментария для решения экономических задач;

- методикой построения, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений и процессов (в части компетенций, соответствующих основным методам).


4. Объём дисциплины и виды учебной работы

Общая трудоёмкость дисциплины составляет 4 зачётных единицы.

Вид промежуточной аттестации – экзамен.

Вид учебной работы	Часы
Общая трудоёмкость дисциплины	144
Аудиторные занятия	51
Лекции (Л)	34
Практические занятия (ПЗ)	17
Самостоятельная работа	93
В семестре	57
В сессию / форма	36
	экзамен

5. Содержание дисциплины

5.1. Содержание разделов дисциплины

1. Линейные модели в экономике.
   

1. Балансовые модели. Вектор валового выпуска, вектор конечного потребления, соотношения баланса, коэффициенты прямых затрат. Уравнение линейного межотраслевого баланса. Модель многоотраслевой экономики Леонтьева.
   
2. Неотрицательные и положительные матрицы. Теорема Фробениуса-Перрона. Число и вектор Фробениуса, их свойства. Продуктивность неотрицательных матриц. Запас продуктивности неотрицательной матрицы.
   
3. Продуктивные модели Леонтьева. Различные критерии продуктивности модели Леонтьева. Вектор полных затрат. Модель равновесных цен.
   
1. Введение в линейное программирование.
   
   1. Общая постановка задачи оптимизации. Целевая функция. Допустимое множество. Допустимое решение. Оптимальное решение. Оптимальное множество.
      
   2. Постановка задачи математического программирования. Классификация задач математического программирования. Постановка задачи линейного программирования.
      
   3. Примеры задач линейного программирования (ЛП): задача о банке, задача о диете, задача об использовании ресурсов, транспортная задача.
      
   4. Общая постановка задачи ЛП и различные формы ее записи (числовая, матричная). Стандартная и каноническая формы задачи ЛП.
      
   5. Геометрия задачи ЛП. Выпуклая многогранная область в . Проектирование выпуклого многогранника на координатные плоскости. Теорема о проекциях. Теорема о существовании оптимального решения задачи ЛП в случае ограниченности целевой функции.
      
   6. Теорема о достижимости оптимального решения задачи ЛП в угловой точке (в случае ограниченности целевой функции). Строение множества оптимальных решений.
      
   7. Графический метод решения задач ЛП при малом числе неизвестных. Линия уровня целевой функции. Алгоритм решения задачи ЛП графическим методом. Сведение задач линейного программирования общего вида к задачам, допускающим решение графическим методом.
      

3. Решение общей задачи линейного программирования.
   

1. Симплекс-метод решения задачи ЛП общего вида. Допустимый вид системы ограничений. Допустимый базис. Свободные и базисные неизвестные. Базисное решение.
   
2. Симплексные таблицы. Алгоритм решения задачи ЛП симплекс-методом. Геометрическая интерпретация симплекс-алгоритма.
   
3. Метод искусственного базиса. Двухфазный симплекс-метод.
   
4. Теорема о конечности симплекс-алгоритма.
   

4. Теория двойственности.
   

1. Постановка взаимно двойственных задач ЛП. Симметричные взаимно двойственные задачи. Экономический смысл двойственности. Основное неравенство для двойственных задач. Основная теорема двойственности и ее следствия. Критерий оптимальности. Теорема равновесия. Условия дополняющей нежесткости.
   
2. Выпуклые многогранные конусы в . Теорема об отделимости. Теорема о следствиях системы линейных неравенств: теорема Фаркаша, теорема Фаркаша-Минковского. Доказательство основной теоремы двойственности.
   
3. Двойственность в экономических задачах. Двойственные цены. Применение двойственности в однопродуктивной задаче.
   
4. Несимметричные двойственные задачи, сведение к симметричной паре. Общая постановка взаимно двойственных задач. Основная теорема двойственности в общей постановке.
   

5. Транспортная задача.
   

1. Транспортная задача ЛП. Открытая и закрытая модель транспортной задачи. Критерий разрешимости транспортной задачи. Методы построения начального опорного плана транспортной задачи (метод СЗ угла, метод минимального тарифа, метод Фогеля).
   
2. Потенциалы, их экономический смысл. Решение транспортной задачи методом потенциалов. Двойственность в транспортной задаче.
   
3. Транспортные задачи с нарушенным балансом запасов и потребностей. Транспортные задачи с ограничениями перевозок.
   
4. Метод дифференциальных рент решения транспортной задачи.
   
5. Примеры решения задач нетранспортного характера, сводимые к транспортным задачам. Распределительные задачи. Венгерский метод.
   
6. Транспортная задача по критерию времени и метод ее решения.
   

6. Оптимизационные задачи на графах.
   

1. Основные понятия теории графов. Оптимизационные задачи на графах. Примеры. Задача о кратчайшем пути. Алгоритм Дейкстры поиска кратчайшего маршрута на графе.
   
2. Задача о максимальном потоке в сети как задача линейного программирования. Алгоритм Форда-Фалкерсона решения задачи о максимальном потоке в сети.
   

5.2. Разделы дисциплины и виды занятий

№ п/п	Наименование раздела (темы) дисциплины	Трудоёмкость в часах
		Всего часов	Аудиторная работа			Внеауди-торная (самостоя-тельная) работа
			Общая	Лекции	Семинары	Общая
1	Линейные модели в экономике	12	6	4	2	6
2	Введение в линейное программирование	12	6	4	2	6
3	Решение общей задачи линейного программирования	16	6	4	2	10
4	Теория двойственности	26	12	8	4	14
5	Транспортная задача	26	12	8	4	14
6	Оптимизационные задачи на графах	16	9	6	3	7
	Экзамен	36	-	-	-	36
	Итого:	144	51	34	17	93

5.3. Разделы дисциплины и междисциплинарные связи с обеспечиваемыми дисциплинами

№ п/п	Наименование обеспечиваемых дисциплин базовой части	Разделы
		1	2	3	4	5	6
1	Методы оптимизации		*	*	*		*
2	Эконометрика	*	*	*	*
3	Теория игр	*	*	*
4	Макроэкономическое планирование и прогнозирование	*		*		*	*
5	Финансовый менеджмент			*			*
6	Финансовые рынки			*	*		*
7	Экономика фирмы			*		*	*

6. Практические (семинарские) занятия


Рабочая учебная программа дисциплины предусматривает 17 часов аудиторных практических занятий (семинаров) (8 занятий по 2 аудиторных часа, за исключением последнего занятия – 1 час).

Подробная тематика семинаров (с указанием соответствующей самостоятельной работы, форм контроля и связи с тематикой лекций) представлена в приложении.

Структура практических занятий в общем такова:

1. Проверка наличия выполненного задания самостоятельной работы.
   
2. Выборочная проверка наличия и правильности выполнения домашнего задания.
   
3. Разбор типичных ошибок, возникших в самостоятельной работе.
   
4. Рассмотрение теоретических оснований для практики текущей темы.
   
5. Разбор практических методов и решение соответствующих задач.
   
6. Корректировка заданий для самостоятельной работы студентов.
   

На некоторых практических занятиях вместо пп. 4 - 6 проводится аудиторная контрольная работа (см. приложение).


7. Самостоятельная работа


Самостоятельная работа студентов по дисциплине состоит из 8 заданий. Подробный перечень заданий для самостоятельной работы (с тематической связью аудиторных занятий, формами контроля и рекомендуемой учебно-методической литературой) приведен в приложении.

Внеаудиторными формами и инструментами самостоятельной работы студентов по дисциплине являются:

• выполнение домашних заданий (практических и теоретических);
  
• выполнение домашних контрольных работ (как средство подготовки
  

к аудиторным контрольным работам);

• подготовка к практическим занятиям как работа с лекционным материалом;
  

• подготовка к экзамену.
  

8. Контрольные вопросы и системы оценивания


Тематика курсовых работ

1. Геометрия задачи линейного программирования.
   
2. Двойственный симплекс-метод и доказательство теоремы двойственности.
   
3. Задачи целочисленного программирования.
   
4. Задачи параметрического линейного программирования в экономике.
   
5. Варианты транспортной задачи. Транспортная задача по критерию времени.
   
6. Методы решения систем линейных неравенств.
   
7. Конечность симплекс алгоритма.
   
8. Сетевые задачи (о почтальоне, коммивояжере, задача размещения).
   
9. Составление кратчайших маршрутов.
   
10. Задача о максимальном потоке в сети.
    
11. Задачи оптимизации в математике и физике.
    
12. Метод ветвей и границ в задаче о коммивояжере.
    
13. Метод ветвей и границ в задаче календарного планирования.
    
14. Основные понятия теории графов.
    
15. Модели сетевого планирования.
    
16. Основные понятия многокритериальной оптимизации.
    
17. Метод блочного программирования.
    
18. Задачи дробно-линейного программирования.
    
19. Задача квадратичного программирования и ее решение симплекс-методом.
    
20. Задача о рюкзаке.
    

Перечень контрольных вопросов к экзамену

1. Модель многоотраслевой экономики Леонтьева.
   
2. Теорема Фробениуса-Перрона. Число и вектор Фробениуса, их свойства.
   
3. Продуктивные модели Леонтьева. Различные критерии продуктивности модели Леонтьева.
   
4. Общая постановка задачи оптимизации.
   
5. Общая постановка задачи математического программирования.
   
6. Общая постановка задачи линейного программирования.
   
7. Каноническая и стандартная форма задач линейного программирования. Приведение задач линейного программирования к стандартной и канонической формам.
   
8. Задача о банке и ее решение графическим способом.
   
9. Задача о диете в канонической и стандартной формах.
   
10. Задача об использовании ресурсов. Что называют матрицей затрат?
    
11. Решите задачу об использовании ресурсов в случае матрицы затрат методом перебора вершин.
    
12. Общая постановка транспортной задачи. Открытая и закрытая модели транспортной задачи.
    
13. Геометрический смысл задачи линейного программирования с -переменными. Теорема о существовании решения задачи линейного программирования в случае ограниченной целевой функции.
    
14. Теорема о достижимости оптимального решения в угловой точке.
    
15. Что такое угловая точка выпуклого множества? Опишите способы отыскания угловых точек выпуклого многогранного множества.
    
16. В чем состоит графический метод решения задачи линейного в случае двух переменных? Какие еще случаи допускают графическое решение?
    
17. Какие случаи возможны для базисного решения задачи линейного программирования? В каких случаях решение задачи линейного программирования получают сразу, в каких нет?
    
18. Что называют проекцией выпуклой многогранной области в 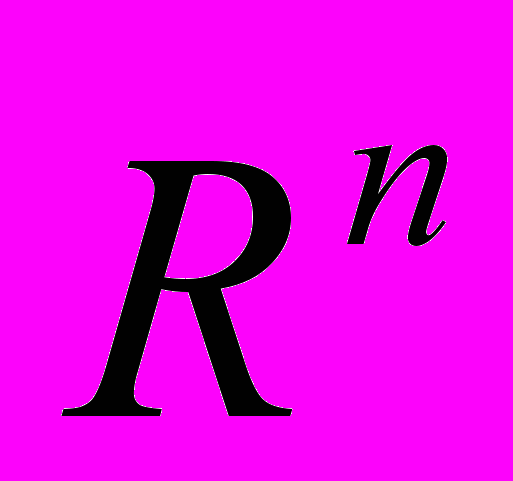на координатную плоскость. Докажите (можно на примере) теорему о проекции.
    
19. Как найти первый базис в задаче линейного программирования?
    
20. Изложите алгоритм решения задачи линейного программирования симплекс-методом.
    
21. Дайте описание симметричных взаимно двойственных задач линейного программирования (в том числе в матричной записи).
    
22. Докажите основное неравенство для двойственных задач.
    
23. Сформулируйте основную теорему двойственности. Какой критерий оптимальности решения вытекает из этой теоремы?
    
24. Сформулируйте и докажите теорему равновесия для двойственных задач.
    
25. Какие двойственные задачи линейного программирования называются несимметричными? Как осуществляется сведение несимметричной пары задач к симметричной?
    
26. Какова общая постановка взаимно двойственных задач? Сформулируйте основную теорему о взаимно двойственных задачах.
    
27. Сформулируйте и докажите теорему отделимости для точки и выпуклого многогранного множества в .
    
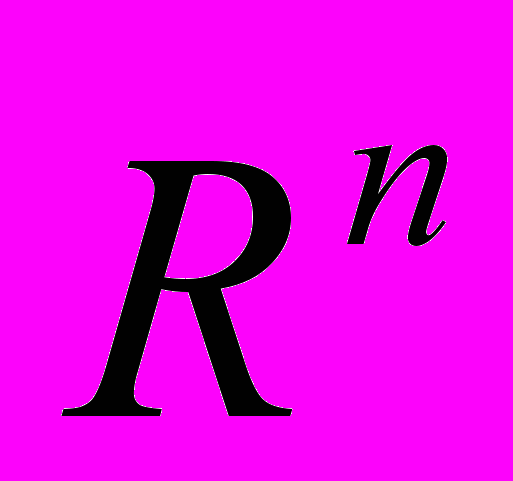28. Множество K{} и его свойства (выпуклость, многогранность).
    
29. Сформулируйте и докажите теорему Фаркаша для однородной системы линейных неравенств.
    
30. Сформулируйте теорему Фаркаша-Минковского для неоднородной системы линейных неравенств в .
    
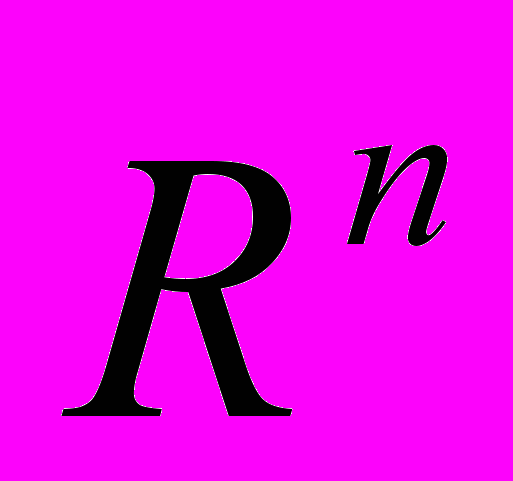31. Докажите основную теорему для симметричных задач, используя теорему Фаркаша-Минковского.
    
32. Укажите методы нахождения исходного плана перевозок в транспортной задаче. Приведите примеры.
    
33. Опишите схему решения транспортной задачи методом потенциалов. Приведите пример.
    
34. Докажите формулу для транспортной задачи.
    
35. Примеры оптимизационных задач на графах.
    
36. Задача о кратчайшем пути. Алгоритм Дейкстры поиска кратчайшего маршрута на графе.
    
37. Задача о максимальном потоке в сети как задача линейного программирования. Алгоритм Форда-Фалкерсона решения задачи о максимальном потоке в сети.
    

Уровень требований и критерии оценок

В качестве оценочных средств программой дисциплины предусматривается:

• текущий контроль (аудиторные контрольные работы, домашние контрольные работы, домашние задания);
  
• промежуточный контроль (экзамен);
  

Итоговая оценка данной части дисциплины проставляется по 100-бальной системе:

- неудовлетворительно – менее 51 балла;

- удовлетворительно – от 51 до 69 баллов;

- хорошо – от 70 до 85 баллов;

- отлично – 86 баллов и выше;

и формируется:

- аттестационными баллами семестра (20)

- экзаменационным баллом (80)

Аттестационный балл семестра складывается из баллов текущей «аттестации» в середине семестра (10) и баллами второй половины семестра «работа в году» (10), каждый из которых учитывает успешность работы студента в семестре (выполнение домашних заданий, аудиторных и домашних контрольных работ, выступления у доски).

9. Учебно-методическое

и информационное обеспечение дисциплины

Рекомендуемая литература

а) основная:

1. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике. Ч.1. Линейная алгебра. Финансы и статистика, 2007.
   
2. Винюков И.А., Попов В.Ю., Пчелинцев С.В. Многочлены и комплексные числа. Собственные значения и собственные векторы. Модель Леонтьева. Учебное пособие для подготовки бакалавров. М.: Финансовая академия при Правительстве РФ, 2009.
   
3. Винюков И.А., Попов В.Ю., Пчелинцев С.В. Линейное программирование. Учебное пособие для подготовки бакалавров. М.: Финансовая академия при Правительстве РФ, 2009.
   
4. Бабайцев В.А. и др. Сборник задач по курсу математики. Под редакцией А.С. Солодовникова и А.В. Браилова. М.: Финансовая академия при Правительстве РФ, 2001.
   
5. Гончаренко В.М., Попов В.Ю. Экономические приложения линейного программирования. Учебное пособие. М.: Финансовая академия при Правительстве РФ, 2003.
   
6. Гончаренко В.М. Математические модели и методы исследования операций. Руководство к решению задач. М.: Финансовая академия при Правительстве РФ, 2006.
   

б) дополнительная:

7. Колемаев В.А. Математические методы и модели исследования операций. Учебник. М.: ЮНИТИ, 2008.
   

10. Приложение

Учебно-методическая карта дисциплины

"Исследование операций"

Наименование раздела	№	Содержание лекций	Содержание семинаров	Самостоятельная работа	Вид контроля
Линейные модели в экономике: 4 ч. лекций, 2 ч. практические занятия 15 ч. самостоятельной работы.	1	Балансовые модели. Уравнение линейного межотраслевого баланса. Модель Леонтьева. Неотрицательные и положительные матрицы. Теорема Фробениуса-Перрона. Число и вектор Фробениуса, их свойства. Продуктивность неотрицательных матриц. Запас продуктивности неотрицательной матрицы.	Практическое занятие по теме лекций № 1-2. [2] § 3.1-3.2.	Решение задач из [2] § 3.1-3.2.	Контроль наличия и выборочная проверка домашнего задания.
	2	Продуктивные модели Леонтьева. Различные критерии продуктивности модели Леонтьева. Вектор полных затрат. Модель равновесных цен.
Введение в линейное программирование: 4 ч. лекций, 2 ч. практические занятия 15 ч. самостоятельной работы.	3	Общая постановка задачи оптимизации. Постановка задачи математического программирования. Классификация задач математического программирования. Общая постановка задачи ЛП. Стандартная и каноническая формы задачи ЛП. Примеры.	Практическое занятие по теме лекций № 3-4. Графический метод решения задач ЛП. [3] § 1.2	Решение задач из [3] § 1.1 – 1.2 Решение задач из [4] § 3.1 - § 3.2.	Контроль наличия и выборочная проверка домашнего задания.
	4	Геометрия задачи ЛП. Теорема о проекциях. Теорема о существовании оптимального решения задачи ЛП в случае ограниченности целевой функции. Теорема о достижимости оптимального решения задачи ЛП в угловой точке
Решение общей задачи линейного программирования: 4 ч. лекций, 2 ч. практические занятия 15 ч. самостоятельной работы.	5	Симплекс-метод решения задачи ЛП общего вида. Симплексные таблицы. Алгоритм решения задачи ЛП симплекс-методом. Примеры.	Практическое занятие по теме лекций №5-6. Симплекс-метод и двухфазный симплекс-метод [3] § 2.1 – 2.2. Контрольная работа № 1	Решение задач из [4] § 3.3 - § 3.4. Домашняя контрольная работа №1.	Проверка домашней контрольной работы №1
	6	Метод искусственного базиса. Двухфазный симплекс-метод. Примеры. Теорема о конечности симплекс-алгоритма.
Теория двойственности 8 ч. лекций, 4 ч. практические занятия, 6 ч. самостоятельной работы.	7	Постановка взаимно двойственных задач ЛП. Симметричные взаимно двойственные задачи. Основное неравенство для двойственных задач. Основная теорема двойственности (формулировка) и ее следствия. Теорема равновесия.	Практическое занятие по теме лекций № 7-8. [3] § 2.3.	Решение задач из [3] § 2.3. Решение задач из [4] § 3.5.	Контроль наличия и выборочная проверка домашнего задания. .
	8	Выпуклые многогранные конусы в . Теорема об отделимости. Теорема о следствиях системы линейных неравенств: теорема Фаркаша, теорема Фаркаша-Минковского. Доказательство основной теоремы двойственности.
	9	Двойственность в экономических задачах. Двойственные цены. Применение двойственности в однопродуктивной задаче.	Практическое занятие по теме лекций № 9-10. [3] § 2.4.	Решение задач из [3] § 2.4. Двойственный симплекс-метод.	Контроль наличия и выборочная проверка домашнего задания. .
	10	Несимметричные двойственные задачи, сведение к симметричной паре. Общая постановка взаимно двойственных задач. Основная теорема двойственности в общей постановке.
Транспортная задача 8 ч. лекций, 4 ч. практические занятия, 9 ч. самостоятельной работы.	11	Транспортная задача ЛП. Открытая и закрытая модель транспортной задачи. Критерий разрешимости транспортной задачи. Методы построения начального опорного плана транспортной задачи.	Практическое занятие по теме лекции №11-12. [3] § 3.1 – 3.2. Контрольная работа № 2.	Домашняя контрольная работа №2.	Проверка домашней контрольной работы №2
	12	Потенциалы, их экономический смысл. Решение транспортной задачи методом потенциалов. Двойственность в транспортной задаче.
	13	Транспортные задачи с нарушенным балансом запасов и потребностей. Транспортные задачи с ограничениями перевозок. Метод дифференциальных рент решения транспортной задачи.	Практическое занятие по темам лекций № 13-14 [5] § 3 (стр. 42 - 49) [6] § 5 (стр.75 - 85)	Решение задач из [5] § 3.	Контроль наличия и выборочная проверка домашнего задания.
	14	Примеры задач линейного программирования, сводимые к транспортным задачам. Распределительные задачи. Венгерский метод. Транспортная задача по критерию времени и метод ее решения.
Оптимизационные задачи на графах 6 ч. лекций, 2 ч. практические занятия, 6 ч. самостоятельной работы.	15	Основные понятия теории графов. Оптимизационные задачи на графах. Примеры. Задача о кратчайшем пути. Алгоритм Дейкстры поиска кратчайшего маршрута на графе.	Практическое занятие по темам лекций №15 – 16. [7] § 7.3 – 7.5	Домашняя контрольная работа №3.	Проверка домашней контрольной работы №3
	16	Задача о максимальном потоке в сети как задача линейного программирования. Алгоритм Форда-Фалкерсона решения задачи о максимальном потоке в сети.
	17	Обзорная лекция.	Контрольная работа №3.