Павлова Ирина Андреевна исследование

Вид материала

Исследование

Содержание Цели работы Область определения функции. Вертикальные асимптоты. Наклонные и горизонтальные асимптоты. Нахождение точки пересечения графика с осью Нахождение промежутков монотонности. Нахождение интервалов выпуклости и вогнутости Нахождение точек пересечения графика с асимптотой. 1) Нахождение области определения функции. 2) Исследование функции на непрерывность. Примеры определения точек нарушения непрерывности Примеры нахождения сингулярных точек функций Пример применения функции Plot в Maple 3) Нахождение точек пересечения функции с осями координат. 4) Исследование функции на границах области определения. Примеры вычисления пределов функций 5) Исследование функции с помощью первой производной. Примеры нахождение минимального значения Примеры нахождения первых производных 6) Исследование функции с помощью второй производной. ... Полное содержание

Подобный материал:

• Бондаренко Ирина Андреевна. Организационно-методические рекомендации, 192.85kb.
• Героя Советского Союза И. Ф. Павлова (гбоу пк №8 им. И. Ф. Павлова) утверждаю директор, 1660.44kb.
• Старостина Светлана Андреевна Правовое регулирование борьбы с преступностью в странах, 2406.73kb.
• Глазер Анна Андреевна Асс. Тяпушова Е. В. исследование, 67kb.
• Акцентуация характера как предпосылка формирования девиантного поведения у подростков, 75.65kb.
• Путилова Ирина Юрьевна, учитель русского языка и литературы Тема : Статистика имен, 394.76kb.
• Халтурина Дарья Андреевна,, 288.78kb.
• Исследование по теме: Автор: Павлова Анна, 9 класс, моу «мсош №16», 251.48kb.
• Российскаяакадемиянау к институт физиологии им. И. П. Павлова, 338.05kb.
• И. П. Павлова и его значение для вокальной подготовки. Пение одна из функций организма,, 29.09kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ


Государственное образовательное учреждение высшего профессионального

образования

«Чувашский государственный педагогический

университет им. И.Я. Яковлева»


Кафедра информатики и вычислительной техники


Павлова Ирина Андреевна


Исследование функций в среде МП Maple


Содержание


Введение


Система Математический Пакет Maple представляет собой программный пакет, систему компьютерной алгебры, которая создана в фирме Waterloo Maple Inc.(Канада), основанной в 1984 году и выпускающей ряд программных продуктов, ориентированных на сложные математические вычисления, визуализацию данных и моделирование. Система Maple предназначена для символьных вычислений, а также имеет ряд средств и для численного решения дифференциальных уравнений и нахождения интегралов. Обладает развитыми графическими средствами. Имеет собственный язык программирования, частично подобный Паскалю.

В самом общем смысле Maple - это среда для выполнения математических расчетов на компьютере. В отличие от языков программирования высокого уровня, таких как Фортран, Бейсик, Си или Паскаль, Maple может решать большое количество математических задач путем введения команд, без всякого предварительного программирования. Кроме того, Maple может оперировать не только приближенными числами, но и точными целыми и рациональными числами. Это позволяет получить ответ с высокой, в идеале с бесконечной, точностью.

Но, что самое важное, решение задач может быть получено аналитически, то есть в виде формул, состоящих из математических символов. Вследствие этого Maple называют также пакетом символьной математики.

К настоящему времени система МП Maple, благодаря усилиям разработчиков, превратилась в мощную вычислительную систему, предназначенную для выполнения сложных проектов. Maple умеет выполнять сложные алгебраические преобразования и упрощения над полем комплексных чисел, находить конечные и бесконечные суммы, произведения, пределы и интегралы, решать в символьном виде и численно алгебраические (в том числе трансцендентные) системы уравнений и неравенств, находить все корни многочленов, решать аналитически и численно системы обыкновенных дифференциальных уравнений и некоторые классы уравнений в частных производных. В Maple включены пакеты подпрограмм для решения задач линейной и тензорной алгебры, Евклидовой и аналитической геометрии, теории чисел, теории вероятностей и математической статистики, комбинаторики, теории групп, интегральных преобразований, численной аппроксимации и линейной оптимизации (симплекс метод) а также задач финансовой математики и многих, многих других задач.

Maple обладает также развитым языком программирования. Это дает возможность пользователю самостоятельно создавать команды и таким образом расширять возможности Maple для решения специальных задач. Хороший текстовый редактор и прекрасные графические средства позволяют профессионально оформить выполненную работу.

Выполнение данной курсовой работы преследует следующие цели и задачи:

Цели работы:

• Определить функциональные возможности системы Математический Пакет Maple, необходимые для исследования математических функций;
  
• Выделить инструментальную среду МП Maple для исследования математических функций;
  
• Определить возможные направления использования программ МП Maple по исследованию математических функций.
  

Задачи работы:

• Изучить среду Математический Пакет Maple;
  
• Дать краткую характеристику МП Maple;
  
• Описать основные функции и возможности МП Maple;
  
• Обобщить материал по исследованию математических функций;
  
• Выделить функции МП Maple, позволяющие осуществлять исследование математических функций;
  
• Охарактеризовать свойства вышеуказанных функций, способы их задания и применения;
  
• Осуществить исследование ряда математических функций в среде МП Maple;
  
• Провести анализ осуществления процесса исследования математических функций в среде МП Maple;
  
• Выяснить возможности системы МП Maple для решения поставленной задачи по исследованию математических функций;
  
• Сделать выводы о возможных направлениях использования программ по исследованию математических функций в МП Maple.
  

§1. Краткая характеристика систем класса Maple

До недавнего времени систему МП Maple называли системой компьютерной алгебры, что указывало на особую роль символьных вычислений и преобразований, которые способна осуществлять эта система. Но такое название сужает сферу применения системы. На самом деле она уже способна выполнять быстро и эффективно не только символьные, но и численные расчеты, причем сочетает это с превосходными средствами графической визуализации и подготовки электронных документов.

По мере распространения математической системы Maple она становится полезной для многих пользователей ПК, вынужденных в силу обстоятельств (работа, учеба, хобби) заниматься математическими вычислениями и всем, что с ними связано. А все это простирается от решения учебных задач в вузах до моделирования сложных физических объектов, систем и устройств, и даже создания художественной графики (например, фракталов).

Maple — типичная интегрированная система, объединяющая в себе:

•  мощный язык программирования (он же язык для интерактивного общения с системой);
  
•  редактор для подготовки и редактирования документов и программ;
  
•  современный многооконный пользовательский интерфейс с возможностью работы в диалоговом режиме;
  
•  мощную справочную систему со многими тысячами примеров;
  
•  ядро алгоритмов и правил преобразования математических выражений;
  
•  численный и символьный процессоры;
  
•  систему диагностики;
  
•  библиотеки встроенных и дополнительных функций;
  
•  пакеты функций сторонних производителей и поддержку некоторых других языков программирования и программ.
  

Ко всем этим средствам имеется полный доступ прямо из программы.

Maple способна решить огромное число задач вообще без какого-либо программирования в общепринятом смысле этого понятия. Достаточно лишь описать алгоритм решения задачи и разбить его на отдельные вопросы, на которые система Maple способна дать ответы. Более того, есть тысячи задач, алгоритмы решения которых уже реализованы в виде функций и команд системы. Тем не менее это вовсе не означает, что в Maple нельзя программировать. На самом деле Maple поддерживает три собственных языка: входной, реализации и программирования.

Maple имеет входной язык сверхвысокого уровня, ориентированный на решение математических задач практически любой сложности. Он служит для задания системе вопросов или, говоря иначе, задания входных данных для последующей их обработки. Это язык интерпретирующего типа и по своей идеологии напоминает добрый старый Бейсик. И такое сходство вовсе не недостаток, а огромное достоинство — ведь именно с Бейсика начался подлинный диалог пользователя напрямую с компьютером! Входной язык имеет большое число заранее определенных математических и графических функций, а также обширную библиотеку, подключаемую по мере необходимости.

Имеет Maple и свой язык процедурного программирования — Maple-язык. Этот язык имеет вполне традиционные средства структурирования программ: операторы циклов, операторы условных и безусловных переходов, операторы сравнения, логические операторы, команды управления внешними устройствами, функции пользователя, процедуры и т. д. Он также включает в себя все команды и функции входного языка, ему доступны все специальные операторы и функции. Многие из них являются весьма серьезными программами, например символьное дифференцирование, интегрирование, разложение в ряд Тейлора, построение сложных трехмерных графиков и т. д.

Синтаксис структурных операторов языка Maple напоминает смесь Бейсика и Паскаля. Это облегчает знакомство с ним тем, кто имеет хотя бы начальный опыт программирования на этих языках. По близким к Бейсику правилам (и при помощи общепринятых математических сокращений) выполняется и ввод математических выражений в диалоговом режиме работы с системой.

Вообще говоря, системы Maple ориентированы на решение сложных задач, хотя и решение в них простых задач вполне возможно и уместно. Система Maple может с успехом применяться для решения самых серьезных математических задач аэродинамики, теории поля, теплопроводности и диффузии, теоретической механики и др. Решение таких задач нередко является многолетним трудом элитных научных коллективов.

Впрочем, поскольку система может быть установлена на любом современном ПК, ее можно (да и нужно) применять как можно чаще и по любому поводу. Это способствует как приобретению практических навыков работы с Maple, так и росту математических познаний тех, кто с ней работает. Это дает Maple обширные возможности в эффективном решении широкого класса математических и научно-технических задач, а также задач в области образования.





§2. Общая схема исследования функций и построения графиков


Сформулируем общую схему исследования функции. Эта схема даёт нам практический способ построения графика функции, отражающего основные черты её поведения.

Пусть дана функция f(x). Для её исследования нужно:

1). Найти её область определения D(f). Если это не слишком сложно, то полезно найти также область значений E(f). (Однако, во многих случаях, вопрос нахождения E(f) откладывается до нахождения экстремумов функции.)

2). Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной, не является ли она периодической.

3). Выяснить, как ведёт себя функция при приближении аргумента x к граничным точкам области определения D(f), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.


4). Если область определения D(f) включает в себя лучи вида (a, +∞) или (-∞, a), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x→+∞ или x→-∞ соответственно.

5). Найти точку пересечения графика с осью Oy (если 0єD(f)). Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью 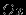, для чего найти корни уравнения f(x)=0 (или убедиться в отсутствии корней). Уравнение f(x)=0 часто удаётся решить лишь приближённо, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.

6). Найти интервалы монотонности функции f(x) (то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f ‘ (x).

На стыках интервалов монотонности найти точки локального экстремума; вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.

7). Найти интервалы выпуклости и вогнутости функции. Это делается с помощью исследования знака второй производной f‘’(x). Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции.

8). В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.

После выяснения свойств функции, упомянутых в пунктах 1 - 8, и нахождения опорных точек (точек пересечения с осями координат, точек графика, соответствующих точкам локального экстремума, точкам перегиба и проч.) мы можем достаточно точно построить график исследуемой функции.

Обсудим теперь подробнее некоторые из этих пунктов.

1). Область определения функции. В некоторых примерах область определения D(f) задаётся в самом условии задачи, например: "Построить график функции, заданной при x є…". Однако часто функция задаётся некоторой формулой, выражающей f(x) как элементарную функцию, вроде:



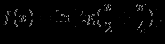
В таком случае принято считать, что областью определения служит максимально широкое множество значений 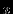, при которых правая часть формулы f(x)=… имеет смысл.

Из этого соглашения по умолчанию есть одно исключение. Если функция имеет вид f(x)=u(x)v(x)или содержит выражения такого рода, то принято считать, что выражение u(x) должно быть положительно, если v(x) принимает значения любого знака, или u(x) неотрицательно, если v(x) положительно. При этом игнорируется тот факт, что выражение u(x)v(x) может иметь смысл и при некоторых других (исключительных) значениях u(x) и v(x), например, когда u(x)<0 и v(x) принимает целое значение.

  Замечание:  При исследовании некоторых функций подробное исследование области определения можно пропустить или ограничиться общими рассуждениями, ввиду сложности точного решения вопроса.

2). Особые свойства функции. Не любая функция обладает такими свойствами, как чётность либо нечётность. Функция заведомо не является ни чётной, ни нечётной, если её область определения несимметрична относительно точки 0 на оси Ox. Точно так же, у любой периодической функции область определения состоит либо из всей вещественной оси, либо из объединения периодически повторяющихся систем промежутков.

Так что если, например, при рассмотрении предыдущего пункта выяснилось, что область определения не обладает свойством симметричности либо периодичности, то заниматься исследованием соответствующих особых свойств функции нет нужды.

Пусть функция f(x) определена на промежутке (a,b).

Если f(-x)=f(x), x(-a,a), то исследуемая функция четная; в этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке (0,a) и отобразить его симметрично относительно оси ординат на (-a,0).


Если f(-x)=-f(x),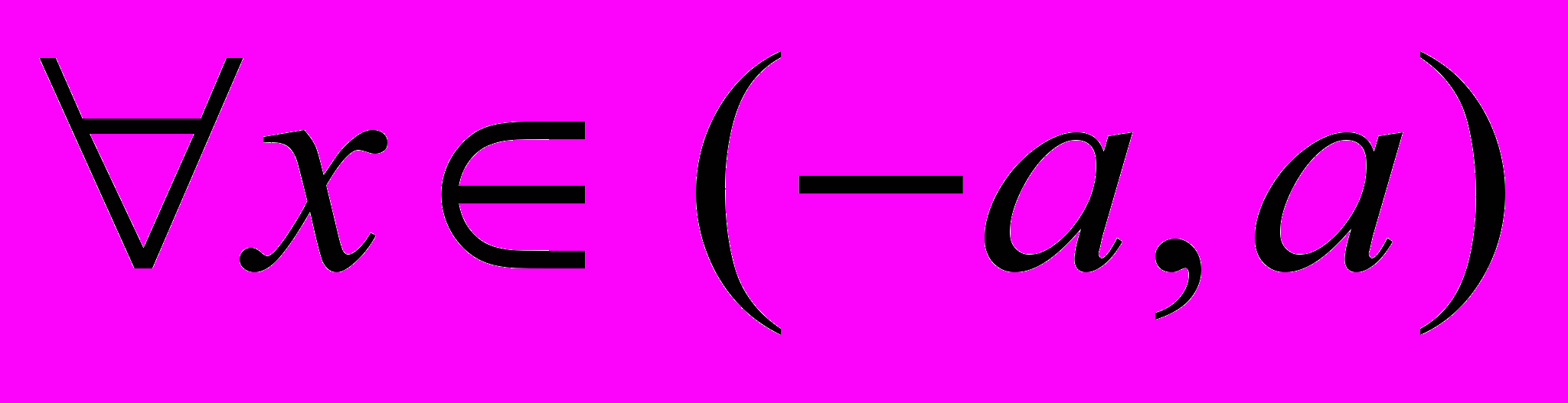, то исследуемая функция нечетная; в этом случае график симметричен относительно начала координат; достаточно построить график функции на промежутке (0,a) и отобразить его симметрично относительно начала координат на (-a,0).

Если (a,b)= 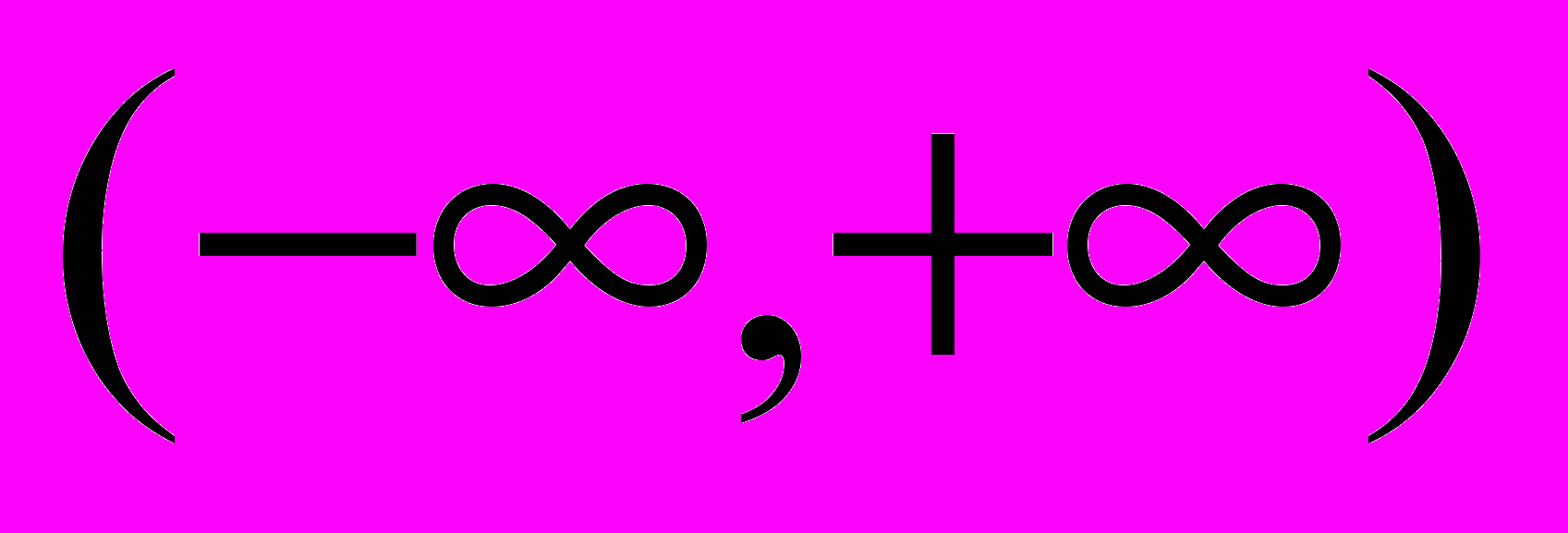и существует такое число T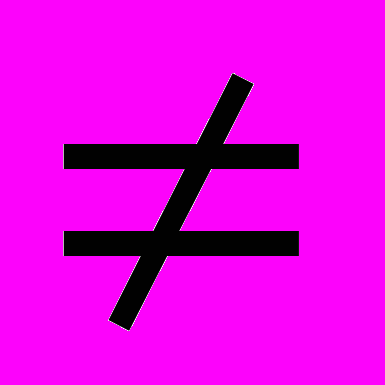0, что f(x+T)=f(x)для любого x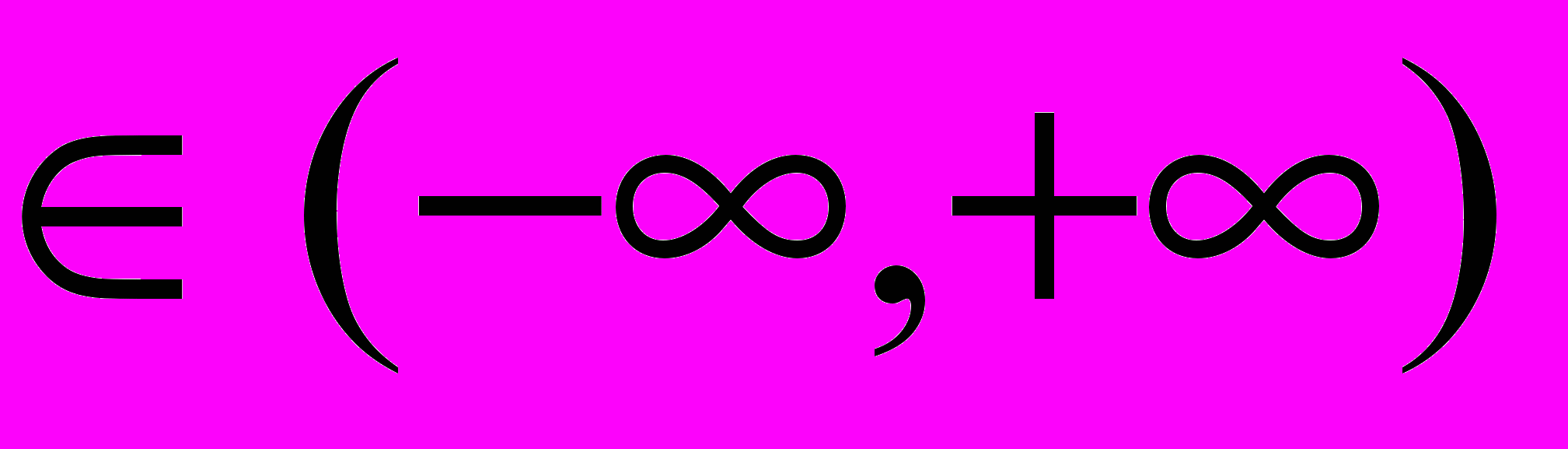, то исследуемая функция периодична с периодом T; в этом случае достаточно построить график функции на промежутке (0,T) и доопределить его по периодичности на всю числовую ось.

3). Вертикальные асимптоты. Если функция f(x) -- элементарная, то на всех интервалах области определения D(f) функция f непрерывна. Значит, вертикальные асимптоты могут появиться только на границах интервалов, составляющих D(f).

4). Наклонные и горизонтальные асимптоты. При их поиске, как и при поиске других асимптотических линий (не обязательно прямых), полезно выделить более просто, чем f(x), устроенную главную часть функции, то есть такую функцию f1(x), что разность f(x)-f1(x) -- бесконечно малая при x → +∞ или x → ─∞. Тогда график главной части y=f1(x) и есть искомая асимптотическая линия. Если ясно, что асимптотическая линия не имеет наклонной либо горизонтальной асимптоты, то её не имеет и исходный график y=f(x). Заметим, что все многочлены 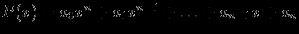(при 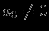и n>=0) не имеют асимптотических линий вида y=kx+b. Следовательно, искать в виде y=kx+b прямолинейные наклонные либо горизонтальные асимптоты у тех графиков, которые имеют асимптотические линии в виде графиков многочленов, в том числе у самих многочленов степени >=2, -- дело бессмысленное: этих прямолинейных асимптот всё равно нет!

5). Нахождение точки пересечения графика с осью Oy состоит в простом вычислении значения функции при . Нахождение же точек пересечения с осью 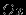может привести к необходимости решить сложное алгебраическое уравнение, что, быть может, удастся сделать лишь приближённо. Отыскав корни функции f(x) и точки разрыва, мы можем определить знак функции на каждом из интервалов между этими точками. Это можно сделать либо вычислив значение функции в какой-нибудь из точек интервала, либо применив метод интервалов, знакомый из школьной программы.

6). Нахождение промежутков монотонности. Для этого находят производную f ‘(x)и решают неравенство f ‘(x)>0. На промежутках, где это неравенство выполнено, функция f(x) возрастает. Там, где выполнено обратное неравенство f ‘(x)<0, функция f(x) убывает. Если два ннтервала возрастания (или убывания) (a,b) и (b,c) примыкают друг к другу в точке 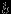и функция f(x) непрерывна в этой точке 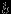, то f(x) возрастает на интервале (a,c).

Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума: там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием -- локальные минимумы.

7). Нахождение интервалов выпуклости и вогнутости ведётся с помощью второй производной. Найдя f’’(x), мы решаем неравенство f’’(x)>0. На каждом из интервалов решения функция будет выпуклой вниз. Решая обратное неравенство f’’(x)<0, мы находим интервалы, на которых функция выпукла вверх (то есть вогнута).

Заодно определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).

8). Нахождение точек пересечения графика с асимптотой. Этот пункт не носит столь уж обязательного характера, однако нахождение таких точек придаёт исследованию функции и построенному её графику законченность и полноту.

Заметим, что получающиеся в процессе исследования функции точки на осях координат и на графике полезно сразу же наносить на чертёж. Это помогает по ходу дела уяснять вид графика. При этом дальнейшие исследования функции имеют характер уточнений, полученных ранее.


§3. Основные функции среды МП Maple

Основой для работы с символьными преобразованиями в Maple является ядро системы. Оно содержит сотни базовых функций и алгоритмов символьных преобразований. Объем ядра достигает 6-7 Мбайт. Имеется также основная библиотека операторов, команд и функций. Многие встроенные в нее функции, как и функции ядра, могут использоваться без какого-либо объявления, другие нуждаются в объявлении.

Дополнительные функции из пакетов могут применяться после объявления подключения пакета с помощью команды with (name), где name — имя применяемого пакета. Общее число функций, с учетом встроенных в ядро и размещенных в пакетах в системе Maple уже превышает 3000. Это означает, что большинство задач может решаться в режиме прямого диалога с системой без использования каких-либо средств программирования.

Maple имеет набор встроенных элементарных математических функций, аргумент х которых может быть целым, рациональным, дробно-рациональным, вещественным или комплексным числом. В ответ на обращение к ним элементарные функции возвращают соответствующее значение.

Чтобы получить подробную информацию о некоторой произвольной функции , необходимо задать команду:

• ?
  

Набор встроенных в ядро системы Maple элементарных математических функций указан в приложении к данной работе.

Рассмотрим набор функций системы Maple, позволяющих осуществить те или иные математические действия, необходимые нам для осуществления исследования элементарных математических функций.

1) Нахождение области определения функции.

Исследование функции, как известно, необходимо начинать с нахождения области её определения, но в системе Maple это сделать невозможно. В связи с этим область определения исследуемых функций будем искать, исследуя их на непрерывность, либо решая соответствующие виды неравенств.

2) Исследование функции на непрерывность.

Для исследования функций на непрерывность Maple имеет функцию iscont, которая записывается в виде:

iscont(f(x), х = а .. b)

iscont(f(x), х = а .. b, 'closed')

iscont(f(x), х = а .. b, 'open')


Она позволяет исследовать функцию f(x) на непрерывность на заданном промежутке [a,b]. Если функция f непрерывна на этом интервале, то в поле вывода появится ответ true – истина; если функция f не является непрерывной на этом интервале, то в поле вывода появится ответ false – ложь. Если задать интервал x=-infinity..+infinity, то функция f будет проверяться на всей числовой оси. В этом случае, если будет получен ответ true, то можно сказать, что функция определена и непрерывна на всей числовой оси. Возможен также результат типа FAIL. Параметр ‘closed’ показывает, что конечные точки должны также проверяться, а указанный по умолчанию параметр 'open' — что они не должны проверяться.

Примеры анализа функций на непрерывность:


> iscont(1/x,x=1..3);



> iscont(1/x,x=-1..1);



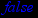
> iscont(1/x,x=0..2,'open');



> iscont(1/x,x=0..2,'closed');




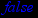
Если исследуемая функция не является непрерывной, необходимо определить точки нарушения её непрерывности. Для этого в Maple имеется функция discont(f,х), позволяющая определить точки разрыва первого и второго рода функции f(x).

Примеры определения точек нарушения непрерывности:

> discont(1/x,x);



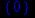
> discont(1/((x-1)*(x-2)*(x-3)),x);




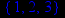
Точки разрыва здесь перечислены в фигурных скобках.

Существует в Maple функция для нахождения точек разрыва второго рода – сингулярных точек. Эта функция записывается как singular (f(x)). Дополнительно в числе параметров может указываться необязательный список переменных.

Примеры нахождения сингулярных точек функций:

> singular(1/x,x);



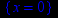
> singular(1/(x-2),x);



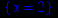
> singular(1/sin(x),x);



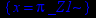
Определить, является ли данная функция непрерывной, можно, построив её график на промежутке от -∞ до +∞. Для построения двумерных графиков в Maple служит функция plot. Она задается в виде:

plot(f, h, v) 

plot(f, h, v, о) ,

где f — визуализируемая функция (или несколько функций), h — переменная с указанием области изменения аргумента функции, v — необязательная переменная с указанием области изменения значений функции, о — параметр или набор параметров, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т. д.). Например для построения графика функции на всей числовой прямой задаём следующую команду:  plot(f(x),x=-infinity..+infinity,y=-infinity..+infinity,color=blue).

Пример применения функции Plot в Maple:

> y:=x->x3-1.5*x2-6*x+1;



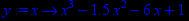
Построим график данной функции.

> plot(y(x),x=-infinity..+infinity,color=blue);




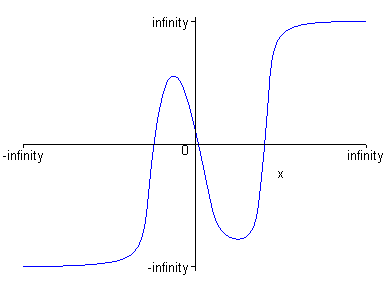
3) Нахождение точек пересечения функции с осями координат.

С помощью функции fsolve( eqns, vars, options) легко находятся значения независимых переменных vars функций eqns, при которых eqns=0 (корни этих функций). При этом данная функция позволяет (в отличие от функции solve) изолировать корни функции eqns указанием примерного интервала их существования.

Эта функция может быть использована со следующими параметрами:

•  maxsols=n — задает нахождение только n корней;
  
•  interval — задается в виде а. .b или х=а. .b, или (х=а. .b, y=c. .d, ...) и обеспечивает поиск корней в указанном интервале.
  

Примеры применения функций solve и fsolve в Maple:

> fsolve(2*sin(x)=Pi/4,x);



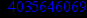
> solve(2*sin(x)=Pi/4,x);



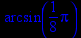
> solve(3*x2-3*x-6,x);



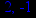
> fsolve(3*x2-3*x-6,x);




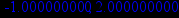
4) Исследование функции на границах области определения.

Для исследования поведения функции на концах интервала исследования необходимо найти пределы данной функции в точках этих концов. Найти пределы исследуемой функции на концах отрезка в Maple можно с помощью команды limit(f(x),x=a) – предел функции f(x) при х, стремящемся к значению a. В результате выполнения данной команды на экране может появиться слово «undefined», которое означает, что предел в данной точке не определён. Тогда можно попробовать найти предел функции в необходимой точке с помощью команд:

limit(f(x), x=a, rigth) – предел функции в точке а справа,

limit(f(x), x=a, left) – предел функции в точке а слева.


Примеры вычисления пределов функций:


> limit(1/x,x=0);



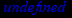
> limit(1/x,x=infinity);



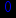
> limit(sin(x)/x,x=0);



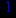
> limit(sin(x),x=infinity);




5) Исследование функции с помощью первой производной.


В Maple для исследования функции на экстремум имеется команда extrema(f,{cond},x,’s’) , где f - функция, экстремумы которой ищутся, в фигурных скобках {cond} указываются ограничения для переменной, х – имя переменной, по которой ищется экстремум, в апострофах ’s’ – указывается имя переменной, которой будет присвоена координата точки экстремума. Если оставить пустыми фигурные скобки {}, то поиск экстремумов будет производиться на всей числовой оси.

Примеры нахождение экстремумов функций:


> extrema(2*x2+3*x-7,{},x);



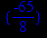
> extrema(x3-1.5*x2-6*x+1,{},x);



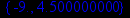
> extrema(1/tan(x)+2*x,{},x);




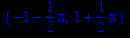
В первой строке вывода приводится экстремум функции, а во второй строке вывода – точка этого экстремума.

 Функция extrema дает неплохие результаты при поиске экстремумов простых аналитических функций, не имеющих особенностей. Однако при анализе сложных функций, содержащих функции со сравнением аргумента (например, abs(x), signum(x) и др.), функция extrema часто отказывается работать и просто повторяет запись обращения к ней.  

К сожалению, команда extrema не может дать ответ на вопрос, какая из точек экстремума есть максимум, а какая – минимум. Для нахождения максимума функции f(x) по переменной х на интервале [x1,x2] используется команда maximize(f,x,x=x1..x2), а для нахождения минимума функции f(x) по переменной х на интервале [x1,x2] используется команда minimize(f, x, x=x1..x2). Если после переменной указать ’infinity’ или интервал x=-infinity..+infinity, то команды maximize и minimize будут искать, соответственно, максимумы и минимумы на всей числовой оси как во множестве вещественных чисел, так и комплексных. Если такие параметры не указывать, то поиск максимумов и минимумов будет производиться только во множестве вещественных чисел. А параметр location (или locationtrue) дает расширенный вывод результатов поиска — выдается не только значение минимума (или максимума), но и значения переменных в этой точке.

Примеры нахождение минимального значения:


> minimize(exp(tan(x)),x=0..10);



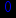
> minimize(x2-3*x+y2+3*y+3);



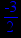
> minimize(1/x,x=1..4);




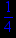
Примеры нахождение максимального значения:


> maximize(exp(tan(x)),x=0..1);



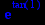
> maximize(x2-3*x+y2+3*y+3);



> maximize(1/x,x=1..4);




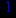
Команды maximize и minimize быстро находят абсолютные экстремумы, но не всегда пригодны для нахождения локальных экстремумов. Команда extrema вычисляет также критические точки, в которых функция не имеет экстремума. В связи с этим целесообразно провести исследование функции с помощью первой производной. Для нахождения первой производной функции в Maple используется команда diff(f(x),x), где f(x) – дифференцируемая функция, х – переменная, по которой происходит дифференцирование.

Примеры нахождения первых производных:


> diff(1/x,x);



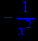
> diff(sin(x),x);



> Diff(tan(x),x);



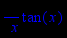
> diff(tan(x),x);



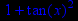
> diff(x3+5*x2+4*x+6,x);



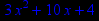
Далее следует найти точки пересечения первой производной функции с осью Ох , а также точки, в которых эта производная не существует. Затем находим интервалы возрастания и убывания, точки экстремума исследуемой функции как в математическом анализе.

6) Исследование функции с помощью второй производной.

В МП Maple не содержится функций, позволяющих определить выпуклость/вогнутость, точки перегиба данной функции. В связи с этим целесообразно провести исследование функции с помощью второй производной. Для нахождения второй производной функции в Maple используется команда diff(f(x),x,x) или diff(f(x),x$2), где f(x) – дифференцируемая функция, х – переменная, по которой происходит дифференцирование.

Примеры нахождения первых производных:

> diff(1/x,x$2);



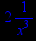
> diff(sin(x),x,x);



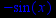
> Diff(tan(x),x,x);



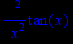
> diff(tan(x),x$2);



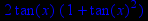
> diff(x3+5*x2+4*x+6,x,x);



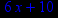
Далее следует найти точки пересечения второй производной функции с осью Ох , а также точки, в которых эта производная не существует. Затем находим интервалы вогнутости и выпуклости и точки перегиба исследуемой функции как в математическом анализе.

7) Нахождение асимптот графика функции.

Рассмотрим пример отыскания асимптот графика функции.


> y:=x->(x2-x+1)/(x-1);



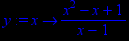
Проверим, является ли функция непрерывной на всей числовой прямой.

> iscont(y(x),x=-infinity..+infinity);



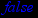
Получили, что данная функция не является непрерывной на всей числовой прямой. Найдём точки нарушения её непрерывности.

> discont(y(x),x);



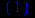
Найдём асимптоты исследуемой функции. Так как в точке х=1 функция терпит разрыв и предел функции в этой точке равен бесконечности, значит, данная точка является вертикальной асимптотой данной функции. Наклонная асимптота имеет вид f=kx+b. Найдём коэффициенты k и b вычислением соответствующих пределов.

> k1:=limit(y(x)/x,x=-infinity);



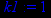
> k1:=limit(y(x)/x,x=infinity);



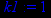
Значит, коэффициент k=1. Найдём коэффициент b.

> k:=1;



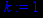
> b:=limit(y(x)-k*x,x=infinity);



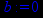
Получили, что коэффициент b=0. Значит, наклонная асимптота имеет вид:

> y:=k*x+b;




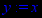
8) Построение графика.


Построение графика функции f(x) – это окончательный этап исследования функции. На рисунке помимо графика исследуемой функции f(x) должны быть нанесены все ее асимптоты, подписаны координаты точек max и min. Построение графика функции в Maple было описано выше.

Отметим, что функция plot может использоваться со следующими параметрами:

COLOR=F – задаёт цвет линии графика; здесь F – цвет на английском языке;

THICKNESS=Y – задаёт толщину линии графика; здесь Y – любое натуральное число;

STYLE=F- задаёт стиль линии графика; здесь F – тип стиля; например: style=line – сплошная линия; style=point – линия в виде рисунка;

COORDS=F – задаёт систему координат, в которой будет построен график; здесь F – тип системы координат, например, coords=polar – полярная система координат; по умолчанию – прямоугольная декартова система координат;

AXES=NON – позволяет чертить график без системы координат;

TICKMARKS=[x, y] – задаёт разметку системы координат; здесь x и y – любые натуральные числа;

SCALING=CONSTRAINED – позволяет сделать одинаковым масштаб графика по осям х и y;

DISCONT=TRUE – позволяет отделить точки на графике, в которых предел функции бесконечен;