Павлова Ирина Андреевна исследование

Вид материала

Исследование

Содержание 4. Рассмотрим функцию y=x+1-1/x-1/x-1.

Подобный материал:

• Бондаренко Ирина Андреевна. Организационно-методические рекомендации, 192.85kb.
• Героя Советского Союза И. Ф. Павлова (гбоу пк №8 им. И. Ф. Павлова) утверждаю директор, 1660.44kb.
• Старостина Светлана Андреевна Правовое регулирование борьбы с преступностью в странах, 2406.73kb.
• Глазер Анна Андреевна Асс. Тяпушова Е. В. исследование, 67kb.
• Акцентуация характера как предпосылка формирования девиантного поведения у подростков, 75.65kb.
• Путилова Ирина Юрьевна, учитель русского языка и литературы Тема : Статистика имен, 394.76kb.
• Халтурина Дарья Андреевна,, 288.78kb.
• Исследование по теме: Автор: Павлова Анна, 9 класс, моу «мсош №16», 251.48kb.
• Российскаяакадемиянау к институт физиологии им. И. П. Павлова, 338.05kb.
• И. П. Павлова и его значение для вокальной подготовки. Пение одна из функций организма,, 29.09kb.

3. Рассмотрим показательную функцию y=(3-х)*exp(x-2).

> restart;

> y:=x->(3-x)*exp(x-2);



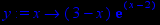
Построим график данной функции.

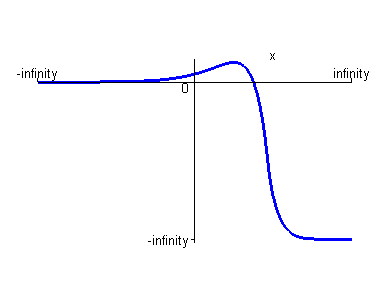
> plot(y(x),x=-infinity..+infinity,color=blue,scaling=constrained);



Проверим, является ли функция непрерывной на всей числовой прямой.

> iscont(y(x),x=-infinity..+infinity);




Найдём сингулярные точки данной функции.

> singular(y(x));



Получили, что данная функция непрерывна на всей числовой прямой. Тогда очевидно, что областью определения данной функции является вся числовая прямая. Исследуем поведение функции на границах её области определения.

> limit(y(x),x=-infinity);



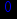
> limit(y(x),x=+infinity);



Получили, что при неограниченном возрастании аргумента х значение функции неограниченно убывает, а при неограниченном убывании аргумента х значение функции стремится к нулю.

Выясним, является ли данная функция чётной или нечётной.

> if y(-x)=y(x) then

print('чётная') elif y(x)=-y(-x) then

print('нечётная')

else

print('Никакая')

fi;



Найдём асимптоты исследуемой функции. Вертикальных асимптот данная функция не имеет, так как областью её определения является вся числовая прямая. Наклонная асимптота имеет вид y=kx+b. Найдём коэффициенты k и b вычислением соответствующих пределов.

> k1:=limit(y(x)/x,x=-infinity);



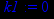
> k2:=limit(y(x)/x,x=infinity);



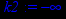
Значит коэффициент k=0. Найдём коэффициент b.

> k:=0;



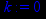
> b:=limit(y(x)-k*x,x=-infinity);



Тогда наклонная асимптота исследуемой функции при х, стремящемся к бесконечности имеет вид:

> y1:=k*x+b;



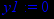
Далее найдём точки пересечения графика функции с осью Ох.

> unassign('x');

> fsolve(y(x)=0,x);



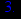
Найдём точки пересечения функции с осью Oy.

> y(0);



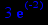
> evalf(%);



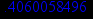
Найдём экстремумы функции.

> extrema(y(x),{},x,'s');

s;





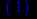
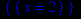
Далее найдём эксиремумы функции с помощью первой производной.

> p1:=diff(y(x),x);



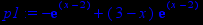
Построим график первой производной.

> plot(p1,x=-infinity..+infinity,color=blue,scaling=constrained);



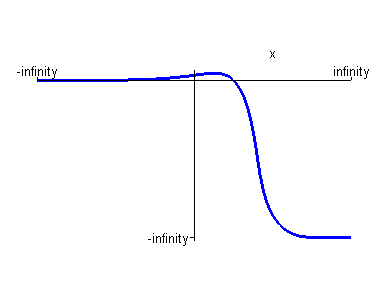
Находим точки пересечения первой производной с осью Ох.

> fsolve(p1,x);



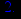
Найдём интервалы возрастания и убывания функции. Для этого найдём значения первой производной на интервалах (-infinity,2) и (2, infinity).

> x:=-10;



> y(x):=p1;



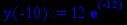
> evalf(%);



> x:=10;



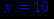
> y(x):=p1;



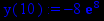
> evalf(%);



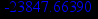
Получили, что при значении аргумента х, принадлежащем интервалу (-infinity,2), значение первой производной функции положительно, значит, исследуемая функция на данном интервале возрастает. При значении аргумента х, принадлежащем интервалу (2, infinity), значение первой производной функции отрицательно, значит, исследуемая функция на данном интервале убывает. Так как при переходе через точку х=2 первая производная исследуемой функции меняет знак с плюса на минус, то отсюда заключаем, что точка х=2 является точкой максимума исследуемой функции. Найдём максимальное значение функции в этой точке.

> ymax:=y(2);




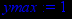
Находим максимальное и минимальное значения исследуемой функции.

> maximize(y(x),x=-infinity..+infinity);



> minimize(y(x),x=-infinity..+infinity);

Найдём производную 2-го порядка.

> p2:=diff(y(x),x$2);



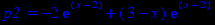
Построим график производной 2-го порядка.

> plot(p2,x=-infinity..infinity,color=blue,scaling=constrained);



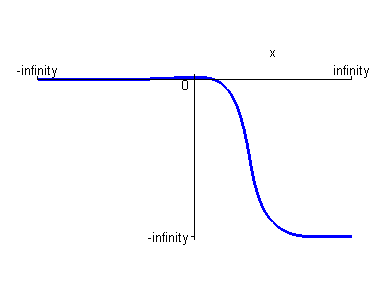
Находим точки пересечения графика производной 2-го порядка с осью Ох.

> fsolve(p2=0,x);



Далее находим интервалы вогнутости вверх и вниз исследуемой функции и точки перегиба функции. Для этого выясним, какие значения принимает вторая производная исследуемой функции на интервалах (-infinity,1) и (1, infinity).

> x:=-10;



> y(x):=p2;



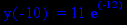
> evalf(%);



> x:=10;



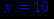
> y(x):=p2;



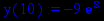
> evalf(%);



Получили, что на интервале (-infinity,1) вторая производная исследуемой функции принимает положительные значения, значит, на этом интервале график данной функции направлен вогнутостью вверх, то есть на данном интервале функция выпукла вниз. На интервале (1, infinity) вторая производная исследуемой функции принимает отрицательные значения, значит, на этом интервале график данной функции направлен вогнутостью вниз, то есть на данном интервале функция выпукла вверх. Так как при переходе через точку х=1 вторая производная исследуемой функции меняет знак, значит, точка х=1 является точкой перегиба исследуемой функции. Найдём значение данной функции в этой точке.

> y(1);



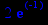
> evalf(%);



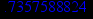
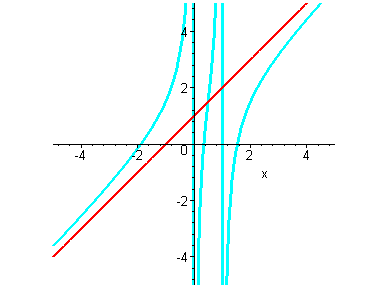
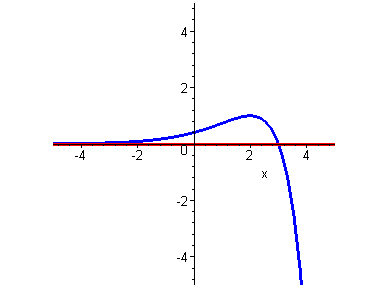
> plot({y(x),k*x+b},x=-5..5,view=[-5..5,-5..5],scaling=constrained,color=[red,blue]);



4. Рассмотрим функцию y=x+1-1/x-1/x-1.

> restart;

> y:=x->x+1-1/x-1/(x-1);



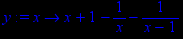
Построим график данной функции.

> plot(y(x),x=-infinity..+infinity,color=blue,scaling=constrained);



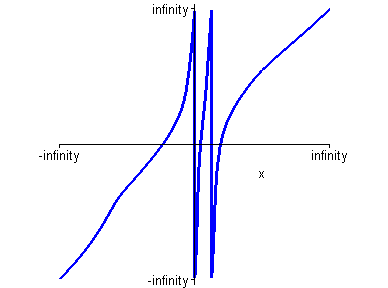
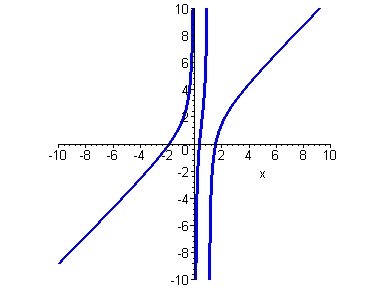
Построим более точный график данной функции.

> plot(y(x),x=-10..10,-10..10,color=blue,discont=true,scaling=constrained);



Проверим, является ли функция непрерывной.

> iscont(y(x),x=-infinity..+infinity);



Получили, что данная функция не является непрерывной на всей числовой прямой. Найдём точки нарушения её непрерывности.

> discont(y(x),x);



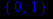
> limit(y(x),x=0,left);



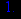
> limit(y(x),x=0,right);



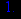
> limit(y(x),x=1,left);




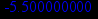
> limit(y(x),x=1,right);



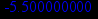
Так как предел исследуемой функции в точках х=0 и х=1 конечен, значит эти точки являются точками разрыва первого рода для данной функции.

Найдём сингулярные точки данной функции.

> singular(y(x));



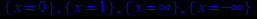
Тогда очевидно, что областью определения данной функции является объединение трёх интервалов (-infinity, 0), (0, 1) и (1, infinity). Исследуем поведение функции на границах её области определения.

> limit(y(x),x=-infinity);



> limit(y(x),x=+infinity);



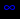
Получили, что при неограниченном возрастании аргумента х значение функции также неограниченно возрастает, а при неограниченном убывании аргумента х значение функции также неограниченно убывает.

Выясним, является ли данная функция чётной или нечётной.

> if y(-x)=y(x) then

print('чётная') elif y(x)=-y(-x) then

print('нечётная')

else

print('Никакая')

fi;



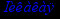
Найдём асимптоты исследуемой функции. Вертикальными асимптотами данной функции являются точки х=0 и х=1. Наклонная асимптота имеет вид y=kx+b. Найдём коэффициенты k и b вычислением соответствующих пределов.

> k1:=limit(y(x)/x,x=-infinity);



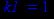
> k2:=limit(y(x)/x,x=infinity);



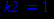
Получили, что коэффициент k=1.Найдём коэффициент b.

> k:=1;



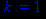
> b1:=limit(y(x)-k*x,x=infinity);



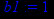
> b2:=limit(y(x)-k*x,x=-infinity);



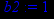
Получили, что коэффициент b=1. Тогда наклонная асимптота данной функции имеет вид:

> b:=1;



> y1:=k*x+b;



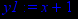
Далее найдём точки пересечения графика функции с осью Ох.


> unassign('x');

> fsolve(y(x)=0,x);



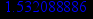
> extrema(y(x),{},x,'s');

s;





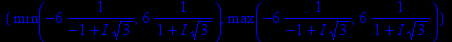
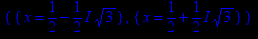
Получили, что действительных точек экстремума данная функция не имеет. Проверим это с помощью первой производной.

> p1:=diff(y(x),x);



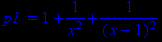
Построим график первой производной.

> plot(p1,x=-infinity..+infinity,color=blue,scaling=constrained);



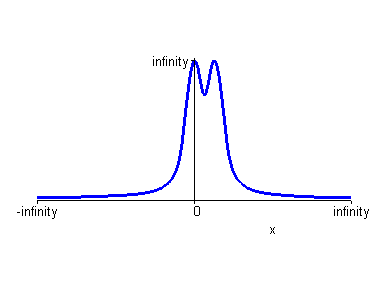
Находим точки пересечения первой производной с осью Ох.

> fsolve(p1=0,x);



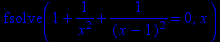
Получили, что точек пересечения с осью Ох первая производная исследуемой функции не имеет. А значит, точек максимума и минимума исследуемая функция не имеет.

Найдём интервалы возрастания и убывания функции. Для этого найдём точки, в которых первая производная не существует.

> discont(p1,x);



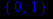
Исследуем поведение первой производной на интервалах (-infinity, 0), (0,1), (1, infinity). Для этого найдём значения первой производной на этих интервалах.

> x:=-10;



> y(x):=p1;



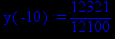
> x:=1/2;



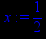
> y(x):=p1;



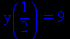
> x:=10;



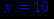
> y(x):=p1;



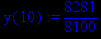
Получили, что при значении аргумента х, принадлежащем интервалу (-infinity,0), значение первой производной функции положительно, значит, исследуемая функция на данном интервале возрастает. При значении аргумента х, принадлежащем интервалу (0,1), значение первой производной функции положительно, значит, исследуемая функция на данном интервале возрастает. При значении аргумента х, принадлежащем интервалу (1, infinity), значение первой производной функции положительно, значит, исследуемая функция на данном интервале снова возрастает.

Найдём экстремумы функции.

Находим максимальное и минимальное значения исследуемой функции.

> maximize(y(x),x=-infinity..+infinity);



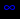
> minimize(y(x),x=-infinity..infinity);



Найдём производную 2-го порядка.

> p2:=diff(y(x),x$2);



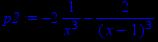
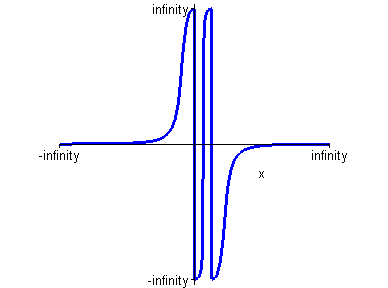
Построим график производной 2-го порядка.

> plot(p2,x=-infinity..infinity,color=blue,scaling=constrained);



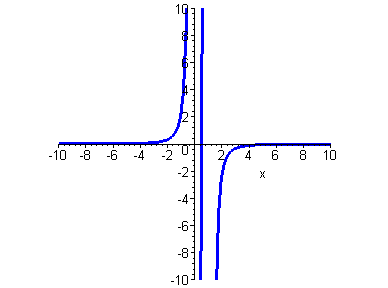
Построим более точный график данной функции.

> plot(p2,x=-10..10,-10..10,color=blue,discont=true);



Находим точки, в которых вторая производная исследуемой функции не существует.

> discont(p2,x);



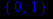
Находим точки пересечения графика производной 2-го порядка с осью Ох.

> fsolve(p2=0,x);



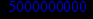
Далее находим интервалы вогнутости вверх и вниз исследуемой функции и точки перегиба функции. Для этого выясним, какие значения принимает вторая производная исследуемой функции на интервалах (-infinity,0), (0, 0.5), (0.5, 1) и (1, infinity).

> x:=-10;



> y(x):=p2;



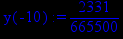
> x:=1/4;



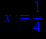
> y(x):=p2;



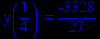
> x:=3/4;



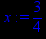
> y(x):=p2;



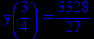
> x:=10;



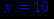
> y(x):=p2;



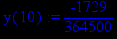
Получили, что на интервале (-infinity,0) вторая производная исследуемой функции принимает положительные значения, значит, на этом интервале график данной функции направлен вогнутостью вверх, то есть функция выпукла вниз. На интервале (0, 0.5) вторая производная исследуемой функции принимает отрицательные значения, значит, на этом интервале график данной функции направлен вогнутостью вниз, то есть функция выпукла вверх. На интервале (0.5, 1) вторая производная исследуемой функции принимает положительные значения, значит, на этом интервале график данной функции направлен вогнутостью вверх, то есть функция выпукла вниз. На интервале (1, infinity) вторая производная исследуемой функции принимает отрицательные значения, значит, на этом интервале график данной функции направлен вогнутостью вниз, то есть функция выпукла вверх. Так как при переходе через точку х= 0.5 вторая производная исследуемой функции меняет знак, значит, точка х=0.5 является точкой перегиба исследуемой функции. Найдём значение данной функции в этой точке.

> y(0.5);



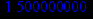
> plot({y(x),k*x+b},x=-5..5,view=[-5..5,-5..5],scaling=constrained,color=[red,cyan]);