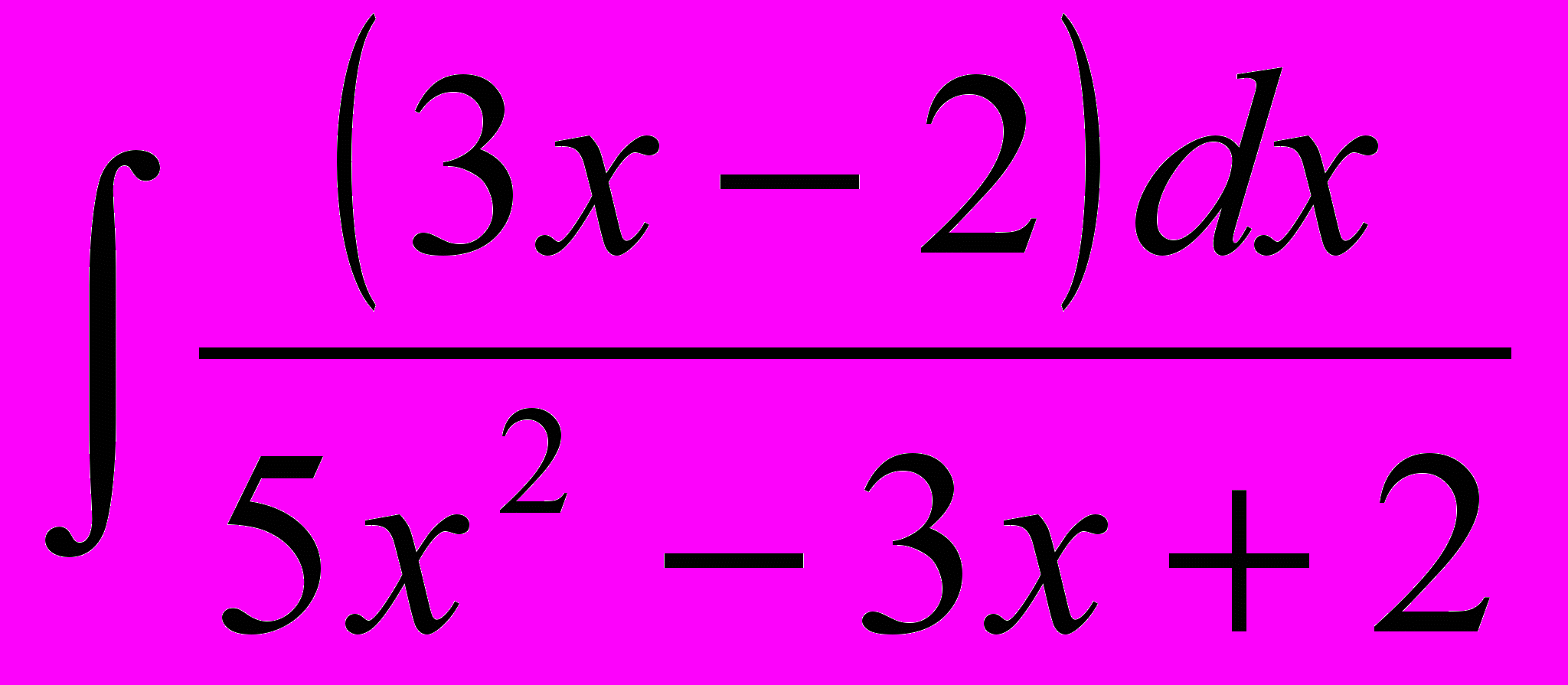План Определение неопределенного интеграла Свойства неопределенного интеграла

Вид материала

Лекция

Содержание 2. Свойства неопределенного интеграла 4. Основные методы вычисления неопределенного интеграла Метод непосредственного интегрирования

Подобный материал:

• Вопросы к экзамену по математическому анализу для студентов 1-го курса специальности, 25.55kb.
• Правила нахождения первообразных. Понятие определенного интеграла. Формула Ньютона-Лейбница., 67.43kb.
• Курсовой проект расчет определенного интеграла, 190.12kb.
• Лекция №6. Расчет переходных процессов с использованием интеграла Дюамеля. Метод переменных, 65.05kb.
• Задачи, приводящие к понятию определенного интеграла. Определенный интеграл и его свойства., 79.79kb.
• Анализа и теории функций календарныйпла нучебных занятий по дисциплине "Высшая математика"., 46.65kb.
• Календарно-тематический план по дисциплине математический анализ 1 (второй семестр), 145.16kb.
• Невропатия, обусловленная моноклональной IgM гаммапатией неопределенного значения, 162.06kb.
• Программа курса лекций, 99.83kb.
• Утверждаю, 111.39kb.

Лекция №8 (2 часа)

Неопределенный интеграл

План

1. Определение неопределенного интеграла
   
2. Свойства неопределенного интеграла
   
3. Таблица интегралов
   
4. Основные методы вычисления неопределенного интеграла
   

1. Определение неопределенного интеграла

В 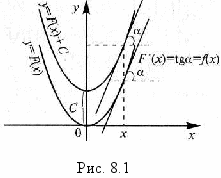дифференциальном исчислении мы решали следующую основную задачу: по данной функции найти ее производную. Рассмотри обратную задачу: дана функция 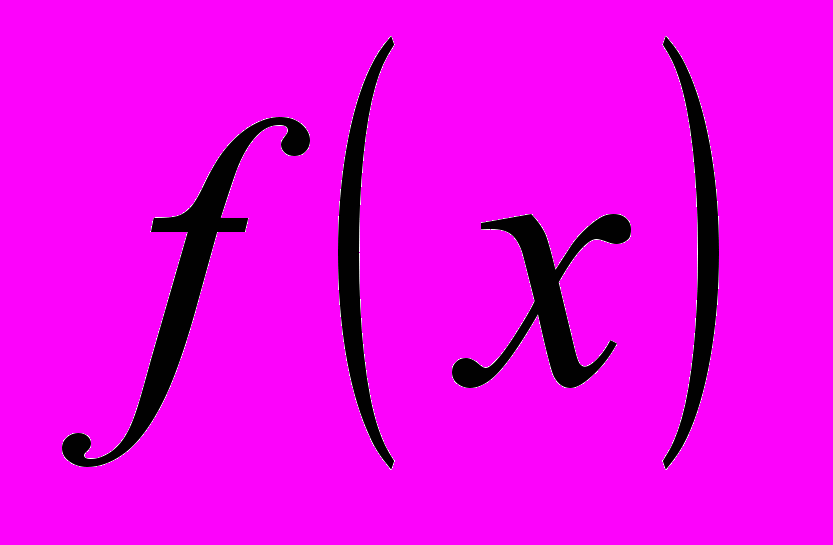; требуется найти такую функцию 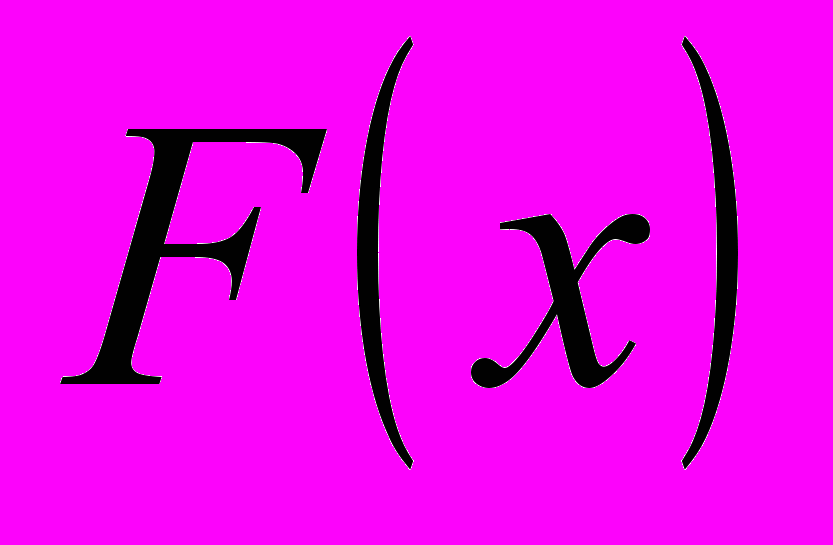, производная которой равна 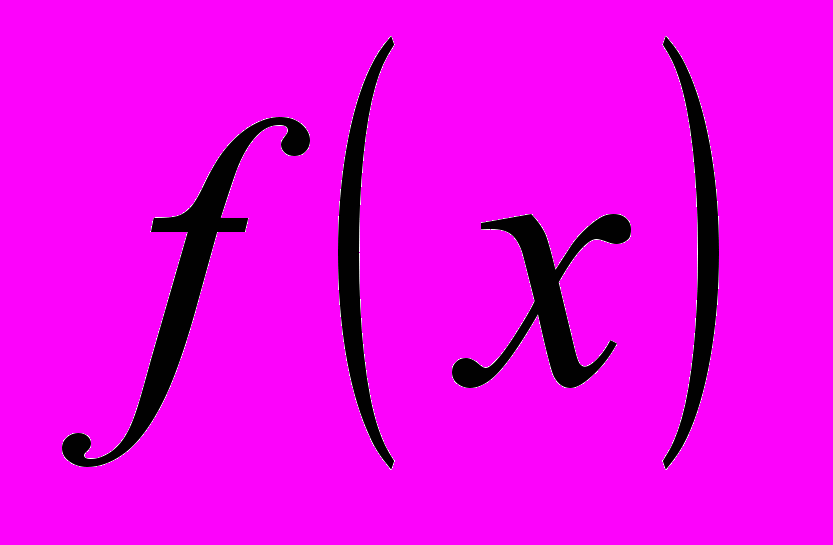, т.е.:

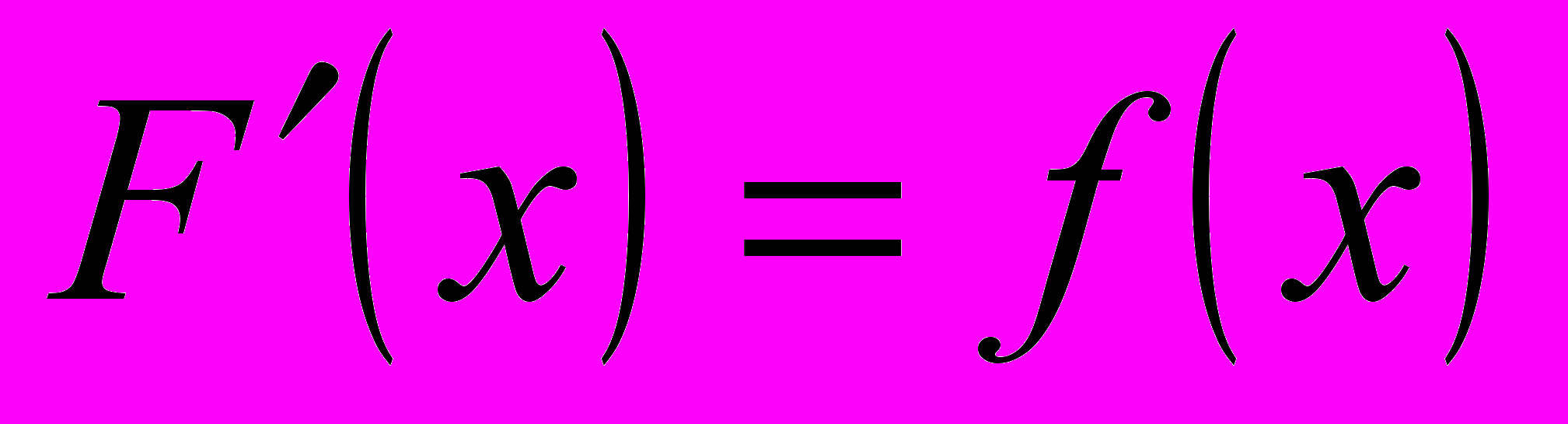(8.1)

Определение 7.1. Функция 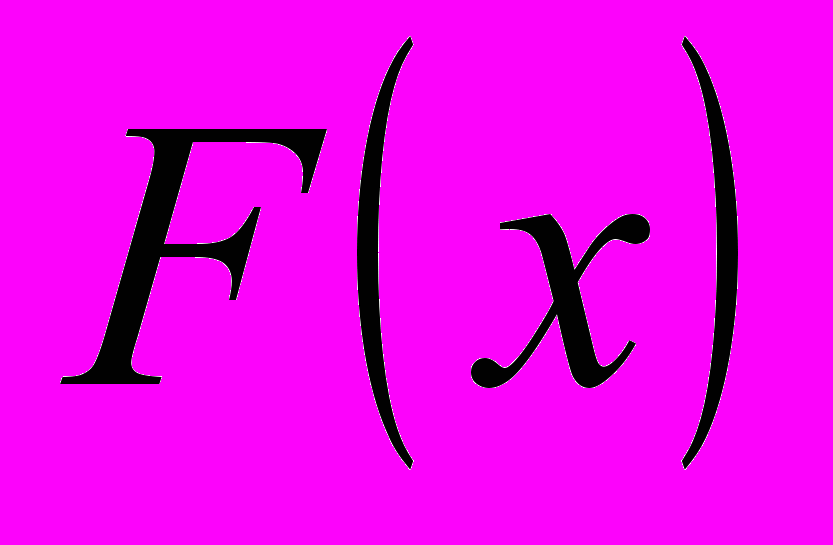называется первообразной от функции 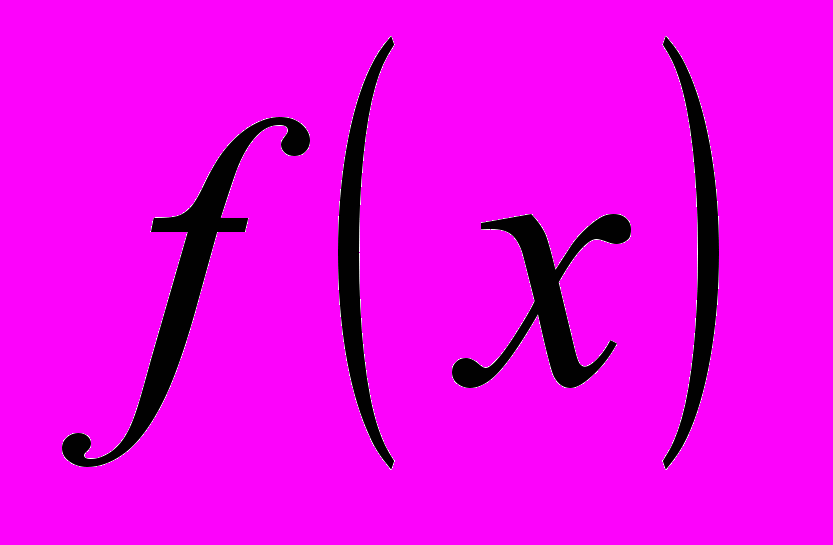на отрезке 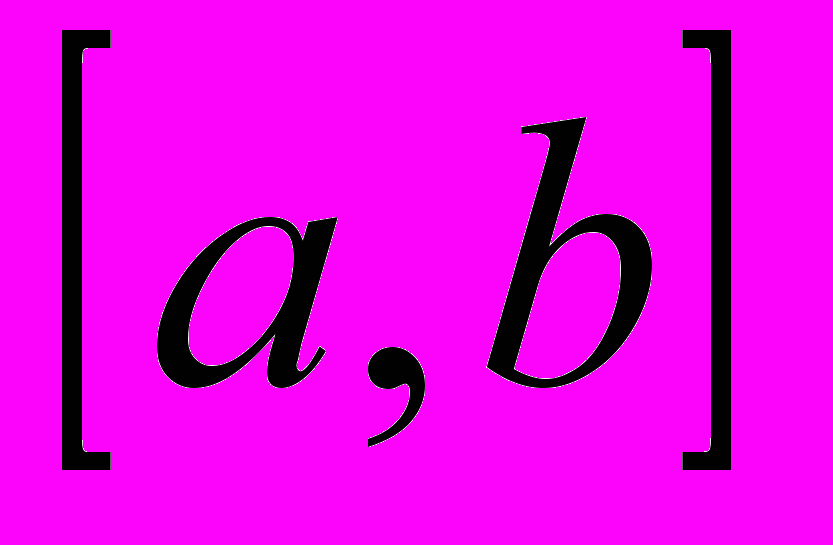, если во всех точках этого отрезка выполняется равенство (8.1).

Пример 8.1. Найти первообразную от функции 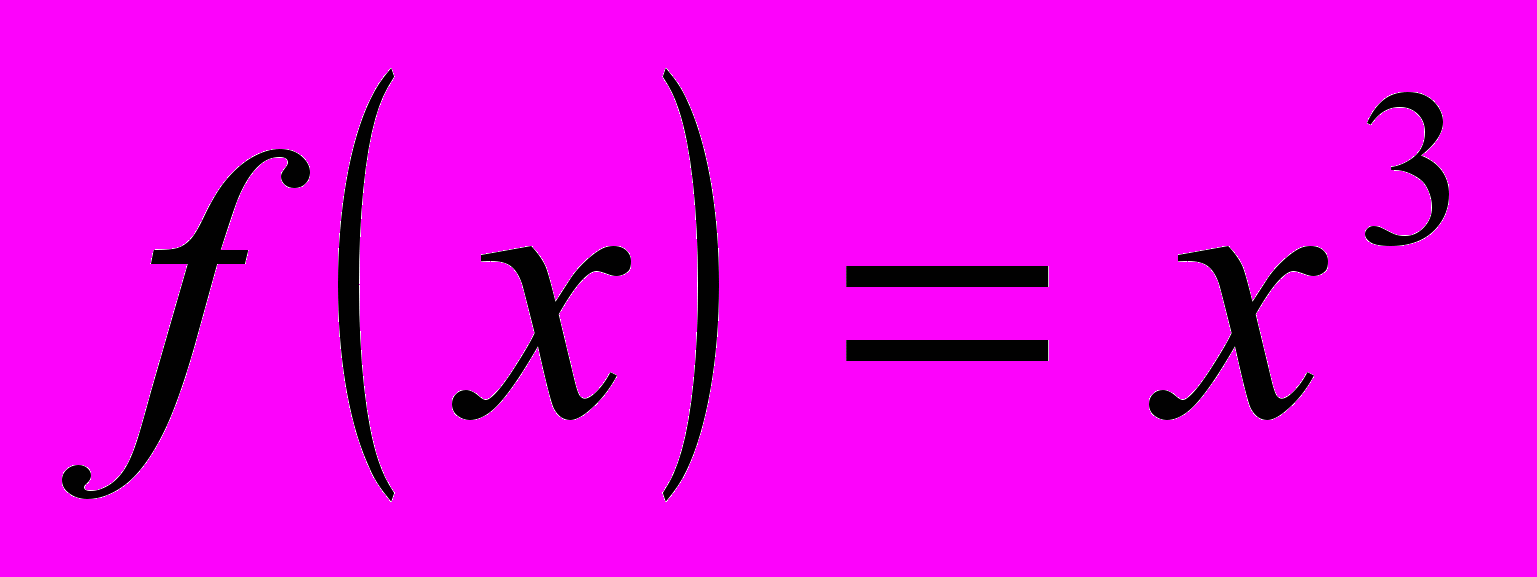. Из определения первообразной следует, что 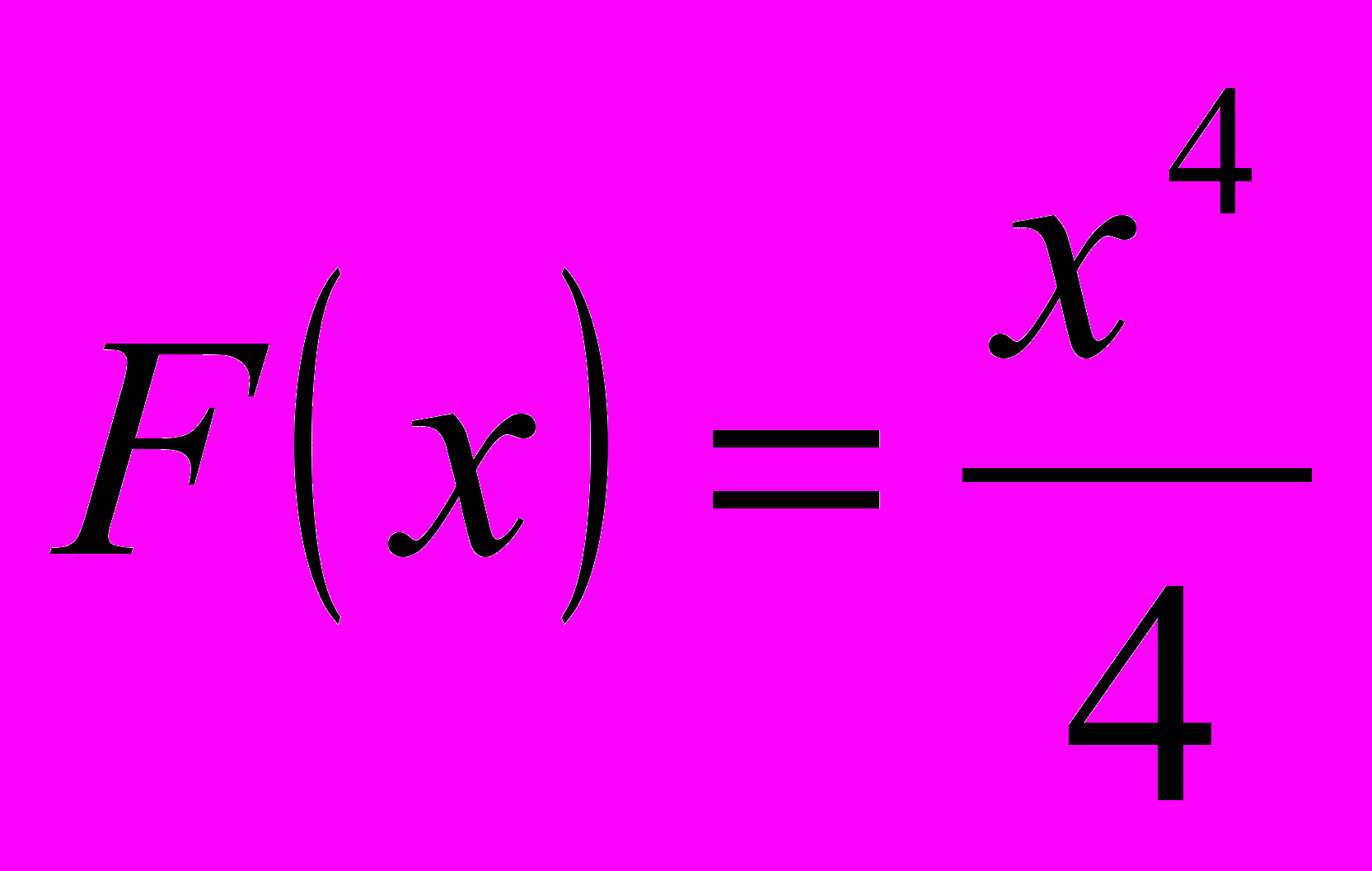- первообразная функции 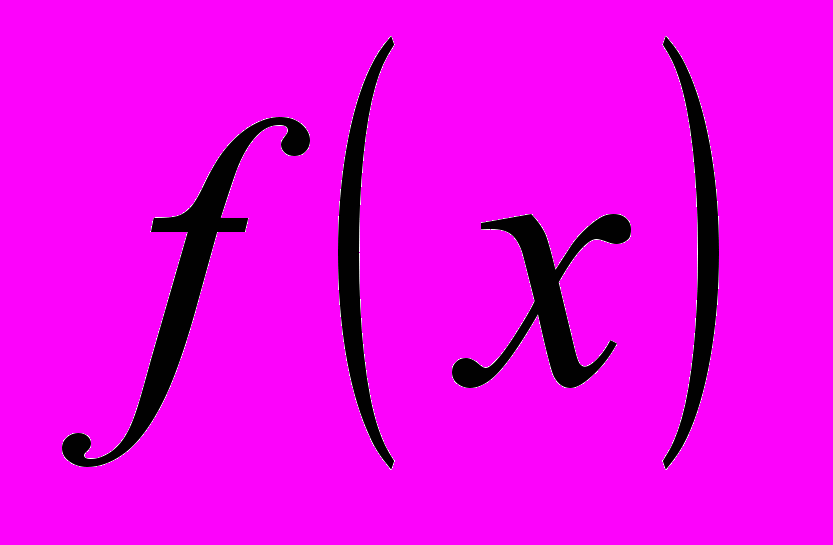, поскольку:

.

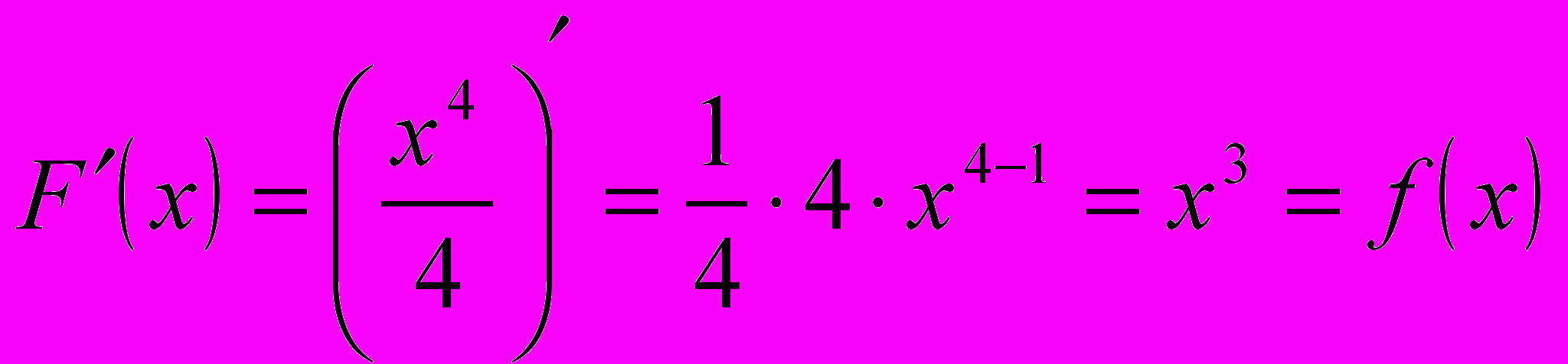Задача отыскания по данной функции ее первообразной решается не однозначно. В рассмотренном примере первообразной для функции 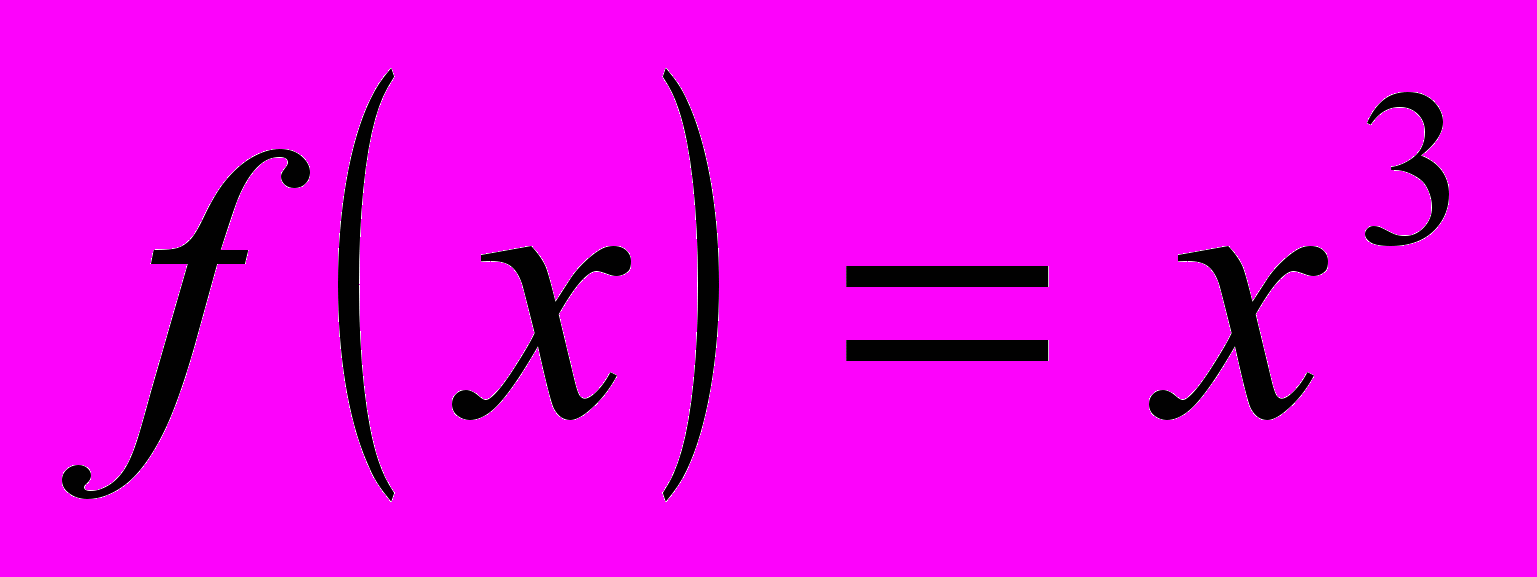является не только функция 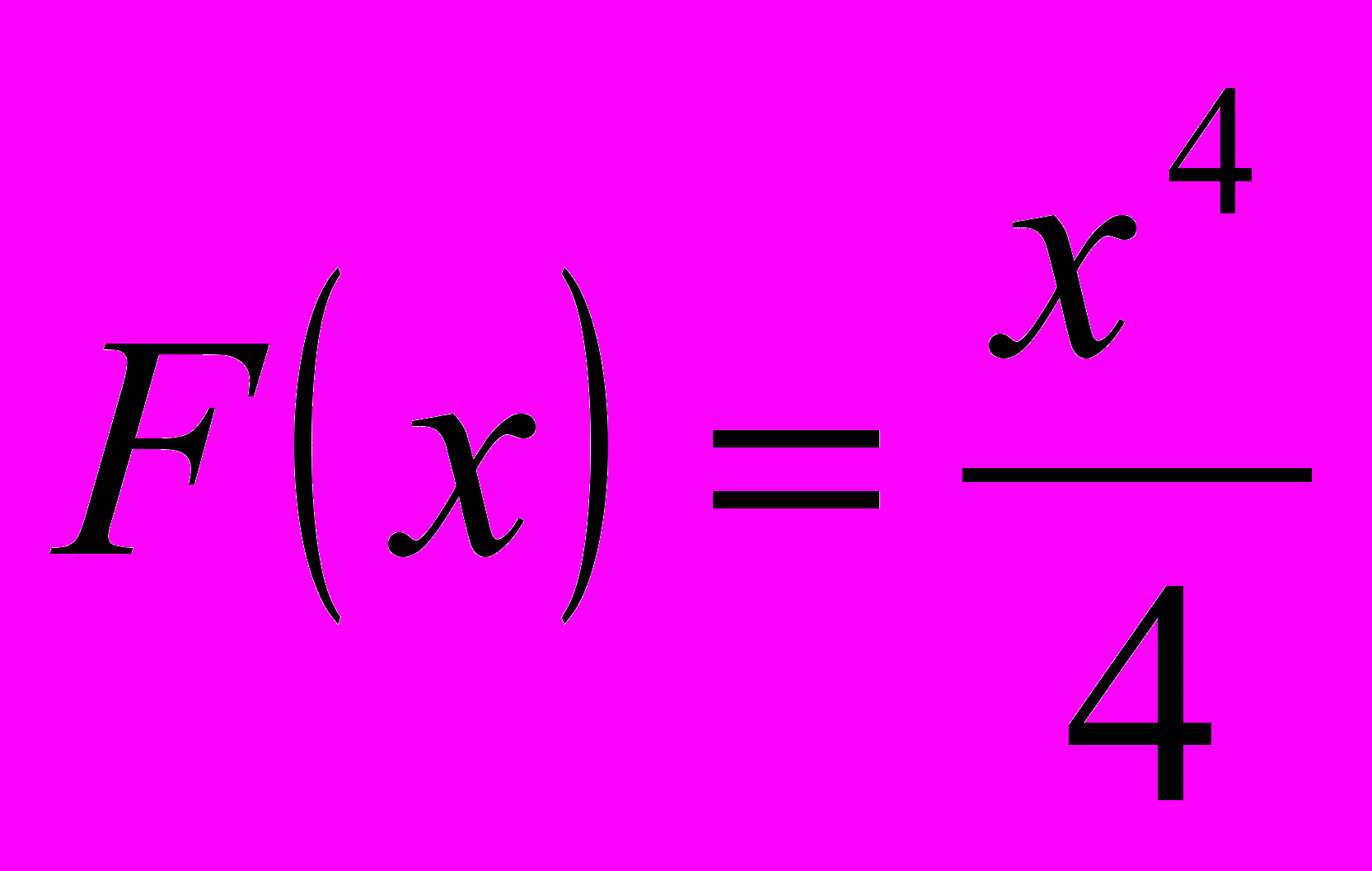, но и , к примеру, 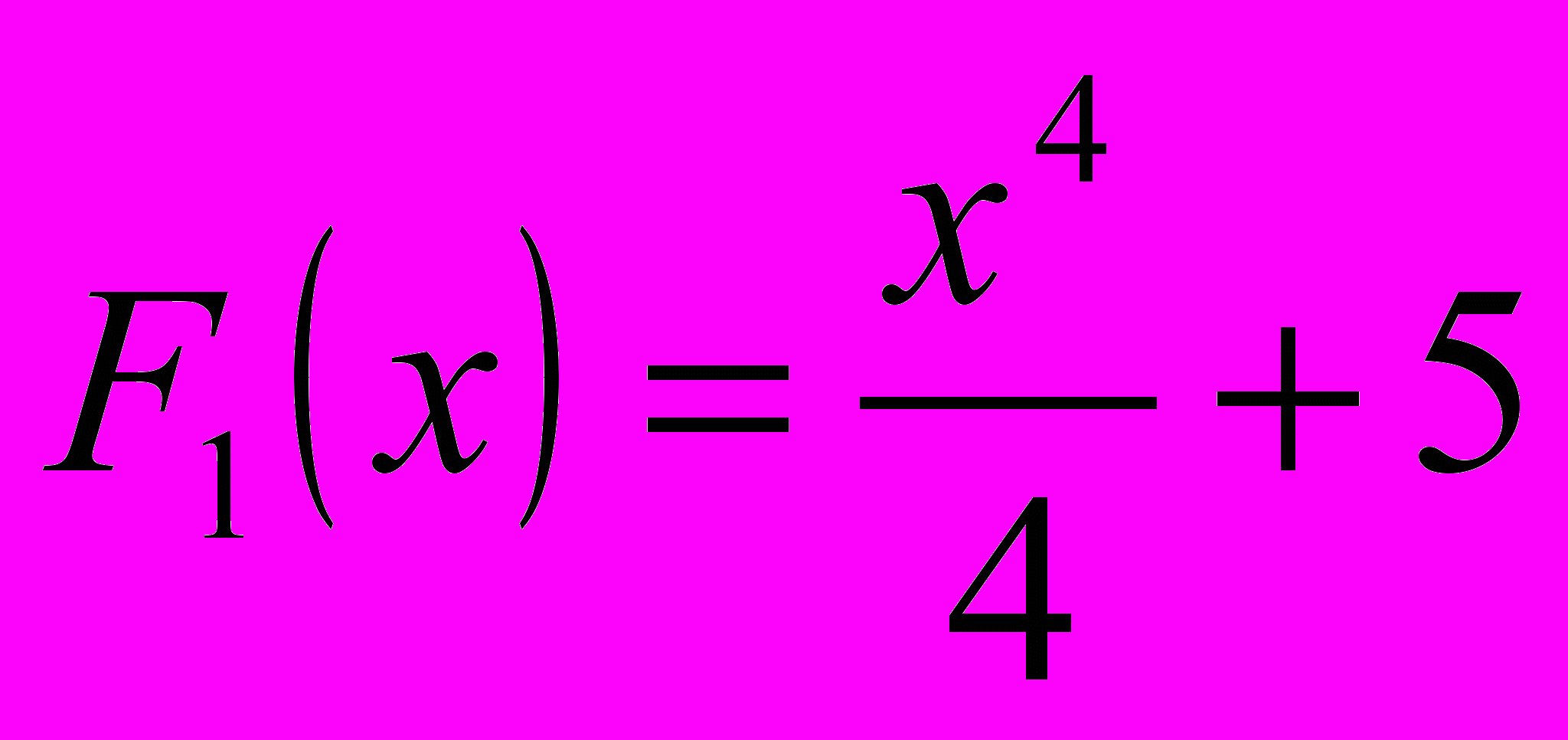и 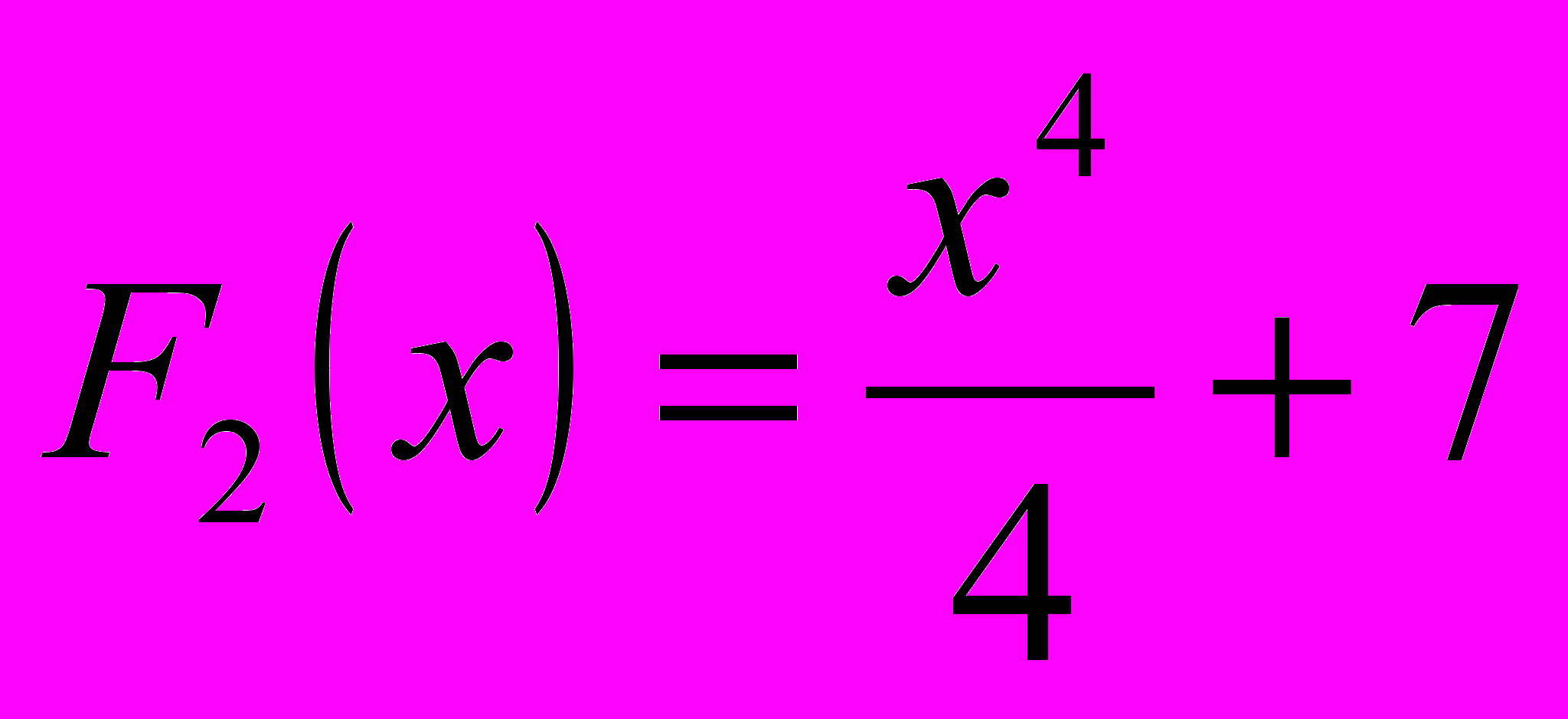и вообщ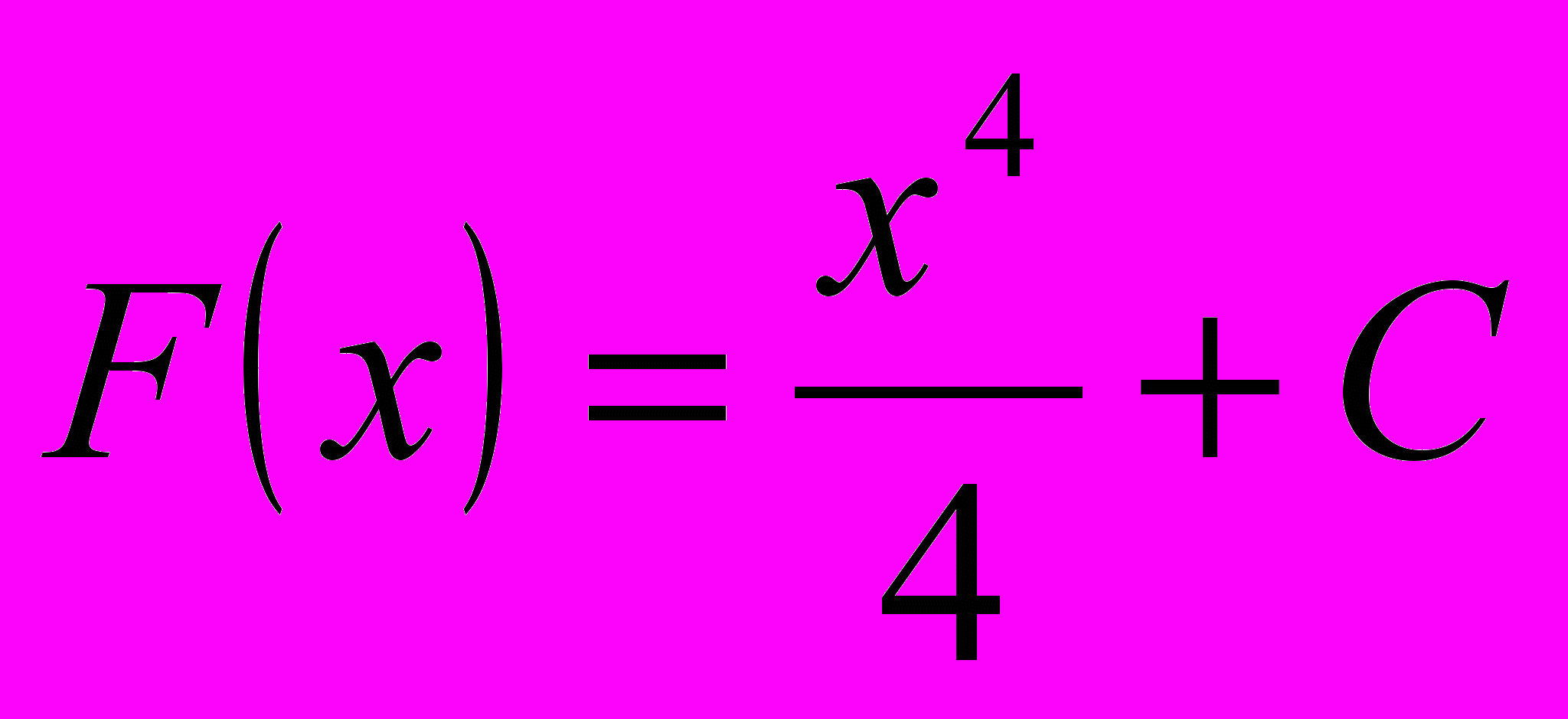е (где - некоторая константа), что можно проверить дифференцированием данных функций.

Теорема 8.1. Если функция 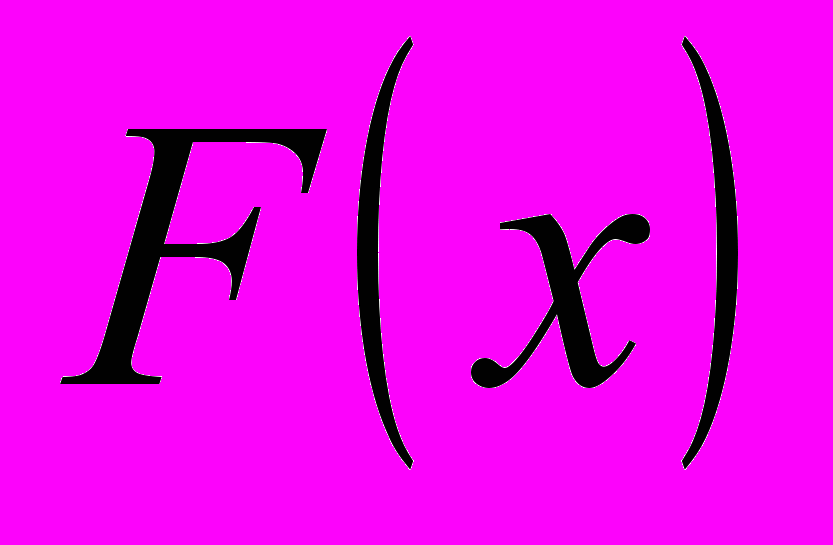первообразная для функции 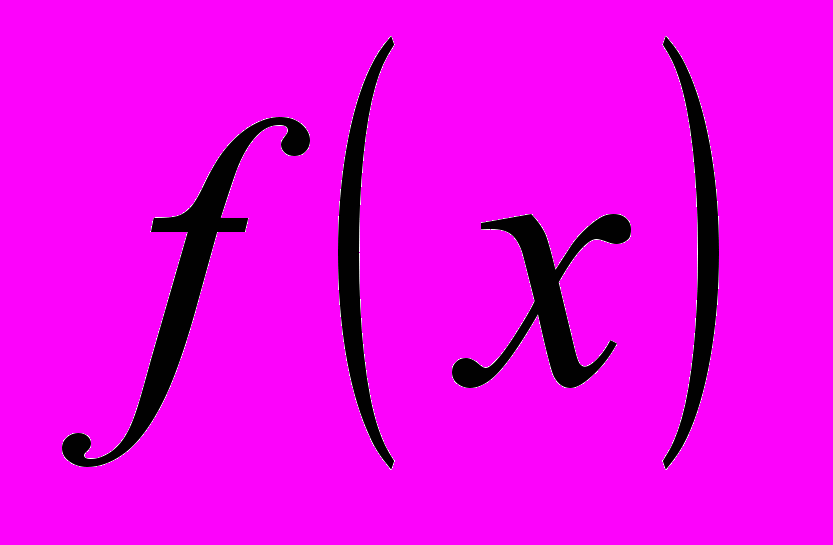на отрезке 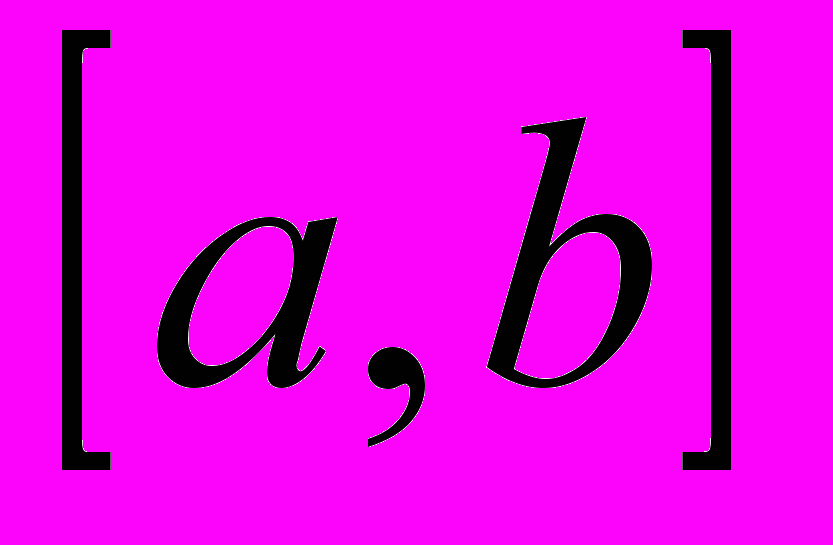, то всякая другая первообразная для функции 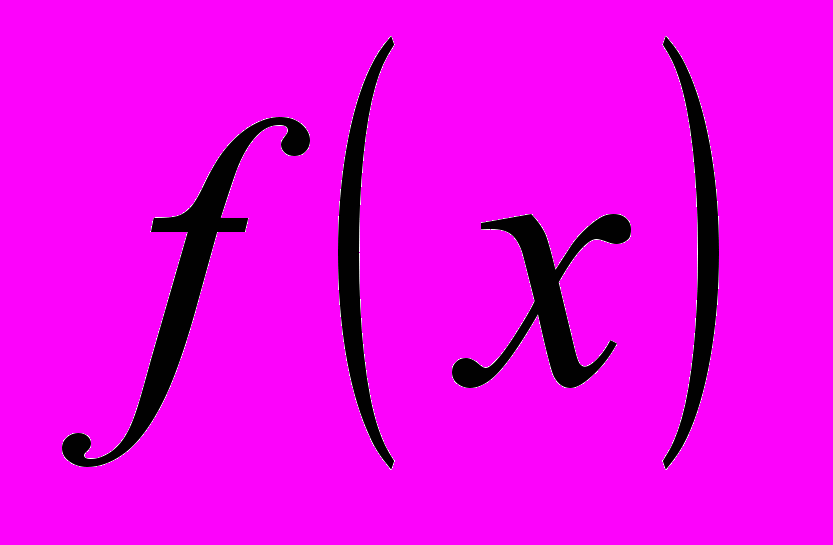отличается от 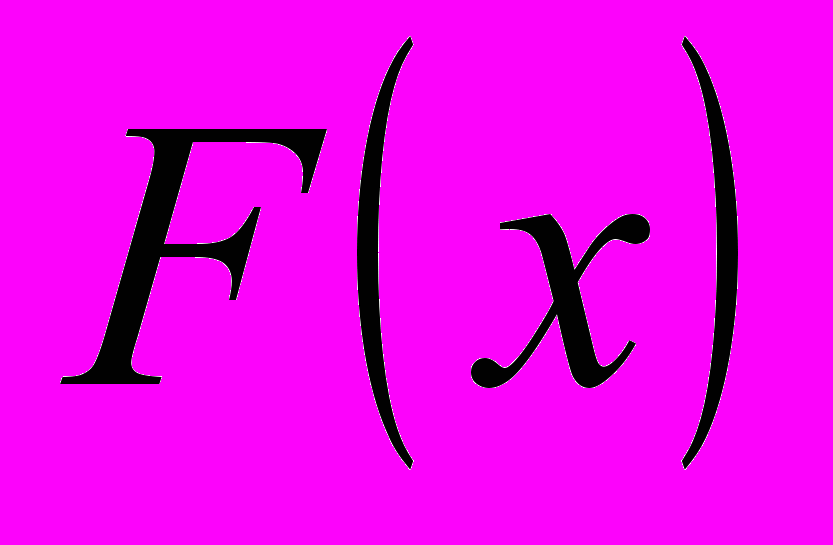на постоянное слагаемое, т.е. может быть представлено в следующем виде:

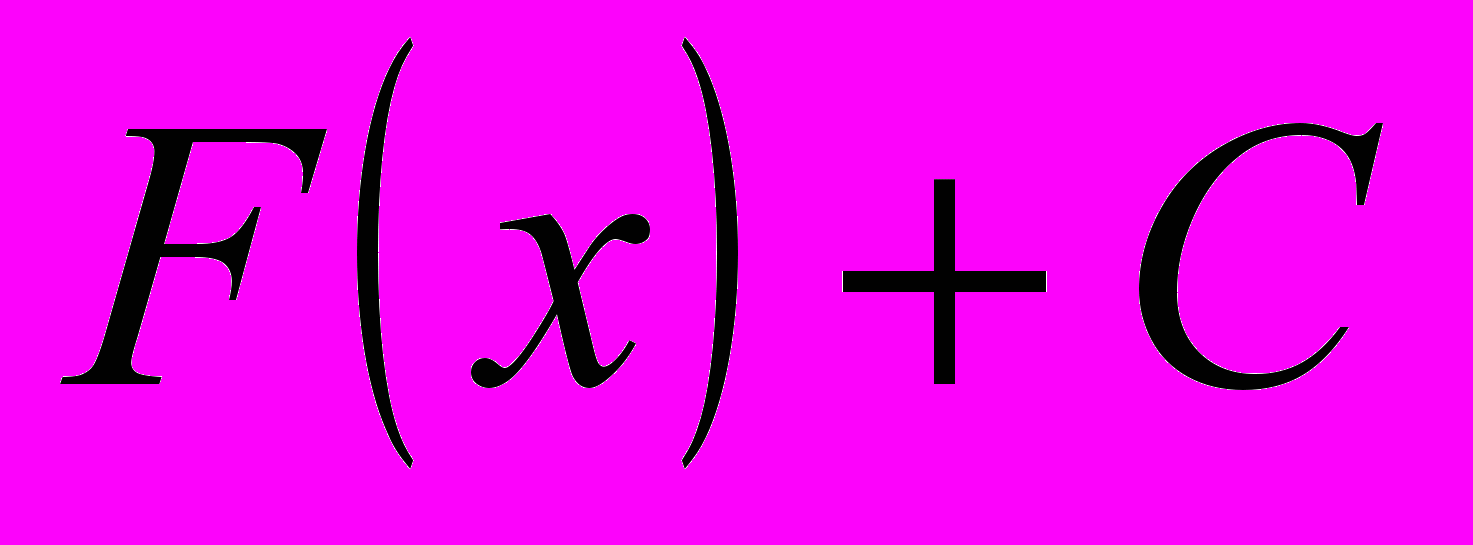(8.2)

Из данной теоремы следует, что выражение (7.2) охватывает совокупность всех первообразных от данной функции.

Введем теперь понятие неопределенного интеграла.

Определение 8.2. Если функция 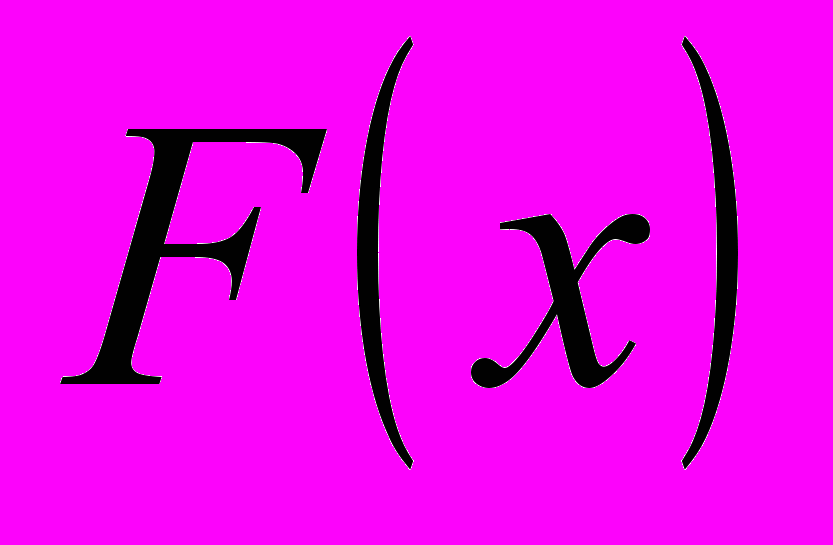является первообразной для функции 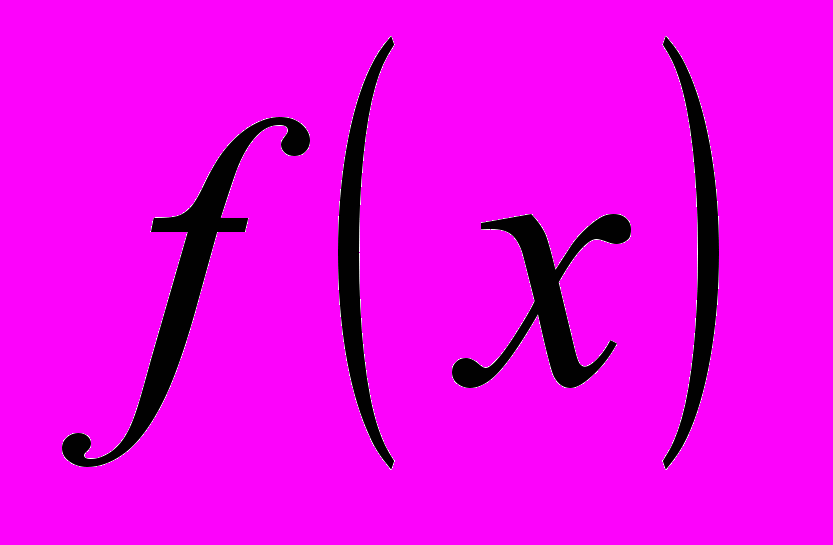, выражение 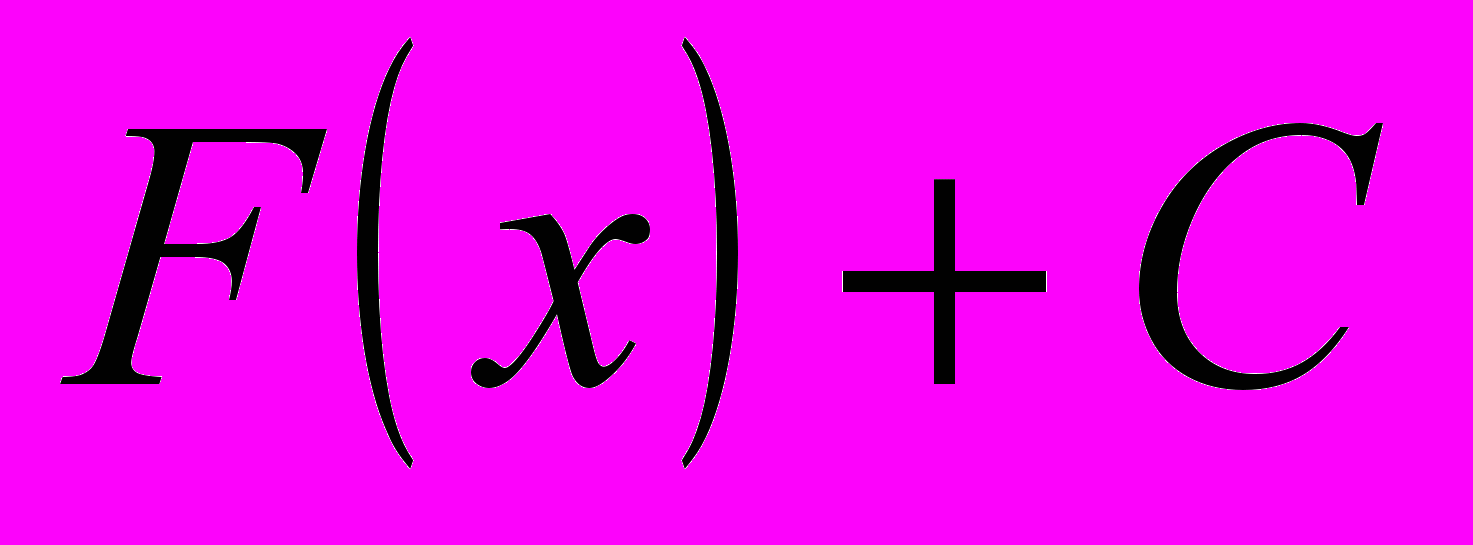называется неопределенным интегралом и обозначается символом 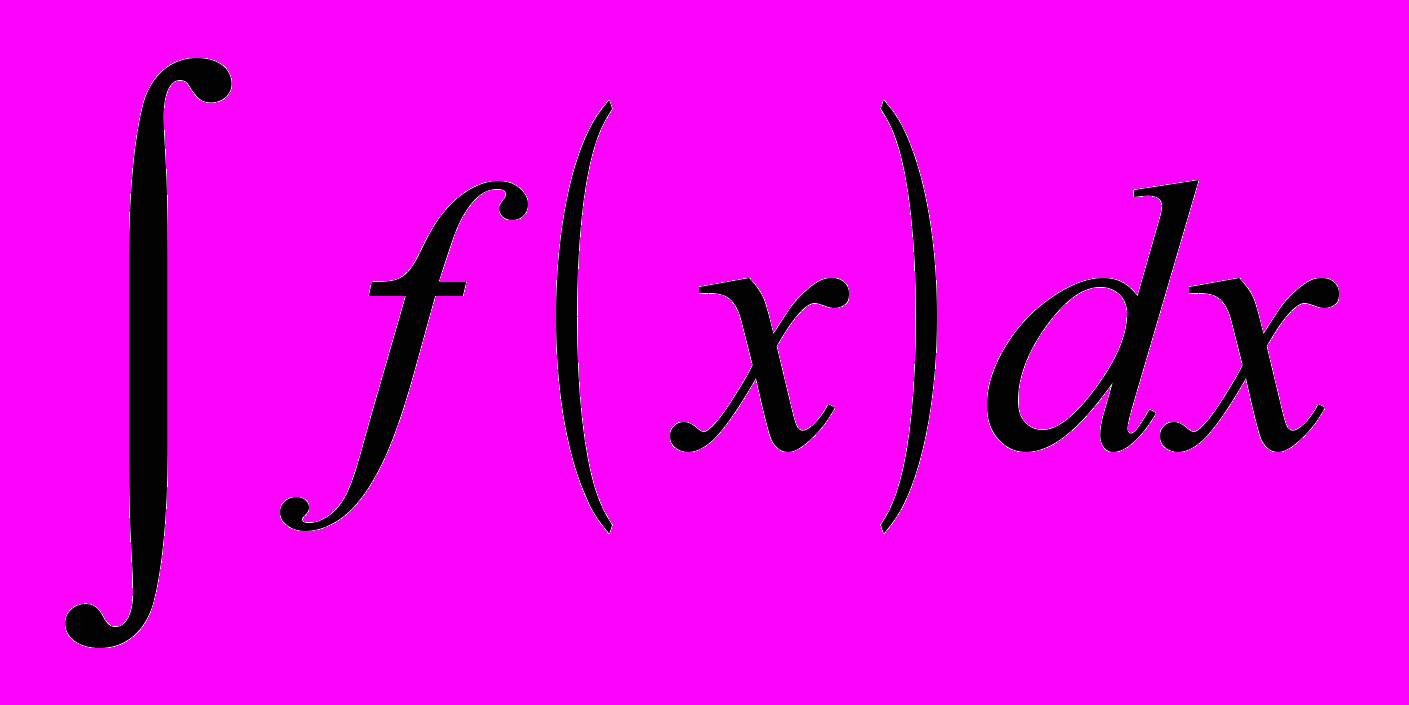. Таким образом можно записать:

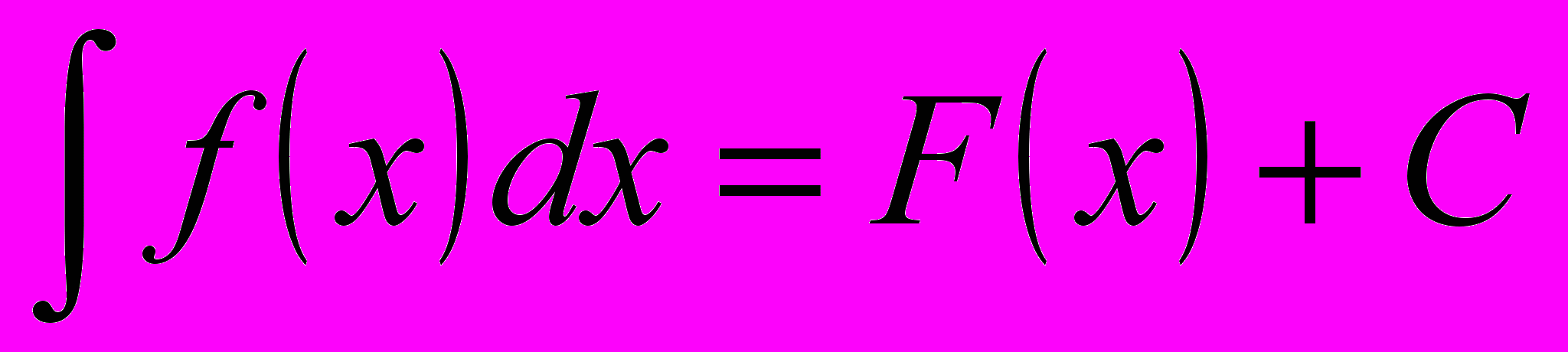(8.3)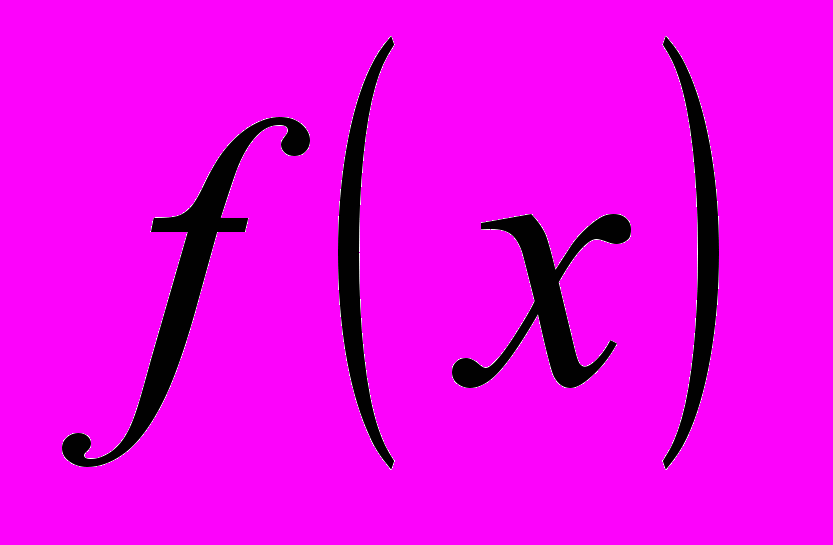

— подынтегральная функция;

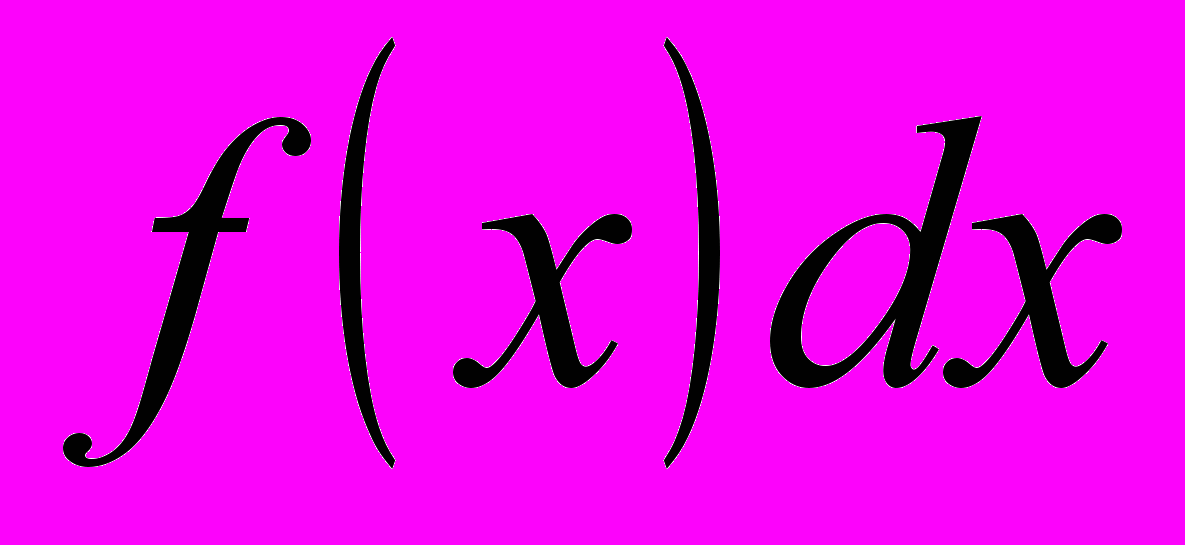— подынтегральное выражение;

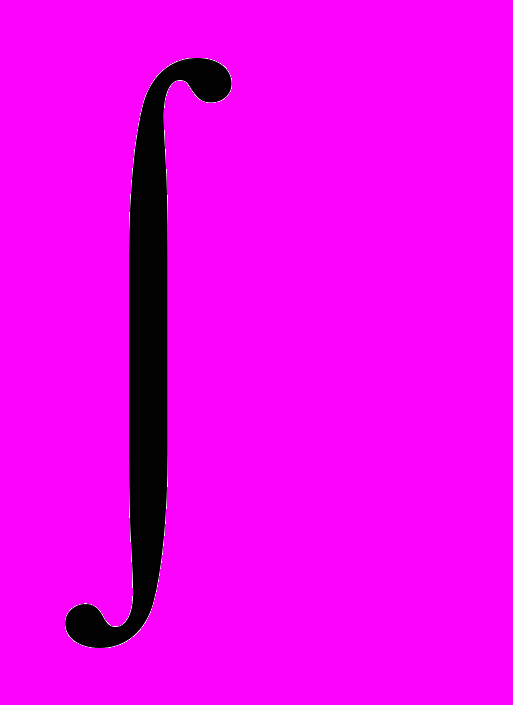— знак неопределенного интеграла;

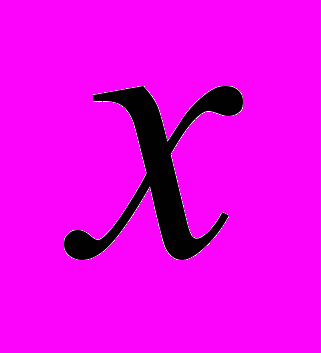— переменная интегрирования.

2. Свойства неопределенного интеграла

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

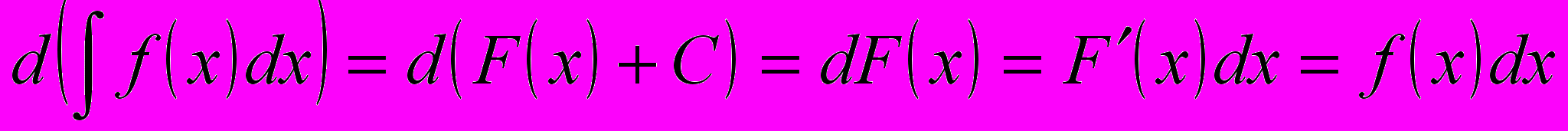(8.4)

2. Производная от неопределенного интеграла равна подынтегральной функции.

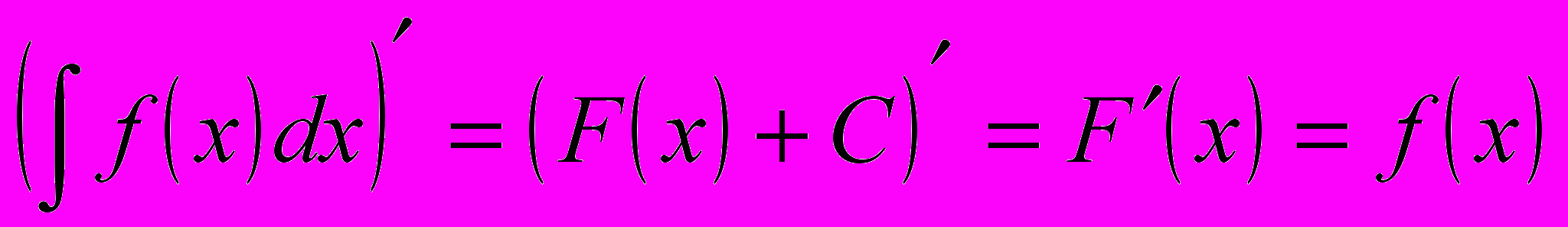(8.5)

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.

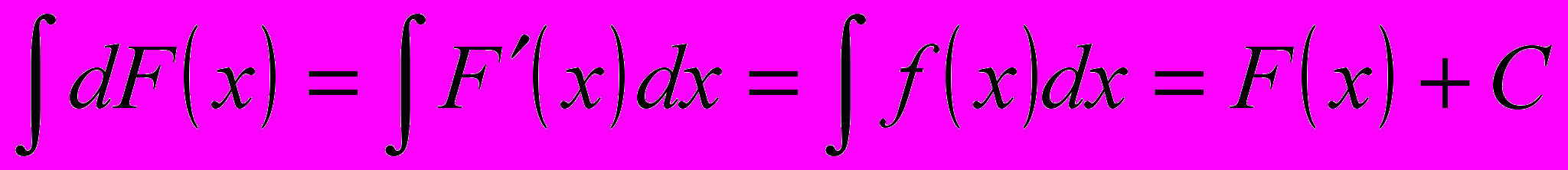(8.6)

4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого в отдельности, т.е.:

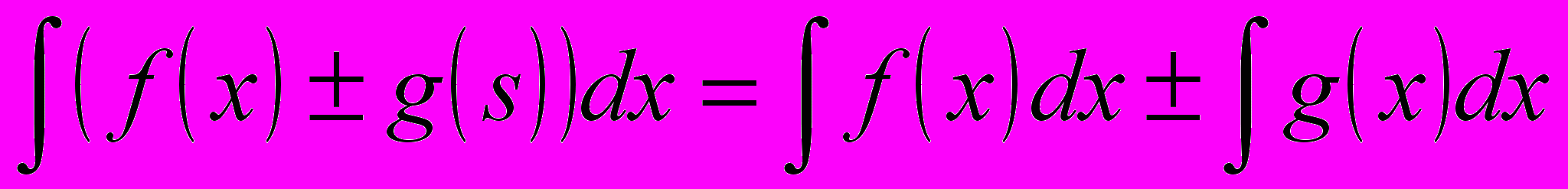(8.7)

5. Постоянный множитель можно вынести за знак неопределенного интеграла, т.е.:

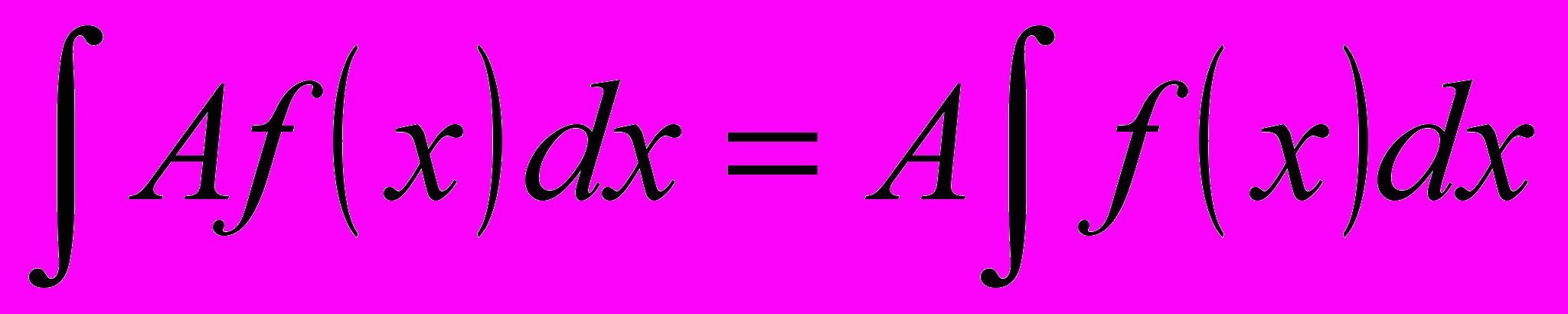(8.8)

3 Таблица интегралов

1.

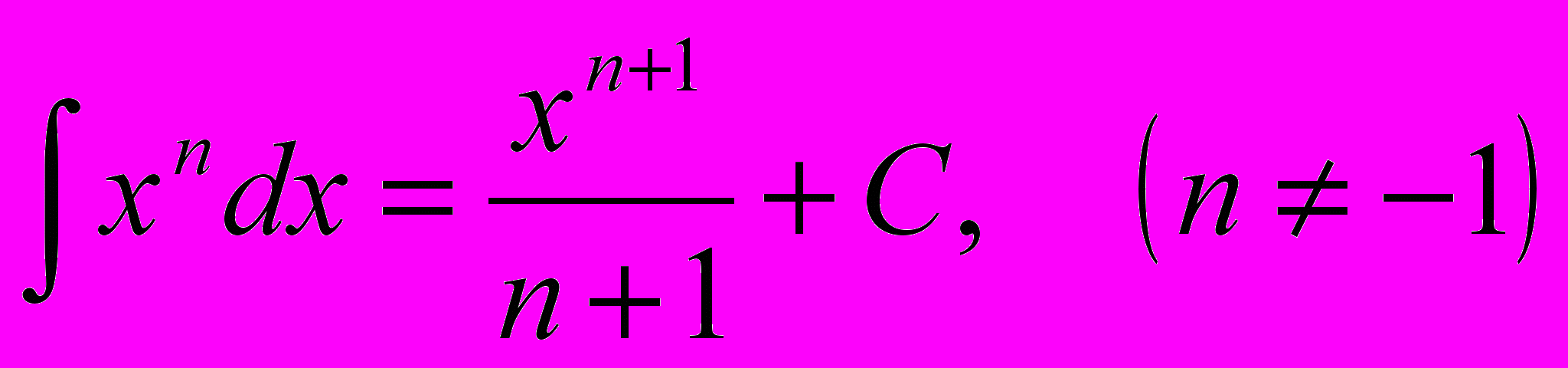
2.

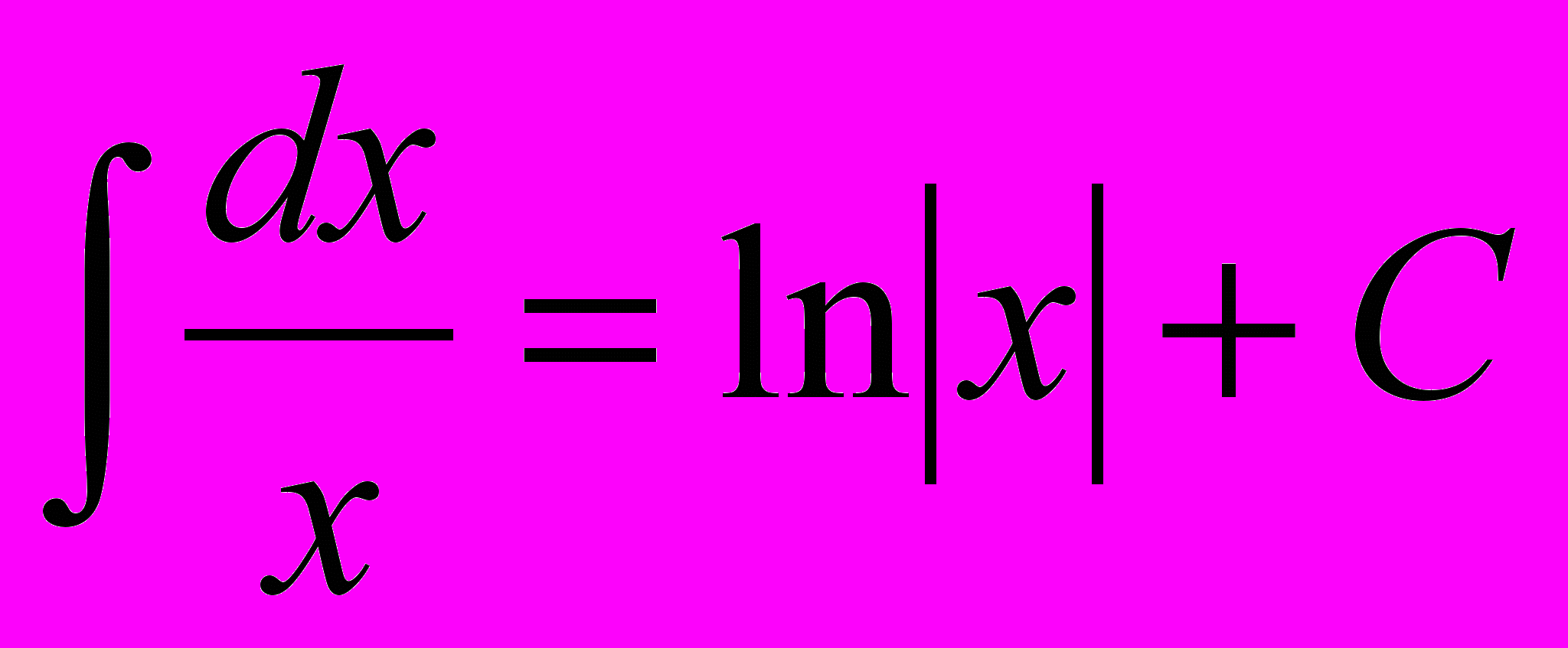
3.

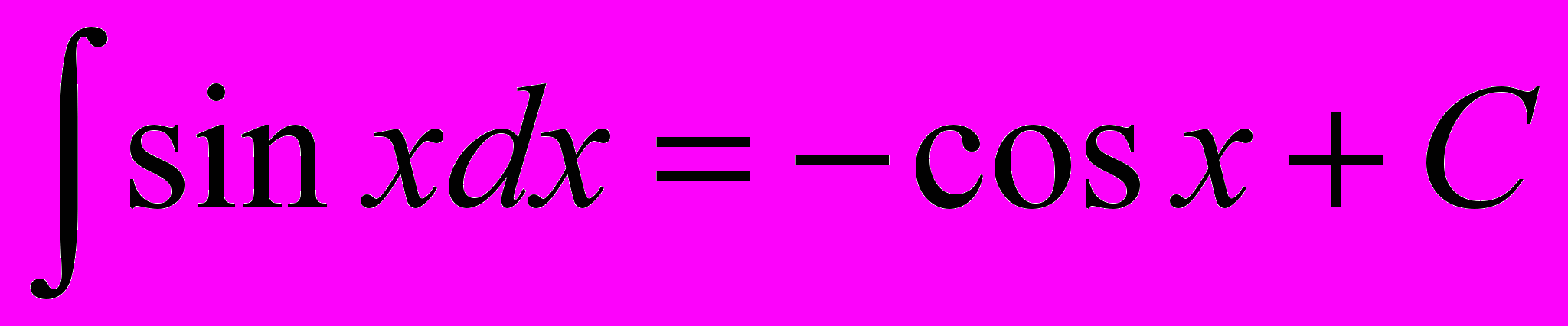
4.

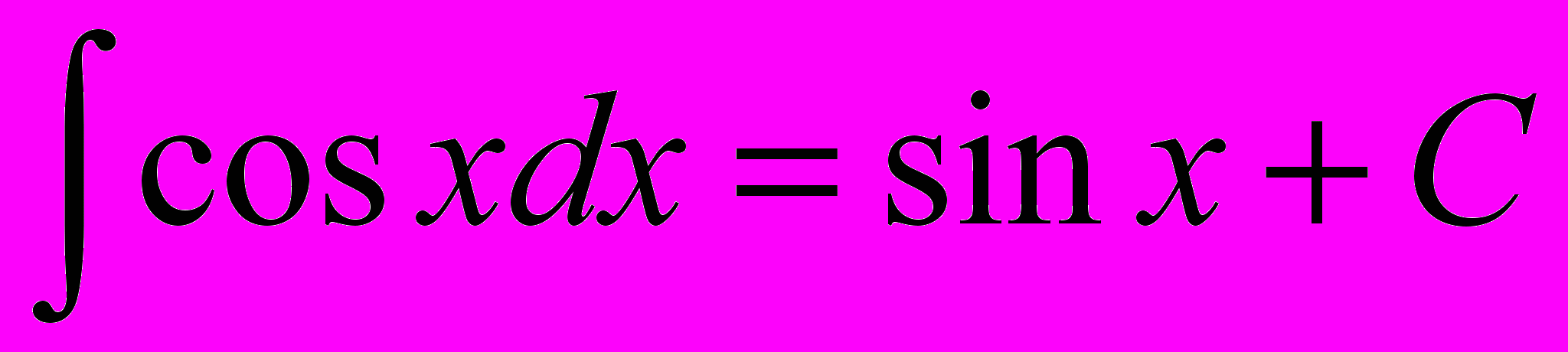
5.

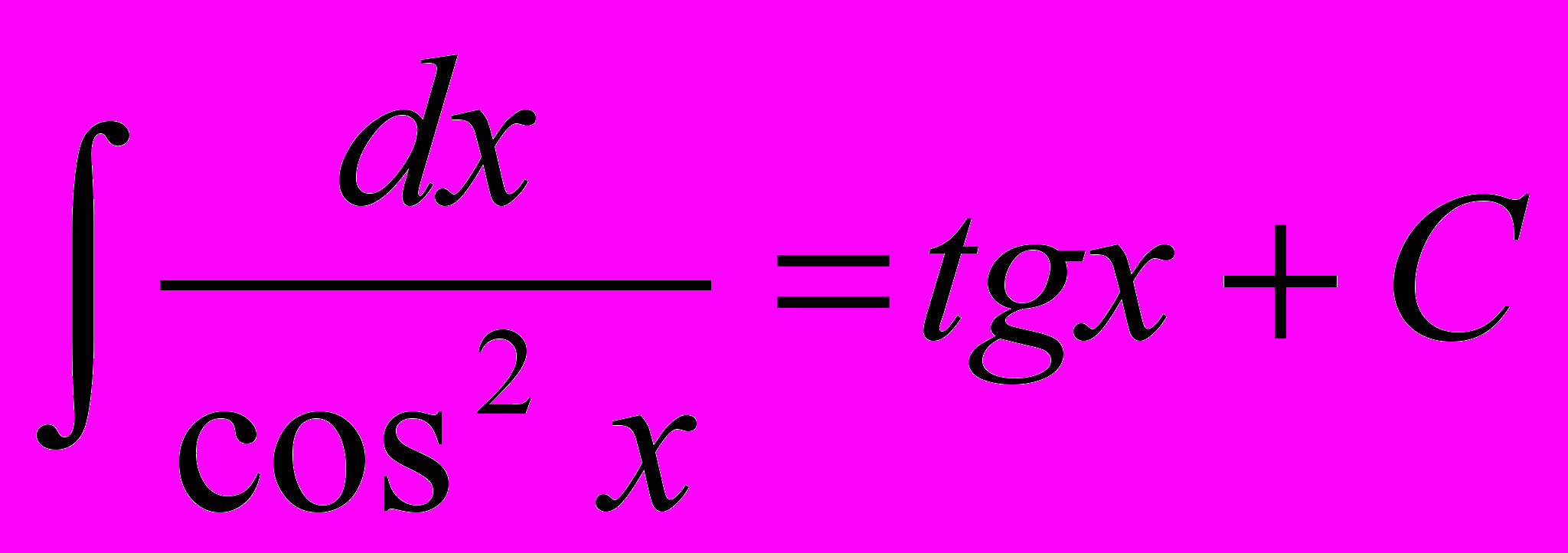
6.

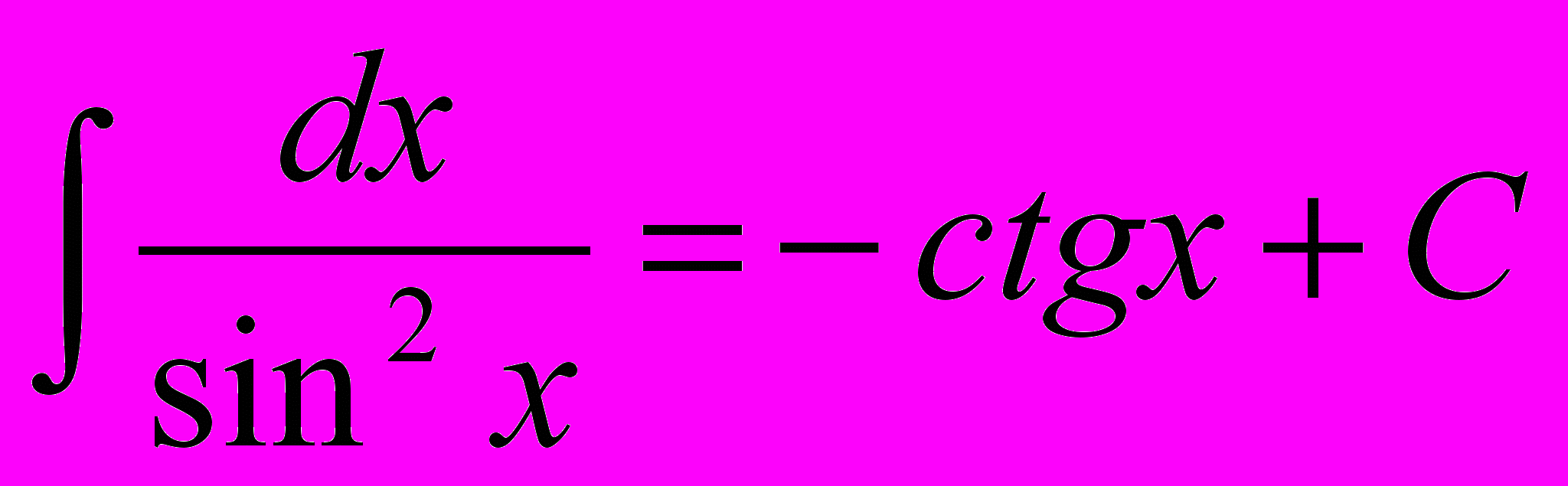
7.

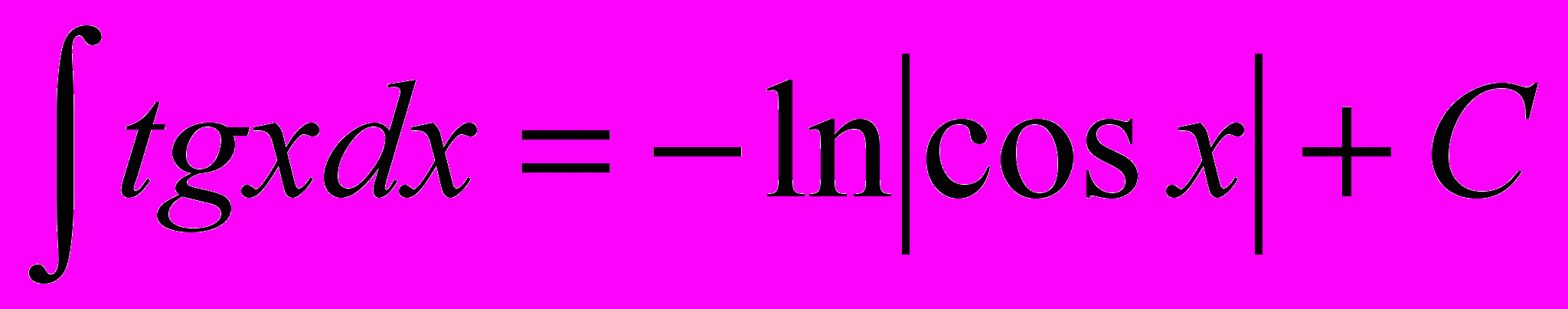
8.

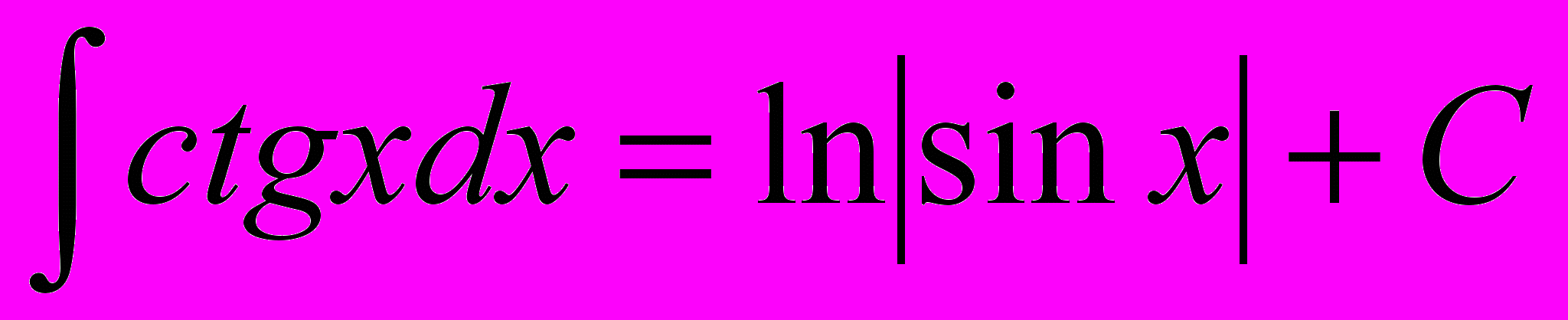
9.

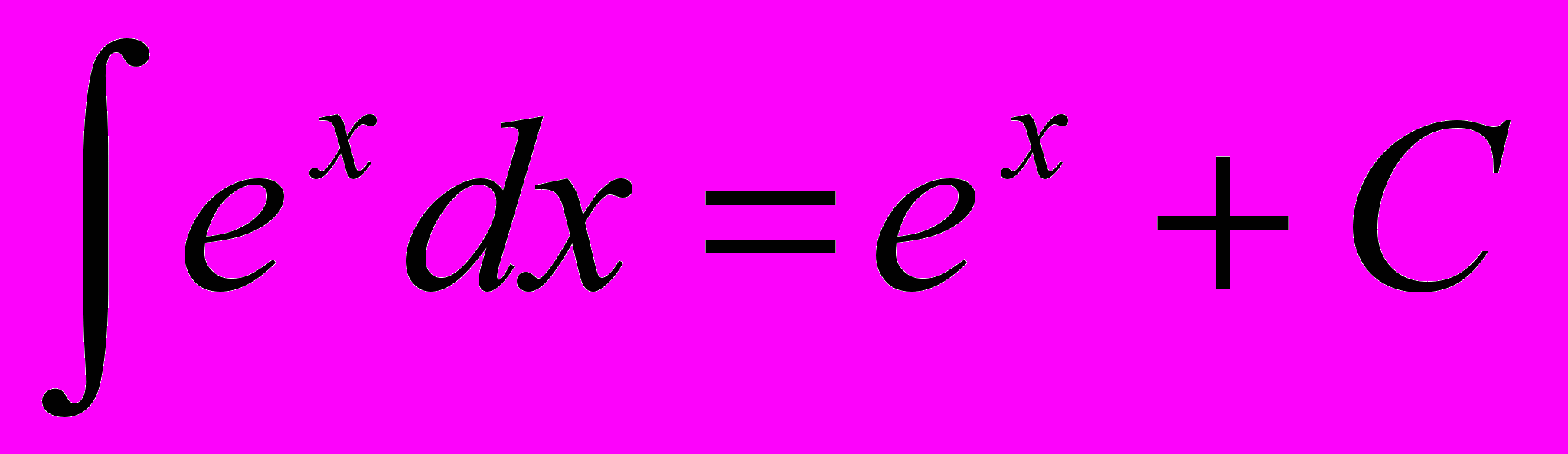
10.

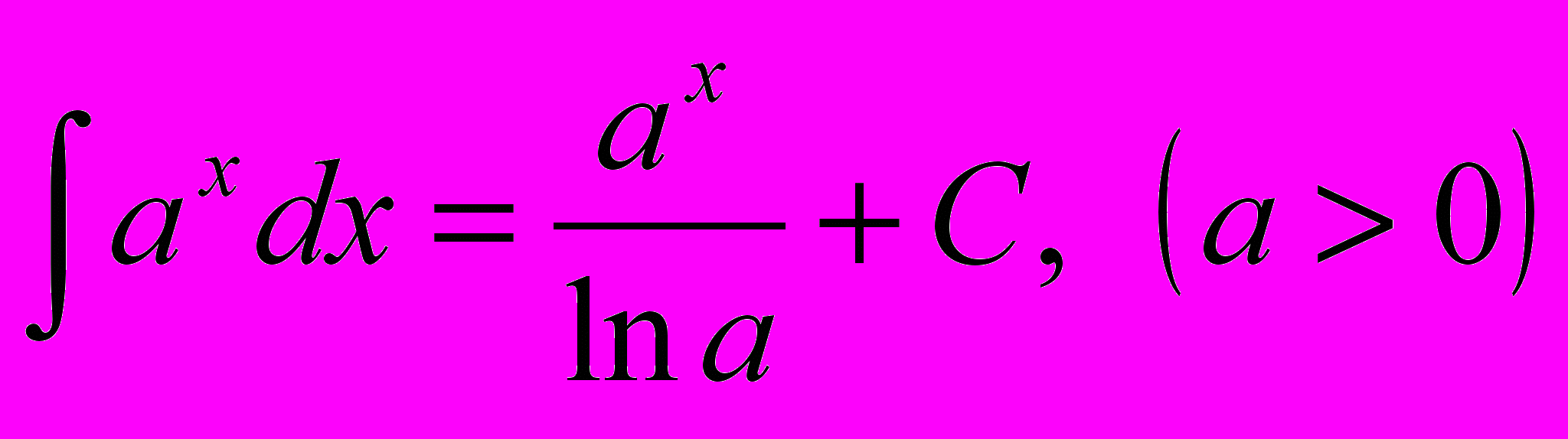
11.

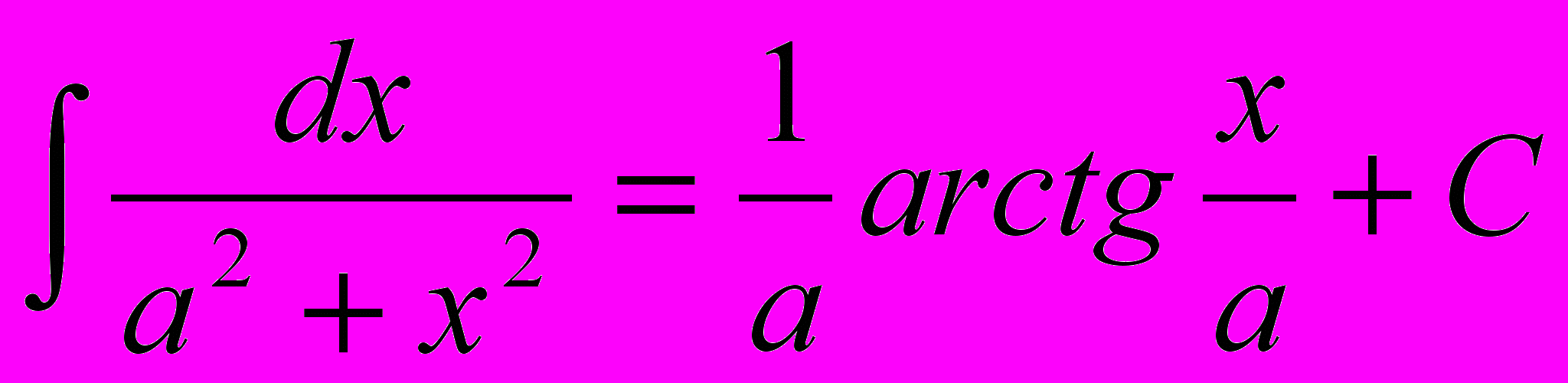
12.

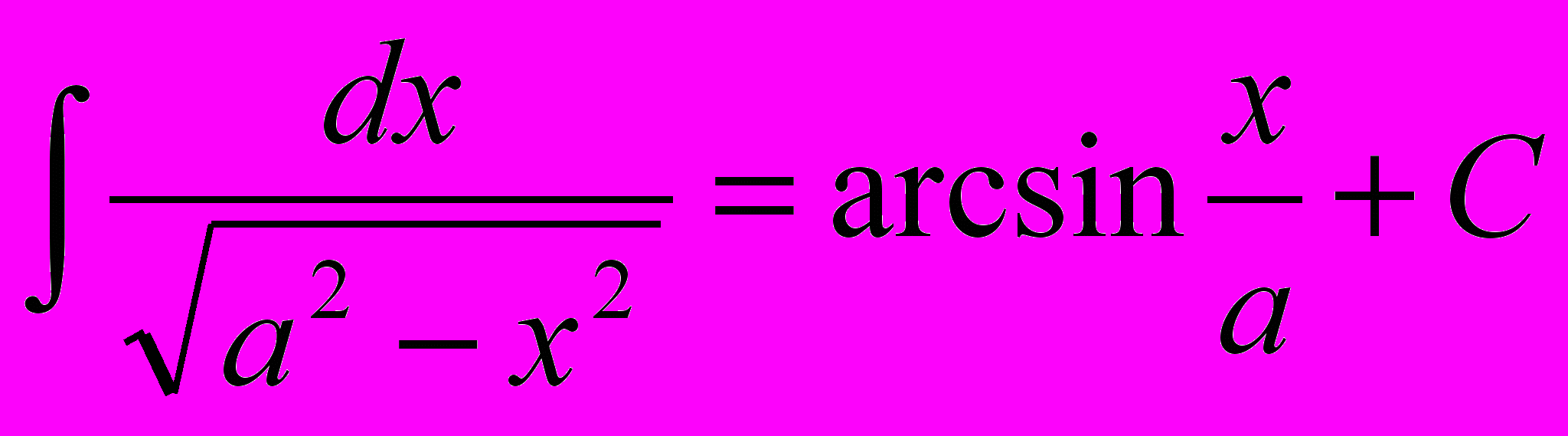
13.

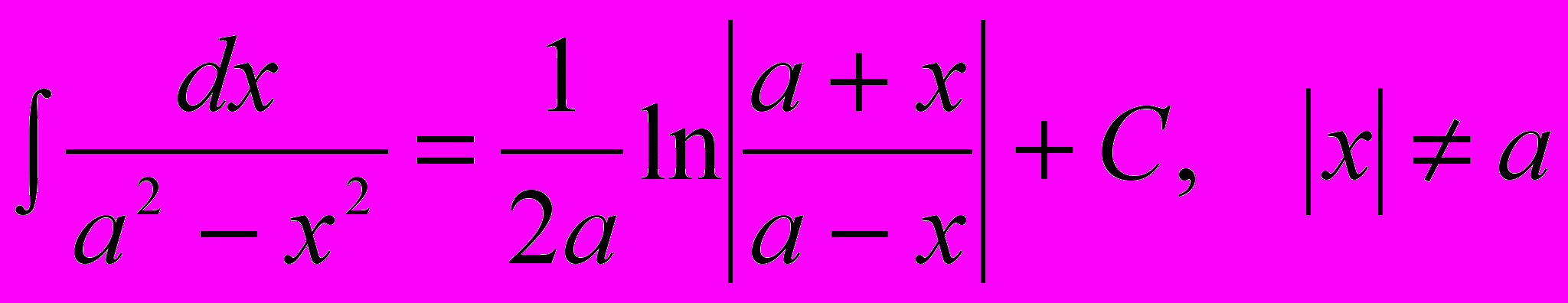
14.

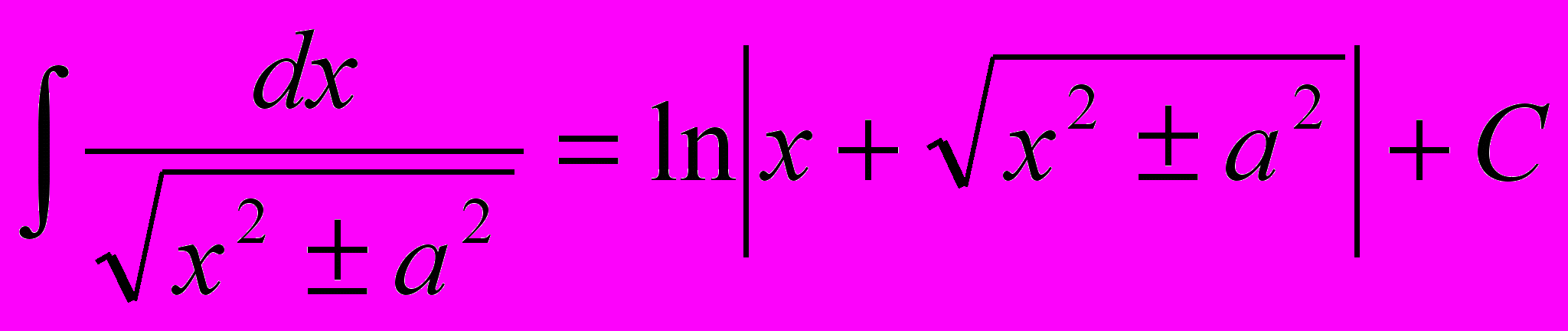
4. Основные методы вычисления неопределенного интеграла

Пусть требуется найти неопределенный интеграл 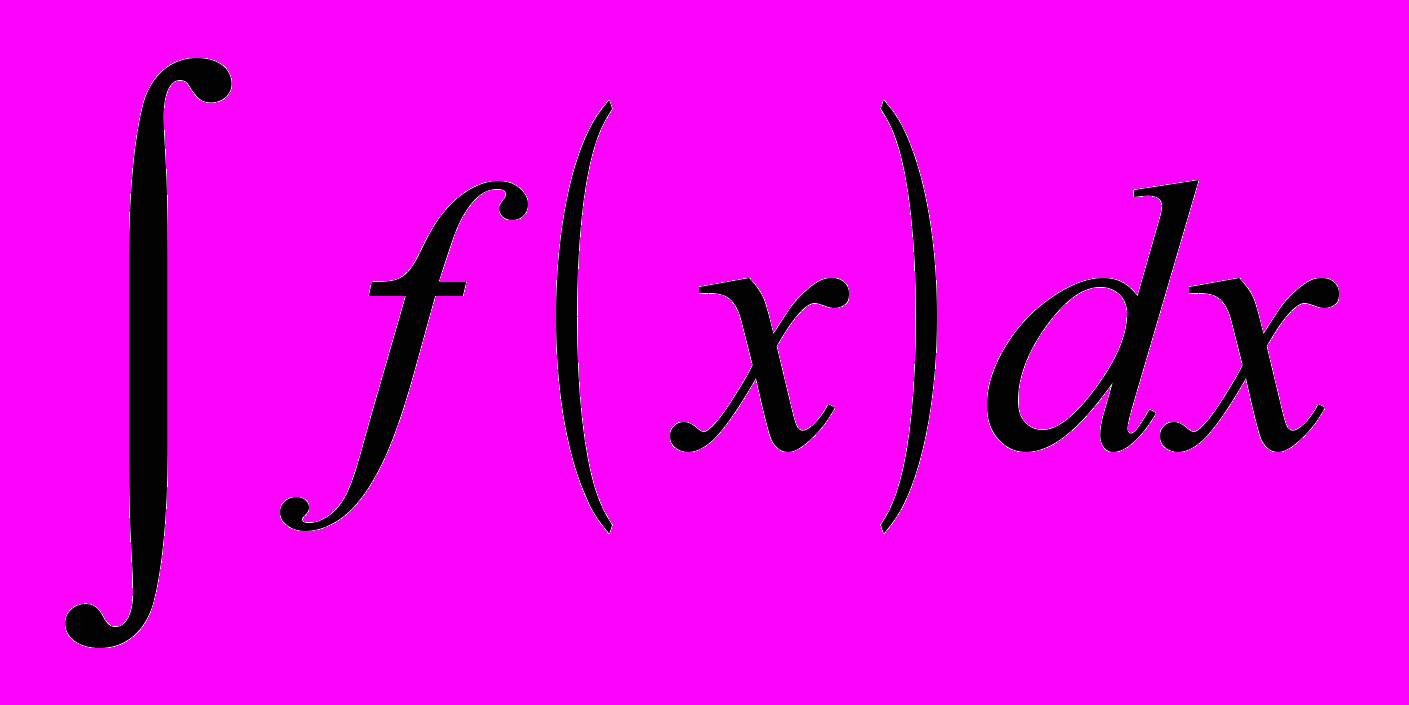, причем непосредственно подобрать первообразную не представляется возможным, но известно, что она существует. В этом случае применяются различные методы интегрирования, благодаря которым исходный интеграл можно привести к интегралу табличного вида. Рассмотрим некоторые из этих методов.

1. Метод непосредственного интегрирования. Используя свойства неопределенного интеграл, а также выполняя элементарные математические преобразования подынтегральной функции, исходный интеграл можно привести к неопределенному интегралу табличного вида.

Пример 8.2. Найти неопределенный интеграл .

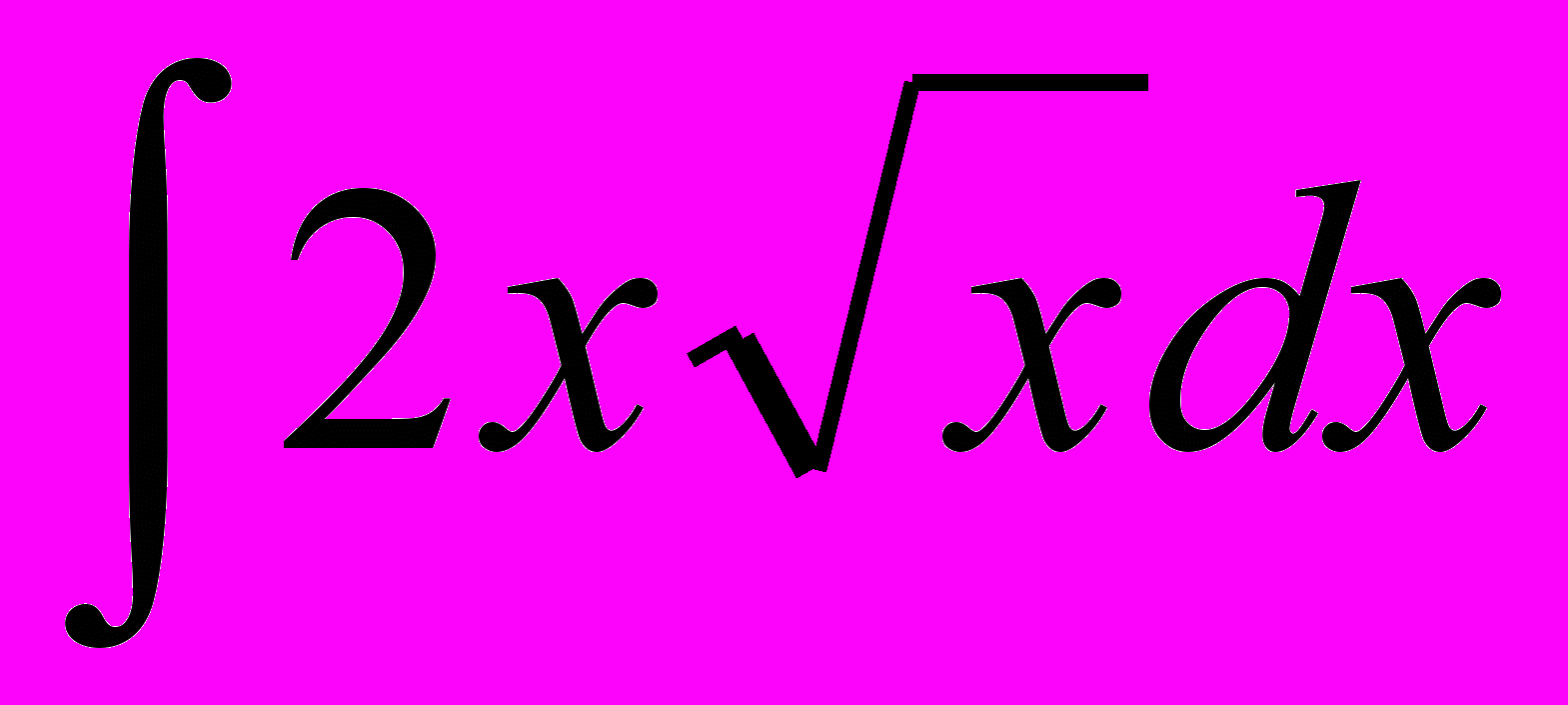Используя пятое свойство неопределенного интеграла, вынесем за знак интеграла постоянную 2. Затем, выполняя элементарные математические преобразования, приведем подынтегральную функцию к степенному виду:

.

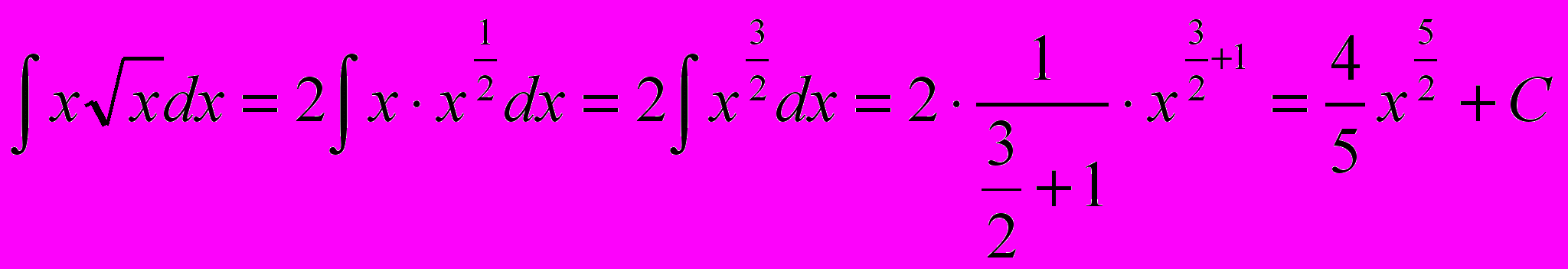2. Замена переменной. Пусть требуется найти неопределенный интеграл 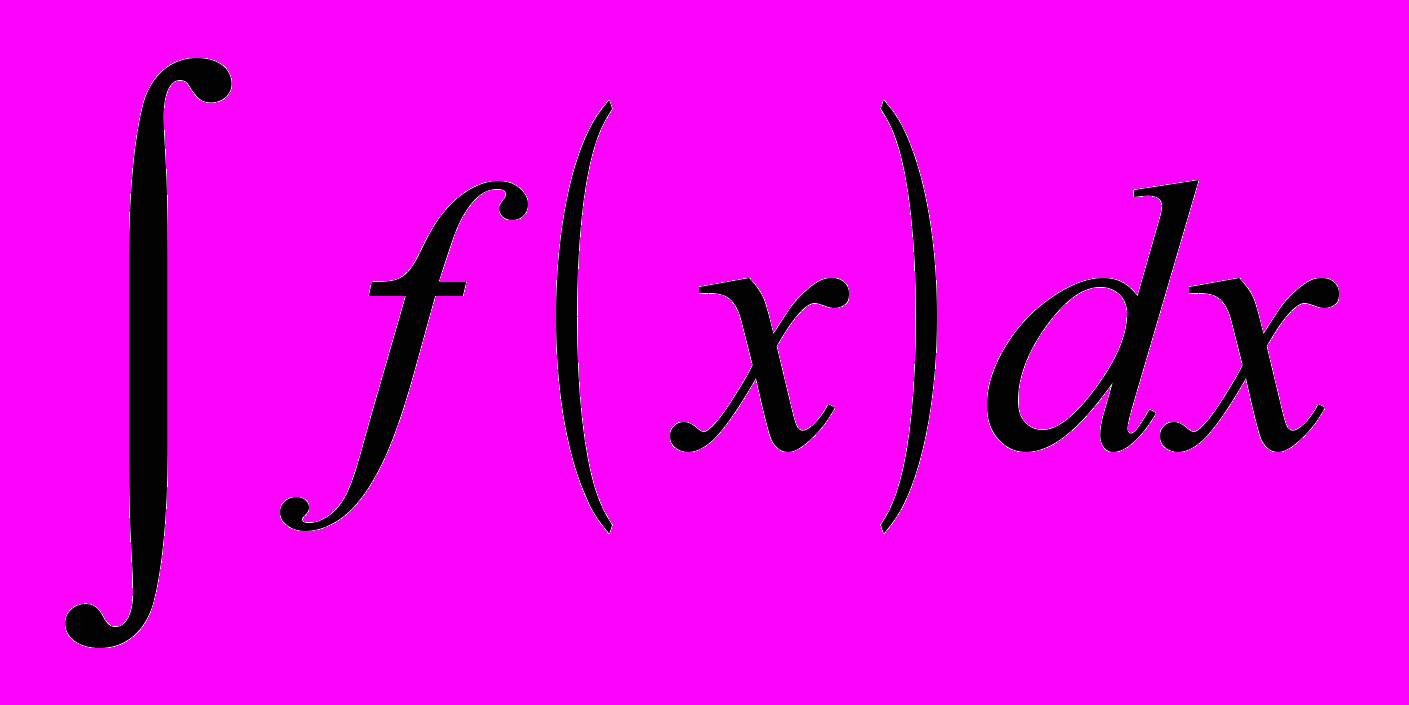. Сделаем замену в подынтегральном выражении, положив 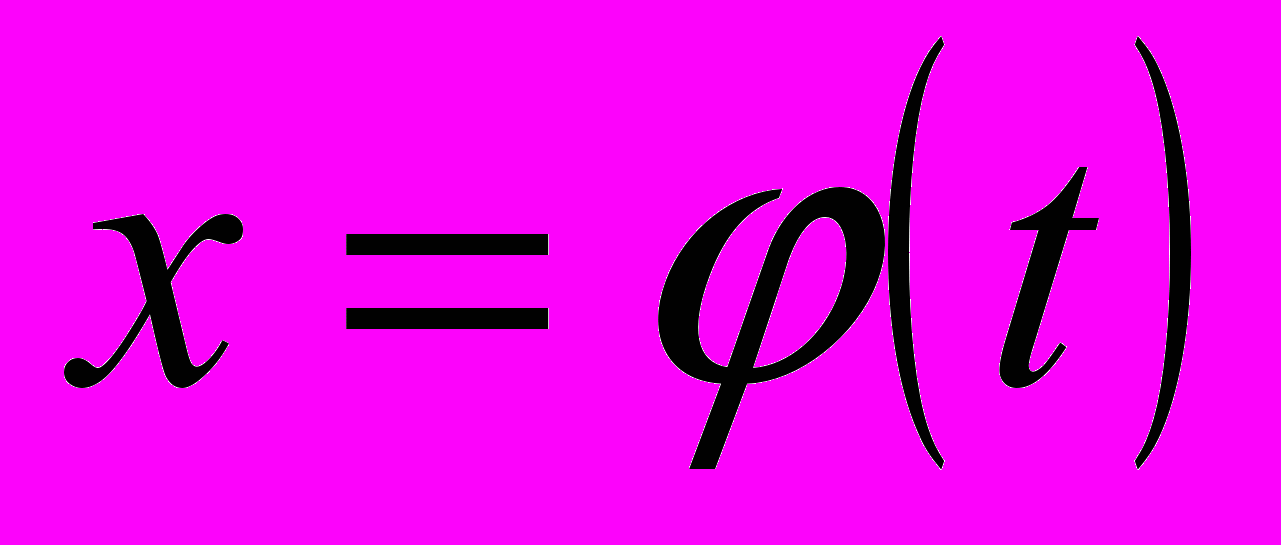, где 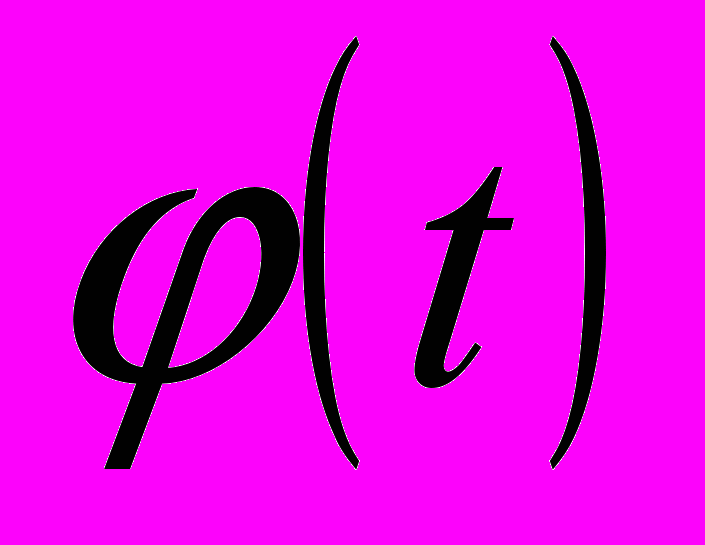— монотонная непрерывная функция, которая имеет непрерывную производную. Тогда 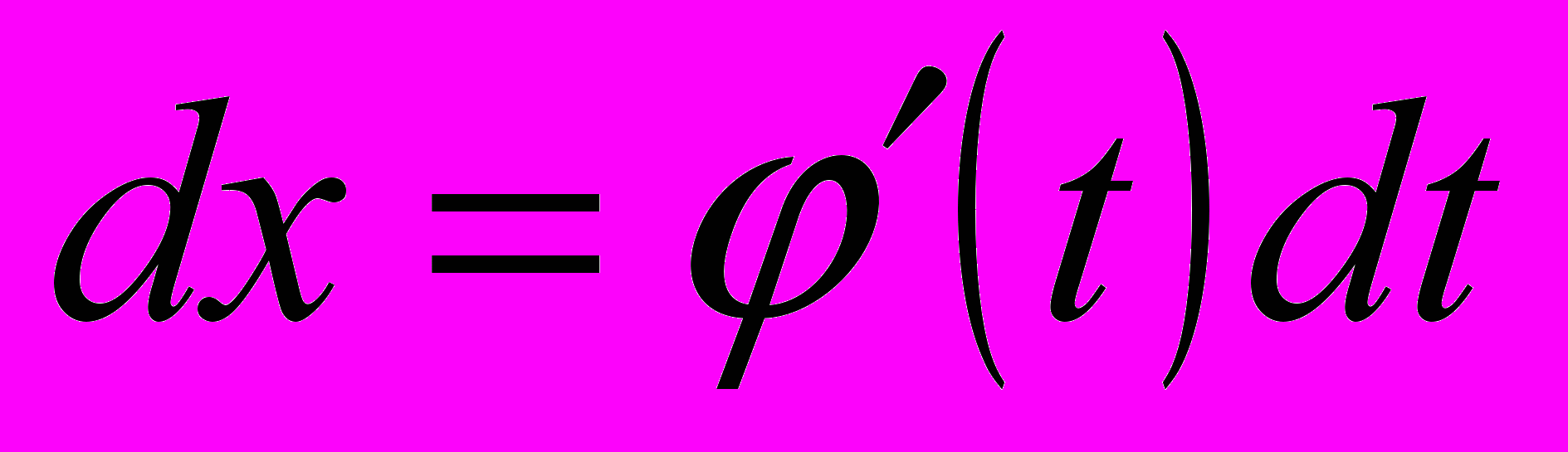. В этом случае имеет следующее равенство:

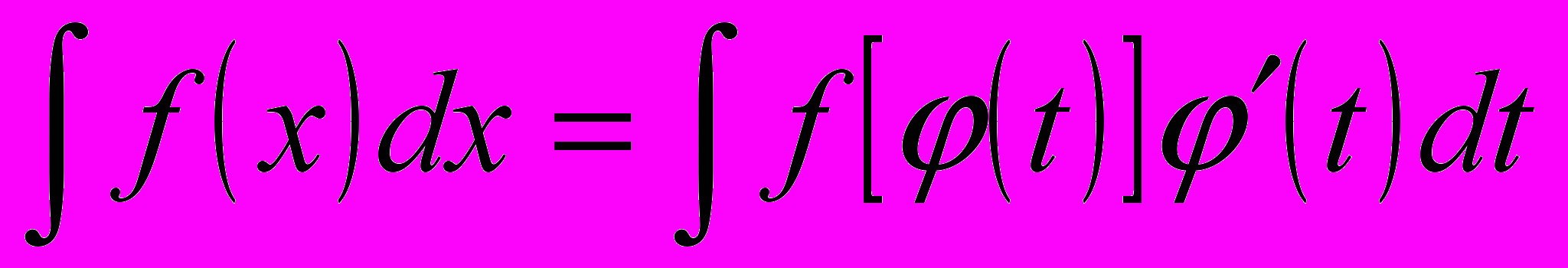(8.9)

Пример 8.3. Найти неопределенный интеграл 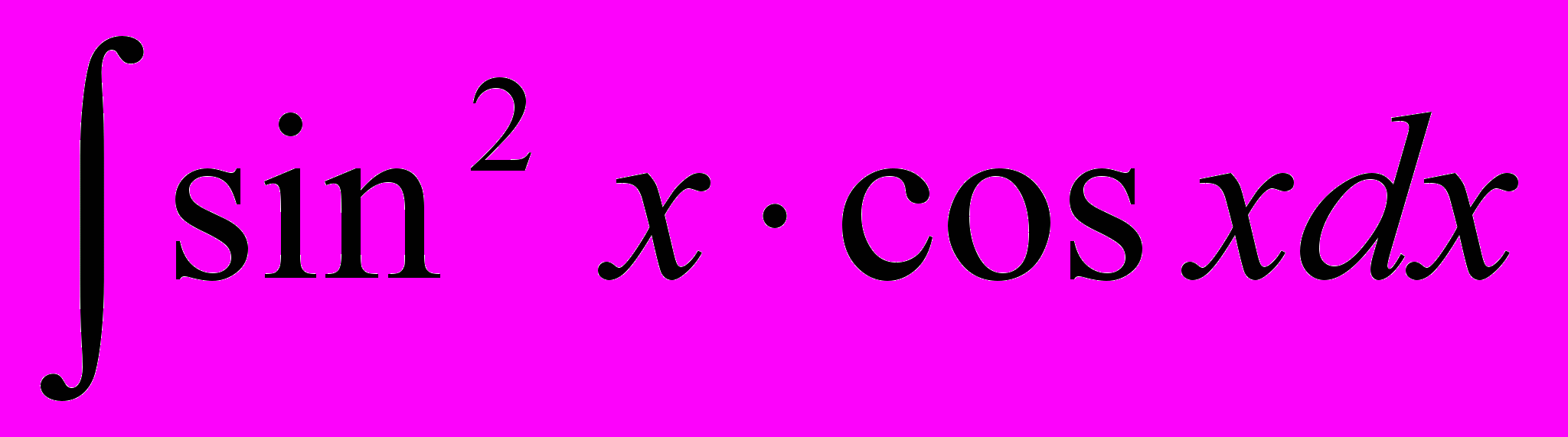, используя метод замены переменной.

Сделаем замену переменной 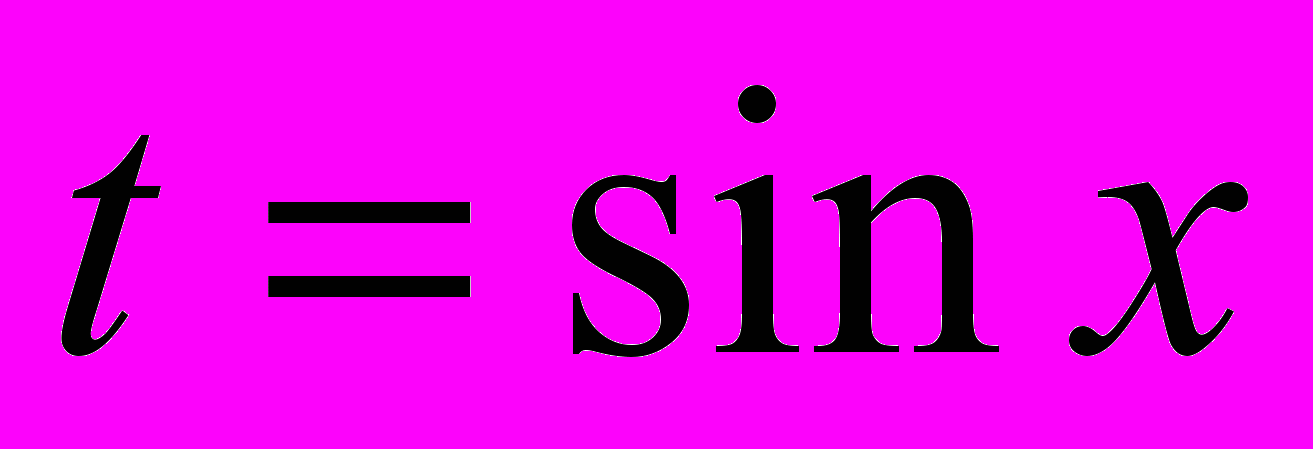, тогда 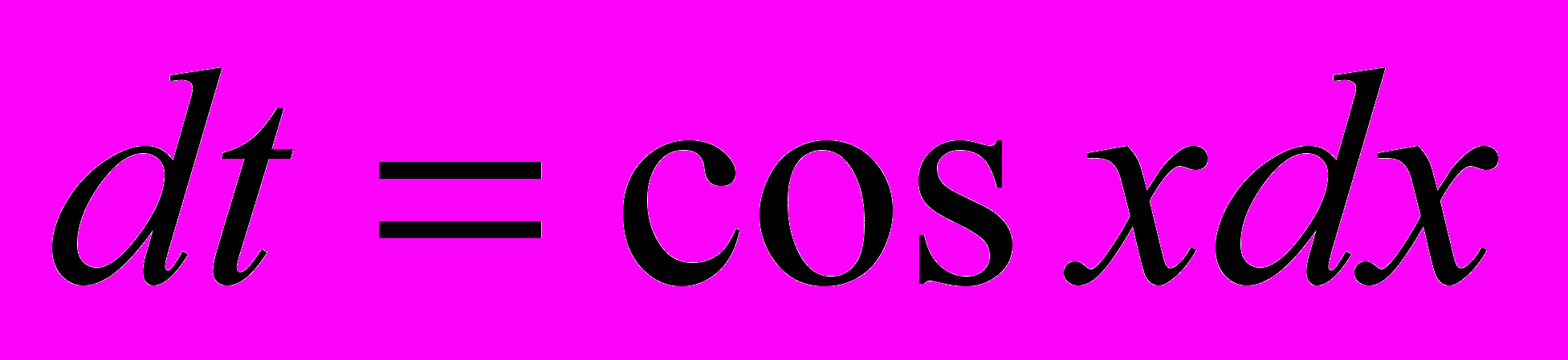. Исходный интеграл примет вид: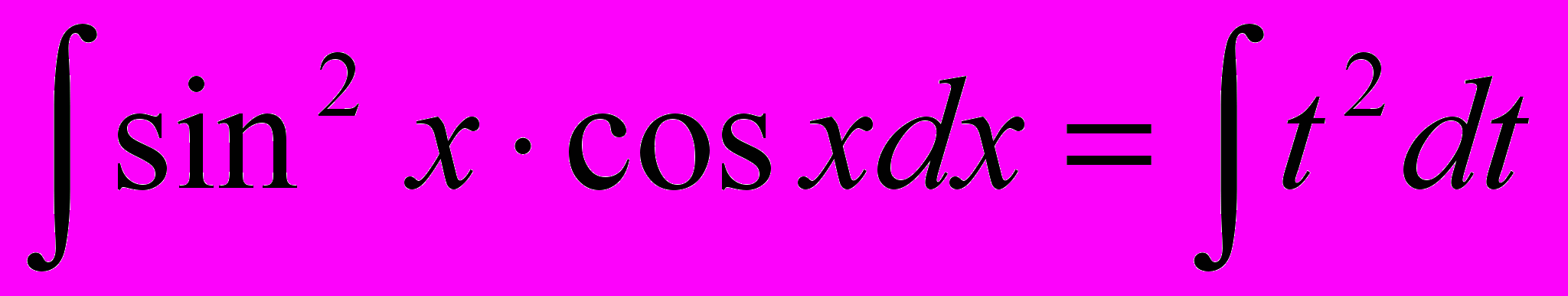



Таким образом, мы получили неопределенный интеграл табличного вида: степенная функция. Используя правило нахождения неопределенного интеграла от степенной функции (см. п.1 в таблице интегралов), найдем:



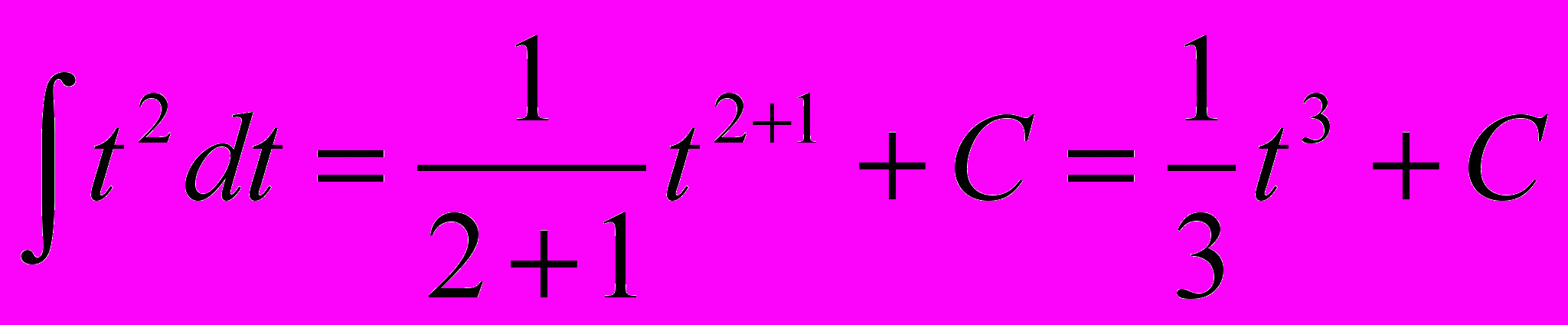
Сделав обратную замену, получим окончательный ответ:



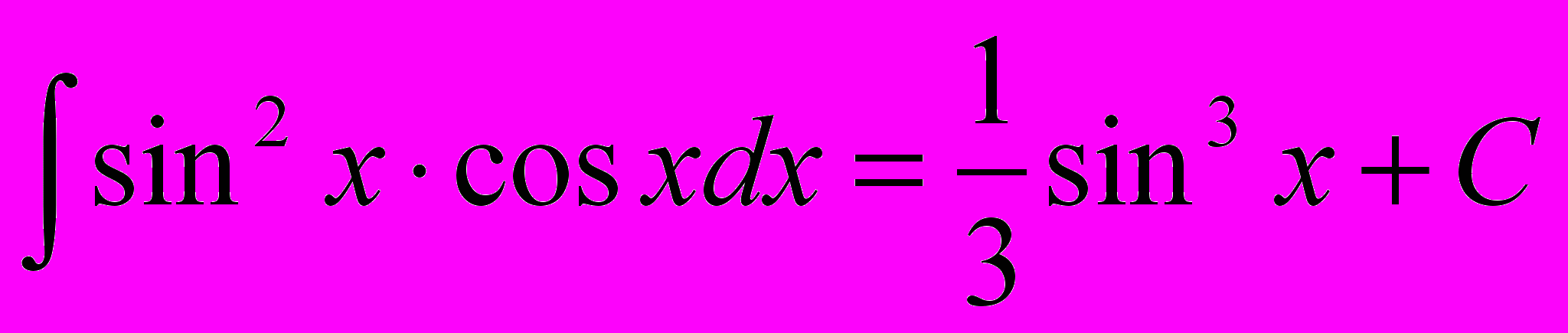
3. Интегрирование по частям. Пусть 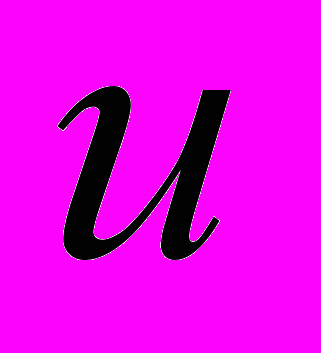и 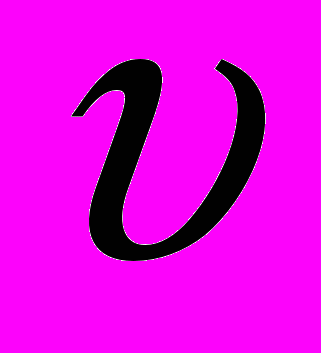— две дифференцируемые функции от переменной 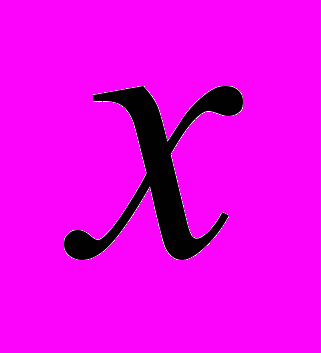. Тогда дифференциал произведения вычисляется по формуле:

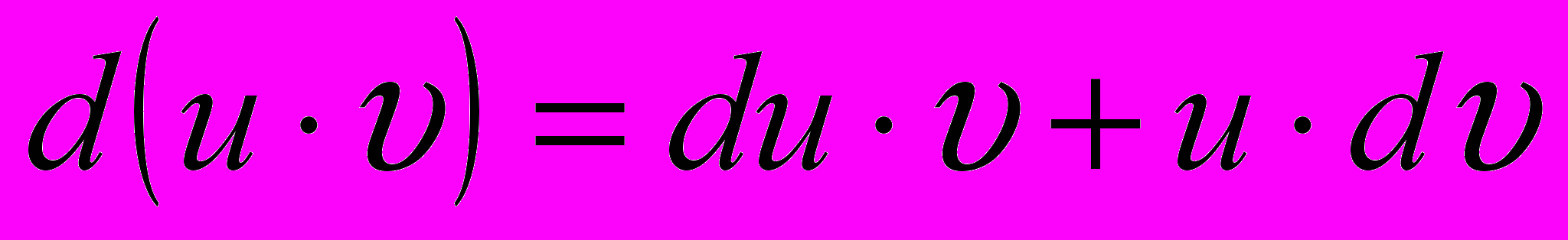(8.10)

Интегрируя, получим:

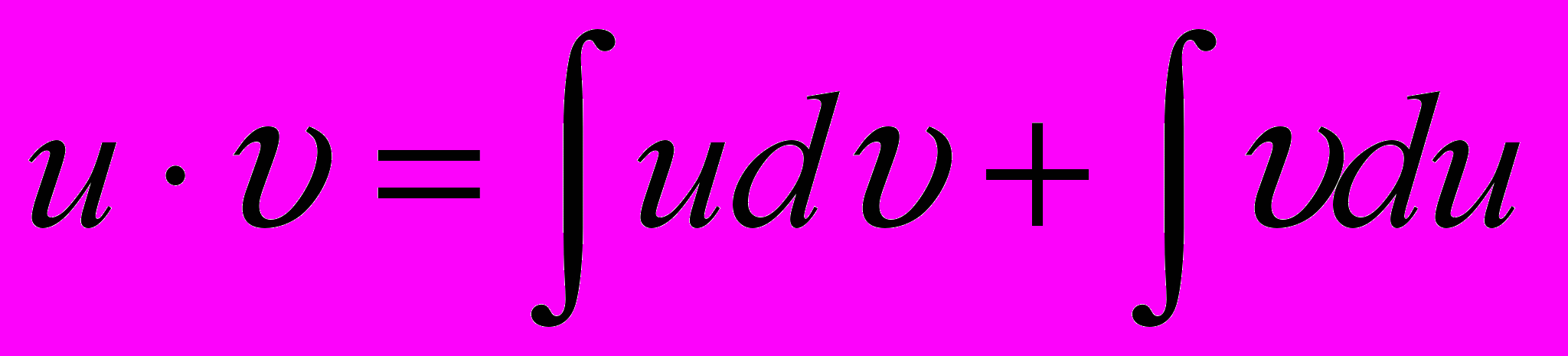(8.11)

Отсюда:

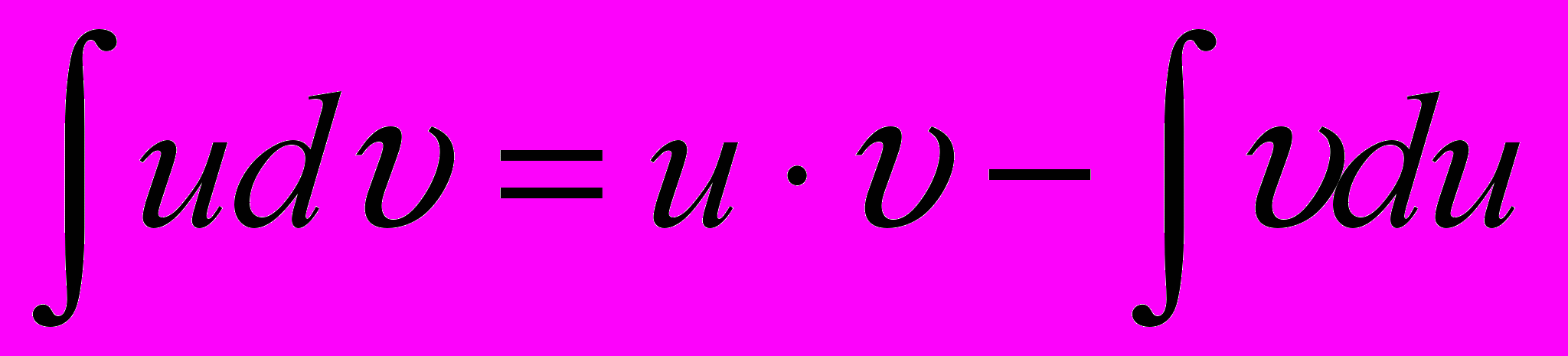(8.12)

Последняя формула называется формулой интегрирования по частям.

Пример 8.4. Найти неопределенный интеграл 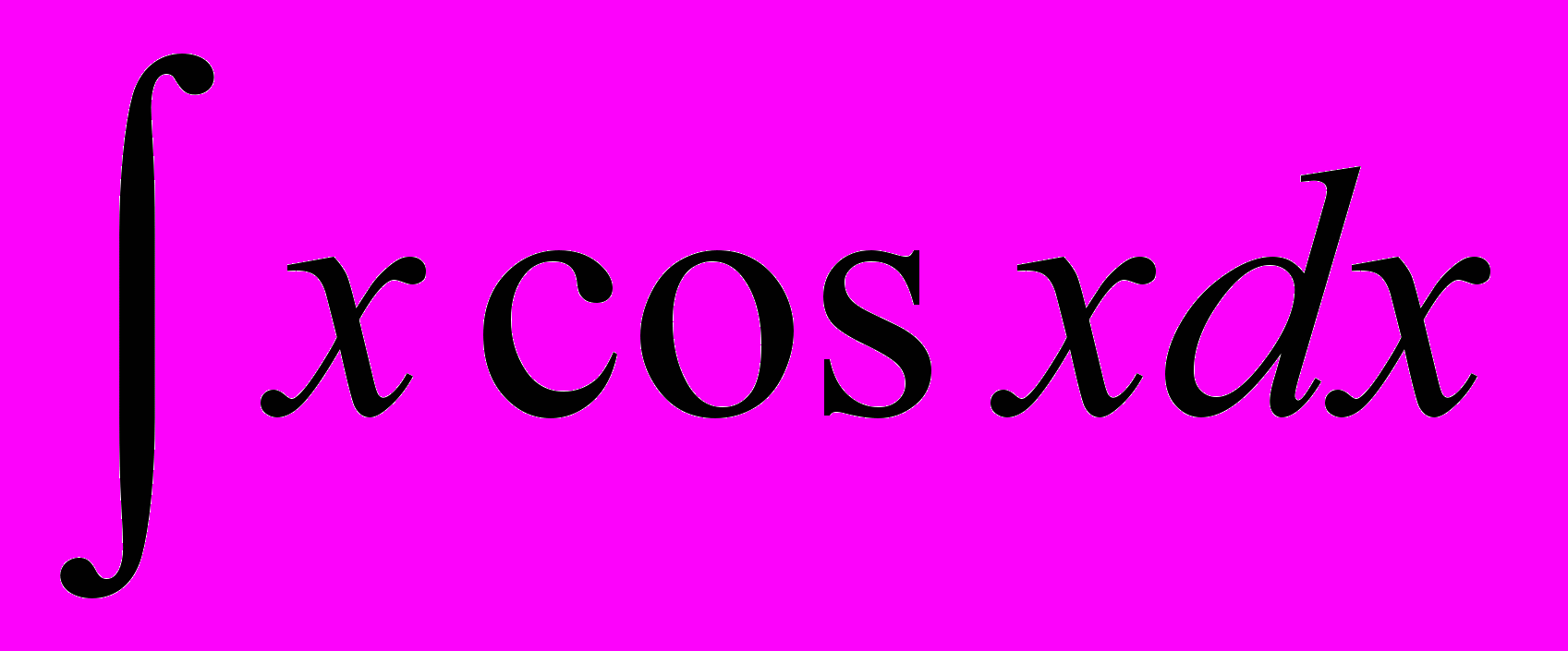, используя метод интегрирования по частям.

Введем следующие обозначения:

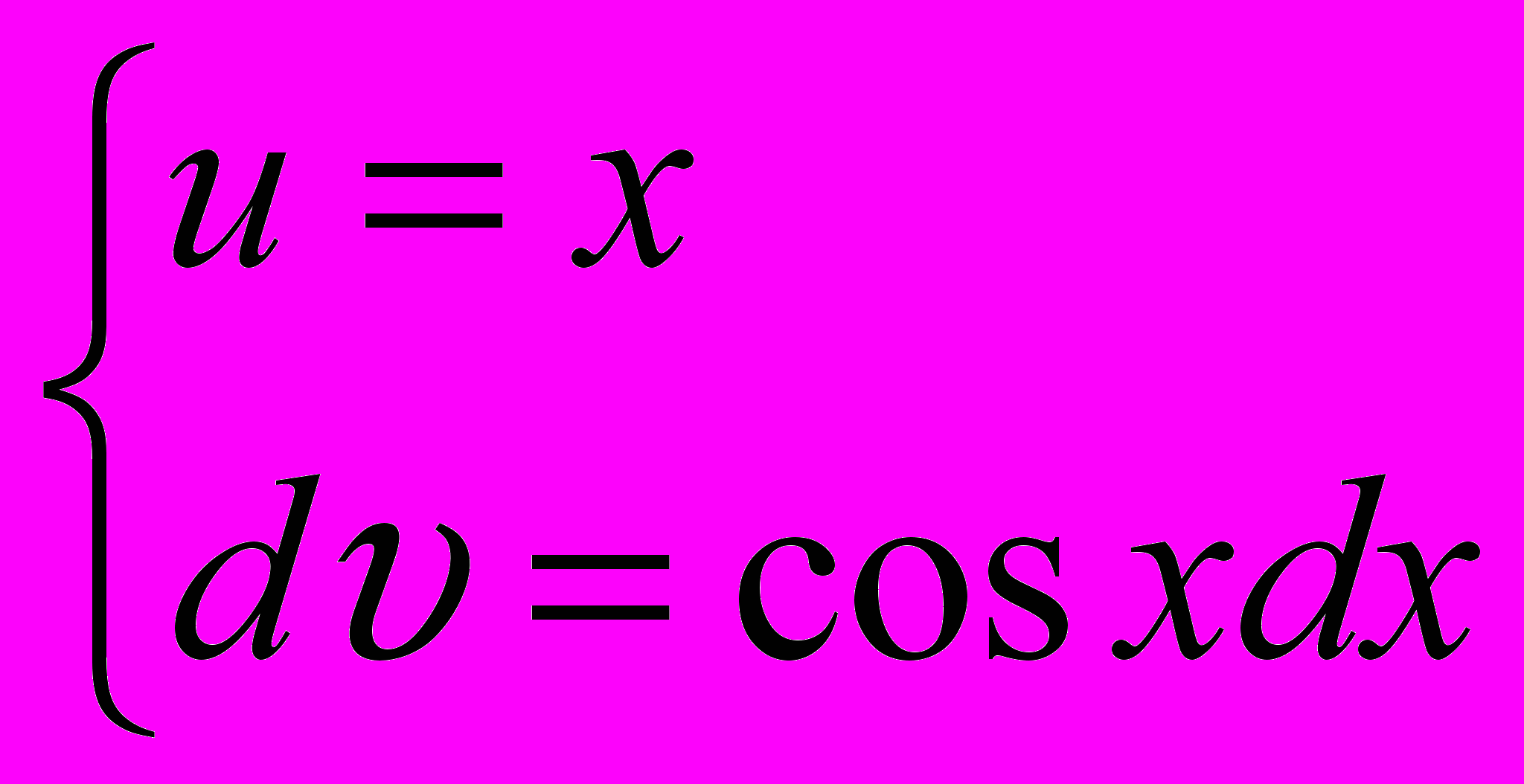(8.13)

Тогда дифференцируя первое выражение и интегрируя второе, получим:

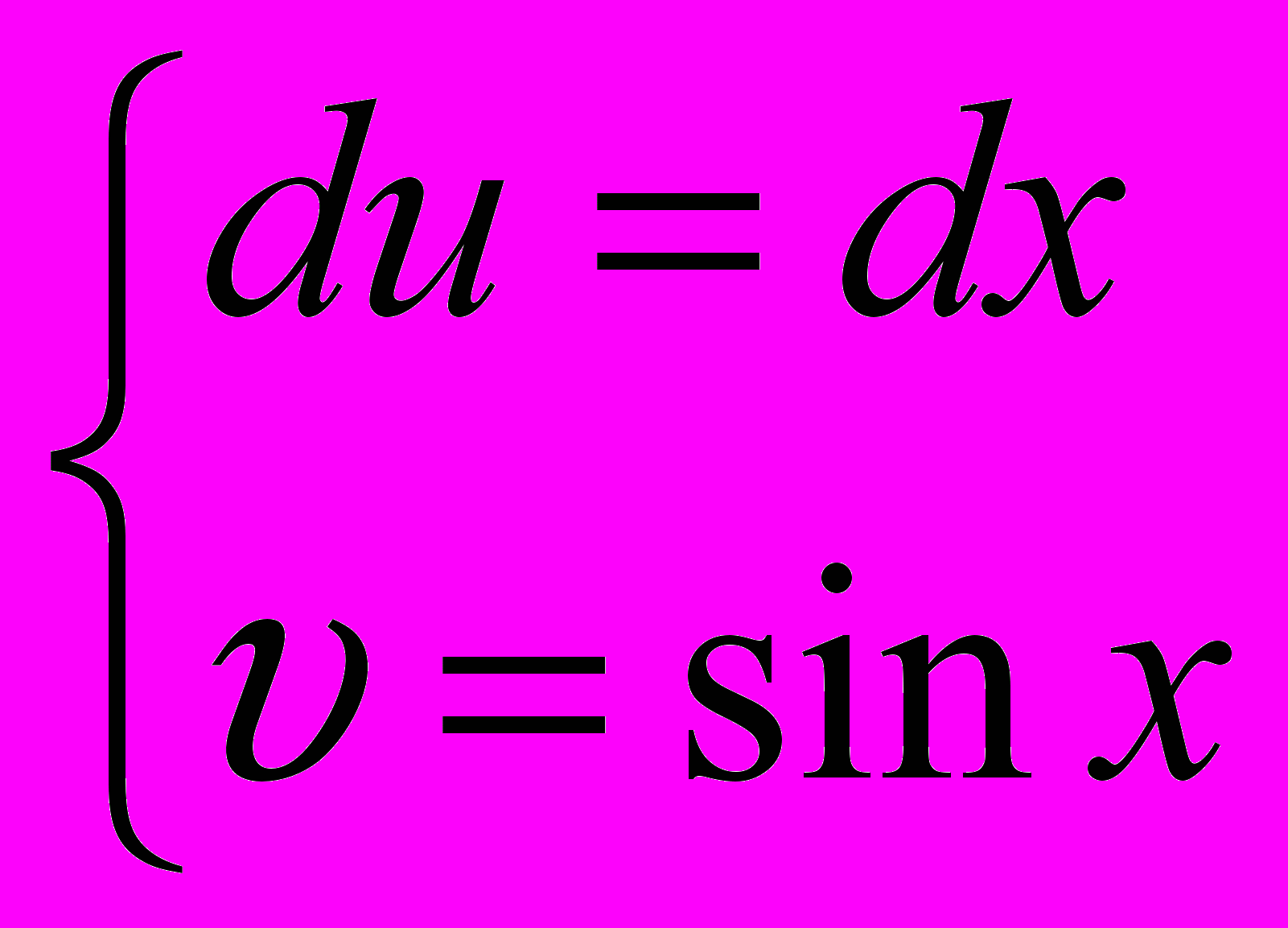(8.14)

Теперь подставив в формулу (8.12) введенные нами обозначения (8.13) и (8.14), получим:



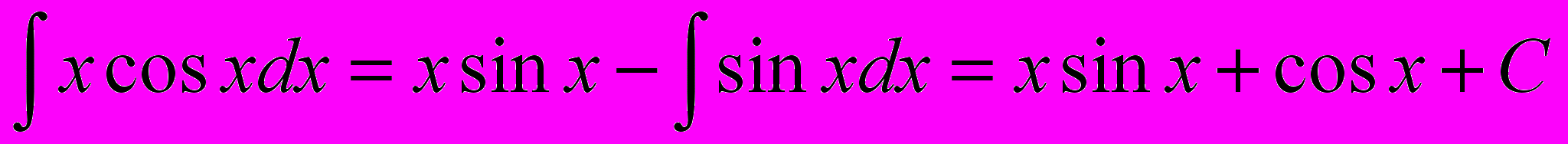
4. Интегралы от некоторых функций, содержащих квадратный трехчлен.

Рассмотрим следующие случаи:

а) В знаменателе интегрируемой функции квадратный трехчлен f(x) = .

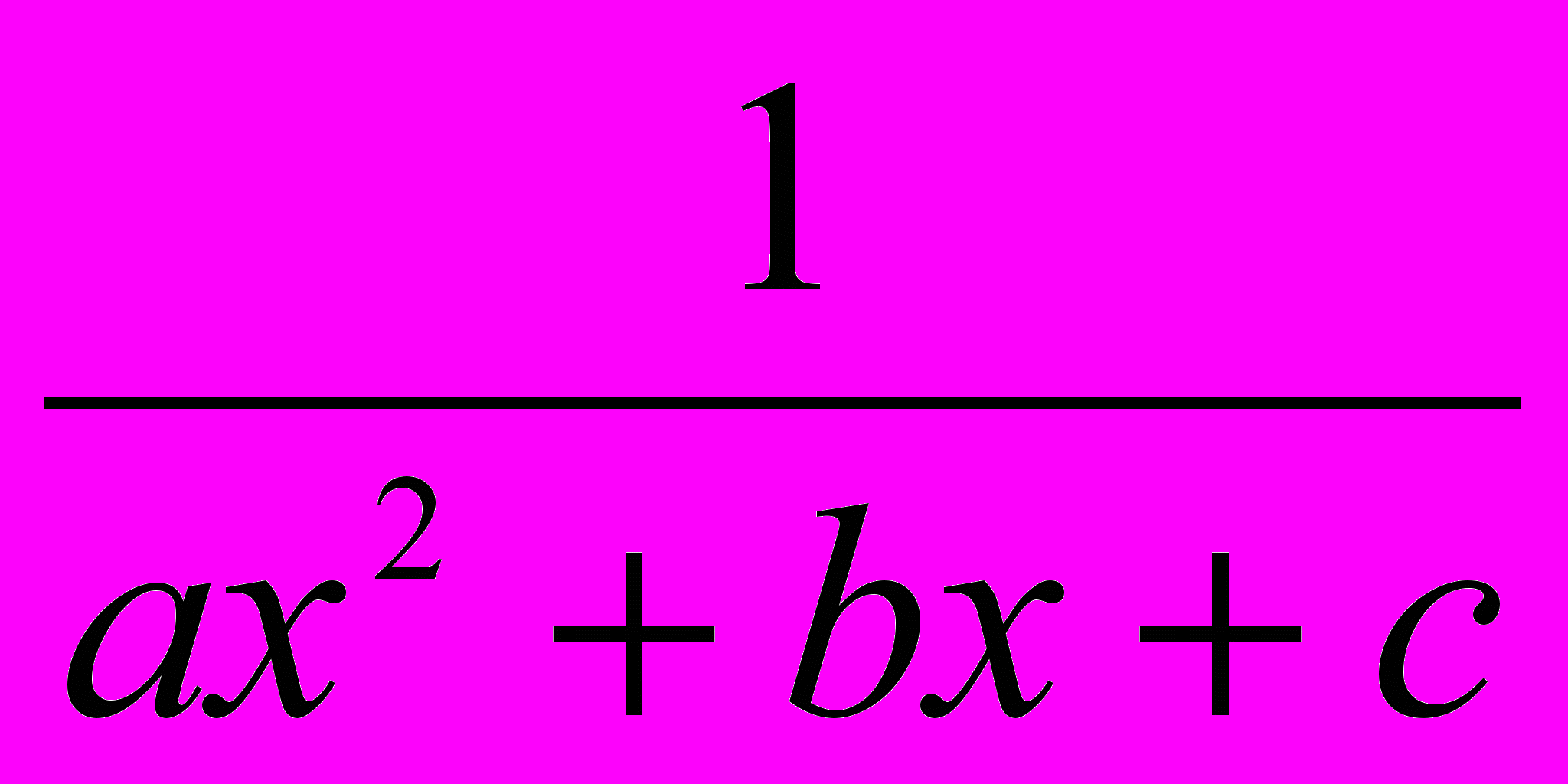Преобразуем его, выделив полный квадрат.

.

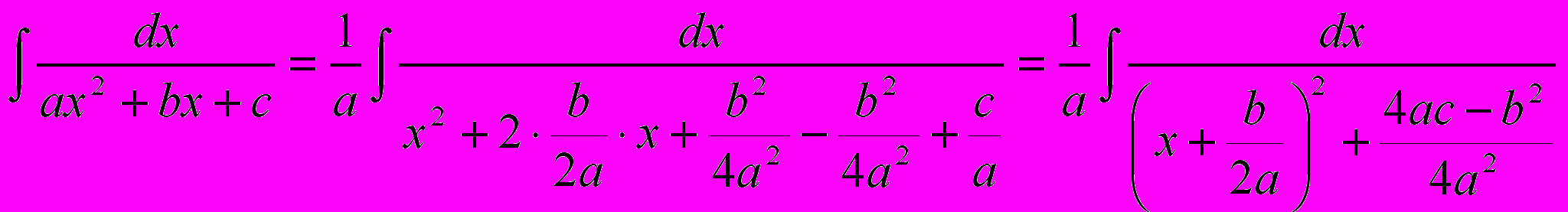Введем обозначение 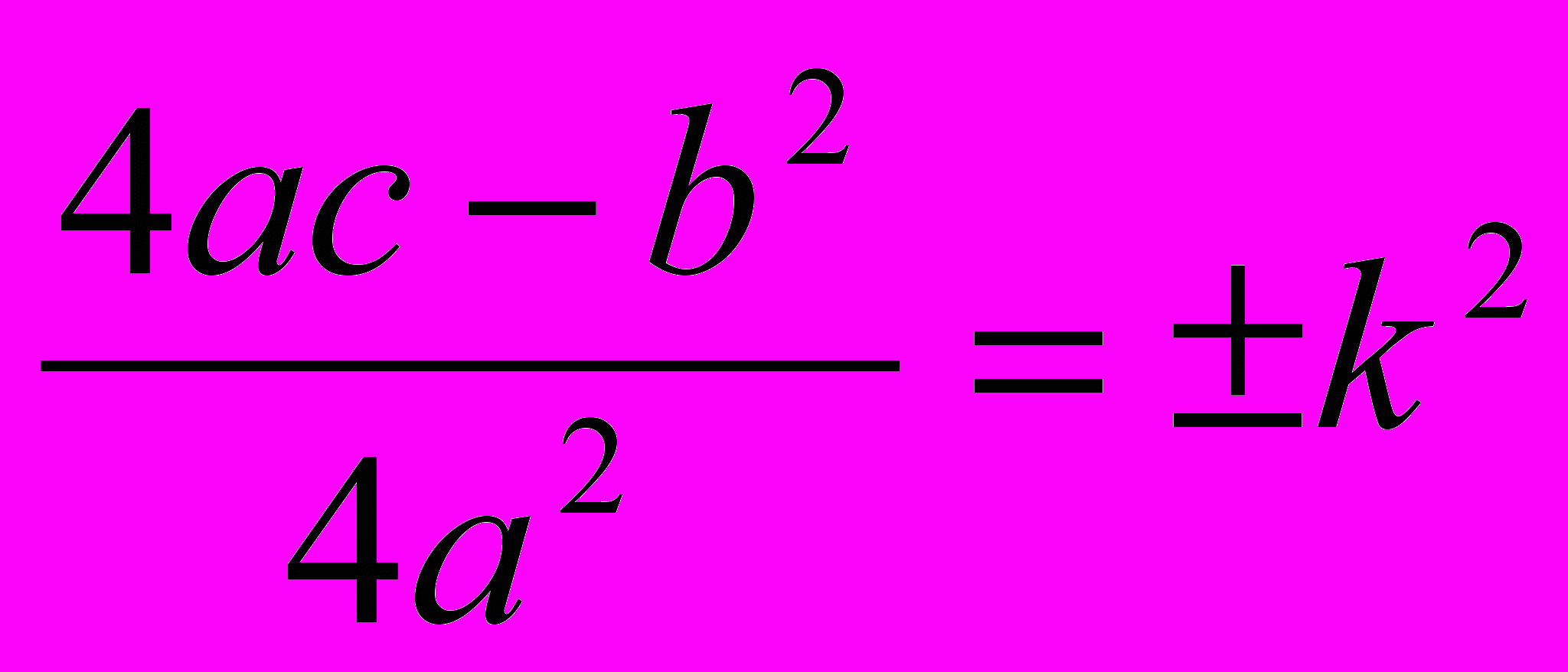. Таким образом, данный интеграл приобретает вид:

.

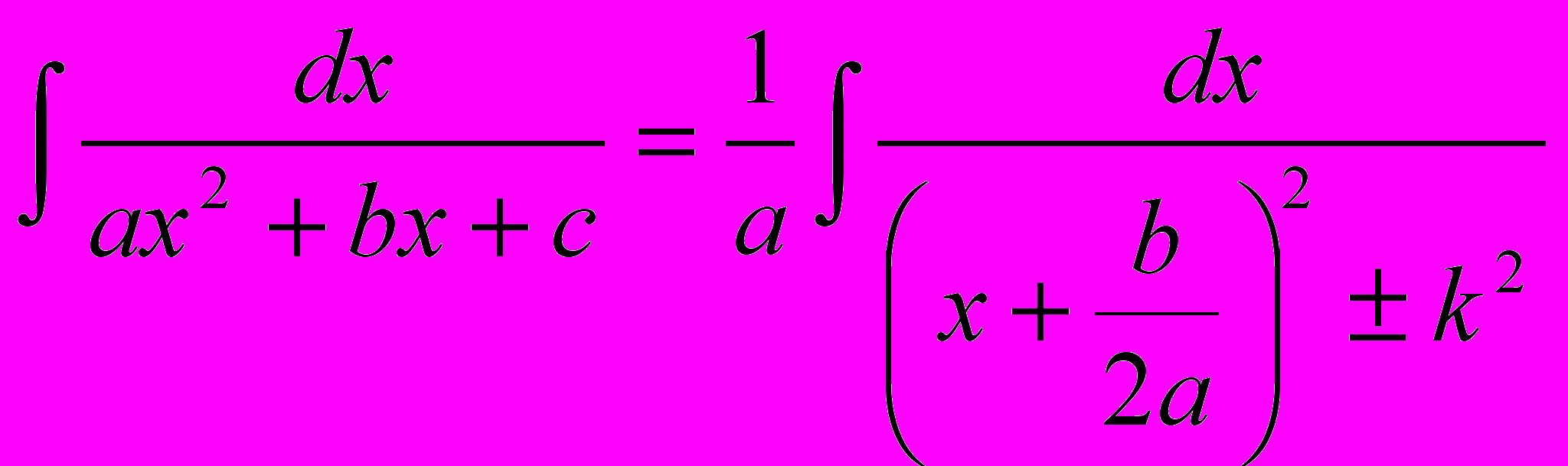Сделаем в последнем интеграле замену переменной:

,

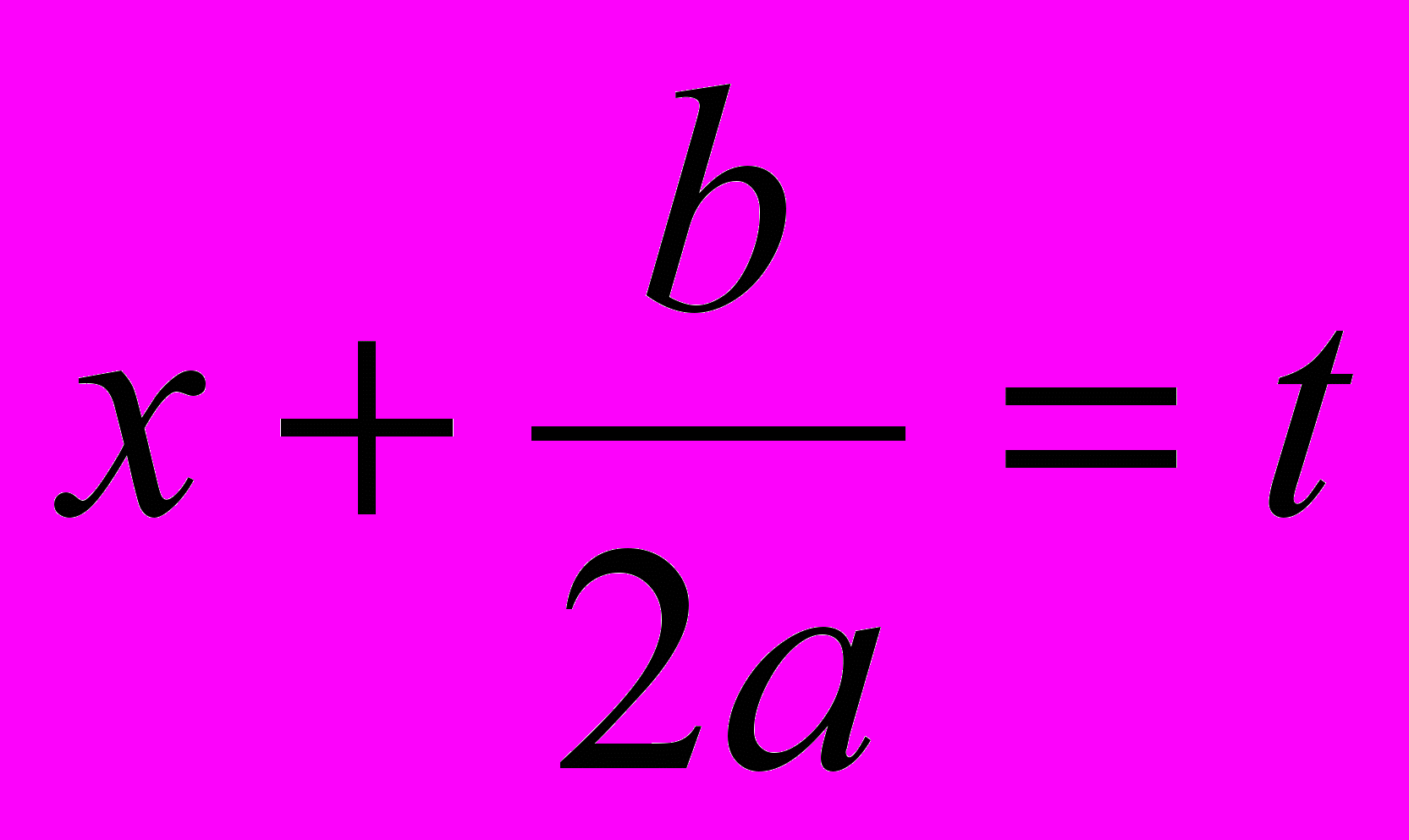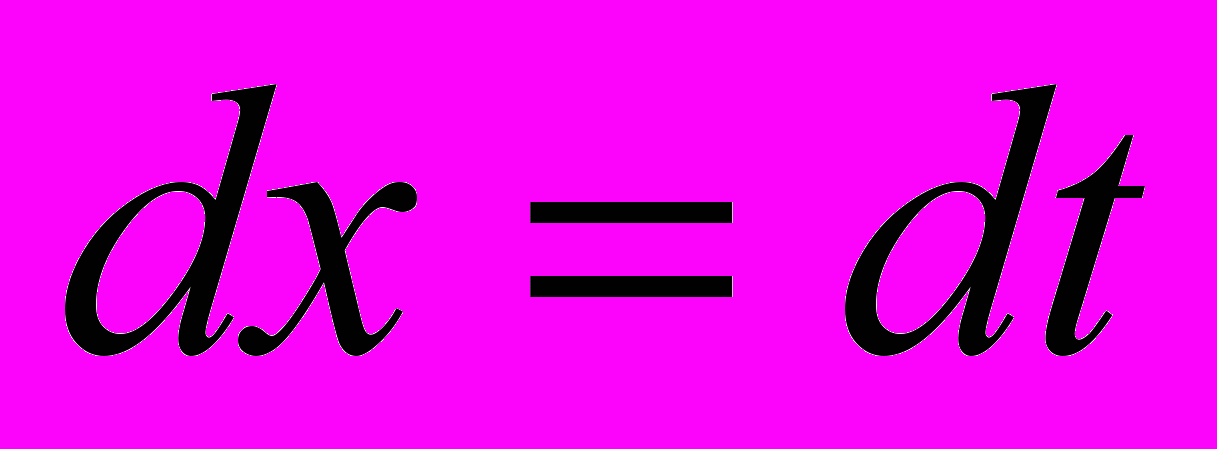
Получим:

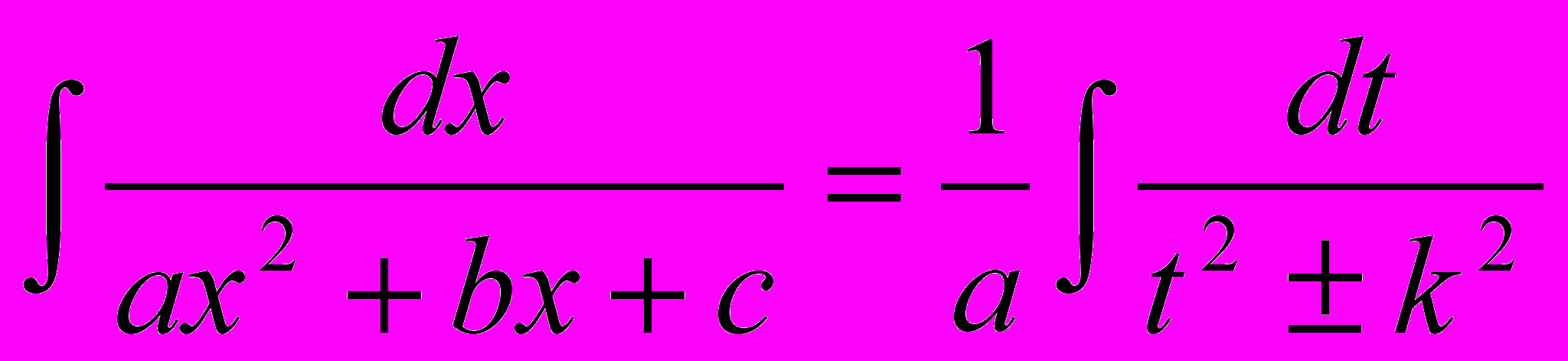. Это – табличный интеграл.

Пример 8.5.

Вычислить интеграл:



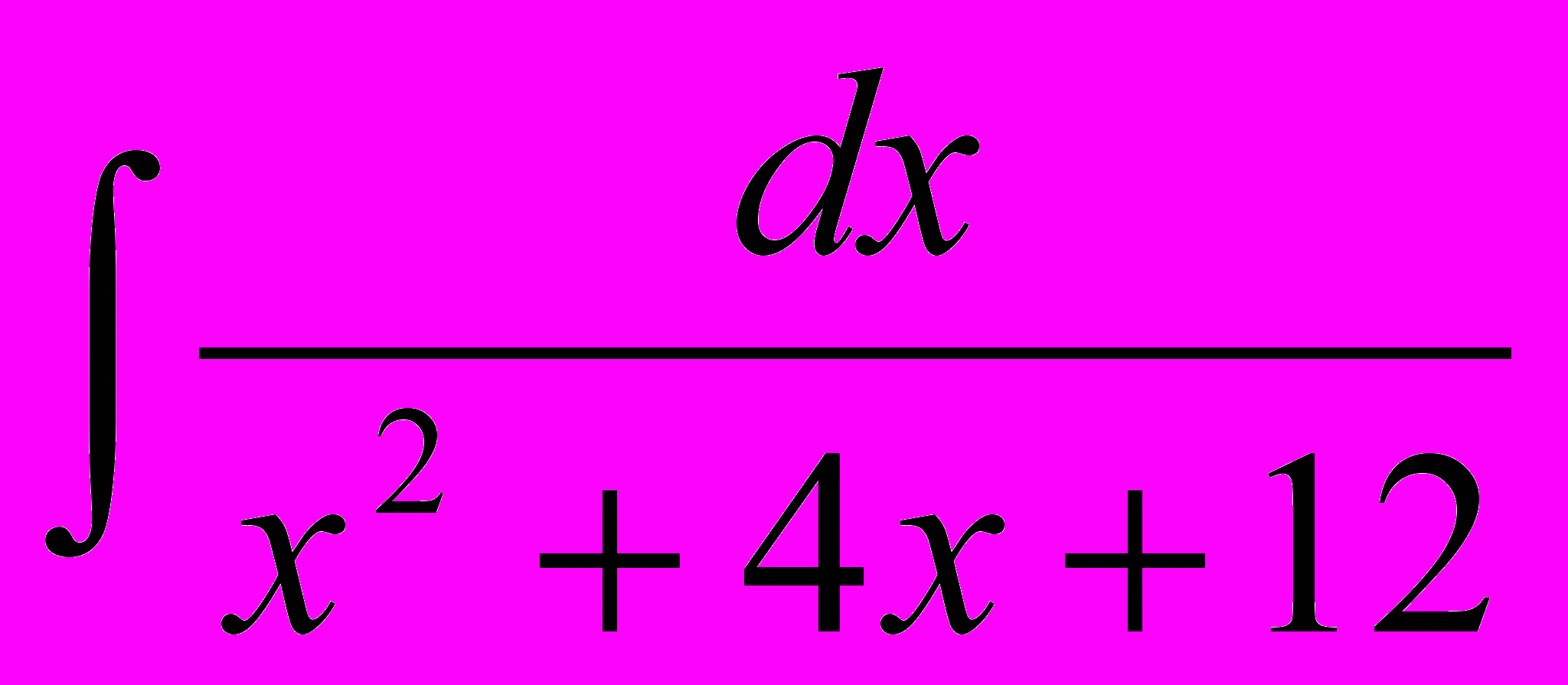
б) Подынтегральная функция имеет вид 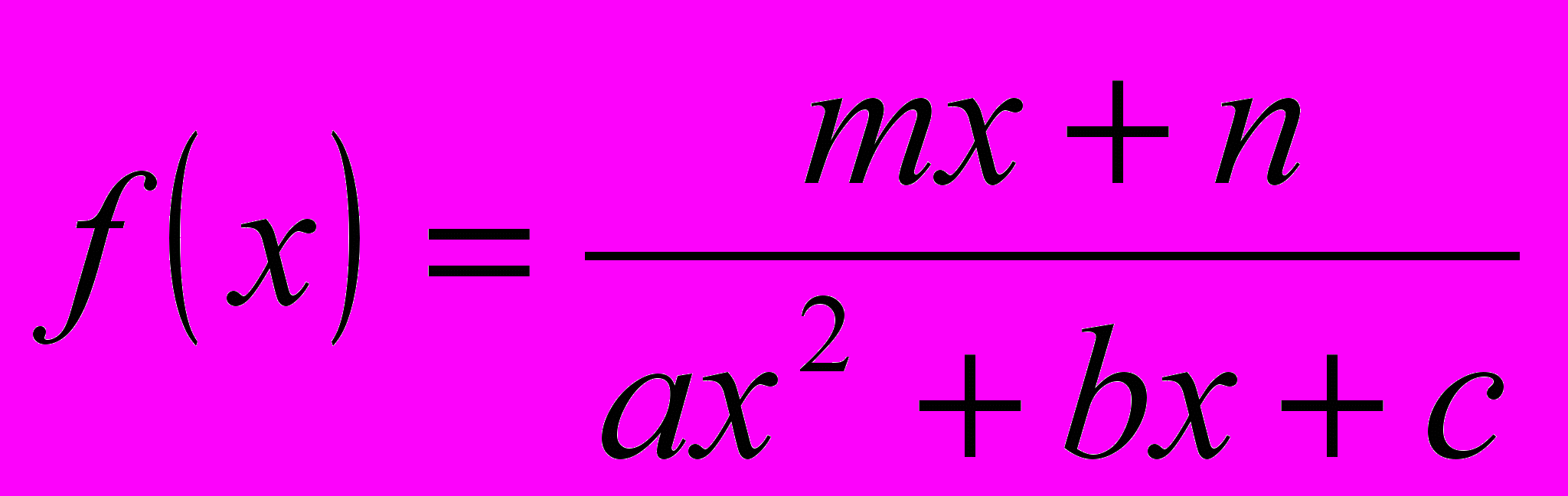. Произведем тождественные преобразования: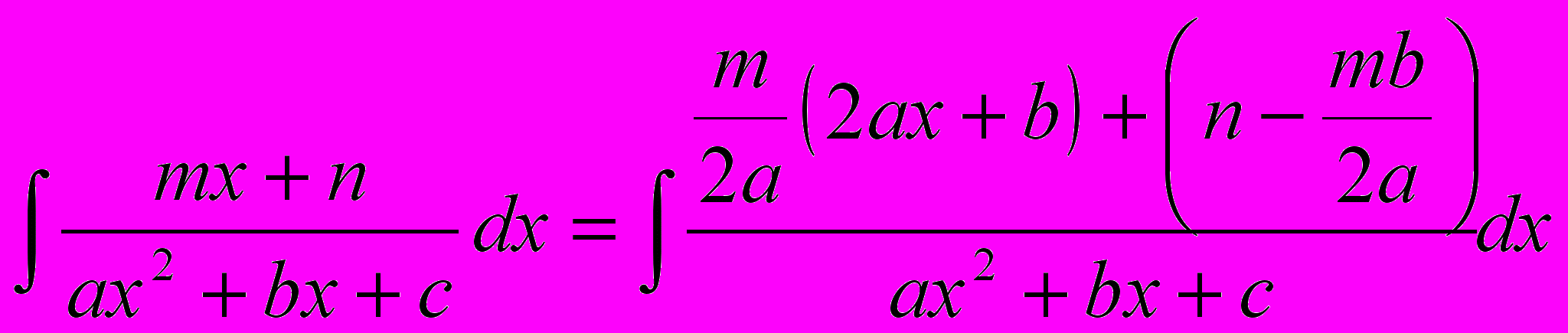



Таким образом, исходный интеграл можно представить в виде суммы:



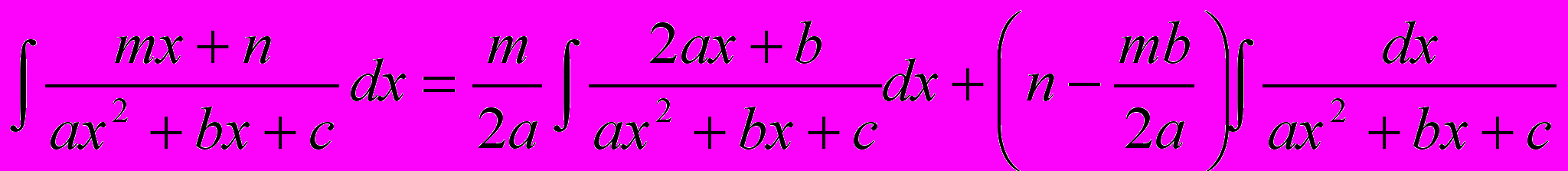
Как вычислять второй интеграл, мы рассмотрели в пункте ; обозначим его через 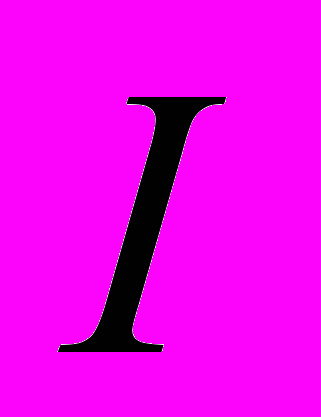. В первом интеграле сделаем замену переменной:

,

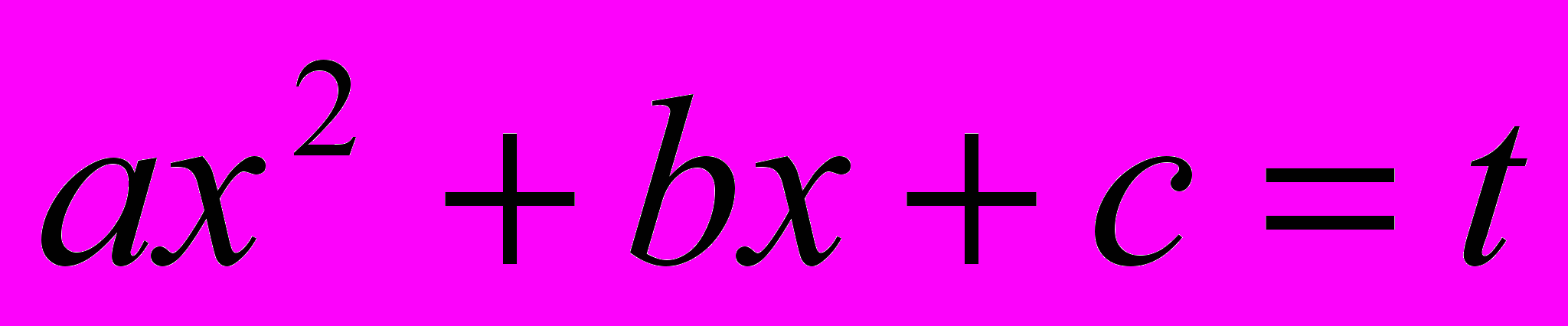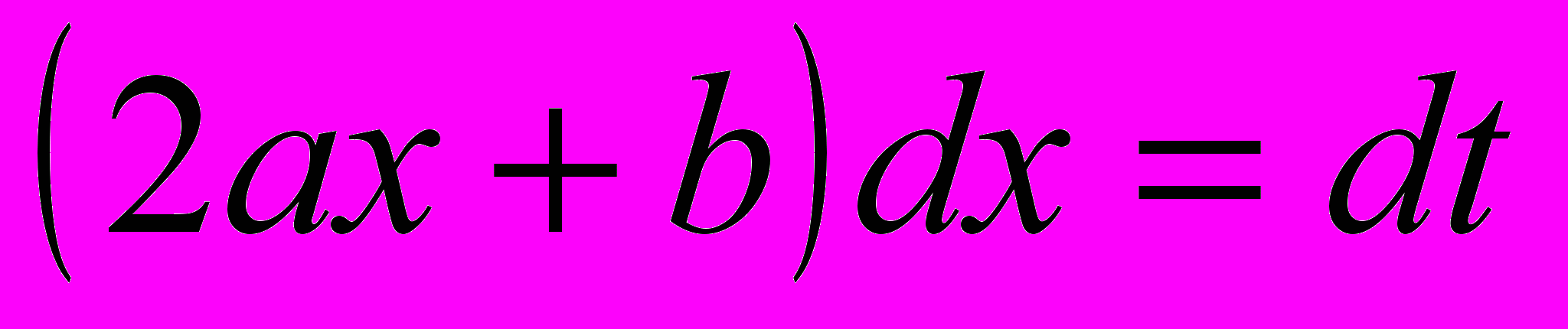
Таким образом:



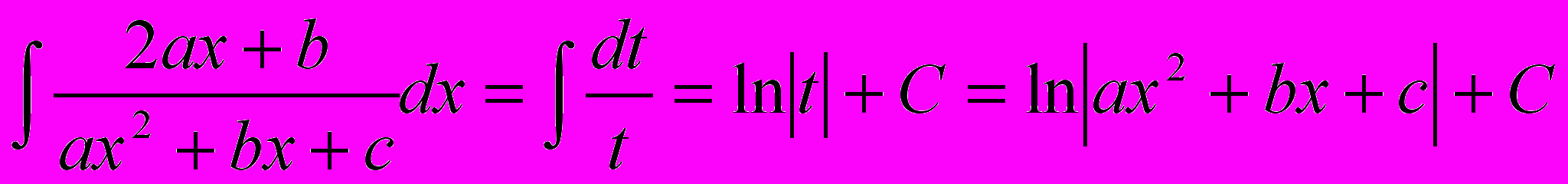
Окончательно получим:



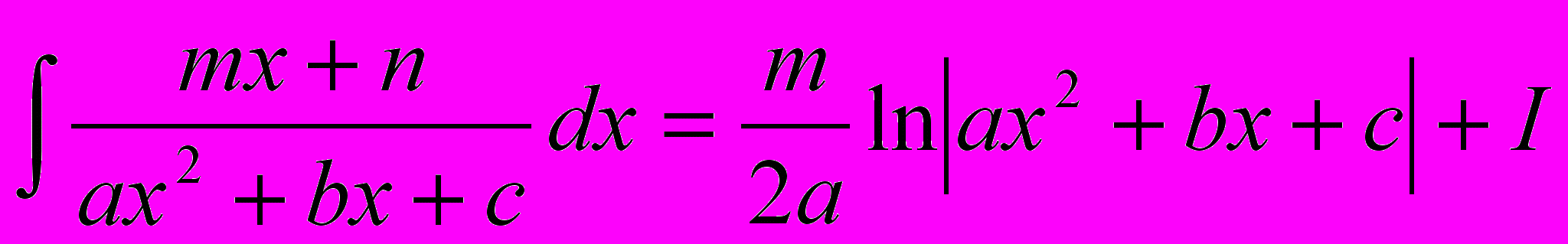
Пример. 7.6