Geum.ru

Интезом системы разрешающих дифференциальных уравнений Сен-Венана на ребрах направленного графа польдерной системы и заданием граничных условий в вершинах графа

Вид материалаДокументы

Содержание


Топологический анализ ПС
X0Y, а для каждого проводящего канала назначается локальная система координат с началом координат в начале открытого проводящего
Синтез разрешающей моделирующей системы уравнений
1 - й контур обхода графа состоит из дуг
Начальные условия
Алгоритм численного решения.
Результаты численных расчетов.
И вершин: 1, 2, 3
Список литературы
Подобный материал:
УДК 626.86.517.97(06)


РАСЧЁТ ПАРАМЕТРОВ СЕТИ ПРОВОДЯЩИХ КАНАЛОВ

ПОЛЬДЕРНЫХ СИСТЕМ


Н.Д. Бобарыкин, Е.Н. Графова, К.С. Латышев*


*Российский государственный университет им. И. Канта,

236040, г. Калининград, ул. А. Невского, 14


Решена задача инвариантного математического моделирования параметров сети открытых проводящих каналов реальных польдерных систем (ПС), основанная на их декомпозиции с последующим синтезом системы разрешающих дифференциальных уравнений Сен-Венана на ребрах направленного графа польдерной системы и заданием граничных условий в вершинах графа.

Приведены результаты численных расчетов параметров реальной польдерной системы, действующей на территории Калининградской области, которая состоит из тринадцати проводящих каналов различной длины и шести контуров обхода графа ПС.


сеть проводящих каналов, графы, польдерная система


Основные задачи математического моделирования параметров проводящих каналов польдерных систем и результаты расчетов для ПС, состоящей из трех разветвленных каналов, приведены в работах [1-2]. Однако на практике осушения переувлажненных земельных массивов приходится иметь дело с большим числом проводящих открытых каналов и более сложной структурой польдерных систем. Поэтому представляется необходимым провести численные расчеты параметров реальной польдерной системы и проанализировать полученные результаты. Рассмотрим основные этапы моделирования сети проводящих каналов ПС.

Топологический анализ ПС проводится на основе теории направленных графов и заключается в теоретико-множественном описании объекта, т.е. декомпозиции исходной постановки на подзадачи. На рис.1 приведена расчетная схема польдерной системы, на которой нумеруются все открытые проводящие каналы, а также начальные и конечные точки каналов. На разработанную схему накладывается структура направленного графа Г. При этом, элементы множества открытых проводящих каналов, как отмечалось выше, являются ребрами графа Г, а множества точек соединения (ветвления) этих каналов – его вершинами.

Для каждого канала задаются его начальные геометрические и физические характеристики, включая подключенные к нему дрены, насосные станции и т.д.

Вся расчетная схема ПС связывается с общей системой координат X0Y, а для каждого проводящего канала назначается локальная система координат с началом координат в начале открытого проводящего канала хi0iуi и осью хi, направленной вдоль проводящего канала.

Исходя из условий минимальности длины циклов графа польдерной системы, рассчитываются контура обхода (циклы) направленного графа ПС. Так, например, на рис.1 приведен один из вариантов сети проводящих каналов польдерной системы, действующей на территории Калининградской области, состоящей из тринадцати проводящих каналов различной длины и шести контуров обходов графа ПС.

Матрица разветвлений каналов ПС формируется с учетом ориентации локальных систем координат отдельных каналов польдерных систем. При таком подходе устраняются трудности, связанные с формализацией математического описания параметров польдерных систем и отпадает необходимость строить расчетные алгоритмы для каждой конкретной задачи, что особенно важно при проектировании и управлении ПС.


У 7

VI


6 VIII

9

V

5 VII 8


IV IX 14

4 10

III XIII

3 X 11 XII 12




II

2


I XI

1



0 13

X


Рис.1. Расчетная схема польдерной системы, состоящей из тринадцати проводящих каналов различной длины и шести контуров обходов графа ПС


Синтез разрешающей моделирующей системы уравнений. Синтез разрешающей системы уравнений в частных производных проводится для каждого открытого канала польдерной системы. Записываются дифференциальные уравнения Сен-Венана в локальных системах координат этих каналов ПС, а затем «собирается» разрешающая система уравнений как совокупность описаний отдельных каналов, входящих в каждый контур обхода графа польдерной системы. Условием «сшивания» уравнений в точках соединения каналов является условие сохранения потока Q прихода и расхода воды в этих узлах.


Таблица 1



№

п/п
Cоединение каналов
Длина,

м

1
1-2
495

2
2-3
1000

3
3-4
1000

4
4-5
1000

5
5-6
1000

6
6-7
2500

7
5-8
1000

8
6-9
3900

9
4-10
3000

10
3-11
2500

11
11-13
2000

12
11-12
1500

13
12-14
1000
1 - Й КОНТУР ОБХОДА ГРАФА СОСТОИТ ИЗ ДУГ:

1, 2, 3, 4, 5, 6 И ВЕРШИН: 1, 2, 3, 4, 5, 6, 7;


2 - Й КОНТУР ОБХОДА ГРАФА СОСТОИТ ИЗ ДУГ:

1, 2, 10, 11 И ВЕРШИН: 1, 2, 3, 11, 13;


3 - Й КОНТУР ОБХОДА ГРАФА СОСТОИТ ИЗ ДУГ:

1, 2, 3, 9 И ВЕРШИН: 1, 2, 3, 4, 10;


4 - Й КОНТУР ОБХОДА ГРАФА СОСТОИТ ИЗ ДУГ:

1, 2, 3, 4, 7 И ВЕРШИН: 1, 2, 3, 4, 5, 8;


5 - Й КОНТУР ОБХОДА ГРАФА СОСТОИТ ИЗ ДУГ:

1, 2, 3, 4, 5, 8 И ВЕРШИН: 1, 2, 3, 4, 5, 6, 9;


6 - Й КОНТУР ОБХОДА ГРАФА СОСТОИТ ИЗ ДУГ:

1, 2, 10, 12, 13 И ВЕРШИН: 1, 2, 3, 11, 12, 14.


Совокупная система дифференциальных уравнений в частных производных интегрируется вдоль контуров обхода, а граничные условия задаются в виде расхода (прихода) воды естественным образом.

Система дифференциальных уравнений Сен-Венана, описывающая уровневый режим воды в каналах, имеет вид:


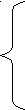; ; (1)

,


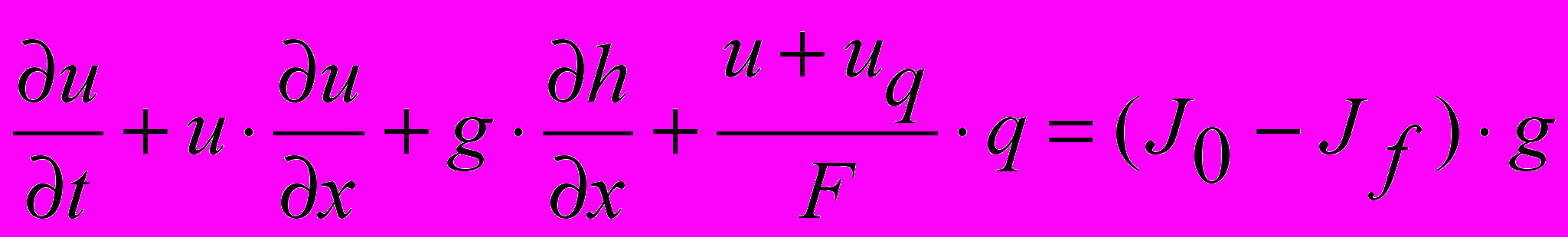где h, u -уровень и скорость движения воды в канале; uq - скорость бокового притока; q - боковой приток; g - ускорение свободного падения; J0 - продольный угол наклона дна; Jf - уклон трения; Q = F·u - расход воды в канале; F - площадь живого сечения, в частности, для сечения канала в виде прямоугольника – F = a · h; а – ширина открытого канала.


Для водоизолированных и горизонтально расположенных проводящих каналов (приток воды в открытые каналы равен нулю q = 0), имеющих прямоугольное сечение, система дифференциальных уравнений Сен-Венана (1), записывается в следующем виде:




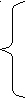
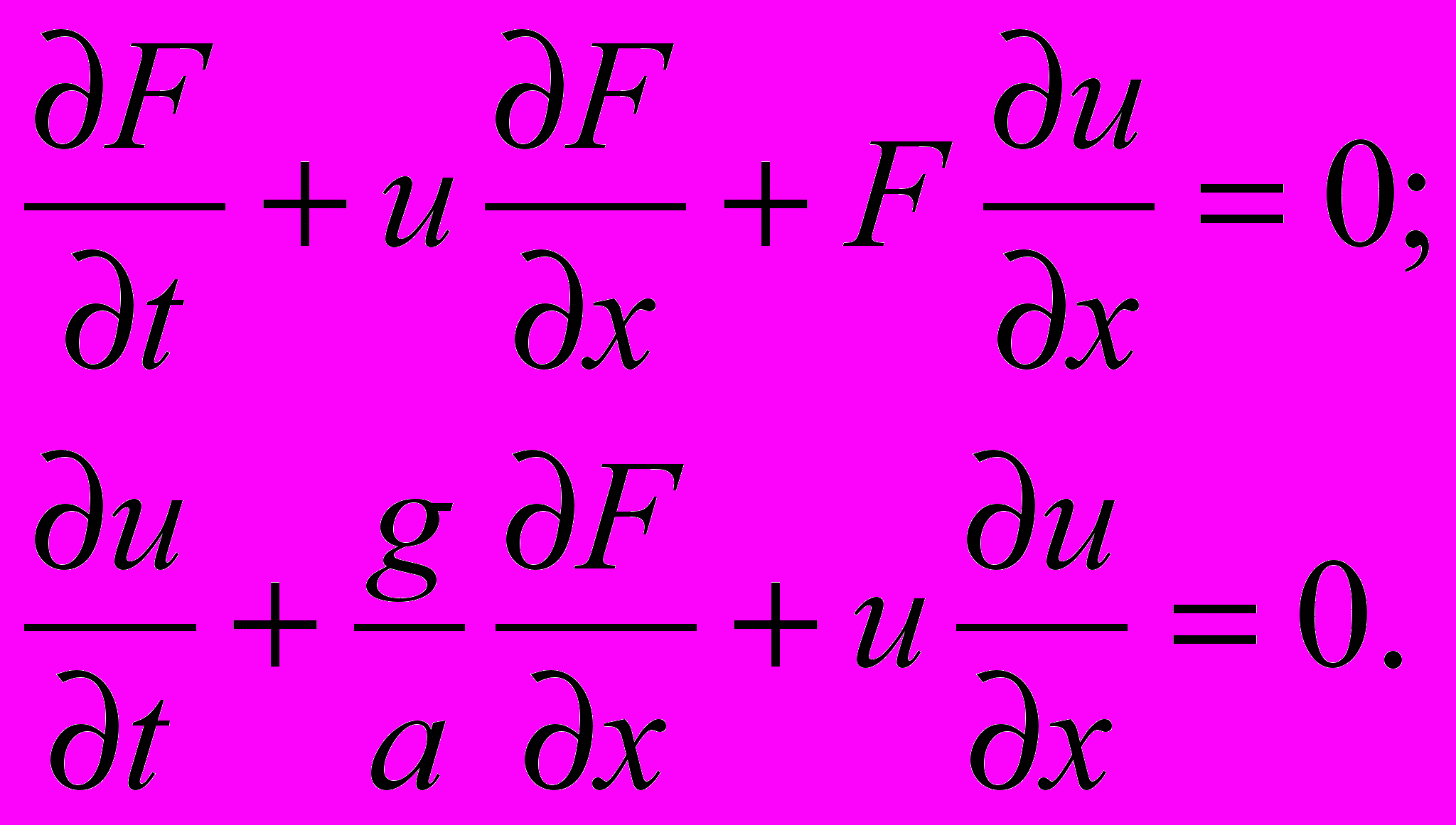
(2)

Приводя систему гиперболических уравнений (2) к каноническому виду, по методике, изложенной в работе [2], получим:

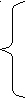
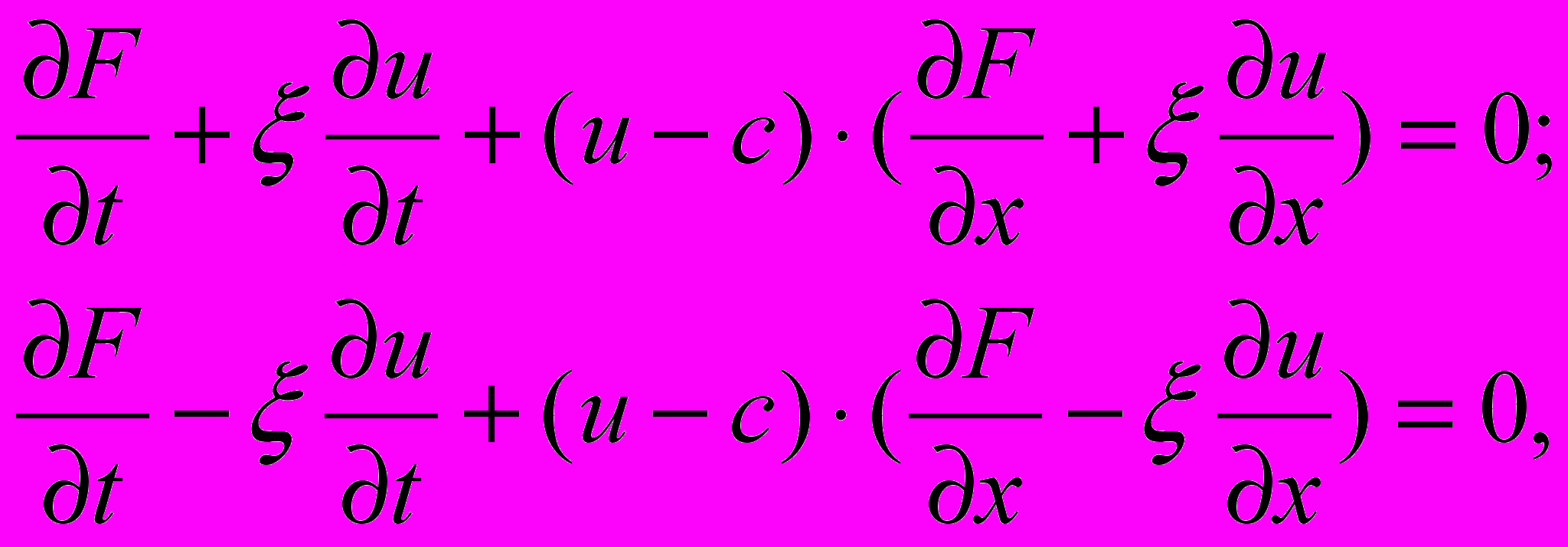(3)

где 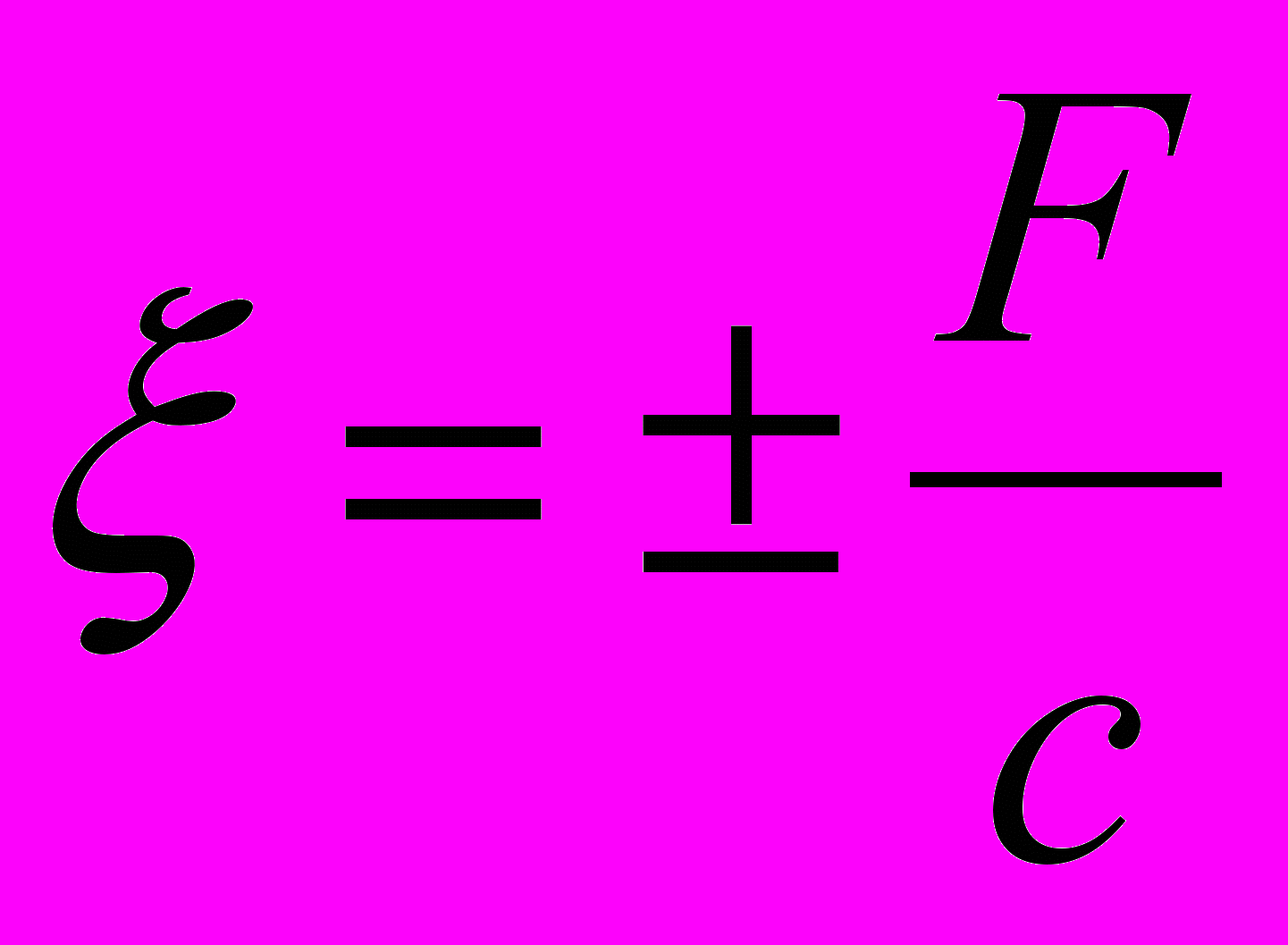; 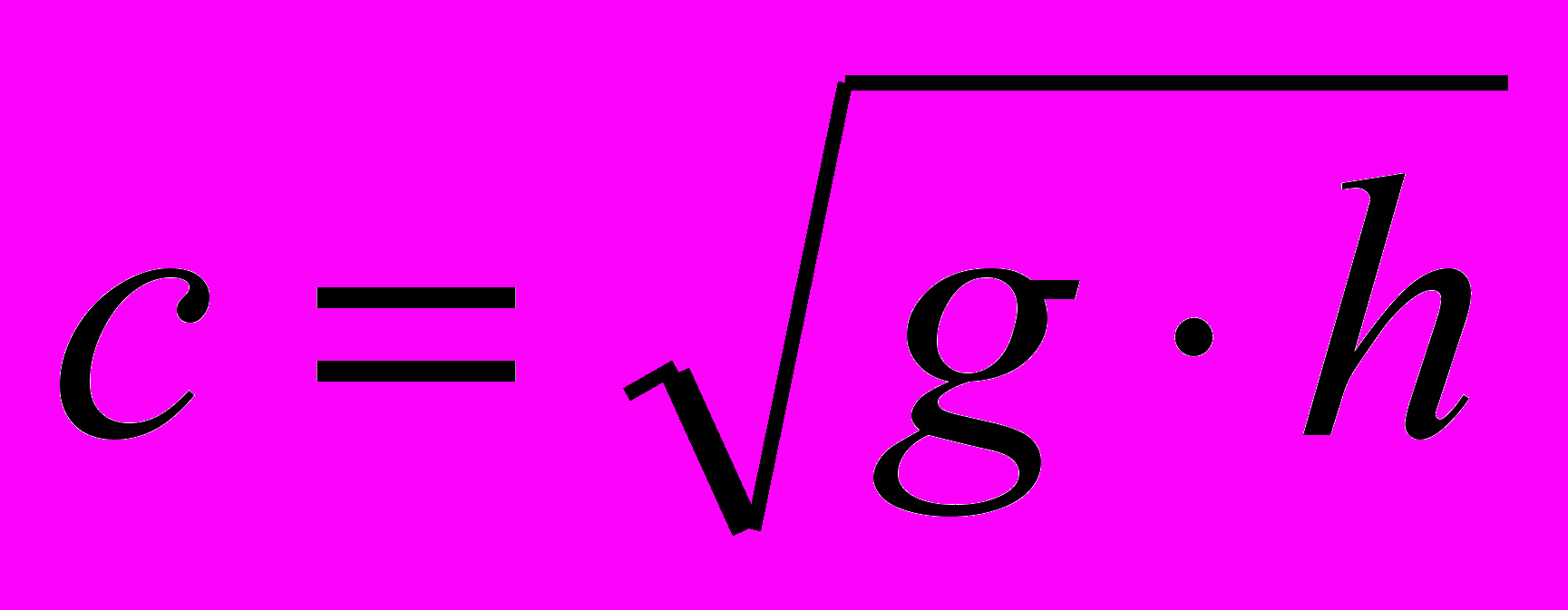- скорость звука в воде.

Начальные условия для системы уравнений (3) задаются следующим образом:

F(x, 0) = 12 м2; u(x, 0) = 0 м/с. (4)

Граничные условия задаются в виде потока воды Q, используя краевые условия 1–го рода. На левой границе контуров обходов графа ПС в начале первого проводящего канала, при наличии насосной станции, задается ее производительность

Q(0, t) = 1.0 м3/с, (5)

а на правой границе контуров обходов графа ПС c учетом непроницаемости торцевых стенок открытых каналов

Q(xn, t) = 0.0 м3/с. (6)

Алгоритм численного решения. Расчет функций Nij и Vij во всех внутренних узлах разностной сетки строится на основе схем бегущего счета и применительно к системе гиперболических уравнений (3), имеют вид:



.

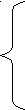
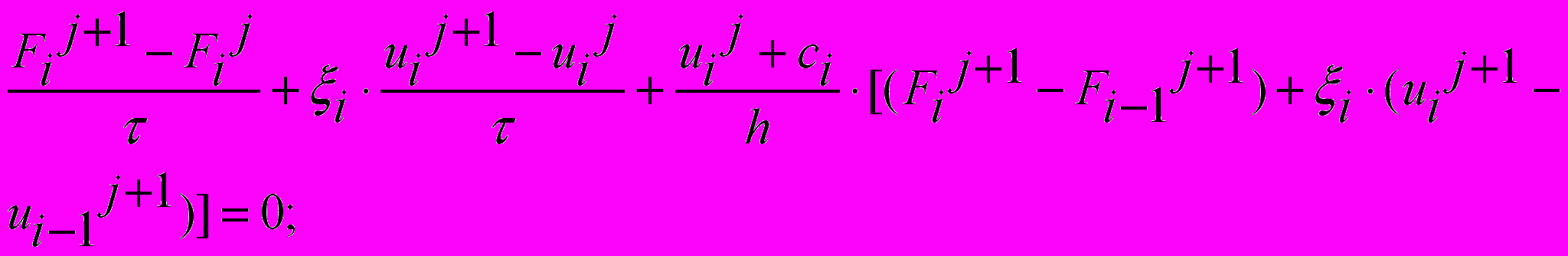
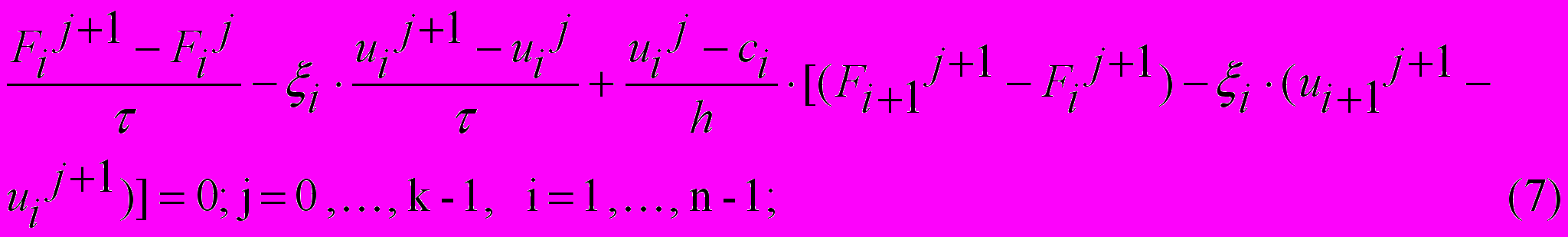где k = 250 – число временных слоев; n – число пространственных узлов.


Система разностных уравнений (7) решается методом матричной прогонки, так как она содержит искомую функцию Fij+1 в трех точках, а именно

Fi-1j+1, Fij+1 и Fi+1j+1 . С этой целью приведем эту систему разностных уравнений к трехточечному виду:


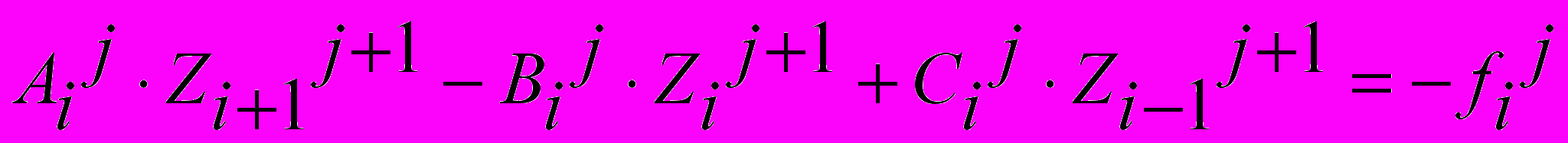; i=1,…,n-1; j=0, …,k-1, (8)

где ; ; ; ;

; .

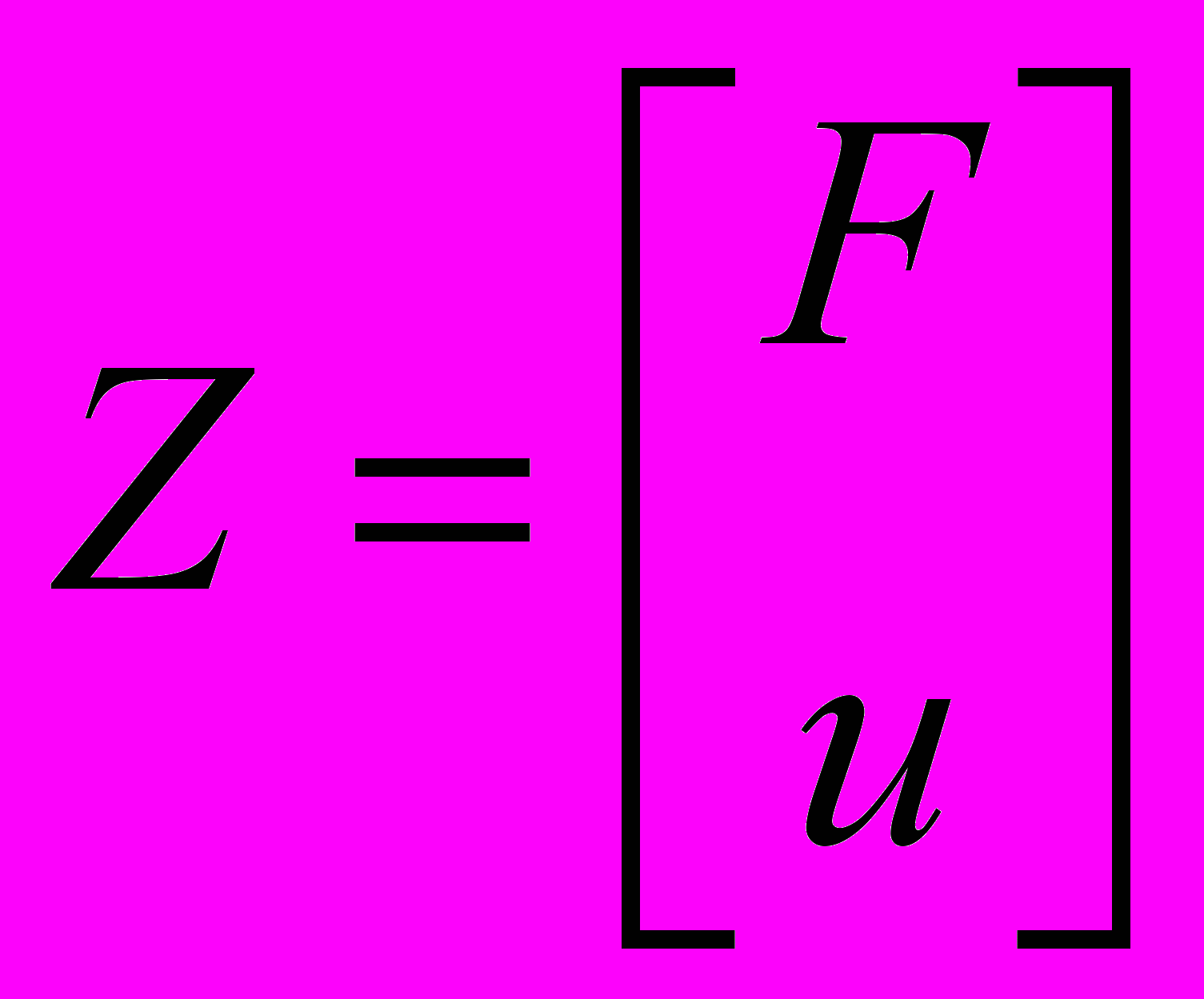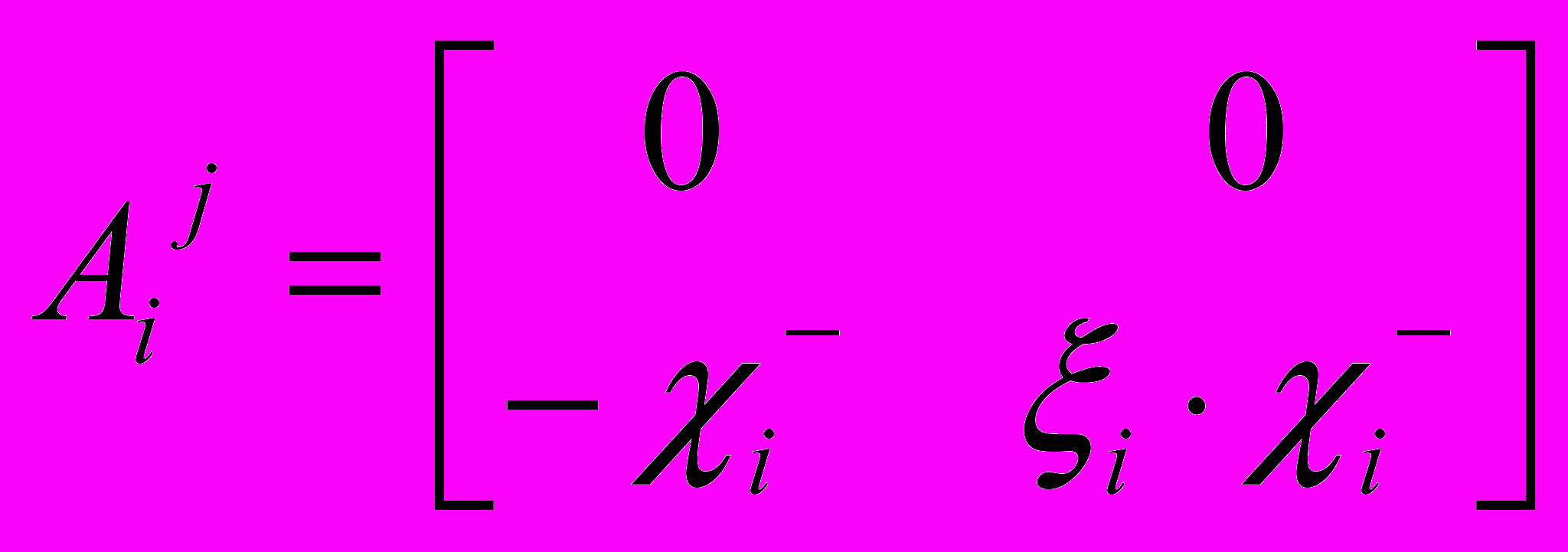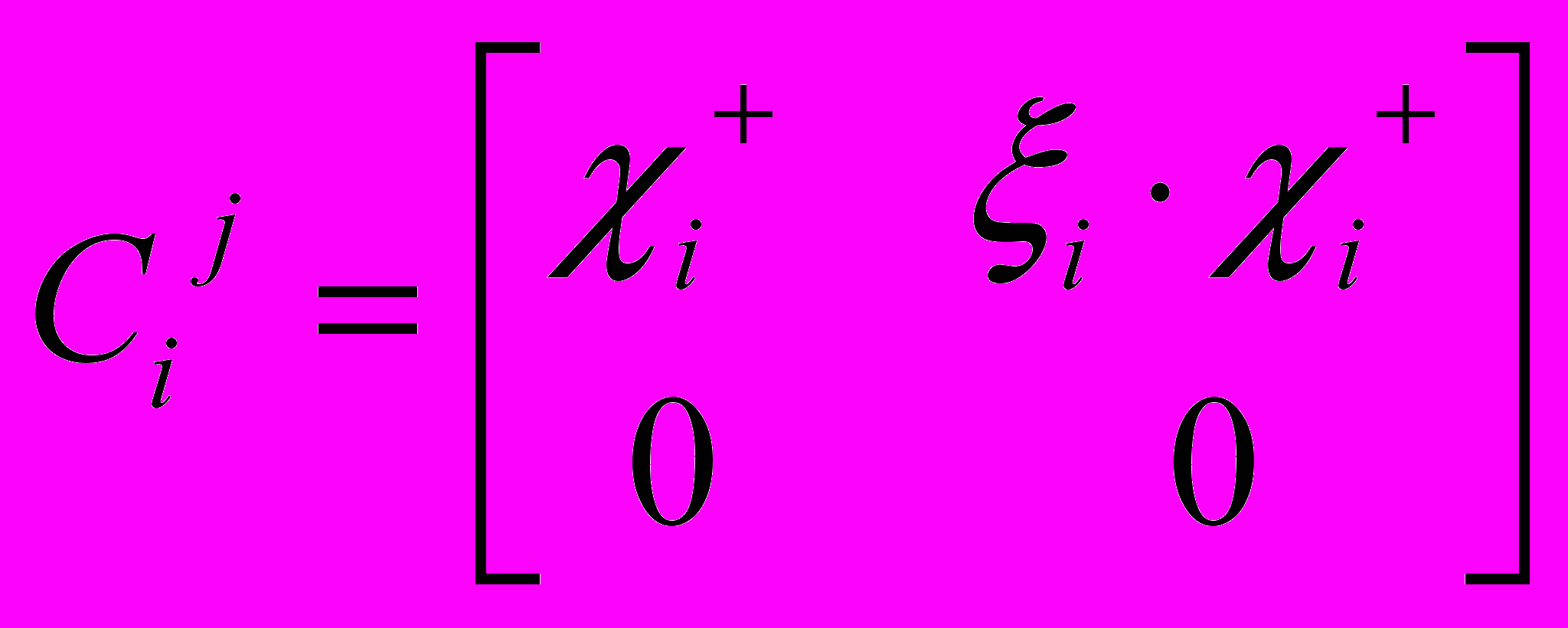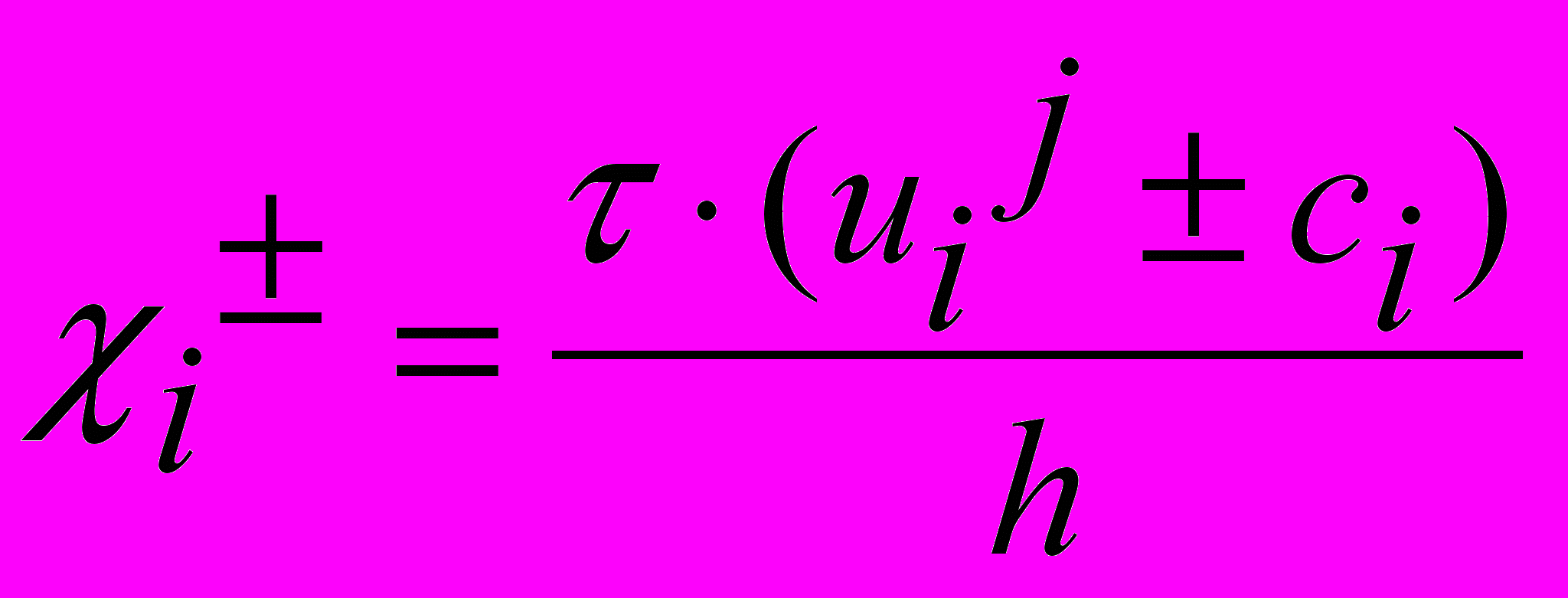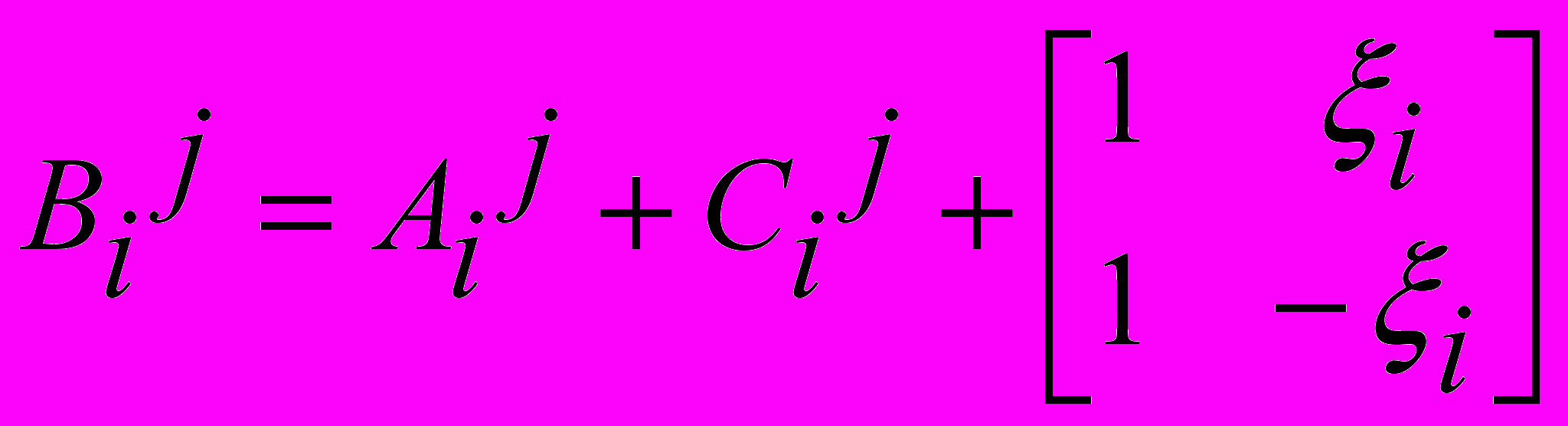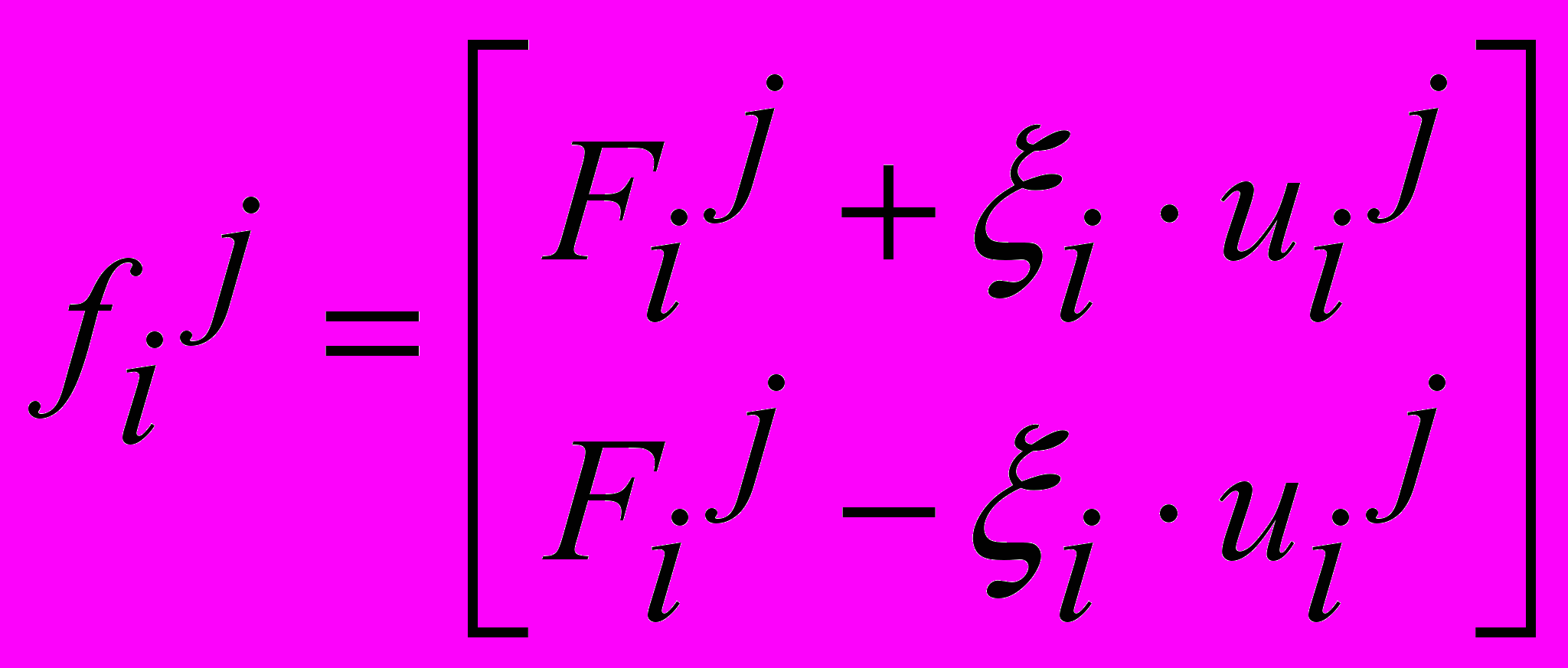Вектор искомых функций Zij+1 определяется рекуррентным соотношением:


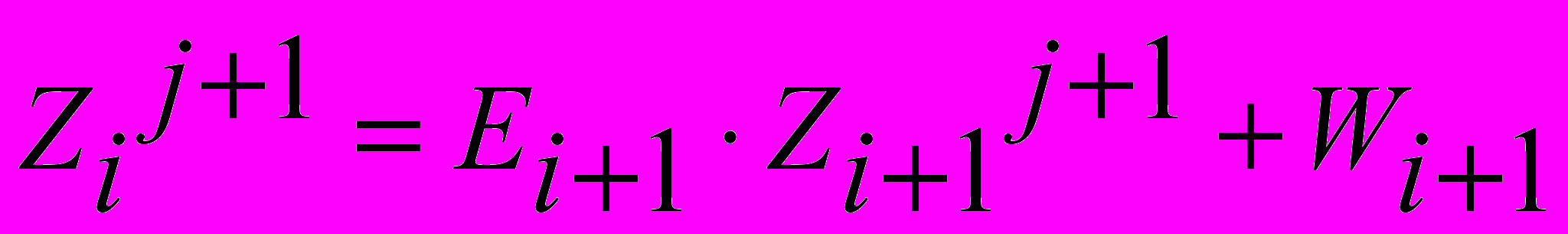; i = n – 1, …, 0; j = 0, …, k –1. (9)


Алгоритмы задания граничных условий и численного интегрирования системы дифференциальных уравнений Сен–Венана вдоль контуров обходов графа Г польдерных систем основаны на схемах бегущего счета и учитывающие наклон характеристик. Суммирования прогоночных коэффициентов при введении новой функции обеспечивает выполнение законов сохранения потоков воды в точках ветвления проводящих каналов польдерных систем [1-2].

Результаты численных расчетов. Проводящие каналы имеют разную длину (см. табл. 1), но одинаковую ширину, равную а = 4 м. При этом шаги интегрирования по координате h = 15 м и по времени τ = 120 с задаются одинаковыми для каждого канала. Это связано с необходимостью с одинаковой точностью аппроксимировать систему дифференциальных уравнений конечно-разностных уравнений, описывающих проводящие каналы различной длины. Действительно, точность аппроксимации дифференциальных уравнений полностью определяется шагами интегрирования по координате h и времени τ и выбранной разностной схемой, так, например, для схем бегущего счета порядок аппроксимации по координате h и времени τ равен единице, т.е. 0(τ, h).

Сравнительно небольшое значение шага интегрирования по времени τ определяется не условием счетной устойчивости алгоритма численного решения системы дифференциальных уравнений, а характерными временами процесса переноса воды в открытых каналах в момент запуска насосной станции. Как показывают численные эксперименты, которые подтверждаются экспериментальными данными, переходной процесс продолжается около одного часа в зависимости от площади живого сечения и длины проводящих каналов (см. рис. 2, b-d).

По нелинейности и связанности системы дифференциальных уравнений Сен-Венана (1), проводились три итерации по всем контурам обхода графа ПС.

Для исследования роли значений геометрических параметров и структуры сети проводящих каналов в пространственно-временные распределения площадей живого сечения F и потоков воды Q, из-за весьма сложности структуры и большого количества взаимодействующих проводящих каналов реальной польдерной системы, рассмотрим два следующих варианта по сложности структуры сети и числу проводящих каналов:

а) водоизолированная сеть проводящих каналов, состоящая из тринадцати проводящих каналов различной длины и шести контуров обходов графа ПС (рис. 1, табл. 1), при включенной насосной станции в начале 1-го канала, производительностью QH = 1.0 м3/с (рис. 2);

б) водоизолированная сеть проводящих каналов, состоящая из четырех проводящих каналов различной длины и трех контуров обходов графа ПС (рис. 3, табл. 2), при включенной насосной станции в начале 1-го канала, производительностью QH = 1.0 м3/с (рис. 4).

На рис. 2 и 4 приведены результаты численных расчетов пространственно-временных распределений площадей живого сечения F и потоков воды Q для открытых проводящих каналов ПС (время t приводится в часах, расстояния – в км). При этом использовались следующие обозначения: F1i1, F2i2, F3i3, F4i1, F5i2, F6i3 и Q1i1, Q2i2, Q3i3, Q4i1, Q5i2, Q6i3 - пространственные распределения площадей живого сечения F и потоков воды Q в каналах вдоль 1, 2, 3, 4, 5 и 6-го контуров обходов графа польдерной системы для момента времени t, равного одному часу; (Fj)1,0, (Fj)5,67, (Fj)6,167, (Fj)7,67, (Fj)10,167, (Fj)11,80, (Fj)13,40 и (Qj)1,0, (Qj)5,67, (Qj)6,80, (Qj)7,35, (Qj)4,65, (Qj)11,80, (Qj)13,40 - временные распределения площадей живого сечения F и потоков воды Q в каналах, для номеров пространственных узлов i, равных 0, 35, 40, 67, 80, 167, что соответствует значениям координат xi – 0 км, 0,525 км, 0,6 км, 1,0 км, 1,2 км, 2,5 км для 1, 5, 6, 7, 10, 11-го и 13-го проводящих каналов.

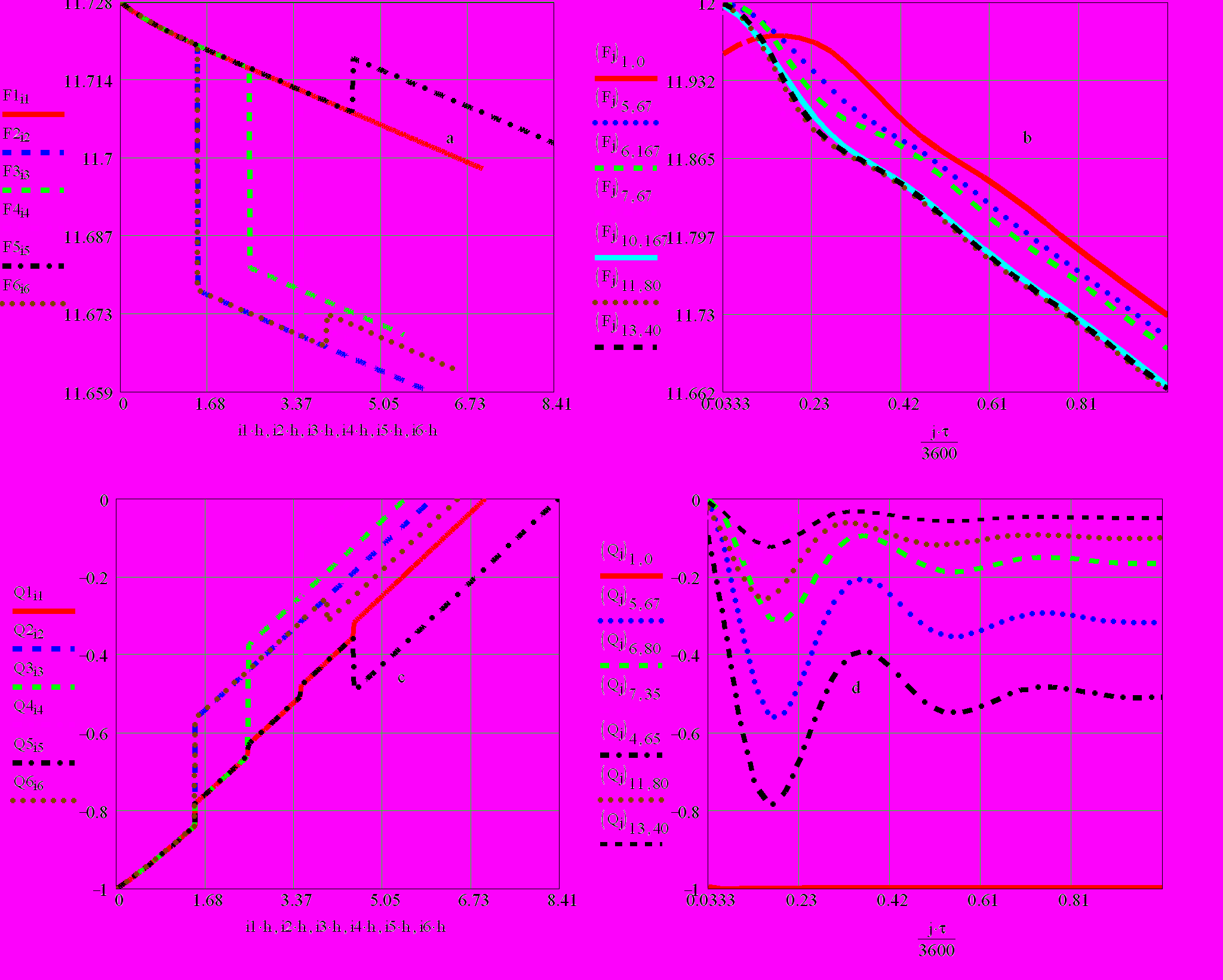Рис. 2. Пространственно-временные распределения площадей живого сечения открытых каналов F, потоков Q и скоростей воды u для тринадцати проводящих каналов различной длины и шести контуров обходов графа ПС


Рассмотрим результаты численных расчетов параметров сети, полученных для первого варианта. Включение насоса, установленного в начале первого канала, порождает волну. Волновой процесс имеет затухающий характер со временем затухания порядка одного часа (см. рис. 2, b-d). По результатам численных расчетов, приведенных на рис.2 b, амплитуда колебаний уровня воды Н (Н= F/a) относительно меньше, чем амплитуды колебания скорости воды в проводящих каналах (здесь и далее - (Qj)5,67 – значение потока воды Q на j-временном слое 5-го канала в 67-м пространственном узле). Сдвиг фаз волновых процессов для различных проводящих каналов польдерной системы обуславливается временем «добегания» волны до соответствующего канала.

Анализ численных расчетов пространственного распределения площадей живого сечения открытых каналов F и потоков воды Q, представленных на

рис. 2, а-с, является весьма затруднительным из-за сложности структуры и большого количества проводящих каналов реальной польдерной системы, (здесь и далее – Q1i1- распределение потока воды Q вдоль 1-го контура обхода графа Г ПС). Поэтому, рассмотрим польдерную систему по второму варианту, имеющую более простую структуру, состоящую из четырех проводящих каналов разной длины (см. табл. 2), расчетная схема которой представлена на рис. 3 (шаги интегрирования по пространству равны h = 15 м, по времени τ = 120 с и проводились три итерации по всем контурам обхода графа ПС).


4

Y III

1 I 2 II

3

IV

5

X

0

Рис.3. Расчетная схема польдерной системы, состоящей из четырех проводящих каналов различной длины и трех контуров обходов графа ПС


Таблица 2


№

п/п
Cоеди-нение каналов
Дли-на,

м

1
1-2
1200

2
2-3
1800

3
2-4
2000

4
2-5
1600



1 - Й КОНТУР ОБХОДА ГРАФА СОСТОИТ ИЗ ДУГ: 1, 2

И ВЕРШИН: 1, 2, 3;

2 - Й КОНТУР ОБХОДА ГРАФА СОСТОИТ ИЗ ДУГ: 1, 3

И ВЕРШИН: 1, 2, 4;


3 - Й КОНТУР ОБХОДА ГРАФА СОСТОИТ ИЗ ДУГ: 1, 4

И ВЕРШИН: 1, 2, 5.


Отметим, что процесс откачки воды из проводящих открытых каналов, как и для реальной польдерной системы (см. рис. 2, b-d), носит затухающей волновой характер со временем затухания примерно равным одному часу при постоянном снижении уровня воды в каналах Н, что соответствует результатам предыдущих расчетов.

Рассмотрим более подробно пространственные распределения площадей живого сечения F и потоков воды Q в проводящих открытых каналах в зависимости от их длины. Отметим, что в точках ветвления проводящих каналов (точка 2, рис. 3) потоки воды Q делятся пропорционально длинам расходящихся каналов (см. рис. 4, с). Такое пространственное перераспределение потоков воды Q в точках соединения проводящих каналов хорошо согласуется с поведением уровня воды F/а в точках разветвления каналов (см. рис. 4, а), так как в более коротких проводящих каналах быстрее падает уровень воды в них и, соответственно, значения потоков имеют меньшие значения по абсолютной величине (знак минус указывает, что поток воды Q направлен в противоположную направлению оси Х сторону).




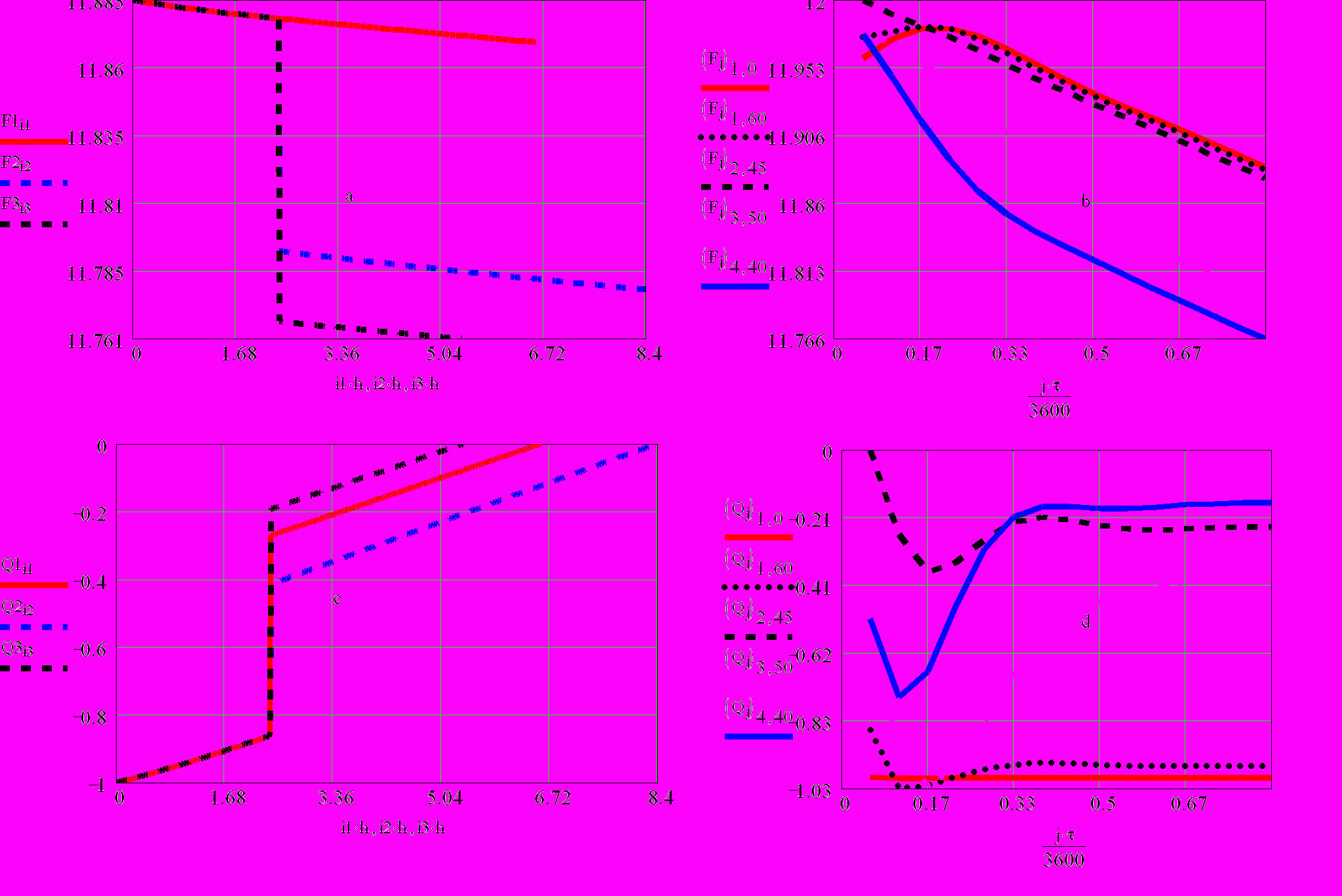
Рис. 4. Пространственно-временные распределения площадей живого сечения открытых каналов F и потоков воды Q для четырех проводящих каналов различной длины и трех контуров обходов графа ПС


Указанные закономерности пространственного распределения уровня воды F/а и потоков воды Q распространяются на сложные сети проводящих каналов польдерных систем, на что указывают результаты численных расчетов таких сетей, приведенных на рис. 2, а-с.

Выводы. Поставлена и решена задача математического моделирования распределения уровня воды в сети проводящих открытых каналов на основе численного решения гиперболической системы дифференциальных уравнений Сен-Венана (1), содержащих инерционные члены. К достоинству данного подхода следует отнести автоматическое выполнение закона сохранения потока воды в точках разветвления каналов и корректную постановку граничных условий. Данная концепция сохранения потока воды в точках ветвления проводящих каналов является основополагающей при сквозном расчете сетей гидродинамических систем, но, тем не менее, она не всегда принимается во внимание авторами численных исследований гидродинамических течений, например [3-4].

Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект №06-01-00396.


СПИСОК ЛИТЕРАТУРЫ


1. Бобарыкин Н. Д. Оптимальное управление режимом грунтовых вод на основе инвариантной нестационарной математической модели польдерных систем (монография) / Н.Д. Бобарыкин. – Калининград: КГТУ, 2004.-168с.

2. Бобарыкин Н.Д. Моделирование движения воды в проводящих каналах польдерных систем / Н.Д. Бобарыкин, К.С. Латышев // Математическое моделирование. РАН.-2005.- Т. 17.- № 9.- С. 27-34.

3. Расчет нестационарных гидродинамических процессов в канале «Сибирь- Средняя Азия»: отчет института гидродинамики СО АН СССР (заключительный), 1986.

4. Булавко А. Г. Водный баланс речных водосборов / А.Г. Булавко. – Л.: Гидрометеоиздат, 1971.


CALCULATIONS of ARGUMENTS of a CONDUCTING CHANNELS WEB FOR POLDER SYSTEMS


N.D. Bobarykin, E.N.Grafova, K.S. Latishev


Is justified and the problem of invariant mathematical modelling of arguments of a opened conducting channels web of substantial polder systems (PS) grounded on their decomposition with consequent synthesizing of a system of Saint-Venant’s authorizing differential equations on ribs of the directional graph polder system and definition of boundary conditions in tops of the graph is resolved.

The results of numerical accounts substantial of a polder system acting on territory of the Kaliningrad area are reduced which one consists of thirteen conducting channels of different length and six outlines of circumvention of the graph of the PS.