Пояснительная записка к курсовому проекту на тему «Решение краевой задачи для системы дифференциальных уравнений с использованием метода Рунге-Кутта» по дисциплине

Вид материала

Пояснительная записка

Содержание СТУДЕНТА ГИП-105Б: Кудряшова В.В. 2.2. Краевая задача 2.3. Постановка задачи Для данного проекта был выбран интерфейс, соответствующий основным требованиям и обеспечивающий легкость работы с ним.

Подобный материал:

• Факультет вычислительной математики и кибернетики, 62.51kb.
• Тема курсовой работы, 36.24kb.
• Пояснительная записка к курсовому проекту на тему «Машина Тьюринга» по дисциплине, 256.01kb.
• Пояснительная записка к курсовому проекту на тему «Ранг матрицы» по дисциплине, 251.76kb.
• Пояснительная записка к курсовому проекту по дисциплине: «Объектно-ориентированное, 43.57kb.
• Пояснительная записка к курсовому проекту на тему «Кодирование информации методом Шеннона-Фано», 253.27kb.
• Пояснительная записка к курсовому проекту на тему «Дизайн интерьера в 3d-max» по дисциплине, 180.66kb.
• Государственная Академия Управления имени С. Орджоникидзе Институт национальной и мировой, 399.35kb.
• Пояснительная записка к курсовому проекту по дисциплине «методы оптимизации», 29.18kb.
• Пояснительная записка к курсовому проекту по дисциплине " системный анализ", 565.1kb.

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОУВПО “Самарский государственный архитектурно-строительный

университет”

Факультет информационных систем и технологий

Кафедра прикладной механики и вычислительной техники


Пояснительная записка


к КУРСОВОМУ ПРОЕКТУ на тему


«Решение краевой задачи для системы дифференциальных уравнений с использованием метода Рунге-Кутта»


по дисциплине


ТЕХНОЛОГИЯ/МЕТОДОЛОГИЯ

НАУЧНЫХ ИССЛЕДОВАНИЙ


СТУДЕНТА ГИП-105Б: Кудряшова В.В.


Подпись, дата Расшифровка подписи

ВЫПОЛНИЛ:

cтудент / /

Модуль сдан в библиотеку кафедры

ПМ и ВТ

Модуль размещен на портале ФИСТ

ПРОВЕРИЛ: / /

ОЦЕНКА


Самара 2009г.


РЕФЕРАТ

Курсовой проект.

Пояснительная записка: 11стр., 3 рис.,3 источника.


”Решение краевой задачи для системы дифференциальных уравнений с использованием метода Рунге-Кутта»


Программой разработки является – Borland Delphi 7.


Цель работы – решение краевой задачи для системы дифференциальных уравнений с использованием метода Рунге-Кутта.

Пользовательский интерфейс приложения разрабатывался на базе языка Borland Delphi 7. Данный язык программирования дает возможность проектировать приложения с простым и надежным пользовательским интерфейсом.


СОДЕРЖАНИЕ

1. ВВЕДЕНИЕ

2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

2.1. РЕШЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МЕТОДОМ РУНГЕ - КУТТА

2.2. КРАЕВАЯ ЗАДАЧА

2.3. ПОСТАНОВКА ЗАДАЧИ

3. ПРАКТИЧЕСКАЯ ЧАСТЬ

4. ЗАКЛЮЧЕНИЕ

5. СПИСОК ИСТОЧНИКОВ И ЛИТЕРАТУРЫ


1.ВВЕДЕНИЕ

Данная программа, написанная на языке программирования Borland Delphi 7, представляет собой решение краевой задачи для системы дифференциальных уравнений с использованием метода Рунге – Кутта.

Цель написания данного курсового проекта – решить краевую задачу для системы дифференциальных уравнений с использованием метода Рунге-Кутта, изобразить графически.

Курсовой проект прост, удобен и практичен в использовании.

Курсовой проект содержит: введение, теоретическую часть, практическую реализацию, заключение, литературу, которая использовалась при написании курсовой работы и приложения.


2.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

2.1. РЕШЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МЕТОДОМ РУНГЕ - КУТТА

Метод позволяет решать системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка следующего вида:

X^’=f(t,X,Y),

Y^’=g(t,X,Y),

которые имеют решение:

X=X(t),

Y=Y(t),

где t - независимая переменная (например, время); X, Y и т.д. - искомые функции (зависимые от t переменные). Функции f, g и т.д. - заданы. Также предполагаются заданными и начальные условия, т.е. значения искомых функций в начальный момент.

Одно диф. уравнение - частный случай системы с одним элементом. Поэтому, далее речь пойдет для определенности о системе уравнений.

Метод может быть полезен и для решения диф. уравнений высшего (второго и т.д.) порядка, т.к. они могут быть представлены системой диф. уравнений первого порядка.

Метод Рунге-Кутта заключается в рекурентном применении следующих формул:

X_k+1=X_k+1/6(k₁+2k₂+2k₃+k₄ ),

X_k+1=X_k+1/6(m₁+2m₂+2m₃+m₄ ),

где

k₁=f (t_k,X_k,Y_k) ∆t,

m₁=g (t_k,X_k,Y_k) ∆t,

k₂=f(t_k+∆t/2, X_k+k₁/2, Y_k+m₁/2) ∆t,

m₂=g(t_k+∆t/2, X_k+k₁/2, Y_k+m₁/2) ∆t,

k₃=f(t_k+∆t/2, X_k+k₂/2, Y_k+m₂/2) ∆t,

m₃=g(t_k+∆t/2, X_k+k₂/2, Y_k+m₂/2) ∆t,

k₄=f(t_k+∆t, X_k+k₃, Y_k+m₃) ∆t.


2.2. КРАЕВАЯ ЗАДАЧА

Краевая задача — дифференциальное уравнение (система дифференциальных уравнений) с заданными линейными соотношениями между значениями искомых функций на начале и конце интервала интегрирования.

Решение краевой задачи ищется в виде суммы линейной комбинации решений однородных задач Коши, соответствующих заданному уравнению при линейно независимых векторах начальных условий, и решения неоднородной задачи Коши с произвольными начальными условиями.

Пример краевой задачи dx/dt = A(t)x+a(t), o≤t≤T

(система неоднородных обыкновенных дифференциальных уравнений с переменными коэффициентами, заданная на участке [0;T])

Граничные условия (общий вид для всех краевых задач): Cx(0) + Dx(T) = B

Где A,C,D — матрицы, x — вектор неизвестных, a — n-вектор (делающий систему неоднородной), B — n-вектор


Общий вид решения:

X(t) = x₀(t)+сумма(от i=1 до n)a_ix_i(t)

Удовлетворение граничных условий достигается за счёт подбора коэффициентов ai. Эти коэффициенты находятся путём решения системы линейных уравнений.

2.3. ПОСТАНОВКА ЗАДАЧИ

Задача данного курсового проекта – разработать программу, решающую систему дифференциальных уравнений методом Рунге-Кутта с построением графиков решения системы, решающую краевую задачу и изобразить график приближения решения методом дихотомии .


3. ПРАКТИЧЕСКАЯ ЧАСТЬ

Для данного проекта был выбран интерфейс, соответствующий основным требованиям и обеспечивающий легкость работы с ним.

На рисунке 1 можно увидеть первоначальный интерфейс программы.




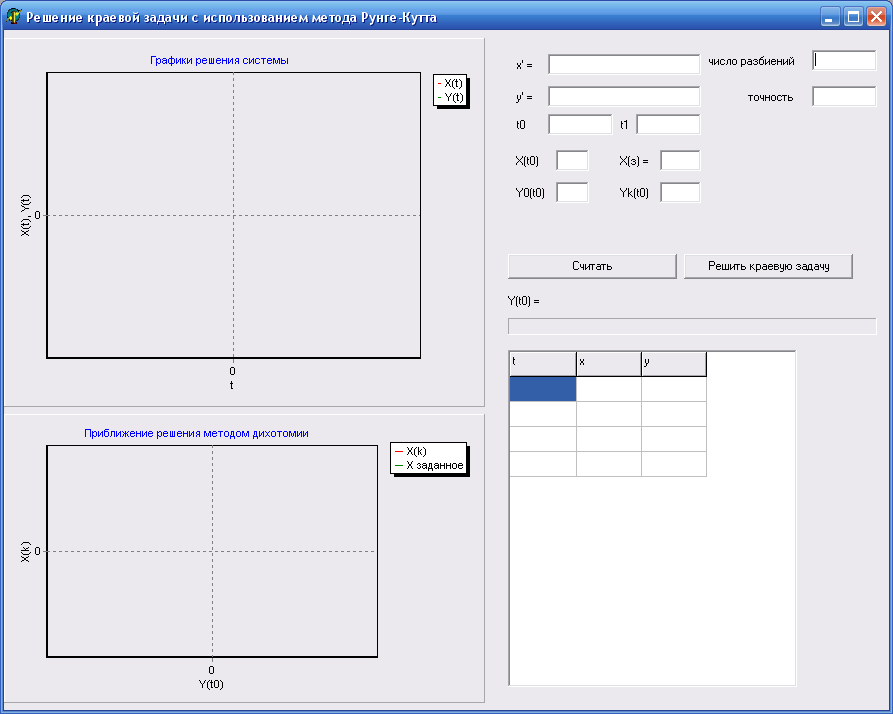
Рисунок 1 – первоначальный интерфейс программы.


Пользователь программы должен ввести систему уравнений (x^’ и y^’) в специальное для этого окно, также диапазон независимой переменной, имеющий начало (t0) и конец (t1), число разбиений, точность, значение функции x от t0 (X(t0)), начальное значение функции y от t0 (Y0(t0)), заданное значение x (x(з)), конечное значение функции y от t0 (Yk(t0)).

После ввода пользователь должен нажать кнопку «считать». Программа решит систему дифференциальных уравнений методом Рунге – Кутта и построит графики решения системы (рисунок 2).



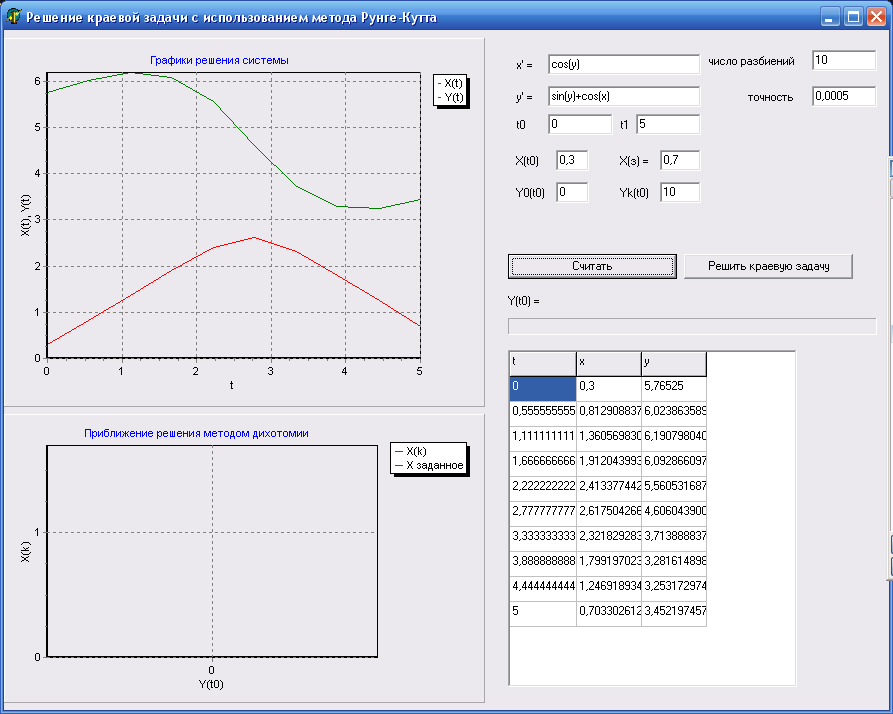
Рисунок 2 – решение системы диф. ур. и построение графиков решения системы.

После нажатия на кнопку «Решить краевую задачу» программа найдёт значение Y(t0) и построит график приближения решения методом дихотомии (рисунок 3).



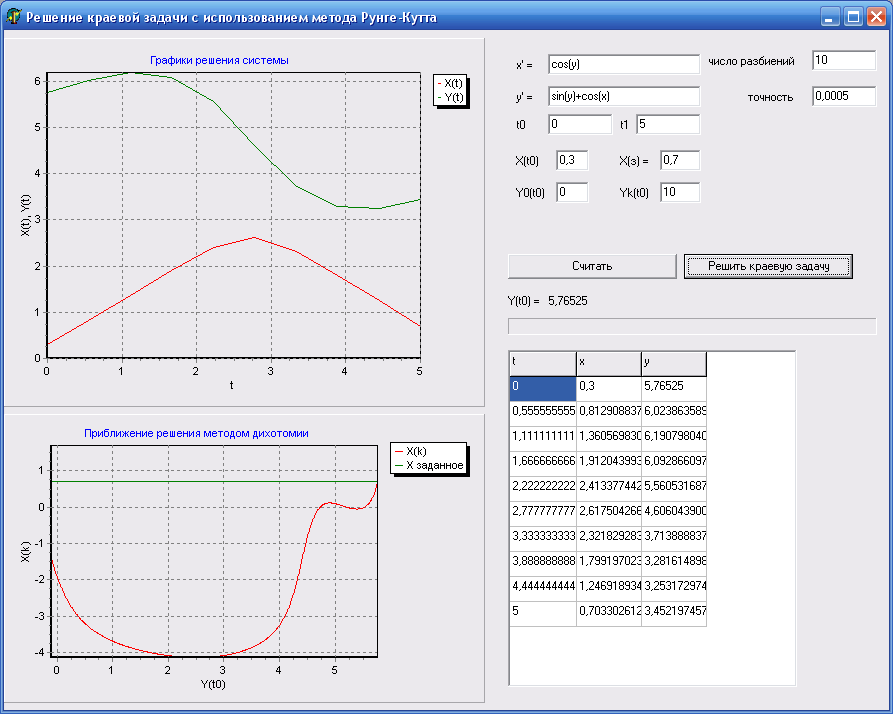
Рисунок 3 – решение краевой задачи.


4. ЗАКЛЮЧЕНИЕ

Данная программа курсовой работы может быть использована как обучающий модуль для студентов факультета «Информационных системы и технологий».


5. СПИСОК ИСТОЧНИКОВ И ЛИТЕРАТУРЫ


1.Пиявский С.А. Информационные системы и технологии в образовании: методические указания к курсовому проектированию «Разработка электронного обучающего модуля» / сост. С.А. Пиявский; Самарс. гос. арх. – строит. ун-т. – Самара, 2007. – 24 с.

2.Пиявский С.А. Методы оптимизации и оптимального управления: Учебное пособие / С.А.Пиявский; Самарск. гос. арх.-строит. ун-т. Самара, 2005. 68 с.

3. ссылка скрыта