Мозжевилов Максим Александрович Разработка модулей генерации заданий и решений по теме «Основы теории чисел» диплом

Вид материала

Диплом

Содержание 2. Практическая часть. 16 Список литературы: 31 1. Аналитическая часть. 1.1. Делители и делимость. Наименьшее общее кратное 1.2. Алгоритм Евклида. 1.3. Простота и факторизация. 1.3. Асимптотический закон распределения простых чисел. 1.4. Функция Эйлера. 1.5. Примеры заданий к рассмотренным темам 2. Практическая часть. 2.2. Цели применения модулей. 2.3. Способы применения модулей. 2.5. Средства разработки модулей Особенности языка 2.7. Интеграция модулей в программный комплекс. Возможности модулей как независимых приложений 2.8. Модуль NOD. Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием деления с остатком, где 2.9. Модуль Asimp. ... Полное содержание

Подобный материал:

• Майзаков Максим Александрович Разработка модулей автоматической генерации заданий, 799.4kb.
• Дидин Максим Александрович Переславль-Залесский Гимназия 7 7 7 7 7 7 7 7 56 диплом, 189.17kb.
• Дидин Максим Александрович Переславль-Залесский Гимназия 10 8 3 10 10 15 8 64 диплом, 103.28kb.
• hulan ucoz, 73.13kb.
• Ок. 365 300 до н э. древнегреческий математик. Работал в Александрии, 72.88kb.
• Разработка урока по теме: «Развитие мышления через постановку проблемно творческих, 84.71kb.
• Курс III семестр- VI всего аудиторных часов 69 ч.,, 47.01kb.
• Отчет о выполеннии ниокр по теме Разработка унифицированных функциональных модулей, 219.08kb.
• Рабочей программы учебной дисциплины «основы теории вероятностей и математической статистики», 46.75kb.
• Рейтинг-план освоения дисциплины «Теория принятия решений» Недели, 83.54kb.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Институт математики и компьютерных наук

Кафедра информационной безопасности


Допустить к защите в ГАК
Заведующий кафедрой
информационной безопасности,
д.т.н.,профессор А.А. Захаров

“____” _________ 2010 г.


Мозжевилов Максим Александрович

Разработка модулей генерации заданий и решений по теме «Основы теории чисел»

(Дипломная работа)


Научный руководитель:

к.ф-м.н.,доцент кафедры ИБ.

__________ Ниссенбаум О.В.

Автор работы:

__________ Мозжевилов М.А.


Тюмень 2010

ВВЕДЕНИЕ

Профессия преподаватель образовалась с древнейших времен. Сначала ценные знания переходили по наследству от отца к сыну в индивидуальном обучении, позже образовывались школы и так начало практиковаться групповое обучение. Это направление развивалось и развивается до сих пор, происходит образование новых различных обучающих структур, система обучения постоянно модернизируется, происходит появление высших учебных заведений.

Актуальность проблем, связанных с преподаванием повышается с каждым днем в связи с развитием системы преподавания, компьютеризацией рабочих мест и росту сферы информационных технологий и компьютерных наук. Одной из таких проблем является отсутствие автоматизации основных аспектов работы преподавателя. В частности: составление и проверка заданий для самостоятельных и контрольных работ.

В 2009 году в Тюменском Государственном Университете на 4 курсе специальности «Компьютерная безопасность» была введена рейтинговая система оценки знаний, была составлена и утверждена новая рабочая учебная программа по дисциплине «Теоретико-числовые методы в криптографии». В этой программе предусмотрены индивидуальные домашние контрольные работы по всем дидактическим единицам курса, т.е. для учебно-методического обеспечения данного курса необходимо разработать не менее 40 индивидуальных домашних контрольных работ. Более того, желательно ежегодное обновление вариантов контрольных работ. Желательно так же автоматизация проверки контрольных работ. Помимо домашних контрольных работ предусмотрены аудиторные контрольные работы, а так же тестирование остаточного знания по предмету, что так же увеличивает количество индивидуальных контрольных заданий.

Мой проект – Разработка модулей генерации заданий и решений по теме «Основы теории чисел» поможет свести к минимуму усилия преподавателя, затраченные на составление, решение и проверку заданий для самостоятельных и контрольных работ по дисциплине «Теоретико-числовые методы в криптографии». Целью создания и внедрения данного проекта является повышение объективности оценки знаний студентов в данной области.

Цель и задачи работы:

Проектирование и разработка модулей автоматической генерации заданий и решений по теме «Основы теории чисел» по дисциплине «Теоретико-числовые методы в криптографии».

Для достижения цели исследования поставим следующие задачи:

• исследовать предметную область;
  
• определить список тем и заданий;
  
• спроектировать и разработать модули генерации заданий и решений;
  
• разработать документацию;
  
• сформировать базу учебных задач.
  

1. Аналитическая часть.

Открытие натуральных чисел было одним из величайших интеллектуальных достижений человечества. Что общего между тремя мамонтами, тремя звездами и тремя вздохами отвергнутого влюбленного? С точки зрения потребительских качеств ничего. Мамонт – это еда, вот она здесь у входа в пещеру, от нее зависит жизнь племени. Звезды в небе, их не потрогаешь, ночью их видно, а днем нет. Вздох вообще нечто не совсем материальное, отдельно от человека не существующее.

Очень не скоро было замечено, что общее между разными предметами и событиями то, что при их перечислении нужно загнуть одно и то же число пальцев на руке, в нашем примере три. Кстати, и до сих пор, (вспомните золотое детство), обучаясь счету, малыши загибают пальцы. С пальцами же связано и возникновение десятичной системы счисления. Кстати, если бы 400 млн. лет назад на берег из океана выползла не пятипалая двоякодышащая рыба, потомками которой мы являемся, а, например, с четырьмя лучами на плавнике, то победила бы восьмеричная система счисления.

Как бы то ни было, человечеством была освоена главная идея, лежащая в основе понятия о натуральном числе. Идея взаимнооднозначного соответствия или биекции между элементами разных множеств.

Множество натуральных чисел сейчас принято обозначать ажурной заглавной буквой N. Натуральными числами являются {1,2,3,…}. Понятие о нуле возникло гораздо позже, чем об остальных целых числах. Ноль обозначает ничто, однако 0 – вполне осязаемый символ ничем не хуже чем 1 или 5. Ноль – это нечто, а обозначает он ничто. Нечто обозначающее ничто – это уже шаг к раздвоению личности и он нормальным людям дался нелегко. Отрицательные числа (понимаемые как долг, как недостача) вошли в сознание людей гораздо проще, так же как и дроби, понимаемые как часть единого целого.

1.1. Делители и делимость.

Для данных целых чисел a и b говорят, что a делит b (или b делится на a), и используют обозначение a|b, если существует такое целое число d, что b = ad. В этом случае a называют делителем b. Любое целое число b > 1 имеет, по крайней мере, два положительных делителя: 1 и b. Под собственным делителем b подразумевают любой положительный делитель, не равный b, а под нетривиальным делителем b – любой положительный делитель, не равный 1 или b. Простым числом, по определению, является целое число, большее 1, которое не имеет положительных делителей, отличных от 1 и самого себя; число называется составным, если оно имеет, по крайней мере, один нетривиальный делитель.

Для простого p и целого неотрицательного числа α мы используем запись p^α|| b, подразумевая, что p^α – наивысшая степень p, делящая b.

Основная теорема арифметики утверждает, что любое натуральное число n может быть записано в виде произведения простых чисел единственным образом (с точностью до перестановки сомножителей). Принято записывать это разложение в виде произведения различных простых сомножителей в соответствующих степенях, располагая простые числа в порядке возрастания. Например, 1200 = 2³∙3∙5²∙7.

Из единственности разложения целых чисел на простые множители следует также простой способ отыскания всех делителей n по его разложению. А именно, любой делитель d числа n должен быть произведением тех же простых сомножителей в степенях, не превышающих степени, точно делящие n. Таким образом, если p^α|| n, то p^β|| d для некоторого β, удовлетворяющего условию 0 ≤ β ≤ α. Например, для нахождения делителей числа 4300 нужно взять 2 в степени 0, 1, 2 или 3, умножить на 3 в степени 0 или 1, на 5 в степени 0, 1 или 2 и на 7 в степени 0 или 1. Число всех сомножителей, таким образом, есть произведение числа способов выбора степени для каждого простого сомножителя, которое, в свою очередь, равно α+1. Иначе говоря, число n = p₁^α1 p₂^α2… p_r^αr имеет (α₁+1) (α₂+1) ... (α_r+1) различных делителей. В частности, у числа 4300 их 48.

Наибольшим общим делителем двух данных целых чисел a и b (обозначаемым НОД(a, b)), не равных одновременно нулю, называется наибольшее целое число d, делящее и a, и b. Если имеются разложения на простые множители двух чисел a и b – легко записать и НОД(a, b). Следует взять все простые числа, входящие в оба разложения, и каждое возвести в степень, равную минимуму из двух соответствующих показателей. Например, сравнивая разложение 10780 = 2²∙5∙7² с приведенным выше разложением числа 4200, получаем, что НОД(4200, 10780) = 2²∙5∙7 = 140.

Наименьшее общее кратное чисел a и b обозначается НОК(a, b) и по определению является наименьшим целым положительным числом, делящимся как на a, так и на b. Имея разложение на простые сомножители чисел a и b, можно получить НОК(a, b), взяв все простые числа, входящие хотя бы в одно из разложений, и каждое возвести в степень, равную максимуму из двух показателей. Легко показать, что НОК(a, b)=|ab|/НОД(a,b).

1.2. Алгоритм Евклида.

При работе с большими числами часто случается, что их разложение на простые множители неизвестно. В частности, важным направлением исследований в теории чисел является отыскание быстрых методов разложения больших чисел на простые множители. К счастью существует сравнительно быстрый способ нахождения НОД (a,b) даже в том случае, когда неизвестны простые делители a или b. он называется алгоритмом Евклида.

Реализация алгоритма Евклида (вариант алгоритма с вычитанием).

Вход: a, b>0.

1. Если a>b Шаг 3
   если a<b Шаг 2
   если a=b Шаг 5 (выход)
   
2. Меняем местами a и b.
   
3. a:=a–b
   
4. Возвращаемся на Шаг 1.
   
5. Выход: a – НОД
   

Ниже приведен пример использования этой реализации алгоритма.

Пример

a=603, b=108

Преобразования алгоритма записаны в таблицу, верхняя строка которой содержит значение переменной a, нижняя – содержимое переменной b. Каждый столбец таблице соответствует состоянию процесса на отдельном шаге.

a	603	495	387	279	171	63	108	45	63	18	45	27	9	18	9
b	108	108	108	108	108	108	63	63	45	45	18	18	18	9	9

Ответ: НОД (603,108)=9.

Реализация алгоритма Евклида (вариант алгоритма с делением с остатком).

Вход: a, b >0.

1. Находим разложение a=bq+r, 0≤r
   
2. если r=0 Шаг 5 (выход)
   
3. a:=b; b:=r.
   
4. Возвращаемся на Шаг 1
   
5. Выход: b – НОД.
   

Пример

a=603, b=108

a	603	108	63	45	27	18
b	108	63	45	27	18	9

603=5·108+63

108=1·63+45

63=1∙45+27

45=1∙27+18

27=1∙18+9

18=2∙9+0

Ответ: НОД (603,108)=9.

Бинарный алгоритм Евклида.

Этот вариант создан специально для реализации на ЭВМ. В нем учитывается, что операция деления на число 2 или на любую степень двойки является весьма быстрой и простой операцией (в двоичной системе счисления операция деления на 2 есть всего лишь битовый сдвиг вправо).

Учтем, что (2^k∙a,2^s∙b)=2^min(k,s)(a,b).

Алгоритм:

Вход: a, b>0.

1. Представим a и b в виде: ; , где a₁, b₁ – нечетные числа.
   k:=min(k₁,k₂).
   
2. Если a₁>b₁ Шаг 4
   a₁< b₁ Шаг 3
   a₁= b₁ Шаг 6
   
3. Меняем местами a₁ и b₁.
   
4. c:=a₁–b₁=2^s∙c₁ (c₁ - нечетное число)
   (Заметим, что с обязательно будет четным, а значит )
   
5. a₁:= b₁ , b₁:=c₁ . Возвращаемся на Шаг 1.
   
6. Выход: (a,b)=2^k∙a₁ .
   

Пример

a=603, b=108

a1	603	27	9
b1	27	9	9
c1	9	9	–

1. a₁=603, k₁=0; b=108=4∙27=2²∙27 k₂=2, b₁=27, k=0

2. a₁=603> b₁=27 Ш4

4. c=603-27=56=64∙9, c₁=9

5. a₁=27; b₁=9 Ш1

1. a₁=27; b₁=9

2. a₁> b₁ Ш4

4. c=a₁–b₁=18=2∙9, c₁=9

5. a₁=9, b₁=9

1. a₁=9, b₁=9, k=0

2. a₁= b₁ Ш6

6. (a,b) = 2º∙9=9

1.3. Простота и факторизация.

Во многих случаях требуется выяснить, является ли большое число n простым. Например, в системе открытого ключа RSA и различных системах, основанных на задаче дискретного логарифмирования в конечных полях, нам нужно найти большое «случайное» простое число. Один из подходов к этому заключается в том, чтобы выбрать большое нечетное целое число n₀, используя генератор случайных чисел, и затем проверять n_0, n₀+2, … на простоту до тех пор, пока мы не найдем первое простое число, большее или равное n₀. Другой тип использования тестов на простоту – выяснение того, является ли некоторое число весьма специального типа простым.

Тест на простоту представляет собой критерий того, что число n не является простым. Если n «проходит» этот тест, то оно, возможно, простое число. Если оно «проходит» целый набор тестов на простоту, то весьма вероятно, что оно действительно является простым. С другой стороны, если n не проходит хотя бы одного теста на простоту, то оно совершенно определенно является составным. Однако при этом остается нерешенной трудная задача нахождения простых делителей числа n (задача факторизации). В общем случае для разложения на множители большого числа, о котором известно, что оно составное (поскольку оно не прошло теста на простоту), требуется гораздо больше времени, чем для нахождения простого числа того же порядка величины. (это – эмпирическое утверждение, а не теорема; ни одного утверждения такого рода не доказано). Надежность криптосистемы RSA основывается на том предположении, что значительно легче найти два чрезвычайно больших простых числа p и q, чем зная n = pq, но не p или q, найти делители числа n.

Существует множество полиномиальных тестов простоты, но большинство из них являются вероятностными (например, тест Миллера-Рабина) и используются для нужд криптографии. Только в 2002 году было доказано, что задача проверки на простоту в общем виде полиномиально разрешима, но предложенный детерминированный алгоритм имеет довольно большую сложность, что затрудняет его практическое применение.

Для некоторых классов чисел существуют специализированные эффективные тесты простоты. Например, для проверки на простоту чисел Мерсенна используется тест Люка-Лемера, а для проверки на простоту чисел Ферма-тест Пепина.

1.3. Асимптотический закон распределения простых чисел.

Современная практическая криптография требует использования больших простых чисел – в некоторых стандартах используются простые числа размером порядка 1024 бита.

Для поиска простых чисел с помощью таких тестов используют следующий подход: из чисел заданного диапазона случайным образом выбирают числа и проверяют их на простоту. Поиск прекращается как только будет найдено простое число. Такой подход называют случайным поиском простых чисел.

Для того чтобы оценить время, которое придется затратить на случайный поиск в заданном диапазоне, необходимо знать, сколько примерно простых чисел в этом диапазоне содержится. Конечно, точное распределение простых чисел в N неизвестно, но некоторые сведения об этом распределении у современной математики имеются.

Более точно на вопрос о распределении простых чисел в N отвечает асимптотический закон распределения простых чисел.

Итак, обозначим π(x) – количество простых чисел, меньших либо равных x. Тогда справедлив

Асимптотический закон простых чисел

.

■

Другими словами, при x→∞, π(x)→x/lnx.

Пример.

Пользуясь асимптотическим законом, вычислим примерное количество простых 512-битных чисел (таких, чтобы старший, 512-й, бит был равен 1). Наименьшее значение 512 битного числа составляет 2⁵¹¹, наибольшее – 2⁵¹²-1. Таким образом, нужно найти приблизительное количество K простых чисел из диапазона (x₁=2⁵¹¹, x₂=2⁵¹²).

K = π(x₂)—π(x₁) ≈ = = = ==.

Тогда вероятность при случайном поиске в заданном диапазоне выбрать простое число составляет

P = ≈ = ≈.

Если же случайный поиск производить только среди нечетных чисел, то

P = ≈ .

То есть для того, чтобы путем случайного перебора среди 512-битных нечетных чисел найти простое, в среднем понадобится 178 итераций. Для 1024-битных чисел поиск среди нечетных чисел потребует в среднем 355 итераций. В общем, при увеличении требуемого размера числа (в битах) в 2 раза, среднее время поиска тоже увеличивается в два раза.

1.4. Функция Эйлера.

Числа a₁,…,a_n называются взаимно простыми, если НОД(a₁,…,a_n)=1. Функция Эйлера φ(a) есть количество чисел ряда 0, 1, …, а–1, взаимно простых с а ().

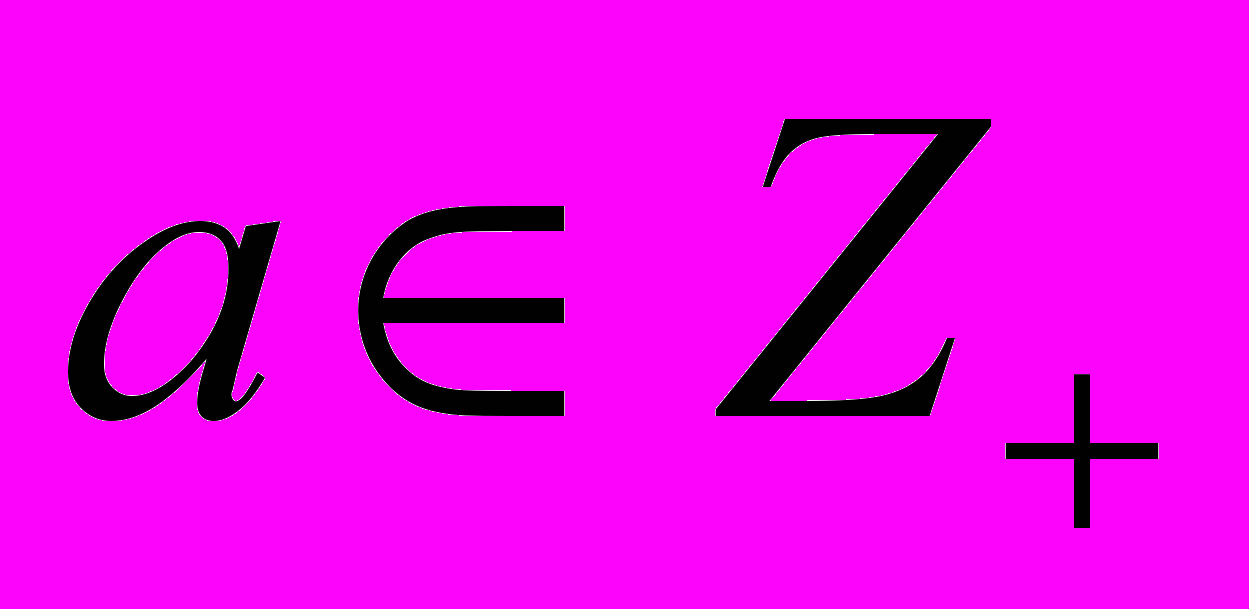φ(1)=1, φ(2)=1, φ(3)=2, φ(4)=2, φ(5)=4, φ(6)=2 и т. д.

Свойства функции Эйлера:

1. φ(1)=1;
   
2. φ(p)=p–1, где р – простое;
   
3. φ(p^α)=p^α–1(p–1) , где р – простое;
   
4. φ(a) – мультипликативная функция.
   

Пример.

Вычислим φ(28350322).

Для того, чтобы вычислить значение функции Эйлера, необходимо найти каноническое разложение аргумента.

28350322=2·14175161=2·7·2025023=2·7²·289289=2·7³·41327=

=2·7³·11·3757=2·7³·11·13·289=2·7³·11·13·17².

φ(28350322)= φ(2·7³·11·13·17²)= φ(2) · φ(7³)· φ(11)· φ(13)· φ(17²)=

=1·7²·6·10·12·17·16=9596160.

Ответ: φ(28 350 322)=9 596 160.

Стоит отметить, что функция Эйлера применяется в криптосистеме RSA. Криптографическая система RSA получила очень широкое распространение и является классическим примером криптографической системы с открытыми ключами.

Открытый ключ состоит из пары чисел (n, e), где n – произведение двух больших простых чисел p и q, а e должно быть меньше числа φ(n)=(p-1)(q-1) и взаимно просто с ним.

Секретный же ключ состоит из пары чисел (n, d), где число d такое, что de ≡ 1 mod φ(n).

1.5. Примеры заданий к рассмотренным темам

Для освоения перечисленных выше тем можно предложить следующие задания:

• Вычислить НОД(a,b) при помощи алгоритма Евклида с вычитанием.
  
• Вычислить НОД(a,b) при помощи алгоритма Евклида с делением с остатком.
  
• Вычислить НОД(a,b) при помощи бинарного алгоритма Евклида.
  
• Вычислить НОД(a,b) при помощи алгоритма Евклида с делением с остатком и бинарного алгоритма Евклида. Сравнить количество итераций.
  
• Найти каноническое разложение числа на простые сомножители.
  
• Вычислить НОК(a,b).
  
• Построить таблицу первых простых чисел с помощью решета Эратосфена.
  
• Разложить дробь в цепную дробь при помощи алгоритма Евклида.
  
• Вычислить примерное количество простых чисел на заданном интервале.
  
• Вычисляет вероятность того, что наугад выбранное число из указанного диапазона будет простым.
  
• Вычисляет, сколько чисел из заданного диапазона следует перебрать, чтобы с определенной вероятностью получить хотя бы одно простое.
  
• Вычислить функцию Эйлера от числа.