Мозжевилов Максим Александрович Разработка модулей генерации заданий и решений по теме «Основы теории чисел» диплом

Вид материала

Список литературы
Приложение 1. Руководство пользователя.
2. Модуль NOD.
Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием вычитания, где
Ответ: НОД(300,283)=1.
Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием деления с остатком, где
3. Модуль ASIMP.
Определить примерное количество простых чисел в диапазоне от a до b, где
Какова вероятность того, что наугад выбранное нечетное число из диапазона от a до b будет простым, если

Подобный материал:

1 2 3 4 5 6 7

ЗАКЛЮЧЕНИЕ

В ходе выполнения дипломной работы мной были изучены материалы по теме «Основы теории чисел» и решена намеченная цель – создание модулей автоматической генерации заданий и решений по данной теме. Для достижения этой цели, мной в ходе выполнения работы были решены следующие задачи:

Выбраны темы и задания, удовлетворяющие требованиям курса обучения дисциплине «Теоретико-числовые методы в криптографии»
Разработаны модули генерации заданий и решений. Данные модули имеют дружественный, интуитивно понятный интерфейс и обладают простотой в использовании.
Составлена документация двух видов. Для пользователя - с иллюстрациями интерфейса и объяснением всех параметров и правил их заполнения. Для программиста - с объяснениями исходного кода, параметров и функций, использующихся в данных модулях.
Реализована интеграция модулей в программный комплекс. Данный комплекс объединяет все модули в одно целое. Имеет дружественный, интуитивно понятный интерфейс и прост в использовании.
Сформированы учебные задания для сборника вариантов контрольных работ по предмету «Теоретико-числовые методы в криптографии».

СПИСОК ЛИТЕРАТУРЫ:

А.В.Рожков, О.В. Ниссенбаум. Теоретико-числовые методы в криптографии: Учебное пособие. Тюмень: Издательство Тюменского государственного университета, 2007. 160с.
Н.Коблиц. Курс теории чисел и криптографии. Москва: Научное изд-во ТВП, 2001, х+254с.
Виноградов И.М. Основы теории чисел. М.: Наука, 1972. 402с.
Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. – М.: МЦНМО, 2003. – 328 с.
Черемушкин А.В. Лекции по арифметическим алгоритмам в криптографии. М.: МЦНМО, 2002. – 104 с.
Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы криптографии. Учебное пособие. М.: Гелиос-АРВ, 2001.
Эндрю Троелсен. С# 2008 и платформа .NET 3.5 Framework = Pro C# 2008 and the .NET 3.5 Framework. — 4-е изд. — М.: Вильямс, 2009. — С. 1368. — ISBN 978-5-8459-1589-4
Герберт Шилдт. C# 3.0: полное руководство = C# 3.0: The Complete Reference. — 4-е изд. — М.: Вильямс, 2009. — С. 992. — ISBN 978-5-8459-1565-8
Кристиан Нейгел, Карли Уотсон и др. Visual C# 2008: базовый курс. Visual Studio® 2008 = Beginning Visual C# 2008. — М.: Диалектика, 2009. — ISBN 978-5-8459-1317-3
Кристиан Нейгел, Билл Ивьен и др. C# 2008 и платформа .NET 3.5 для профессионалов = Professional C# 2008. — М.: Диалектика, 2008. — ISBN 978-5-8459-1458-3

Приложение 1. Руководство пользователя.

1. Модуль EILER.

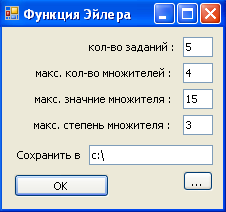
Рисунок 4

На рисунке 4 представлен интерфейс модуля EILER.

Модуль предназначен для генерации заданий и решений на тему вычисления функции Эйлера. Модуль случайным образом генерирует аргумент и вычисляет функцию Эйлера этого аргумента и выводит результаты решения в текстовый файл.

Задания генерируются по следующей формуле:

n = p₁^a¹ p₂^a² … p_k^a^k

где p – это простое число, значение которого генерируется случайным образом из диапазона простых чисел от 2 до значения указанного в параметре макс. значение множителя; a – степень множителя, значение которой генерируется случайным образом из диапазона чисел от 1 до значения заданного в параметре макс. степень множителя; k – это количество множителей, значение этого параметра принимает случайное число из диапазона чисел от 1 до значения указанного в параметре макс. количество множителей.

Модуль имеет следующие параметры:

Кол-во заданий
- Это количество заданий, которые будут сгенерированы в результате работы модуля.
- Может быть только целым положительным числом.
- Значение по умолчанию – 5.
- Минимальное возможное значение – 1.
- Максимальное возможное значение – 29.
Макс. кол-во множителей
- Это максимально возможное количество простых сомножителей, входящих в каноническое разложение аргумента.
- Может быть только целым положительным числом.
- Минимальное значение – 1.
- Максимальное значение – 168.
- Значение по умолчанию – 4.
- Значение этого параметра прямо пропорционально влияет на сложность генерируемых заданий.
Макс. значение множителя
- Это максимальное значение, которое может принять каждый простой сомножитель аргумента, при генерации заданий.
- Может быть только целым положительным числом.
- Значение по умолчанию – 15.
- Минимальное значение – зависит от параметра макс.количество множителей, при вводе которого программа сама введет минимально допустимое значение данного параметра.
- Максимальное значение – 997.
- Значение этого параметра прямо пропорционально влияет на сложность генерируемых заданий.
Макс. степень множителя
- Это максимальная степень, в которой простой сомножитель входит в каноническое разложение аргумента.
- Может быть только целым положительным числом.
- Значение по умолчание – 3.
- Минимальное значение – 1.
- Максимальное значение – 5.
Сохранить в
- Это место, куда будут сохранены сгенерированные файлы задания и решения.
- Значение по умолчанию – место, откуда был запущен данный модуль.
- Для выбора места сохранения нужно нажать на кнопку с тремя точками.

После ввода всех параметров, следует нажать на кнопку ОК. Модуль сгенерирует файлы и сохранит их в указанном месте, после чего появится информационное сообщение о готовности файлов и месте их сохранения, как показано на рисунке 5.

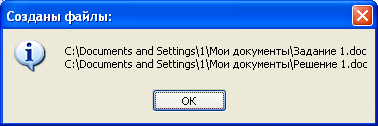
Рисунок 5

Пример работы модуля.

Установлены следующие входные параметры:

кол-во заданий – 3;
макс. кол-во множителей – 4;
макс. значение множителя – 15;
макс. степень множителя – 3.

Содержание сгенерированного файла с заданиями:

Вычислить функцию φ(n).

а) n=9295;

б) n=6552;

в) n=28014525.

Содержание сгенерированного файла с решениями:

Вычислить функцию φ(n).

а) n=9295.

Решение:

n=5∙11∙13².

φ(n)=4∙10∙13∙12 = 6240.

Ответ: φ(9295) = 6240.

б) n=6552.

Решение:

n=2³∙3²∙7∙13.

φ(n)=2²∙3∙2∙6∙12 = 1728.

Ответ: φ(6552) = 1728.

в) n=28014525.

Решение:

n=3³∙5²∙7³∙11².

φ(n)=3²∙2∙5∙4∙7²∙6∙11∙10 = 11642400.

Ответ: φ(28014525) = 11642400.

2. Модуль NOD.

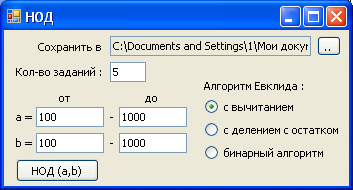
Рисунок 6

На рисунке 6 представлен интерфейс модуля NOD.

Модуль предназначен для вычисления наибольшего общего делителя двух чисел и имеет следующие параметры:

Сохранить в
- Это место, куда будут сохранены сгенерированные файлы задания и решения.
- Значение по умолчанию – место, откуда был запущен данный модуль.
- Для выбора места сохранения нужно нажать на кнопку с тремя точками.
Кол-во заданий
- Это количество заданий, которые будут сгенерированы в результате работы модуля.
- Может быть только целым положительным числом.
- Значение по умолчанию – 5.
- Минимальное возможное значение – 1.
- Максимальное возможное значение – 29.
от
- Это нижняя граница диапазона чисел, используемых для генерации значений a и b.
- Может быть только целым положительным числом.
- Значение по умолчанию – 100.
- Минимальное возможное значение – 1.
- Максимальное возможное значение – 1000000.
до
- Это верхняя граница диапазона чисел, используемых для генерации значений a и b.
- Может быть только целым положительным числом.
- Значение по умолчанию – 1000.
- Минимальное возможное значение – 1.
- Максимальное возможное значение – 1000000.
Метод вычисления
- Определяет, какой алгоритм будет использован для вычисления наибольшего общего делителя чисел a и b.
- Вычитание – алгоритм Евклида с использованием вычитания.
- Деление с остатком – алгоритм Евклида с использованием деления с остатком.
- Бинарный алгоритм – бинарный алгоритм Евклида.

После ввода всех параметров, следует нажать на кнопку НОД(a,b). Модуль сгенерирует файлы и сохранит их в указанном месте, после чего появится информационное сообщение о готовности файлов и месте их сохранения, как это показано на рисунке 5(стр.32).

Пример работы модуля.

Установлены следующие входные параметры:

количество заданий – 2;
a = от 1 до 500;
b = от 1 до 500;
алгоритм Евклида – с вычитанием.

Содержание сгенерированного файла с заданиями:

Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием вычитания, где:

а) a = 300, b = 283;

б) a = 239, b = 314.

Содержание сгенерированного файла с решениями:

Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием вычитания, где:

а) a = 300, b = 283.

Решение:

a	300	17	283	266	249	232	215	198	181	164	147	130	113	96
b	283	283	17	17	17	17	17	17	17	17	17	17	17	17
79	62	45	28	11	17	6	11	5	6	1
17	17	17	17	17	11	11	6	6	5	5

Ответ: НОД(300,283)=1.

б) a = 239, b = 314.

Решение:

a	239	314	75	239	164	89	14	75	61	47	33	19	5	14
b	314	239	239	75	75	75	75	14	14	14	14	14	14	5
9	4	5	1
5	5	4	4

Ответ: НОД(239,314)=1.

Установлены следующие входные параметры:

количество заданий – 2;
a = от 1 до 500;
b = от 1 до 500;
алгоритм Евклида – с делением с остатком.

Содержание сгенерированного файла с заданиями:

Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием деления с остатком, где:

а) a = 411, b = 489;

б) a = 311, b = 127.

Содержание сгенерированного файла с решениями:

Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием деления с остатком, где:

а) a = 411, b = 489.

Решение:

a	411	489	411	78	21	15	6
b	489	411	78	21	15	6	3

411=0∙489+411

489=1∙411+78

411=5∙78+21

78=3∙21+15

21=1∙15+6

15=2∙6+3

6=2∙3+0

Ответ: НОД(411,489)=3.

б) a = 311, b = 127.

Решение:

a	311	127	57	13	5	3	2
b	127	57	13	5	3	2	1

311=2∙127+57

127=2∙57+13

57=4∙13+5

13=2∙5+3

5=1∙3+2

3=1∙2+1

2=2∙1+0

Ответ: НОД(311,127)=1.

Установлены следующие входные параметры:

количество заданий – 2;
a = от 1 до 500;
b = от 1 до 500;
алгоритм Евклида – бинарный алгоритм.

Содержание сгенерированного файла с заданиями:

Вычислить НОД(a,b) при помощи бинарного алгоритма Евклида, где:

а) a = 154, b = 246;

б) a = 83, b = 449.

Содержание сгенерированного файла с решениями:

Вычислить НОД(a,b) при помощи бинарного алгоритма Евклида, где:

а) a = 154, b = 246.

Решение:

154=2¹∙77, k₁=1; 246=2¹∙123, k₂=1.

=> k=min(k₁,k₂)=1, a₁=max(123,77)=123, b₁=min(123,77)=77.

c=123-77=46=2¹∙23, c₁=23, a₁=max(b₁,c₁)=77, b₁=min(b₁,c₁)=23.

c=77-23=54=2¹∙27, c₁=27, a₁=27, b₁=23.

c=27-23=4=2²∙1, c₁=1, a₁=23, b₁=1.

c=23-1=22=2¹∙11, c₁=11, a₁=11, b₁=1.

c=11-1=10=2¹∙5, c₁=5, a₁=5, b₁=1.

c=5-1=4=2²∙1, c₁=1, a₁=1, b₁=1.

Ответ: НОД(154,246)=2^k∙b₁=2¹∙1=2.

б) a = 83, b = 449.

Решение:

83=2⁰∙83, k₁=0; 449=2⁰∙449, k₂=0.

=> k=min(k₁,k₂)=0, a₁=max(449,83)=449, b₁=min(449,83)=83.

c=449-83=366=2¹∙183, c₁=183, a₁=max(b₁,c₁)=183, b₁=min(b₁,c₁)=83.

c=183-83=100=2²∙25, c₁=25, a₁=83, b₁=25.

c=83-25=58=2¹∙29, c₁=29, a₁=29, b₁=25.

c=29-25=4=2²∙1, c₁=1, a₁=25, b₁=1.

c=25-1=24=2³∙3, c₁=3, a₁=3, b₁=1.

c=3-1=2=2¹∙1, c₁=1, a₁=1, b₁=1.

Ответ: НОД(83,449)=2^k∙b₁=2⁰∙1=1.

3. Модуль ASIMP.

Данный модуль выполняет задания, основанные на асимптотическом законе распределения простых чисел. Для генерации заданий и решений, необходимо указать нужный вариант задания и ввести параметры, определяющие сложность и количество заданий, а так же указать место, где буду сохранены текстовые файлы, сгенерированные в результате работы модуля.

На рисунке 7 представлен интерфейс модуля ASIMP.

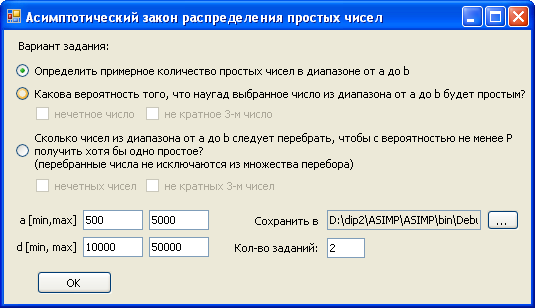
Рисунок 7

Модуль имеет следующие параметры:

Вариант задания
- Определяет вид задания.
- Во втором и третьем вариантах имеются дополнительные параметры для выбираемых чисел:
  - выбираются нечетные числа;
  - выбираются не кратные 3-м числа.
a[min, max]
- Параметр а – это нижняя граница диапазона чисел.
- min и max – нижняя и верхняя границы диапазона чисел используемых для генерации значения параметра a.
- Может быть только целым положительным числом.
- Значение по умолчанию – от 500 до 5000.
- Минимальное возможное значение – 100.
- Максимальное возможное значение – 10000.
d[min, max]
- Параметр d – это длина диапазона чисел (b = a + d).
- min и max – нижняя и верхняя границы диапазона чисел используемых для генерации значения параметра d.
- Может быть только целым положительным числом.
- Значение по умолчанию – от 10000 до 50000.
- Минимальное возможное значение – 1000.
- Максимальное возможное значение – 1000000.
Сохранить в
- Это место, куда будут сохранены сгенерированные файлы задания и решения.
- Значение по умолчанию – место, откуда был запущен данный модуль.
- Для выбора места сохранения нужно нажать на кнопку с тремя точками.
Кол-во заданий
- Это количество заданий, которые будут сгенерированы в результате работы модуля.
- Может быть только целым положительным числом.
- Значение по умолчанию – 5.
- Минимальное возможное значение – 1.
- Максимальное возможное значение – 29.

вариант задания – определить примерное количество простых чисел в диапазоне от a до b;
a = от 500 до 5000;
d = от 10000 до 50000;
количество заданий – 2.

Содержание сгенерированного файла с заданиями:

Определить примерное количество простых чисел в диапазоне от a до b, где:

а) a = 4900, b = 33000;

б) a = 4500, b = 21000.

Содержание сгенерированного файла с решениями:

Определить примерное количество простых чисел в диапазоне от a до b, где:

а) a = 4900, b = 33000.

Решение:

Примерное количество простых чисел в диапазоне от 4900 до 33000 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 2595,1.

Ответ: K ≈ 2595,1.

б) a = 4500, b = 21000.

Решение:

Примерное количество простых чисел в диапазоне от 4500 до 21000 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 1575,11.

Ответ: K ≈ 1575,11.

Установлены следующие входные параметры:

вариант задания – какова вероятность того, что наугад выбранное нечетное число из диапазона от a до b будет простым;
a = от 500 до 5000;
d = от 10000 до 50000;
количество заданий – 2.

Содержание сгенерированного файла с заданиями:

Какова вероятность того, что наугад выбранное нечетное число из диапазона от a до b будет простым, если:

а) a = 1300, b = 42000;

б) a = 2400, b = 37000.

Содержание сгенерированного файла с решениями:

Какова вероятность того, что наугад выбранное нечетное число из диапазона от a до b будет простым, если:

а) a = 1300, b = 42000.

Решение:

Примерное количество простых чисел в диапазоне от 1300 до 42000 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 3764,05.

Количество чисел, больших 1300 и меньших 42000, есть 40700. Доля нечетных чисел есть 1/2. Тогда всего перебирается чисел 20350. Вероятность случайного выбора простого числа есть

P = 3764,05 / 20350 ≈ 0,18.

Ответ: P ≈ 0,18.

б) a = 2400, b = 37000.

Решение:

Примерное количество простых чисел в диапазоне от 2400 до 37000 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 3209,2.

Количество чисел, больших 2400 и меньших 37000, есть 34600. Доля нечетных чисел есть 1/2. Тогда всего перебирается чисел 17300. Вероятность случайного выбора простого числа есть

P = 3209,2 / 17300 ≈ 0,19.

Ответ: P ≈ 0,19.

Установлены следующие входные параметры:

вариант задания – Сколько чисел из диапазона от a до b следует перебрать, чтобы с вероятностью не менее p получить хотя бы одно простое? (перебранные числа не исключаются из множества перебора);
a = от 500 до 5000;
d = от 10000 до 50000;
количество заданий – 2.

Содержание сгенерированного файла с заданиями:

Сколько чисел из диапазона от a до b следует перебрать, чтобы с вероятностью не менее p получить хотя бы одно простое? (перебранные числа не исключаются из множества перебора).

а) a = 3200, b = 24000, p = 0,7;

б) a = 4400, b = 38000, p = 0,995.

Содержание сгенерированного файла с решениями:

Сколько чисел из диапазона от a до b следует перебрать, чтобы с вероятностью не менее p получить хотя бы одно простое? (перебранные числа не исключаются из множества перебора).

а) a = 3200, b = 24000, p = 0,7.

Решение:

Примерное количество простых чисел в диапазоне от 3200 до 24000 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 1983,1.

Количество чисел, больших 3200 и меньших 24000, есть 20800. Вероятность случайного выбора простого числа есть

P = 1983,1 / 20800 ≈ 0,1.

Вероятность достичь успеха хотя бы в одном из n испытаний есть 1-(1-P)ⁿ ≥ p. Тогда n ≥ log_(1-P)(1-p), т.е n ≥ ln(1-p) / ln(1-P) ≥ 12,02 => n=13.

Ответ: требуется 13 испытаний.

б) a = 4400, b = 38000, p = 0,995.

Решение:

Примерное количество простых чисел в диапазоне от 4400 до 38000 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 3079,01.

Количество чисел, больших 4400 и меньших 38000, есть 33600. Вероятность случайного выбора простого числа есть

P = 3079,01 / 33600 ≈ 0,09.

Вероятность достичь успеха хотя бы в одном из n испытаний есть 1-(1-P)ⁿ ≥ p. Тогда n ≥ log_(1-P)(1-p), т.е n ≥ ln(1-p) / ln(1-P) ≥ 55,13 => n=56.

Ответ: требуется 56 испытаний.

a	300	17	283	266	249	232	215	198	181	164	147	130	113	96
b	283	283	17	17	17	17	17	17	17	17	17	17	17	17
79	62	45	28	11	17	6	11	5	6	1
17	17	17	17	17	11	11	6	6	5	5

a	239	314	75	239	164	89	14	75	61	47	33	19	5	14
b	314	239	239	75	75	75	75	14	14	14	14	14	14	5
9	4	5	1
5	5	4	4

a	300	17	283	266	249	232	215	198	181	164	147	130	113	96
b	283	283	17	17	17	17	17	17	17	17	17	17	17	17
79	62	45	28	11	17	6	11	5	6	1
17	17	17	17	17	11	11	6	6	5	5

a	239	314	75	239	164	89	14	75	61	47	33	19	5	14
b	314	239	239	75	75	75	75	14	14	14	14	14	14	5
9	4	5	1
5	5	4	4

Blog

Мозжевилов Максим Александрович Разработка модулей генерации заданий и решений по теме «Основы теории чисел» диплом

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ:

Приложение 1. Руководство пользователя.

a	300	17	283	266	249	232	215	198	181	164	147	130	113	96
b	283	283	17	17	17	17	17	17	17	17	17	17	17	17
79	62	45	28	11	17	6	11	5	6	1
17	17	17	17	17	11	11	6	6	5	5

a	239	314	75	239	164	89	14	75	61	47	33	19	5	14
b	314	239	239	75	75	75	75	14	14	14	14	14	14	5
9	4	5	1
5	5	4	4