Мозжевилов Максим Александрович Разработка модулей генерации заданий и решений по теме «Основы теории чисел» диплом

Вид материала

2. Практическая часть.
2.2. Цели применения модулей.
2.3. Способы применения модулей.
2.5. Средства разработки модулей
Особенности языка
2.7. Интеграция модулей в программный комплекс.
Возможности модулей как независимых приложений
2.8. Модуль NOD.
Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием деления с остатком, где
2.9. Модуль Asimp.
Пример работы модуля ASIMP.
Определить примерное количество простых чисел в диапазоне от a до b, где
2.10. Модуль Eiler.

Подобный материал:

1 2 3 4 5 6 7

2. Практическая часть.

2.1. Предметная область.

Современная криптография в значительной мере использует результаты таких дисциплин как алгебра, теория чисел, теория сложности. Студентам, изучающим криптографию всерьез, необходимо знание ее математических основ, поскольку ничто так не помогает знанию как понимание, а понимание алгоритмов криптографии и криптоанализа невозможно без понимания идей, которые в них заложены.

Для разработки модулей генерации заданий и решений по теме «Основы теории чисел» были выбраны следующие темы:

Делители и делимость.
Асимптотический закон распределения простых чисел.
Функция Эйлера.

Данные темы являются обязательными в изучении дисциплины «Теоретико-числовые методы в криптографии».

Теоретические результаты данных разделов являются основой для поиска и проверки простых чисел, которые широко применяются в различных областях криптографии. Большие простые числа используются в криптографии с открытым ключом. Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL. Простые числа также используются в хеш-таблицах и для генерации псевдослучайных чисел. Получение случайных простых чисел является неотъемлемой частью процедур выработки ключей во многих криптографических алгоритмах, включая RSA и ElGamal. А также функция Эйлера применяется в криптосистеме RSA для выработки открытого и секретного ключа.

Из выбранных тем, для реализации модулей, были сформулированы следующие задания:

Вычислить наибольший общий делитель двух чисел.
- используя алгоритм с вычитанием;
- используя алгоритм с делением с остатком;
- используя бинарный алгоритм.
Вычислить примерное количество простых чисел в заданном промежутке.
Вычислить вероятность того, что наугад выбранное число из заданного диапазона будет простым.
- выбирается только нечетное число;
- выбирается только не кратное 3-м число;
- выбирается только нечетное и не кратное 3-м число;
- выбирается любое число из заданного диапазона.
Вычислить сколько чисел из заданного диапазона следует перебрать, чтобы с определенной вероятностью получить хотя бы одно простое.
- перебираются только нечетные числа;
- перебираются только числа не кратные 3-м;
- перебираются только нечетные и не кратные 3-м числа;
- перебираются все числа из заданного диапазона.
Вычислить функцию Эйлера от числа.

Данные задания направлены на формирование у студента умений и навыков, необходимых для лучшего усвоения теоретического материала по выбранным темам.

2.2. Цели применения модулей.

Для одного потока студентов, в общей сложности необходимо сформировать примерно 1000 заданий по теме «Основы теории чисел». Поэтому преподаватель вынужден прилагать уйму усилий, чтобы подготовить проверочные материалы для студентов. В результате усталости и переутомления нередко возникают случаи, когда преподаватель при составлении или проверке заданий не замечает ошибки там, где они есть или наоборот, видит ошибку там, где ее нет, вследствие чего знания студентов могут быть оценены не правильно.

Модули автоматической генерации заданий и решений в первую очередь призваны облегчить труд преподавателя, путем снижения затрат времени и сил на подготовку и проверку заданий для самостоятельных и контрольных работ, что позволит дать максимально адекватную оценку знаниям, а так же выявить пробелы в знаниях студентов.

Применение модулей:

текущий контроль знаний;
обучение;
самопроверка.

Для итогового контроля знаний и для проверки остаточных знаний, безусловно, лучше подходит тестирование, но для текущего контроля знаний лучше подойдут контрольные работы, т.к. они позволяют преподавателю определить не только уровень знаний и оценку студента, но и причины неуспеваемости и пробелы в знаниях данного студента. Самостоятельное выполнение студентом заданий с последующей проверкой по готовому решению, полученному от преподавателя, подходит для самопроверки и обучения студентов. Таким образом, задания, в виде контрольных работ весьма полезны в обучении дисциплине «Теоретико-числовые методы в криптографии».

2.3. Способы применения модулей.

Текстовые проверочные работы.

В результате работы модуля формируются два текстовых файла. В одном файле записаны сгенерированные задания для студентов, а во втором достаточно подробное решение этих заданий. Таким образом, для проведения проверочной работы, преподавателю достаточно распечатать сгенерированные модулем файлы и раздать студентам распечатки с заданиями, а распечатки с решениями позволят преподавателю достаточно быстро и с меньшими усилиями проверить работы студентов и выявить ошибки и неточности в их решении.

Обучение

Выявленные пробелы в знаниях студентов во время проверочных работ, позволят преподавателю в дальнейшем ходе обучения сделать упор на те моменты, которые были плохо усвоены, чтобы восполнить пробелы в знаниях студентов. А также в процессе обучения гораздо легче усваивать новый материал, рассматривая его на наглядных примерах, которые с легкостью могут быть получены при помощи модулей генерации заданий и решений.

Самоконтроль.

Многие студенты хотят быть уверены в том, что они поняли тему и научились правильно решать задания или же просто хотят «набить руку» перед предстоящей контрольной работой. В этом им, безусловно, помогут готовые решения заданий, созданные модулями генерации заданий и решений.

2.4. Апробация.

В ходе проведения проверки модулей генерации заданий и решений по теме «Основы теории чисел» на корректность составления и правильность решения заданий было выявлено, что все сгенерированные задания и решения, предоставленные для проверки группе студентов 5 курса специальности «Компьютерная безопасность», составлены корректно и решены правильно.

После чего была сформирована база контрольных работ по предмету «Теоретико-числовые методы в криптографии», часть из которых была использована для проведения самостоятельной работы среди студентов 4 курса специальности «Компьютерная безопасность» в феврале 2010. А также некоторые из сформированных заданий были использованы для прорешивания на практических занятиях по предмету «Теоретико-числовые методы в криптографии» в феврале 2010 года.

2.5. Средства разработки модулей

В качестве средства разработки модулей генерации заданий и решений на тему «Основы теории чисел» был выбран объектно-ориентированный язык программирования – С#.

C# разработан в 1998—2001 годах группой инженеров под руководством Андерса Хейлсберга в компании Microsoft как основной язык разработки приложений для платформы Microsoft .NET. Компилятор C# входит в стандартную установку самой .NET, поэтому программы на нём можно создавать и компилировать даже без инструментальных средств, вроде Visual Studio.

C# относится к семье языков с C-подобным синтаксисом, из них его синтаксис наиболее близок к C++ и Java. Язык имеет статическую типизацию, поддерживает полиморфизм, перегрузку операторов (в том числе операторов явного и неявного приведения типа), делегаты, атрибуты, события, свойства, обобщённые типы и методы, итераторы, анонимные функции с поддержкой замыканий, LINQ, исключения, комментарии в формате XML.

Переняв многое от своих предшественников — языков C++, Java, Delphi, Модула и Smalltalk — С#, опираясь на практику их использования, исключает некоторые модели, зарекомендовавшие себя как проблематичные при разработке программных систем: так, C# не поддерживает множественное наследование классов (в отличие от C++).

Особенности языка

C# разрабатывался как язык программирования прикладного уровня для CLR (Common Language Runtime – «общеязыковая исполняющая среда») и, как таковой, зависит, прежде всего, от возможностей самой CLR. Это касается, прежде всего, системы типов C#, которая отражает FCL (Framework Class Library – стандартная библиотека классов платформы «.NET Framework»). Присутствие или отсутствие тех или иных выразительных особенностей языка диктуется тем, может ли конкретная языковая особенность быть транслирована в соответствующие конструкции CLR. Так, с развитием CLR от версии 1.1 к 2.0 значительно обогатился и сам C#; подобного взаимодействия следует ожидать и в дальнейшем. (Однако эта закономерность была нарушена с выходом C# 3.0, представляющим собой расширения языка, не опирающиеся на расширения платформы .NET.) CLR предоставляет C#, как и всем другим .NET-ориентированным языкам, многие возможности, которых лишены «классические» языки программирования. Например, сборка мусора не реализована в самом C#, а производится CLR для программ, написанных на C# точно так же, как это делается для программ на VB.NET, J# и др.

2.6. Документация

Для каждого модуля разработана подробная документация для пользователей. Описываются правила заполнения входных параметров программы, значения каждого параметра и его влияние на остальные параметры. Руководство пользователя приведено в Приложении 1.

Поскольку данный проект имеет перспективы на дальнейшее развитее, составлена документация для программиста, в которой описываются все параметры, переменные и функции, использующиеся в каждом модуле. Это облегчит работу для будущих программистов, которые будут заниматься разработкой дополнительных модулей на различные темы и дисциплины или усовершенствованием существующих модулей. Документация программиста приведена в Приложении 2.

2.7. Интеграция модулей в программный комплекс.

Основной целью данного проекта является разработка модулей в виде библиотек функций - DLL (Dynamic-link library – динамически подключаемая библиотека), подключаемых к программному комплексу. Это позволяет создавать полноценные контрольные работы, состоящие из различных тем, список которых определяется подключенными модулями. Вместе с этим каждый из модулей имеет возможность работать независимо от программного комплекса генерации контрольных работ.

Возможности модулей как независимых приложений:

Регулирование уровня сложности и количества генерируемых заданий путем изменения входных параметров.
Создание текстовых файлов c заданиями и решениями в указанном месте.

Возможности программного комплекса.

Подключение необходимых модулей к системе.
Работа со всеми модулями как с одним целым.
Регулирование уровня сложности и количества генерируемых заданий для каждого подключенного модуля.
Создание текстовых файлов, содержащих в себе задания и решения всех подключенных к системе модулей.

2.8. Модуль NOD.

На рисунке 1 представлен интерфейс модуля NOD.

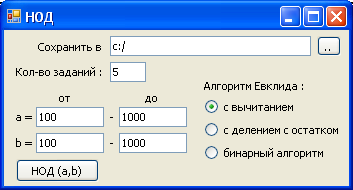
Рисунок 1. Интерфейс модуля NOD.

Данный модуль находит наибольший общий делитель двух чисел, используя при этом выбранный вариант алгоритма Евклида:

алгоритм с вычитанием;
алгоритм с делением с остатком;
бинарный алгоритм.

Задание генерируется путем выбора двух случайных чисел из указанных диапазонов для каждого из чисел. Решение генерируется в соответствии с выбранным алгоритмом. Файлы с заданием и решением генерируются в указанном месте.

Пример работы модуля NOD.

Установлены следующие входные параметры:

количество заданий – 2;
a = от 1 до 100;
b = от 1 до 100;
алгоритм Евклида – с делением с остатком.

Содержание сгенерированного файла с заданиями:

Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием деления с остатком, где:

а) a = 85, b = 9;

б) a = 97, b = 51.

Содержание сгенерированного файла с решениями:

Вычислить НОД(a,b) при помощи алгоритма Евклида с использованием деления с остатком, где:

а) a = 85, b = 9.

Решение:

a	85	9	4
b	9	4	1

85=9∙9+4

9=2∙4+1

4=4∙1+0

Ответ: НОД(85,9)=1.

б) a = 97, b = 51.

Решение:

a	97	51	46	5
b	51	46	5	1

97=1∙51+46

51=1∙46+5

46=9∙5+1

5=5∙1+0

Ответ: НОД(97,51)=1.

Установлены следующие входные параметры:

количество заданий – 2;
a = от 50 до 500;
b = от 100 до 200;
алгоритм Евклида – бинарный алгоритм.

Содержание сгенерированного файла с заданиями:

Вычислить НОД(a,b) при помощи бинарного алгоритма Евклида, где:

а) a = 297, b = 114;

б) a = 63, b = 134.

Содержание сгенерированного файла с решениями:

Вычислить НОД(a,b) при помощи бинарного алгоритма Евклида, где:

а) a = 297, b = 114.

Решение:

297=2⁰∙297, k₁=0; 114=2¹∙57, k₂=1.

=> k=min(k₁,k₂)=0, a₁=max(297,57)=297, b₁=min(297,57)=57.

c=297-57=240=2⁴∙15, c₁=15, a₁=max(b₁,c₁)=57, b₁=min(b₁,c₁)=15.

c=57-15=42=2¹∙21, c₁=21, a₁=21, b₁=15.

c=21-15=6=2¹∙3, c₁=3, a₁=15, b₁=3.

c=15-3=12=2²∙3, c₁=3, a₁=3, b₁=3.

Ответ: НОД(297,114)=2^k∙b₁=2⁰∙3=3.

б) a = 63, b = 134.

Решение:

63=2⁰∙63, k₁=0; 134=2¹∙67, k₂=1.

=> k=min(k₁,k₂)=0, a₁=max(67,63)=67, b₁=min(67,63)=63.

c=67-63=4=2²∙1, c₁=1, a₁=max(b₁,c₁)=63, b₁=min(b₁,c₁)=1.

c=63-1=62=2¹∙31, c₁=31, a₁=31, b₁=1.

c=31-1=30=2¹∙15, c₁=15, a₁=15, b₁=1.

c=15-1=14=2¹∙7, c₁=7, a₁=7, b₁=1.

c=7-1=6=2¹∙3, c₁=3, a₁=3, b₁=1.

c=3-1=2=2¹∙1, c₁=1, a₁=1, b₁=1.

Ответ: НОД(63,134)=2^k∙b₁=2⁰∙1=1.

2.9. Модуль Asimp.

На рисунке 2 представлен интерфейс модуля ASIMP.

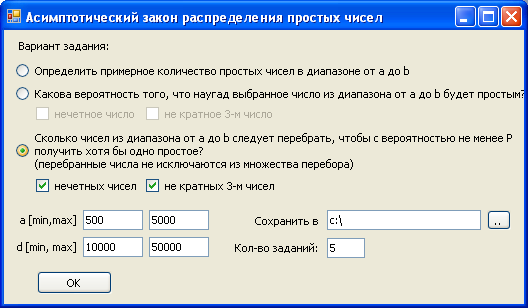
Рисунок 2. Интерфейс модуля ASIMP.

Данный модуль выполняет три варианта заданий, основанных на асимптотическом законе распределения простых чисел:

вычисляет примерное количество простых чисел в заданном диапазоне;
вычисляет вероятность того, что наугад выбранное число из указанного диапазона будет простым; при этом есть возможность задать ограничение на выбираемое наугад число:
- выбирается только нечетное число;
- выбирается только не кратное 3-м число;
- выбирается нечетное и некратное 3-м число;
- выбирается любое число из заданного диапазона;
вычисляет, сколько чисел из заданного диапазона следует перебрать, чтобы с определенной вероятностью получить хотя бы одно простое; при этом есть возможность задать ограничение на перебираемые числа:
- выбираются только нечетные числа;
- выбираются только не кратные 3-м числа;
- выбираются нечетные и некратные 3-м числа;
- выбираются любые числа из заданного диапазона.

На основе введенных входных параметров программы генерируются файлы с заданиями и решениями этих заданий.

Пример работы модуля ASIMP.

Установлены следующие входные параметры:

вариант задания – вычисляет, сколько чисел из заданного диапазона следует перебрать, чтобы с определенной вероятностью получить хотя бы одно простое
- выбираются нечетные и некратные 3-м числа;
a = от 500 до 5000;
d = от 10000 до 50000;
количество заданий – 2.

Содержание сгенерированного файла с заданиями:

Сколько нечетных и не кратных 3-м чисел из диапазона от a до b следует перебрать, чтобы с вероятностью не менее p получить хотя бы одно простое? (перебранные числа не исключаются из множества перебора).

а) a = 2700, b = 40000, p = 0,8;

б) a = 1300, b = 50000, p = 0,95.

Содержание сгенерированного файла с решениями:

Сколько нечетных и не кратных 3-м чисел из диапазона от a до b следует перебрать, чтобы с вероятностью не менее p получить хотя бы одно простое? (перебранные числа не исключаются из множества перебора).

а) a = 2700, b = 40000, p = 0,8.

Решение:

Примерное количество простых чисел в диапазоне от 2700 до 40000 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 3433,05.

Количество чисел, больших 2700 и меньших 40000, есть 37300. Доля нечетных и не кратных 3-м чисел есть 1/3. Тогда всего перебирается чисел 12433,33. Вероятность случайного выбора простого числа есть

P = 3433,05 / 12433,33 ≈ 0,28.

Вероятность достичь успеха хотя бы в одном из n испытаний есть 1-(1-P)ⁿ ≥ p. Тогда n ≥ log_(1-P)(1-p), т.е n ≥ ln(1-p) / ln(1-P) ≥ 4,98 => n=5.

Ответ: требуется 5 испытаний.

б) a = 1300, b = 50000, p = 0,95.

Решение:

Примерное количество простых чисел в диапазоне от 1300 до 50000 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 4439,86.

Количество чисел, больших 1300 и меньших 50000, есть 48700. Доля нечетных и не кратных 3-м чисел есть 1/3. Тогда всего перебирается чисел 16233,33. Вероятность случайного выбора простого числа есть

P = 4439,86 / 16233,33 ≈ 0,27.

Вероятность достичь успеха хотя бы в одном из n испытаний есть 1-(1-P)ⁿ ≥ p. Тогда n ≥ log_(1-P)(1-p), т.е n ≥ ln(1-p) / ln(1-P) ≥ 9,38 => n=10.

Ответ: требуется 10 испытаний.

Установлены следующие входные параметры:

вариант задания – вычисляет примерное количество простых чисел в заданном диапазоне;

a = от 100 до 1000;
d = от 5000 до 10000;
количество заданий – 2.

Содержание сгенерированного файла с заданиями:

Определить примерное количество простых чисел в диапазоне от a до b, где:

а) a = 300, b = 8700;

б) a = 750, b = 6300.

Содержание сгенерированного файла с решениями:

Определить примерное количество простых чисел в диапазоне от a до b, где:

а) a = 300, b = 8700.

Решение:

Примерное количество простых чисел в диапазоне от 300 до 8700 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 906,5.

Ответ: K ≈ 906,5.

б) a = 750, b = 6300.

Решение:

Примерное количество простых чисел в диапазоне от 750 до 6300 есть

K = π(b) - π(a) = b/ln(b) - a/ln(a) ≈ 606,85.

Ответ: K ≈ 606,85.

2.10. Модуль Eiler.

На рисунке 3 представлен интерфейс модуля EILER.

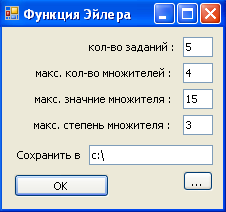
Рисунок 3. Интерфейс модуля EILER.

Данный модуль вычисляет функцию Эйлера числа, которое генерируется на основе введенных параметров и сохраняет в указанном месте файлы с заданиями и решениями. При генерации задания, модуль генерирует каноническое разложение числа на основе введенных параметров, которое затем используется и для решения.

Задания генерируются по следующей формуле:

n = p₁^a¹ p₂^a² … p_k^a^k

где p – это простое число, значение которого генерируется случайным образом из диапазона простых чисел от 2 до значения указанного в параметре макс. значение множителя; a – степень множителя, значение которой генерируется случайным образом из диапазона чисел от 1 до значения заданного в параметре макс. степень множителя; k – это количество множителей, значение этого параметра принимает случайное число из диапазона чисел от 1 до значения указанного в параметре макс. количество множителей.

Пример работы модуля EILER.

Установлены следующие входные параметры:

кол-во заданий – 2;
макс. кол-во множителей – 4;
макс. значение множителя – 15;
макс. степень множителя – 3.

Содержание сгенерированного файла с заданиями:

Вычислить функцию φ(n).

а) n=25350;

б) n=7700;

Содержание сгенерированного файла с решениями:

Вычислить функцию φ(n).

а) n=25350.

Решение:

n=2∙3∙5²∙13².

φ(n)=1∙2∙5∙4∙13∙12 = 6240.

Ответ: φ(25350) = 6240.

б) n=7700.

Решение:

n=2²∙5²∙7∙11.

φ(n)=2∙5∙4∙6∙10 = 2400.

Ответ: φ(7700) = 2400.

Blog

Мозжевилов Максим Александрович Разработка модулей генерации заданий и решений по теме «Основы теории чисел» диплом

2. Практическая часть.