Geum.ru

Комп’ютерне моделювання фізичних процесів Для студентів ІV курсу спеціальності 070100 Фізика Суми-2009р

Вид материалаДокументы

Содержание


Структура програми
Аудиторних занять
Самостійна робота
Структура залікового кредиту курсу
Теми практичних занять
Розподіл балів, що присвоюються студентам
Зміст самостійної роботи
Теоретичні питання до заліку
Орієнтовні теми курсових робіт
Перелік літератури, рекомендованої для вивчення курсу
Подобный материал:

Міністерство освіти і науки України

Сумський державний педагогічний університет

імені А.С.Макаренка


Методичні матеріали

щодо кредитно-модульної системи

організації навчального процесу зі спеціального курсу

«Комп’ютерне моделювання фізичних процесів»

Для студентів ІV курсу спеціальності

6.070100 Фізика


Суми-2009р.

УДК 519.61, 519.62, 519.63, 519.65, 519.688


Методичні матеріали щодо кредитно-модульної системи організації навчального процесу зі спеціального курсу «Комп’ютерне моделювання фізичних процесів» для студентів ІV курсу спеціальності 6.070100-Фізика/ Уклад.: Пономарьов О.Г. – Вид. центр СумДПУ імені А.С.Макаренка, 2009. - 12 с.


Укладач: Пономарьов ОГ. – кандидат фізико-математичних наук, доцент кафедри експериментальної і теоретичної фізики СумДПУ імені А.С.Макаренка;


Затверджено вченою радою фізико-математичного факультету СумДПУ імені А.С.Макаренка

Протокол №__________від_______________2009р.

СТРУКТУРА ПРОГРАМИ

НАВЧАЛЬНОЇ ДИСЦИПЛІНИ

«КОМП’ЮТЕРНЕ МОДЕЛЮВАННЯ ФІЗИЧНИХ ПРОЦЕСІВ»


І. Опис предмета навчальної дисципліни

Предмет: комп’ютерне моделювання фізичних процесів


Курс 4

Підготовка бакалаврів
Напрям, спеціальність, освітньо-кваліфікаційний рівень
Характеристика навчальної дисципліни

Кількість кредитів, відповідних ECTS: 4,5


Змістових модулів: 3


Загальна кількість годин: 162


Тижневих годин:

4 (ІІ семестр)
Шифр та назва напрямку: 0701 – Фізика


Шифр та назва спеціальності:

6.070100 – Фізика


Освітньо-кваліфікаційний рівень: бакалавр

За вибором студента


Рік підготовки: 4


Семестри: 8


Лекції (теоретична підготовка): 36 годин


Практичні: 30 годин


Індивідуальні: 6 годин


Самостійна робота: 90 години


Вид підсумкового контролю:

ІІ семестр – залік


Мета: Метою та завданням навчального курсу є: вивчення теоретичних основ обчислювальної математики, чисельних методів рішення як звичайних диференційних рівнянь так і рівнянь в частинних похідних, отримання навиків програмування цих завдань на ПОК, навчитися фізичний процес адекватно зображати в вигляді математичної моделі, отримати її рішення та аналізувати результати.


У результаті вивчення дисципліни студенти повинні:

знати:
  • методи інтерполяції і апроксимації функції;
  • методи чисельного інтегрування та диференціювання функції;
  • чисельні методи рішення систем лінійних алгебраїчних рівнянь;
  • чисельні методи рішення нелінійних рівнянь і задач оптимізації;
  • чисельні методи рішення звичайних диференційних рівнянь;
  • чисельні методи рішення задач математичної фізики.


вміти:
  • аналізувати літературу з проблем чисельного моделювання фізичних процесів;
  • моделювати фізичні процеси за допомогою математичних моделей;
  • застосовувати чисельні методи рішення отриманих математичних зображень фізичного процесу;
  • розробляти алгоритм чисельного рішення;
  • програмувати розроблений алгоритм.


ВСТУП

Дана програма визначає об’єм знань студента зі спеціального курсу комп’ютерного моделювання фізичних процесів, яки є необхідними для проведення розрахунків складних систем і процесів, яки описуються диференційними рівняннями. Курс комп’ютерного моделювання фізичних процесів розширює знання в області дискретної математики, дає навики опису складних фізичних процесів за допомогою математичного апарату, складання алгоритму вирішення завдання, та переклад алгоритму на одну з мов програмування, отримання результатів за допомогою комп’ютера та проведення їх аналізу.

Програма курсу розрахована на ІІ семестр четвертого року навчання студентів спеціальності «Фізика» та забезпечуються такою кількістю годин:





ІІ семестр, годин
Всього

Аудиторних занять
66
66

Лекцій
36
36

Практичних занять
30
30

Індивідуальних занять
6
6

Самостійна робота
90
90

Всього
162
162

Форма семестрового контролю
залік




ІІ СЕМЕСТР


Змістовий модуль І

Елементи дискретного аналізу


Тема 1.1. Інтерполяція і наближення функцій.

Зміст. Постановка задачі наближення функцій. Інтерполяційний многочлен Лагранжа. Інтерполяційна формула Ньютона. Інтерполяція зі згладжуванням. Метод найменших квадратів. Інтерполяція функцій однієї змінної за допомогою кубічного сплайна. Інтерполяція фінітними функціями з компактним носієм. В-сплайни. Кусково-кубічна інтерполяція зі згладжуванням.


Тема 1.2. Методи чисельного інтегрування і диференціювання функцій.

Зміст. Чисельне диференціювання функцій. Питання пов’язані з чисельним диференціюванням функцій. Чисельне диференціювання за допомогою формули Ньютона. Застосування формули Грегорі-Ньютона. Застосування формули Стірлінга. Чисельне інтегрування функцій. Методи трапецій і Сімпсона. Квадратурні формули Гауса. Інтегрування засноване на інтерполяції функцій.


Змістовий модуль ІІ

Чисельні методи рішення систем рівнянь.


Тема 2.1. Чисельні методи рішення систем лінійних алгебраїчних рівнянь.

Зміст. Прями методі рішення систем алгебраїчних рівнянь. Рішення систем лінійних рівнянь по формулам Крамера. Рішення систем лінійних рівнянь по схемі Гауса. Рішення систем лінійних рівнянь з застосуванням LU-розкладу матриці рівняння. Оцінка достовірності отриманого рішення прямими методами. Процедура ітераційного уточнення рішення. Ітераційні методі рішення систем алгебраїчних рівнянь. Ітераційний процес Якобі (проста ітерація). Принцип побудови ітераційних процесів. Метод Зейделя. Метод верхньої релаксації.

Тема 2.2. Чисельні методи рішення нелінійних рівнянь і задач оптимізації.

Зміст. Методи знаходження нулів нелінійних рівнянь. Нелінійні алгебраїчні рівняння описуючи фізичні процеси. Принцип побудови одно-крокових ітераційних процесів. Метод поділу відрізку надвоє. Метод січної. Метод Ньютона. Метод простої ітерації. Находження комплексних коренів. Чисельні методи задач оптимізації. Питання пов’язані з задачами оптимізації. Градієнтні методи.


Тема 2.3. Чисельні методи рішення звичайних диференційних рівнянь.

Зміст. Чисельні методи рішення задач Коші. Розклад рішення в ряд Тейлора. Методи Рунге-Кутта. Методи з контролем похибки на крокі. Інтегрування систем рівнянь. Дослідження властивостей скінчено-різносних методів на модельних задачах. Чисельні методи рішення крайових задач для звичайних диференційних рівнянь. Найпростіші методи рішення крайової задачі. Рішення крайової сіткової задачі. Постановка крайових задач для лінійних систем. Алгоритми рішення крайових задач для систем першого порядку. Методи диференційної ортогональної прогонки. Оцінка похибки чисельних методів рішення звичайних диференційних рівнянь. Дослідження властивостей скінчено-різносних методів на модельних задачах. Оцінка похибки одно-крокових методів. Оцінка похибки при рішенні крайової задачі методом прогонки.


Змістовий модуль ІІІ

Чисельні методи розв’язання задач моделювання фізичних процесів.


Тема 3.1. Загальні відомості теорії скінченно-різносних схем.

Зміст. Апроксимація. Явна та неявна апроксимація. Рахункова стійкість. Абсолютна та умовна стійкість. Теорема збіжності. Скінченно-різносні аналоги деяких задач математичної фізики. Задачі Діріхле та Неймана для двомірного рівняння Пуасона. Проблема граничних умов. Різницеві схеми для рівнянь теплопровідності та коливань. Схема Кранка-Ніколсона.


Тема 3.2. Моделювання задач електростатики.

Зміст. Інтегральний метод теорії потенціалів. Формула Гріна. Інтегральне зображення диференційної крайової задачі. Фундаментальне рішення для двохвимірного рівняння Лапласа в Декартових і циліндричних координатах. Задача простого слою. Чисельне представлення інтегрального рівняння простого слою. Метод колокації. Апроксимація поверхневої густини зарядів В-сплайнами. Чисельне диференціювання потенціалу.


Тема 3.3. Моделювання задач руху заряджених часток в електромагнітних полях.

Зміст. Завдання початкових даних для заряджених часток. Регулярний та випадковий розподіл часток в початковому фазовому просторі. Емітуюча поверхня. Урахування просторового заряду. Числова схема розрахунку руху заряджених часток в обчислених полях.


Структура залікового кредиту курсу


№
Тема
Кількість годин, відведених на

лекції
прак
тичні
індивід. Заняття
самост.

роботу
Вид контролю

І
Змістовий модуль І. Елементи дискретного аналізу
8
6
2
20



1.1.
Інтерполяція і наближення функцій.
4
3



12
залік

1.2.
Методи чисельного інтегрування і диференціювання функцій.
4
3



8
залік

ІІ
Змістовий модуль ІІ. Чисельні методи рішення систем рівнянь.
12
12
2
34



2.1.
Чисельні методи рішення систем лінійних алгебраїчних рівнянь.
4
4



8
залік

2.2.
Чисельні методи рішення нелінійних рівнянь і задач оптимізації.
4
4



10
залік

2.3.
Чисельні методи рішення звичайних диференційних рівнянь.
4
4



16
залік

ІІІ
Змістовий модуль ІІІ. Чисельні методи розв’язання задач моделювання фізичних процесів.
16
12
2
36



3.1.
Загальні відомості теорії скінченно-різносних схем.
4
4



16
залік

3.2.
Моделювання задач електростатики.
6
4



10
с/р

3.3.
Моделювання задач руху заряджених часток в електромагнітних полях.
6
4



10
с/р

Усього
36
30
6
90





ТЕМИ ПРАКТИЧНИХ ЗАНЯТЬ


Модуль

№
Тема
Год.
Прим.

Змістовий модуль І.
1
Розробка алгоритму для комп’ютерної програми інтерполяції довільної табульованої функції за допомогою многочлену Лагранжа.
2



2
Розробка алгоритму чисельного інтегрування функцій методами трапецій, Сімпсона та квадратурними формулами Гауса.
2



Змістовий модуль ІІ.
3
Розробка алгоритму для комп’ютерної програми рішення систем лінійних рівнянь по схемі Гауса.
2



4
Розробка алгоритму для комп’ютерної програми ітераційного рішення систем алгебраїчних рівнянь методом Зейделя.
2



5
Розробка алгоритму для комп’ютерної програми знаходження нулів нелінійних рівнянь методами Ньютона та простої ітерації для задовільної функції.
2



6
Розробка алгоритму для комп’ютерної програми розрахунку задовільної задачі Коші.
2



7
Розробка алгоритму для комп’ютерної програми розрахунку задовільної крайової задачі методом прогонки.
2



Змістовий модуль ІІІ.
8
Розробка алгоритму для комп’ютерної програми для отримання рішення рівняння теплопровідності за допомогою різницевих схем.
2



9
Розробка алгоритму для комп’ютерної програми для отримання рішення рівняння коливань за допомогою різницевих схем.
2



10
Ознайомлення з програмою розрахунку електростатичних полів LAPLAS-2.
6



11
Ознайомлення з програмою моделювання задач руху заряджених часток в електромагнітних полях.

6





Розподіл балів, що присвоюються студентам:
Відвідув. лекцій
Відвідув. практичних
Відповіді
Заліки
Всього

ЗМ І.
3
4
2
20
29

ЗМ ІІ.
4
8
3
30
45

ЗМ ІІІ.
5
8
3
10
26

Усього
12
20
8
60
100



ЗМІСТ САМОСТІЙНОЇ РОБОТИ


Тема 1: Інтерполяція і наближення функцій. (12 год.)


Завдання для самостійної роботи:
  1. Розробити програму інтерполяції довільної табульованої функції за допомогою многочлену Лагранжа.
  2. Провести табулювання функції (вираз функції задано в індивідуальному завданні). За допомогою розроблених програм зобразити інтерполяційні функції с застосуванням однієї з графічних програм (ORIGIN).

Методичні рекомендації:
  1. Застосувати алгоритм розроблений на практичних заняттях.
  2. Провести табулювання інтерполяційних функцій.

Література:
  1. Н.С. Бахвалов Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). – М.: Наука, 1973, 632с.
  2. И.Н. Молчанов Машинные методы решения прикладних задач. Алгебра, приближение функций. – Киев: Наукова думка, 1987, 288с.
  3. Г.И. Марчук Методы вычислительной математики. – М.: Наука, 1989, 608с.
  4. Ильин В.П. Численные методы решения задач электрофизики. -М.:Наука, 1985. - 202c.


Тема 2: Методи чисельного інтегрування і диференціювання функцій. ( 8 год.)


Завдання для самостійної роботи:
  1. Розробити програми інтегрування функцій методоми трапецій та Сімпсона.
  2. За допомогою розроблених програм провести чисельне інтегрування функції (вираз функції задано в індивідуальному завданні). Провести порівняльний аналіз з точним значенням інтегралу для кожного числового метода.

Методичні рекомендації:
  1. Застосувати алгоритми розроблені на практичних заняттях.
  2. Провести попереднє табулювання функцій.

Література:
  1. Бахвалов Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). – М.: Наука, 1973, 632с.
  2. Молчанов Машинные методы решения прикладних задач. Алгебра, приближение функций. – Киев: Наукова думка, 1987, 288с.
  3. Г.Н.Воробьева, А.Н.Данилова Практикум по вычислительной математике. – М.: Высшая школа, 1990, 208с.


Тема 3: Чисельні методи рішення систем лінійних алгебраїчних рівнянь. ( 16 год.)


Завдання для самостійної роботи:
  1. Розробити комп’ютеру програму та провести рішення системи лінійних рівнянь заданих в індивідуальному завданні методом Гауса.
  2. Розробити комп’ютеру програму та провести рішення системи лінійних рівнянь заданих в індивідуальному завданні методом Зейделя.
  3. Провести порівняльний аналіз точності рішення системи лінійних рівнянь запропонованими методами на підставі нев’язкі рішення.

Методичні рекомендації:
  1. Застосувати алгоритми програм розроблені на практичних заняттях.
  2. Нев’язка рішення 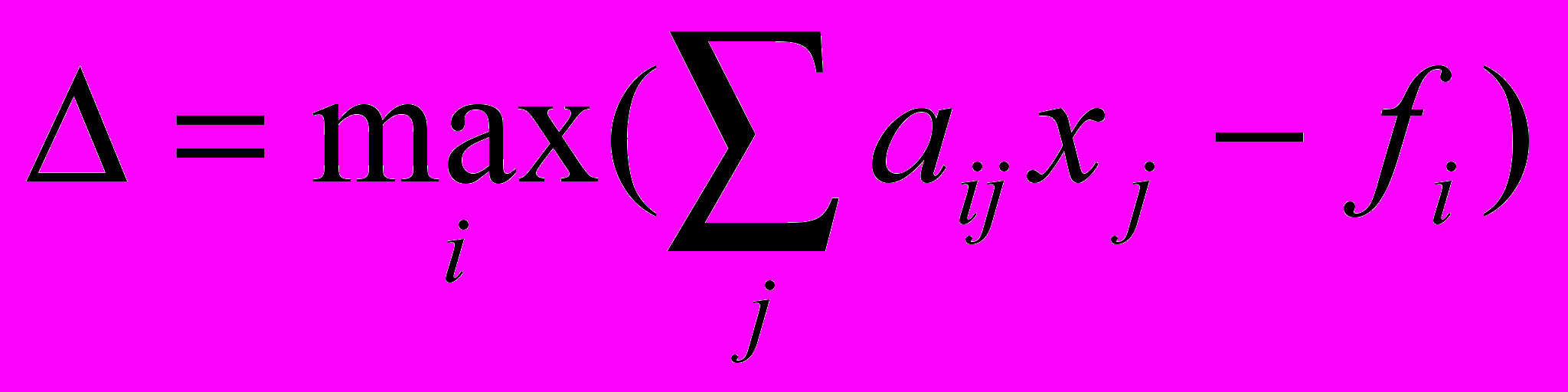, де xj – чисельне рішення

Література:
  1. Бахвалов Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). – М.: Наука, 1973, 632с.
  2. Молчанов Машинные методы решения прикладних задач. Алгебра, приближение функций. – Киев: Наукова думка, 1987, 288с.
  3. Г.Н.Воробьева, А.Н.Данилова Практикум по вычислительной математике. – М.: Высшая школа, 1990, 208с.


Тема 4: Чисельні методи рішення нелінійних рівнянь і задач оптимізації. ( 12 год.)


Завдання для самостійної роботи:
  1. Розробити комп’ютеру програму та знайти нулі нелінійних рівнянь заданих в індивідуальному завданні методом Ньютона.

Методичні рекомендації:

1. Застосувати результати практичних занять.

Література:
  1. Бахвалов Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). – М.: Наука, 1973, 632с.
  2. Молчанов Машинные методы решения прикладних задач. Алгебра, приближение функций. – Киев: Наукова думка, 1987, 288с.
  3. Г.Н.Воробьева, А.Н.Данилова Практикум по вычислительной математике. – М.: Высшая школа, 1990, 208с.


Тема 5: Чисельні методи рішення звичайних диференційних рівнянь. ( 18 год.)


Завдання для самостійної роботи:
  1. Вирішити задачу руху пучка протонів з енергії 1Мев і відносним розкидом по енергії 10-3 в магнітної квадрупольної лінзі. Скалярний магнітний потенціал має вигляд 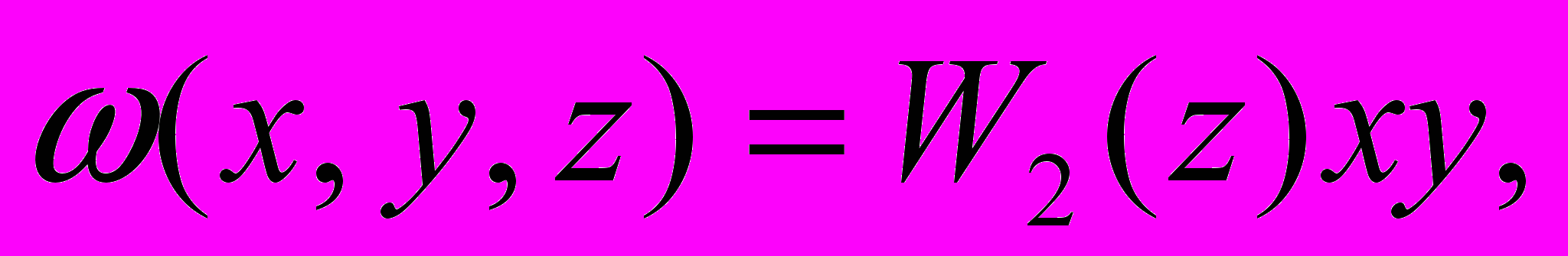де 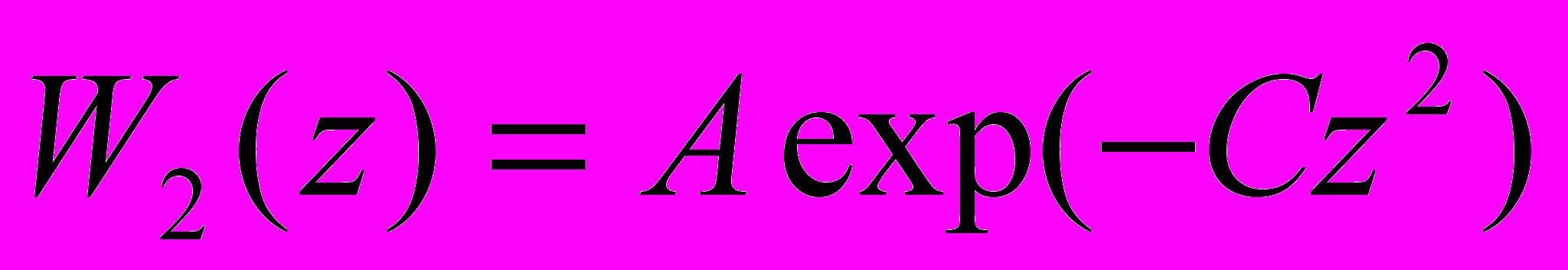. Пучок колімується за допомогою двох круглих коліматорів об’єктного з радіусом r і кутового з радіусом R. Коліматори розташовані на відстані D. Відстань від об’єктного коліматора до центра лінзи L (L>> D), -L
  2. Знайти рішення крайової задачі для звичайного диференційного рівняння методом прогонки. Робота 7, завдання 1-12, стор. 159, [3].

Методичні рекомендації:
  1. Траєкторні рівняння руху пучка в стаціонарному магнітному полі мають вигляд

,

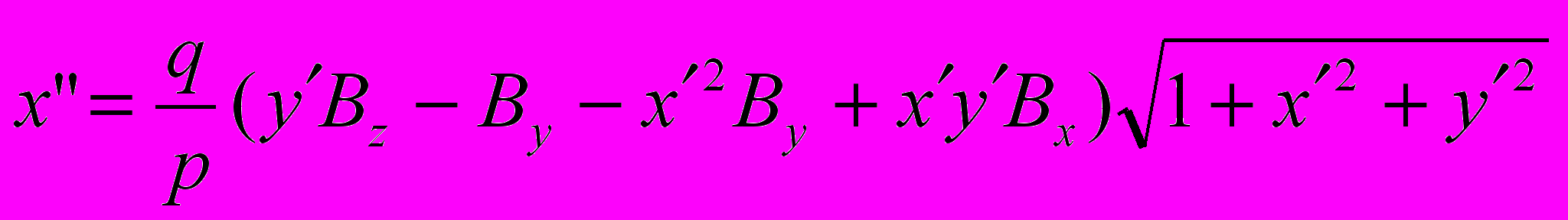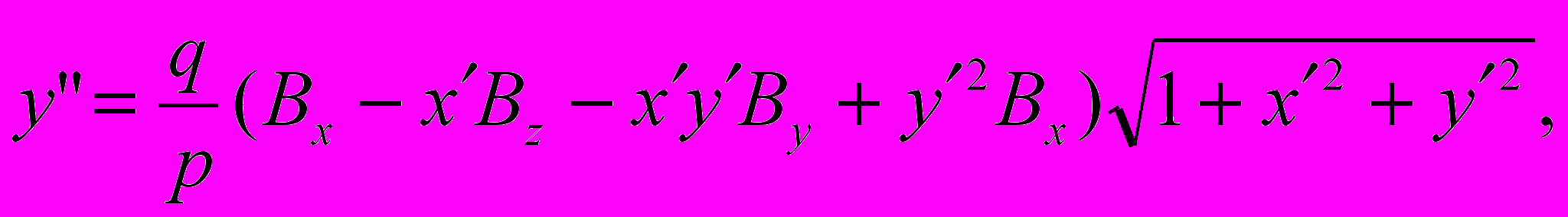де q,p заряд та імпульс частинки, Вx(y,z) складові вектора магнітної індукції.

Література:
  1. Бахвалов Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). – М.: Наука, 1973, 632с.
  2. Молчанов Машинные методы решения прикладних задач. Алгебра, приближение функций. – Киев: Наукова думка, 1987, 288с.
  3. Г.Н.Воробьева, А.Н.Данилова Практикум по вычислительной математике. – М.: Высшая школа, 1990, 208с.


Тема 6: Чисельні методи рішення задач моделювання фізичних процесів. ( 26 год.)


Завдання для самостійної роботи:
  1. Розробити програму розрахунку диференційних рівнянь з крайовими умовами для рівнянь коливань. Вираз рівняння і крайові умови задано в індивідуальному завданні. Коливання струни представити в графічному вигляді за допомогою одної з графічних програм (ORIGIN).
  2. Розробити програму розрахунку диференційних рівнянь з крайовими умовами для рівнянь теплопровідності. Вираз рівняння і крайові умови задано в індивідуальному завданні. Розповсюдження теплового потоку представити в графічному вигляді за допомогою одної з графічних програм (ORIGIN).
  3. Підготувати початкові дані для оптичної схеми електронної гармати.
  4. Провести розрахунок розподілу потенціалу і його чотирьох похідних вздовж оптичної вісі електронної гармати с застосуванням розрахункової програми LAPLAS-2.
  5. Підготувати попередні дані фазового простору електронів з емітуючої поверхні.
  6. Провести розрахунок руху пучка в електронної гармати з урахуванням просторового заряду за допомогою розрахункової програми EGUN.

Методичні рекомендації:

1. Застосувати алгоритми та програми, з якими було ознайомлено на практичних заняттях.

Література:
  1. Г.И. Марчук Методы вычислительной математики. – М.: Наука, 1989, 608с.
  2. Г.Н.Воробьева, А.Н.Данилова Практикум по вычислительной математике. – М.: Высшая школа, 1990, 208с.
  3. Курбатов П.А., Аринчин С.А. Численный расчет электромагнитных полей. -М.:Энергоатомиздат,1984. - 168c.
  4. Ильин В.П. Численные методы решения задач электрофизики. -М.:Наука, 1985. - 202c.


Даною програмою передбачається виконання 6-х заліків.


Методи навчання: лекції, розробка алгоритмів, розробка комп’ютерних програм, проведення розрахунків.


ТЕОРЕТИЧНІ ПИТАННЯ ДО ЗАЛІКУ

  1. Інтерполяційний многочлен Лагранжа.
  2. Інтерполяційна формула Ньютона.
  3. Інтерполяція зі згладжуванням. Метод найменших квадратів.
  4. Інтерполяція функцій однієї змінної за допомогою кубічного сплайна.
  5. Чисельне диференціювання функцій с застосуванням формули Стірлінга.
  6. Чисельне інтегрування функцій методами трапецій і Сімпсона.
  7. Чисельне інтегрування функцій квадратурними формулами Гауса.
  8. Рішення систем лінійних рівнянь по схемі Гауса.
  9. Оцінка достовірності отриманого рішення прямими методами. Процедура ітераційного уточнення рішення.
  10. Рішення систем алгебраїчних рівнянь с застосуванням ітераційного процесу Якобі (проста ітерація).
  11. Рішення систем алгебраїчних рівнянь с застосуванням ітераційного процесу Зейделя.
  12. Знаходження нулів нелінійних рівнянь методом поділу відрізку надвоє.
  13. Знаходження нулів нелінійних рівнянь методом Ньютона.
  14. Находження комплексних коренів.
  15. Чисельні методи рішення задач Коші. Методи Рунге-Кутта.
  16. Чисельні методи рішення задач Коші. Методи з контролем похибки на крокі.
  17. Чисельні методи рішення крайових задач для звичайних диференційних рівнянь. Рішення крайової сіткової задачі Діріхле.
  18. Чисельні методи рішення крайових задач для звичайних диференційних рівнянь. Рішення крайової сіткової задачі Неймана.
  19. Загальні сведення теорії скінченно-різносних схем. Апроксимація. Рахункова стійкість. Теорема збіжності.
  20. Різницева схема для рівняння теплопровідності.
  21. Різницева схема для рівняння коливань.
  22. Схема Кранка-Ніколсона.
  23. Інтегральний метод теорії потенціалів. Формула Гріна. Інтегральне зображення диференційної крайової задачі.
  24. Фундаментальне рішення для двохвимірного рівняння Лапласа в Декартових і циліндричних координатах. Задача простого слою.
  25. Моделювання задач електростатики. Чисельне представлення інтегрального рівняння простого слою. Метод колокації. Апроксимація поверхневої густини зарядів В-сплайнами.


ОРІЄНТОВНІ ТЕМИ КУРСОВИХ РОБІТ
  1. Моделювання розподілу електростатичного поля в прискорюючой структурі з аксіальною симетрією.
  2. Моделювання електростатичного поля в квадрупольної лінзі з порушеннями квадрупольної симетрії .
  3. Моделювання процесу зондоформування іонного пучка в ядерному скануючому мікрозонді.
  4. Моделювання руху пучка іонів в системі транспортування аналітичного прискорюючого комплексу.



ПЕРЕЛІК ЛІТЕРАТУРИ, РЕКОМЕНДОВАНОЇ ДЛЯ ВИВЧЕННЯ КУРСУ

„Комп’ютерне моделювання фізичних процесів”


№

п/п
Література
Кількість екземплярів

(у бібліотеці)

1
2
3





Основна література



1.
Н.С. Бахвалов Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). – М.: Наука, 1973, 632с.
Електронний носій

2.
Г.И. Марчук Методы вычислительной математики. – М.: Наука, 1989, 608с.
Електронний носій

4.
Курбатов П.А., Аринчин С.А. Численный расчет электромагнитных полей.

-М.:Энергоатомиздат,1984. - 168c.
Електронний носії

5.
Ильин В.П. Численные методы решения задач электрофизики. -М.:Наука, 1985. - 202c.
Електронний носій





Допоміжна література



1.
И.Н. Молчанов Машинные методы решения прикладних задач. Алгебра, приближение функций. – Киев: Наукова думка, 1987, 288с.
Електронний носій

2.
Васильев Ф.П. Лекции по методам решения экстремальных задач. Изд-во Московского университета, 1974. - 376с.
Електронний носій