Робоча навчальна програма для студентів спеціальності 070201 «Радіофізика І електроніка» Затверджено

Вид материала

Документы

Содержание Завдання для самостійної роботи Рекомендована література Семінари № 1,2. Рівняння дифузії Рекомендована література Завдання для самостійної роботи Завдання для самостійної роботи Завдання для самостійної роботи Модульна контрольна робота № 4 (2 год). Завдання для самостійної роботи Семінар № 7. Сферичні функції Завдання для самостійної роботи Семінар № 8. Циліндричні функції Рекомендована література Завдання для самостійної роботи Завдання для самостійної роботи Лекція № 11. Фундаментальний розв'язок рівняння дифузії Завдання для самостійної роботи Завдання для самостійної роботи Рекомендована література Модульна контрольна робота № 6 (2 год). ... Полное содержание

Подобный материал:

• Робоча навчальна програма для студентів спеціальності 070201 «Радіофізика І електроніка», 386.16kb.
• Робоча навчальна програма для студентів спеціальності 070201 «Радіофізика І електроніка», 429.28kb.
• Робоча навчальна програма для студентів спеціальності 070201 «Радіофізика І електроніка», 157.66kb.
• Робоча навчальна програма для студентів спеціальності 070201 «Радіофізика І електроніка», 396.61kb.
• Робоча навчальна програма для студентів спеціальності 070201 «Радіофізика І електроніка», 273.51kb.
• Робоча навчальна програма для студентів спеціальності 070201 "радіофізика І електроніка", 339.63kb.
• Робоча навчальна програма для студентів спеціальності 070201, 236.33kb.
• Робоча навчальна програма для студентів спеціальності 07201 ­­- радіофізика І електроніка, 246.07kb.
• Робоча програма навчальної дисципліни Програмування та математичне моделювання Для, 240.3kb.
• Робоча навчальна програма для студентів спеціальності 070204 прикладна фізика Затверджена, 219.58kb.

Тема № 1. «Класифікація рівнянь матфізики»


Лекція № 1. Класифікація рівнянь матфізики (1 год).

Основнi роздiли фiзики, закони яких виражаються у виглядi рiвнянь з частинними похiдними. Основні поняття теорії диференціальних рівнянь з частинними похідними.


Завдання для самостійної роботи (8 год).

Вивчення матеріалів лекції, вивчення класифiкацiї та канонiчного вигляду лiнiйних диференцiальних рiвнянь з частинними похiдними другого порядку за рекомендованою літературою.


Рекомендована література: [6,7,18,23].


Тема № 2. «Рівняння дифузії»


Лекція № 2. Рівняння дифузії (1 год).

Метод вiдокремлення змiнних для лiнiйних диференцiальних рiвнянь з частинними похiдними. Розв'язання рiвняння дифузiї на вiдрiзку методом вiдокремлення змiнних.


Семінари № 1,2. Рівняння дифузії (3 год).

Розв'язання рiвняння дифузiї на вiдрiзку методом вiдокремлення змiнних.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [6,7,18,23].


Тема № 3. «Хвильове рівняння»


Лекція № 3. Хвильове рівняння (1 год).

Розв'язання хвильового рівняння на вiдрiзку методом вiдокремлення змiнних.


Семінар № 3. Хвильове рівняння (2 год).

Розв'язання хвильового рiвняння на вiдрiзку методом вiдокремлення змiнних.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [6,7,18,23].


Тема № 4. «Рівняння Лапласа»


Лекція № 4. Рівняння Лапласа (1 год).

Розв'язання рiвнянь Лапласа в прямокутнику та крузi методом вiдокремлення змiнних.


Семінар № 4. Рівняння Лапласа (1 год).

Розв'язання рiвнянь Лапласа в прямокутнику та крузi методом вiдокремлення змiнних


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [6,7,18,23].


Тема № 5. «Рівняння Гельмгольца»


Лекція № 5. Рівняння Гельмгольца (2 год).

Розв'язання рiвнянь Лапласа в прямокутнику та крузi методом вiдокремлення змiнних. Рiвняння Гельмгольця в прямокутнику. Системи координат, в яких вiдокремлюються змiнни для двохвимiрного рiвняння Гельмгольця.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, виконання домашнього завдання.


Рекомендована література: [6,7,18,23].


Контрольні запитання

1. Основнi роздiли фiзики, закони яких виражаються у виглядi рiвнянь з частинними похiдними: електродинамiка, механiка та термодинамiка суцiльного середовища (гiдро- та аеродинамiка, теорiя пружностi, теорiя дифузiї та теплопровiдностi), квантова механiка та теорiя поля.
   
2. Основнi поняття та означення теорiї диференцiальних рiвнянь з частинними похiдними.
   
3. Лiнiйнi диференцiальнi рiвняння з частинними похiдними. Принцип суперпозицiї. Класифiкацiя та канонiчний вид лiнiйного диференцiального рiвняння з частинними похiдними другого порядку. Характеристики. 
   
4. Метод вiдокремлення змiнних для лiнiйних диференцiальних рiвнянь з частинними похiдними.
   
5. Приклади застосування метода вiдокремлення змiнних. Розв'язання рiвняння дифузiї на вiдрiзку методом вiдокремлення змiнних.
   
6. Розв'язання хвильового рiвняння на вiдрiзку методом вiдокремлення змiнних.
   
7. Розв'язання рiвнянь Лапласа в прямокутнику та крузi методом вiдокремлення змiнних. Рiвняння Гельмгольця в прямокутнику.
   
8. Системи координат, в яких вiдокремлюються змiнни для двохвимiрного рiвняння Гельмгольця
   

Модульна контрольна робота № 4 (2 год).

Контрольна робота СРС (2 год).


Змістовий модуль №5 «Метод відокремлення змінних-2»


Тема № 6. «Узагальнені гіпергеометричні функції»


Лекція № 6. Узагальнені гіпергеометричні функції (3 год).

Узагальненi гiпергеометричнi функцiї: означення та основнi властивостi. Зв'язок узагальнених гiпергеометричних функцiй з елементарними та спецiальними функцiями. Асимптотична поведiнка узагальнених гiпергеометричних функцiй. Виродження узагальнених гiпергеометричних функцiй. Узагальнене гiпергеометричне рiвняння.


Завдання для самостійної роботи (7 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [19,21].


Тема № 7. «Сферичні функції»


Лекція № 7. Сферичні функції (4 год).

Сферичнi функцiї. Гармонiчнi полiноми та їх властивостi. Означення сферичних функцiй. Ортогональнiсть та повнота системи сферичних функцiй на сферi одиничного радiусу. Диференцiальне рiвняння сферичних функцiй. Загальний вигляд розв'язку рiвняння Лапласа в сферичних координатах. Розклад фундаментального розв'язку рiвняння Лапласа в ряд по сферичних функцiях. Розв'язок задачi Дiрiхле для рiвняння Лапласа в кулi методом вiдокремлення змiнних.


Семінар № 7. Сферичні функції (4 год).

Розв’язання рiвняння Лапласа в сферичних координатах. Розклад фундаментального розв'язку рiвняння Лапласа в ряд по сферичних функцiях. Розв'язок задачi Дiрiхле для рiвняння Лапласа в кулi методом вiдокремлення змiнних.


Завдання для самостійної роботи (7 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [6,7,18,23].


Тема № 8. «Циліндричні функції»


Лекція № 8. Циліндричні функції (5 год).

Цилiндричнi функцiї. Означення та класифiкацiя цилiндричних функцiй. Спiввiдношення мiж цилiндричними функцiями Беселя, Неймана та Ганкеля. Диференцiальне рiвняння для цилiндричних функцiй. Загальний вигляд розв'язку рiвняння Лапласа в цилiндричних координатах. Розв'язок задачi Дiрiхле для рiвняння Лапласа в цилiндрi методом вiдокремлення змiнних.


Семінар № 8. Циліндричні функції (4 год).

Розв'язок задачi Дiрiхле для рiвняння Лапласа в цилiндрi методом вiдокремлення змiнних.


Завдання для самостійної роботи (7 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [6,7,18,23].


Контрольні запитання

1. Узагальненi гiпергеометричнi функцiї: означення та основнi властивостi.
   
2. Зв'язок узагальнених гiпергеометричних функцiй з елементарними та спецiальними функцiями.
   
3. Виродження узагальнених гiпергеометричних функцiй.
   
4. Узагальнене гiпергеометричне рiвняння.
   
5. Гармонiчнi полiноми та їх властивостi.
   
6. Означення сферичних функцiй. Ортогональнiсть та повнота системи сферичних функцiй на сферi одиничного радiусу.
   
7. Диференцiальне рiвняння сферичних функцiй. Загальний вигляд розв'язку рiвняння Лапласа в сферичних координатах.
   
8. Розклад фундаментального розв'язку рiвняння Лапласа в ряд по сферичних функцiях.
   
9. Розв'язок задачi Дiрiхле для рiвняння Лапласа в кулi методом вiдокремлення змiнних.
   
10. Означення та класифiкацiя цилiндричних функцiй. Спiввiдношення мiж цилiндричними функцiями Беселя, Неймана та Ганкеля.
    
11. Диференцiальне рiвняння для цилiндричних функцiй.
    
12. Цилiндричнi функцiї у випадку, коли незалежна змiнна прямує до нуля або до нескiнченностi.
    
13. Метод перевалу.
    
14. Ортогональнiсть i повнота системи цилiндричних функцiй на вiдрiзку.
    
15. Загальний вигляд розв'язку рiвняння Лапласа в цилiндричних координатах.
    
16. Розв'язок задачi Дiрiхле для рiвняння Лапласа в цилiндрi методом вiдокремлення змiнних.
    

Модульна контрольна робота № 5 (2 год).

Контрольна робота СРС (2 год).


Змістовий модуль №6 «Методи узагальнених функцій»


Тема № 9. «Означення і основні властивості узагальнених функцій»


Лекція № 9. Узагальнені функції (5 год).

Узагальненi функцiї. Основнi функцiї та їх властивостi. Ядро осереднення. Означення та приклади регулярних i сингулярних узагальнених функцiй. Диференцiювання та iнтегрування узагальнених функцiй. Замiна змiнних в узагальнених функцiях. Множення узагальнених функцiй на основну функцiю. Згортка узагальнених функцiй. Регуляризацiя узагальнених функцiй. Перетворення Фур'є узагальнених функцiй. Функцiя Хевiсайда та -функцiя Дiрака: їх означення, властивостi та фiзична iнтерпретацiя.


Семінар № 9. Узагальнені функції (4 год).

Операції з узагальненими функціями. Замiна змiнних в узагальнених функцiях. Множення узагальнених функцiй на основну функцiю. Згортка узагальнених функцiй. Регуляризацiя узагальнених функцiй. Перетворення Фур'є узагальнених функцiй. Функцiя Хевiсайда та -функцiя Дiрака: їх означення, властивостi та фiзична iнтерпретацiя.


Завдання для самостійної роботи (5 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [7,8,18,23].


Тема № 10. «Фундаментальний розв’язок лінійного диференціального»


Лекція № 10. Фундаментальний розв’язок лінійного диференціального рівняння (3 год).

Фундаментальний розв'язок. Означення фундаментального розв'язку лiнiйного диференцiального рiвняння. Теорема про iснування та єдинiсть розв'язку лiнiйного диференцiального рiвняння iз сталими коефiцiєнтами. Фундаментальний розв'язок лiнiйного диференцiального рiвняння iз звичайними похiдними. Розв'язок задачi Кошi для лiнiйного диференцiального рiвняння за допомогою фундаментального розв'зку


Семінар № 10. Фундаментальний розв’язок (4 год).

Фундаментальний розв'язок лiнiйного диференцiального рiвняння iз звичайними похiдними. Розв'язок задачi Кошi для лiнiйного диференцiального рiвняння за допомогою фундаментального розв'зку.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [7,8,18,23].


Тема № 11. «Фундаментальний розв’язок рівняння дифузії»


Лекція № 11. Фундаментальний розв'язок рівняння дифузії (2 год).

Рiвняння дифузiї. Фундаментальний розв'язок рiвняння дифузiї в n-вимiрному просторi. Розв'язок задачi Кошi для рiвняння дифузiї.


Семінар № 11. Фундаментальний розв'язок рівняння дифузії (2 год).

Розв’язування задач Коші для рівняння дифузії рівняння методом фундаментального розв’язку.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [7,8,18,23].


Тема № 12. «Фундаментальний розв’язок хвильового рівняння»


Лекція № 12. Фундаментальний розв'язок хвильового рівняння (4 год).

Хвильове рiвняння. Фундаментальний розв'язок хвильового рiвняння в n-вимiрному просторi, зокрема в 1-,2-,3-вимiрних просторах. Метод спуска. Розв'язок задачi Кошi та межових задач з однорiдними межовими умовами для хвильового рiвняння в n-вимiрному просторi. Збудження хвиль точковим джерелом.


Семінар № 12. Фундаментальний розв'язок хвильового рівняння (2 год).

Розв’язування задач Коші для рівняння хвильового рівняння методом фундаментального розв’язку.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [7,8,18,23].


Тема № 13. «Фундаментальний розв’язок рівняння Лапласа»


Лекція № 13. Рівняння Лапласа (4 год).

Рiвняння Лапласа та Пуасона. n-вимiрнi сферичнi координати та фундаментальний розв'язок рiвняння Лапласа в n-вимiрному просторi. Функцiя Грiна задачi Дiрiхле. Функцiя Грiна для n-вимiрного пiвпросторi та n-вимiрнї кулi. Розв'язок задачi Дiрiхле в n-вимiрному пiвпросторi за допомогою функцiї Грiна. Розв'язок задачi Дiрiхле в n-вимiрнiй кулi за допомогою функцiї Грiна


Семінар № 13. Рівняння Лапласа (2 год).

Розв'язок задачi Дiрiхле в n-вимiрному пiвпросторi за допомогою функцiї Грiна. Розв'язок задачi Дiрiхле в n-вимiрнiй кулi за допомогою функцiї Грiна


Рекомендована література: [7,8,18,23].


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Контрольні запитання

1. Узагальненi функцiї. Основнi функцiї та їх властивостi.
   
2. Ядро осереднення. Означення та приклади регулярних i сингулярних узагальнених функцiй.
   
3. Диференцiювання та iнтегрування узагальнених функцiй.
   
4. Замiна змiнних в узагальнених функцiях.
   
5. Множення узагальнених функцiй на основну функцiю.
   
6. Згортка узагальнених функцiй.
   
7. Регуляризацiя узагальнених функцiй.
   
8. Перетворення Фур'є узагальнених функцiй. Θ-функцiя Хевiсайда та δ-функцiя Дiрака: їх означення, властивостi та фiзична iнтерпретацiя.
   
9. Означення фундаментального розв'язку лiнiйного диференцiального рiвняння.
   
10. Фундаментальний розв'язок лiнiйного диференцiального рiвняння iз звичайними похiдними.
    
11. Розв'язок задачi Кошi для лiнiйного диференцiального рiвняння за допомогою фундаментального розв'зку.
    
12. Фундаментальний розв'язок рiвняння дифузiї в n-вимiрному просторi.
    
13. Фундаментальний розв'язок хвильового рiвняння в n-вимiрному просторi, зокрема в 1-,2-,3-вимiрних просторах.
    
14. Розв'язок задачi Кошi для хвильового рiвняння в n-вимiрному просторi. Збудження хвиль точковим джерелом.
    
15. n-вимiрнi сферичнi координати та фундаментальний розв'язок рiвняння Лапласа в n-вимiрному просторi.
    
16. Функцiя Грiна задачi Дiрiхле. Функцiя Грiна для n-вимiрного пiвпросторi та n-вимiрнї кулi. Розв'язок задачi Дiрiхле в n-вимiрному пiвпросторi за допомогою функцiї Грiна.
    
17. Розв'язок задачi Дiрiхле в n-вимiрнiй кулi за допомогою функцiї Грiна.
    

Модульна контрольна робота № 6 (2 год).

Контрольна робота СРС (2 год).


Організація самостійної роботи студентів


Перелік питань змістових модулів, винесених на самостійну роботу:

• Змістовий модуль № 1, тема № 2.
  

Тема: «Елементарні функції комплексної змінної та їх властивості».

План:

1. Функці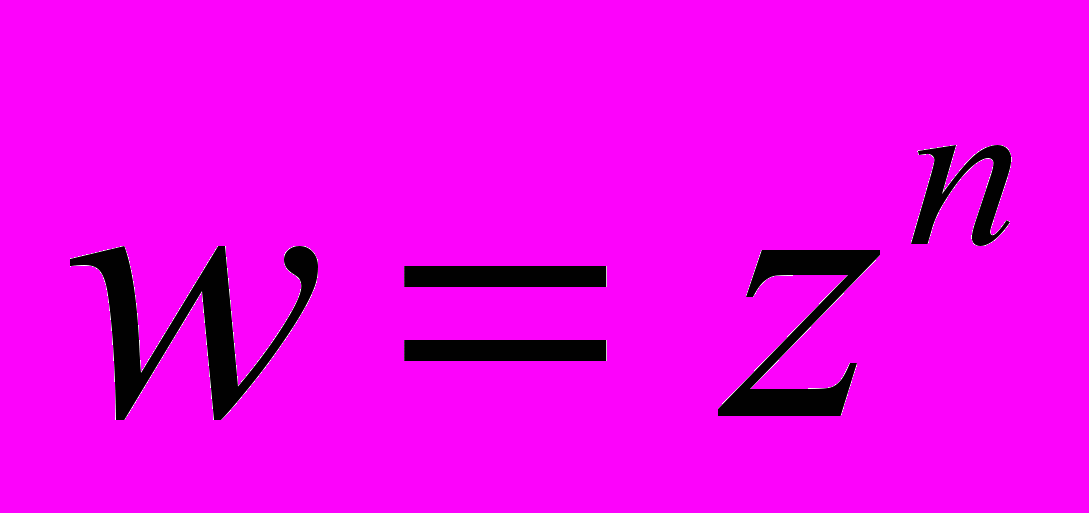ї і 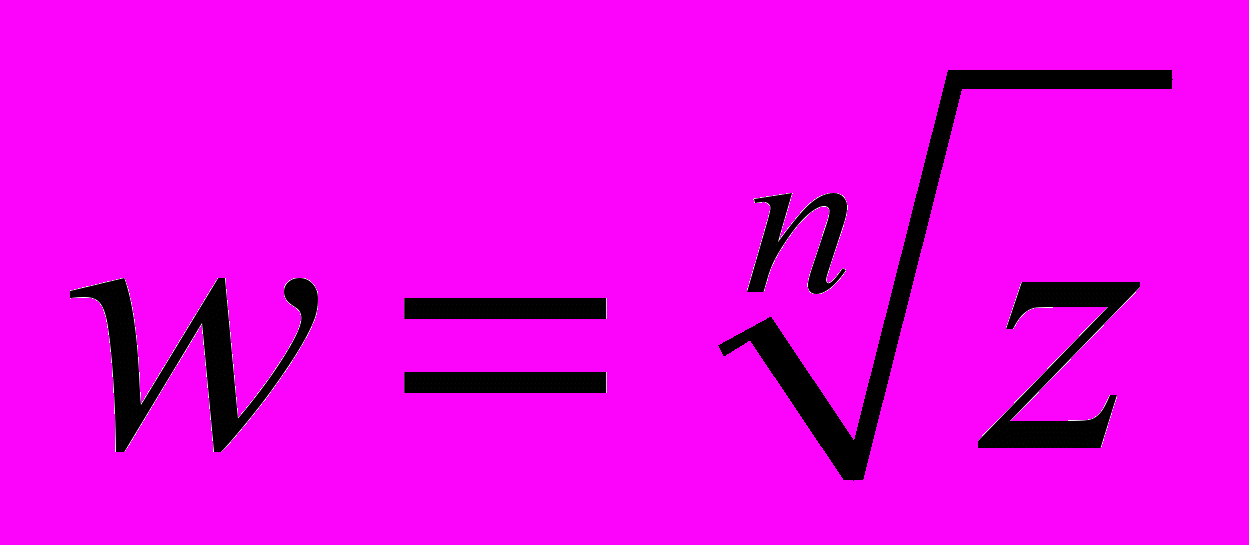[1, п.6, стор. 23-27];
   
2. Функція Жуковського 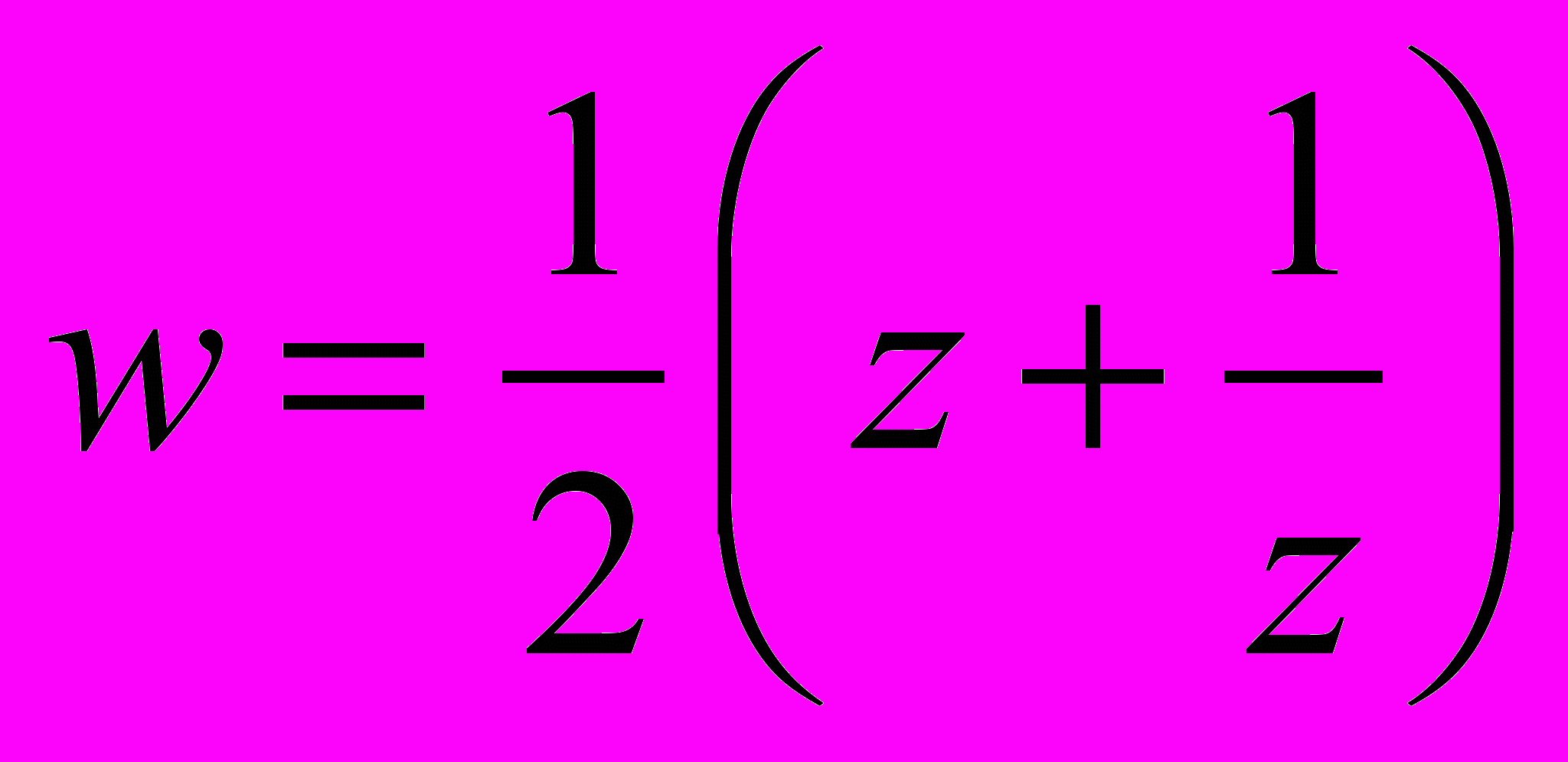[1, п.7, стор. 27-30];
   
3. Показникова функція і логарифм [1, п.8, стор. 30-34];
   
4. Тригонометричні і гіперболічні функції [1, п.9, стор. 34-39];
   
5. Узагальнена степенева функція 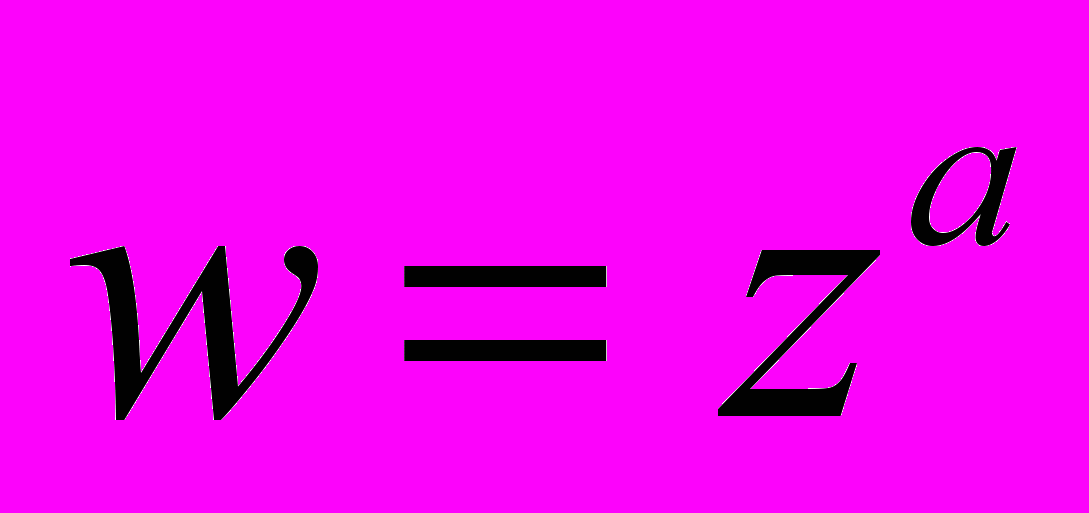[1, п.10, стор. 39-40].
   

• Змістовий модуль № 2, тема № 8.
  

Тема: «Логарифмічний лишок».

План:

1. Означення логарифмічного лишка [2, § 3.1, стор. 143-144];
   
2. Принцип аргументу. Підрахунок кількості нулів аналітичної функції. Теорема Руше [1, п.75, стор. 424-425] ; [2, § 3.2, стор. 145-147].
   

• Змістовий модуль № 3, тема № 11.
  

Тема: «Гармонічні функції».

План:

1. Означення та властивості гармонічних функцій; побудова гармонічної функції за спряженою [1, п.41, п.42, стор. 186-200], [2, § 7.1, стор. 184-185];
   
2. Інваріантність оператора Лапласа відносно конформних відображень [2, §7.2, стор. 185-187].
   

• Змістовий модуль № 3, тема № 10.
  

Тема: «Канонічний вигляд лiнiйних диференцiальнi рiвняння з частинними похiдними другого порядку».


План:

1. Означення лiнiйного диференцiального рiвняння. Принцип лінійної суперпозицiї. [6, §1.1, стор. 11-12]; [7,§ 1.1.9, стор. 28-30]; [8, § 1.11, стор. 38-41].
   
2. Класифікація лiнiйних диференцiальнi рiвняння з частинними похiдними другого порядку. Три типи рівнянь. Характеристики. [6, § 1.1, стор. 11-18], [7, § 1.3.1, стор. 43-45] [7, § 1.3.3, стор. 46-47], [8, § 3.1, стор. 56-58], [8, § 3.3, стор. 60-61].
   
3. Зведення до канонiчного вигляду лiнiйного диференцiального рiвняння з частинними похiдними другого порядку [6,§ 1.3, стор. 20-22], [7, § 1.3.4, стор. 47-53], [8, § 3.4, стор. 61-67].
   
4. Приклади [6, Задачи к главе I, стор. 22-23], [7, § 1.3.5. Пример. Уравнение Трикоми, стор. 53-54], [8, § 3.5. Пример. Уравнение Трикоми, стор. 67-68].
   

Перелік питань, які виносяться на іспит

1. Основнi поняття та означення теорiї диференцiальних рiвнянь з частинними похiдними. Принцип суперпозицiї для лiнiйних диференцiальних рiвнянь та приклади його застосування.
   
2. Класифiкацiя та канонiчний вид лiнiйного диференцiального рiвняння з частинними похiдними другого порядку. Характеристики.
   
3. Метод вiдокремлення змiнних для лiнiйних диференцiальних рiвнянь з частинними похiдними та приклади його застосування.
   
4. Розв'язок рiвняння дифузiї на вiдрiзку методом вiдокремлення змiнних. Приклад.
   
5. Розв'язок хвильового рiвняння на вiдрiзку методом вiдокремлення змiнних. Приклад.
   
6. Розв'язок рiвняння Лапласа та Пуассона в прямокутнику методом вiдокремлення змiнних. Приклад.
   
7. Розв'язок рiвняння Лапласа та Пуассона в крузi та кiльцi методом вiдокремлення змiнних. Приклад.
   
8. Розв'язок рiвняння Гельмгольця в прямокутнику методом вiдокремлення змiнних. Системи координат, в яких вiдокремлюються змiнни для двовимiрного рiвняння Гельмгольця. Приклад.
   
9. Гармонiчнi полiноми та їх властивостi. Означення сферичних функцiй.
   
10. Ортогональнiсть та повнота системи сферичних функцiй на сферi одиничного радiусу. Диференцiальне рiвняння сферичних функцiй.
    
11. Представлення фундаментального розв'язку рiвняння Лапласа у виглядi ряду по сферичних функцiях у випадку, коли особлива точка фундаментального розв'язку i центр координат не спiвпадають.
    
12. Загальний вигляд розв'язку рiвняння Лапласа в сферичних координатах.
    
13. Розв'язок задачi Дiрiхле для рiвняння Лапласа в кулi методом вiдокремлення змiнних. Приклад.
    
14. Означення та класифiкацiя цилiндричних функцiй. Спiввiдношення мiж цилiндричними функцiями Беселя, Неймана та Ханкеля. Iнтегральнi зображення цилiндричних функцiй.
    
15. Цилiндричнi функцiї у випадку, коли незалежна змiнна прямує до нуля або до нескiнченностi. Метод перевалу. Приклади.
    
16. Диференцiальне рiвняння для цилiндричних функцiй. Ортогональнiсть i повнота системи цилiндричних функцiй на вiдрiзку. Ряди Фур'є-Бесселя.
    
17. Загальний вигляд розв'язку рiвняння Лапласа в цилiндричних координатах.
    
18. Розв'язок задачi Дiрiхле для рiвняння Лапласа в цилiндрi методом вiдокремлення змiнних. Приклад.
    
19. Означення узагальнених функцiй. Основнi функцiї та їх властивостi. Ядро осереднення. Означення та приклади регулярних та сингулярних узагальнених функцiй.
    
20. Диференцiювання узагальнених функцiй. Приклади.
    
21. Замiна змiнних в узагальнених функцiях. Приклади. Множення узагальнених функцiй на основну функцiю. Приклади.
    
22. Згортка та перетворення Фур'є узагальнених функцiй. Приклади.
    
23. Означення -функцiї та її фiзична iнтерпретацiя. Диференцiювання та замiна змiнної в -функцiї. Множення -функцiї на основну функцiю. Згортка -функцiї з узагальненими функцiями. Перетворення Фур'є вiд -функцiї.
    
24. Означення фундаментального розв'язку лiнiйного диференцiального рiвняння. Теорема про iснування та єдинiсть розв'язку лiнiйного диференцiального рiвняння iз сталими коефiцiєнтами.
    
25. Фундаментальний розв'язок лiнiйного диференцiального рiвняння iз звичайними похiдними. Розв'язок задачi Кошi для лiнiйного диференцiального рiвняння за допомогою фундаментального розв'зку.
    
26. Фундаментальний розв'язок рiвняння дифузiї в n-вимiрному просторi. Розв'язок задачi Кошi та межових задач з однорiдними межовими умовами для рiвняння дифузiї.
    
27. Метод спуска. Приклади.
    
28. Фундаментальний розв'язок хвильового рiвняння в 1-вимiрному просторi. Розв'язок задачi Кошi.
    
29. Фундаментальний розв'язок хвильового рiвняння в 2-вимiрному просторi. Розв'язок задачi Кошi.
    
30. Фундаментальний розв'язок хвильового рiвняння в 3-вимiрному просторi. Розв'язок задачi Кошi. Збудження хвиль точковим джерелом.
    
31. n-вимiрнi сферичнi координати та фундаментальний розв'язок рiвняння Лапласа в n-вимiрному просторi.
    
32. Функцiя Грiна задачi Дiрiхле. Розв'язок задачi Дiрiхле за допомогою функцiї Грiна. Функцiя Грiна для n-вимiрного пiвпросторi та n-вимiрнї кулi.
    
33. Розв'язок задачi Дiрiхле в n-вимiрному пiвпросторi за допомогою функцiї Грiна. Приклад.
    
34. Розв'язок задачi Дiрiхле в n-вимiрнiй кулi за допомогою функцiї Грiна. Приклад.
    
35. Узагальненi гiпергеометричнi функцiї: означення та основнi властивостi. Зв'язок узагальнених гiпергеометричних функцiй з елементарними та спецiальними функцiями. Виродження узагальнених гiпергеометричних функцiй. Узагальнене гiпергеометричне рiвняння.
    

Перелік джерел інформації


а) основна література:

1. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. - М: Наука. 1987. - 688 с.
   
2. Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. - М: Наука. 1979. - 320 с.
   
3. Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. - М: Наука. 1982. - 488 с.
   
4. Евграфов М.А., Бежанов К.А., Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Сборник задач по теории аналитических функций. - М: Наука. 1972. 416 с.
   
5. Волковыский Л.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории функций комплексного переменного. - М: Наука. 1970. 320 с.
   
6. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М: 1972. - 736 с.
   
7. Владимиров В.С., Жаринов В.В. Уравнения математической физики. М: ФИЗМАТЛИТ, 2000. - 400 с.
   
8. Владимиров В.С., Уравнения математической физики. М: Наука,1971.
   

б) додаткова література

9. Бицадзе А.В. Основы теории аналитических функций комплексного переменного. - М: Наука. 1984. 320 с.
   
10. Евграфов М.А. Аналитические функции. - М: Наука. 1968. 472 с.
    
11. Привалов И.И. Введение в теорию функций комплексного переменного. - М: Наука. 1999. - 432 с.
    
12. Гурвиц А., Курант Р. Теория функций. - М: Наука. 1968. 648 с.
    
13. Шабат Б.В. Введение в комплексный анализ. ч. 1,2. - М: Наука. 1976.
    
14. Голубев В.В. Лекции по аналитической теории дифференциальных уравнений. - М.- Л.: ГИТТЛ. 1950. 436 с.
    
15. Бицадзе А.Б. Уравнения математической физики. 2-е изд. М: Наука, 1982. – 336 с.
    
16. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. М: Наука. - 1972. - 688 с.
    
17. Владимиров В.С., Михайлов В.П., Вашарин А.А., Каримова Х.Х., Сидоров Ю.В., Шабунин М.И. Сборник задач по уравнениям математической физики. - 2-е изд. - М: Наука. 1982. - 256 с.
    
18. Юрачкiвський А.П., Грязнова В.О. Метод вiдокремлення змiнних у задачах математичної фiзики: Навч. посiбник для студентiв природничих факультетiв. - К.: РВЦ "Київський унiверситет", 1988. - 142 с.
    
19. Бiлоколос Є.Д., Юрачкiвський А.П., Шека Д.Д. Спецiальнi функцiї в задачах математичної фiзики. - К.: ВПЦ "Київський унiверситет", 2000. - 92 с.
    
20. Боголюбов А.Н., Кравцов В.В. Задачи математической физики: уч. пособие. - М: Изд-во МГУ. - 1998. - 350 с.
    
21. Бейтман Г., Ердейи А. Высшие трансцендентные функции. Т.1 М.: Н. – 1973.
    

б) джерела іnternet

22. ссылка скрыта(ссылка скрыта)
    
23. Білоколос Є.Д., Шека Д.Д., Збірник задач з курсу «рівняння математичної фізики. - К: 2004. (pd.unіv.kіev.ua/downloads/publ/matphys_problems.pdf)